TopCoder problem "SilverDistance" used in SRM 456 (Division I Level One , Division II Level Two)

Problem Statement
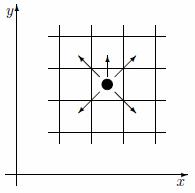
	In Japanese Chess, there is a piece called Silver. A Silver piece located in cell (x,y) can move to any of the following cells in one step: (x-1,y+1), (x,y+1), (x+1,y+1), (x-1,y-1), (x+1,y-1). In other words, it can move one cell in any of the four diagonal directions, or it can move one cell vertically in the positive y direction. Initially, there's a Silver piece in cell (sx,sy) of an infinitely large board. Return the minimal number of steps required to move to cell (gx,gy).
Definition
	Class: SilverDistance Method: minSteps Parameters: int, int, int, int Returns: int Method signature: int minSteps(int sx, int sy, int gx, int gy) (be sure your method is public)
Constraints
-	sx, sy, gx and gy will each be between -1,000,000 and 1,000,000 inclusive.
Examples
0)
	1 0 1 9 Returns: 9 Move up vertically in the positive y direction 9 times.
1)
	0 0 -4 3 Returns: 5 Follow the path : (0,0) -> (-1,1) -> (-1,2) -> (-2,3) -> (-3,2) -> (-4,3)
2)
	0 0 5 8 Returns: 8 Move up vertically in the postive y direction 3 times, then move diagonally up and to the right 5 times.
3)
	-487617 826524 892309 -918045 Returns: 1744571
4)
	-27857 31475 -27857 31475 Returns: 0 The Silver is already in the goal.

Problem url:

Problem stats url:

Writer:

Testers:

Problem categories: