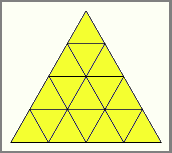
Petya likes triangles. He draws a trianglar grid using the following process: He starts off with an equilateral triangle. He then draws points on the edges of this triangle, dividing each edge up into N equal-length segments. Next, he connects each pair of points that is at equal distance from some vertex of the triangle with a straight line, ending up with N*N smaller equilateral triangles. An example of this figure with N = 4 is shown below.
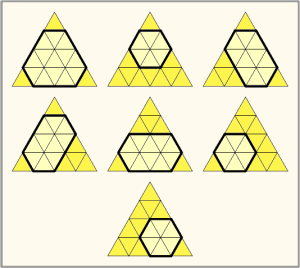
However, he likes hexagons more than he likes triangles. How many non-degenerate convex hexagons can be formed using the line segments in his figure? This number can be very big, so return it modulo 1000000007. |