Problem Statement |
| | NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.
Taro and Hanako are playing Rabbit Puzzle. There are three rabbits and three nests on a line. You are given a long[] rabbits, where each element is the initial position of a single rabbit, and a long[] nests, where each element is the position of a single nest.
They must perform the following routine exactly K times:
- Choose two different rabbits A and B, located at points a and b, respectively.
- A jumps over B and lands at point 2*b-a.
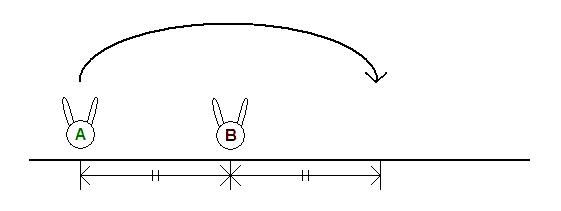
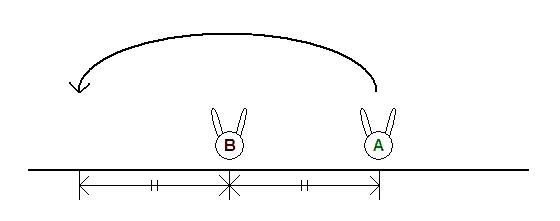
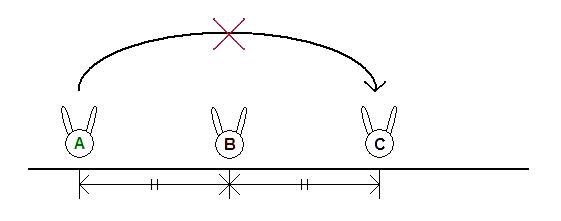
The jump is not allowed if another rabbit is already at point 2*b-a.
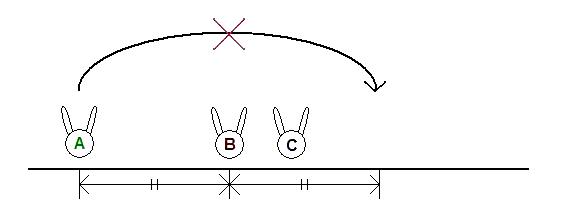
The jump is also not allowed if A jumps over more than one rabbit.
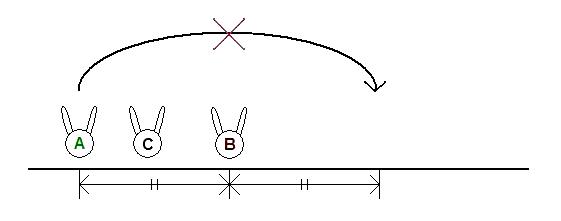
The goal of the puzzle is to have every rabbit be in a nest after the K routines. Note that the i-th rabbit doesn't necessarily have to be in the i-th nest. Return the number of ways to solve this puzzle, modulo 1,000,000,007. Two ways are considered different if at least one jump is different.
|
| |
Definition |
| | | Class: | RabbitPuzzle | | Method: | theCount | | Parameters: | long[], long[], int | | Returns: | int | | Method signature: | int theCount(long[] rabbits, long[] nests, int K) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | rabbits will contain exactly 3 elements. |
| - | Each element of rabbits will be between -10^18 and 10^18, inclusive. |
| - | rabbits will be sorted in strictly ascending order. |
| - | nests will contain exactly 3 elements. |
| - | Each element of nests will be between -10^18 and 10^18, inclusive. |
| - | nests will be sorted in strictly ascending order. |
| - | K will be between 1 and 100, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: 1 | | The only solution is moving a rabbit from 5 to 11. |
|
|
| 1) | |
| | |
| 2) | |
| | | Returns: 0 | | They must use exactly 2 jumps. It's impossible to solve this puzzle. |
|
|
| 3) | |
| | | Returns: 0 | | This puzzle is also impossible. |
|
|
| 4) | |
| | | Returns: 0 | | This puzzle is also impossible. |
|
|
| 5) | |
| | |
| 6) | |
| | {67, 281, 2348} | {235, 1394, 3293} | 83 |
| Returns: 167142023 | |
|
| 7) | |
| | {-1000000000000000000, 999999999999999998, 999999999999999999} | {-1000000000000000000, 999999999999999999, 1000000000000000000} | 5 |
| Returns: 29 | |
|




