Problem Statement |
| | NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.
You are given a white rectangle of size width by height. A green horizontal line (parallel to the width of the rectangle) is drawn through the middle of the rectangle so that it divides the rectangle into two congruent rectangles. This line extends infinitely out of the rectangle. You are asked to place red and blue disks (a disk is a circle and its interior) on the rectangle so that the entire rectangle is covered. The center of every disk must be placed on the green line, not necessarily within the rectangle bounds. Disks are placed sequentially from left to right, i.e., the center of each next placed disk must lie strictly to the right of the center of the last previously placed disk. Each disk is placed on top of all previously placed disks, i.e., when a disk is placed it covers any parts of previously placed disks that overlap. To challenge yourself, you have decided to only allow disk placements that satisfy the following additional constraint.
Every point covered by a newly placed disk must either
- not be covered by any previous disk or
- if covered by some previous disk then the topmost previous disk covering this point must be a different color than the newly placed disk.
You are given int[] red and int[] blue. The number of elements in red and blue corresponds to the number of red and blue disks you have, respectively. Each element of red or blue is the diameter of a red or blue disk, respectively. Note that each disk can only be used at most once. Find the smallest number of disks that can be placed as described above such that every point in the rectangle is covered by at least one disk. Return -1 if this is not possible. |
| |
Definition |
| | | Class: | ColoringRectangle | | Method: | chooseDisks | | Parameters: | int, int, int[], int[] | | Returns: | int | | Method signature: | int chooseDisks(int width, int height, int[] red, int[] blue) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | width and height will be between 1 and 10000, inclusive. |
| - | red will contain between 1 and 50 elements, inclusive. |
| - | blue will contain between 1 and 50 elements, inclusive. |
| - | Every element of red will be between 1 and 10000, inclusive. |
| - | Every element of blue will be between 1 and 10000, inclusive. |
| - | To avoid precision problems, if the answer for an input is X >= 1, then it will be possible to cover a rectangle with height of height and width of width + 1e-5 with X disks (given the same set of disks). Furthermore, for any input with answer X, it will not be possible to cover a rectangle with height of height and width of width - 1e-5 using fewer than X disks from the same set (or using any amount of disks if X is -1). |
| |
Examples |
| 0) | |
| | | Returns: 3 | A possible placement is as follows:
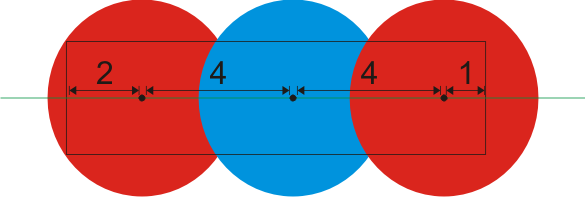 |
|
|
| 1) | |
| | 30 | 5 | {4,10,7,8,10} | {5,6,11,7,5} |
| Returns: 4 | |
|
| 2) | |
| | | Returns: -1 | | There are not enough blue disks. |
|
|
| 3) | |
| | | Returns: 1 | | The blue disk alone is enough to cover the rectangle. |
|
|
| 4) | |
| | |
