Problem Statement |
| | NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.
Little John has drawn a rectangle. On the top edge, he draws n dots at different places and numbers them 1 through n from left to right. On the bottom edge, he also draws n dots at different places and numbers them 1 through n from left to right.
John will then draw n straight line segments. For each segment, he will first choose a dot on the top edge that has not been chosen earlier. Then, he will choose a dot on the bottom edge that has not been chosen earlier. Finally, he will connect those two dots to form a straight line segment.
John has drawn several of the n segments so far. You are given int[]s startDot and endDot. startDot[i] is the number of the top dot chosen for the i-th segment which has already been drawn, and endDot[i] is the number of the bottom dot chosen for that segment. For each remaining segment, John will randomly choose an available top dot and an available bottom dot (each available top dot has an equal probability of being chosen, and each available bottom dot has an equal probability of being chosen). Return the expected number of distinct pairs of line segments that cross each other in the final drawing. |
| |
Definition |
| | | Class: | DrawingLines | | Method: | countLineCrossings | | Parameters: | int, int[], int[] | | Returns: | double | | Method signature: | double countLineCrossings(int n, int[] startDot, int[] endDot) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The returned value must have an absolute or relative error less than 1e-9. |
| |
Constraints |
| - | n will be between 2 and 10000, inclusive. |
| - | startDot and endDot will each contain between 1 and 50 elements, inclusive. |
| - | startDot and endDot will contain the same number of elements. |
| - | startDot and endDot will each contain less than n elements. |
| - | Each element of startDot will be between 1 and n, inclusive. |
| - | Each element of endDot will be between 1 and n, inclusive. |
| - | All elements of startDot will be distinct. |
| - | All elements of endDot will be distinct. |
| |
Examples |
| 0) | |
| | | Returns: 1.5 | There are four possible ways for Little John to pick the dots :
- [Top 1]-[Bottom 1] [Top 3]-[Bottom 2]
- [Top 1]-[Bottom 2] [Top 3]-[Bottom 1]
- [Top 3]-[Bottom 1] [Top 1]-[Bottom 2]
- [Top 3]-[Bottom 2] [Top 1]-[Bottom 1]
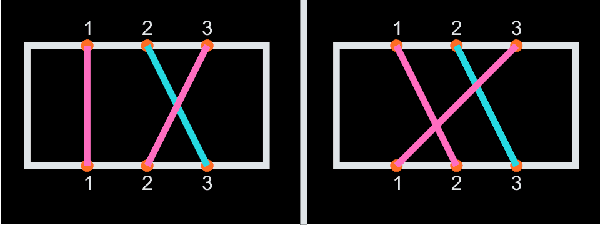
The first and the fourth ways correspond to the left picture, while the second and the third ways correspond to the right picture. The blue line is the line initially drawn by Little John.
In the left configuration, there is 1 pair of segments that cross each other. In the right configuration, there are 2 pairs of segments that cross each other. Hence, the expected number of crossed pairs is 1.5. |
|
|
| 1) | |
| | |
| 2) | |
| | |
| 3) | |
| | |
