Problem Statement |
| | You are going to decorate a very large white board with square sheets of colored paper.
Each sheet of paper can be of any non-zero size.
You have chosen N colors, numbered 0 to N - 1,
and you will use exactly one sheet of each color.
You are given four int[]s, xa, ya, xb, and yb,
each containing exactly N elements.
The sheet of paper with color i must be placed so that its center
is at either (xa[i], ya[i]) or (xb[i], yb[i]).
All sides of the paper must be parallel to the coordinate axes,
and no two sheets of paper can overlap each other
(Two squares overlap if their intersection has a non-zero area).
Return the maximum possible size of the smallest of the N sheets of paper.
The size of a square sheet of paper is its side length.
If you cannot place all N sheets, then return 0 instead.
|
| |
Definition |
| | | Class: | ColorfulDecoration | | Method: | getMaximum | | Parameters: | int[], int[], int[], int[] | | Returns: | int | | Method signature: | int getMaximum(int[] xa, int[] ya, int[] xb, int[] yb) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | It can be proved that the answer is always an integer. |
| |
Constraints |
| - | xa will contain between 2 and 50 elements, inclusive. |
| - | xa, ya, xb, and yb will contain the same number of elements. |
| - | Each element of xa, ya, xb, and yb will be between 0 and 1,000,000,000, inclusive. |
| |
Examples |
| 0) | |
| | { 10, 0, 7 } | { 0, 19, 6 } | { 20, 10, 25 } | { 20, 35, 25 } |
| Returns: 19 | 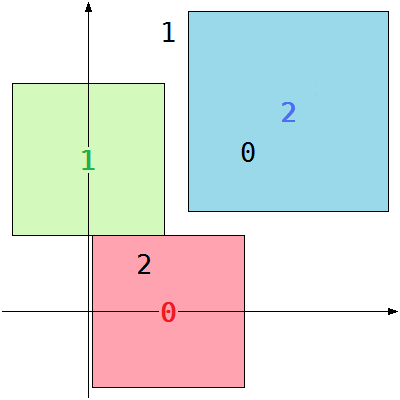
In the picture above, the numbers represent the candidates for the center of each color.
Choose (10, 0) for color 0, (0, 19) for color 1, and (25, 25) for color 2. The paper with color 2 could be larger, but the size of the smallest sheet cannot exceed 19.
|
|
|
| 1) | |
| | { 464, 20 } | { 464, 10 } | { 464, 3 } | { 464, 16 } |
| Returns: 461 | | (xa[i], ya[i]) and (xb[i], yb[i]) might be the same.
|
|
|
| 2) | |
| | { 0, 0, 1, 1 } | { 0, 0, 1, 1 } | { 1, 1, 0, 0 } | { 1, 1, 0, 0 } |
| Returns: 0 | | No matter how we choose to place the squares, at least two of them will have the same center. This means we cannot place four sheets of non-zero size without overlapping, so we return 0.
|
|
|
| 3) | |
| | { 0, 3, 0, 5, 6 } | { 1, 6, 0, 8, 5 } | { 6, 1, 7, 4, 7 } | { 5, 9, 2, 8, 9 } |
| Returns: 3 | |
|
| 4) | |
| | { 1000000000, 0 } | { 0, 1000000000 } | { 0, 1000000000 } | { 0, 1000000000 } |
| Returns: 1000000000 | |
|
