Problem Statement
There are four types of matrix shifts: left, right, top and bottom. Performing the left shift on the matrix, we shift each of its columns one position to the left and put the first column in place of the last one. Similarly, right shift results in shifting each column to the right and placing the last one in place of the first. Top shift takes each row one position up and puts the first row in place of the last, and bottom shift shifts all the rows one position down and puts the last row in place of the first row. Note that if a matrix has only one row, then top and bottom shifts do not change the matrix in any way. Similarly, if a matrix has a single column, then right and left shifts have no effect.
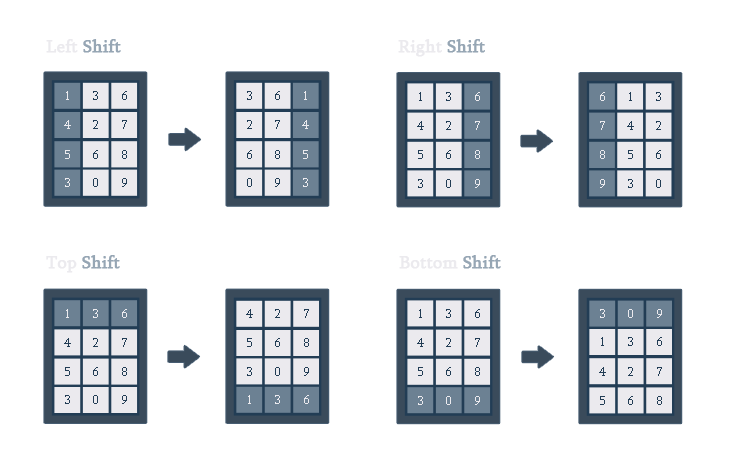
You are given a String[] matrix, where the j-th character of the i-th element is the digit in row i, column j. Compute and return the minimum possible total number of shifts that Manao should perform to accomplish his task. If there is no way to obtain a matrix with the upper left element equal to value, return -1 instead.
Definition
| Class: | MatrixShiftings |
| Method: | minimumShifts |
| Parameters: | String[], int |
| Returns: | int |
| Method signature: | int minimumShifts(String[] matrix, int value) |
| (be sure your method is public) | |
Constraints
Examples
| ||
Returns: 2 | ||
| ||
| ||
Returns: 2 | ||
| ||
| ||
Returns: 3 | ||
| ||
| ||
Returns: -1 | ||
| ||
| ||
Returns: 6 | ||