TopCoder problem "TurretPlacement" used in Member SRM 465 (Division I Level One , Division II Level Two)

Problem Statement
	NOTE: This problem statement contains images that may not display properly if viewed outside of the applet. The celebrated general Archibald Waving took charge of the third army in the occidental front. After losing the first two armies, Waving has become obsessed with finding the optimal way to construct the army's two gun towers. The towers have square-shaped bases. It is possible to construct towers of various sizes, and hence the size of the base square may also vary. However, only those bases are allowed whose sides are of integer length. Each tower may be centered only at points picked from a given set of points described by int[]s x and y where the i-th point is (x[i], y[i]). Moreover, the areas of the bases of the towers should not overlap (the squares are allowed to touch each other). Note that in order to achieve this, you may select squares whose sides are not parallel to the co-ordinate axes. Waving wants to know the number of ways in which he can position and construct the two towers. Two ways are considered different if at least one of the picked center points differs or if at least one of the picked square side sizes differs. Since it is possible to shoot in all directions from a tower, two ways differing only in the orientation of the base squares are not considered different. Help Waving by returning the total number of different ways to place the two towers.
Definition
	Class: TurretPlacement Method: count Parameters: int[], int[] Returns: long Method signature: long count(int[] x, int[] y) (be sure your method is public)
Constraints
-	x and y will contain between 2 and 50 elements, inclusive.
-	y will contain as many elements as x.
-	Each element of x and y will be between -10000 and 10000, inclusive.
-	Each of the points described by x and y will be unique.
Examples
0)
	{0,2} {0,2} Returns: 10 There are 10 different size combinations that can be used for the two towers as detailed in the following image. Note that in some cases it is necessary to orient towers in a way such that their sides are not paralel to the coordinate axis.
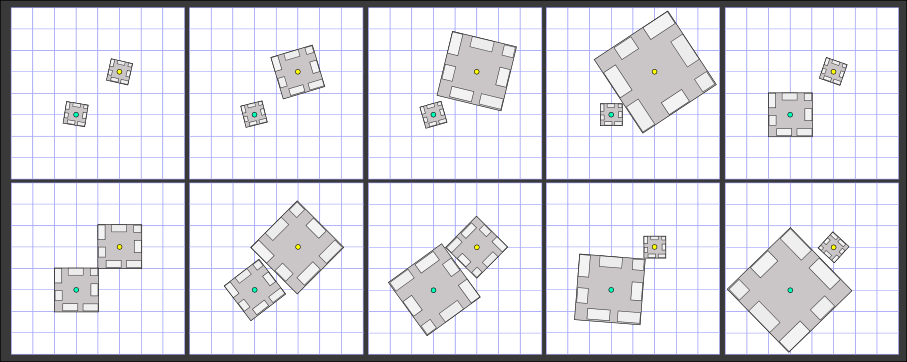1)
	{0,1,2} {0,1,0} Returns: 8
2)
	{1,2,3,0} {-1,-5,-7,100} Returns: 65137
3)
	{9998,-10000,10000,0} {9998,10000,10000,0} Returns: 2799564895

Problem url:

Problem stats url:

Writer:

Testers:

Problem categories: