TopCoder problem "PrefixTree" used in Member SRM 491 (Division I Level Two)



Problem Statement

    

A prefix tree (also called trie) is a rooted tree data structure used to efficiently store a set of words, S. In a trie every edge has a letter associated with it. Every node in the trie is associated with the string which we get when we read all the edge letters on the path from the root to this node. So the root of the trie is associated with the empty string and every leaf of the trie is associated with some word from S.



A trie is constructed so that from each node at most one child edge is associated with each letter. So not only do all the descendants of a node have a common prefix (which is the string associated with this node) but also every word with this string as prefix is the descendant of this node. It is necessary that for every word from S there is a node in trie with which is this word associated.



An example of a trie for the set of words {"aab", "ca"}:



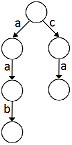
It is not hard to see that if we change the order of letters in the given words then we will get a different trie (constructed from these different words) which might possibly have fewer nodes.

For example the trie constructed from words {"aab","ca"} would have 6 nodes (see image above), but if we change "ca" to "ac" then the trie would have only 5 nodes:



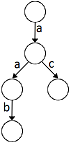
Given String[] words which represents the set of words. You are allowed to permute the letters in each word in any way you like. Find the optimal permutation of the letters of the words so the trie constructed from them would have the minimal number of nodes. Return this number of nodes.

 

Definition

    
Class:PrefixTree
Method:getNumNodes
Parameters:String[]
Returns:int
Method signature:int getNumNodes(String[] words)
(be sure your method is public)
    
 

Constraints

-words will contain between 1 and 16 elements, inclusive.
-Each element of words will contain between 1 and 50 characters.
-Each element of words will consist of lowercase letters ('a'-'z').
 

Examples

0)
    
{"topcoder"}
Returns: 9
With only one word, every permutation gives the same answer.
1)
    
{"topcoder","topcoder"}
Returns: 9
Words in the input can repeat. The optimal permutation is the one in which the words are equal.
2)
    
{"aab","ca"}
Returns: 5
Example from the problem statement. The optimum is if we change "ca" to "ac".
3)
    
{"aab","ca","ba"}
Returns: 5
The optimum is when the words are: "aba", "ac", "ab".
4)
    
{"ab","cd","ef"}
Returns: 7
Sometimes nothing can be optimized.
5)
    
{"a","aa","aaa"}
Returns: 4
One word can be also a prefix of another word.

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11009

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14244&pm=11009

Writer:

Mimino

Testers:

Rustyoldman , ivan_metelsky , rng_58 , wrong

Problem categories:

Dynamic Programming, String Manipulation