TopCoder problem "TimeTravellingGardener" used in SRM 492 (Division I Level One , Division II Level Two)

Problem Statement
	NOTE: This problem statement contains images that may not display properly if viewed outside of the applet. There are N trees arranged in a straight horizontal line. They are numbered 0 through N-1 from left to right. The distance between tree i and tree (i+1) is distance[i], and the initial vertical height of tree i is height[i]. Each tree is assumed to be a perfect vertical segment. Your goal is to make the topmost points of all the trees collinear. To do this, you can choose any number of trees and have them travel back to a time when they were shorter. You can decrease the height of each chosen tree to any non-negative value (not necessarily an integer). You will operate on each tree individually, so the trees do not all have to decrease in height by the same amount. The trees that you do not choose will all remain at their original heights. Return the minimum number of trees you must send back in time to achieve this goal.
Definition
	Class: TimeTravellingGardener Method: determineUsage Parameters: int[], int[] Returns: int Method signature: int determineUsage(int[] distance, int[] height) (be sure your method is public)
Notes
-	Two or more points are collinear if they lie on a single straight line.
Constraints
-	distance will contain between 1 and 49 elements, inclusive.
-	Each element of distance will be between 1 and 1000, inclusive.
-	The number of elements in height will be one plus the number of elements in distance.
-	Each element of height will be between 1 and 1000, inclusive.
Examples
0)
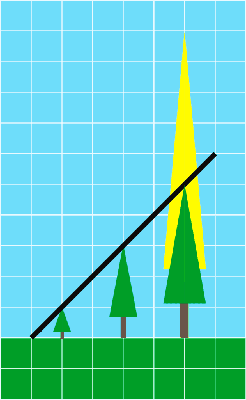
	{2,2} {1,3,10} Returns: 1
1)
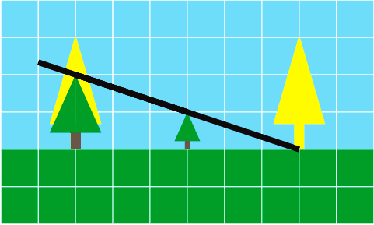
	{3,3} {3,1,3} Returns: 2
2)
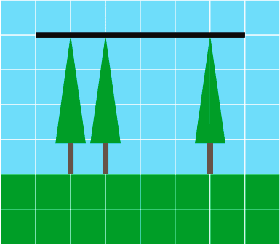
	{1,3} {4,4,4} Returns: 0
3)
	{4,2} {9,8,5} Returns: 1
4)
	{476,465,260,484} {39,13,8,72,80} Returns: 3
5)
	{173,36,668,79,26,544} {488,743,203,446,444,91,453} Returns: 5
6)
	{2,4,2,2,4,2,4,2,2,4} {2,2,10,10,10,16,16,22,22,28,28} Returns: 6

Problem url:

Problem stats url:

Writer:

Testers:

Problem categories: