Problem Statement
Rabbit Taro wants to color the vertices of a cube. He thinks the cube will be beautiful if:
- Each vertex is colored by a color that is suitable for it.
- No two adjacent vertices have the same color.
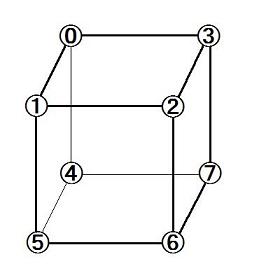
There are N types of colors. You are given a String[] colors. The j-th color is suitable for the i-th vertex if the j-th character of the i-th element of colors is 'Y'. Return the number of different ways to color the cube.
Definition
| Class: | CubeColoring |
| Method: | theCount |
| Parameters: | String[] |
| Returns: | long |
| Method signature: | long theCount(String[] colors) |
| (be sure your method is public) | |
Notes
Constraints
Examples
| ||
Returns: 0 | ||
| ||
| ||
Returns: 1 | ||
| ||
| ||
Returns: 250 | ||
| ||
Returns: 0 | ||
| ||
| ||
Returns: 611480 | ||