TopCoder problem "BunnyComputer" used in SRM 487 (Division I Level One , Division II Level Two)



Problem Statement

    Bunnies like programming and they often practice for contests.



There is a special computer named B-Computer, which all bunnies are eager to use. All bunnies want to solve a difficult problem using B-Computer. Because they type very fast, each of them wants to solve the problem according to the following process that consists of 3 stages (no delay is allowed between subsequent stages):
  1. Use B-Computer for exactly one time unit.
  2. Think and calculate on paper for exactly k time units, not using B-Computer.
  3. Use B-Computer for exactly one time unit again to complete.
B-Computer cannot be used by more than one bunny at the same time, but when a bunny is thinking and calculating on paper, another bunny may use B-Computer.



A day is divided into a number of equal time units, and each time unit has an associated positive integer value called preference. You are given a int[] preference, which contains the preference values for a day. The number of elements in preference is the number of time units in the day, and the i-th element of preference is the preference of the i-th time unit.



Bunnies want to design a B-Computer schedule for a single day so that the sum of preferences of time units in which one of them uses B-Computer is maximized. The schedule must be such that each bunny uses B-computer exactly as described above and both time units at which the same bunny uses B-computer are in the same day. Return the maximum possible sum of preferences. You can assume that there are infinitely many bunnies.
 

Definition

    
Class:BunnyComputer
Method:getMaximum
Parameters:int[], int
Returns:int
Method signature:int getMaximum(int[] preference, int k)
(be sure your method is public)
    
 

Constraints

-preference will contain between 1 and 50 elements, inclusive.
-Each element of preference will be between 1 and 1,000,000, inclusive.
-k will be between 1 and 50, inclusive.
 

Examples

0)
    
{ 3, 1, 4, 1, 5, 9, 2, 6 }
2
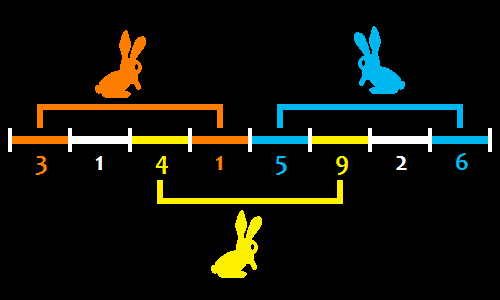
Returns: 28
The sum is maximized when three bunnies use B-Computer as follows:
  • One bunny uses B-Computer during the 1-st time unit and again during the 4-th time unit.
  • One bunny uses B-Computer during the 3-rd time unit and again during the 6-th time unit.
  • One bunny uses B-Computer during the 5-th time unit and again during the 8-th time unit.
1)
    
{ 3, 1, 4, 1, 5, 9, 2, 6 }
1
Returns: 31
2)
    
{ 1, 2, 3, 4, 5, 6 }
3
Returns: 14
3)
    
{ 487, 2010 }
2
Returns: 0
No bunnies can use B-Computer.

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11157

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14240&pm=11157

Writer:

lyrically

Testers:

PabloGilberto , ivan_metelsky , soul-net

Problem categories:

Simple Math, Simple Search, Iteration