Problem Statement |
| | Cat Taro likes dice. He has a die which is a 1 x 1 x 1 cube where each face contains a number between 1 and 6. Each number appears on exactly one face, and the sum of the numbers on opposite faces is always 7.
There is an infinitely large board which is divided into 1 x 1 cells. The board has a coordinate system in which the x-coordinate (the first coordinate) increases from left to right, while the y-coordinate (the second coordinate) increases from bottom to top. Taro initially places the die on the cell with coordinates (0, 0). The die shows '1' on the top face, '2' on the front face, and '3' on the left face (so the bottom face shows '6', the back face shows '5', and the right face shows '4').
Taro wants to move this die to cell (goalx, goaly) by performing a sequence of rotations. There are two ways to rotate the die:
- Rotate toward the right. This operation moves the die from cell (x, y) to cell (x+1, y).
- Rotate toward the top. This operation moves the die from cell (x, y) to cell (x, y+1).
For example, if Taro's first rotation is toward the right, then the die will move to cell (1, 0) and the top face will show '3'.
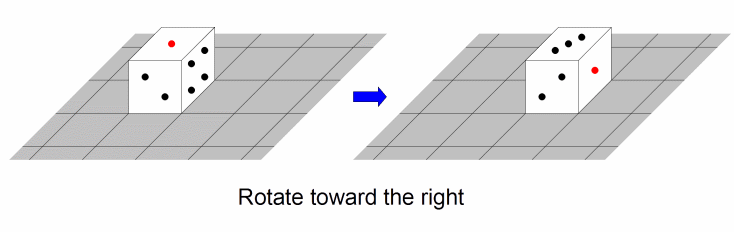
Return the number of sequences of rotations which move the die to cell (goalx, goaly), such that the following conditions are satisfied:
- The die must show '1' again on the top face when it reaches (goalx, goaly).
- The die must not show '1' on the top face before it reaches (goalx, goaly).
|
| |
Definition |
| | | Class: | DiceRotation | | Method: | theCount | | Parameters: | int, int | | Returns: | int | | Method signature: | int theCount(int goalx, int goaly) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The answer will always fit in a signed 32-bit integer. |
| |
Constraints |
| - | goalx will be between 1 and 1,000,000,000, inclusive. |
| - | goaly will be between 1 and 1,000,000,000, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: 2 | There are two ways to move the die to cell (2,2) that satisfy the conditions:
- right -> right -> up -> up
- up -> up -> right -> right
|
|
|
| 1) | |
| | |
| 2) | |
| | |
| 3) | |
| | |
| 4) | |
| | |
