Problem Statement |
| | Fox Ciel likes sequences. One day, she invented a new type of sequence and named it the fox sequence. A sequence seq containing N elements is called a fox sequence if and only if there exist four integers a, b, c and d such that 0 < a < b <= c < d < N-1 and the following five conditions are met:
- seq[0], seq[1], ... , seq[a] forms an arithmetic progression with a positive common difference. An arithmetic progression is a sequence where the difference between successive elements is equal. The difference between successive elements is called the common difference. Note that 0 is neither positive nor negative.
- seq[a], seq[a+1], ... , seq[b] forms an arithmetic progression with a negative common difference.
- seq[b], seq[b+1], ... , seq[c] are all equal.
- seq[c], seq[c+1], ... , seq[d] forms an arithmetic progression with a positive common difference.
- seq[d], seq[d+1], ... , seq[N-1] forms an arithmetic progression with a negative common difference.
In the following image, the top 3 sequences are fox sequences, while the bottom 3 sequences are not:
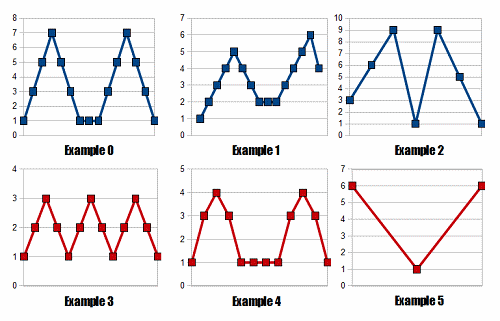
You are given a sequence seq. Return "YES" if it is a fox sequence, or "NO" if it is not (all quotes for clarity). |
| |
Definition |
| | | Class: | FoxSequence | | Method: | isValid | | Parameters: | int[] | | Returns: | String | | Method signature: | String isValid(int[] seq) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | seq will contain between 1 and 50 elements, inclusive. |
| - | Each element of seq will be between 1 and 2,000, inclusive. |
| |
Examples |
| 0) | |
| | {1,3,5,7,5,3,1,1,1,3,5,7,5,3,1}
|
| Returns: "YES" | This is the top-left sequence of the image shown in the statement. The next five examples are also from that image. |
|
|
| 1) | |
| | {1,2,3,4,5,4,3,2,2,2,3,4,5,6,4}
|
| Returns: "YES" | |
|
| 2) | |
| | |
| 3) | |
| | {1,2,3,2,1,2,3,2,1,2,3,2,1}
|
| Returns: "NO" | |
|
| 4) | |
| | {1,3,4,3,1,1,1,1,3,4,3,1}
|
| Returns: "NO" | |
|
| 5) | |
| | |
