TopCoder problem "FoxJumping" used in SRM 498 (Division I Level Three)



Problem Statement

    Fox Ciel likes to jump around in large fields. She is currently at point (0, 0) of a field, and she wants to land at point (Tx, Ty) using exactly R jumps.



In one jump, she can move 0, 1, 2, ..., Mx units in the positive x direction and 0, 1, 2, ..., My units in the positive y direction. All jumps must have a non-zero distance. In addition, there are some jumps which she is not good at. These jumps are described in the int[] bad. If bad contains the number b, it means she cannot make a diagonal jump where she moves exactly b units in the positive x direction and b units in the positive y direction. Each element of bad will be a multiple of 10.



For instance, if Mx=12, My=11, bad={10} and she is at point (0, 0), then the only points she can jump to are the green ones shown below:







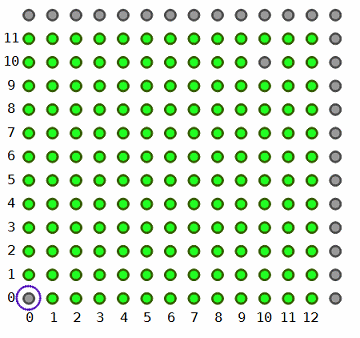
Return the number of ways she can start at (0, 0), jump exactly R times, and land at (Tx, Ty), modulo 10,007. Two ways are considered to be different if there is an index i, 0 <= i < R, such that Ciel lands at different points after the i-th (0-based) jump in these ways.
 

Definition

    
Class:FoxJumping
Method:getCount
Parameters:int, int, int, int, int, int[]
Returns:int
Method signature:int getCount(int Tx, int Ty, int Mx, int My, int R, int[] bad)
(be sure your method is public)
    
 

Constraints

-Tx and Ty will each be between 1 and 800, inclusive.
-Mx and My will each be between 1 and 800, inclusive.
-R will be between 1 and 1,600, inclusive.
-bad will contain between 0 and 50 elements, inclusive.
-Each element of bad will be between 1 and min(Mx, My), inclusive, and be a multiple of 10.
-All elements of bad will be distinct.
 

Examples

0)
    
2
2
1
1
2
{}
Returns: 1
There is only 1 way to reach the destination.



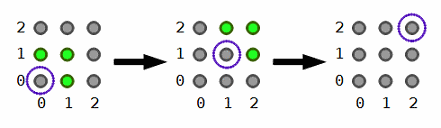1)
    
2
2
1
1
3
{}
Returns: 6
The following are the 6 ways she can reach her destination. Note that when she jumps, she must move a distance of at least one unit.



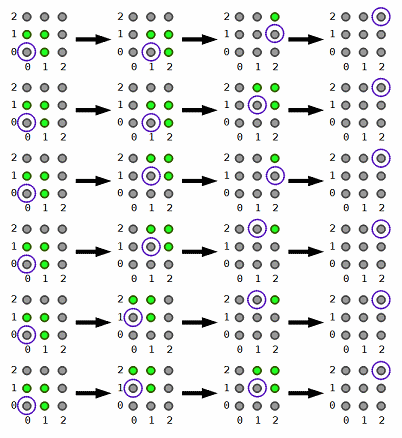2)
    
10
10
10
10
1
{}
Returns: 1

She can jump only once, so there is 1 way to reach the destination.

3)
    
10
10
10
10
1
{10}
Returns: 0

This case is almost the same as the previous one. However, in this case, the required jump is a bad jump, so she cannot reach the destination in a single jump.

4)
    
11
11
11
11
2
{10}
Returns: 140
5)
    
123
456
70
80
90
{30, 40, 20, 10, 50}
Returns: 6723

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11223

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14427&pm=11223

Writer:

ir5

Testers:

PabloGilberto , ivan_metelsky , pieguy

Problem categories:

Dynamic Programming, Math