TopCoder problem "HexagonPuzzle" used in SRM 495 (Division II Level Three)



Problem Statement

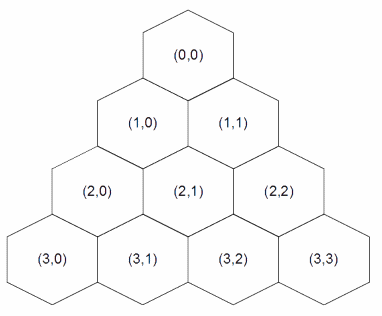
    Cat Taro has a triangle board divided into hexagonal cells. The board contains N rows numbered 0 through N-1 from top to bottom, where the i-th row contains (i+1) hexagonal cells numbered (i,0) through (i,i) from left to right. For example, if N = 4, the board looks like the picture below.







Each cell contains a token. Rabbit Hanako locked some cells so that tokens in those cells can't be moved. You are given a String[] board containing exactly N elements. For all i between 0 and N-1, inclusive, the i-th element of board will contain exactly (i+1) characters. If the j-th character of the i-th element of board is 'X', the cell (i,j) is locked. If the j-th character of the i-th element of board is '.', the cell (i,j) is unlocked.



Cat Taro can perform the following operation an arbitrary number of times: Choose three distinct unlocked cells A, B and C. These three cells must have a common vertex. Move the token in cell A to cell B, the token in cell B to cell C and the token in cell C to cell A.







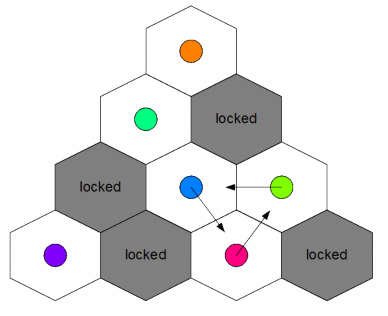
Return the number of different board states he can achieve by performing operations as described above, modulo 1,000,000,007. Two states are different if there exists at least one token that is placed in a different cell in one state than it is in the other state.
 

Definition

    
Class:HexagonPuzzle
Method:theCount
Parameters:String[]
Returns:int
Method signature:int theCount(String[] board)
(be sure your method is public)
    
 

Constraints

-board will contain between 1 and 50 elements, inclusive.
-The i-th (0-indexed) element of board will contain exactly i+1 characters.
-Each character in board will be '.' or 'X'.
 

Examples

0)
    
{".",
 ".X",
 "X..",
 ".X.X"}

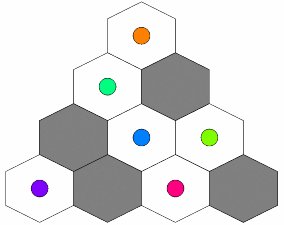
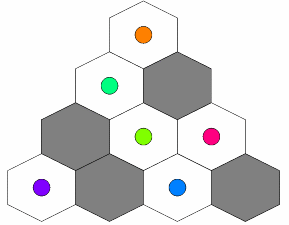
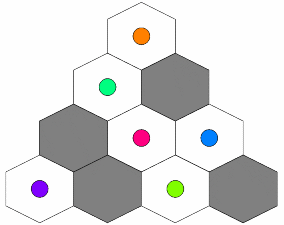
Returns: 3
Example from the problem statement.



He can achieve the following three board states.



  
1)
    
{"X"}

Returns: 1
Taro can't perform any operation.
2)
    
{".",
 "..",
 "...",
 ".X.."}

Returns: 20160
3)
    
{".",
 "..",
 "XXX",
 "..X.",
 ".X..X",
 "XXXX..",
 "..X.X.X",
 "..X.XX.."}

Returns: 108
4)
    
{".",
 "..",
 "...",
 "....",
 ".....",
 "......",
 ".......",
 "........"}
Returns: 261547992

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11303

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14424&pm=11303

Writer:

rng_58

Testers:

PabloGilberto , ivan_metelsky , soul-net

Problem categories:

Math