Problem Statement |
| | Nick likes to draw fractals. For the special occasion of Single Round Match 500, he decided to draw the 500th generation of his favorite fractal.
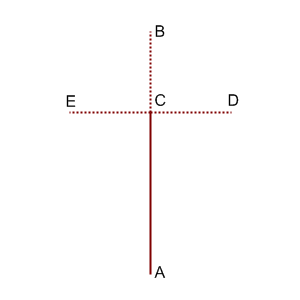
Each generation of the fractal can be described as a set of segments on the plane. Some of these segments are called final and all other are considered to be non-final. In each non-final segment, one of its endpoints is chosen and called the root of this segment. In pictures below, solid and dotted lines are used to represent final and non-final segments, correspondingly.
The first generation consists of one segment with endpoints (0, 0) and (0, 81). This segment is non-final and its root is (0, 0).

The i-th generation, i >= 2, is produced from the (i-1)-th generation as follows. All final segments from the (i-1)-th generation are included into the i-th generation without any changes. For each non-final segment from the (i-1)-th generation, let A and B be its endpoints, with A being its root. The following steps are then done:
- The point C is drawn on the segment AB so that the length of segment AC is twice as large as the length of segment BC.
- Segment CD is drawn as the rotation of segment CB around point C by 90 degrees clockwise.
- Segment CE is drawn as the rotation of segment CB around point C by 90 degress counter-clockwise.
- Segment AC is included in the i-th generation as a final segment.
- Segments CB, CD and CE are included in the i-th generation as non-final segments. The root of each of these three segments is point C.
The second and third generations of this fractal are shown on the picture below.
Consider a rectangle R on the plane that consists of points (x, y), such that x1 <= x <= x2 and y1 <= y <= y2. Let S be the set of all segments of the 500-th generation of the fractal described above (both final and non-final ones). Return the total length of all parts of segments from S that belong to rectangle R. |
| |
Definition |
| | | Class: | FractalPicture | | Method: | getLength | | Parameters: | int, int, int, int | | Returns: | double | | Method signature: | double getLength(int x1, int y1, int x2, int y2) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The returned value must have an absolute or relative error less than 1e-9. |
| |
Constraints |
| - | x1 will be between -100 and 100, inclusive. |
| - | x2 will be between x1+1 and 100, inclusive. |
| - | y1 will be between -100 and 100, inclusive. |
| - | y2 will be between y1+1 and 100, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: 53.0 | | Only one part of fractal segments belongs to this rectangle: (0, 0) - (0, 53). |
|
|
| 1) | |
| | | Returns: 0.0 | | No parts of fractal segments belong to this rectangle. |
|
|
| 2) | |
| | | Returns: 21.0 | | Two parts of fractal segments belong to this rectangle: (-10, 54) - (10, 54) and (0, 54) - (0, 55). Note that parts that lie on the rectangle's border also belong to the rectangle. |
|
|
| 3) | |
| | |


