TopCoder problem "Archimedes" used in SRM 151 (Division I Level One)

Problem Statement
	The Greek mathematician Archimedes of Syracuse (287-212 B.C.) was most likely the first in finding a way to systematically (iteratively) approximate the value of Pi, the ratio between the perimeter and the diameter of a circle. He inscribed and circumscribed regular polygons in/around a circle and calculated their perimeter. These are lower (inscribed polygon) and upper (circumscribed polygon) bounds for the perimeter of the circle, and therefore can be used to calculate lower and upper bounds for Pi. He then found a formula for directly calculating the perimeter of inscribed and circumscribed polygons with 2*n sides only using the values previously calculated for polygons with n sides. You now have a slightly simpler task, considering only inscribed polygons. You are given an int numSides, the number of sides of a regular polygon that is inscribed in a circle. Return a double, the approximated value for Pi when the perimeter of that polygon is used as an approximation for the perimeter of the circle. 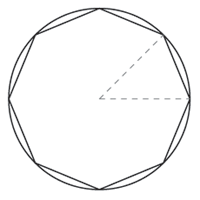[Image showing a circle with an 8-sided regular polygon inscribed]
Definition
	Class: Archimedes Method: approximatePi Parameters: int Returns: double Method signature: double approximatePi(int numSides) (be sure your method is public)
Notes
-	Perimeter of a circle: 2 * PI * radius
-	Perimeter of a n-sided regular polygon: n * sidelength
-	Reminder how doubles are evaluated: If your result is within 1e-9 of the expected result, your solution will be evaluated as correct. If your result is between (1+1e-9) * expected and (1-1e-9) * expected, it will be evaluated as correct.
Constraints
-	numSides will be between 3 and 100000, inclusive.
Examples
0)
	3 Returns: 2.598076211353316
1)
	8 Returns: 3.0614674589207183
2)
	17280 Returns: 3.1415926362832276

Problem url:

Problem stats url:

Writer:

Testers:

Problem categories: