Problem Statement |
| | This problem contains images
Elwood has a little sister named Casey. Although being quite young, Casey not only likes Modern Art, but also creates little pieces of art by herself. Her latest favorites are drawings on squared paper. She wants her new creations to be composed of only one basic shape that is used in all orientations:

[Image showing Casey's basic shape in all orientations.]
She draws her shapes into rectangles on her paper. For a rectangle of a given size, she wants to fill the entire rectangle
in all different ways. Elwood immediately recognizes that even for small rectangles there might be many different fillings.
But Casey, like little sisters sometimes do, doesn't believe him, so she asks you to exactly calculate how many drawings
she has to do for a rectangle of a given size.
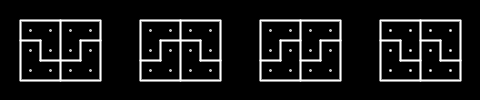
[Image showing all four possible fillings of a 3x4 rectangle.]
Given an int length and an int width describing the size of Casey's rectangle, return the number of different ways this rectangle can be filled using Casey's basic shape. The rectangle is oriented, so count symmetrical fillings multiple times as done in the example above. |
| |
Definition |
| | | Class: | CaseysArt | | Method: | howManyWays | | Parameters: | int, int | | Returns: | double | | Method signature: | double howManyWays(int length, int width) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | Reminder:
If your result is within 10-9 of the expected result, your solution will be evaluated as correct.
If your result is between (1+10-9)*expected and (1-10-9)*expected, it will be evaluated as correct. |
| |
Constraints |
| - | length will be between 1 and 18, inclusive. |
| - | width will be between 1 and 15, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: 4.0 | | This is the rectangle shown in the problem description. |
|
|
| 1) | |
| | | Returns: 4.0 | | This is the rectangle shown in the problem description rotated. |
|
|
| 2) | |
| | | Returns: 0.0 | | A rectangle of size 2x2 can't be filled. |
|
|
| 3) | |
| | |

