TopCoder problem "TopCan" used in SRM 209 (Division I Level Two)

Problem Statement
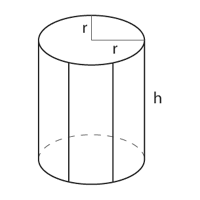
	This problem contains an image. TopCan, Inc. is a major producer of food. It produces all kinds of food than can be filled into a can: pineapples, mushrooms, peas, etc. However, business is not going well, so they are looking for ways to make production cheaper. An important expense factor is the amount of material needed for producing the can, which directly depends on the surface area of the can. Currently, cans are produced in all imaginable shapes and sizes, but to reduce cost, the company thinks about producing only cans in the shape of a cylinder (as shown below). So to be able to decide whether production should be changed TopCan wants to know, for a given volume, the minimal surface area possible of such a can. As the company's brightest employee, this task has been assigned to you. Given an int volume, return a double, the minimal surface area possible of a cylinder that has the given volume.
Definition
	Class: TopCan Method: minSurface Parameters: int Returns: double Method signature: double minSurface(int volume) (be sure your method is public)
Notes
-	Consider the material the can is made of to be infinitely thin.
-	Some formulas for your convenience: r: radius of the circle being the base of the cylinder h: height of the cylinder Volume V = h * PI * r2 Surface S = 2 * PI * r * (r + h)
-	If not provided by a library, use the value of 2*acos(0) for PI.
-	Reminder: If your result is within 10-9 of the expected result, your solution will be evaluated as correct. If your result is between (1+10-9)*expected and (1-10-9)*expected, it will be evaluated as correct.
Constraints
-	volume will be between 1 and 100000, inclusive.
Examples
0)
	10 Returns: 25.694955950835347 For a volume of 10, the cylinder has a height of about 2.3351 and the base circle has a radius of about 1.1675.
1)
	20 Returns: 40.78820010663257

Problem url:

Problem stats url:

Writer:

Testers:

Problem categories: