Problem Statement |
| | Often, a large task can be broken down into a number of smaller tasks, some of which are dependent on others. For example, developing a substantial piece of software might be broken down into 4 tasks: the database component, the server component, the client component, and integration of the three components. Each component can be written independently, but the final task of integrating the three components cannot be started until each of the components is finished.
We can think of these dependencies as a directed acyclic graph (DAG), where each node represents a task, and each directed edge represents a dependency. For example, the following graph represents the above example:
DB------>--\
\
Server------>Integration
/
Client-->--/
Your task is to determine how fast some set of tasks can be completed, given that you can work on at most 2 tasks at a time, and once you start working on a task, you must work on that task until it is finished. You are to write a method, fastest, which will take a DAG representing the dependencies of the tasks and the amount of time that each task takes to complete, and should return the smallest amount of time in which every task may be finished.
The DAG will be given to you as a String[], dag. Each element of dag will be formatted as "<time>:<d0>,<d1>,...", where each <di> indicates that the task represented by this element of dag is dependent on the task represented by the dith element of dag.
|
| |
Definition |
| | | Class: | Scheduling | | Method: | fastest | | Parameters: | String[] | | Returns: | int | | Method signature: | int fastest(String[] dag) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | dag will contain between 1 and 12 elements, inclusive. |
| - | Each element of dag will be formatted as "<time>:<d0>,<d1>,...", where each <di> is between 0 and the number of elements in dag-1, inclusive (with no extra leading 0's anywhere). |
| - | Each <time> will be between 1 and 10, inclusive. |
| - | No element of dag will contain more than one occurrence of the same <di>. |
| - | Each element of dag will contain between 2 and 50 characters, inclusive. |
| - | dag will represent a directed acyclic graph. |
| |
Examples |
| 0) | |
| | {"3:","2:","4:","7:0,1,2"} |
| Returns: 12 | This represents the following DAG (numbers represent the time it takes to complete a task represented by a node).
3-->--\
\
2------->7
/
4-->--/
This is similar to the example in the problem statement. Task 3 may not be started until tasks 0, 1, and 2 are all completed. So, the best way to do this is to start by doing both tasks 0 and 2. Then, at time 3, task 0 is completed, and you can start working on task 1. At time 4, you complete task 2, but there is nothing more to do, so at that point you are only working on one task. Then, at time 5, task 1 completes, and you can work on task 3, which completes at time 12.
Here is a table showing a timeline for one of the best ways to do it:
| Tasks being
Time | worked on or
| started
------+------
0 | 0,2
3 | 1,2
4 | 1
5 | 3
12 | done
|
|
|
| 1) | |
| | {"9:","8:","6:","4:","7:","7:0,1,2,3,4","3:2,3"} |
| Returns: 24 | This one is a little more complicated. It represents the following DAG (plugin users - please view the image in the applet):
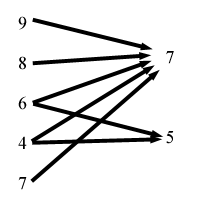
|
|
|
| 2) | |
| | { "10:", "5:", "5:1", "5:1", "5:2,3" } |
| Returns: 20 | |
|
| 3) | |
| | {"1:","2:","4:","8:","6:","3:","7:","5:","9:","5:","10:","3:"} |
| Returns: 32 | |
|
