Problem Statement |
| |
This problem contains an image. If you don't see it, view the problem description in the applet instead.
In the future, farmers won't have to rely on primitive scarecrows
to keep the birds away from their crops. A new revolutionary
invention, an "electronic scarecrow", will make sure the birds
stay out of the farmers' fields forever.
If you have three electronic scarecrows located on a field so that they form
a triangle, a bird won't be able to fly inside this area because it will get
zapped by a laser beam coming out from the scarecrows. Of course, if you have
more scarecrows, the whole area that is surrounded by these scarecrows becomes protected
(this area is known as the convex hull). Consider the picture below:
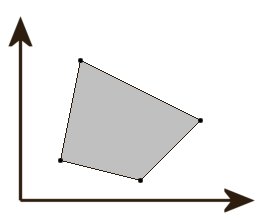
The black dots represents electronic scarecrows and the area shaded
gray is the part of the field that is inaccessible to the birds.
This sounds great, but there are two drawbacks. First, the scarecrows are of
course very expensive, so a farmer can't afford very many of them. Second, they are
quite heavy and need firm soil to stand on, and must also be in range of a
power outlet. This severely limits the number of locations the farmer
can place such scarecrows.
Given the coordinates of possible locations for the scarecrows
and the maximum number of scarecrows the farmer can afford to buy,
calculate the largest area that can be guarded by these scarecrows.
The farmer's field is a rectangular area, and all locations given
will be inside this area.
Create a class ElectronicScarecrows containing the method largestArea which takes
a int[] x and a int[] y, the coordinates of
possible locations for the scarecrows (element i in x and y
correspond to the coordinates of the ith location) and an int n,
the maximum number of scarecrows the farmer can afford to buy. The method should return a
double containing the largest area the scarecrows can cover. You may safely
assume that it will always be possible to put the scarecrows so they will cover an area
strictly greater than 0.
|
| |
Definition |
| | | Class: | ElectronicScarecrows | | Method: | largestArea | | Parameters: | int[], int[], int | | Returns: | double | | Method signature: | double largestArea(int[] x, int[] y, int n) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The area of a simple polygon with corners at (x1,y1), (x2,y2), ..., (xm,ym) - in clockwise or counterclockwise direction - is the absolute value of ((x1*y2 - x2*y1) + (x2*y3 - x3*y2) + ... + (xm*y1 - x1*ym))/2 |
| - | A solution will be judged correct if the absolute or relative error is within 1e-9. |
| |
Constraints |
| - | x will contain between 3 and 40 elements, inclusive. |
| - | y will contain between 3 and 40 elements, inclusive. |
| - | x will contain the same number of elements as y. |
| - | Each element in x will be between 0 and 1000, inclusive. |
| - | Each element in y will be between 0 and 1000, inclusive. |
| - | No location will appear more than once. |
| - | n will be between 3 and 40, inclusive. |
| - | It will be possible to select the coordinates so that an area strictly greater than 0 is covered. |
| |
Examples |
| 0) | |
| | {2,1,6,5,3,7,9} | {2,5,1,5,7,6,4} | 4 |
| Returns: 24.0 | | Selecting the points (2,2), (6,1), (9,4) and (3,7) will yield an area of 24 (this corresponds to the picture in the figure above).
|
|
|
| 1) | |
| | {183,229,723,510,395,936,447,328} | {1000,823,0,412,786,446,312,286} | 15 |
| Returns: 347200.0 | | The farmer can afford more scarecrows than there are possible locations for him to put them.
|
|
|
| 2) | |
| | {33,36,26,8,12,8,28,19,8,37,9,22,31,30,25} | {12,8,6,16,27,7,31,33,35,22,22,36,29,22,32} | 8 |
| Returns: 740.5 | |
|
| 3) | |
| | {327,196,744,91,709,38,944,300,927,715,835,874,958,667,748,511,377,956,184,956,
809,925,12,45,184,180,169,374,914,398,954,875,286,422,76,315,497,209,512,938} | {913,843,73,213,903,444,444,905,352,54,194,207,373,57,105,959,932,480,843,424,
140,661,578,616,851,132,135,936,676,23,578,737,74,959,724,924,955,854,958,376} | 25 |
| Returns: 685819.5 | |
|
