Problem Statement
Warning: Embedded in this problem statement are images that may not be visible if you are using a plugin. For best results, view this problem in the standard Arena editor.
"To heck with this quipu!" exclaimed Tupac the Incan philosopher. He was trying to record the contents of his household using the knot language of Peru, but the rules were too complicated. Who besides a tax collector could keep track of all the fixed knots, transient knots, and rhetorical knots?
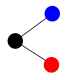
After some thought, Tupac contrived a simpler scheme that would encode each inventory item on a length of string using a sequence of square knots and bow knots. For one particular collection of four items, he tied the following four strings, where 's' stands for a square knot and 'b' for a bow knot: {"bsb", "bbs", "sbbs", "sbs"}.
This took 13 knots. Tupac now gathered the strings into a quipu by tying them at one end with a top knot, making a grand total of 14 knots. The result of his efforts is depicted in the following image, where the bow knots are colored blue; the square knots, red; and the top knot, black.
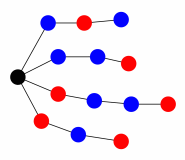
"The top knot is important," explained Tupac to his wife, Cuxi, "because it shows me where to start reading each item."
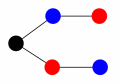
"Let me see that," said Cuxi, reaching for the quipu. "I can record the same four items using fewer knots."
Once Cuxi had cut off some parts of the quipu and reknotted a few others, it emerged like so.
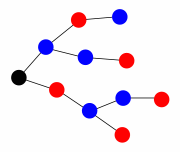
Her husband goggled at this feat. "Three knots fewer!" he cried. "And it encodes exactly the same inventory!"
Tupac saw that if he began from the top knot and followed a path through the quipu from left to right until the end of a string, he could spell out any inventory item, but nothing that wasn't in the inventory. This was an improvement over the original quipu, in which he sometimes found himself reading the wrong item and therefore having to backtrack to the top knot.
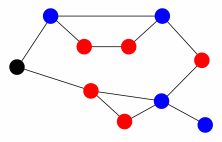
"I can do better yet," said Cuxi, "if I join some strings at the other end of the quipu. Watch this." After some more cutting and reknotting, she produced the following configuration.
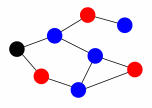
Cuxi stated emphatically that you weren't supposed to pursue a looping path through the quipu. "Follow the grain of the string from beginning to end," she said, "and make sure you don't double back. The quipu only works in one direction."
She also pointed out that the paths were deterministic: at every knot where the quipu bifurcated, there was a choice of two different knots. This guaranteed that any inventory item could be found without backtracking or pursuing several paths at once.
Tupac was pleased to confirm that Cuxi's abbreviated quipu was functionally equivalent to the original. He could begin reading from the top knot and proceed strictly from left to right through the knots, following one of four distinct paths that spelled out exactly the items of the inventory.
"I can't make it any smaller," said Cuxi, "but a quipu with eight knots is an improvement over the original fourteen. So I'm pretty good. I'm only worried about cases where one item in the inventory is a prefix of another."
"There will never be such a case," said Tupac. "As it happens, my inventory encoding has the property that no item can be a prefix of another."
You are given a String[] describing a collection of inventory items encoded under Tupac's system. Calculate the smallest number of knots, including the top knot, that must be tied to make a deterministic binary quipu for this inventory.
Definition
| Class: | BinaryQuipu |
| Method: | fewestKnots |
| Parameters: | String[] |
| Returns: | int |
| Method signature: | int fewestKnots(String[] inventory) |
| (be sure your method is public) | |
Notes
Constraints
Examples
| ||
Returns: 8 | ||
| ||
| ||
Returns: 3 | ||
| ||
| ||
Returns: 5 | ||
| ||
| ||
Returns: 5 | ||
| ||
| ||
Returns: 10 | ||
| ||
| |
Returns: 181 | |