Problem Statement |
| |
Every moviegoer is familiar with the tense scene in the air control
tower where a green phosphorescent screen shows a radial arm sweeping
around to update the position of a brightly glowing spot. A more modern
but less dramatic technology is omnidirectional radar, which diffuses
its signal in all directions at once in order to discern the positions
of several distinct bodies. Like the traditional system, this kind of
radar does not work in a continuous fashion, but periodically emits a
burst of radio waves.
Observe that if a single object traveling at constant speed is within
range of the radar, two consecutive readings suffice to identify its
path. If several objects are within range, then two readings alone are
inadequate, since they lead to multiple interpretations. Three consecutive
readings, however, will often allow one to determine the paths of a set
of objects traveling at constant speed.
You are given six int[]s describing three consecutive
readings from an omnidirectional radar installation that pulses at
one-second intervals. The first two int[]s contain the
first set of readings, specifying the x and y coordinates
in meters of each blip on the radar grid. The second and third pair
of int[]s describe the coordinates of the same number of
radar blips at consecutive intervals. Although within each pair, the nth
element of the x int[] refers to the same point as
the nth element of the y int[], there
isn't necessarily any correspondence in the order of coordinate pairs
between any two sets of readings.
If these readings are not consistent with the interpretation that every
radar blip corresponds to an object moving in a straight line at constant
speed within radar range, or if there are several such interpretations,
return an empty int[]. Otherwise, return a int[]
containing the speed in meters per second of each object in the order
established by the first set of readings. Round your results to the
nearest m/s, with 0.5 rounding up.
|
| |
Definition |
| | | Class: | PulseRadar | | Method: | deduceSpeeds | | Parameters: | int[], int[], int[], int[], int[], int[] | | Returns: | int[] | | Method signature: | int[] deduceSpeeds(int[] x1, int[] y1, int[] x2, int[] y2, int[] x3, int[] y3) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | Assume that all objects are moving in the same plane. |
| - | Some objects may be stationary. |
| - | In the case of multiple interpretations that would all result in the same int[] of speeds, you should still return an empty int[]. |
| |
Constraints |
| - | x1 has between 1 and 10 elements, inclusive |
| - | y1, x2, y2, x3, and y3 each have the same number of elements as x1 |
| - | each element of x1, y1, x2, y2, x3, and y3 is between -1000 and 1000, inclusive |
| - | no set of readings includes two radar blips at the same location |
| |
Examples |
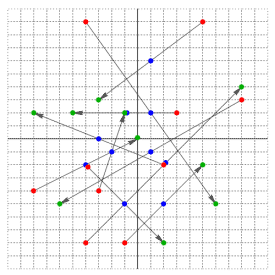
| 0) | |
| | {-8, -7, 9, -5} | {2, -1, -2, -6} | {-2, -3, 8, 1} | {-3, 1, 4, -2} | {4, 1, 7, 7} | {-8, 3, 10, 2} |
| Returns: { 8, 4, 6, 7 } | There is a unique interpretation of the objects' linear motion. In this and all further diagrams, red dots depict the first set of readings, blue dots the second, and green the third.
|
|
|
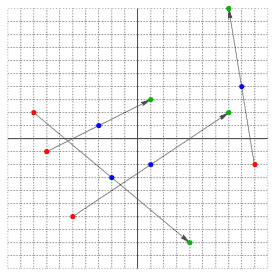
| 1) | |
| | {-7, -2, 2, 0} | {8, -2, -2, -6} | {-5, -1, 3, -1} | {9, 1, -4, -8} | {-3, 1, 5, -2} | {10, 5, -6, -10} |
| Returns: { } | It cannot be the case that each object is moving in a straight line
at constant speed.
|
|
|
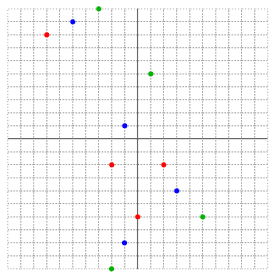
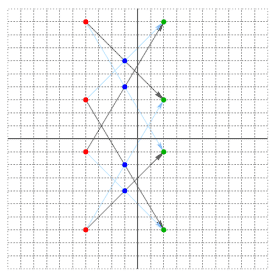
| 2) | |
| | {-4, -4, -4, -4} | {9, 3, -1, -7} | {-1, -1, -1, -1} | {6, -2, 4, -4} | {2, 2, 2, 2} | {3, -7, 9, -1} |
| Returns: { } | There are several interpretations of the objects' linear motion.
|
|
|
| 3) | |
| | {5, -4, 2, -1, 8, -4, -8, 3, -3, -4} | {9, 9, -2, -8, 3, -8, -4, 2, -4, -2} | {-2, 2, 1, 2, 1, -1, -3, 1, -4, -1} | {-1, -5, 6, -2, 2, 2, 0, -1, -2, -5} | {8, 5, -1, -3, 6, -5, 2, 0, -6, -8} | {4, -2, 2, 3, -5, 2, -8, 0, -5, 2} |
| Returns: { 5, 9, 5, 4, 8, 8, 4, 4, 3, 4 } | |
|
| 4) | |
| | {-300, 466} | {-600, 866} | {466, 100} | {866, -450} | {500, 466} | {-300, 866} |
| Returns: { 427, 0 } | |
|