TopCoder problem "RecursiveGraph" used in SRM 188 (Division I Level Three)

Problem Statement

This problem statement contains an image which will not display correctly for plugin users.

You will be given an undirected graph which may contain several smaller copies of itself. These copies, or "children", will in turn recursively contain the same number of children, creating a graph with an infinite number of nodes. You are to find the shortest path through this graph.

At each level down, the edges of children have half the weight of their parent, rounded down. Once you recurse deep enough into the graph, all edges eventually have a weight of zero.

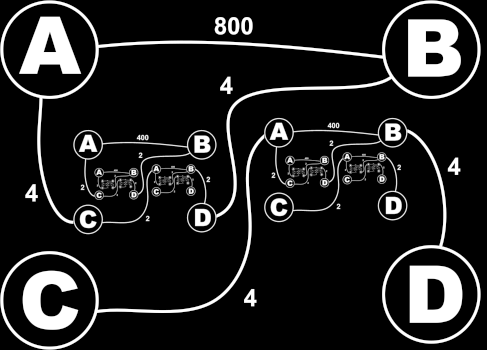
For example, consider the graph pictured above with 4 top-level nodes (A, B, C, and D), and 2 recursive children. Notice that each child has two smaller copies inside of it, and each of those children has two smaller copies inside of it, repeating infinitely. In this graph, there is a direct path from node A to B with distance 800. However, there is a shorter path from A to B that goes through C and D in the left-side child of the top-level graph. Within the left-side child, the path from C to D goes through A and B in its right-side child. The length of this 5-edge path is 4 + 2 + 200 + 2 + 4 = 212.

However, there is an even shorter path, bypassing the third-level edge from A to B with cost 200. By replacing this edge with the same 5-edge path two levels down, there is a 9-edge path with distance 4 + 2 + 1 + 0 + 50 + 0 + 1 + 2 + 4 = 64. Similarly, the edge with cost 50 can be bypassed again by recursing farther into the graph. By going down deep enough to the point where all edges have zero weight, the edge cost can be bypassed completely, resulting in a shortest path from A to B of length 4 + 2 + 1 + 0 + ... + 0 + 1 + 2 + 4 = 14.

Graphs will contain up to 10 top-level nodes ('A' through 'J'), and each parent graph at each level may contain up to 9 child graphs, smaller copies of itself, numbered ('1' through '9'). The graph will be specified by a list of edges in the top-level graph. Edges are specified by two nodes, followed by a weight. Either node may optionally be followed by a single digit, representing a connection to a node in the corresponding recursive copy of the graph.

The graph pictured above would be specified as:


    "A B 800" (connecting A and B in every copy of the graph)
    "A C1 4"  (connecting A in every copy to C in its first child)
    "D1 B 4"  (connecting B in every copy to D in its first child)
    "C A2 4"  (connecting C in every copy to A in its second child)
    "B2 D 4"  (connecting D in every copy to B in its second child)

There will be no edge that directly connects two nodes of the same child. For example, the edge "A3 B3 10" would be illegal, but the edge "A4 B5 20" is allowed. A top-level edge implies corresponding edges in all copies of the graph at all levels. Likewise, an edge connecting a top-level node to a copy implies corresponding connections between parents and children at all levels, and an edge connecting nodes of two different children implies corresponding edges between nodes in those two children at all levels.

Given a list of edges, a starting node, and an ending node, return the length of the shortest path between the starting and ending nodes. Return -1 if there is no such path, or if the distance of the shortest path is greater than 1,000,000,000.

Definition

Class:	RecursiveGraph
Method:	shortestPath
Parameters:	String[], char, char
Returns:	int
Method signature:	int shortestPath(String[] edges, char start, char end)
(be sure your method is public)

Notes

The shortest path may descend recursively down many levels.

All edges are undirected. The order of a pair of nodes in the input is not significant.

There can be no edges that connect nodes between levels with depths that differ by more than 1.

Constraints

edges will contain between 1 and 50 elements, inclusive.

Each element of edges will be formatted as "<node> <node> <weight>".

Each <node> is a character between 'A' and 'J', inclusive, optionally followed by a digit between '1' and '9', inclusive.

Each <weight> is an integer from 0 to 1000, inclusive, and will not have any leading zeros.

There will be at most 10 top-level nodes (letters 'A' through 'J').

At each level, there will be at most 9 copies of the graph embedded directly in itself (nodes with digits '1' through '9').

There will not be more than one edge between the same two nodes.

There will not be an edge connecting two nodes of the same recursive copy, i.e. "A1 B1 5" would be illegal input.

start and end will each be a character between 'A' and 'J', inclusive, and will be nodes which appear in edges.

Examples

{"A B 20",
"C D 13",
"A C1 1",
"D1 C2 2",
"D2 B 3"}

'A'

'B'

Returns: 18

This graph has 4 top-level nodes, plus two copies of itself. There are two paths from A to B. The direct path across the first edge has a cost of 20. However, the path through the two copies (A->C1->D1->C2->D2->B) has a weight of 1 + 6 + 2 + 6 + 3 = 18. Remember, the edges from C to D in the children have half the weight (rounded down) of the edge from C to D in their parent.

{"A B 800",
"A C1 4",
"D1 B 4",
"C A2 4",
"B2 D 4"}

'A'

'B'

Returns: 14

This is the example from the problem statement.

{"A A1 1",
"B B1 1"}

'A'

'B'

Returns: -1

No matter how far down you recurse, there is no path from A to B.

{ "A E1 10", "H2 J 11",
"E F 50", "F1 G2 5", "G H 60",
"A C4 12", "D4 J 13",
"C E1 14", "F1 D 15",
"E G8 6", "F H8 8" }

'J'

'A'

Returns: 49

{ "E H 3", "C J 3", "D E9 0", "H9 A 0", "A C3 0", "J3 F 0" }

'D'

'F'

Returns: 2

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2365

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4760&pm=2365

Writer:

legakis

Testers:

lbackstrom , brett1479

Problem categories:

Graph Theory