Problem Statement
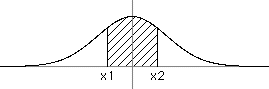
Given two real numbers x1 and x2, calculate an approximation to the integral of e-x^2 evaluated between the limits from x1 to x2, which is accurate to the nearest 0.00001. Return the answer in a String, as a fixed point number with exactly five digits to the right of the decimal point and exactly one digit to the left of the decimal point.
For example: x1 = -0.5 and x2 = 0.5 returns "0.92256"
Definition
| Class: | NumericalIntegral |
| Method: | integrate |
| Parameters: | double, double |
| Returns: | String |
| Method signature: | String integrate(double x1, double x2) |
| (be sure your method is public) | |
Notes
- e-x^2 can be calculated in C++ with exp(-x*x) in math.h.
- e-x^2 can be calculated in C# with Math.Exp(-x*x). The Math class is in the System namespace.
- e-x^2 can be calculated in Java with Math.exp(-x*x).
- e-x^2 can be calculated in Visual Basic with Exp(-x*x) in the System.Math namespace.
Constraints
Examples
| ||
Returns: "0.92256" | ||
| ||
| ||
Returns: "0.09967" | ||
| ||
Returns: "0.00000" | ||
| ||
| ||
Returns: "0.00010" | ||