Warning: Embedded in this problem statement is an image that may
not be visible if you are using a plugin. For best results, view this
problem in the standard Arena editor.
The left-handed Finnish hockey player Slaapi Shotti has a spectacular move
where he fires the puck from the blue line, off the boards, and into the
net. The relevant portion of an international hockey rink is shown below.
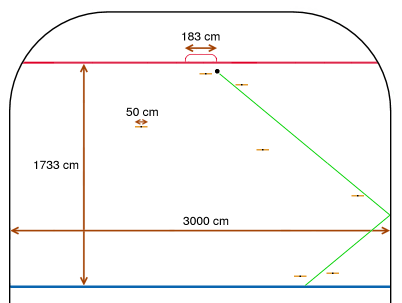
The rink is 3000 centimeters (cm) wide. The distance between the blue
line and the goal line is 1733 cm. Centered on the goal line is the
goal itself, which is 183 cm wide and marked with a goalpost at each
end. When Slaapi shoots, the puck will travel in a straight line from
a given point on the blue line, rebound symmetrically from the right
border of the rink, and continue traveling in a straight line. We shall
model the puck and the goalposts as infinitesimal points on the ice.
Positioned on the ice are up to nine players, whom we model as line
segments that are 50 cm long and parallel to the blue line. Each player
must stand on or below the goal line, at least one centimeter above
the blue line, and at least one centimeter away from the sides. Players
may overlap or coincide. In order for Slaapi to score a goal, the puck
may not intersect a player's line segment at any point, including its
endpoints. For the purposes of player position as well as puck rebound,
you may ignore the curvature of the rink and assume that the boards are
perfectly straight, forming a rectangle with the blue line and goal line.
Slaapi must shoot the puck from the point on the blue line whose distance
from the left border of the rink is given by the int
puckCoord. You are also given two int[]s,
xCoords and yCoords. The distance in centimeters of the
nth player's midpoint from the left border of the rink is given by
the nth element of xCoords, and the distance of his midpoint
from the blue line is given by the nth element of yCoords.
Calculate the angle, measured counterclockwise from the blue line,
at which Slaapi must shoot the puck so that its point of intersection
with the goal line is between the goalposts, inclusively, and as close
as possible to the right goalpost. Return your answer in degrees as a
double value with an absolute or relative error of 1.0e-9.
Return -1.0 if Slaapi cannot score a goal in the prescribed manner.
The input is guaranteed to be such that the rightmost gap through which
Slaapi can score, if any, is at least 1.0e-6 cm wide at the goal line.
| 