Problem Statement |
| | This problem contains images which will not display correctly for plugin users. Please use the applet to view the problem statement and examples.
Given a set of two-dimensional points with integer coordinates, determine if they uniquely determine a square. In other words, determine if there is exactly one square that can be constructed so that each specified point is exactly on an edge or vertex of the square. Return "consistent" if exactly one such square exists, "inconsistent" if no such square exists, and return "ambiguous" if more than one such square is possible. To simplify the problem a bit, input will contain at least five points. The coordinates of the points are specified in two int[]s, x and y. The i'th point is specified by (x[i],y[i]).
For example:
x={0,0,2,3,5,5,3,2}
y={2,3,0,0,3,2,5,5}
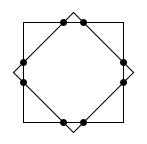
Returns "ambiguous" since two squares can be constructed such that each passes through all eight points, as shown in the figure.
|
| |
Definition |
| | | Class: | SquarePoints | | Method: | determine | | Parameters: | int[], int[] | | Returns: | String | | Method signature: | String determine(int[] x, int[] y) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The possible squares may be at any orientation(s). |
| |
Constraints |
| - | x will have between 5 and 50 elements inclusive. |
| - | y will have between 5 and 50 elements inclusive. |
| - | x and y will have the same number of elements. |
| - | Each element of x and y will be between -1000 and 1000 inclusive. |
| - | Each point (x[i],y[i]) must be distinct from all the other points. |
| |
Examples |
| 0) | |
| | {0,0,2,3,5,5,3,2} | {2,3,0,0,3,2,5,5} |
| Returns: "ambiguous" | |
|
| 1) | |
| | {0,0,10,10,4} | {0,10,0,10,5} |
| Returns: "inconsistent" | 
No way to make a square with all the points here. |
|
|
| 2) | |
| | {1,1,1,1,1,1,1,1,1,1,1,1,1,2,3,4,5,6,7,8,9,10,11,12,13,
13,13,13,13,13,13,13,13,13,13,13,13,12,11,10,9,8,7,6,5,4,3,2} | {1,2,3,4,5,6,7,8,9,10,11,12,13,13,13,13,13,13,13,13,13,13,13,13,13,
12,11,10,9,8,7,6,5,4,3,2,1,1,1,1,1,1,1,1,1,1,1,1} |
| Returns: "consistent" | 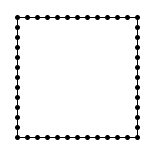
This is an extremely well determined square. |
|
|
| 3) | |
| | { 0,4,8,-5,-1,3} | { 0,3,6,15,18,21} |
| Returns: "consistent" | 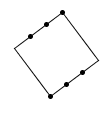
Exactly one square fits here. |
|
|
| 4) | |
| | { 0,4,8,-5,-1,3,16} | { 0,3,6,15,18,21,12} |
| Returns: "inconsistent" | 
No square is possible. |
|
|
| 5) | |
| | {0,4,8,-5,-1} | {0,3,6,15,18} |
| Returns: "ambiguous" | 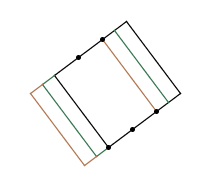
More than one square is possible. Three of them are shown here. |
|
|
| 6) | |
| | {998,-1000,-998,1000,999} | {1000,998,-1000,-998,0} |
| Returns: "inconsistent" | | Almost a square, but not quite. |
|
|
| 7) | |
| | {0,1,2,0,100} | {0,0,0,1,140} |
| Returns: "consistent" | |
|
| 8) | |
| | |
| 9) | |
| | {0,1,2,0,2,0} | {0,0,0,2,2,3} |
| Returns: "inconsistent" | |
|





