Problem Statement |
| |
This problem uses subscripts and superscripts which may not display properly for plugin users.
We've all heard the riddle "How far can a dog run into the woods?", where the expected answer is "halfway". However, this is only correct if worded as "How far can a dog run directly into the woods?". We're here today to solve the actual problem, where "running into" is defined as moving in a way such that for any two times t1>0 and t2>0, t1<t2 if and only if distance(position(t1))>distance(position(t2)), where distance(p) is the distance (in a straight line) from the center of the woods to a position, and position(t) is the dog's position at time t. Complicating (and making more realistic) our problem are the trees in the woods. Each tree is defined by x and y coordinates, and a diameter. As any dog owner can attest, it is in a dog's nature to run in circles. Our dog is slightly demented, so his nature is to run in clockwise circles centered at the center of the woods until he hits a tree. If he hits a tree, he runs counterclock-wise around the tree until he is able to travel clockwise tangent to the center of the woods.
You are to create a class DogWoods, with a method howFar, which takes int[]s containing the x and y coordinates, and the diameters of each tree. The method will also take parameters startx and starty, which are the starting x and y coordinates for the dog. The ith element of x corresponds to the ith element of y, which corresponds to the ith element of diameter. The dog is determined to have reached the center of the woods when the dog's distance to the center is <= 10 units. Your method must return the distance that would be travelled by the dog, while obeying his nature, before he reaches the center of the woods. Your return value must be within 1e-9 relative or absolute error of the correct value.
The location (0,0) is the center of the woods, with the positive x axis extending to the right, and the positive y axis extending up (a standard Cartesian plane).
If the dog would run an infinitely long distance while obeying his nature, then your method should return -1.
Given two circles with the following equations,
(x - x0)2 + (y - y0)2 = r02 (A circle centered at (x0,y0) with radius r0)
x2 + y2 = r12 (A circle centered at (0,0) with radius r1)
their points of intersection are given by:
x = x0 / 2 - x0(r02 - r12) / 2d + y0p / 2d
y = y0 / 2 - y0(r02 - r12) / 2d - x0p / 2d
and
x = x0 / 2 - x0(r02 - r12) / 2d - y0p / 2d
y = y0 / 2 - y0(r02 - r12) / 2d + x0p / 2d
where
d = x02 + y02
p = sqrt(((r0 + r1)2 - d)(d - (r1 - r0)2))
|
| |
Definition |
| | | Class: | DogWoods | | Method: | howFar | | Parameters: | int[], int[], int[], int, int | | Returns: | double | | Method signature: | double howFar(int[] x, int[] y, int[] diameter, int startx, int starty) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The dog will always obey his nature as described. |
| - | The dog may not run through any part of a tree. |
| - | Trees are to be considered exactly round. |
| - | The dog should be treated as a mathematical point. I.e., it has no diameter. |
| - | The distance around a circle is pi * diameter. |
| - | pi ~ 3.14159265358979. |
| |
Constraints |
| - | x, y, and diameter will all have the same number of elements. |
| - | x will have between 1 and 50 elements, inclusive. |
| - | Every element of x and y will be between -1000 and 1000, inclusive. |
| - | Every element of diameter will be between 1 and 100, inclusive. |
| - | startx and starty and will be between -1000 and 1000, inclusive. |
| - | The closest that the perimeter of any two trees will be to each other is 1e-6. |
| - | For any two trees a and b, the distance of the closest point to the center of a will not be within 1e-6 of the distance of the furthest point to the center of b. |
| - | No tree will completely cover the circle of diameter 20 at the center of the woods. |
| - | For every tree, the circle of diameter 20 will either not intersect that tree, or it will intersect by at least 1e-6 units at the greatest width of intersection. |
| - | The dog will not start in the midst of a tree. |
| |
Examples |
| 0) | |
| | | Returns: 23.64281561414452 | The dog travels until it meets the tree, covering 18.431923291703267 units, and then travels around the tree until it is within 10 units of the center, for another 5.2108923224412536 units.
In the image, the red lines represents the dog's path, the black circle the tree, and the blue circle the center of the forest.
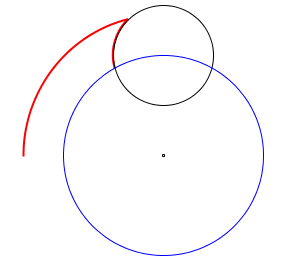 |
|
|
| 1) | |
| | {40,15,-5}
| {7,25,11} | {26,12,23} | 0 | -49 |
| Returns: 531.3835950099849 | In this image, the red lines represents the dog's path, the black circles the trees, and the blue circle the center of the forest.
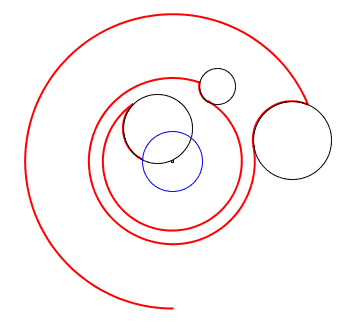 |
|
|
| 2) | |
| | | Returns: -1.0 | | The dog can continue spiraling around the center never meeting a tree. |
|
|
| 3) | |
| | | Returns: 0.0 | | The dog started within 10 units of the center, and therefore cannot travel any further. |
|
|
| 4) | |
| | {-220,-204,-187,-11,16,211,-180,87,272,-118,-1,16,187,113,71,217,-12,78} | {232,-162,60,-125,-22,-266,-120,-242,87,-148,50,-218,161,-232,249,215,11,-79} | {53,8,77,74,4,42,36,31,73,84,67,59,33,18,94,87,13,59} | 51 | -255 |
| Returns: 3564.170613418495 | |
|

