Problem Statement |
| |
You are working for a company that manufactures high-resolution grids of sensors, such as those used in digital cameras. While the probability of any one sensor being defective is low, it is likely that a very large grid of sensors will have a few defects. For consumer products, this is just accepted, and sometimes the artifacts caused by non-functioning sensors can be hidden with filtering in software.
For high-end products, however, your company wishes to provide defect-free sensor grids. They plan to do this by making extremely high-resolution grids, locating the defective sensors, and then finding a (hopefully) large rectangular region within that grid that does not contain any defects.
Given the width and height of the sensor grid, and the locations of all defects, find the rectangular region in the grid with the largest area (width times height) that does not contain any defective sensors. The locations of the defects are given as zero-indexed coordiantes, where (0,0) is the upper-left corner of the sensor grid. Return a int[] with 4 elements, in this order: the x coordinate of the upper-left corner of the rectangle, the y coordinate of the upper-left corner of the rectangle, the width of the rectangle, and the height of the rectangle. If there are more than one rectangle with the same largest area, return the one with smallest y coordinate. If there are more than one with the same largest area and smallest y coordinate, return the one with the smallest x coordinate. If there are more than one with the same largest area and upper-left corner, return the one with the greatest width.
|
| |
Definition |
| | | Class: | SensorGrid | | Method: | largestRectangle | | Parameters: | int, int, int[], int[] | | Returns: | int[] | | Method signature: | int[] largestRectangle(int width, int height, int[] x, int[] y) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | "upper-left" refers to the corner closest to (0,0). |
| - | The width is measured parallel to the x axis, and the height is measured parallel to the y axis. |
| - | The ith point (starting at point 0) is given by (x[i], y[i]). |
| |
Constraints |
| - | width will be between 1 and 40000, inclusive. |
| - | height will be between 1 and 40000, inclusive. |
| - | x will contain between 1 and 50 elements, inclusive. |
| - | y will contain the same number of elements as x. |
| - | Each element of x will be between 0 and width-1, inclusive. |
| - | Each element of y will be between 0 and height-1, inclusive. |
| - | There will be no duplicate points. |
| - | There will be at least one functional sensor. |
| |
Examples |
| 0) | |
| | 9 | 7 | { 1, 5, 1, 5, 3, 7, 3, 7 } | { 0, 0, 2, 2, 4, 4, 6, 6 } |
| Returns: { 2, 0, 3, 4 } | Four 3x4 rectangles fit between the defects, as show in the following figure:

Of these, two have the smallest y coordiante (zero), and of those two, the rectangle at position (2,0) has the smallest x coordinate. |
|
|
| 1) | |
| | | Returns: { 0, 0, 5, 4 } | Two rectangles with the same area fit between the defects, as show in the following figure:
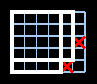
They both have the same upper-left position, so we return the one with the larger width.
|
|
|
| 2) | |
| | 17 | 16 | { 1, 3, 5, 7, 11, 13, 15,
1, 3, 5, 7, 11, 13, 15,
1, 3, 5, 7, 11, 13, 15,
1, 3, 5, 7, 11, 13, 15,
1, 3, 5, 7, 11, 13, 15,
1, 3, 5, 7, 11, 13, 15,
1, 3, 5, 7, 11, 13, 15 }
| { 1, 1, 1, 1, 1, 1, 1,
3, 3, 3, 3, 3, 3, 3,
5, 5, 5, 5, 5, 5, 5,
7, 7, 7, 7, 7, 7, 7,
10, 10, 10, 10, 10, 10, 10,
12, 12, 12, 12, 12, 12, 12,
14, 14, 14, 14, 14, 14, 14 } |
| Returns: { 8, 0, 3, 16 } | |
|

