TopCoder problem "Crossings" used in SRM 217 (Division I Level Two)

Problem Statement
	You are watching a car race. Each car starts at a different point on the x-axis, travels at the same speed, and starts at the same time. However, each car is travelling along a different road (which extends to infinity in one direction, and is stopped by the x-axis in the other direction), and each road has its own direction specified by an angle between 1 and 179, inclusive. An angle of 90 indicates that the road heads directly in the positive y direction, while an angle of 1 indicates that the road heads just a little bit north of the positive x direction. 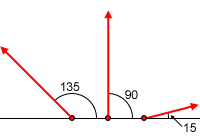Sometimes, two or more roads intersect at some point. When this happens, the car that reaches the intersection first is able to block the intersection so that no other cars can pass through it. If two cars arrive at an intersection at the same time, the car that appears earlier in the input (lower index) will be the only car to pass through. 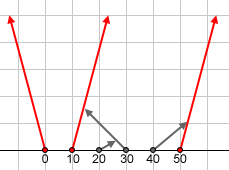In this picture, the cars following the red paths at 0, 10 and 50 pass all intersections, while the cars following the gray paths are stopped (see example 0). You will be given two int[]s, positions, and angles, where the ith car corresponds to the ith element of positions and the ith element of angles. The ith element of positions is the x coordinate of the ith car. The ith element of angles is the angle in degrees between the x-axis and the road that the ith car travels on. Your method should return a int[] containing the 0-based indices of all the cars that will pass all the intersections along their roads. Your return should be sorted in ascending order.
Definition
	Class: Crossings Method: getOut Parameters: int[], int[] Returns: int[] Method signature: int[] getOut(int[] positions, int[] angles) (be sure your method is public)
Constraints
-	positions and angles will contain the same number of elements.
-	Each element of positions will be between 0 and 1000000, inclusive.
-	Each element of angles will be between 1 and 179, inclusive.
-	Each element of positions will be unique.
Examples
0)
	{0, 40, 20, 10, 30, 50} {105, 40, 30, 75, 135, 75} Returns: { 0, 3, 5 } The example from the problem statement.
1)
	{0, 40, 20} {40, 40, 140} Returns: { 0, 1 }
2)
	{10, 20} {89, 91} Returns: { 0 }

Problem url:

Problem stats url:

Writer:

Testers:

Problem categories: