Problem Statement |
| | This problem contains images.
In chess the queen reigns supreme over all other pieces. She has mastered the techniques of the rook and the bishop, thus allowing her to move any number of steps diagonally, vertically, or horizontally. Since a single queen controls such a large area, it is hard to put multiple queens on the board without them getting in each others' way (two queens are "in each others' way" if one can reach the other in a single move). For this reason there is a famous challenge requiring n queens to be placed on an n-by-n chess board such that no two queens interfere with each other.
In this problem you will implement a particular randomized solution. The board is setup as follows starting with column 1 on the left, and ending with column n on the right:
- 1) Choose a random number R between 1 and n inclusive.
- 2) Place a queen in row R of the current column (row 1 is the top; row n is the bottom).
An alteration step works as follows:
- 1) Compute T, the number of columns containing reachable queens.
- 2) Choose a random number K between 1 and T inclusive. Let C
denote the Kth column, counting from the left, that contains a reachable queen.
In effect, we have randomly chosen one of the reachable queens.
- 3) For each of the n positions in column C,
compute how many queens from other columns can currently reach that position.
- 4) Move the queen in column C to the position in column C reachable
by the fewest number of queens. If multiple positions are tied, continue to step 5, otherwise the alteration step is complete.
- 5) Compute P, the number of positions that tied in step 4.
- 6) Choose a random number Q between 1 and P inclusive. Counting from the top down,
move the queen to the Qth of the tied positions in 4.
Note that an alteration step may not cause any movement at all. You will return how many alteration steps are required before no two queens interfere with one another. The ith random value used in the algorithms above will be (a(i) % Up)+1 where Up is the inclusive upper bound on the random number required and a(i) is given by the following formula:
- a( 1 ) = 1 ,
- a( k+1 ) = ( 16807 * a( k ) ) % 2147483647 for k > 0.
Here % denotes modulus or remainder. Use a 64-bit integral type to correctly compute the a(j) values. Random values 1 through n will be used to setup the board, while the remaining values will be used to perform the alteration steps. Make sure to follow the algorithm carefully thus ensuring each random value is used at the correct time. Specifically, make sure you do not continue on to step 5 unless directed to do so. If no alteration steps are required, return 0. |
| |
Definition |
| | | Class: | QueenInterference | | Method: | numSteps | | Parameters: | int | | Returns: | int | | Method signature: | int numSteps(int n) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | n must be between 4 and 100 inclusive. |
| - | n will not be 17. |
| |
Examples |
| 0) | |
| | | Returns: 4 | The first 5 random numbers are 2,3,5,4,4 thus producing the following initial configuration.
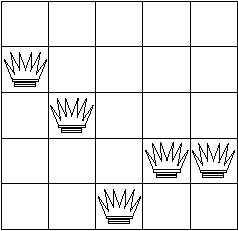
Alteration Step 1:
All 5 queens are reachable, so we choose a random number between 1 and 5 inclusive. The number we get is 1, so we shall work on the leftmost column. Computing reachabilities we arrive at the following scores.
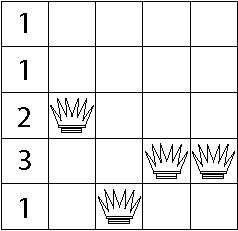
Since there are 3 positions reachable by 1 queen, we retrieve another random number between 1 and 3 inclusive. The number turns out to be 3 so the queen is placed on the lowest of the 3 potential spots.
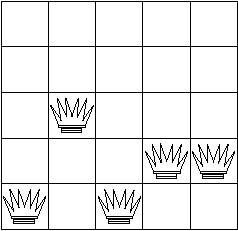
Alteration Step 2:
Since only 4 queens are still reachable we choose a random number between 1 and 4 inclusive.
The next two random values are 1 and 3 so the previous steps are repeated and the board remains unchanged.
Alteration Step 3:
Again we choose a random number between 1 and 4 inclusive, but this time we get 4. Column 5 is the fourth column containing a reachable queen. We thus compute how many queens can reach each position in that column.
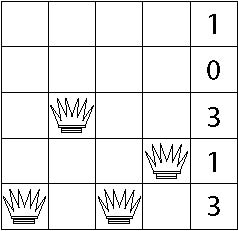
Row 2 is the least reachable, so the queen is moved there.
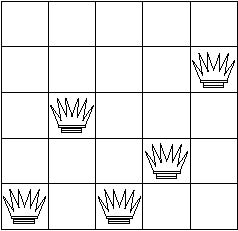
Alteration Step 4:
Now there are 3 reachable queens so we choose a random number between 1 and 3 inclusive. We get the number 2 thus causing us to alter column 3 (the second column from the left containing a reachable queen). Now we compute how many queens can reach each position.
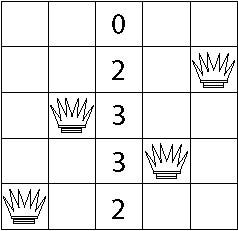
Only the topmost position is reachable by 0 queens so we move the queen there.
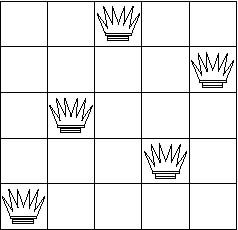
Now the board is complete, so we return 4.
|
|
|
| 1) | |
| | |
| 2) | |
| | |






