|
NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.
Given a regular grid of size W x H with various squares blocked out,
find a path from point (0,0) to point (W,H)
that does not pass through any of the blocked-out squares.
The path must consist only of 90-degree arcs (quarters of circles).
The radius of each arc must be an integer,
and therefore begin and end on an integer grid point.
The tangents at each end of every arc must be parallel to the x or y axis.
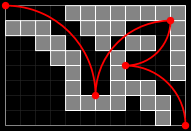
Arcs may intersect the corner of a blocked-out square
and even pass between two that share a corner
(as shown in the examples below),
but may not pass through the interior of any blocked-out square.
The grid will be given as a String[],
with a '.' representing an empty square
and a '#' representing a blocked-out square.
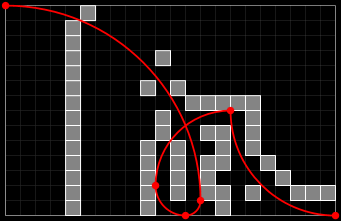
For example, given the following 12 x 8 grid:
{ "....########",
"###..###...#",
"..##..#.##.#",
"...##..#...#",
"....#..#...#",
"....#..###..",
"....####.##.",
"..........#." }
there is a path from (0,0) to (12,8) consisting of 4 arcs,
as shown in the following figure:
Find the path that contains the fewest number of arcs,
and return the number of arcs in that path.
If there is no path, return -1.
|