Problem Statement |
| | The problem statement contains an image.
More and more electronic devices can be connected to the internet. So far, most of them don't support
wireless networking, which means you have to pull TP (twisted pair) cables in your
apartment. You also have to use hubs, which split a cable from one connection to four other connections.
A connection can either be the internet connection, an electronic device or a hub.
All cables must be pulled on the floor along the walls, and all connections will be at the floor near a wall.
There will be a single internet connection in the apartment, and all electronic devices (there will always
be more than one) must be connected to it through one or more hubs. The hubs may be interconnected as well.
Given the design of an apartment as a top-down view, the number of hubs at your disposal, the location of the internet
connection and the locations of all electronic devices, determine the least amount of TP cable
needed. You may place the hubs anywhere along a wall. Several hubs can be placed at the exact
same location, and hubs can be at the same location as other existing connections.
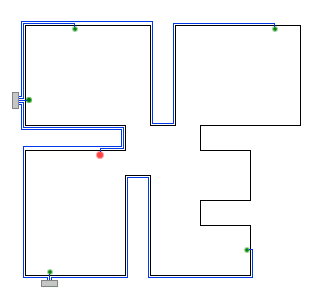
Consider the image below, showing the design of an apartment from a top-down view. The red dot marks
the internet connection, the green dots mark electronic devices, the gray boxes the positions of the hubs,
and the blue lines TP cable. Note that the dots, boxes and lines are slightly separated from
the wall on the image, but this is for clarification only.
The apartment design will be given as a String[] describing the top-down view as
a simple polygon. All lines in the polgyon will be either horizontal or vertical. Each element will be in the form
"<x> <y>" describing a point in the polygon. The points
will be given in either clockwise or counter-clockwise order.
The connections will also be given as a String[], where each element will be in
the format "<x> <y>". The first element will be the location
of the internet connection, and the other elements the locations of the electronic devices.
Create a class CableWoes containing the method leastTPCable which takes a String[]
design, the apartment design, a String[] connections, the locations
of the connections, and an int hubs, the number of hubs at your disposal.
The method should return an int, the least amount of TP cable needed to be pulled.
If it's not possible to connect all devices to the internet, return -1 (see example 4).
|
| |
Definition |
| | | Class: | CableWoes | | Method: | leastTPCable | | Parameters: | String[], String[], int | | Returns: | int | | Method signature: | int leastTPCable(String[] design, String[] connections, int hubs) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | Not all hubs at your disposal need to be used, see example 3. |
| - | The coordinates in connections are not necessarily unique, see example 2. |
| |
Constraints |
| - | design will contain between 4 and 50 elements, inclusive. |
| - | connections will contain between 3 and 50 elements, inclusive. |
| - | Each element in design and connections will be in the format "<x> <y>". |
| - | The elements in design will be unique. |
| - | design will describe a simple polygon containing only horizontal and vertical lines. No lines in the polygon will intersect or overlap other lines. |
| - | All coordinates in connections will be on a line in the polygon describing the apartment. |
| - | Each <x> and <y> in design and connections will be an integer between 0 and 1000, inclusive, and will not contain any leading zeros. |
| - | hubs will be between 1 and 20, inclusive. |
| |
Examples |
| 0) | |
| | {"1 1","6 1","6 5","7 5","7 1","12 1","12 5","8 5",
"8 6","10 6","10 8","8 8","8 9","10 9","10 11",
"6 11","6 7","5 7","5 11","1 11","1 6","5 6","5 5","1 5"} | {"4 6","1 4","3 1","11 1","10 10","2 11"} | 2 |
| Returns: 66 | | This is the example in the picture. Hubs have been placed at "1 4" and "2 11".
|
|
|
| 1) | |
| | {"1 1","6 1","6 5","7 5","7 1","12 1","12 5","8 5",
"8 6","10 6","10 8","8 8","8 9","10 9","10 11",
"6 11","6 7","5 7","5 11","1 11","1 6","5 6","5 5","1 5"} | {"4 6","1 4","3 1","11 1","10 10","2 11"} | 3 |
| Returns: 59 | | Same as above, except that we now have three hubs at our disposal. Even though we don't need three hubs, using them all decreases the cable length a bit. The hubs should be placed at "1 4", "2 11" and "4 6".
|
|
|
| 2) | |
| | {"0 0","1 0","1 1000","0 1000"} | {"0 500","1 500","0 500","1 500"} | 1 |
| Returns: 2002 | | No matter where the hub is placed along the wall, the same amount of cable is needed. Note that the distance between "0 500" and "1 500" is 1001 and not 1, since the cable must go around the whole wall.
|
|
|
| 3) | |
| | {"0 0","0 10","10 10","10 0"} | {"0 0","0 10","10 10","10 0","0 0","0 10","10 10","10 0"} | 15 |
| Returns: 30 | | Only 4 of the 15 hubs are needed to get the optimal solution. |
|
|
| 4) | |
| | {"0 0","0 10","10 10","10 0"} | {"5 0","5 0","5 0","5 0","5 0","5 0","5 0"} | 1 |
| Returns: -1 | |
|
