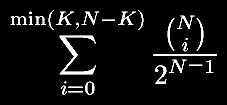TopCoder problem "LargeSignTest" used in SRM 231 (Division I Level Two)

Problem Statement
	A sign test is a test that is performed to determine if the results of an experiment are statistically significant. In particular, it looks at a number of similar trials, where each trial's outcome is either positive or negative. It calculates the probability that the results of your experiments would be at least as unbalanced as they actually turned out to be if the outcomes of each trial were totally random - a 50% chance of being positive and a 50% chance of being negative. For example, the probability of the five trials being split 4-1 or 5-0 is 12/32: 2 out of 32 times the results will be 5 negatives or 5 positives and 10 out of 32 times the results will have 4 negatives or 4 positives. Hence, the p-value of an outcome with 4 positives and 1 negative is 12/32 = 0.375. 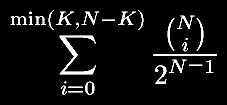To make this more concrete, the p-value of N trials, K of which are negative can be calculated as where the numerator of the fraction is the binomial coefficient: N!/(i!(N-i)!). There is one exception to this though: when K*2 is equal to N, the p-value is simply 1 (the above equation gives the wrong result). This is all quite simple, when N and K are small, but what if they are rather large? Your task is to compute the p-value, given N and K, where 0<=K<=N<=1,000,000 and 0<N. You should return this value as a percentage with exactly one digit after the decimal point (don't forget the percent sign). You should use standard rounding when formatting your return. You need not worry about borderline cases as the constraints ensure that the percentage will not be within 1e-3 of XX.X5, where each X represents a digit.
Definition
	Class: LargeSignTest Method: pvalue Parameters: int, int Returns: String Method signature: String pvalue(int N, int K) (be sure your method is public)
Constraints
-	N will be between 1 and 1,000,000, inclusive.
-	K will be between 0 and N, inclusive.
-	The percentage will not be within 1e-3 of XX.X5, where each X represents a digit.
Examples
0)
	5 4 Returns: "37.5%" The p-value in this case is (choose(5,0)+choose(5,1))/2N-1 = (1+5)/16 = 6/16 = 3/8 = 37.5%
1)
	10 5 Returns: "100.0%"
2)
	1000000 400000 Returns: "0.0%"
3)
	20 5 Returns: "4.1%"

Problem url:

Problem stats url:

Writer:

Testers:

Problem categories: