Problem Statement |
| |
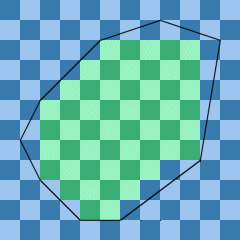
A convex polygon is placed on a large checkerboard with the polygon vertices lying on the grid intersections.
Calculate the number of light and dark squares lying entirely inside the polygon. Assume that the polygon
edges are infinitely thin. In the picture below, 28 light squares and 26 dark squares are enclosed by the polygon.
The upper left corner (coordinates 0,0) will always be a dark square.
Create a class CheckerPolygon containing the method countSquares which takes two int[],
X and Y, describing the convex polygon. Element i in X and Y is the coordinate
for the ith vertex in the polygon. The method should return a int[] containing
exactly two elements: the first element is the number of light squares entirely enclosed by the polygon, and
the second element the number of dark squares entirely enclosed by the polygon.
|
| |
Definition |
| | | Class: | CheckerPolygon | | Method: | countSquares | | Parameters: | int[], int[] | | Returns: | int[] | | Method signature: | int[] countSquares(int[] X, int[] Y) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The vertices in the polygon may be ordered clockwise or counter-clockwise. |
| |
Constraints |
| - | X and Y will contain between 3 and 50 elements, inclusive. |
| - | X will contain the same number of elements as Y. |
| - | Each element in X and Y will be between 0 and 10000, inclusive. |
| - | The polygon described by X and Y will be convex. |
| - | There will not be three points lying on the same line. |
| |
Examples |
| 0) | |
| | {1,2,5,8,11,10,6,4,2} | {7,5,2,1,2,8,11,11,9} |
| Returns: {26, 28} | | This is the example in the problem statement.
|
|
|
| 1) | |
| | {1,5000,5001,10000,10000,5001,5000,1} | {4999,0,0,4999,5000,9999,9999,5000} |
| Returns: {25000000, 24990001} | |
|
| 2) | |
| | |
| 3) | |
| | {537,127,987,2390} | {173,98,12,107} |
| Returns: {90908, 90911} | |
|
