|
We are given a disc of radius discRadius and want to cover it using
numDiscs small discs - i.e., place the small discs flat above the original
disc in such a way that no point of the original disc is visible (assuming
the small discs are opaque). All smaller discs we use for the covering
have the same radius.
We perform the covering using the following procedure:
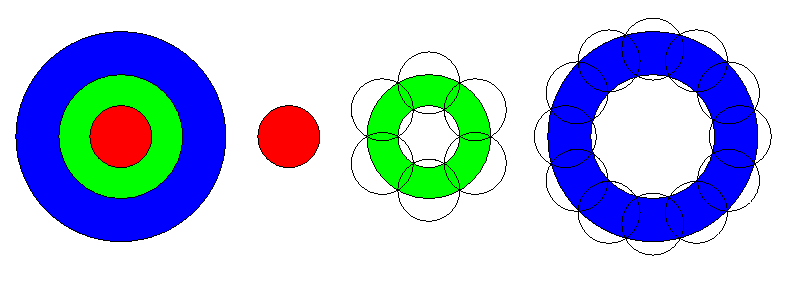
- In the first step, we split the disc into several rings using concentric
circles (with the same center as the original disc). Note that the innermost
"ring" will have an inner radius 0, and thus will actually be a
disc. We are free to split the disc into as many rings and at
whatever positions we want (i.e., use circles of arbitrary radii). The example
below shows a disc split into three rings (blue, green and red).
- In the second step, we regard each of the rings independently, and try to
cover each of them using some number of the small discs. We can either
use one small disc, which has to be centered at the center of the original
disc, or use three or more discs, whose centers must be the vertices of a
regular polygon centered at the center of the original disc. The example
below shows one such case: The innermost ring (red, actually a disc) is
covered by one small disc (which has the same radius as the red disc),
the green ring is covered by 6 small discs centered at the vertices of
a regular hexagon around the center, and the outermost blue ring
is covered by 12 small discs centered at the vertices of a regular 12-gon.
Please note that we try to cover each ring totally independently of
the others, i.e., ignore that parts in one ring may have been covered
already by the discs used to cover another ring (in the example
below, the discs used to cover the green ring would also cover parts
of the blue and red rings, but we ignore this fact).
In summary, we have the freedom to choose the number and size of the rings
that the original disc is split into, how many of the numDiscs discs are
used for covering each of the rings, and the distance from the center at
which the small discs for each ring are placed. We will have to choose these
parameters such that a covering using this procedure is possible using
the smallest possible discs.
Given discRadius, the radius of the original disc, and numDiscs,
the total number of small discs to use, return the minimum radius that
the small discs must have so that a covering using the above procedure
is possible.
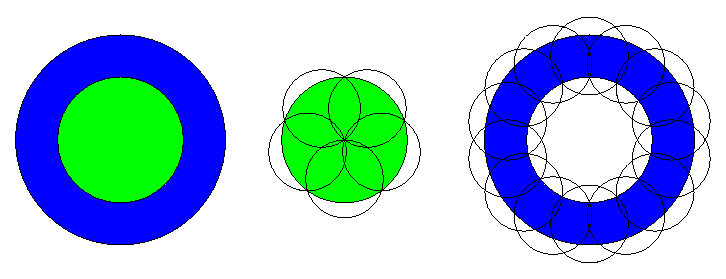
The example shown above is only one possibility to cover the original
disc using 19 small discs (which turns out to be the optimal one for
the used procedure). The figure below shows as an example another
(non-optimal) possibility: here, the original disc is split only into
two rings, and 5 of the small discs are used to cover the inner (green)
ring, the other 14 small discs are used to cover the outer (blue) ring.
It is clear here that too much space is wasted in the outer ring (that
ring was chosen too narrow), so this can not be an optimal solution.
|