|
NOTE: This problem statement contains an image that may not display properly if viewed outside of the applet.
You will be given the map of a maze, with exactly two openings on the boundary.
Your task is to add mirrors to the maze in such an arrangement that if a laser is shined through one opening in the boundary, it will exit through the other opening.
Your method should return the least number of mirrors necessary to be added in order to accomplish this.
If no solution is possible, return -1.
The maze will consist of walls ('#'), open spaces ('.'), and mirrors ('/' and '`')
arranged on a regular grid.
The laser may only travel though open spaces and reflect off of mirrors.
If it hits a wall, the light will be absorbed.
You may only place mirrors on open spaces.
Mirrors are always at a 45-degree angle to the axes of the maze, and deflect the laser at a right angle.
For example, given the following maze:
#######
##....#
##.##.#
##.##.#
......#
##.####
##.####
There are three arrangements of mirrors that will deflect the laser from one opening in the boundary to
the other:
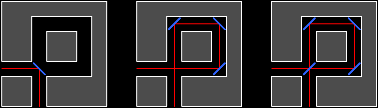
These three solutions require 1, 3, and 4 mirrors, respectively. The least number of mirrors needed is
1, so 1 is the correct answer.
The map may have mirrors already placed, which you may use but cannot move. For example, given the following map:
#######
##....#
##.##.#
##.##.#
../...#
##.####
##.####
there is only one solution (the third arrangement in the figure above).
Three more mirrors must be added, so the correct answer in this case is 3.
| 