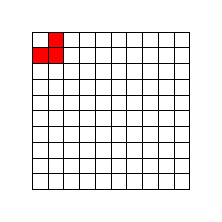
You are given a rectangular board consisting of width times height small squares. Return the number of different ways there are to cut a k-polyomino out of this board, so that the remaining part remains connected.
A k-polyomino is a connected set of k squares. The figure below shows as an example all possible pentominoes (5-polyominoes) ignoring any translations, rotations or reflections.
Connected means side-connected here (both in the polyomino definition and in the requirement for the remaining part of the board) - i.e., you must be able to go from any square to any other by only going through squares and square-sides but not square-corners.

For two ways of cutting a polyomino out of the grid to be different and be counted separately it suffices if at least one grid square is included in the first polyomino but not in the other.
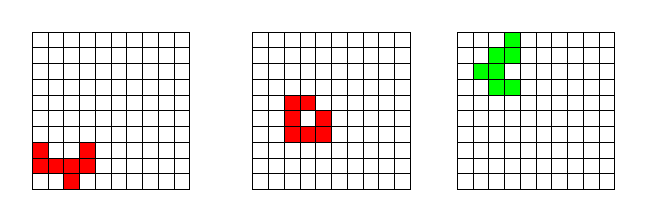
The example below shows some polyomino cuts for k=7. The two on the left (red) are not counted, since they leave the remaining grid disconnected, while the one on the right (green) is counted.
|