Problem Statement |
| | You are given two polygons, described by two String[]s polygon1 and polygon2. The elements of polygonx (x=1 or 2) consist of two space separated integers describing the coordinates of the vertices of polygon x in counterclockwise order.
Both polygons will be convex and have non-zero areas. Furthermore the two polygons will be such that a vertex of one polygon won't lie on the sides of the other.
Return the area of the overlap of the two polygons.
|
| |
Definition |
| | | Class: | ConvexPolygons | | Method: | overlap | | Parameters: | String[], String[] | | Returns: | double | | Method signature: | double overlap(String[] polygon1, String[] polygon2) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | A polygon being convex means: every straight line joining any two interior points of the polygon is entirely contained in the interior of the polygon. |
| - | A return value with either an absolute or relative error of less than 1e-9 is considered correct. |
| |
Constraints |
| - | polygon1 and polygon2 each have between 3 and 50 elements, inclusive. |
| - | Each element of polygon1 and polygon2 has length between 1 and 50, inclusive. |
| - | Each element of polygon1 and polygon2 consists of two space separated integers with values between -1000 and 1000, inclusive. |
| - | Both polygons will be convex and have non-zero areas. |
| - | Both polygons will be such that a vertex of one polygon won't lie on the sides of the other. |
| - | The points described by polygon1 and polygon2 will be in counterclockwise order. |
| |
Examples |
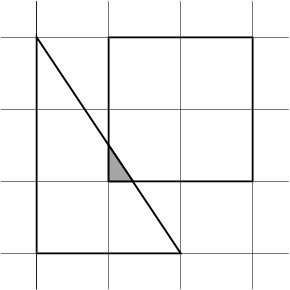
| 0) | |
| | {"00 00","02 00","00 03"} | {"1 1","3 1","3 3", "1 3"} |
| Returns: 0.08333333333333326 | |
|
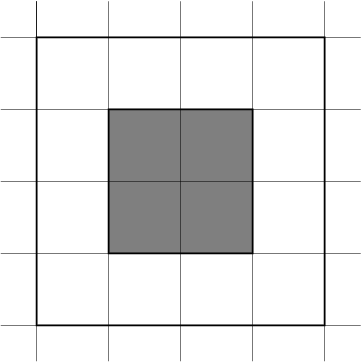
| 1) | |
| | {"-1 -1","1 -1","1 1","-1 1"} | {"-2 -2","0 -2","2 -2","2 0","2 2","0 2","-2 2","-2 0"} |
| Returns: 4.0 | When one polygon encloses the other, the overlap is the area of the smaller one.
|
|
|
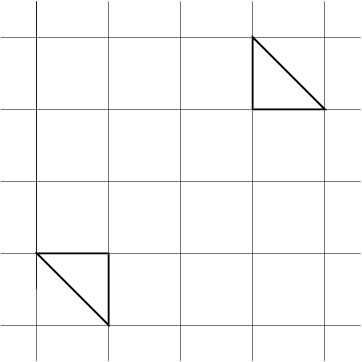
| 2) | |
| | {"-1 -1","-2 -1","-1 -2"} | {"1 1","2 1","1 2"} |
| Returns: 0.0 | They don't overlap.
|
|
|
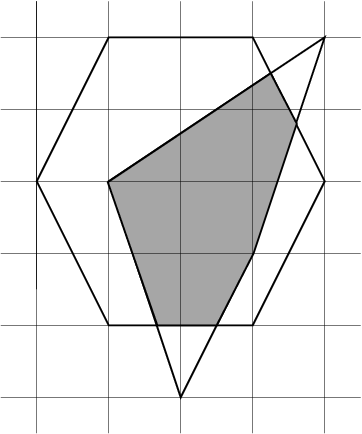
| 3) | |
| | {"-2 0","-1 -2","1 -2","2 0","1 2","-1 2"} | {"0 -3","1 -1","2 2","-1 0"} |
| Returns: 5.233333333333333 | |
|