Problem Statement |
| | NOTE: This problem statement contains an image that may not display properly if viewed outside of the applet.
In a one dimensional mountainous landscape you want to build a watchtower. This watchtower must fulfill one condition: it must be possible to oversee the whole landscape from it. The landscape is described by two int[]s positions and heights. The elements of positions are sorted in strictly ascending order. The height at the i-th element of positions is the i-th element of heights; the intermediate heights are obtained by interpolation.
You are allowed to build the watchtower on the landscape wherever you like. To save expenses, you want to build it at a position such that the necessary height of the watchtower needed to oversee the whole landscape is minimized. Return this minimal height.
|
| |
Definition |
| | | Class: | WatchTower | | Method: | minHeight | | Parameters: | int[], int[] | | Returns: | double | | Method signature: | double minHeight(int[] positions, int[] heights) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | Your return value must have an absolute or relative error less than 1e-9. |
| |
Constraints |
| - | positions and heights each contain between 2 and 50 elements, inclusive. |
| - | positions and heights each contain the same number of elements. |
| - | Each element of positions and heights is between 0 and 1,000,000, inclusive. |
| - | The elements of positions are all distinct and sorted in strictly ascending order. |
| |
Examples |
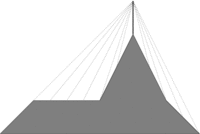
| 0) | |
| | { 1,2,4,5,6,7 } | { 1,2,2,4,2,1 } |
| Returns: 1.0 | Just build the watchtower at the highest point.
|
|
|
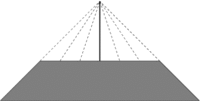
| 1) | |
| | { 10,20,49,59 } | { 0,10,10,0 } |
| Returns: 14.5 | Build the watchtower right in the middle.
|
|
|
| 2) | |
| | { 0,2,4,6,8,10 } | { 0,1,3,6,10,11 } |
| Returns: 0.0 | A zero height watchtower at position 8 can oversee the whole landscape.

|
|
|


