| Suppose you have half of a chessboard as depicted below with 0 or more rooks placed on it. No two rooks can share a row or column.
Beginning with the lower left corner, we travel along the edge of the board. Below, the different positions we move through during this process are numbered.
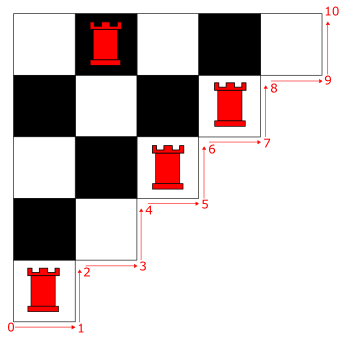
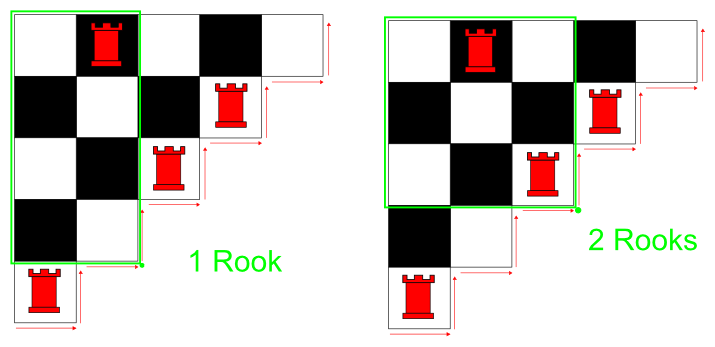
At each corner, we count how many rooks are above and to the left of our position. Examples illustrating how the rooks are counted are given below.
By travelling from position to position we obtain a sequence of integers. For the above board, our sequence would be
0, 1, 0, 1, 1, 2, 1, 2, 1, 1, 0.
In this problem we reverse the process. Instead, you are given the sequence and must return the corresponding half-chessboard.
Given a sequence of 2n+1 integers, you will return a String[] with n elements. Element k (0-based), which corresponds to row k of the board, will contain precisely n-k characters. 'R' should be used to denote a rook and '.' should be used to denote an empty square. If more than one board is possible, choose the one where the rook in row 0 is furthest to the left (if such a rook exists). If multiple boards are still possible, choose the one where the rook in row 1 is furthest to the left, and so forth. If no board is possible, return an empty String[]. The sequence will be given in seqBeg and seqEnd. The elements of seqBeg all come before the elements of seqEnd. For example, if
seqBeg = { 0, 1, 0, 1, 1, 2, 1 }
seqEnd = { 2, 1, 1, 0}
then the resulting 11 element input sequence is the same as featured in the example above. | 
