TopCoder.com Algorithm Problems Searcher

ProductAndSum

Brute Force, Dynamic Programming, Math

Used in:

SRM 500

Used as:

Division I Level Three

Writer:

Chmel_Tolstiy

Testers:

PabloGilberto , ivan_metelsky , Smylic

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11345

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14429&pm=11345

Problem Statement

NOTE: This problem statement contains superscripts that may not display properly if viewed outside of the applet.

A positive integer is called nice if the sum of its digits is equal to S and the product of its digits is equal to 2^p2 * 3^p3 * 5^p5 * 7^p7. Return the sum of all nice integers, modulo 500,500,573.

Definition

Class:	ProductAndSum
Method:	getSum
Parameters:	int, int, int, int, int
Returns:	int
Method signature:	int getSum(int p2, int p3, int p5, int p7, int S)
(be sure your method is public)

Constraints

-

p2, p3, p5 and p7 will each be between 0 and 100, inclusive.

-

S will be between 1 and 2,500, inclusive.

Examples

0)

Returns: 26

There are two nice integers: 22 and 4. Their sum is 26.

1)

Returns: 110109965

A single nice integer is 1,111,111,111.

2)

Returns: 610

41 + 14 + 221 + 212 + 122 = 610.

3)

Returns: 0

There are no nice integers in this case.

4)

Returns: 61610122

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FractalPicture

Brute Force, Geometry, Recursion, Simple Math, Simulation

Used in:

SRM 500

Used as:

Division I Level Two

Writer:

Chmel_Tolstiy

Testers:

PabloGilberto , ivan_metelsky , Smylic

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11344

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14429&pm=11344

Problem Statement

Nick likes to draw fractals. For the special occasion of Single Round Match 500, he decided to draw the 500th generation of his favorite fractal.

Each generation of the fractal can be described as a set of segments on the plane. Some of these segments are called final and all other are considered to be non-final. In each non-final segment, one of its endpoints is chosen and called the root of this segment. In pictures below, solid and dotted lines are used to represent final and non-final segments, correspondingly.

The first generation consists of one segment with endpoints (0, 0) and (0, 81). This segment is non-final and its root is (0, 0).

The i-th generation, i >= 2, is produced from the (i-1)-th generation as follows. All final segments from the (i-1)-th generation are included into the i-th generation without any changes. For each non-final segment from the (i-1)-th generation, let A and B be its endpoints, with A being its root. The following steps are then done:

The point C is drawn on the segment AB so that the length of segment AC is twice as large as the length of segment BC.
Segment CD is drawn as the rotation of segment CB around point C by 90 degrees clockwise.
Segment CE is drawn as the rotation of segment CB around point C by 90 degress counter-clockwise.
Segment AC is included in the i-th generation as a final segment.
Segments CB, CD and CE are included in the i-th generation as non-final segments. The root of each of these three segments is point C.

The second and third generations of this fractal are shown on the picture below.

Consider a rectangle R on the plane that consists of points (x, y), such that x1 <= x <= x2 and y1 <= y <= y2. Let S be the set of all segments of the 500-th generation of the fractal described above (both final and non-final ones). Return the total length of all parts of segments from S that belong to rectangle R.

Definition

Class:	FractalPicture
Method:	getLength
Parameters:	int, int, int, int
Returns:	double
Method signature:	double getLength(int x1, int y1, int x2, int y2)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

x1 will be between -100 and 100, inclusive.

-

x2 will be between x1+1 and 100, inclusive.

-

y1 will be between -100 and 100, inclusive.

-

y2 will be between y1+1 and 100, inclusive.

Examples

0)

-1

Returns: 53.0

Only one part of fractal segments belongs to this rectangle: (0, 0) - (0, 53).

1)

Returns: 0.0

No parts of fractal segments belong to this rectangle.

2)

-10

Returns: 21.0

Two parts of fractal segments belong to this rectangle: (-10, 54) - (10, 54) and (0, 54) - (0, 55). Note that parts that lie on the rectangle's border also belong to the rectangle.

3)

Returns: 2999.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GeometricProgressions

Math, Simulation

Used in:

SRM 500

Used as:

Division II Level Three

Writer:

Chmel_Tolstiy

Testers:

PabloGilberto , ivan_metelsky , Smylic

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11343

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14429&pm=11343

Problem Statement

NOTE: This problem statement contains superscripts that may not display properly if viewed outside of the applet.

You are given two geometric progressions S1 = (b1*q1ⁱ, 0 <= i <= n1-1) and S2 = (b2*q2ⁱ, 0 <= i <= n2-1). Return the number of distinct integers that belong to at least one of these progressions.

Definition

Class:	GeometricProgressions
Method:	count
Parameters:	int, int, int, int, int, int
Returns:	int
Method signature:	int count(int b1, int q1, int n1, int b2, int q2, int n2)
(be sure your method is public)

Constraints

-

b1 and b2 will each be between 0 and 500,000,000, inclusive.

-

q1 and q2 will each be between 0 and 500,000,000, inclusive.

-

n1 and n2 will each be between 1 and 100,500, inclusive.

Examples

0)

Returns: 6

The progressions in this case are (3, 6, 12, 24, 48) and (6, 12, 24, 48, 96). There are 6 integers that belong to at least one of them: 3, 6, 12, 24, 48 and 96.

1)

Returns: 9

This time the progressions are (3, 6, 12, 24, 48) and (2, 6, 18, 54, 162). Each of them contains 5 elements, but integer 6 belongs to both progressions, so the answer is 5 + 5 - 1 = 9.

2)

Returns: 2

The progressions are (1) and (0).

3)

Returns: 100500

Each element of the second progression belongs to the first progression as well.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ColorfulRabbits

Simple Math

Used in:

SRM 499

Used as:

Division I Level One , Division II Level Two

Writer:

lyrically

Testers:

PabloGilberto , ivan_metelsky , nika

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11327

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14428&pm=11327

Problem Statement

Cat Pochi visited a town of rabbits and asked some of the rabbits the following question: "How many rabbits in this town other than yourself have the same color as you?". The rabbits all replied truthfully, and no rabbit was asked the question more than once. You are given the rabbits' replies in the int[] replies. Return the minimum possible number of rabbits in this town.

Definition

Class:	ColorfulRabbits
Method:	getMinimum
Parameters:	int[]
Returns:	int
Method signature:	int getMinimum(int[] replies)
(be sure your method is public)

Constraints

-

replies will contain between 1 and 50 elements, inclusive.

-

Each element of replies will be between 0 and 1,000,000, inclusive.

Examples

0)

{ 1, 1, 2, 2 }

Returns: 5

If there are 2 rabbits with a color and 3 rabbits with another color, Pochi can get this set of replies.

1)

{ 0 }

Returns: 1

A poor lonely rabbit.

2)

{ 2, 2, 44, 2, 2, 2, 444, 2, 2 }

Returns: 499

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OneDimensionalBalls

Graph Theory, Simple Math, Simple Search, Iteration

Used in:

SRM 496

Used as:

Division I Level Two

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11318

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14425&pm=11318

Problem Statement

There is an infinite axis with N balls on it. The balls are moving with equal positive velocity, some of them in the positive direction of the axis and some in the opposite. The balls are small enough to be treated as points on the axis. If two balls meet at a point, they do not collide, and instead, they each continue moving in the same direction and at the same speed as before.

Manao is shown a picture of the axis taken at some moment of time. All the balls are at different points in the picture. The balls are numbered from 0 to N-1 and the i-th ball is at point firstPicture[i].

Some time after the first picture is taken, several balls are added to the axis and another picture is taken. Yet again, no two balls share a point in this picture. The balls seem indistinguishable and their coordinates are given in int[] secondPicture in ascending order.

For each ball in the second picture, Manao has to guess whether it is present on the first one as well, and if so, say its number. Sometimes, this can't be determined unambiguously, so any valid guess is welcome. A guess is valid if the balls could move in the way described above and appear in the named locations in the second picture. Two guesses are different if there is a ball in the second picture which Manao identifies differently in these guesses. Return the number of valid guesses for the given pictures.

Definition

Class:	OneDimensionalBalls
Method:	countValidGuesses
Parameters:	int[], int[]
Returns:	long
Method signature:	long countValidGuesses(int[] firstPicture, int[] secondPicture)
(be sure your method is public)

Constraints

-

firstPicture will contain N elements, where N is between 1 and 50, inclusive.

-

Each element of firstPicture will be between 0 and 100,000,000, inclusive.

-

Elements in firstPicture will be distinct.

-

secondPicture will contain between N and 50 elements, inclusive.

-

Each element of secondPicture will be between 0 and 100,000,000, inclusive.

-

Elements in secondPicture will be in strictly ascending order.

Examples

0)

{12,11}

{10,11,13}

Returns: 3

There are 2 balls in the first picture at points 12 and 11, respectively. One more ball is added in the second picture. The following three guesses are valid:

1) The ball at point 10 is ball 0, the ball at point 11 is the new one, the ball at point 13 is ball 1.

2) The ball at point 10 is ball 1, the ball at point 11 is ball 0, the ball at point 13 is the new one.

3) The ball at point 10 is ball 1, the ball at point 11 is the new one, the ball at point 13 is ball 0.

1)

{1,2,3}

{1,2,3}

Returns: 0

Each picture contains the same number of balls, so they must contain the same set of balls. However, given that some time has passed between the shots, and the balls move with equal positive velocity, there is no way for them to have interchanged positions.

2)

{1,3}

{1,3}

Returns: 1

If the balls move in opposite directions, they will interchange their positions at some moment.

3)

{7234}

{6316,689156,689160,689161,800000,1000001}

Returns: 6

Ball 0 could be any of the balls in the second picture.

4)

{6,2,4}

{1,2,3,4,5,7,8}

Returns: 7

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AdditionGame

Greedy, Simple Math, Simple Search, Iteration

Used in:

SRM 498

Used as:

Division II Level One

Writer:

ir5

Testers:

PabloGilberto , ivan_metelsky , sl2 , pieguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11317

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14427&pm=11317

Problem Statement

Fox Ciel is playing a game called Addition Game.

Three numbers A, B and C are written on a blackboard, and Ciel initially has 0 points. She repeats the following operation exactly N times: She chooses one of the three numbers on the blackboard. Let X be the chosen number. She gains X points, and if X >= 1, the number X on the blackboard becomes X-1. Otherwise, the number does not change.

Return the maximum number of points she can gain if she plays optimally.

Definition

Class:	AdditionGame
Method:	getMaximumPoints
Parameters:	int, int, int, int
Returns:	int
Method signature:	int getMaximumPoints(int A, int B, int C, int N)
(be sure your method is public)

Constraints

-

A, B and C will each be between 1 and 50, inclusive.

-

N will be between 1 and 150, inclusive.

Examples

0)

Returns: 13

The three numbers written on the blackboard are (3, 4, 5). One possible optimal strategy is as follows:

Ciel chooses 5. She gains 5 points, and the numbers become (3, 4, 4).
Ciel chooses 4. She gains 4 points, and the numbers become (3, 3, 4).
Ciel chooses 4. She gains 4 points, and the numbers become (3, 3, 3).

She gains a total of 5+4+4=13 points.

1)

Returns: 3

One optimal strategy is to choose a 1 in each of the first three turns, for a total of 3 points. The numbers then become (0, 0, 0). After that, she won't be able to gain any more points.

2)

Returns: 1140

The only optimal strategy is to choose the following numbers: 48, 47, 46, ..., 11, 10, 9.

3)

Returns: 446

4)

Returns: 57

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FoxStones

Math

Used in:

SRM 498

Used as:

Division I Level Two

Writer:

ir5

Testers:

PabloGilberto , ivan_metelsky , pieguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11316

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14427&pm=11316

Problem Statement

Fox Ciel has a rectangular board separated into 1x1 cells. The board is N cells wide and M cells high. Columns are numbered 1 to N from left to right, and rows are numbered 1 to M from top to bottom. A cell in column x, row y is said to have coordinates (x, y). Each cell contains a stone, and all stones are different. Also, some cells are marked. These marked cells are given in the int[]s sx and sy, where (sx[i], sy[i]) are the coordinates of the i-th marked cell.

Ciel is interested to know how many layouts of the same stones on this board are similar to the current layout. Two layouts are considered to be similar if, for each possible pairing of a stone and a marked cell, the distance between the stone and the marked cell is the same in both layouts. The distance between cells with coordinates (xA, yA) and (xB, yB) is defined as max{|xA-xB|, |yA-yB|}, where |z| is the absolute value of z.

Return the number of layouts that are similar to the current layout, modulo 1,000,000,009. Note that according to the definition above, the current layout is similar to itself, so it should also be counted.

Definition

Class:	FoxStones
Method:	getCount
Parameters:	int, int, int[], int[]
Returns:	int
Method signature:	int getCount(int N, int M, int[] sx, int[] sy)
(be sure your method is public)

Constraints

-

N and M will each be between 1 and 200, inclusive.

-

sx and sy will each contain between 1 and 50 elements, inclusive.

-

sx and sy will contain the same number of elements.

-

Each element of sx will be between 1 and N, inclusive.

-

Each element of sy will be between 1 and M, inclusive.

-

No two cells represented by sx and sy will have the same coordinates.

Examples

0)

{3}

{1}

Returns: 4

There are 4 similar layouts:

1)

{2}

{1}

Returns: 6

2)

{1,2,3}

{1,2,3}

Returns: 8

3)

{5,6,7,8,9,10}

{11,12,13,14,15,16}

Returns: 410850247

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AlternatingLane

Dynamic Programming, Math

Used in:

Member SRM 494

Used as:

Division I Level Two , Division II Level Three

Writer:

ivan_metelsky

Testers:

eleusive , gojira_tc

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11309

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14423&pm=11309

Problem Statement

Mr. Green owns a beautiful park full of trees. Recently, he arranged a new lane in the park and planted N trees along the lane. The trees are numbered from 0 to N-1 in the order that they occur along the lane. It is known that once the i-th tree grows up, its height in meters will be a random integer uniformly distributed between low[i] and high[i], inclusive.

Mr. Green has quite a strange conception about beauty. In particular, he is very fond of so called alternating sequences of integers, which are defined by the following rules:

Every sequence of 1 integer is alternating.
A sequence of 2 integers (A, B) is alternating if and only if A is not equal to B.
A sequence of 3 integers (A, B, C) is alternating if and only if (A C) or (A > B and B < C).
A sequence of L, L > 3, integers (A[0], A[1], ..., A[L-1]) is alternating if and only if each triple of consecutive integers in the sequence form an alternating sequence. In other words, each of the sequences (A[0], A[1], A[2]), (A[1], A[2], A[3]), ..., (A[L-3], A[L-2], A[L-1]) must be alternating.

Mr. Green measures the beauty of an alternating sequence as the sum of absolute differences between all pairs of its consecutive elements. In other words, for a sequence (A[0], A[1], ..., A[L-1]), its beauty is equal to |A[0] - A[1]| + |A[1] - A[2]| + ... + |A[L-2] - A[L-1]|. Note that the beauty of a sequence consisting of 1 element is equal to 0.

Once all the trees grow up, Mr. Green will write down their heights in the order that they occur along the lane. If the resulted sequence of integers is alternating, then he will be satisfied with the resulting lane. Otherwise, he will cut some trees down so that the sequence formed by the remaining trees is alternating. If there are several ways to obtain an alternating sequence, he will choose a way among them that results in a sequence with maximum possible beauty.

Return the expected value of the beauty of the resulting sequence.

Definition

Class:	AlternatingLane
Method:	expectedBeauty
Parameters:	int[], int[]
Returns:	double
Method signature:	double expectedBeauty(int[] low, int[] high)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

low will contain between 1 and 50 elements, inclusive.

-

high will contain the same number of elements as low.

-

Each element of low and high will be between 1 and 100,000, inclusive.

-

For each valid index i, low[i] will be less than or equal to high[i].

Examples

0)

{1}

{100}

Returns: 0.0

Here we have only 1 tree, so the beauty of the resulting sequence will be 0.

1)

{1, 1, 1}

{2, 2, 2}

Returns: 1.0

Once all the trees grow up, 8 different lanes are possible with equal probability. In cases (1, 1, 1) and (2, 2, 2), Mr. Green will cut 2 trees and the beauty will be 0. In cases (1, 1, 2), (2, 2, 1), (1, 2, 2), (2, 1, 1), he will cut the middle tree and the beauty will be 1. Finally, in cases (1, 2, 1) and (2, 1, 2), he won't cut any trees and the beauty will be 2. Therefore, the answer is (4/8) * 1 + (2/8) * 2 = 1.

2)

{1, 3, 5, 7, 9}

{2, 4, 6, 8, 10}

Returns: 8.0

Here, Mr. Green will always leave only the first and the last trees.

3)

{4, 3, 3, 7}

{10, 7, 7, 7}

Returns: 6.171428571428572

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StrangeElevator

Dynamic Programming, Math

Used in:

SRM 495

Used as:

Division I Level Three

Writer:

rng_58

Testers:

PabloGilberto , ivan_metelsky , soul-net

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11305

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14424&pm=11305

Problem Statement

When cat Taro went to an internship, he found a strange elevator in the office's skyscraper. The skyscraper contains 58 floors. The elevator is composed of 2 boxes and these 2 boxes move together. When the lower box stops at the x-th floor, the upper box always stops at the (x+1)-th floor. The lower box stops only on odd floors (1st, 3rd, 5th, ..., 57th). The upper box stops only on even floors (2nd, 4th, 6th, ..., 58th). He is very interested by this elevator, and he wants to compute the number of possible elevators composed of N boxes in a skyscraper of height H.

The elevators must satisfy the following conditions:

For each floor, exactly one box stops at that floor.
The distance between 2 boxes is an integer and never changes. More formally, for each pair of boxes (A,B), there must be some integer d such that box B always stops at the (x+d)-th floor when box A stops at the x-th floor. If the (x+d)-th floor doesn't exist, box A must not stop at the x-th floor.

Two elevators are different if the following is true. When the bottommost box is at the first floor, there exists an i such that a box is at the i-th floor in one elevator and no box is at the i-th floor in the other elevator. You are given two integers H and N. Return the number of possible elevators that have N boxes in a skyscraper of height H, modulo 1,000,000,007.

Definition

Class:	StrangeElevator
Method:	theCount
Parameters:	int, int
Returns:	int
Method signature:	int theCount(int H, int N)
(be sure your method is public)

Constraints

-

H will be between 1 and 1,000,000,000, inclusive.

-

N will be between 1 and H, inclusive.

Examples

0)

Returns: 2

The following two elevators are possible:

When the lower box stops at the 1st, 3rd, ..., 57th floor, the upper box stops at the 2nd, 4th, ..., 58th floor, respectively.
When the lower box stops at the 1st, 2nd, ..., 29th floor, the upper box stops at the 30th, 31st, ..., 58th floor, respectively.

1)

Returns: 1

The only box always stops at the 1st floor.

2)

Returns: 2

The following two elevators are possible:

When the lowest box stops at the 1st, the 4th and the 7th floor, the middle box stops at the 2nd, the 5th and the 8th floor, and the topmost box stops at the 3rd, the 6th and the 9th floor, respectively.
When the lowest box stops at the 1st, the 2nd and the 3rd floor, the middle box stops at the 4th, the 5th and the 6th floor, and the topmost box stops at the 7th, the 8th and the 9th floor, respectively.

3)

Returns: 30

4)

58585858

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HexagonPuzzle

Math

Used in:

SRM 495

Used as:

Division II Level Three

Writer:

rng_58

Testers:

PabloGilberto , ivan_metelsky , soul-net

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11303

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14424&pm=11303

Problem Statement

Cat Taro has a triangle board divided into hexagonal cells. The board contains N rows numbered 0 through N-1 from top to bottom, where the i-th row contains (i+1) hexagonal cells numbered (i,0) through (i,i) from left to right. For example, if N = 4, the board looks like the picture below.

Each cell contains a token. Rabbit Hanako locked some cells so that tokens in those cells can't be moved. You are given a String[] board containing exactly N elements. For all i between 0 and N-1, inclusive, the i-th element of board will contain exactly (i+1) characters. If the j-th character of the i-th element of board is 'X', the cell (i,j) is locked. If the j-th character of the i-th element of board is '.', the cell (i,j) is unlocked.

Cat Taro can perform the following operation an arbitrary number of times: Choose three distinct unlocked cells A, B and C. These three cells must have a common vertex. Move the token in cell A to cell B, the token in cell B to cell C and the token in cell C to cell A.

Return the number of different board states he can achieve by performing operations as described above, modulo 1,000,000,007. Two states are different if there exists at least one token that is placed in a different cell in one state than it is in the other state.

Definition

Class:	HexagonPuzzle
Method:	theCount
Parameters:	String[]
Returns:	int
Method signature:	int theCount(String[] board)
(be sure your method is public)

Constraints

-

board will contain between 1 and 50 elements, inclusive.

-

The i-th (0-indexed) element of board will contain exactly i+1 characters.

-

Each character in board will be '.' or 'X'.

Examples

0)

{".",
 ".X",
 "X..",
 ".X.X"}

Returns: 3

Example from the problem statement.

He can achieve the following three board states.

1)

{"X"}

Returns: 1

Taro can't perform any operation.

2)

{".",
 "..",
 "...",
 ".X.."}

Returns: 20160

3)

{".",
 "..",
 "XXX",
 "..X.",
 ".X..X",
 "XXXX..",
 "..X.X.X",
 "..X.XX.."}

Returns: 108

4)

{".",
 "..",
 "...",
 "....",
 ".....",
 "......",
 ".......",
 "........"}

Returns: 261547992

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PalindromfulString

Brute Force, Recursion, Simple Math

Used in:

SRM 496

Used as:

Division II Level Three

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11296

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14425&pm=11296

Problem Statement

A palindrome is a string that is the same whether it is read from left to right or from right to left.

Consider a string of length N which contains only uppercase letters. Write down all of its contiguous substrings of length M (a separate substring must be written down for each starting position, even if some of these substrings are the same strings). If at least K of the substrings you have written down are palindromes, we call the string palindromful.

Return the number of different palindromful strings of length N.

Definition

Class:	PalindromfulString
Method:	count
Parameters:	int, int, int
Returns:	long
Method signature:	long count(int N, int M, int K)
(be sure your method is public)

Constraints

-

N will be between 2 and 11, inclusive.

-

M will be between 2 and N, inclusive.

-

K will be between 0 and 11, inclusive.

Examples

0)

Returns: 26

For a string of length 2, the only substring of length 2 is the string itself. Therefore, in this case we need to count palindromes of length 2, which are "AA", "BB", ..., "ZZ".

1)

Returns: 676

This time there can be no palindrome among the substrings, so any string of length 2 will do.

2)

Returns: 1326

Either the first two or the last two characters of the string should be equal, with no restrictions on the remaining one. This gives us 2*26*26=1352 variants, of which 26 are strings consisting entirely of the same character and therefore duplicated.

3)

Returns: 676

We're looking for palindromes of length 4.

4)

Returns: 4310176

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StonesGame

Greedy, Simple Math

Used in:

SRM 493

Used as:

Division I Level One , Division II Level Two

Writer:

maksay

Testers:

PabloGilberto , ivan_metelsky , K.A.D.R

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11292

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14422&pm=11292

Problem Statement

Romeo and his friend Strangelet are playing a game. There are N stones in a row, all of which are black except for the M-th one, which is white (all positions in this problem are 1-based). The players alternate turns, and Romeo plays first. On each turn, a player must choose exactly K consecutive stones, one of which must be white, and reverse their order. The winner is the first player who puts the white stone in the L-th position. Return "Romeo" if Romeo can win regardless of how Strangelet plays, and return "Strangelet" if Strangelet can win regardless of Romeo's strategy. Otherwise, return "Draw" since neither player can win if both players play optimally. All quotes are for clarity only.

Definition

Class:	StonesGame
Method:	winner
Parameters:	int, int, int, int
Returns:	String
Method signature:	String winner(int N, int M, int K, int L)
(be sure your method is public)

Constraints

-

N will be between 2 and 1,000,000, inclusive.

-

M, K and L will each be between 1 and N, inclusive.

-

M and L will be different.

Examples

0)

Returns: "Draw"

There are three stones and the stone in position 1 is white. To win the game, a player must put the white stone in position 2. However, since K is 1, each player can only choose a single stone to reverse, so it is impossible to move the white stone from its original position. Therefore, neither player can win.

1)

Returns: "Romeo"

Romeo can win on his first move by reversing the order of the first two stones.

2)

Returns: "Strangelet"

Romeo's only possible move is to reverse the last two stones. This puts the white stone in position 4. Strangelet can then reverse the third and fourth stones, putting the white stone in position 3 and winning the game.

3)

Returns: "Draw"

This is similar to the previous example, but here, the white stone must be moved to position 2. As in the previous example, Romeo's first move will put the white stone in position 4. This time, Strangelet will then move it back to position 5 because otherwise, Romeo would move it to position 2 and win. This sequence of moves will repeat infinitely and neither player will win.

4)

Returns: "Romeo"

5)

Returns: "Strangelet"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FoxMakingDice

Simple Math, Simple Search, Iteration

Used in:

Member SRM 491

Used as:

Division I Level One

Writer:

wrong

Testers:

Rustyoldman , ivan_metelsky , Mimino , rng_58

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11234

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14244&pm=11234

Problem Statement

Fox Jiro likes dice. He wants to make his own dice. Each die he wants to make is a cube. Each of the 6 faces has an integer between 1 and N, inclusive. No two faces have same number. Also the following condition must be satisfied: for all faces, the sum of the numbers on opposite faces must be equal and the sum must be greater than or equal to K.

He realized that there are many ways to make such dice. He wants to know how many ways there are. Please help Jiro to make a program that is given two integers N and K and returns the number of different dice satisfying the condition mentioned above.

Two dice are considered the same if you can rotate one to form the other.

Definition

Class:	FoxMakingDice
Method:	theCount
Parameters:	int, int
Returns:	long
Method signature:	long theCount(int N, int K)
(be sure your method is public)

Notes

-

The answer will always fit in a signed 64-bit integer.

Constraints

-

N will be between 1 and 1,000, inclusive.

-

K will be between 1 and 2,000, inclusive.

Examples

0)

Returns: 2

You can make normal dice. There are two ways to arrange the numbers.

1)

Returns: 0

You cannot make 6 sided dice with 5 numbers.

2)

Returns: 20625666000

3)

Returns: 879075732

4)

Returns: 4506149340

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Starport

Simple Math

Used in:

SRM 490

Used as:

Division I Level One , Division II Level Two

Writer:

Chmel_Tolstiy

Testers:

PabloGilberto , ivan_metelsky , pieguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11227

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14243&pm=11227

Problem Statement

A new starport has just started working. Starting from some moment of time (call it minute 0), a new spaceship arrives at the starport every M minutes. In other words, spaceships arrive at the starport at minutes 0, M, 2*M, 3*M and so on.

Similarly, starting from minute 0 and repeating each N minutes, all arrived spaceships that are still placed at the port are teleported to the shed. If a spaceship arrives at the exact same minute when such a teleportation happens, it will be teleported immediately. Otherwise it will need to wait until the next teleportation happens.

Let the waiting time of a spaceship be the time between its arrival and its teleportation to the shed. Return the average waiting time of a spaceship in minutes. See notes for an exact definition.

Definition

Class:	Starport
Method:	getExpectedTime
Parameters:	int, int
Returns:	double
Method signature:	double getExpectedTime(int N, int M)
(be sure your method is public)

Notes

-

Let W(i) be the waiting time for the spaceship that arrives at minute M * i. The average waiting time can be defined as the limit of (W(0) + W(1) + ... + W(P - 1)) / P when P tends to positive infinity. This limit will always exist.

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

N and M will each be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 1.0

Spaceships arrive at the starport at minutes 0, 2, 4, 6, 8, and so on. Teleportations are done at minutes 0, 4, 8, and so on. The waiting times for the spaceships are, correspondingly, 0, 2, 0, 2, 0, and so on, so the expected waiting time is 1.

1)

Returns: 2.0

2)

Returns: 2.5

3)

Returns: 6170.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FoxJumping

Dynamic Programming, Math

Used in:

SRM 498

Used as:

Division I Level Three

Writer:

ir5

Testers:

PabloGilberto , ivan_metelsky , pieguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11223

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14427&pm=11223

Problem Statement

Fox Ciel likes to jump around in large fields. She is currently at point (0, 0) of a field, and she wants to land at point (Tx, Ty) using exactly R jumps.

In one jump, she can move 0, 1, 2, ..., Mx units in the positive x direction and 0, 1, 2, ..., My units in the positive y direction. All jumps must have a non-zero distance. In addition, there are some jumps which she is not good at. These jumps are described in the int[] bad. If bad contains the number b, it means she cannot make a diagonal jump where she moves exactly b units in the positive x direction and b units in the positive y direction. Each element of bad will be a multiple of 10.

For instance, if Mx=12, My=11, bad={10} and she is at point (0, 0), then the only points she can jump to are the green ones shown below:

Return the number of ways she can start at (0, 0), jump exactly R times, and land at (Tx, Ty), modulo 10,007. Two ways are considered to be different if there is an index i, 0 <= i < R, such that Ciel lands at different points after the i-th (0-based) jump in these ways.

Definition

Class:	FoxJumping
Method:	getCount
Parameters:	int, int, int, int, int, int[]
Returns:	int
Method signature:	int getCount(int Tx, int Ty, int Mx, int My, int R, int[] bad)
(be sure your method is public)

Constraints

-

Tx and Ty will each be between 1 and 800, inclusive.

-

Mx and My will each be between 1 and 800, inclusive.

-

R will be between 1 and 1,600, inclusive.

-

bad will contain between 0 and 50 elements, inclusive.

-

Each element of bad will be between 1 and min(Mx, My), inclusive, and be a multiple of 10.

-

All elements of bad will be distinct.

Examples

0)

{}

Returns: 1

There is only 1 way to reach the destination.

1)

{}

Returns: 6

The following are the 6 ways she can reach her destination. Note that when she jumps, she must move a distance of at least one unit.

2)

{}

Returns: 1

She can jump only once, so there is 1 way to reach the destination.

3)

{10}

Returns: 0

This case is almost the same as the previous one. However, in this case, the required jump is a bad jump, so she cannot reach the destination in a single jump.

4)

{10}

Returns: 140

5)

{30, 40, 20, 10, 50}

Returns: 6723

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AppleTrees

Dynamic Programming, Math

Used in:

Member SRM 489

Used as:

Division I Level Three

Writer:

rng_58

Testers:

liympanda , eleusive , ivan_metelsky , vexorian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11213

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14242&pm=11213

Problem Statement

Rabbit Hanako likes apples. She decided to plant apple trees along a straight road.

The road has D candidate positions for planting apple trees. These positions are numbered 0 through D-1, from left to right. The distance between position x and position y is |x-y| meters (|x-y| denotes the absolute value of x-y). She wants to plant N apple trees numbered from 0 to N-1 in different positions. The trees may be planted in any order. The i-th tree won't grow if there are other trees which are closer than r[i] meters. In other words, if i and j are distinct, the distance between the i-th tree and the j-th tree must be at least max(r[i],r[j]) meters.

Return the number of ways to plant all apple trees modulo 1,000,000,007.

Definition

Class:	AppleTrees
Method:	theCount
Parameters:	int, int[]
Returns:	int
Method signature:	int theCount(int D, int[] r)
(be sure your method is public)

Constraints

-

D will be between 1 and 100,000, inclusive.

-

r will contain between 1 and 40 elements, inclusive.

-

Each element of r will be between 1 and 40, inclusive.

Examples

0)

{40}

Returns: 10

There are 10 candidate positions for the only tree.

1)

{1, 1, 1, 1}

Returns: 24

Trees must be planted in different positions, so the number of ways to plant all trees is 4! = 24.

2)

{1, 1, 2}

Returns: 4

The following 4 ways are possible:

Plant the 0th tree in position 0, the 1st tree in position 1, and the 2nd tree in position 3.
Plant the 0th tree in position 1, the 1st tree in position 0, and the 2nd tree in position 3.
Plant the 0th tree in position 2, the 1st tree in position 3, and the 2nd tree in position 0.
Plant the 0th tree in position 3, the 1st tree in position 2, and the 2nd tree in position 0.

3)

{5, 8}

Returns: 2550

4)

{4, 8, 9}

Returns: 28830

5)

{21, 37, 23, 13, 32, 22, 9, 39}

Returns: 923016564

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DiceRotation

Math

Used in:

Member SRM 489

Used as:

Division I Level Two

Writer:

rng_58

Testers:

liympanda , eleusive , ivan_metelsky , vexorian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11212

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14242&pm=11212

Problem Statement

Cat Taro likes dice. He has a die which is a 1 x 1 x 1 cube where each face contains a number between 1 and 6. Each number appears on exactly one face, and the sum of the numbers on opposite faces is always 7.

There is an infinitely large board which is divided into 1 x 1 cells. The board has a coordinate system in which the x-coordinate (the first coordinate) increases from left to right, while the y-coordinate (the second coordinate) increases from bottom to top. Taro initially places the die on the cell with coordinates (0, 0). The die shows '1' on the top face, '2' on the front face, and '3' on the left face (so the bottom face shows '6', the back face shows '5', and the right face shows '4').

Taro wants to move this die to cell (goalx, goaly) by performing a sequence of rotations. There are two ways to rotate the die:

Rotate toward the right. This operation moves the die from cell (x, y) to cell (x+1, y).
Rotate toward the top. This operation moves the die from cell (x, y) to cell (x, y+1).

For example, if Taro's first rotation is toward the right, then the die will move to cell (1, 0) and the top face will show '3'.

Return the number of sequences of rotations which move the die to cell (goalx, goaly), such that the following conditions are satisfied:

The die must show '1' again on the top face when it reaches (goalx, goaly).
The die must not show '1' on the top face before it reaches (goalx, goaly).

Definition

Class:	DiceRotation
Method:	theCount
Parameters:	int, int
Returns:	int
Method signature:	int theCount(int goalx, int goaly)
(be sure your method is public)

Notes

-

The answer will always fit in a signed 32-bit integer.

Constraints

-

goalx will be between 1 and 1,000,000,000, inclusive.

-

goaly will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 2

There are two ways to move the die to cell (2,2) that satisfy the conditions:

right -> right -> up -> up
up -> up -> right -> right

1)

Returns: 2

2)

Returns: 2

3)

Returns: 2

4)

1000000000

1000000000

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BallsConverter

Math, Simple Search, Iteration

Used in:

Member SRM 489

Used as:

Division I Level One

Writer:

rng_58

Testers:

liympanda , eleusive , ivan_metelsky , vexorian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11211

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14242&pm=11211

Problem Statement

Rabbit Hanako invented a machine called the Balls Converter.

This machine accepts N types of balls. First, Hanako puts some balls into the machine. While the machine contains at least two balls, it chooses two different balls, throws them away, and creates a new ball. The types of the two balls that the machine throws away determine the type of the new ball. If it throws away a type-i ball and a type-j ball, the type of the new ball is described by convert[i][j]. If convert[i][j] is 'A', 'B', ..., 'Z', the type of the new ball is 0, 1, ..., 25, respectively. If convert[i][j] is 'a', 'b', ..., 'x', the type of the new ball is 26, 27, ..., 49, respectively.

If the type of the last ball can be always determined uniquely from the initial configuration of the box (regardless of which balls the machine throws away at each step), it's called a good machine. If the machine is good, return "Good". Otherwise return "Bad".

Definition

Class:	BallsConverter
Method:	theGood
Parameters:	String[]
Returns:	String
Method signature:	String theGood(String[] convert)
(be sure your method is public)

Constraints

-

convert will contain between 1 and 50 elements, inclusive.

-

Each element of convert will contain exactly N characters, where N is the number of elements in convert.

-

convert[i][j] will be equal to convert[j][i] for all valid i and j.

-

Each character in convert will be a letter corresponding to an integer between 0 and N-1, inclusive, where N is the number of elements in convert.

Examples

0)

{"AB", "BA"}

Returns: "Good"

The parity of the number of type-1 ball never changes. If the machine contains even number of type-1 balls at first, the last ball will be type-0. If the machine contains odd number of type-1 balls at first, the last ball will be type-1.

1)

{"BA", "AA"}

Returns: "Bad"

For example, if the machine contains one type-0 ball and two type-1 balls, the type of the last ball can't be uniquely determined. If two type-1 balls are chosen in the first operation, the last ball will be type-1. If one type-0 ball and one type-1 ball are chosen in the first operation, the last ball will be type-0.

2)

{"ACB", "CBA", "BAC"}

Returns: "Bad"

3)

{"AAAA", "ABBB", "ABCC", "ABCD"}

Returns: "Good"

4)

{"AAAAAAAAAAAAAAAAAAAAAAAAAAAAAA",
"ABCDEFGHIJKLMNOPQRSTUVWXYZabcd",
"ACEGIKMOQSUWYacACEGIKMOQSUWYac",
"ADGJMPSVYbADGJMPSVYbADGJMPSVYb",
"AEIMQUYcCGKOSWaAEIMQUYcCGKOSWa",
"AFKPUZAFKPUZAFKPUZAFKPUZAFKPUZ",
"AGMSYAGMSYAGMSYAGMSYAGMSYAGMSY",
"AHOVcFMTaDKRYBIPWdGNUbELSZCJQX",
"AIQYCKSaEMUcGOWAIQYCKSaEMUcGOW",
"AJSbGPYDMVAJSbGPYDMVAJSbGPYDMV",
"AKUAKUAKUAKUAKUAKUAKUAKUAKUAKU",
"ALWDOZGRcJUBMXEPaHSdKVCNYFQbIT",
"AMYGSAMYGSAMYGSAMYGSAMYGSAMYGS",
"ANaJWFSBObKXGTCPcLYHUDQdMZIVER",
"AOcMaKYIWGUESCQAOcMaKYIWGUESCQ",
"APAPAPAPAPAPAPAPAPAPAPAPAPAPAP",
"AQCSEUGWIYKaMcOAQCSEUGWIYKaMcO",
"AREVIZMdQDUHYLcPCTGXKbOBSFWJaN",
"ASGYMASGYMASGYMASGYMASGYMASGYM",
"ATIbQFYNCVKdSHaPEXMBUJcRGZODWL",
"AUKAUKAUKAUKAUKAUKAUKAUKAUKAUK",
"AVMDYPGbSJAVMDYPGbSJAVMDYPGbSJ",
"AWOGcUMEaSKCYQIAWOGcUMEaSKCYQI",
"AXQJCZSLEbUNGdWPIBYRKDaTMFcVOH",
"AYSMGAYSMGAYSMGAYSMGAYSMGAYSMG",
"AZUPKFAZUPKFAZUPKFAZUPKFAZUPKF",
"AaWSOKGCcYUQMIEAaWSOKGCcYUQMIE",
"AbYVSPMJGDAbYVSPMJGDAbYVSPMJGD",
"AcaYWUSQOMKIGECAcaYWUSQOMKIGEC",
"AdcbaZYXWVUTSRQPONMLKJIHGFEDCB"}

Returns: "Good"

5)

{"AAAAAFAAAAAAAAAAAAAAAAAXAAAAcAAAAAAAAAAnAAAAAAAvAA",
"ABBBBFBBBBBLBBBBQBBBBBBXYBBBcBBBBBBBBBBnBBBBBBBvwB",
"ABCCCFCCCCCLMCOCQRCCCCCXYCCCcCCCCCCCCCCnCCCCsCCvwC",
"ABCDEFGHDDDLMDODQRSDUVWXYDDbcdDfghDDklDnopDrsDDvwx",
"ABCEEFEEEEELMEOEQRSEUVWXYEEbcEEfEhEEklEnEpEEsEEvwE",
"FFFFFFFFFFFFFFFFFFFFFFFXFFFFcFFFFFFFFFFFFFFFFFFvFF",
"ABCGEFGGGGGLMGOGQRSGUVWXYGGbcGGfGhGGklGnGpGGsGGvwG",
"ABCHEFGHHHHLMHOHQRSHUVWXYHHbcdHfHhHHklHnHpHHsHHvwH",
"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwx",
"ABCDEFGHJJJLMJOJQRSJUVWXYJJbcdJfghJJklJnopJrsJJvwx",
"ABCDEFGHKJKLMNOPQRSTUVWXYZKbcdefghijklmnopqrsKKvwx",
"ALLLLFLLLLLLLLLLLLLLLLLXLLLLcLLLLLLLLLLnLLLLLLLvwL",
"ABMMMFMMMMMLMMOMQMMMMMMXYMMMcMMMMMMMMMMnMMMMMMMvwM",
"ABCDEFGHNJNLMNOPQRSTUVWXYZNbcdefghijklmnopqrsNNvwx",
"ABOOOFOOOOOLOOOOQOOOOOOXYOOOcOOOOOOOOOOnOOOOOOOvwO",
"ABCDEFGHPJPLMPOPQRSTUVWXYZPbcdPfghiPklmnopPrsPPvwx",
"AQQQQFQQQQQLQQQQQQQQQQQXQQQQcQQQQQQQQQQnQQQQQQQvwQ",
"ABRRRFRRRRRLMRORQRRRRRRXYRRRcRRRRRRRRRRnRRRRRRRvwR",
"ABCSSFSSSSSLMSOSQRSSSSSXYSSScSSSSSSSSSSnSSSSsSSvwS",
"ABCDEFGHTJTLMTOTQRSTUVWXYTTbcdTfghiTklTnopTrsTTvwx",
"ABCUUFUUUUULMUOUQRSUUUWXYUUUcUUUUhUUklUnUUUUsUUvwU",
"ABCVVFVVVVVLMVOVQRSVUVWXYVVbcVVfVhVVklVnVVVVsVVvwV",
"ABCWWFWWWWWLMWOWQRSWWWWXYWWWcWWWWhWWkWWnWWWWsWWvwW",
"XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXvXX",
"AYYYYFYYYYYLYYYYQYYYYYYXYYYYcYYYYYYYYYYnYYYYYYYvwY",
"ABCDEFGHZJZLMZOZQRSTUVWXYZZbcdZfghiZklZnopZrsZZvwx",
"ABCDEFGHaJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwx",
"ABCbbFbbbbbLMbObQRSbUbWXYbbbcbbfbhbbklbnbbbbsbbvwb",
"cccccccccccccccccccccccXcccccccccccccccccccccccvcc",
"ABCdEFGddddLMdOdQRSdUVWXYddbcddfdhddkldndpddsddvwd",
"ABCDEFGHeJeLMeOPQRSTUVWXYZebcdefghijklmnoperseevwx",
"ABCffFfffffLMfOfQRSfUfWXYfffcffffhffklfnffffsffvwf",
"ABCgEFGHgggLMgOgQRSgUVWXYggbcdgfghggklgngpggsggvwg",
"ABChhFhhhhhLMhOhQRShhhhXYhhhchhhhhhhkhhnhhhhshhvwh",
"ABCDEFGHiJiLMiOiQRSiUVWXYiibcdifghiiklinopirsiivwx",
"ABCDEFGHjJjLMjOPQRSTUVWXYZjbcdjfghijklmnopjrsjjvwx",
"ABCkkFkkkkkLMkOkQRSkkkkXYkkkckkkkkkkkkknkkkkskkvwk",
"ABCllFlllllLMlOlQRSlllWXYlllcllllhllkllnllllsllvwl",
"ABCDEFGHmJmLMmOmQRSTUVWXYZmbcdmfghimklmnopmrsmmvwx",
"nnnnnFnnnnnnnnnnnnnnnnnXnnnncnnnnnnnnnnnnnnnnnnvnn",
"ABCoEFGHoooLMoOoQRSoUVWXYoobcdofghooklonoporsoovwx",
"ABCppFpppppLMpOpQRSpUVWXYppbcppfphppklpnpppSsppvwp",
"ABCDEFGHqJqLMqOPQRSTUVWXYZqbcdefghijklmnopqrsqqvwx",
"ABCrEFGHrrrLMrOrQRSrUVWXYrrbcdrfghrrklrnrSrrsrrvwx",
"ABsssFsssssLMsOsQRsssssXYssscssssssssssnsssssssvws",
"ABCDEFGHtJKLMNOPQRSTUVWXYZtbcdefghijklmnopqrsttvwx",
"ABCDEFGHuJKLMNOPQRSTUVWXYZubcdefghijklmnopqrstuvwx",
"vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv",
"AwwwwFwwwwwwwwwwwwwwwwwXwwwwcwwwwwwwwwwnwwwwwwwvww",
"ABCxEFGHxxxLMxOxQRSxUVWXYxxbcdxfghxxklxnxpxxsxxvwx"}

Returns: "Bad"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheBoringGameDivOne

Advanced Math, Brute Force, Dynamic Programming, Encryption/Compression, Geometry, Graph Theory, Greedy, Math, Recursion, Search, Simple Math, Simple Search, Iteration, Simulation, Sorting, String Manipulation, String Parsing

Used in:

SRM 488

Used as:

Division I Level Three

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , ivan_metelsky , nika

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11205

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14241&pm=11205

Problem Statement

John and Brus are very bored. That's why they decided to invite their friend and play a boring shooter game. John and Brus are on the first team and the friend is the only player of the second team. The game consists of X rounds. During a round players may shoot each other, but a player can't shoot himself. If a player shoots some player from the opposite team his score is increased by one and if he shoots his teammate his score is decreased by one. Once a player is shot, he can't shoot other players and other players can't shoot him until the end of the current round. A round ends when all the players on one of the teams are shot.

You are given six integers. scoreJ, scoreB and scoreF are scores of John, Brus and the friend respectively. killedJ, killedB and killedF are the number of times John, Brus and the friend were shot respectively. Return the int[] containing exactly two elements, where the first element is the smallest possible value of X and the second element is the largest possible value of X. If there are no possible values of X, return an empty int[].

Definition

Class:	TheBoringGameDivOne
Method:	find
Parameters:	int, int, int, int, int, int
Returns:	int[]
Method signature:	int[] find(int scoreJ, int killedJ, int scoreB, int killedB, int scoreF, int killedF)
(be sure your method is public)

Constraints

-

scoreJ will be between -1000 and 1000, inclusive.

-

scoreB will be between -1000 and 1000, inclusive.

-

scoreF will be between -1000 and 1000, inclusive.

-

killedJ will be between 0 and 1000, inclusive.

-

killedB will be between 0 and 1000, inclusive.

-

killedF will be between 0 and 1000, inclusive.

Examples

0)

Returns: {2, 3 }

The possible scenario with two rounds is: friend kills John, Brus kills friend, round ends, friend kills Brus, John kills friend, round ends. And with three rounds - John kills friend, round ends, Brus kills friend, round ends, friend kills John, friend kills Brus, round ends.

1)

Returns: {0, 0 }

No rounds here.

2)

-2

Returns: { }

This is impossible.

3)

-1

Returns: {8, 9 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheBoredomDivTwo

Advanced Math, Encryption/Compression

Used in:

SRM 488

Used as:

Division II Level One

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , ivan_metelsky , nika

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11194

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14241&pm=11194

Problem Statement

John and Brus are bored. They have n+m common friends. The first n of them are bored and other m are not. John chooses the j-th (1-based) friend for a talk. If the friend is not bored, he becomes bored after the talk. Brus does the same with the b-th (1-based) friend. Note that John and Brus can't choose the same friend.

You have to find the number of bored friends after the talks.

Definition

Class:	TheBoredomDivTwo
Method:	find
Parameters:	int, int, int, int
Returns:	int
Method signature:	int find(int n, int m, int j, int b)
(be sure your method is public)

Constraints

-

n will be between 1 and 47, inclusive.

-

m will be between 1 and 47, inclusive.

-

j will be between 1 and n+m, inclusive.

-

b will be between 1 and n+m, inclusive.

-

j and b will be different.

Examples

0)

Returns: 2

The first friend is already bored and the second friend becomes bored after the talk with Brus.

1)

Returns: 2

Here John and Brus choose two friends that are already bored.

2)

Returns: 3

All the friends become bored.

3)

Returns: 5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheBoredomDivOne

Simple Math, Simple Search, Iteration

Used in:

SRM 488

Used as:

Division I Level One

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , ivan_metelsky , nika

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11193

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14241&pm=11193

Problem Statement

John and Brus are bored. They have n+m common friends. n of them are bored and m are not. Every hour John and Brus randomly choose two different friends A and B. If there are several possible pairs (A, B), each one has the same probability of being chosen. After that, John has a talk with friend A and Brus has a talk with friend B. For each of two chosen friends, if the friend is not bored, he becomes bored after the talk.

You have to find the expected time for all the friends to become bored.

Definition

Class:	TheBoredomDivOne
Method:	find
Parameters:	int, int
Returns:	double
Method signature:	double find(int n, int m)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

n will be between 1 and 47, inclusive.

-

m will be between 1 and 47, inclusive.

Examples

0)

Returns: 1.0

There are two friends overall. Since John and Brus always choose different friends for a talk, both friends will be bored after one hour.

1)

Returns: 1.5

Here John and Brus can choose two friends that are already bored, so the expectation is more than 1 hour.

2)

Returns: 2.0

3)

Returns: 13.831068977298521

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BuyingFlowers

Brute Force, Search, Simple Math

Used in:

Member SRM 489

Used as:

Division II Level Two

Writer:

fushar

Testers:

liympanda , eleusive , ivan_metelsky , vexorian , rng_58

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11191

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14242&pm=11191

Problem Statement

Teddy loves roses and Tracy loves lilies. They wish to plant these flowers in a large garden.

However, the only florist in town sells these flowers in packets which are represented by int[]s roses and lilies. The i-th packet contains roses[i] roses and lilies[i] lilies. Each packet can be bought only once.

Teddy and Tracy wish to buy some flowers and arrange them into a rectangular grid. This grid must be arranged such that each cell contains exactly one flower, and any two cells which share an edge must contain different kinds of flowers. Additionally, Teddy and Tracy must use all the flowers they buy.

Teddy and Tracy love square-shaped grids, so they wish to buy a set of packets such that they can arrange the flowers into the most square-like grid possible. More precisely, they wish to arrange the flowers into an R x C grid, where R and C are positive integers, such that |R-C| (|R-C| denotes the absolute value of R-C) is minimized. Return this minimum absolute value, or -1 if no valid arrangement exists.

Definition

Class:	BuyingFlowers
Method:	buy
Parameters:	int[], int[]
Returns:	int
Method signature:	int buy(int[] roses, int[] lilies)
(be sure your method is public)

Constraints

-

roses and lilies will contain the same number of elements, between 1 and 16, inclusive.

-

Each element of roses and lilies will be between 0 and 10000, inclusive.

-

The total number of flowers in each packet represented by roses and lilies will be greater than 0.

Examples

0)

{2, 4}

{4, 2}

Returns: 1

Buying all the packets to get 6 roses and 6 lilies, they can create a 3 x 4 grid with the following arrangement:

  RLRL
  LRLR
  RLRL

The difference of the height and the width of this arrangement is 1.

1)

{2, 7, 3}

{3, 4, 1}

Returns: 0

Buying the first and the third packets, they can create the following square arrangement:

  RLR
  LRL
  RLR

2)

{4, 5, 2, 1}

{6, 10, 5, 9}

Returns: -1

No valid grid can be created.

3)

{1, 208, 19, 0, 3, 234, 1, 106, 99, 17}

{58, 30, 3, 5, 0, 997, 9, 615, 77, 5}

Returns: 36

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BunnyComputer

Simple Math, Simple Search, Iteration

Used in:

SRM 487

Used as:

Division I Level One , Division II Level Two

Writer:

lyrically

Testers:

PabloGilberto , ivan_metelsky , soul-net

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11157

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14240&pm=11157

Problem Statement

Bunnies like programming and they often practice for contests.

There is a special computer named B-Computer, which all bunnies are eager to use. All bunnies want to solve a difficult problem using B-Computer. Because they type very fast, each of them wants to solve the problem according to the following process that consists of 3 stages (no delay is allowed between subsequent stages):

Use B-Computer for exactly one time unit.
Think and calculate on paper for exactly k time units, not using B-Computer.
Use B-Computer for exactly one time unit again to complete.

B-Computer cannot be used by more than one bunny at the same time, but when a bunny is thinking and calculating on paper, another bunny may use B-Computer.

A day is divided into a number of equal time units, and each time unit has an associated positive integer value called preference. You are given a int[] preference, which contains the preference values for a day. The number of elements in preference is the number of time units in the day, and the i-th element of preference is the preference of the i-th time unit.

Bunnies want to design a B-Computer schedule for a single day so that the sum of preferences of time units in which one of them uses B-Computer is maximized. The schedule must be such that each bunny uses B-computer exactly as described above and both time units at which the same bunny uses B-computer are in the same day. Return the maximum possible sum of preferences. You can assume that there are infinitely many bunnies.

Definition

Class:	BunnyComputer
Method:	getMaximum
Parameters:	int[], int
Returns:	int
Method signature:	int getMaximum(int[] preference, int k)
(be sure your method is public)

Constraints

-

preference will contain between 1 and 50 elements, inclusive.

-

Each element of preference will be between 1 and 1,000,000, inclusive.

-

k will be between 1 and 50, inclusive.

Examples

0)

{ 3, 1, 4, 1, 5, 9, 2, 6 }

Returns: 28

The sum is maximized when three bunnies use B-Computer as follows:

One bunny uses B-Computer during the 1-st time unit and again during the 4-th time unit.
One bunny uses B-Computer during the 3-rd time unit and again during the 6-th time unit.
One bunny uses B-Computer during the 5-th time unit and again during the 8-th time unit.

1)

{ 3, 1, 4, 1, 5, 9, 2, 6 }

Returns: 31

2)

{ 1, 2, 3, 4, 5, 6 }

Returns: 14

3)

{ 487, 2010 }

Returns: 0

No bunnies can use B-Computer.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RectangleAvoidingColoring

Brute Force, Simple Math

Used in:

Member SRM 485

Used as:

Division I Level Two

Writer:

ivan_metelsky

Testers:

mohamedafattah , gojira_tc , sl2

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11149

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14238&pm=11149

Problem Statement

There is an N x M board divided into 1 x 1 cells. The rows of the board are numbered from 0 to N-1, and the columns are numbered from 0 to M-1. The cell located in row r and column c has coordinates (r, c).

In a coloring of the board, each cell on the board is colored white or black. A coloring is called rectangle-avoiding if it is impossible to choose 4 distinct cells of the same color so that their centers form a rectangle whose sides are parallel to the sides of the board. In other words, a coloring is rectangle-avoiding if, for each a, b, c, and d with 0 <= a < b < N, 0 <= c < d < M, there is at least one white cell and at least one black cell among the cells (a, c), (a, d), (b, c) and (b, d).

You are given a String[] board representing a board. The j-th character of the i-th element of board represents cell (i, j), and it can be 'W', 'B' or '?'. Here, 'W' indicates a white cell, 'B' indicates a black cell and '?' indicates an uncolored cell. For each uncolored cell, you may choose to color it either white or black. Return the number of different rectangle-avoiding colorings that can be achieved. If it is impossible to achieve a rectangle-avoiding coloring, return 0.

Definition

Class:	RectangleAvoidingColoring
Method:	count
Parameters:	String[]
Returns:	long
Method signature:	long count(String[] board)
(be sure your method is public)

Notes

-

Two colorings are different if there is a cell on the board that is colored white in one coloring and black in the other coloring.

-

The answer will always fit into a 64-bit signed integer data type.

Constraints

-

board will contain between 1 and 50 elements, inclusive.

-

Each element of board will contain between 1 and 50 characters, inclusive.

-

All elements of board will contain the same number of characters.

-

Each character in each element of board will be 'W', 'B' or '?'.

Examples

0)

{"??",
 "??"}

Returns: 14

Since each cell can be black or white, there are 2^4 = 16 ways to color this board. Of them, only 2 monochromatic colorings are not rectangle-avoiding, so the answer is 16 - 2 = 14.

1)

{"B?",
 "?B"}

Returns: 3

It is the same board as in previous example, but colors for some cells are already predefined. There are 4 ways to color the remaining cells and in one of them the board becomes completely black. Therefore the answer is 4 - 1 = 3.

2)

{"WW",
 "WW"}

Returns: 0

This board is already colored and the coloring is not rectangle-avoiding.

3)

{"??B??",
 "W???W",
 "??B??"}

Returns: 12

4)

{"??",
 "W?",
 "W?",
 "?W",
 "W?"}

Returns: 16

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AfraidOfEven

Simple Math

Used in:

Member SRM 485

Used as:

Division I Level One , Division II Level Two

Writer:

ivan_metelsky

Testers:

mohamedafattah , gojira_tc , sl2

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11146

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14238&pm=11146

Problem Statement

A sequence of integers a[0], a[1], ..., a[N-1], where N >= 3, is called an arithmetic progression if the difference between any two successive terms in the sequence is a constant. More precisely, it is an arithmetic progression if a[i] - a[i-1] = a[i+1] - a[i] for every integer i such that 0 < i < N-1.

Sasha and Pasha are students sharing the same room. Once, when Pasha had left the room, Sasha was in a good mood. So he took a piece of chalk and wrote an arithmetic progression on the blackboard. The progression consisted of at least 4 elements, all of which were positive integers. Then Sasha went to class, and Pasha came back.

Pasha is a very nice person, but there's one problem with him -- he's frightened of even numbers! So, when he returned, he decided to make all the numbers on the board odd. He did this by repeatedly finding an arbitrary even number X, erasing it, and writing X/2 in its place. He continued to perform this step until no even numbers remained.

Your task is to help Sasha restore the initial progression. You will be given a int[] seq, where the i-th element is the i-th number in the sequence written on the blackboard after Pasha's actions. Return an int[] whose i-th element is the i-th number in a sequence that Sasha could have originally written on the blackboard. The constraints will ensure that at least one such sequence exists. If there are several such sequences, choose the one among them whose int[] representation is lexicographically smallest.

Definition

Class:	AfraidOfEven
Method:	restoreProgression
Parameters:	int[]
Returns:	int[]
Method signature:	int[] restoreProgression(int[] seq)
(be sure your method is public)

Notes

-

The lexicographically smaller of two different int[]s containing the same number of elements is the one with a smaller number at the first position where they differ.

-

It is guaranteed that all elements of the resulting int[] will fit into a 32-bit signed integer data type.

Constraints

-

seq will contain between 4 and 50 elements, inclusive.

-

Each element of seq will be between 1 and 1000, inclusive.

-

Each element of seq will be odd.

-

There will exist at least one arithmetic progression from which Pasha would produce exactly the sequence described by seq.

Examples

0)

{1, 1, 3, 1, 5}

Returns: {1, 2, 3, 4, 5 }

If the progression written by Pasha was {1, 2, 3, 4, 5}, then Sasha would divide 2 by 2 once and 4 by 2 twice to produce exactly {1, 1, 3, 1, 5}. Note that Pasha could have written other progressions, e.g., {2, 4, 6, 8, 10}, but {1, 2, 3, 4, 5} has the lexicographically smallest int[] representation.

1)

{9, 7, 5, 3, 1}

Returns: {9, 7, 5, 3, 1 }

It is possible that all terms in the original progression were odd. In this case Pasha wouldn't perform any replacements.

Note that an arithmetic progression doesn't have to be an increasing sequence.

2)

{999, 999, 999, 999}

Returns: {999, 999, 999, 999 }

A sequence where all terms are the same is also an arithmetic progression.

3)

{7, 47, 5, 113, 73, 179, 53}

Returns: {14, 47, 80, 113, 146, 179, 212 }

4)

{749, 999, 125, 1}

Returns: {1498, 999, 500, 1 }

Some elements of the original progression could be greater than 1000.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumberMagic

Greedy, Math

Used in:

SRM 484

Used as:

Division I Level Three

Writer:

rng_58

Testers:

PabloGilberto , ivan_metelsky , pieguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11133

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14237&pm=11133

Problem Statement

NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.

Taro shows a magic trick to Hanako.

Taro: Hello Hanako. I'll show you a magic trick. Please imagine a positive integer less than or equal to 16.

Hanako: OK. I imagined it.

Taro: (Taro shows card 1 to Hanako.) Does this card contain your number?

Hanako: Yes.

Taro: (Taro shows card 2 to Hanako.) Does this card contain your number?

Hanako: No.

Taro: (Taro shows card 3 to Hanako.) Does this card contain your number?

Hanako: Yes.

Taro: (Taro shows card 4 to Hanako.) Does this card contain your number?

Hanako: Yes.

Taro: Your number is 5!

(Card 1 contains 1, 2, 3, 4, 5, 6, 7 and 8. Card 2 contains 1, 2, 3, 4, 9, 10, 11 and 12. Card 3 contains 1, 2, 5, 6, 9, 10, 13 and 14. Card 4 contains 1, 3, 5, 7, 9, 11, 13 and 15.)

Let's generalize this magic trick. Hanako imagines a positive integer less than or equal to N. Each card must contain exactly M different integers between 1 and N, inclusive. Taro must be able to determine Hanako's number correctly using her answers to his questions. Return the minimal number of cards required to perform this magic trick successfully every time.

Definition

Class:	NumberMagic
Method:	theMin
Parameters:	int, int
Returns:	int
Method signature:	int theMin(int N, int M)
(be sure your method is public)

Constraints

-

N will be between 2 and 1,000,000,000, inclusive.

-

M will be between 1 and N-1, inclusive.

Examples

0)

Returns: 4

The example from the statement.

1)

Returns: 1

Write 1 on the only card. If Hanako answers "yes", her number is 1. If she answers "no", her number is 2.

2)

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RabbitNumber

Brute Force, Math

Used in:

SRM 484

Used as:

Division I Level One , Division II Level Two

Writer:

rng_58

Testers:

PabloGilberto , ivan_metelsky , pieguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11131

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14237&pm=11131

Problem Statement

When cat Taro and rabbit Hanako were practicing hard for SRM 484, they noticed an interesting property of 484. They called it Rabbit Number.

Let S(n) be the sum of the digits of n. For example, S(484) = 4+8+4 = 16 and S(22) = 2+2 = 4. A positive integer x is called a Rabbit Number if S(x*x) = S(x)*S(x). For example, 22 is a Rabbit Number because S(484) = S(22)*S(22).

Return the number of Rabbit Numbers between low and high, inclusive.

Definition

Class:	RabbitNumber
Method:	theCount
Parameters:	int, int
Returns:	int
Method signature:	int theCount(int low, int high)
(be sure your method is public)

Constraints

-

low will be between 1 and 1,000,000,000, inclusive.

-

high will be between low and 1,000,000,000, inclusive.

Examples

0)

Returns: 1

22 is a Rabbit Number because

S(22*22) = S(484) = 16

S(22) * S(22) = 4 * 4 = 16

1)

Returns: 0

484 is not a Rabbit Number because

S(484*484) = S(234256) = 22

S(484) * S(484) = 16 * 16 = 256

2)

Returns: 12

3)

Returns: 24

4)

1000000000

1000000000

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EvaluatingElections

Greedy, Simple Math

Used in:

TCO10 Final

Used as:

Division I Level One

Writer:

misof

Testers:

SnapDragon , Rustyoldman , marek.cygan , timmac , ivan_metelsky , Egor

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11124

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14287&pm=11124

Problem Statement

Election day is coming in everyone's favorite country, Absurdistan. The elections consist of three steps.

This week anyone can register a political party.
The country is divided into districts. The next week each party will be able to register a candidate in each of the districts.
After that week there is the election day. Each district contains at least one eligible voter. By law, each of the eligible voters has to vote for one of the candidates who are registered in their district. The candidate who receives the most votes is elected to represent the district in the national parliament. In case of a tie nobody is elected from that district.

A party is considered to win the elections if the number of elected candidates belonging to the party is strictly greater than the total number of elected candidates belonging to all other parties.

You have just founded a new party. It will have a candidate in each of the districts.

You are given a int[] districts containing the number of eligible voters in each district. Compute and return the smallest total number X such that if X people vote for your party you are sure to win the elections.

Definition

Class:	EvaluatingElections
Method:	evaluate
Parameters:	int[]
Returns:	int
Method signature:	int evaluate(int[] districts)
(be sure your method is public)

Constraints

-

districts will contain between 1 and 50 elements, inclusive.

-

Each element in districts will be between 1 and 999, inclusive.

Examples

0)

{47}

Returns: 24

You need to win this district, and with 24 votes you can be sure that you'll win it.

1)

{9,9}

Returns: 14

Imagine the following scenario in which your party gets a total of 13 votes: In district #1 your party gets all 9 votes, in district #2 you get 4 votes and one of the other parties gets 5. In that case your party would not win the elections. On the other hand, with 14 votes you are sure to win both districts.

2)

{1,1,1,1,1,1}

Returns: 4

You need to win more than a half, i.e., at least four of these six districts.

3)

{2,2,2,2,2,2}

Returns: 7

Clearly, 6 votes are not enough: for example, if you get one vote in each region, there will be six ties and nobody will get elected. With 7 votes for your party there are several ways how these can be distributed. We can easily check that in each of them you are sure to win the elections.

For example, you can get both votes in two of the regions and a single vote in three other regions. In that case, you won in two regions, and you forced a tie in three other regions, leaving at most one region for some other party.

4)

{8,10,12}

Returns: 21

With 21 votes for your party you are almost sure to win in at least two regions, and thereby to win the elections. The only case when this does not happen is the case when you get all 12 votes in the largest region and half of the votes in each of the other two. But in this case you won one region and no opponent can win any other region, which still means you win the elections.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AverageAverage

Brute Force, Simple Math, Simple Search, Iteration

Used in:

Member SRM 482

Used as:

Division II Level One

Writer:

pieguy

Testers:

ivan_metelsky , boba5551 , it4.kp , abal9002

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11121

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14235&pm=11121

Problem Statement

Given a int[] numList, for each non-empty subset of numList, compute the average of its elements, then return the average of those averages.

Definition

Class:	AverageAverage
Method:	average
Parameters:	int[]
Returns:	double
Method signature:	double average(int[] numList)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

numList will contain between 1 and 8 elements, inclusive.

-

All elements of numList will be between -1000 and 1000, inclusive.

-

All elements of numList will be distinct.

Examples

0)

{1,2,3}

Returns: 2.0

The non-empty subsets of numList are: {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, and {1,2,3}, whose respective averages are: 1, 2, 3, 1.5, 2, 2.5, and 2. The average of the averages is 2.

1)

{42}

Returns: 42.0

There is only one non-empty subset to consider.

2)

{3,1,4,15,9}

Returns: 6.4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BatchSystemRoulette

Greedy, Math

Used in:

SRM 481

Used as:

Division I Level Two

Writer:

vexorian

Testers:

PabloGilberto , ivan_metelsky , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11119

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14234&pm=11119

Problem Statement

In the past, whole organizations depended on a single, big computer to do all the computational work. In a particular case, a computer has a list of pending jobs which is described by int[] duration and String[] user, each with n elements. duration[i] is the total time in minutes required to complete the i-th job and user[i] is a string that identifies the user that requested that job. A user may request multiple jobs. The computer may only process one job at a time. The waiting time for a user is defined as the time that this user has to wait before all of the jobs (s)he requested are finished. The computer will always pick a schedule to process the jobs in such a way that the average of waiting times over all users is minimized. If there are multiple schedules that can accomplish the minimum average waiting time, the computer will pick any of them with equal probability.

We need a way to estimate how long the computer will take to finish each of the jobs. Your method must return a double[] containing n elements. The i-th element of your return must be the expected time in minutes before the computer finishes processing the i-th job.

Definition

Class:	BatchSystemRoulette
Method:	expectedFinishTimes
Parameters:	int[], String[]
Returns:	double[]
Method signature:	double[] expectedFinishTimes(int[] duration, String[] user)
(be sure your method is public)

Notes

-

User names are case sensitive. A user named "Bob" is different from a user named "bob". See example 1 for clarification.

-

Each element of the returned value must have an absolute or relative error less than 1e-9.

Constraints

-

duration will contain between 1 and 50 elements, inclusive.

-

user will contain the same number of elements as duration.

-

Each element of duration will be between 1 and 1000000000, inclusive.

-

Each element of user will contain between 1 and 50 characters, inclusive.

-

Each element of user will contain only letters ('a'-'z','A'-'Z') and at most one space character that will not be a leading or trailing space.

Examples

0)

{3, 2, 4, 1}

{"Gil Grissom", "Sarah Sidle", "Warrick Brown", "Catherine Willows"}

Returns: {6.0, 3.0, 10.0, 1.0 }

There is only one optimal way to schedule the jobs: {3, 1, 0, 2}.

1)

{3, 2, 4, 1}

{"mac taylor", "Mac Taylor", "Mac Taylor", "Peyton Driscoll"}

Returns: {4.0, 8.0, 9.0, 1.0 }

This time, there are two different ways to schedule the jobs that are optimal: {3, 0, 1, 2} and {3, 0, 2, 1}.

2)

{13, 14, 15, 56, 56}

{"Tim Speedle", "Tim Speedle", "Tim Speedle", "Horatio Caine", "YEEEAAAAAAAAAAH"}

Returns: {27.5, 28.0, 28.5, 126.0, 126.0 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PermutationSignature

Greedy, Simple Math

Used in:

SRM 497

Used as:

Division I Level One , Division II Level Two

Writer:

misof

Testers:

SnapDragon , Rustyoldman , marek.cygan , timmac , ivan_metelsky , Egor , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11115

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14426&pm=11115

Problem Statement

The signature of a permutation is a string that is computed as follows: for each pair of consecutive elements of the permutation, write down the letter 'I' (increasing) if the second element is greater than the first one, otherwise write down the letter 'D' (decreasing).

For example, the signature of the permutation {3,1,2,7,4,6,5} is "DIIDID".

Your task is to reverse this computation: You are given a String signature containing the signature of a permutation. Find and return the lexicographically smallest permutation with the given signature. If no such permutation exists, return an empty int[] instead.

Definition

Class:	PermutationSignature
Method:	reconstruct
Parameters:	String
Returns:	int[]
Method signature:	int[] reconstruct(String signature)
(be sure your method is public)

Notes

- For any positive integer N, a permutation of N elements is a sequence of length N that contains each of the integers 1 through N exactly once.

- To compare two permutations A and B, find the smallest index i such that A[i] and B[i] differ. If A[i] < B[i], we say that A is lexicographically smaller than B, and vice versa.

Constraints

- signature will contain between 1 and 50 characters, inclusive.

- Each character in signature will be either 'I' or 'D'.

Examples

0)

"IIIII"

Returns: {1, 2, 3, 4, 5, 6 }

1)

"DI"

Returns: {2, 1, 3 }

There are two permutations with this signature: {3,1,2} and {2,1,3}. You must return the lexicographically smaller one.

2)

"IIIID"

Returns: {1, 2, 3, 4, 6, 5 }

3)

"DIIDID"

Returns: {2, 1, 3, 5, 4, 7, 6 }

This is the signature from the problem statement. Note that the correct answer is not the permutation from the problem statement.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DistantPoints

Geometry, Math, Simple Search, Iteration

Used in:

TCO10 Semi 1

Used as:

Division I Level One

Writer:

gojira_tc

Testers:

SnapDragon , Rustyoldman , marek.cygan , timmac , ivan_metelsky , Egor

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11077

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14284&pm=11077

Problem Statement

There is a square on a plane with (0,0) as its lower left and (2^N+2, 2^N+2) as its upper right corner. It is known that K distinct points have to be painted. Each of them should be strictly inside the square and should have integral coordinates. The first point to be painted is always (1,1). For each of the next points, the one from which the Euclidean distance to the closest already painted point is maximum should be chosen. In case of ties, the leftmost point should be painted. If there are still several possibilities, the lowermost point is chosen. Return int[] with exactly two elements, the X and Y coordinates of the K-th point to be painted.

Definition

Class:	DistantPoints
Method:	getKth
Parameters:	int, int
Returns:	int[]
Method signature:	int[] getKth(int N, int K)
(be sure your method is public)

Notes

-

The Euclidean distance between two points (x1,y1) and (x2,y2) is equal to the square root of (x1-x2)^2+(y1-y2)^2.

Constraints

-

N will be between 2 and 10, inclusive.

-

K will be between 1 and the amount of points inside the square with side length 2^N+2, inclusive.

Examples

0)

Returns: {17, 17 }

The square stretches from (0,0) to (18,18). After you paint (1,1), the farthest point within the square is (17,17).

1)

Returns: {1, 17 }

Now there are two candidates. Both upper-left and bottom-right points within the square are equally distant from the already painted two, so we choose the leftmost one.

2)

Returns: {9, 9 }

After you paint all the corners, the best choice is the center of the square.

3)

Returns: {1, 3 }

4)

Returns: {33, 32 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BestApproximationDiv2

Search, Simple Math

Used in:

SRM 483

Used as:

Division II Level Three

Writer:

espr1t

Testers:

PabloGilberto , ivan_metelsky , gojira_tc

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11073

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14236&pm=11073

Problem Statement

Elly is not a big fan of mathematical constants. Most of them are infinite, and therefore hard to memorize. Fractions, on the other hand, are often easier to remember and can provide good approximations. For example, 22/7 = 3.1428... is one way to approximate Pi. Unfortunately, it's only accurate to 2 places after the decimal point, so it doesn't help at all. A slightly better example is 355/113 = 3.14159292... which is correct up to 6 digits after the decimal point.

Elly understands that working with infinite decimal fractions is going to be very difficult, so she first wants to find a good way to approximate floating point numbers with decimal representations that are finite. Your task is to help her in this mission. You will be given a String number containing the decimal representation of a non-negative fraction strictly less than 1 (possibly with trailing zeros). More precisely, number will be formatted "0.dd...d" (quotes for clarity) where each d is a decimal digit ('0'-'9') and the number of d's is between 1 and 48, inclusive.

Given a fraction F = A/B, where 0 <= A < B, its quality of approximation with respect to number is calculated as follows:

Let S be the decimal fraction (infinite or finite) representation of F.
Let N be the number of digits after the decimal point in number. If number has trailing zeros, all of them are considered to be significant and are counted towards N.
If S is infinite or the number of digits after the decimal point in S is greater than N, only consider the first N decimals after the decimal point in S. Truncate the rest of the digits without performing any kind of rounding.
If the number of digits after the decimal point in S is less than N, append trailing zeroes to the right side until there are exactly N digits after the decimal point.
The quality of approximation is the number of digits in the longest common prefix of S and number. The longest common prefix of two numbers is the longest string which is a prefix of the decimal representations of both numbers with no extra leading zeroes. For example, "3.14" is the longest common prefix of 3.1428 and 3.1415.

Elly doesn't like long approximations either, so you are only allowed to use fractions where the denominator is less than or equal to maxDen. Find an approximation F = A/B of number such that 1 <= B <= maxDen, 0 <= A < B, and the quality of approximation is maximized. Return a String formatted "A/B has X exact digits" (quotes for clarity) where A/B is the approximation you have found and X is its quality. If there are several such approximations, choose the one with the smallest denominator among all of them. If there is still a tie, choose the one among those with the smallest numerator.

Definition

Class:	BestApproximationDiv2
Method:	findFraction
Parameters:	int, String
Returns:	String
Method signature:	String findFraction(int maxDen, String number)
(be sure your method is public)

Constraints

-

maxDen will be between 1 and 100,000, inclusive.

-

number will contain between 3 and 50 characters, inclusive.

-

number will consist of a digit '0', followed by a period ('.'), followed by one or more digits ('0'-'9').

Examples

0)

"0.141592658"

Returns: "1/7 has 3 exact digits"

3 plus the current approximation yields an approximation of Pi.

1)

"0.1337"

Returns: "0/1 has 1 exact digits"

Not a lot of options here.

2)

"0.1234567891011121314151617181920"

Returns: "10/81 has 8 exact digits"

3)

"0.42"

Returns: "3/7 has 3 exact digits"

This one can be represented in more than one way. Be sure to choose the one with the lowest denominator.

Note that 21/50 is an even more accurate approximation (it is, in fact, exact), but it has the same number of matching digits (all three) and has a greater denominator.

4)

"0.420"

Returns: "21/50 has 4 exact digits"

All trailing zeros in number are significant.

5)

"0.141592658"

Returns: "16/113 has 7 exact digits"

A better approximation for the decimal part of Pi.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ShrooksOnTheBoard

Dynamic Programming, Math

Used in:

TCO10 Wildcard

Used as:

Division I Level Three

Writer:

dkorduban

Testers:

SnapDragon , Rustyoldman , marek.cygan , timmac , ivan_metelsky , Egor

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11072

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14286&pm=11072

Problem Statement

A K-shrook is a fairy chess piece that can move horizontally in both directions for at most K squares. Here is an illustration of 2-shrook possible moves:

Two K-shrooks attack each other if one of them can reach the other shrook's square in one move. You are given a board with H rows and W columns. Find out the number of ways to place an arbitrary positive amount of K-shrooks on this board so that no two of them attack each other. Return this number modulo 100003.

Definition

Class:	ShrooksOnTheBoard
Method:	count
Parameters:	int, int, int
Returns:	int
Method signature:	int count(int K, int H, int W)
(be sure your method is public)

Constraints

- K will be between 1 and 1,000,000,000, inclusive.

- H will be between 1 and 1,000,000,000, inclusive.

- W will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 4

The possible placements are "S..", ".S.", "..S" and "S.S".

1)

Returns: 8

There can not be more than 1 shrook in a row.

2)

Returns: 56963

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ColorfulJewelry

Math

Used in:

TCO10 Final

Used as:

Division I Level Three

Writer:

lyrically

Testers:

SnapDragon , Rustyoldman , marek.cygan , timmac , ivan_metelsky , Egor

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11061

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14287&pm=11061

Problem Statement

Some jewels are placed in a rectangular grid on an infinite plane. You are given String[] jewels describing the jewels. If the j-th character of the i-th element of jewels is 'R', 'G' or 'B', there is a red, green or blue jewel at the center of the j-th cell of the i-th row of the grid, respectively. Jewels of the same color cannot be distinguished.

Alice draws two squares on this plane. Their sides must be parallel to the axis and have length k. She is allowed to draw squares so that some part of them are on the outside of the grid. Then she will get the jewels which lie in the inside of at least one of the two squares. Note that the inside of a square does not contain its boundary. She wants to make a chain of jewels, using some of the jewels she will get. She does not have to use all of the jewels she will get. A chain is a row of one or more jewels. Chains are non-directional. For example, chains R-G-B and B-G-R are considered equal. How many different chains are possible, considering all the chains from all possible square locations? Return the answer modulo 1,000,000,009.

Definition

Class:	ColorfulJewelry
Method:	getChains
Parameters:	String[], int
Returns:	int
Method signature:	int getChains(String[] jewels, int k)
(be sure your method is public)

Notes

-

For the purposes of this problem, a jewel is considered to be a single point.

Constraints

-

jewels will contain between 1 and 44 elements, inclusive.

-

Each element of jewels will contain the same number of characters.

-

Each element of jewels will contain between 1 and 44 characters, inclusive.

-

Each character in jewels will be either 'R', 'G' or 'B'.

-

k will be between 1 and 44, inclusive.

Examples

0)

{ "RGB" }

Returns: 6

Alice can get at most two jewels. The possible chains are: R, G, B, R-G, R-B, G-B.

1)

{ "RGB" }

Returns: 9

Alice can get all the three jewels.

2)

{ "RGB" }

Returns: 9

3)

{ "RRRRR", 
  "RGGRR", 
  "RGGGG", 
  "RRRGG" }

Returns: 280

4)

{ "RRRRRRRRRR", 
  "RRRRRRRRRR", 
  "RRRRRRRRRR", 
  "RRRRRRRRRR", 
  "RRRRRRRRRR", 
  "RRRRRRRRRR", 
  "RRRRRRRRRR", 
  "RRRRRRRRRR", 
  "RRRRRRRRRR", 
  "RRRRRRRRRR" }

Returns: 68

5)

{ "RRRGGGGG", 
  "RRRGGGGG", 
  "RRRGGBBB", 
  "GGGGGBBB", 
  "GGGGGBBB" }

Returns: 613435159

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SignalIntelligence

Encryption/Compression, Greedy, Math, Sorting

Used in:

SRM 480

Used as:

Division II Level Three

Writer:

dolphinigle

Testers:

PabloGilberto , ivan_metelsky , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11059

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14159&pm=11059

Problem Statement

Gogo has been hired by the newly founded TopCoder Security Agency (TSA) and has been tasked to encrypt a signal code generated by a radar.

The signal will consist of several positive integers. The order of integers within the signal is not important and therefore should not be preserved during encryption. However, there may be duplicate integers, and the number of occurrences of each integer is important and must be preserved during encryption.

Gogo's idea is to encrypt these integers into a String that consists only of digits '1' and '0'. The encryption scheme is as follows:

Start with an infinite String consisting solely of '0' characters. The characters within the string are indexed from left to right 1, 2, 3, ... .
For each input integer X in the signal, Gogo will allocate it within the string. To do this, he will select an index 2^p, where p is a non-negative integer that he may choose arbitrarily, but in such way that characters at indices between 2^p and 2^p + X - 1, inclusive, are all equal to '0'. The allocating procedure consists of replacing all these characters with '1's. This newly created sequence of consecutive '1' characters is said to represent the allocated integer X.
In order to allow unique decryption, the following property must hold after all numbers from the signal are allocated. For every two integers from the input signal, there must be at least one '0' character between the sequences of '1's that represent these integers.

After all numbers are allocated within the string properly, the '1' character with the largest index is found and all '0' characters to the right of it are removed. The obtained finite string is the result of the encryption procedure.

Given integers to encrypt in int[] numbers, return the length of the shortest string that encrypts them and can be obtained according to the scheme described above. It is guaranteed that this length will not exceed 2^62.

Definition

Class:	SignalIntelligence
Method:	encrypt
Parameters:	int[]
Returns:	long
Method signature:	long encrypt(int[] numbers)
(be sure your method is public)

Constraints

-

numbers will contain between 1 and 50 elements, inclusive.

-

Each element of numbers will be between 1 and 1,000,000,000, inclusive.

-

The answer will not exceed 2^62.

Examples

0)

{1,2,3}

Returns: 8

The string "11011101" encrypts the given numbers and has a length of 8. There is no shorter string that encrypts these numbers.

1)

{4,4,2,2}

Returns: 19

The elements in numbers might not be distinct.

2)

{1000000000,1000000000,1000000000,1000000000,1000000000,
1000000000,1000000000,1000000000,1000000000,1000000000,
1000000000,1000000000,1000000000,1000000000,1000000000,
1000000000,1000000000,1000000000,1000000000,1000000000}

Returns: 281475976710655

The answer may be very big, but it will not exceed 2^62.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EnclosingSquare

Math

Used in:

TCO10 Final

Used as:

Division I Level Two

Writer:

lyrically

Testers:

SnapDragon , Rustyoldman , marek.cygan , timmac , ivan_metelsky , Egor

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11044

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14287&pm=11044

Problem Statement

Find the area of the minimum square in the plane, such that its 4 vertices are distinct lattice points and there are exactly n lattice points strictly inside it. If there is no such square, return 0 instead.

Definition

Class:	EnclosingSquare
Method:	getMinimum
Parameters:	long
Returns:	long
Method signature:	long getMinimum(long n)
(be sure your method is public)

Notes

-

A lattice point in the coordinate plane is a point whose x-coordinate and y-coordinate are both integers.

Constraints

-

n will be between 0 and 1,000,000,000,000, inclusive.

Examples

0)

Returns: 5

The square below contains exactly 4 lattice points strictly inside itself and has an area of 5.

1)

Returns: 0

There is no such square.

2)

1000000000000

Returns: 1000000000001

3)

Returns: 104

4)

Returns: 90

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CalculationCards

Dynamic Programming, Math

Used in:

TCO10 Wildcard

Used as:

Division I Level Two

Writer:

lyrically

Testers:

SnapDragon , Rustyoldman , marek.cygan , timmac , ivan_metelsky , Egor

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11040

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14286&pm=11040

Problem Statement

There are some cards in a box which are specified by a String[] cards. One of the operators '+', '-' or '*' is written on the left half of each card and a digit is written on the right half of each card. You draw all cards from the box randomly, one by one. At each step each of the remaining cards has the same probability of being drawn. Then you align the cards from left to right in the order you have drawn them. Finally, add a zero at the left of the cards and calculate the value of this expression. For example, if you have drawn "+1", "-2" and "*3" (in this order), the expression is "0 + 1 - 2 * 3", whose value is -5. Return the expected value.

Definition

Class:	CalculationCards
Method:	getExpected
Parameters:	String[]
Returns:	double
Method signature:	double getExpected(String[] cards)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

cards will contain between 1 and 50 elements, inclusive.

-

Each element of cards will contain exactly 2 characters.

-

The first character in each element of cards will be either '+', '-' or '*'.

-

The second character in each element of cards will be a digit ('0' - '9').

Examples

0)

{ "+1", "-2", "*3" }

Returns: -1.6666666666666667

One of the following expressions will be made with equal probability:

0 + 1 - 2 * 3 = -5
0 + 1 * 3 - 2 = 1
0 - 2 + 1 * 3 = 1
0 - 2 * 3 + 1 = -5
0 * 3 + 1 - 2 = -1
0 * 3 - 2 + 1 = -1

1)

{ "+1", "+2", "+3" }

Returns: 6.0

The value will always be 6.

2)

{ "+3", "-7", "*4", "+6" }

Returns: 3.5

3)

{ "+1", "*2", "*3" }

Returns: 3.1666666666666665

4)

{ "*7", "-2", "*0", "+3", "*8" }

Returns: 5.633333333333334

5)

{ "+1", "*9", "*9", "*9", "*9", "*9", "*9", "*9", "*9", "*9", "*9" }

Returns: 3.5660295009090906E8

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MovieSeating

Simple Math

Used in:

SRM 483

Used as:

Division II Level Two

Writer:

espr1t

Testers:

PabloGilberto , ivan_metelsky , gojira_tc

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11035

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14236&pm=11035

Problem Statement

Elly and some of her friends (possibly none) are going to the movies. Their company consists of numFriends people, including Elly. Since they don't want to be spread across the entire hall, they decided to sit either in the same row or in the same column (though not necessarily next to one another).

Your are given a String[] hall representing the layout of seats in the theater that are already taken. The j-th character of the i-th element of hall will be '#' if the seat at row i, column j is already taken and '.' if it is empty.

Return the number of different ways for Elly and her friends to choose numFriends different empty seats so that their seating requirement is fulfilled. Two ways are considered different if there exists a person in their company that will sit in different seats in these two ways.

Definition

Class:	MovieSeating
Method:	getSeatings
Parameters:	int, String[]
Returns:	long
Method signature:	long getSeatings(int numFriends, String[] hall)
(be sure your method is public)

Constraints

-

numFriends will be between 1 and 8, inclusive.

-

hall will contain between 1 and 50 elements, inclusive.

-

Each element of hall will contain between 1 and 50 characters, inclusive.

-

All elements of hall will contain the same number of characters.

-

Each character in hall will be either '.' or '#'.

Examples

0)

{ ".#..",
  ".##.",
  "...." }

Returns: 34

Here the movie hall has 3 rows and 4 columns. The second seat in the first row is taken, as well as the seats in the middle of the second row.

1)

{ "..#",
  ".##",
  "..." }

Returns: 16

Elly and her friend can sit in two ways in the first row, they cannot sit in the second row, and they can sit in six ways in the third row. If they choose to sit in the same column, they can do it in six ways in the leftmost column, two ways in the middle column, and not in the rightmost column because there is only one seat.

2)

{ "..####..", 
  ".###.##.",
  ".######.",
  "#.#.#.#." }

Returns: 0

There are enough places for the company, but since they want to sit in the same row or same column, none of the possible seatings satisfies them.

3)

{ "........" }

Returns: 40320

Just enough seats for all of them.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheAirTripDivOne

Graph Theory, Simple Math

Used in:

SRM 479

Used as:

Division I Level Two

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , ivan_metelsky , gojira_tc

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11030

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14158&pm=11030

Problem Statement

In some country there are n cities numbered from 1 to n. There are also several types of flights between them. Each flight type is characterized with 5 integers A, B, F, T and P. All flights of this type depart from city A and arrive at city B (without changing planes in any intermediate cities). Each flight type is one-directional, so it is impossible to fly from city B to city A using the same flight type. All flights of the same type depart with some periodicity. More precisely, the first flight of this type departs from A at time F, the next flight departs at time F + P, then at F + 2P, and so on (there are infinitely many flights of the same type). Each flight of the same type has the same flight time T. I.e., if a plane departs from A at time T₀, then it arrives to B at time T₀ + T.

The description of all flight types is given in String[] flights. Concatenate the elements of this String[] in the same order as they are given without any delimiters between its elements to get a single String. This String will contain a single space separated list of flight type descriptions. Each such description will be of the form "A,B,F,T,P" (quotes for clarity), where the meaning of integers A, B, F, T and P is exactly the same as defined in the previous paragraph.

John would like to travel from city 1 to city n where his friend Brus is waiting for him. Unfortunately, there are no direct flights from 1 to n, so he will have to use several flights to reach city n. He can't use any other transport besides planes, so the departure city of each next flight he takes must be the same as the arrival city of the previous flight he has taken. Moreover, in order for him to be able to change planes, the departure time of each next flight must be strictly greater than the arrival time of the previous flight. If he arrives at some city at time T₁ and then departs at time T₂, the waiting time in this city is equal to T₂ - T₁. John defines the safety of his route from 1 to n as the minimum of waiting times over all cities where he changes flights.

John wants to arrive at city n no later than at time moment time. If there are several routes that achieve this goal, he wants to choose the route among them with the maximum possible safety. Return this maximum possible safety. If there are no such routes, return -1.

Definition

Class:	TheAirTripDivOne
Method:	find
Parameters:	int, String[], int
Returns:	int
Method signature:	int find(int n, String[] flights, int time)
(be sure your method is public)

Constraints

-

n will be between 3 and 477, inclusive.

-

flights will contain between 1 and 47 elements, inclusive.

-

Each element of flights will contain between 1 and 47 characters, inclusive.

-

The concatenation of all elements of flights will be a single space separated list of flight type descriptions without leading or trailing spaces.

-

Each flight type description will be of form "A,B,F,T,P" (quotes for clarity), where A, B, F, T and P are integers formatted with no extra leading zeros.

-

In each flight type, A and B will be distinct integers between 1 and n, inclusive.

-

In each flight type, F, T and P will be between 1 and 1,000,000,000, inclusive.

-

There will be no flight from city 1 to city n.

-

time will be between 1 and 1,000,000,000, inclusive.

Examples

0)

{"1,2,1,4,7 ", "2,3,9,1,10"}

Returns: 14

The optimal way is to take the first flight at time 1 and the second one at time 19.

1)

{"1,2,1,1,1 2,3,2,1,98"}

Returns: -1

Since John needs a strictly positive time to change a flight, it is possible to get to city 3 only at time 101.

2)

{"47,74,1,1,1"}

Returns: -1

It is impossible to reach the destination at all.

3)

{"1,3,15,17,11 1,3,14,16,14 5,7,12,18,18 1,6,13,1", 
 "6,12 1,2,18,14,13 5,6,10,10,18 3,1,10,10,10 1,3",
 ",17,16,10 2,3,16,18,16 6,1,15,12,10 2,1,15,18,1",
 "0 4,7,10,16,15 6,3,10,14,10 1,6,19,19,15 1,4,12",
 ",10,14 4,7,10,18,14 2,3,16,12,12 1,3,14,10,19 3",
 ",7,17,10,12 2,1,14,12,16 4,3,19,11,12 1,6,10,18",
 ",12 2,3,16,12,10 6,2,10,18,12 5,1,14,18,12 5,1,",
 "18,10,10 3,2,19,15,10 7,4,16,19,14 6,3,16,12,10",
 " 5,7,14,13,13 1,3,12,10,16 5,7,16,18,15 6,2,18,",
 "12,14 3,2,10,18,16 4,2,18,18,14 1,5,10,18,16 2,",
 "3,10,19,16 1,4,11,18,15 2,1,15,15,14 7,2,10,12,",
 "10"}

Returns: 33

Note that there can be multiple flight types with the same departure city and the same arrival city.

4)

{"1,4,10,8,2 4,6,14,8,2 6,2,8,1",
 "0,1 2,7,19,5,1 ",
 "1,5,15,17,11 5,3,10,1",
 "0,18 3,7,12,18,18"}

Returns: 35

Take the flight from city 1 to city 4 at time 10 to arrive at city 4 at time 18. Then take the flight from city 4 to city 6 at time 54 to arrive at city 6 at time 62. Next take the flight from city 6 to city 2 at time 97 to arrive at city 2 at time 107. Finally, take the flight from city 2 to city 7 at time 142 to arrive at city 7 exactly at time 147. The safety of this route is min{54 - 18, 107 - 62, 142 - 107} = 35.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheCoffeeTimeDivOne

Greedy, Simple Math, Simulation, Sorting

Used in:

SRM 479

Used as:

Division I Level One

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , ivan_metelsky , gojira_tc

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11028

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14158&pm=11028

Problem Statement

John and Brus are flying on an airplane and now it's coffee time.

There are n seats in the plane numbered from 1 to n, one seat in each row. All seats are occupied, thus there are n passengers overall (including John and Brus). A stewardess will serve a cup of coffee or tea to each passenger. She needs to serve tea to all passengers whose seat numbers are listed in int[] tea, and she needs to serve coffee to all other passengers.

A coffee and tea machine is located just before the first seat of the plane. The stewardess has a flask that can contain enough coffee or tea to serve at most 7 passengers. Initially, the stewardess is located near the coffee and tea machine and the flask is empty.

The stewardess can perform the following kinds of actions:

Move from the coffee and tea machine to seat 1 or move from seat 1 to the coffee and tea machine. Each of these two actions takes 1 second.
Move from seat i, i > 1, to seat i-1. It takes 1 second.
Move from seat i, i < n, to seat i+1. It takes 1 second.
If she is near seat i, the passenger at this seat has not yet been served and the current type of drink in the flask is the same as the drink this passenger wants, she can serve this passenger with a cup of drink he/she wants. It takes 4 seconds.
If she is near the coffee and tea machine and the flask is empty, she can fill the flask with either tea or coffee (but not both simultaneously). It takes 47 seconds. Note that she can fill the flask partially (to serve less than 7 passengers), but it still takes 47 seconds.

Given int n and int[] tea, return the minimal time needed for the stewardess to serve all passengers with proper drinks and return to the coffee and tea machine.

Definition

Class:	TheCoffeeTimeDivOne
Method:	find
Parameters:	int, int[]
Returns:	long
Method signature:	long find(int n, int[] tea)
(be sure your method is public)

Constraints

-

n will be between 2 and 44,777,777, inclusive.

-

tea will contain between 1 and 47 elements, inclusive.

-

Each element of tea will be between 1 and n, inclusive.

-

All elements of tea will be distinct.

Examples

0)

{1}

Returns: 108

The stewardess will serve coffee in 47+2+4+2=55 seconds and tea in 47+1+4+1=53 seconds.

1)

{2, 1}

Returns: 59

Here she only needs to serve tea.

2)

{1, 2, 3, 4, 5, 6, 7}

Returns: 261

The stewardess will fill the flask three times overall: once with tea and two times with coffee.

3)

{1, 10, 6, 2, 4}

Returns: 891

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RandomApple

Dynamic Programming, Math

Used in:

Member SRM 478

Used as:

Division I Level Three

Writer:

rng_58

Testers:

liympanda , konqueror , ivan_metelsky , keshav_57

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11026

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14187&pm=11026

Problem Statement

Taro likes apples very much. He has N boxes numbered from 0 to N-1. There are K different types of apples numbered from 0 to K-1. You are given three String[]s, hundred, ten and one. Concatenate j-th characters in hundred[i], ten[i] and one[i] in this order to get a string that represents the number of j-th type apples in Box i (it may have leading zero(s)). This number will be between 0 and 199, inclusive.

He decided to choose one apple from his boxes, and he does so in the following way:

First Step: He chooses a non-empty subset of his N boxes randomly and transfers all apples from those boxes to another box (this is a box other than the original N boxes and it is initially empty). Each non-empty subset of boxes has the same probability of being chosen.
Second Step: He chooses one apple from the new box randomly. Each apple in the box has the same probability of being chosen.

Return a double[] that contains exactly K elements and whose i-th element is the probability that Taro chooses an i-th type apple.

Definition

Class:	RandomApple
Method:	theProbability
Parameters:	String[], String[], String[]
Returns:	double[]
Method signature:	double[] theProbability(String[] hundred, String[] ten, String[] one)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

N will be between 1 and 50, where N is the number of elements in hundred.

-

K will be between 1 and 50, where K is the number of characters in hundred[0].

-

ten and one will contain exactly N elements.

-

Each element in hundred, ten and one will contain exactly K characters.

-

Each character in hundred will be '0' or '1'.

-

Each character in ten and one will be a digit ('0'-'9').

-

Each box will contain at least one apple.

Examples

0)

{"00"}

{"00"}

{"58"}

Returns: {0.38461538461538464, 0.6153846153846154 }

There is only one box which contains 5 type-0 apples and 8 type-1 apples. The probability of choosing a type-0 apple is 5 / 13.

1)

{"00", "00"}

{"00", "00"}

{"21", "11"}

Returns: {0.5888888888888889, 0.4111111111111111 }

If he chooses only box 0 in the first step, the probability of choosing a type-0 apple is 2 / 3.

If he chooses only box 1 in the first step, the probability of choosing a type-0 apple is 1 / 2.

If he chooses both boxes in the first step, the probability of choosing a type-0 apple is 3 / 5.

So the probability of choosing a type-0 apple is (2 / 3 + 1 / 2 + 3 / 5) / 3 = 53 / 90.

2)

{"0000", "0000", "0000"}

{"2284", "0966", "9334"}

{"1090", "3942", "4336"}

Returns: 
{0.19685958571981937, 0.24397246802233483, 0.31496640865458775, 0.24420153760325805 }

3)

{"01010110", "00011000", "00001000", "10001010", "10111110"}

{"22218214", "32244284", "68402430", "18140323", "29043145"}

{"87688689", "36101317", "69474068", "29337374", "87255881"}

Returns: 
{0.11930766223754977, 0.14033271060661345, 0.0652282589028571, 0.14448118133046356, 0.1981894622733832, 0.10743462836879789, 0.16411823601857622, 0.06090786026175882 }

4)

{"10"}

{"00"}

{"00"}

Returns: {1.0, 0.0 }

One box with 100 type-0 apples and no type-1 apples.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BestApproximationDiv1

Simple Search, Iteration

Used in:

SRM 483

Used as:

Division I Level One

Writer:

espr1t

Testers:

PabloGilberto , ivan_metelsky , gojira_tc

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11023

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14236&pm=11023

Problem Statement

Elly is not a big fan of mathematical constants. Most of them are infinite, and therefore hard to memorize. Fractions, on the other hand, are often easier to remember and can provide good approximations. For example, 22/7 = 3.1428... is one way to approximate Pi. Unfortunately, it's only accurate to 2 places after the decimal point, so it doesn't help at all. A slightly better example is 355/113 = 3.14159292... which is correct up to 6 digits after the decimal point.

Elly understands that working with infinite decimal fractions is going to be very difficult, so she first wants to find a good way to approximate floating point numbers with decimal representations that are finite. Your task is to help her in this mission. You will be given a String number containing the decimal representation of a non-negative fraction strictly less than 1. There will be exactly 6 digits after the decimal point in number (trailing zeros are possible and significant). More precisely, number will be formatted "0.dddddd" (quotes for clarity) where each d is a decimal digit ('0'-'9').

Given a fraction F = A/B, where 0 <= A < B, its quality of approximation with respect to number is calculated as follows:

Let S be the decimal fraction (infinite or finite) representation of F.
If S is infinite or the number of digits after the decimal point in S is greater than 6, only consider the first 6 decimals after the decimal point in S. Truncate the rest of the digits without performing any kind of rounding.
If the number of digits after the decimal point in S is less than 6, append trailing zeroes to the right side until there are exactly 6 digits after the decimal point.
The quality of approximation is the number of digits in the longest common prefix of S and number. The longest common prefix of two numbers is the longest string which is a prefix of the decimal representations of both numbers with no extra leading zeroes. For example, "3.14" is the longest common prefix of 3.1428 and 3.1415.

Elly doesn't like long approximations either, so you are only allowed to use fractions where the denominator is less than or equal to maxDen. Find an approximation F = A/B of number such that 1 <= B <= maxDen, 0 <= A < B, and the quality of approximation is maximized. Return a String formatted "A/B has X exact digits" (quotes for clarity) where A/B is the approximation you have found and X is its quality. If there are several such approximations, choose the one with the smallest denominator among all of them. If there is still a tie, choose the one among those with the smallest numerator.

Definition

Class:	BestApproximationDiv1
Method:	findFraction
Parameters:	int, String
Returns:	String
Method signature:	String findFraction(int maxDen, String number)
(be sure your method is public)

Constraints

-

maxDen will be between 1 and 1000, inclusive.

-

number will contain exactly 8 characters.

-

number will consist of a digit '0', followed by a period ('.'), followed by exactly six digits ('0'-'9').

Examples

0)

"0.141592"

Returns: "1/7 has 3 exact digits"

3 plus the current approximation yields an approximation of Pi.

1)

"0.133700"

Returns: "0/1 has 1 exact digits"

Not a lot of options here.

2)

"0.123456"

Returns: "10/81 has 7 exact digits"

3)

"0.420000"

Returns: "21/50 has 7 exact digits"

This one can be represented in more than one way. Be sure to choose the one with the lowest denominator.

4)

"0.909999"

Returns: "10/11 has 4 exact digits"

Even though 91/100 is a much closer approximation, 10/11 matches up to 3 digits, and 91/100 only to one.

5)

"0.141592"

Returns: "16/113 has 7 exact digits"

A better approximation for the decimal part of Pi.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CarrotJumping

Math

Used in:

Member SRM 478

Used as:

Division I Level One , Division II Level Two

Writer:

rng_58

Testers:

liympanda , konqueror , ivan_metelsky , keshav_57

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11022

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14187&pm=11022

Problem Statement

Rabbits often feel hungry, so when they go out to eat carrots, they jump as quickly as possible.

Initially, rabbit Hanako stands at position init. From position x, she can jump to either position 4*x+3 or 8*x+7 in a single jump. She can jump at most 100,000 times because she gets tired by jumping.

Carrots are planted at position x if and only if x is divisible by 1,000,000,007 (i.e. carrots are planted at position 0, position 1,000,000,007, position 2,000,000,014, and so on). Return the minimal number of jumps required to reach a carrot. If it's impossible to reach a carrot using at most 100,000 jumps, return -1.

Definition

Class:	CarrotJumping
Method:	theJump
Parameters:	int
Returns:	int
Method signature:	int theJump(int init)
(be sure your method is public)

Constraints

-

init will be between 1 and 1,000,000,006, inclusive.

Examples

0)

125000000

Returns: 1

She can jump from 125000000 to 1000000007.

1)

281250001

Returns: 2

281250001 -> 1125000007 -> 9000000063

2)

18426114

Returns: 58

3)

Returns: 478

4)

705616876

Returns: 100000

5)

852808441

Returns: -1

She can't reach any carrot by making at most 100,000 jumps.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KiwiJuice

Dynamic Programming, Math

Used in:

Member SRM 478

Used as:

Division I Level Two

Writer:

rng_58

Testers:

liympanda , konqueror , ivan_metelsky , keshav_57

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11019

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14187&pm=11019

Problem Statement

Taro has prepared delicious kiwi fruit juice. He poured it into N bottles numbered from 0 to N-1. Each bottle has a capacity of C liters, and he poured bottles[i] liters of kiwi juice into the i-th bottle initially. Taro will sell these bottles after performing an arbitrary number of operations of the following type (possibly zero). In each operation, he chooses two distinct bottles A and B, and pours kiwi juice from bottle A to bottle B until either bottle A becomes empty or bottle B becomes full, whichever happens earlier.

If a bottle contains x liters of kiwi juice at the end (where x is an integer between 0 and C, inclusive), then Taro can sell the bottle for prices[x] dollars. Return the maximum amount of money he can earn.

Definition

Class:	KiwiJuice
Method:	theProfit
Parameters:	int, int[], int[]
Returns:	int
Method signature:	int theProfit(int C, int[] bottles, int[] prices)
(be sure your method is public)

Constraints

-

C will be between 1 and 49, inclusive.

-

bottles will contain between 1 and 15 elements, inclusive.

-

Each element of bottles will be between 0 and C, inclusive.

-

prices will contain exactly C + 1 elements.

-

Each element of prices will be between 0 and 1,000,000, inclusive.

Examples

0)

{5, 8}

{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10}

Returns: 10

If Taro pours kiwi juice from bottle 0 to bottle 1, then bottle 0 will contain 3 liters of kiwi juice and bottle 1 will contain 10 liters of kiwi juice. He can sell bottle 1 for 10 dollars.

1)

{5, 8}

{0, 0, 0, 0, 0, 10, 10, 10, 10, 10, 10}

Returns: 20

Sell both bottles without pouring.

2)

{4, 5, 3, 7}

{14, 76, 12, 35, 6, 94, 26, 3, 93, 90, 420}

Returns: 625

It is possible that a bottle containing lesser juice is more expensive.

3)

{0}

{1000000, 1000000}

Returns: 1000000

4)

{2, 47, 24, 14, 0, 32, 9, 12, 31, 46, 39, 12, 16, 22, 29}

{428668, 995687, 128567, 37241, 496916, 238624, 304781, 997819, 85856, 417008,
398570, 951499, 750349, 333625, 927594, 188616, 942498, 259414, 654344, 354809,
25303, 226854, 98578, 207140, 305527, 358343, 393213, 256248, 282644, 103327,
667191, 103402, 609183, 619323, 189127, 518006, 778846, 400460, 128334, 795097,
605203, 669142, 121825, 934404, 837430, 554265, 610818, 546228, 80784, 949440}

Returns: 12873962

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ProductsOfDigits

Dynamic Programming, Simple Math

Used in:

TCO10 Round 4

Used as:

Division I Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11015

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14282&pm=11015

Problem Statement

Given a positive integer N, let P(N) denote the product of all digits in the decimal representation of N. For example, P(4256) = 4 * 2 * 5 * 6 = 240, P(2112) = 2 * 1 * 1 * 2 = 4 and P(100) = 1 * 0 * 0 = 0.

Consider the infinite sequence S = (P(1), P(2), P(3), ...). Given a int[] prod containing exactly M elements, find the first occurrence of (prod[0], prod[1], ..., prod[M-1]) in S as a consecutive subsequence. In other words, return the smallest positive index X such that P(X + i) = prod[i] for all i between 0 and M-1, inclusive. The constraints will guarantee that at least one such X exists.

Definition

Class:	ProductsOfDigits
Method:	firstOccurrence
Parameters:	int[]
Returns:	long
Method signature:	long firstOccurrence(int[] prod)
(be sure your method is public)

Notes

-

It can be shown that under the constraints of this problem, the return value will always fit within a 64-bit signed integer datatype.

Constraints

-

prod will contain between 1 and 50 elements, inclusive.

-

Each element of prod will be between 0 and 1,000,000,000, inclusive.

-

There will be at least one occurrence of (prod[0], ..., prod[M-1]) in S as a consecutive subsequence, where M is the number of elements in prod.

Examples

0)

{1, 2, 3, 4, 5}

Returns: 1

Since P(1) = 1, P(2) = 2, ..., P(5) = 5, we have that S starts with an occurrence of (1, 2, 3, 4, 5).

1)

{9, 0, 1}

Returns: 9

P(9) = 9, P(10) = 0, P(11) = 1.

2)

{0, 0, 0, 0}

Returns: 100

All numbers between 100 and 103, inclusive, have a 0 in their decimal representations.

3)

{288}

Returns: 489

4 * 8 * 9 = 288.

4)

{108864, 127008, 145152, 163296, 0, 22680, 45360, 68040, 90720}

Returns: 789946

5)

{1}

Returns: 1

6)

{0, 1, 2, 3, 4, 5}

Returns: 10

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

YetAnotherRobotSimulation

Brute Force, Dynamic Programming, Math

Used in:

TCO10 Semi 2

Used as:

Division I Level One

Writer:

gojira_tc

Testers:

SnapDragon , Rustyoldman , marek.cygan , timmac , ivan_metelsky , Egor

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11014

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14285&pm=11014

Problem Statement

Manao has constructed a robot which can move on a plane and has a remote control device. The only instructions the robot understands are "UP", "DOWN", "LEFT" and "RIGHT". If (x, y) is the robot's current location, then after receiving an "UP" instruction, it will move to (x, y+1). Similarly, after receiving "DOWN", "LEFT" and "RIGHT" instructions, it will move to (x, y-1), (x-1, y) and (x+1, y), correspondingly. Unfortunately, it seems that the robot's receiving device sometimes malfunctions. When an instruction is sent to the robot, there is a 1/2 probability that it receives an instruction and performs it, and there is a 1/2 probability that its receiving device malfunctions, in which case the robot will remain in its current position.

The robot is initially located in (0,0). You are given a set of points on the plane. The coordinates of the i-th point are (locationsX[i], locationsY[i]). Manao wants to get his robot in one of these locations. In order to do it, he will choose a fixed sequence containing exactly L instructions and will send all of them, in order, to the robot (some of the instructions might be performed by the robot and some might be ignored due to the malfunction). The quality of a sequence is defined as the probability that the robot finishes in one of the given locations after Manao sends the entire sequence of instructions. Return the maximum possible quality of a sequence of length L.

Definition

Class:	YetAnotherRobotSimulation
Method:	getMaximumProbability
Parameters:	int, int[], int[]
Returns:	double
Method signature:	double getMaximumProbability(int L, int[] locationsX, int[] locationsY)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

-

You can assume that when Manao sends an instruction to the robot, whether its receiving device will malfunction or not does not depend on the robot's behaviour for each of the previously sent instructions.

Constraints

-

L will be between 1 and 50, inclusive.

-

locationsX will contain between 1 and 50 elements, inclusive.

-

Each element of locationsX will be between -100 and 100, inclusive.

-

locationsY will contain the same number of elements as locationsX.

-

Each element of locationsY will be between -100 and 100, inclusive.

-

Points (locationsX[i], locationsY[i]) will be distinct.

Examples

0)

{1,2,2}

{1,1,0}

Returns: 0.5

One of the optimal sequences is {"UP","RIGHT","RIGHT"}. If the robot's receiving device malfunctions at the first instruction, then the remaining two instructions should surely be performed in order to reach location 2. The probability of this case is 1/8. On the other hand, if the first instruction is successfully accomplished, only failing both of the remaining instructions will get the robot nowhere, which means a 3/8 success chance. Summing these up, we obtain 1/2.

1)

{0,0,0,0}

{0,1,2,3}

Returns: 0.9375

A possible strategy is pushing "UP" four times and "DOWN" once.

2)

{0}

{0}

Returns: 0.5

Sometimes malfunctioning is desirable.

3)

{2,3,3}

{1,1,0}

Returns: 0.41015625

4)

{6,7,12,-21,5,5,2,4}

{4,5,-2,4,5,12,5,7}

Returns: 0.1323284485260956

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BunnyExam

Brute Force, Graph Theory, Simple Math

Used in:

SRM 487

Used as:

Division I Level Two

Writer:

lyrically

Testers:

PabloGilberto , ivan_metelsky , soul-net

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11011

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14240&pm=11011

Problem Statement

Bunnies like programming and they sometimes make useful devices.

One group of bunnies made a device called RandomAnswerer for their final exam. They cannot solve any of the problems, so they will try to answer the questions randomly.

There are m problems numbered 1 through m. The answer for each problem will be one of the integers between 1 and k, inclusive. We also know the following:

The answer to problem x is different from that of problem x + 1, where 1 <= x < m.
We have a int[] linkage containing N * 2 elements. For each i, where 0 <= i < N, the answer to problem linkage[i * 2] is the same as that of linkage[i * 2 + 1]. Note that all elements in linkage are distinct.

RandomAnswerer makes a sequence of m answers and shows it to the bunnies. Both the sequence produced by RandomAnswerer and the sequence of correct answers are chosen among all possible sequences of m answers that agree with the information above, randomly (all of them have the same probability of being chosen) and independently. Return the expected number of correct answers bunnies get. If there is any contradiction in the information, i.e., there are no sequences of answers that agree with all of it, return -1.0 instead.

Definition

Class:	BunnyExam
Method:	getExpected
Parameters:	int, int, int[]
Returns:	double
Method signature:	double getExpected(int m, int k, int[] linkage)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

m and k will each be between 1 and 1,000,000,000, inclusive.

-

linkage will contain between 0 and 20 elements, inclusive.

-

linkage will contain an even number of elements.

-

Each element of linkage will be between 1 and m, inclusive.

-

All elements of linkage will be distinct.

Examples

0)

{ 1, 3 }

Returns: 1.5

Here problems 1 and 2 have different answers, problems 2 and 3 have different answers and problems 1 and 3 have the same answer.

The answers will be either (1, 2, 1) or (2, 1, 2), so the number of correct answers bunnies get will be 3 or 0 with equal probability.

1)

{ 1, 4 }

Returns: -1.0

This is impossible.

2)

{ }

Returns: 0.25

linkage may be empty.

3)

1000000000

{ 11, 13, 2010, 487 }

Returns: -1.0

4)

{ 32, 16, 8, 4, 2, 1 }

Returns: -1.0

5)

{ 1, 3, 7, 9, 13, 10, 6, 2  }

Returns: 4.333333333333333

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BottlesOnShelf

Math, Simple Search, Iteration

Used in:

Member SRM 491

Used as:

Division II Level Three

Writer:

Mimino

Testers:

Rustyoldman , ivan_metelsky , rng_58 , wrong

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11008

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14244&pm=11008

Problem Statement

There are N bottles on a shelf (numbered from 1 to N). Some little kids are playing football near the shelf. Sometimes it happens that their ball hits the shelf and every bottle with an index between left[i] and right[i], inclusive, that is also divisible by damage[i] falls on the ground and breaks.

Given N and the arrays left, right and damage. The ball has hit the shelf exactly M times, where M is the size of each of the three arrays. Count and return the number of bottles broken by the kids.

Definition

Class:	BottlesOnShelf
Method:	getNumBroken
Parameters:	int, int[], int[], int[]
Returns:	int
Method signature:	int getNumBroken(int N, int[] left, int[] right, int[] damage)
(be sure your method is public)

Constraints

-

N will be between 1 and 1,000,000,000, inclusive.

-

left, right and damage will each contain between 1 and 18 elements, inclusive.

-

left, right and damage will contain the same number of elements.

-

Each element of left and right will be between 1 and N, inclusive.

-

For each i, left[i] will be less than or equal to right[i].

-

Each element of damage will be between 1 and 42, inclusive.

Examples

0)

{1}

{7}

{2}

Returns: 3

Every second bottle has been broken by the kids. The shelf looks like this (.-unbroken, X-broken):

    .X.X.X.

1)

{1,1}

{7,7}

{2,3}

Returns: 4

Every bottle dividible by 2 or 3 has been broken.

    .XXX.X.

2)

{1,1,1}

{7,7,7}

{2,3,6}

Returns: 4

Now every bottle divisible by 6 has been broken also, but the result is the same as in last example.

    .XXX.X.

3)

{1,6}

{5,10}

{1,7}

Returns: 6

From the first half of the shelf, every bottle has been broken. From the second half only the bottle with number 7 has been broken.

    XXXXX.X...

4)

{4}

{4}

{7}

Returns: 0

None bottle has been broken.

5)

1000000000

{1}

{1000000000}

{1}

Returns: 1000000000

Every bottle has been broken.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OneDigitDifference

Simple Math

Used in:

Member SRM 491

Used as:

Division II Level One

Writer:

Mimino

Testers:

Rustyoldman , ivan_metelsky , rng_58 , wrong

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11007

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14244&pm=11007

Problem Statement

We say that two integer numbers differ from each other by one digit, when in their decimal notation, possibly with leading zeros, they will differ in exactly one position. For example numbers 128 and 28 differ by one digit:

But numbers 2047 and 40 differ by two digits:

Given the number N, find and return the smallest possible non-negative number M, such that number N and M differ from each other by exactly one digit.

Definition

Class:	OneDigitDifference
Method:	getSmallest
Parameters:	int
Returns:	int
Method signature:	int getSmallest(int N)
(be sure your method is public)

Constraints

-

N will be between 0 and 2,000,000,000, inclusive.

Examples

0)

Returns: 0

0 is the smallest non-negative number and differs by only one digit.

1)

Returns: 1

The result number is not always smaller than N.

2)

900000123

Returns: 123

Leading zeros in the result are okay:

900000123

000000123

3)

Returns: 0

Leading zeros are okay also with 0 as a result:

4)

Returns: 7

5)

1907654321

Returns: 907654321

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ChickenOracle

Simple Math, Simple Search, Iteration

Used in:

SRM 481

Used as:

Division I Level One , Division II Level Two

Writer:

vexorian

Testers:

PabloGilberto , ivan_metelsky , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=11004

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14234&pm=11004

Problem Statement

This time, instead of solving an easy problem with a known solution, you will be in charge in solving an old problem with a solution which was unknown to this date. The old question is whether the egg or the chicken came first. This question has been very difficult to answer over the ages, but a chance has finally come: It is said that a new oracle has appeared which knows everything.

You tried asking the question to the oracle, but the oracle refused to answer, arguing that it has already answered the question to n other people and is tired of answering that question. Not to give up, you decided to interview each of the n people. Of them, eggCount people told you that the answer was "The egg", while the remaining n-eggCount people claimed that the answer was "The chicken". Confused by the results, you asked the oracle a second time. The oracle still refused to answer the question, but instead explained the results: In order to hide the truth to those unworthy, the oracle has intentionally given the wrong answer to exactly lieCount people. On the other hand, also to avoid sharing the secret, exactly liarCount people (not necessarily those that were told the right answer by the oracle) have intentionally given you the opposite answer to the one given to them by the oracle.

You are still suspiscious that the explanation given by the oracle is another lie. Given ints n, eggCount, lieCount and liarCount, find out if scenarios exist such that "The egg" or "The chicken" is the correct answer. If there exist scenarios such that either answer is correct, return "Ambiguous" (quotes for clarity). If only one answer has a possible scenario, return "The egg" or "The chicken" (quotes for clarity) depending on the answer. If neither of the answers has a possible scenario, return "The oracle is a lie".

Definition

Class:	ChickenOracle
Method:	theTruth
Parameters:	int, int, int, int
Returns:	String
Method signature:	String theTruth(int n, int eggCount, int lieCount, int liarCount)
(be sure your method is public)

Constraints

-

n will be between 1 and 1000000, inclusive.

-

eggCount, lieCount and liarCount will each be between 0 and n, inclusive.

Examples

0)

Returns: "The egg"

In this case, every person has answered correctly.

1)

Returns: "The oracle is a lie"

According to the oracle, it has told the correct answer to all 60 people and then 30 of them lied to you. However, it contradicts the fact that 40 people have told you one answer and 20 people have told another one.

2)

Returns: "The chicken"

3)

Returns: "Ambiguous"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

QuickSort

Dynamic Programming, Math, Recursion

Used in:

SRM 486

Used as:

Division I Level Two

Writer:

soul-net

Testers:

PabloGilberto , battyone , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10996

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14239&pm=10996

Problem Statement

The purpose of this problem is to evaluate the performance of randomized quick sort in a given instance. Randomized quick sort is an algorithm that takes as input an array of N distinct integers and sorts them in ascending order. We will only consider inputs where all elements to be sorted are different.

The randomized quick sort we will evaluate works as follows:

quick-sort(L)
   if L has less than 2 elements
      return L
   otherwise:
      let P be an element of L chosen at random with uniform distribution
      let L0 be the list of all elements of L that are strictly less than P, in the same relative order as in L
      let L1 be the list of all elements of L that are strictly greater than P, in the same relative order as in L
      let L2 be quick-sort(L0)
      let L3 be quick-sort(L1)
      return the concatenation of L2, P and L3, in that order

We will define the cost of a call to quick-sort(L) as its individual cost, plus the cost of each of its recursive calls (if any). The individual cost of a call to quick-sort(L) is the number of elements less than P that are located to the right of P in L plus the number of elements greater than P that are located to the left of P in L.

You will be given a int[] L, which represents the input to be evaluated. Return the expected cost of quick-sort(L) when run over that list.

Definition

Class:	QuickSort
Method:	getEval
Parameters:	int[]
Returns:	double
Method signature:	double getEval(int[] L)
(be sure your method is public)

Notes

- The returned value must have an absolute or relative error less than 1e-9.

Constraints

- L will contain between 1 and 50 elements, inclusive.

- Each element of L will be between 1 and 50, inclusive.

- All elements of L will be different.

Examples

0)

{1,2,3,4,5}

Returns: 0.0

With the elements in sorted order, the cost is 0 for any possible combination of pivot selections.

1)

{1,2,4,3,5,6}

Returns: 1.0

The 3 and the 4 need to be swapped. That can only happen when P=3 or P=4 are selected. All other selections for P add 0 cost, so the overall cost is always 1.

2)

{3,2,1}

Returns: 2.6666666666666665

If the first choice is P=1, the cost will be 2 for {2,3} being on its left plus 1 for recursively sorting the {3,2} list. If the first choice is P=3, an analogous situation also leads to an overall cost of 3. If the first choice is P=2, however, the cost is two because all other elements are in the wrong position, but after that, the recursive calls are free of charge because both lists have one element. Therefore, the expected cost is 2/3*3 + 1/3*2 = 2+2/3.

3)

{50,40,30,20,10,15,25,35,45}

Returns: 11.07698412698413

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RepresentableNumbers

Math

Used in:

TCO10 Round 2

Used as:

Division I Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10994

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14280&pm=10994

Problem Statement

Let's call a positive integer A totally odd if each digit in its decimal notation is odd, i.e., one of 1, 3, 5, 7, 9. For example, integers 9, 513, 77777 are totally odd and integers 2 and 99990 are not.

A positive integer N is called representable if it can be represented as N = A + B, where both A and B are totally odd numbers. For example, 2 = 1 + 1 and 4752 = 1377 + 3375 are representable, while 3 and 220 are not.

Given an int X, return the smallest representable number that is greater than or equal to X.

Definition

Class:	RepresentableNumbers
Method:	getNext
Parameters:	int
Returns:	int
Method signature:	int getNext(int X)
(be sure your method is public)

Constraints

-

X will be between 1 and 100,000,000, inclusive.

Examples

0)

Returns: 2

1 is not representable, and 2 = 1 + 1 is representable.

1)

Returns: 1000

999 is not representable, and 1000 = 999 + 1 is representable.

2)

Returns: 2000

2000 = 1999 + 1 is representable.

3)

Returns: 4222222

All numbers between 4201234 and 4222221 are not representable, and 4222222 = 3111111 + 1111111 is representable.

4)

10101010

Returns: 10102222

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OneRegister

Greedy, Simple Math

Used in:

SRM 486

Used as:

Division I Level One , Division II Level Two

Writer:

soul-net

Testers:

PabloGilberto , battyone , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10992

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14239&pm=10992

Problem Statement

You've designed a computer and implemented all the common arithmetic operators: addition, subtraction, multiplication and integer division. However, your budget was very limited, so you could only afford to place a single register in the computer. The register can store any non-negative integer value. Since there is only one register, there is no need to identify the store location or the operands of each operation or its result. The programming language has four instructions: '+', '-', '*' and '/'. Each instruction performs the corresponding operation using the value in the register as both its parameters. It then stores the result in the same register, overwriting the previous content.

A program for your computer is a sequential list of zero or more instructions. You want to show that, even with its limitations, your newly constructed computer is powerful. You will be given two ints s and t. Return the shortest program that finishes with a value of t in the register if it contained s before executing. If there is more than one possible answer, return the one that comes earliest lexicographically. If there is no program that can do the job, return ":-(" (quotes for clarity) instead.

Definition

Class:	OneRegister
Method:	getProgram
Parameters:	int, int
Returns:	String
Method signature:	String getProgram(int s, int t)
(be sure your method is public)

Notes

-

A string comes lexicographically earlier than another one of the same length if and only if it contains a symbol with a lower ASCII code in the first position at which they differ. The operators in ascending order of ASCII code are: '*', '+', '-' and '/'.

-

If the division operation is used when the register contains a zero, the program will give an error and terminate with a zero value in the register.

Constraints

-

s and t will be between 1 and 1000000000 (10^9), inclusive.

Examples

0)

Returns: "+*+"

The program executes as follows:

 Reg | Ins | Res
-----+-----+-----
   7 |  +  |  14
  14 |  *  | 196
 196 |  +  | 392

1)

Returns: "/+***"

2)

Returns: "**"

3)

Returns: ""

A trivial program.

4)

Returns: ":-("

No solution.

5)

Returns: "/"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheChroniclesOfAmber

Math, Search

Used in:

TCO10 Round 3

Used as:

Division I Level Two

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10990

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14281&pm=10990

Problem Statement

There is an amazing series of stories called "The Chronicles of Amber" written by Roger Zalazny. The stories tell us about the princes and princesses of the kingdom of Amber. The princes possess superhuman abilities and magical artifacts. For example, each prince carries a deck of Tarot cards, where each trump card has the image of a prince. A prince can contact another prince using a trump card, and if the second prince agrees, the first prince will teleport instantaneously to the exact location of the second prince. This teleportation is called a connection, and at any given time T, only a single connection can happen in the entire kingdom. Note that T is not necessarily an integer, so if two times, t₁ and t₂, are different but very close to each other, a connection can happen at t₁ and another connection can happen at t₂.

A battle between the forces of Amber and Chaos is about to begin, and each prince of Amber has been assigned a location where he must be during the battle. The territory where the battle will occur can be represented as an infinite plane, where locations are points on the plane. The i-th prince is currently located at point (princeX[i], princeY[i]), but he must be at point (destinationX[i], destinationY[i]). Princes can travel using two methods: riding, and teleporting as described above. Princes ride at a speed of 1 distance unit per second. The riding distance between any two locations is the Euclidean distance between their points. Princes can all ride simultaneously.

Assume that each prince has a complete deck of Tarot cards and can therefore make a connection with any other prince. All the princes have united for the sake of the great battle, and will agree to all connection requests. The princes want to move in such a way that they all reach their destination points as soon as possible. More precisely, they consider a moment in time, T (measured in seconds, where the initial time is 0), to be enough for them to reach their destination points if they can collaborate and organize their riding and/or teleports so that each of them will be at his respective destination point at exactly moment T. Return the smallest moment in time, T₀, such that all moments T > T₀ are enough for them to reach their destination points.

Definition

Class:	TheChroniclesOfAmber
Method:	minimumTime
Parameters:	int[], int[], int[], int[]
Returns:	double
Method signature:	double minimumTime(int[] princeX, int[] princeY, int[] destinationX, int[] destinationY)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

princeX will contain between 1 and 50 elements, inclusive.

-

Each element of princeX will be between 0 and 10000, inclusive.

-

princeY will contain the same number of elements as princeX.

-

Each element of princeY will be between 0 and 10000, inclusive.

-

destinationX will contain the same number of elements as princeX.

-

Each element of destinationX will be between 0 and 10000, inclusive.

-

destinationY will contain the same number of elements as princeX.

-

Each element of destinationY will be between 0 and 10000, inclusive.

Examples

0)

{1,5,5}

{0,0,0}

{1,1,0}

{4,2,3}

Returns: 4.0

One of the possible scenarios for this testcase is the following. Prince 0 starts riding directly north toward his destination point while the other two princes remain stationary. When he gets to point (1,2), prince 1 makes a connection with him and teleports to (1,2), which is prince 1's destination. When he gets to point (1,3), prince 2 makes a connection with him and teleports to (1,3). Prince 2 then starts riding west. Prince 0 reaches his destination of (1,4) at the same time that prince 2 reaches his destination of (0,3).

Note that even though time moment 4 is itself enough for the princes to reach their destination points, the least T₀ satisfying the problem's conditions is still 4.

1)

{0,0,0}

{1,2,3}

{0,0,0}

{0,2,4}

Returns: 1.0

Tarot cards will not help here. Princes 0 and 2 just have to ride to their destination points.

2)

{0,0,0}

{1,2,3}

{0,0,0}

{4,2,0}

Returns: 1.0

The solution is as follows. First prince 1 teleports to prince 2's location, then prince 2 teleports to prince 0's location and finally prince 0 teleports to prince 1's location. After this, they move directly to their destination points. In this case, each moment T > 1 is enough for them to reach their destination points, so the correct return value is T₀ = 1.

3)

{0,3,5}

{0,4,0}

{3,5,0}

{4,0,0}

Returns: 4.47213595499958

Each prince is located in the other's destination point. The optimal strategy is: prince 2 teleports to prince 0's location, then prince 0 teleports to prince 1's location, and then prince 1 rides to his destination point.

4)

{3629,6751,8655,5115,7809,6759,7133,1810,6102,2539,1777,242}

{5294,180,988,7780,1635,7904,845,7405,4800,2567,4795,2339}

{8723,9275,6705,5875,7981,7666,1158,4135,17,2984,5086,3570}

{6166,53,5980,4499,412,9074,8190,847,650,9158,9116,4396}

Returns: 2622.582696503582

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BankLottery

Dynamic Programming, Simple Math

Used in:

TCO10 Round 4

Used as:

Division I Level One

Writer:

vexorian

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10988

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14282&pm=10988

Problem Statement

Most of the local Feudalian banks have started using a lottery system instead of paying interest in the traditional way. It's a less expensive system for the banks, and most people don't seem to notice the difference. One bank's current system works as follows.

After the end of each week, the bank holds a drawing. Each bank account holder is given 1 ticket per dollar in his balance. After all the tickets have been distributed, one ticket is chosen randomly. Every ticket has an equal probability of being chosen. The chosen ticket's owner wins weeklyJackpot dollars, which is immediately added to his balance.

You have just opened an account at the bank and would like to know your expected balance at some point in the future. Somehow, you were able to access the current balances of all the account holders at the bank. These balances are given in the int[] accountBalance. Your initial balance is accountBalance[0], and each of the remaining elements of accountBalance is the balance of another person at the bank. For the purposes of this problem, assume that no transactions other than those caused by the lottery system will occur, and assume that no accounts will be closed or created. Return your expected balance after weekCount weeks.

Definition

Class:	BankLottery
Method:	expectedAmount
Parameters:	int[], int, int
Returns:	double
Method signature:	double expectedAmount(int[] accountBalance, int weeklyJackpot, int weekCount)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

accountBalance will contain between 1 and 50 elements, inclusive.

-

Each element of accountBalance will be between 0 and 100000, inclusive.

-

At least one element of accountBalance will be greater than 0.

-

weeklyJackpot will be between 1 and 1000, inclusive.

-

weekCount will be between 1 and 1000, inclusive.

Examples

0)

{100,100}

Returns: 200.0

1)

{2,2,2}

Returns: 2.6666666666666665

In the first week, there is a 1/3 probability that the balances will become {3,2,2}, a 1/3 probability that they will become {2,3,2} and a 1/3 probability that they will become {2,2,3}.

In week 2, {3,2,2} will have an expected value of around 3.4286 for account 0. {2,3,2} and {2,2,3} both yield an expected value of around 2.2857 for account 0. The total expected value is around 2.66667.

2)

{1,2,3,4,5,6,7,8,9,10}

Returns: 37.36363636363636

3)

{0,200,200,0,300,300,600}

Returns: 0.0

With no money in the account, the probability to win the lottery will always be 0.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SequenceOfCommands

Brute Force, Simple Math, Simulation

Used in:

SRM 473

Used as:

Division I Level One , Division II Level Two

Writer:

misof

Testers:

PabloGilberto , bmerry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10979

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14155&pm=10979

Problem Statement

You are standing on some arbitrary point in the infinite plane.

You are given a String[] commands that contains the commands you have to execute. Each character of each element of commands is one command. The commands must be executed in the given order: first you execute all commands in the first element of commands one by one, then those in the second element, etc.

There are only three types of commands: 'S' means "step forward", 'L' means "turn 90 degrees to the left", and 'R' means "turn 90 degrees to the right". All your steps have the same length.

You will be executing the commands forever: after you execute the last character of the last element of commands, you will always start from the beginning again.

We say that your path is bounded if there is some positive real number R such that while executing the infinite sequence of steps you will never leave the circle with radius R steps and center at your starting location.

Given the String[] commands, your method should determine whether your path will be bounded or not. Return the String "bounded" (quotes for clarity) if the path is bounded and "unbounded" if it is not.

Definition

Class:	SequenceOfCommands
Method:	whatHappens
Parameters:	String[]
Returns:	String
Method signature:	String whatHappens(String[] commands)
(be sure your method is public)

Constraints

- commands will contain between 1 and 50 elements, inclusive.

- Each element in commands will contain between 1 and 50 characters, inclusive.

- Each character in each element of commands will be one of 'S', 'L', and 'R'.

Examples

0)

{"L"}

Returns: "bounded"

You are standing on the same spot forever, and in each step you take a turn 90 degrees to the left. This path is clearly bounded.

1)

{"SRSL"}

Returns: "unbounded"

Imagine that you start executing the commands facing to the north. While following this sequence you will repeatedly execute the following steps: make a step to the north, rotate right, make a step to the east, and rotate left (to face north again).

Given enough time, this path will take you arbitrarily far away from the spot where you started, hence it is unbounded.

2)

{"SSSS","R"}

Returns: "bounded"

While executing this sequence of commands, you will be walking along the boundary of a small square.

3)

{"SRSL","LLSSSSSSL","SSSSSS","L"}

Returns: "unbounded"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ChildlessNumbers

Brute Force, Math, Simple Search, Iteration

Used in:

SRM 473

Used as:

Division II Level Three

Writer:

misof

Testers:

PabloGilberto , bmerry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10978

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14155&pm=10978

Problem Statement

Let D(X) denote the sum of digits of the positive integer X. For example, D(4007) = 4 + 0 + 0 + 7 = 11.

Take any positive integer X, and let Y = X / D(X). If Y is an integer, we say that Y is the parent of X (and that X is a child of Y). For example, if X=12 then X / D(X) = 12 / (1+2) = 4, hence 4 is the parent of 12.

Note that multiple numbers can have the same parent. For example, 4 is also the parent of 36, as 36/(3+6) = 36/9 = 4.

We say that a number Y is childless if there is no positive integer X such that Y is the parent of X.

You are given two ints A and B. Find and return the count of all childless numbers that lie between A and B, inclusive.

Definition

Class:	ChildlessNumbers
Method:	howMany
Parameters:	int, int
Returns:	int
Method signature:	int howMany(int A, int B)
(be sure your method is public)

Constraints

-

A will be between 1 and 1,000,000,000, inclusive.

-

B will be between A and 1,000,000,000, inclusive.

-

B-A will be between 0 and 10,000, inclusive.

Examples

0)

Returns: 0

Each of the numbers {4,5,6,7} has at least one child. For example, 54 / (5+4) = 6, hence 6 is not childless.

1)

Returns: 0

E.g., 333 / (3+3+3) = 37.

2)

Returns: 3

In this range there are three childless numbers: 62, 63, and 65. For the other two we have 732 / (7+3+2) = 732/12 = 61 and 320 / (3+2+0) = 320/5 = 64.

3)

Returns: 1

The only childless number in this range is 276.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RightTriangle

Math, Search

Used in:

SRM 473

Used as:

Division I Level Two

Writer:

misof

Testers:

PabloGilberto , bmerry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10976

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14155&pm=10976

Problem Statement

Consider a circle in the plane.

You are given an int places. This is the number of places that are equally spaced along the perimeter of the circle, i.e., the distance between any two consecutive places is equal. The places are numbered 0 to places-1 in clockwise order, starting at an arbitrary place.

We will now draw red points in some of the places. The number of red points is given as an int points. As the number of points may be large, we will generate them using a simple process that is described below.

Finally, once all points are generated, your task is to find and return the number of right triangles that have all three vertices in red points.

To generate the points, you are given three ints a, b, and c. For n = 0, 1, 2, 3, ..., points-1, execute the following steps:

Compute P[n] = (a*n*n + b*n + c) modulo places.
Starting at P[n], find the first place in the clockwise direction that does not contain a red point.
Put a red point onto that place.

Definition

Class:	RightTriangle
Method:	triangleCount
Parameters:	int, int, int, int, int
Returns:	long
Method signature:	long triangleCount(int places, int points, int a, int b, int c)
(be sure your method is public)

Notes

-

A right triangle is a triangle with non-zero area in which one of the angles is exactly 90 degrees.

-

For any valid input the answer fits into a long (i.e., a signed 64-bit integer variable).

Constraints

-

places will be between 1 and 1,000,000, inclusive.

-

points will be between 0 and 100,000, inclusive.

-

points will not be greater than places.

-

a will be between 0 and 1,000,000, inclusive.

-

b will be between 0 and 1,000,000, inclusive.

-

c will be between 0 and 1,000,000, inclusive.

Examples

0)

Returns: 0

The points are placed on places 0, 3, and 6. The resulting triangle is not a right triangle (in fact, it is equilateral).

1)

Returns: 1

This time the red points are on places 0, 5, and 20. The only triangle determined by these points is a right triangle.

2)

Returns: 4

This time the formula for the next place always gives the output 1. Hence the points are placed on places 1, 2, 3, and 0, in this order. Each of the four triangles determined by these points is a right triangle.

3)

Returns: 0

An awful lot of obtuse triangles.

4)

Returns: 6980

Watch out for integer overflow when computing P[n].

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OnTheFarmDivTwo

Brute Force, Simple Math

Used in:

SRM 473

Used as:

Division II Level One

Writer:

misof

Testers:

PabloGilberto , bmerry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10974

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14155&pm=10974

Problem Statement

There are some chickens and some cows in Farmer John's yard.

John's daughter Susie counted that all the animals in the yard have a total of 3 heads. John's son Billy counted their legs and got a total of 8. Using their answers, Farmer John easily determined that there have to be exactly 2 chickens and 1 cow.

Write a method that will solve a general version of Farmer John's problem. You are given two ints heads and legs. Compute the number of chickens and the number of cows. Return a int[] with two elements: first the number of chickens, then the number of cows. If there is no solution, return an empty int[] instead.

Definition

Class:	OnTheFarmDivTwo
Method:	animals
Parameters:	int, int
Returns:	int[]
Method signature:	int[] animals(int heads, int legs)
(be sure your method is public)

Notes

-

If the solution exists, it is always unique.

-

A chicken has 1 head and 2 legs. A cow has 1 head and 4 legs.

Constraints

-

heads will be between 0 and 1,000,000, inclusive.

-

legs will be between 0 and 1,000,000, inclusive.

Examples

0)

Returns: {2, 1 }

Two chickens and a cow have a total of three heads and eight legs.

1)

Returns: {0, 10 }

Ten cows.

2)

Returns: { }

This test case has no solution because the number of legs is too large (or the number of heads is too small).

3)

Returns: { }

No set of animals can have one head and three legs.

4)

Returns: {0, 0 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SumRectangle

Simple Math, Simple Search, Iteration

Used in:

TCO10 Qual 3

Used as:

Division I Level One

Writer:

misof

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10948

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14278&pm=10948

Problem Statement

A sum rectangle is a rectangle divided into a grid of unit squares. Each square contains a number, and the numbers in neighboring squares always satisfy the following property:

The number in any square S that is neither in the bottom row nor in the right column can be computed as the sum of the following three numbers:

The number in the square directly below S.
The number in the square directly to the right of S.
The number in the other square adjacent to the previous two squares (the one diagonally down and to the right of S).

An example of a correctly filled sum rectangle:

+----+----+----+----+----+
| 88 | 57 | 33 | 10 |  5 |
+----+----+----+----+----+
| 18 | 13 | 11 | 12 | -7 |
+----+----+----+----+----+
|  1 |  4 | -2 |  1 | 18 |
+----+----+----+----+----+

For example, in the top left corner we have 88 = 18 + 57 + 13.

We have a secret sum rectangle. You will be given a int[] leftColumn containing the leftmost number in each row of our rectangle, from the top to the bottom. You will also be given an int[] topRow containing the topmost number in each column of our rectangle, from the left to the right. Compute and return the number in the bottom right corner. If the input is such that this number cannot be determined uniquely, return 0 instead.

Definition

Class:	SumRectangle
Method:	getCorner
Parameters:	int[], int[]
Returns:	int
Method signature:	int getCorner(int[] leftColumn, int[] topRow)
(be sure your method is public)

Notes

-

You may assume that the return value will always fit into an int (i.e., a 32-bit signed integer data type).

Constraints

-

leftColumn will contain between 1 and 10 elements, inclusive.

-

Each element of leftColumn will be between 0 and 100, inclusive.

-

topRow will contain between 1 and 10 elements, inclusive.

-

Each element of topRow will be between 0 and 100, inclusive.

-

Element 0 of leftColumn will be equal to element 0 of topRow.

Examples

0)

{88,18,1}

{88,57,33,10,5}

Returns: 18

This is the rectangle from the problem statement. The lower right corner is uniquely determined by the left column and the top row.

1)

{0,0,0,0}

{0,0,0,0}

Returns: 0

The only correct way to fill this rectangle is to place a zero into each square.

2)

{6,1}

{6,2}

Returns: 3

This is the smallest non-trivial case:

+----+----+
|  6 |  2 |
+----+----+
|  1 | ?? |
+----+----+

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TwoSidedCards

Graph Theory, Math

Used in:

SRM 472

Used as:

Division I Level Two

Writer:

rng_58

Testers:

PabloGilberto , ivan_metelsky , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10947

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14154&pm=10947

Problem Statement

There are N cards which are initially blank. First, Taro writes a distinct number between 1 and N, inclusive, on the front side of each card. The number he writes on the i-th card is taro[i]. Then, Hanako turns over all the cards and writes a distinct number between 1 and N, inclusive, on the back side of each card. The number she writes on the i-th card is hanako[i].

Now you must determine the number of distinct ways that the N cards can be arranged in a row. The cards can be placed in any order and each card can be oriented so that either its front side or back side is displayed. Two arrangements are considered distinct if the i-th card in the row shows a different number in one arrangement than it does it in the other. Return the number of distinct possible arrangements, modulo 1,000,000,007.

Definition

Class:	TwoSidedCards
Method:	theCount
Parameters:	int[], int[]
Returns:	int
Method signature:	int theCount(int[] taro, int[] hanako)
(be sure your method is public)

Constraints

-

N will be between 1 and 50, inclusive, where N is the number of elements in taro.

-

Each element of taro will be between 1 and N, inclusive.

-

taro will contain no duplicate elements.

-

hanako will contain exactly N elements.

-

Each element of hanako will be between 1 and N, inclusive.

-

hanako will contain no duplicate elements.

Examples

0)

{1, 2, 3}

{1, 3, 2}

Returns: 12

If the front side of each card is displayed, the cards will be (1,2,3), and you can get (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1) by changing the order.

If the back side of the second card is displayed, the cards will be (1,3,3), and you can get (1,3,3), (3,1,3), (3,3,1) by changing the order.

If the back side of the third card is displayed, the cards will be (1,2,2), and you can get (1,2,2), (2,1,2), (2,2,1) by changing the order.

If the back sides of both the second and third cards are displayed, the cards will be (1,3,2), and you can get (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1) by changing the order.

In total, there are 12 possibilities: (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1), (1,3,3), (3,1,3), (3,3,1), (1,2,2), (2,1,2), (2,2,1).

1)

{1, 2, 3}

{1, 2, 3}

Returns: 6

You can make 123, 132, 213, 231, 312, 321.

2)

{1, 2}

{2, 1}

Returns: 4

You can make 11, 12, 21, 22.

3)

{5, 8, 1, 2, 3, 4, 6, 7}

{1, 2, 3, 4, 5, 6, 7, 8}

Returns: 2177280

4)

{41, 22, 17, 36, 26, 15, 10, 23, 33, 48, 49, 9, 34, 6, 21, 2, 46, 16, 25, 3, 24, 13, 40, 37, 35,
50, 44, 42, 31, 12, 29, 7, 43, 18, 30, 19, 45, 32, 39, 14, 8, 27, 1, 5, 38, 11, 4, 20, 47, 28}

{19, 6, 23, 35, 17, 7, 50, 2, 33, 36, 12, 31, 46, 21, 30, 13, 47, 22, 44, 4, 25, 24, 3, 15, 20,
48, 10, 28, 26, 18, 5, 45, 49, 16, 40, 42, 43, 14, 1, 37, 29, 8, 41, 38, 9, 11, 34, 32, 39, 27}

Returns: 529165844

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SnowPlow

Graph Theory, Simple Math

Used in:

TCO10 Round 2

Used as:

Division I Level One

Writer:

misof

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10946

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14280&pm=10946

Problem Statement

Even though it is June, the city of SnowVille is facing some serious trouble: last night, lots of snow covered all the roads in the city.

The road network looks as follows: There are N important places in the city. The places are labeled 0 through N-1. Each road in the city connects two of these places. Each pair of places is connected by at most one road. Each road can contain one or more car lanes. Each road is bidirectional and the number of lanes is the same for both directions.

Sadly, all the snow plows except for one were already decommissioned for the summer. The one snow plow that is still available is in a depot at place 0.

Whenever the snow plow drives along a road, it is able to clean a single lane going in the direction in which it travels. Hence if you want to clean an entire road with K lanes going in each direction, the snow plow must drive along this road at least K times in each direction.

You are given a String[] roads that describes the road network: If there is no road between places i and j, character j of element i of roads is '0'. The maximum number of lanes a road can have in each direction is 9. If there is a road with k lanes in each direction, character j of element i of roads is 'k' (that is, '1' if there is one lane, '2' if there are two lanes, etc.)

Traversing a single lane of any single road takes the snow plow exactly one minute. Return the least number of minutes in which the snow plow can clean all lanes on all roads. If cleaning all lanes on all roads is impossible, return -1 instead.

Definition

Class:	SnowPlow
Method:	solve
Parameters:	String[]
Returns:	int
Method signature:	int solve(String[] roads)
(be sure your method is public)

Notes

- The snow plow is allowed to drive along a lane it already cleared.

- The road network does not have to be planar.

Constraints

- The number of places N will be between 2 and 50, inclusive.

- roads will contain exactly N elements.

- Each element of roads will contain exactly N characters.

- Each character of each element of roads will be between '0' and '9', inclusive.

- roads will be symmetric, i.e., for each i and j: character i of element j of roads will be equal to character j of element i of roads.

- For each i, character i of element i of roads will be '0'.

Examples

0)

{"010000",
 "101000",
 "010100",
 "001010",
 "000101",
 "000010"}

Returns: 10

The important places are connected as follows: 0-1-2-3-4-5. The only optimal solution is for the snow plow to travel from 0 to 5 and back.

1)

{"010000",
 "101000",
 "010100",
 "001020",
 "000201",
 "000010"}

Returns: 12

This time the road between places 3 and 4 has two lanes in each direction. One possible optimal schedule for the snow plow is to visit the places in the order 0,1,2,3,4,5,4,3,4,3,2,1,0, each time using a new lane.

2)

{"031415",
 "300000",
 "100000",
 "400000",
 "100000",
 "500000"}

Returns: 28

This time the snow plow can clean all lanes simply by going back and forth between 0 and each of the neighboring places a suitable number of times.

3)

{"0100",
 "1000",
 "0001",
 "0010"}

Returns: -1

There is no way to reach the road 2-3, so clearly there is no solution.

4)

{"0101",
 "1001",
 "0000",
 "1100"}

Returns: 6

In this case the road network consists of the roads 0-1, 0-3, and 1-3. It can be cleared for example by doing a circle in one direction (0-1-3-0) followed by a circle in the other direction. Note that place 2 remains unvisited.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TwoRegisters

Math, Search

Used in:

TCO10 Round 1

Used as:

Division I Level Two

Writer:

soul-net

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10937

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14279&pm=10937

Problem Statement

You have a very simple computer whose memory consists only of two registers X and Y. Each of them can store a positive integer. The computer is so simple that it only has two different instructions (between brackets is the name of each instruction):

[X] X := X + Y
[Y] Y := X + Y

As you may have imagined, both instructions compute the sum of both registers and store the result in one of them, overwriting its previous content. A program for this computer is simply a sequential list of zero or more instructions. When a program starts in this computer, both registers are initialized to 1. For instance, if the program is "XXYYX" then the following happens:

  X | Y | ins | execute
----+---+-----+------------
  1 | 1 | [X] | X := X + Y
----+---+-----+------------
  2 | 1 | [X] | X := X + Y
----+---+-----+------------
  3 | 1 | [Y] | Y := X + Y
----+---+-----+------------
  3 | 4 | [Y] | Y := X + Y
----+---+-----+------------
  3 | 7 | [X] | X := X + Y
----+---+-----+------------
 10 | 7 |

You will be given an int r. Return the shortest program for the described computer that makes register X end with value r. Register Y may contain any value. If there are several such programs, return the one that comes earliest lexicographically.

Definition

Class:	TwoRegisters
Method:	minProg
Parameters:	int
Returns:	String
Method signature:	String minProg(int r)
(be sure your method is public)

Notes

- A String comes lexicographically earlier than another one of the same length if and only if it contains a letter closer the beginning of the alphabet in the first position at which they differ.

Constraints

- r will be between 1 and 1000000 (10⁶), inclusive.

Examples

0)

Returns: "XXYYX"

The example in the problem statement.

1)

Returns: "XX"

2)

Returns: "XYYYYXX"

3)

Returns: "XYXYXYX"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Passwords

Dynamic Programming, Math

Used in:

TCO10 Round 3

Used as:

Division I Level Three

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10934

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14281&pm=10934

Problem Statement

A password is a sequence of alphanumeric characters. Count the number of different passwords of length N which contain at least L lowercase characters, at least U uppercase characters and at least D digits. Return this number modulo 1,000,000,009.

Definition

Class:	Passwords
Method:	countValid
Parameters:	int, int, int, int
Returns:	int
Method signature:	int countValid(int N, int L, int U, int D)
(be sure your method is public)

Constraints

-

N will be between 1 and 200,000, inclusive.

-

L will be between 0 and N, inclusive.

-

U will be between 0 and N, inclusive.

-

D will be between 0 and N, inclusive.

Examples

0)

Returns: 100

The only valid passwords are those consisting of digits only. There are 100 2-digit sequences.

1)

Returns: 40560

A valid password will contain exactly one lowercase and one uppercase letter and one digit. Since they can come in any order, there are 3!*26*26*10 = 40560 possible combinations.

2)

Returns: 5029440

This time, the exact number of characters of each type is undefined.

3)

Returns: 818019214

4)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SieveOfEratosthenes

Math, Search

Used in:

TCO10 Round 3

Used as:

Division I Level One

Writer:

soul-net

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10931

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14281&pm=10931

Problem Statement

The Sieve of Erathosthenes is an ancient method used to find all prime numbers between 2 and a given upper bound maxNum, inclusive. It works like this:

make a list of all numbers between 2 and maxNum, inclusive
for x = 2 to maxNum
   if x is not scratched
      for y = 2 to maxNum/x
         if x*y is not scratched, scratch x*y
      end for
   end if
end for

In this fashion, every composite number in the range will get scratched while every prime number will remain unscratched. Return the last number which gets scratched when the Sieve of Eratosthenes is run with the given maxNum.

Definition

Class:	SieveOfEratosthenes
Method:	lastScratch
Parameters:	int
Returns:	int
Method signature:	int lastScratch(int maxNum)
(be sure your method is public)

Constraints

-

maxNum will be between 4 and 2000000000 (2*10⁹), inclusive.

Examples

0)

Returns: 15

When x=2, the numbers 4, 6, 8, 10, 12, 14, 16, and 18 are scratched. When x=3, only 9 and 15 are scratched (other multiples like 6 and 12 were already scratched in a previous step). For x=5,7,11,13 and 17, there are no new scratches. Therefore, the answer is 15.

1)

Returns: 4

2, 3 and 5 are all primes, so the only scratched number is 4.

2)

Returns: 91

3)

Returns: 361

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CrazyLine

Greedy, Math, Sorting

Used in:

SRM 486

Used as:

Division II Level Three

Writer:

soul-net

Testers:

PabloGilberto , battyone , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10926

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14239&pm=10926

Problem Statement

A rigorous teacher makes all his students stand in a line before entering the classroom. Being a rigorous teacher, he makes the students line up in non-descending order by height. One time, while the students were lining up, the teacher had to go to the bathroom. The students took the opportunity to play with the teacher's head and make a crazy line. They defined the craziness of a line as the sum of the absolute difference in height between each pair of consecutive students. Since a line ordered by height has minimum craziness, they of course decided to arrange themselves in a line with maximum craziness.

You are given a int[] heights, where each element is the height of a single student. Return the maximum possible craziness of a line made by those students.

Definition

Class:	CrazyLine
Method:	maxCrazyness
Parameters:	int[]
Returns:	int
Method signature:	int maxCrazyness(int[] heights)
(be sure your method is public)

Constraints

- heights will contain between 1 and 50 elements, inclusive.

- Each element of heights will be between 1 and 1000, inclusive.

Examples

0)

{5,10,25,40,25}

Returns: 100

If the line is arranged in this order: 25-10-40-5-25, the sum of the differences is 15+30+35+20=100.

1)

{2,3,5,7,11,13,17,19}

Returns: 82

The following order is optimal: 7-17-5-13-2-19-3-11.

2)

{1,1,1,1,1,1,501}

Returns: 1000

Make sure to place the tall guy in the middle.

3)

{1000,1000,1000,1000,1000,1000,1000,1000,1000}

Returns: 0

There is not much difference.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RobotSimulation

Simple Math, Simulation

Used in:

TCO10 Qual 1

Used as:

Division I Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , soul-net

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10921

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14294&pm=10921

Problem Statement

There is an infinite field divided into 1x1 squares. A robot is standing in one of the squares.

You are going to make the robot move according to the following algorithm. Create a String S by concatenating times copies of the given String program. Then, go through all the characters of S from beginning to end. For each character, move the robot to an adjacent square in the direction indicated by the character. 'U' means up, 'D' means down, 'L' means left and 'R' means right.

After you have gone through all the characters of S, determine which squares have been visited by the robot. A square is considered visited if the robot has been in it at least once. The starting and ending squares are considered visited. Return the total number of visited squares.

Definition

Class:	RobotSimulation
Method:	cellsVisited
Parameters:	String, int
Returns:	int
Method signature:	int cellsVisited(String program, int times)
(be sure your method is public)

Constraints

-

program will contain between 1 and 10 characters, inclusive.

-

Each character in program will be one of 'U', 'D', 'L' or 'R'.

-

times will be between 1 and 200,000,000, inclusive.

Examples

0)

"RRR"

Returns: 301

The robot will move to the right 300 times, so 301 squares will be visited.

1)

"DDU"

Returns: 102

The robot will move according to the pattern "DDU" 100 times. Initially, we have 1 visited square. The first time the pattern "DDU" is applied, it adds 2 new squares, and each subsequent time this pattern is applied, only 1 new square is added. Therefore the total number of visited squares is 1 + 2 + 1 * 99 = 102.

2)

"URLD"

Returns: 3

After each repetition of the pattern "URLD", the robot returns to the initial cell. So the answer here doesn't depend on times and is always equal to 3.

3)

"UUDUDDLLDR"

Returns: 7

4)

"UUDUDDLLDR"

12345678

Returns: 37037039

5)

"RRUUULLDD"

Returns: 10810815

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheMoviesLevelOneDivOne

Simple Math

Used in:

SRM 469

Used as:

Division I Level One

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10898

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14152&pm=10898

Problem Statement

John and Brus are going to a theater to see a very interesting movie. They would like to have seats next to each other in the same row. The theater contains n rows, with m seats in each row. Rows are numbered 1 to n from front to back, and seats are numbered 1 to m from left to right. Some of the seats are already reserved, but John and Brus can book any of the available seats.

You are given int[]s row and seat. The i-th elements of row and seat are the row number and seat number of the i-th reserved seat. All remaining seats are available. Return the number of ways for John and Brus to book two available seats next to each other in the same row.

Definition

Class:	TheMoviesLevelOneDivOne
Method:	find
Parameters:	int, int, int[], int[]
Returns:	long
Method signature:	long find(int n, int m, int[] row, int[] seat)
(be sure your method is public)

Notes

-

Two bookings are considered different only if one contains a seat that the other does not contain. In other words, they don't need to decide which seat John sits in and which seat Brus sits in.

Constraints

-

n and m will each be between 1 and 1,000,000,000, inclusive.

-

row will contain between 1 and 47 elements, inclusive.

-

row and seat will contain the same number of elements.

-

Each element of row will be between 1 and n, inclusive.

-

Each element of seat will be between 1 and m, inclusive.

-

All pairs (row[i], seat[i]) will be distinct.

Examples

0)

{1, 2}

{2, 3}

Returns: 1

The first and the second seat in the second row are the only two free seats next to each other in the same row.

1)

{1, 1, 1, 2, 2, 2}

{1, 2, 3, 1, 2, 3}

Returns: 0

There are no free seats in the theater.

2)

{1}

{1}

Returns: 23

3)

{1, 9, 6, 10, 6, 7, 9, 3, 9, 2}

{7, 7, 3, 3, 7, 1, 5, 1, 6, 2}

Returns: 54

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

JingleRingle

Greedy, Simple Math

Used in:

TCO10 Qual 2

Used as:

Division I Level One

Writer:

Nickolas

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10896

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14277&pm=10896

Problem Statement

Your favorite online game operates on two types of currency - jingles and ringles. They are obtained from different sources, and players can trade them in an exchange market. Each individual trade is the result of an agreement between two people - a seller who wants to sell 1 jingle and a buyer who wants to buy it for an agreed upon integer price of X ringles. Each trade is executed as follows:

The buyer pays X ringles to the seller.
The seller pays 1 jingle to the buyer.
The seller pays a tax of floor((X * tax) / 100) ringles to the game host. The buyer pays no taxes.

You have a lot of ringles and no jingles, and you want to perform several trades to make a profit. The exchange market is described as two sets of offers. Offers from buyers are given in the int[] buyOffers, where each element is the price that some buyer is willing to pay for 1 jingle. Offers from sellers are given in the int[] sellOffers, where each element is the price some seller wants to receive for 1 jingle. You are also given the tax rate tax.

Return the maximum profit in ringles you can get after accepting some of these offers and paying the applicable taxes. Note that you can accept as many offers from sellers as you wish, but you can only accept offers from buyers if you already have enough jingles to sell. If you can't make a positive profit, return 0.

Definition

Class:	JingleRingle
Method:	profit
Parameters:	int[], int[], int
Returns:	int
Method signature:	int profit(int[] buyOffers, int[] sellOffers, int tax)
(be sure your method is public)

Notes

-

floor(X) is the largest integer which is less than or equal to X.

-

Assume that you have enough ringles to accept all offers from sellers.

Constraints

-

buyOffers and sellOffers will each contain between 0 and 50 elements, inclusive.

-

Each element of buyOffers and sellOffers will be between 100 and 10000, inclusive.

-

tax will be between 0 and 20, inclusive.

Examples

0)

{1000, 1024}

{990, 1011}

Returns: 34

You can accept offer 0 from sellOffers and buy 1 jingle for 990 ringles, and then accept offer 1 from buyOffers and sell this jingle for 1024 ringles. There are no taxes here, so your profit is 34 ringles.

1)

{1000, 1001, 1002}

{980, 981, 982}

Returns: 2

Accepting any of buyOffers makes you pay 20 ringles in taxes. If you accept offer 0 from sellOffers and offer 2 from buyOffers, you can get a profit of 2 ringles.

2)

{100, 120, 140}

{150, 170, 200}

Returns: 0

All offers from sellOffers are higher than offers from buyOffers, so no profitable trades can be done.

3)

{}

{}

Returns: 0

There are no offers.

4)

{1692, 3281, 862}

{2701, 2819, 2582, 1918, 638, 601, 1128, 2760, 1949, 3074,
  615, 2221, 1691, 3226, 1351, 1329, 556, 1060, 898, 1080,
 2494, 2379, 3148, 737, 1412, 3290, 1594, 1314, 959, 3192,
 1326, 932, 1103, 937, 1670, 2017, 1403, 1282, 2949, 2940,
 2557, 940, 2561, 1248, 2385, 541, 2382, 1309, 831}

Returns: 3905

You can accept all offers from buyOffers.

5)

{5016, 7212, 7613, 1590, 2942, 5155, 5898, 8113, 2001, 2348,
  671, 5167, 7524, 2467, 4294, 3628, 4480, 5872, 5230, 3732,
 4637, 6419, 1431, 6335, 1652, 3005, 2125, 2193, 2183, 5856,
 1795, 5441, 2079, 7114, 2290, 4025, 5943, 1695}

{2407, 5602, 1350}

Returns: 13195

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SequenceMerger

Math, Search, Sorting

Used in:

TCO10 Qual 1

Used as:

Division I Level Three

Writer:

soul-net

Testers:

PabloGilberto , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10887

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14294&pm=10887

Problem Statement

In this problem, you will be given descriptions of several integer sequences, and you will be required to return elements at certain positions of the union of all the given sequences. The union of several sequences is a sequence containing all the elements of those sequences, sorted in non-decreasing order. For each integer x, the number of occurrences of x in the union is equal to the total number of occurrences of x in all the given sequences. For example, if we are given sequences (3, 2, 2, 3), (1) and (5, 7, 1), their union is the sequence (1, 1, 2, 2, 3, 3, 5, 7).

Each of the given sequences will be an arithmetic sequence, a geometric sequence or an explicit sequence.

An arithmetic sequence is described by three positive integers A, B and C. The sequence contains exactly C elements: A, A+B, A+B+B, ..., A+B*(C-1). Formally, the sequence is { A+B*x | x an integer between 0 and C-1, inclusive}.
A geometric sequence is described by three positive integers A, B and C. The sequence contains exactly C elements: A, A*B, A*B*B, ..., A*B^(C-1). Formally, the sequence is { A*B^x | x an integer between 0 and C-1, inclusive}.
An explicit sequence is just a non-empty sequence of arbitrary positive integers.

Each sequence will be represented as a String, where the first character is 'A', 'G' or 'E', denoting arithmetic, geometric or explicit sequences, respectively. The second character will always be a space. After that is a list of positive integers, where each integer is written with no leading zeroes, consecutive integers are separated by a single space, and there are no leading or trailing spaces. In the case of arithmetic and geometric sequences, this list will always contain exactly three integers, A, B and C, in that order, as described above for each type of sequence. For explicit sequences, the list will contain one or more integers, explicitly representing the members of the sequence.

You will be given a String[] seqs, where each element represents a sequence as described in the previous paragraph, and a int[] positions, which contains a list of 1-based positions. Return a int[] containing the same number of elements as positions, such that its i-th element is the element at position positions[i] of the union of all the sequences in seqs. If the union contains less than positions[i] elements or if the element at position positions[i] of the union is strictly greater than 1000000000 (10^9), the i-th element of the return must be -1 instead. See examples for further clarification.

Definition

Class:	SequenceMerger
Method:	getVal
Parameters:	String[], int[]
Returns:	int[]
Method signature:	int[] getVal(String[] seqs, int[] positions)
(be sure your method is public)

Notes

-

The elements of the given sequences don't necessarily fit within 32-bit or 64-bit integer types.

Constraints

-

positions will contain between 1 and 50 elements, inclusive.

-

Each element of positions will be between 1 and 1000000000 (10^9), inclusive.

-

seqs will contain between 1 and 50 elements, inclusive.

-

Each element of seqs will contain between 3 and 50 characters, inclusive.

-

Each element of seqs will be formatted as described in the problem statement.

Examples

0)

{"E 1 1000000000 1000000001"}

{1,2,3,4}

Returns: {1, 1000000000, -1, -1 }

The sequence here has only 3 elements. The first two elements are returned normally. The element at position 3 is strictly greater than 1000000000, so you must return -1 in that place. There is no element at position 4, so you must also return -1 there.

1)

{"A 1 1 10", "G 1 2 4"}

{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}

Returns: {1, 1, 2, 2, 3, 4, 4, 5, 6, 7, 8, 8, 9, 10, -1 }

The arithmetic sequence is 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. The geometric sequence is 1, 2, 4, 8. Therefore, the resulting sequence is 1, 1, 2, 2, 3, 4, 4, 5, 6, 7, 8, 8, 9, 10.

2)

{"A 1000000000 1000000000 1000000000","G 100000000000000000 1000000000000 100000000000000", "E 1000000000000000 10000000 10 1111"}

{1,2,3,4,5,6,7,8,9,10}

Returns: {10, 1111, 10000000, 1000000000, -1, -1, -1, -1, -1, -1 }

Watch out for big numbers.

3)

{"G 1 1 999999999", "E 2"}

{1,999999999,1000000000}

Returns: {1, 1, 2 }

A lot of 1s and a 2.

4)

{"A 100 341 1524", "G 1 3 45235", "E 653 87 12341 8785 123 543"}

{100000,1,10,10000,100,1000}

Returns: {-1, 1, 441, -1, 28403, 334621 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RabbitProgramming

Dynamic Programming, Math

Used in:

SRM 475

Used as:

Division I Level Three

Writer:

lyrically

Testers:

PabloGilberto , ivan_metelsky , keshav_57

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10880

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14156&pm=10880

Problem Statement

Rabbits often feel lonely, so they enjoy participating in programming contests together.

Rabbit Iris is the head coach of her university's programming team. The big annual contest is going to be held next month, so she decided to hold a preliminary contest to help her decide who to put in the team.

The preliminary contest is now over, and the submissions are being reviewed. You are given a int[] points, and a String[] standings. Each element of points represents a single problem from the contest. For the j-th problem:

If points[j] is positive, then all submissions for this problem have been reviewed, and the point value of the problem is points[j]. The j-th character of the i-th element of standings is 'Y' if rabbit i correctly solved the problem, or 'N' if he did not.
If points[j] is negative, then none of the submissions for this problem have been reviewed yet, and the point value of the problem is -points[j]. The j-th character of the i-th element of standings is 'Y' if rabbit i submitted a solution (which may or may not be correct) for this problem, or 'N' if he did not.

A rabbit's score is the sum of the point values for the problems which he solved correctly. Once all the submissions are reviewed, the rabbits will be ranked according to their scores. Rabbits with higher scores will be ranked higher than rabbits with lower scores. If two rabbits have the same score, then the lower-numbered rabbit will be ranked higher. The top qualified ranking rabbits will be qualified to be members of the team. Among them, Iris will arbitrarily select selected rabbits to actually be in the team. If you consider all the possible scenarios for the problems which have not yet been reviewed, how many different teams are possible?

Definition

Class:	RabbitProgramming
Method:	getTeams
Parameters:	int[], String[], int, int
Returns:	long
Method signature:	long getTeams(int[] points, String[] standings, int qualified, int selected)
(be sure your method is public)

Notes

-

Two teams are considered different if and only if at least one rabbit belongs to exactly one of the teams.

Constraints

-

points will contain between 1 and 50 elements, inclusive.

-

Each element of points will be between -100,000 and 100,000, inclusive.

-

No element of points will be 0.

-

standings will contain between 1 and 50 elements, inclusive.

-

Each element of standings will contain exactly N characters, where N is the number of elements in points.

-

Each character in standings will be either 'Y' or 'N'.

-

qualified will be between 1 and the number of elements in standings, inclusive.

-

selected will be between 1 and qualified, inclusive.

Examples

0)

{ 1, -10 }

{ "NY", 
  "YN", 
  "YN",
  "YN" }

Returns: 5

If rabbit 0's submission for problem 1 is correct, rabbits 0, 1, and 2 are qualified, and teams { 0, 1 }, { 0, 2 }, { 1, 2 } are possible.

If it is incorrect, rabbits 1, 2, and 3 are qualified, and teams { 1, 2 }, { 1, 3 }, { 2, 3 } are possible.

1)

{ -250, -500, -1000 }

{ "YYY", 
  "YNY", 
  "YYN", 
  "YYN", 
  "YNN" }

Returns: 10

Any pairs of rabbits can be chosen.

2)

{ 5, -12, 5, -15, 10, -20, 3, -25, 7, -32, 21, -45 }

{ "YYYYYYYYYNYY", 
  "YYYNYYYYYNNN", 
  "YYYNYNYYNNYN", 
  "YYYYYNYYYYNN", 
  "YYNNYNYNYYNN", 
  "YYYNNNYYNNNN", 
  "YYNNNNYYNNNN", 
  "NNYNYYYNYNNN", 
  "NNNNNNYYYNNN", 
  "YYYNNNYYYNNN" }

Returns: 99

Example from a real programming contest.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RabbitIncreasing

Math

Used in:

SRM 475

Used as:

Division I Level Two

Writer:

lyrically

Testers:

PabloGilberto , ivan_metelsky , keshav_57

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10879

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14156&pm=10879

Problem Statement

Rabbits often feel lonely, even though they breed a lot.

A male rabbit and a female rabbit were born in July (the 7th month) of year 1, in a certain country. They were the only rabbits in the entire country, so they became a couple.

In March (the 3rd month) of every year, each couple who is strictly more than 1 year old will breed one male and one female rabbit. That is, couples born in year y will start breeding in the year y + 2.

Then, in April (the 4th month) of every year, all newly born rabbits will form couples among themselves. Each rabbit will be a member of exactly one couple, and each couple will contain one male and one female rabbit.

You are given a int[] leaving. Each element of leaving is a year in which half of all couples will leave the country in November (the 11th month). If there are an odd number of couples, n, then (n + 1) / 2 couples will leave. Older couples always have priority when leaving. This means that every couple who leaves will have an age greater than or equal to every couple who stays.

How many couples are in this country in December (the 12th month) of year k? Return the answer modulo 1,000,000,009.

Definition

Class:	RabbitIncreasing
Method:	getNumber
Parameters:	int[], int
Returns:	int
Method signature:	int getNumber(int[] leaving, int k)
(be sure your method is public)

Constraints

-

leaving will contain between 1 and 50 elements, inclusive.

-

k will be between 1 and 10,000,000, inclusive.

-

Each element of leaving will be between 1 and k, inclusive.

-

Elements of leaving will be sorted in strictly increasing order.

Examples

0)

{ 3 }

Returns: 1

The first couple will breed a pair of rabbits in March of year 3. Since there are 2 couples in November, 1 old pair will leave.

1)

{ 5, 9 }

Returns: 6

In November of year 5, 3 out of 5 couples will leave.

In November of year 9, 5 out of 10 couples will leave.

2)

{ 5, 10, 15 }

Returns: 212

3)

{ 2 }

10000000

Returns: 0

4)

{ 195, 211, 227, 230, 260, 
  297, 346, 350, 403, 411, 
  428, 485, 594, 606, 876 }

Returns: 975206486

There are a lot of rabbits. Be sure to return the answer modulo 1,000,000,009.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RabbitStepping

Simple Math

Used in:

SRM 475

Used as:

Division I Level One , Division II Level Two

Writer:

lyrically

Testers:

PabloGilberto , ivan_metelsky , keshav_57

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10878

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14156&pm=10878

Problem Statement

Rabbits often feel lonely, so one group of rabbits decided to gather together and play a game.

The game is played on a horizontal row of N cells (N >= 2), numbered 0 to N - 1 from left to right. Each cell is colored white, black or red. You are given a String field of length N, where the i-th character is the color of cell i ('W' for white, 'B' for black and 'R' for red).

There are r rabbits playing the game. The rabbits choose their starting cells randomly such that no two rabbits are on the same cell. Each subset of r distinct cells has the same probability of being chosen as their starting cells. The size of the field is the number of cells it contains (which is initially N). The following is repeated while the size of the field is greater than 2:

Each rabbit steps onto a neighboring cell. Since each cell potentially has up to two neighboring cells, the following rules are used to determine which cell the rabbit will choose:
- If a rabbit is on cell 0, she must step onto cell 1.
- If a rabbit is on cell size - 1 or size - 2, she must step onto the left neighboring cell.
- All other rabbits choose which neighboring cell to step onto according to the color of the cell they are currently on:
  - White: She must step onto the left neighboring cell.
  - Black: She must step onto the right neighboring cell.
  - Red: If this is her first move, she must step onto the left neighboring cell. Otherwise, she must return to the cell she was on immediately before she was on the current cell.
After all rabbits finished their steps, for each cell that contains more than one rabbit, all rabbits on that cell will be removed from the field.
The rightmost cell will disappear (causing the size of the field to decrease by 1). By the rules above, this cell will always be empty.

When the game ends, 0, 1 or 2 rabbits will remain on the field. Return the expected number of rabbits left on the field when the game ends.

Definition

Class:	RabbitStepping
Method:	getExpected
Parameters:	String, int
Returns:	double
Method signature:	double getExpected(String field, int r)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

field will contain between 2 and 17 characters, inclusive.

-

Each character in field will be either 'W', 'B', or 'R'.

-

r will be between 1 and N, inclusive, where N is the number of characters in field.

Examples

0)

"WRBRW"

Returns: 0.8

The initial positions of the rabbits are cells { 0, 1, 2, 3 }, { 0, 1, 2, 4 }, { 0, 1, 3, 4 }, { 0, 2, 3, 4 }, or { 1, 2, 3, 4 }.

For example, if { 0, 1, 2, 4 } is chosen, they will step as follows and 2 rabbits will remain on the field:

1)

"WWB"

Returns: 1.3333333333333333

2)

"WW"

Returns: 1.0

No moves will be performed, and one rabbit will remain alone on the field.

3)

"BBBBBBBBBB"

Returns: 0.9523809523809523

4)

"RRBRRWRRBRRW"

Returns: 0.9696969696969697

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MallSecurity

Brute Force, Graph Theory, Math

Used in:

Member SRM 468

Used as:

Division I Level Three

Writer:

keshav_57

Testers:

Rustyoldman , ivan_metelsky , mohamedafattah , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10877

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14183&pm=10877

Problem Statement

The first mall of the kingdom is about to be inaugurated in a few days. The king wants to make sure that the mall is highly secured.

The mall has N floors, numbered 1 to N. Each floor has stations which allow people to enter or leave the floor to which the station belongs. All escalators in the mall begin and end at stations of adjacent floors. To make movement of people easier, super-escalators connect stations in floor 1 to stations in floor N. Each escalator or super-escalator can be used to go upwards as well as downwards. If the i-th floor has K_i stations then the stations are numbered from 1 to K_i. The escalators and super-escalators are constructed in such a way that a person can reach any station from any other station using them.

The king wants to have as many guards in the mall as possible to make it secure. Guards can only be placed at stations and at most 1 guard can be placed at a station. Moreover, the people of the kingdom become panicky if they see more than one guard at a time. Hence, there should be no such escalator (or super-escalator) such that guards are placed at both its end stations.

You are given a String[] escDescription which when concatenated represents a comma (',') separated list of escalators and super-escalators. Every escalator (or super-escalator) is of the form "A B C". If C is less than N, the String represents an escalator from station A of floor C, to station B of floor C+1. If C is equal to N, then the String represents a super-escalator from station A of floor C (= N), to station B of floor 1. Help the king by returning the maximum number of guards he can place in the mall.

Definition

Class:	MallSecurity
Method:	maxGuards
Parameters:	int, String[]
Returns:	int
Method signature:	int maxGuards(int N, String[] escDescription)
(be sure your method is public)

Constraints

-

N will be between 10 and 50, inclusive.

-

The total number of stations in the mall will not exceed 100.

-

escDescription will contain between 1 and 50 elements, inclusive.

-

Each element of escDescription will contain between 1 and 50 characters, inclusive.

-

The concatenation of the elements of escDescription will be a comma separated list of escalators and super-escalators.

-

Each escalator and super-escalator will be given as "A B C" (quotes for clarity), where A, B and C are positive integers with no leading zeros.

-

In each escalator and super-escalator description, A will be a valid number of station located on floor C.

-

In each escalator and super-escalator description, B will be a valid number of station located on floor C + 1 (or on floor 1, if C = N).

-

In each escalator and super-escalator description, C will be between 1 and N, inclusive.

-

Each floor will have at least 1 station.

-

The stations on each floor will be numbered from 1 to K, inclusive, where K is the total number of stations on this floor.

-

Each pair of stations will be connected with at most one escalator or super-escalator.

-

It will be possible to reach any station from any other station using escalators and super-escalators.

Examples

0)

{"1 1 1,1 1 2,1 1 3,1 1 4,1 1 5,1 1 6,1 1 7,1 1 8,1 ", 
 "1 9,1 1 10"}

Returns: 5

There are 10 floors and each floor has only one station. The stations on adjacent floors are connected with escalators. The stations on floor 1 and on floor 10 are connected with a super-escalator. You can place 5 guards on stations of the following floors: 1, 3, 5, 7 and 9. Another solution is to place them on floors 2, 4, 6, 8, 10.

1)

{"1 1 1,1 1 2,1 1 3,1 1 4,1 1 5,1 1 6,1 1 7,1 1 8,1 ", 
 "1 9,1 1 10"}

Returns: 6

This time there are 11 floors and there's no super-escalator. You can place 6 guards on stations of the following floors: 1, 3, 5, 7, 9, 11.

2)

{"1 1 7,1 2 9,2 1", 
 " 8,1 2 6,1 1 8,1 2 3,1 2 2,2 ", 
 "2 4,1 1 1,2 1 2,3 2 3,1 1 5,2 1 1,4 ", 
 "1 7,1 1 10,3 2 5,1 2 5,3 3 1,", 
 "3 2 8,3 1 2,1 1 3,4 4 2,2", 
 " 4 6,4 2 5,2 3 3,6 4 1,5 2 8,1 3 6,1 3 7,", 
 "4 3 8,1 3 8,5 2 3,4 2 8,2 6 7,1 3 9,", 
 "1 1 4,6 1 1,2 3 1,5 1 5,6 1 8,5 ", 
 "2 2,3 2 10,3 3 9,1 5 2,4 1 1,1 5 10"}

Returns: 25

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CarelessSecretary

Dynamic Programming, Math

Used in:

SRM 477

Used as:

Division II Level Three

Writer:

keshav_57

Testers:

PabloGilberto , ivan_metelsky , mohamedafattah

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10875

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14157&pm=10875

Problem Statement

The king needs to distribute instructions to all his ministers. Since each minister requires a unique set of instructions, he writes a personalized letter for each minister and hands them off to his secretary to deliver.

Unfortunately, the king's secretary is a really careless fellow. He forgets that each minister has his own personalized letter, and he delivers a random letter to each minister instead. After he realizes his mistake, he begins to call the ministers one by one and asks them if they got the correct letter. So far, he has called K of the N ministers, and to his horror, none of the K ministers has received the correct letter.

The king is furious with his secretary, but he decides to give him one last chance to save his job. He asks the secretary the following question. In how many ways was it possible for him to distribute the letters so that the current situation would arise? In other words, how many different ways could the letters have been distributed such that a wrong letter went to each of the K ministers that has been called so far? Two ways are considered different if at least one minister gets a different letter. If the secretary can answer this question correctly, he can keep his job. Your job is to help the secretary by calculating the correct answer for him. Since the answer can be very large, return the answer modulo 1,000,000,007.

Definition

Class:	CarelessSecretary
Method:	howMany
Parameters:	int, int
Returns:	int
Method signature:	int howMany(int N, int K)
(be sure your method is public)

Constraints

-

N will be between 1 and 1000, inclusive.

-

K will be between 1 and N, inclusive.

-

K will be between 1 and 12, inclusive.

Examples

0)

Returns: 1

There are two ministers, and one of them must not get his own letter. Therefore, the only possibility is that they get each other's letters.

1)

Returns: 4

The minister who must not get his own letter might get any of the two remaining letters. For each possibility, there are 2 ways to give the letters to the other ministers. Hence, the answer is 2*2 = 4.

2)

Returns: 2

Three ministers, and none of them get their own letters.

3)

Returns: 2790

4)

Returns: 322560

5)

Returns: 466134693

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Islands

Simple Math, Simple Search, Iteration

Used in:

SRM 477

Used as:

Division I Level One , Division II Level Two

Writer:

keshav_57

Testers:

PabloGilberto , ivan_metelsky , mohamedafattah

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10874

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14157&pm=10874

Problem Statement

The king is trying to find new ways to generate revenue, and he is currently exploring tourism as one potential avenue. The kingdom is a group of islands, and the amount of revenue that can be generated depends on the combined total length of beaches on all the islands.

You are given a String[] kingdom consisting of '.' or '#' characters. '#' represents a land mass, whereas '.' represents water. kingdom[i][j] represents a regular-hexagon shaped area with each side of unit length. Since the cells are hexagonal in shape, the odd-numbered rows (0-based) are 'shifted' towards the right. A beach is a segment which has water on one side, and land on the other.

An example String[] and the corresponding image are given below to illustrate. The beaches are marked in red.

{"..#.##",
 ".##.#.",
 "#.#..."}

Return the combined total length of beaches on all the islands.

Definition

Class:	Islands
Method:	beachLength
Parameters:	String[]
Returns:	int
Method signature:	int beachLength(String[] kingdom)
(be sure your method is public)

Constraints

-

kingdom will contain between 1 and 50 elements, inclusive.

-

Each element of kingdom will contain between 1 and 50 characters, inclusive.

-

Each element of kingdom will contain the same number of characters.

-

Each character in kingdom will be either '.' or '#'.

Examples

0)

{".#...#.."}

Returns: 4

There are two small islands with water on two sides of each island.

1)

{"..#.##", 
 ".##.#.", 
 "#.#..."}

Returns: 19

The example in the problem statement.

2)

{"#...#.....",
 "##..#...#."}

Returns: 15

3)

{"....#.",
 ".#....",
 "..#..#",
 "####.."}

Returns: 24

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LotteryPyaterochka

Dynamic Programming, Simple Math

Used in:

SRM 466

Used as:

Division I Level Two

Writer:

Chmel_Tolstiy

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10863

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14150&pm=10863

Problem Statement

Alice likes lotteries. Her favorite lottery is Pyaterochka, which is very popular in Belarus. Each ticket in this lottery is a rectangular grid with N rows and 5 columns, where each cell contains an integer between 1 and 5*N, inclusive. All integers within a single ticket are distinct.

After the tickets are distributed, the lottery organizers randomly choose 5 distinct integers, each between 1 and 5*N, inclusive. Each possible subset of 5 integers has the same probability of being chosen. These integers are called the winning numbers. A ticket is considered a winner if and only if it has a row which contains at least 3 winning numbers.

Alice will buy a single ticket. Each possible ticket has the same probability of being sold. Return the probability that she will buy a winning ticket.

Definition

Class:	LotteryPyaterochka
Method:	chanceToWin
Parameters:	int
Returns:	double
Method signature:	double chanceToWin(int N)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

N will be between 1 and 100, inclusive.

Examples

0)

Returns: 1.0

Any ticket contains just one line with some permutation of numbers 1, 2, 3, 4, 5. Ony one set of winning numbers is possible - {1, 2, 3, 4, 5}. So the only line of any ticket contains all 5 winning numbers, and therefore each ticket is a winner.

1)

Returns: 1.0

For any set of winning numbers chosen, there's exactly one line in any ticket that contains at least 3 winning numbers.

2)

Returns: 0.5004995004995004

3)

Returns: 0.13161551092585574

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LotteryCheating

Brute Force, Simple Math, String Manipulation

Used in:

SRM 466

Used as:

Division I Level One , Division II Level Two

Writer:

Chmel_Tolstiy

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10862

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14150&pm=10862

Problem Statement

Bob likes to play the lottery, but it's so hard to win without cheating. Each lottery ticket has an identifier which contains exactly n decimal digits. If an identifier contains only '0's, it is considered a winning ticket. Otherwise, the identifier is interpreted as a positive integer X written in decimal notation (possibly with leading zeros). If X has an odd number of positive integer divisors, it is a winning ticket, otherwise, it is not. A positive integer is a divisor of X if it divides X evenly.

Unfortunately, Bob only has enough money to buy one ticket, and he cannot see the identifier before buying a ticket. Therefore, he decides to cheat by buying a ticket and modifying its identifier to make it a winning ticket. In a single change operation, he can choose one digit, erase it, and print some other digit in the same position. No other types of modifications are allowed. He can perform any number of these change operations, but he wants to perform as few as possible to minimize the risk of getting caught.

You are given a String ID, the initial identifier on Bob's ticket. Return the minimal number of change operations necessary to transform the identifier into a winning one. If the initial identifier is already a winner, return 0.

Definition

Class:	LotteryCheating
Method:	minimalChange
Parameters:	String
Returns:	int
Method signature:	int minimalChange(String ID)
(be sure your method is public)

Constraints

-

ID will contain between 1 and 10 characters, inclusive.

-

Each character in ID will be between '0' and '9', inclusive.

Examples

0)

"1"

Returns: 0

1 is the only divisor of this identifier. Since there are an odd number of divisors, it is already a winning ticket, and no changes are necessary.

1)

"1234"

Returns: 2

One possible solution is to transform "1234" into "1024". As 1024 is 2^10, it has 11 divisors: 2^0, 2^1, ..., 2^10.

2)

"9000000000"

Returns: 1

Bob can change the '9' into a '0'. The resulting identifier "0000000000" contains only '0's, so it is a winning ticket.

3)

"4294967296"

Returns: 0

The initial identifier represents the integer 2^32, so it has 33 divisors.

4)

"7654321"

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HanoiGoodAndBad

Recursion, Simple Math, Simulation

Used in:

Member SRM 482

Used as:

Division I Level Two

Writer:

pieguy

Testers:

ivan_metelsky , boba5551 , it4.kp , abal9002

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10858

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14235&pm=10858

Problem Statement

The Towers of Hanoi puzzle consists of 3 pegs and a number of disks of distinct radii. The 3 pegs are the source, spare, and target. Initially, all disks are on the source peg, in ascending order by radius from top to bottom. The goal is to move all disks to the target peg, subject to the following rules:

Only one disk may be moved at a time.
No disk may be placed on top of a smaller disk.
A move consists of taking the highest disk from one peg, and placing it onto another peg above any disks already on that peg.

Dave and Earl are each solving a Towers of Hanoi puzzle with N disks. Dave makes as few moves as possible, solving the puzzle in only 2^N-1 moves. Earl, on the other hand, encounters every possible configuration of disks exactly once during the course of solving it, thereby requiring 3^N-1 moves to solve it. Pseudocode for their respective solutions are:

solve_Dave(source, target, spare, N)
{
	if(N>0)
	{
		solve_Dave(source, spare, target, N-1)
		move a disk from source to target
		solve_Dave(spare, target, source, N-1)
	}
}

solve_Earl(source, target, spare, N)
{
	if(N>0)
	{
		solve_Earl(source, target, spare, N-1)
		move a disk from source to spare
		solve_Earl(target, source, spare, N-1)
		move a disk from spare to target
		solve_Earl(source, target, spare, N-1)
	}
}

Given N, and the number of moves Dave has made toward the solution, return the number of moves Earl must make in order to reach the same configuration of disks as Dave.

Definition

Class:	HanoiGoodAndBad
Method:	moves
Parameters:	int, int
Returns:	int
Method signature:	int moves(int N, int Dave)
(be sure your method is public)

Constraints

-

N will be between 1 and 19, inclusive.

-

Dave will be bewteen 0 and 2^N-1, inclusive.

Examples

0)

Returns: 2

Dave begins by moving a disk from the source peg to the target peg. Earl begins by moving a disk from the source peg to the spare peg, then to the target peg.

1)

Returns: 80

It takes Dave 15 moves to completely solve the puzzle with 4 disks, and Earl 80 moves.

2)

Returns: 16418

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BaseConfusion

Math, Recursion

Used in:

Member SRM 482

Used as:

Division II Level Three

Writer:

pieguy

Testers:

ivan_metelsky , boba5551 , it4.kp , abal9002

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10856

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14235&pm=10856

Problem Statement

Dave writes the numbers from M to N (inclusive) on a piece of paper in base B (see notes for details). Then he hands the paper to Earl and asks Earl to compute the sum of the numbers. Earl, however, mistakenly assumes the numbers are written in base B+1. Return the value Earl will come up with.

For example, if M is 14, N is 18, and B is 3, Dave would write:

112

120

121

122

200

Then Earl would sum the values (expressed here in base 10):

22

24

25

26

32

For a result of 129.

Definition

Class:	BaseConfusion
Method:	sum
Parameters:	int, int, int
Returns:	long
Method signature:	long sum(int M, int N, int B)
(be sure your method is public)

Notes

-

The number a_na_n-1...a₁a₀ in base B corresponds to the value a_n*Bⁿ + a_n-1*B^n-1 + ... + a₁*B + a₀. For example 120 in base 3 corresponds to the value 1 * 3² + 2 * 3 + 0 = 15 in decimal, while 120 in base 4 corresponds to the value 1 * 4² + 2 * 4 + 0 = 24 in decimal.

-

When writing numbers in bases higher than 10, it may be necessary to represent digits higher than 9. In such cases letters (a, b, c, ...) are used to represent (10, 11, 12, ...) as needed.

-

The return value is guaranteed to fit within a 64-bit signed integer datatype.

Constraints

-

M and N will be between 1 and 350000000, inclusive.

-

M will be less than or equal to N.

-

B will be between 3 and 16, inclusive.

Examples

0)

Returns: 129

The example from the problem statement.

1)

Returns: 55

Earl produces the correct answer in this case.

2)

Returns: 121

3)

Returns: 3141592653

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IsolatedPrimes

Advanced Math

Used in:

Marathon Match 58

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10844

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14226&pm=10844

Problem Statement

A prime number is a number that is divisible by only itself and one. In this problem we will say that a prime number p is x-isolated at distance (a,b) if there there are at most x primes (including p) between (p-a) and (p+b), inclusive. You are given the numbers a, b and x. Your task is to find the smallest prime p between a+2 and 2⁶³-1-b, inclusive, such that p is x-isolated at distance (a,b), and return a String which contains its decimal notation. For example, for x=2 and a=b=5, the smallest possible value is 23, as the only primes in [18,28] are 19 and 23.

Your score for each individual test case will simply be the value you return (or 0 if your value does not meet the criteria above). Invalid returns (a string which is not a prime number, a number outside of the bounds or a number which is not sufficiently isolated) result in a score of 0 and don't contribute to the overall score. Assuming your return is valid for a test case, it's contribution to your overall score will be BEST/YOU, where BEST is the best (lowest) value found for this test case by any competitors and YOU is your value. The total score will simply be the sum of these ratios over all test cases.

Definition

Class:	IsolatedPrimes
Method:	findPrime
Parameters:	int, int, int
Returns:	String
Method signature:	String findPrime(int x, int a, int b)
(be sure your method is public)

Notes

-

java.math.BigInteger.isProbablePrime(200) is used for primality testing.

-

If a test case has no valid returns, everyone will receive a 0 for that test.

Constraints

-

x is chosen uniformly at random in [1,500]

-

a and b are chosen uniformly at random in [4x,25x]

-

The size of your code is limited to 100K (102400 bytes)

-

The time limit is 20 seconds. The memory limit is 1024M.

Examples

0)

"1"

Returns: "x = 2
a = 5
b = 5
"

1)

"2"

Returns: "x = 410
a = 5954
b = 1916
"

2)

"3"

Returns: "x = 400
a = 4067
b = 9810
"

3)

"4"

Returns: "x = 87
a = 922
b = 630
"

4)

"5"

Returns: "x = 76
a = 1127
b = 546
"

5)

"6"

Returns: "x = 312
a = 7649
b = 4383
"

6)

"7"

Returns: "x = 449
a = 3232
b = 8777
"

7)

"8"

Returns: "x = 489
a = 11822
b = 8438
"

8)

"9"

Returns: "x = 126
a = 2399
b = 1183
"

9)

"10"

Returns: "x = 500
a = 12500
b = 12500
"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TurretPlacement

Simple Math, Simple Search, Iteration

Used in:

Member SRM 465

Used as:

Division I Level One , Division II Level Two

Writer:

vexorian

Testers:

ivan_metelsky , gojira_tc , boba5551 , keshav_57

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10840

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14182&pm=10840

Problem Statement

NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.

The celebrated general Archibald Waving took charge of the third army in the occidental front. After losing the first two armies, Waving has become obsessed with finding the optimal way to construct the army's two gun towers. The towers have square-shaped bases. It is possible to construct towers of various sizes, and hence the size of the base square may also vary. However, only those bases are allowed whose sides are of integer length. Each tower may be centered only at points picked from a given set of points described by int[]s x and y where the i-th point is (x[i], y[i]). Moreover, the areas of the bases of the towers should not overlap (the squares are allowed to touch each other). Note that in order to achieve this, you may select squares whose sides are not parallel to the co-ordinate axes.

Waving wants to know the number of ways in which he can position and construct the two towers. Two ways are considered different if at least one of the picked center points differs or if at least one of the picked square side sizes differs. Since it is possible to shoot in all directions from a tower, two ways differing only in the orientation of the base squares are not considered different. Help Waving by returning the total number of different ways to place the two towers.

Definition

Class:	TurretPlacement
Method:	count
Parameters:	int[], int[]
Returns:	long
Method signature:	long count(int[] x, int[] y)
(be sure your method is public)

Constraints

-

x and y will contain between 2 and 50 elements, inclusive.

-

y will contain as many elements as x.

-

Each element of x and y will be between -10000 and 10000, inclusive.

-

Each of the points described by x and y will be unique.

Examples

0)

{0,2}

{0,2}

Returns: 10

There are 10 different size combinations that can be used for the two towers as detailed in the following image. Note that in some cases it is necessary to orient towers in a way such that their sides are not paralel to the coordinate axis.

1)

{0,1,2}

{0,1,0}

Returns: 8

2)

{1,2,3,0}

{-1,-5,-7,100}

Returns: 65137

3)

{9998,-10000,10000,0}

{9998,10000,10000,0}

Returns: 2799564895

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LateProfessor

Brute Force, Math, Simulation

Used in:

SRM 467

Used as:

Division I Level One , Division II Level Two

Writer:

vexorian

Testers:

PabloGilberto , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10823

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14151&pm=10823

Problem Statement

Punctuality is not exactly one of Dr. Wesley's strengths. His student John always shows up for class at the scheduled starting time, but he never knows when Dr. Wesley will arrive. This is a problem for John because he cannot stay in the same place doing nothing for a long period of time. Therefore, he has come up with the following method to reduce the amount of time he spends waiting by the classroom door.

John arrives at time 0.
John waits for Dr. Wesley to arrive.
If after waitTime seconds Dr. Wesley has not arrived yet, John goes to take a walk for walkTime seconds.
John therefore arrives back to the classroom exactly at time waitTime + walkTime.
If Dr. Wesley has not arrived yet, John waits another waitTime seconds and then proceeds to take a new walk. The process is repeated until John becomes aware that Dr. Wesley has arrived.

Overall, John stands in front of the class door from time 0 to time waitTime, inclusive, then from time walkTime + waitTime to time walkTime + 2*waitTime, inclusive, and so on. At all other time moments he walks outside.

This has solved John's patience issues, but it has caused a new problem. When John returns from a walk, if Dr. Wesley is already in the classroom, it will appear that John has arrived late to class. Dr. Wesley does not like that, and he will deny John access to the class if he arrives lateTime or more seconds after the time at which Dr. Wesley arrived.

There are multiple variables that affect Dr. Wesley's arrival time, but for the purpose of the problem, assume that the arrival time will be a real number chosen uniformly from bestArrival to worstArrival, inclusive. Return the probability that John will be denied access to Dr. Wesley's class.

Definition

Class:	LateProfessor
Method:	getProbability
Parameters:	int, int, int, int, int
Returns:	double
Method signature:	double getProbability(int waitTime, int walkTime, int lateTime, int bestArrival, int worstArrival)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

waitTime, walkTime, lateTime and worstArrival will each be between 1 and 10000000, inclusive.

-

bestArrival will be between 0 and worstArrival, inclusive.

Examples

0)

Returns: 0.4

The professor will arrive at some random moment between 0 and 50 seconds, inclusive. During this interval, these are John's activities:

He waits from time 0 to time 20, inclusive.
He takes a walk between times 20 and 50, non-inclusive.
He arrives back at time 50.

John will only be too late if the professor arrives while he is away, and more than 10 seconds before he returns. This only happens if the professor arrives strictly between times 20 and 40. The probability that this will happen is (40-20)/(50-0) = 0.4.

1)

Returns: 0.42857142857142855

If the professor arrives between 30 and 40 seconds or between 70 and 90 seconds, John will be late to the class.

2)

Returns: 0.0

John's walking time is 40 seconds. Hence, even if the professor arrives while John is taking a walk, John will always be less than 50 seconds late.

3)

Returns: 0.6637270828498492

4)

Returns: 1.0

Dr. Wesley will always arrive at time 90 seconds. John will arrive at time 100 seconds after taking two different walks. Since the time difference is equal to 10 seconds, John will be too late.

5)

Returns: 0.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumberNeighbours

Simple Math, Simple Search, Iteration

Used in:

Member SRM 465

Used as:

Division II Level One

Writer:

boba5551

Testers:

timmac , ivan_metelsky , gojira_tc , vexorian , keshav_57

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10821

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14182&pm=10821

Problem Statement

The celebrated general Archibald Waving took charge of the second army in the occidental front. After losing the first army, Waving has become obsessed with effective organization of the army. As a part of this endeavor he has assigned numbers to each of his soldiers. He has also devised a rule which allows two soldiers to work together if and only if the numbers assigned to the soldiers are neighbouring numbers. Two numbers x and y are neighbouring numbers if there exists a permutation of digits of x and a permutation of digits of y such that they are equal if we ignore the leading zeros in the permutations. For example, the numbers 40020 and 204 are neighboring. To see this, permute the digits of 40020 to achieve 00042 and the digits of 204 to achieve 042. If you ignore the leading zeros, both numbers become equal to 42, so they are neighboring.

You are given a int[] numbers representing soldiers' numbers. Waving needs to pick two soldiers to send a telegram. He would like to know how many different pairs of soldiers are there who can work together to accomplish the task. Help Waving by returning the number of pairs of neighbouring numbers in the int[] numbers.

Definition

Class:	NumberNeighbours
Method:	numPairs
Parameters:	int[]
Returns:	int
Method signature:	int numPairs(int[] numbers)
(be sure your method is public)

Constraints

-

numbers will contain between 2 and 50 elements, inclusive.

-

Each element of numbers will be between 1 and 1,000,000, inclusive.

-

All elements of numbers will be distinct.

Examples

0)

{10, 1, 100, 20, 2, 3}

Returns: 4

The pairs of neighbouring numbers are (10, 1), (1, 100), (20, 2) and (10, 100).

1)

{204, 42, 40020, 200}

Returns: 3

2)

{1, 10, 100, 1000, 10000, 100000, 1000000}

Returns: 21

Any two numbers are neighbouring.

3)

{3, 33, 333, 3333}

Returns: 0

There are no two numbers that are neighbouring.

4)

{1024, 4021, 204, 303, 33, 603, 36, 55, 505}

Returns: 4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Cryptography

Encryption/Compression, Math, Sorting

Used in:

SRM 480

Used as:

Division II Level One

Writer:

dolphinigle

Testers:

PabloGilberto , ivan_metelsky , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10814

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14159&pm=10814

Problem Statement

TopCoder Security Agency (TSA, established today) has just invented a new encryption system! This encryption system takes as its input a list of numbers to encrypt.

You work at TSA and your task is to implement a very important part of the encryption process. You are allowed to pick one number in the input list and increment its value by 1. This should be done in such way that the product of all numbers in the list after this change becomes as large as possible.

Given the list of numbers as int[] numbers, return the maximum product you can obtain. It is guaranteed that the return value will not exceed 2^62.

Definition

Class:	Cryptography
Method:	encrypt
Parameters:	int[]
Returns:	long
Method signature:	long encrypt(int[] numbers)
(be sure your method is public)

Constraints

-

numbers will contain between 2 and 50 elements, inclusive.

-

Each element of numbers will be between 1 and 1000, inclusive.

-

The return value will not exceed 2^62.

Examples

0)

{1,2,3}

Returns: 12

If we increment the first number, we get 2*2*3 = 12. If we increment the second, we get 1*3*3 = 9. If we increment the third, we get 1*2*4 = 8. Hence, the correct return value is 12.

1)

{1,3,2,1,1,3}

Returns: 36

The elements of numbers are not necessarily unique.

2)

{1000,999,998,997,996,995}

Returns: 986074810223904000

The answer may be very big, but will not exceed 2^62.

3)

{1,1,1,1}

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FriendTour

Dynamic Programming, Greedy, Math

Used in:

SRM 476

Used as:

Division I Level Two

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10806

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14186&pm=10806

Problem Statement

Social networks have become an integral part of our lives, and Manao is no exception. Back in the times when Facebook had no news feed, Manao was spending much of his time traversing his friends' profiles. As you might know, a profile is a page which contains various information about the user. It also shows some subset of his friends. To be more precise, if a user has less than K friends, the page shows them all and if not, then only K friends are shown. The subset of K friends is chosen from the set of all friends every time somebody visits the profile, and all subsets have equal probability of being chosen.

Manao liked to perform tours of his friends' profiles. He started the tour at his profile and clicked on one of the friends visible on his page, thus moving to that friend's profile. From there, he again chose one of his friends from those visible on that page and moved to that person's profile, and so on. Manao never visited the profiles of people who were not his friends and never clicked on any of his friends' profiles twice. The tour was finished when he was not able to proceed because no unvisited profiles of his friends were visible. If Manao visited profiles of all his friends during the tour, it is considered to be completed, otherwise the tour is ruined.

Manao lives in Manglisi and there are a total of N people from Manglisi registered at Facebook (including Manao). We shall number them from 1 to N, where Manao is number 1. It is known that all friends of each person from Manglisi also live in Manglisi. You are given a String[] friends containing N elements, where the i-th element (1-based) is a space-separated list of friends of the i-th person. Manao knows the list of friends of everybody in advance. Return the probability that Manao performs a complete tour if he behaves optimally, i.e., in such a way that this probability is maximized.

Definition

Class:	FriendTour
Method:	tourProbability
Parameters:	String[], int
Returns:	double
Method signature:	double tourProbability(String[] friends, int K)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

friends will contain between 2 and 36 elements, inclusive.

-

Each element of friends will contain between 1 and 36 characters, inclusive.

-

Each element of friends will contain a space-separated list of distinct integers without leading zeros.

-

Each of the numbers in friends will be between 1 and N, inclusive. Number i will never occur in element i (1-based) of friends.

-

If number i is present in friends[j], then number j will be present in friends[i] (both indices are 1-based).

-

K will be between 1 and 36, inclusive.

Examples

0)

{"2 3 4",
 "1 3 4",
 "1 2 4",
 "1 2 3"}

Returns: 0.2222222222222222

Manao has three friends, who are all also friends with each other. Every time a profile is viewed, only one friend is shown. No matter which friend appears on Manao's profile first, the probability that Manao will continue his tour from that friend's profile is 2/3 and the probability that Manao will visit the last friend left is 1/3, which results in a total of 2/9.

1)

{"2 3 4",
 "1 3 4",
 "1 2 4",
 "1 2 3"}

Returns: 0.6666666666666666

This time, two friends are shown on each profile. No matter how Manao chooses between unvisited profiles, there is a 1/3 probability that he won't be able to complete the tour.

2)

{"3 2 4",
 "3 5 1",
 "5 2 1 4",
 "3 1 5",
 "3 2 4"}

Returns: 0.3333333333333333

Note that the friend numbers in the lists don't have to follow in increasing order. Also, unlike the previous examples, this time the outcome depends on Manao's strategy.

3)

{"3 2 4",
 "3 5 1",
 "5 2 1 4",
 "3 1 5 6",
 "3 2 4",
 "4"}

Returns: 0.3055555555555556

4)

{"6 5 4 2",
 "1 6 3 5",
 "5 4 2",
 "3 1 5",
 "2 4 3 1 6",
 "1 2 5"}

Returns: 0.73125

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BuildingWalls

Math, Simple Search, Iteration

Used in:

TCHS10 Round 3

Used as:

Division I Level Three

Writer:

vexorian

Testers:

PabloGilberto , ivan_metelsky , StevieT

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10799

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14229&pm=10799

Problem Statement

Building walls with bricks can sometimes be fun, but not in this problem. You have several bricks, some of which are 2 units wide and some of which are 3 units wide. All the bricks are 1 unit high. Your objective is to build a perfect rectangular wall with no empty spaces inside. You can stack the bricks in any pattern you want, but you are not allowed to rotate them. You are not required to use all your bricks.

You are given ints twoBricks and threeBricks, the number of 2 unit wide and 3 unit wide bricks you have, respectively. Return the total number of different perfect walls you can build. Two walls are considered different if at least one of their dimensions (width or height) is different.

Definition

Class:	BuildingWalls
Method:	countPossibilities
Parameters:	int, int
Returns:	int
Method signature:	int countPossibilities(int twoBricks, int threeBricks)
(be sure your method is public)

Constraints

-

twoBricks and threeBricks will each be between 0 and 100000, inclusive.

-

twoBricks + threeBricks will be at least 1.

Examples

0)

Returns: 3

Three different walls of height 1 can be made: One of width 2, one of width 3 and one of width 5.

1)

Returns: 11

The following sizes in (width, height) pairs are possible: (2,1), (3,1), (4,1), (5,1), (6,1), (7,1), (8,1), (10,1), (2,2), (3,2), (5,2) .

2)

Returns: 20

3)

Returns: 92

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CornersDecoding

Encryption/Compression, Math

Used in:

TCHS10 Round 2

Used as:

Division I Level Three

Writer:

Nickolas

Testers:

PabloGilberto , ivan_metelsky , StevieT

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10796

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14225&pm=10796

Problem Statement

Corners compression is a method of compressing black-and-white images to a list of so-called corners which works as follows.

The image to be compressed is a rectangular grid of pixels, where each pixel is either black or white. First the image is padded with a row of white pixels on the top and on the bottom and a column of white pixels on the left and on the right. All the following processing is done with the padded image.

Image rows are numbered from 0 (top row) to H-1 (bottom row), and image columns are numbered from 0 (left column) to W-1 (right column). Each pair of indices (i, j), 0 <= i < H-1, 0 <= j < W-1, defines a 2x2 block of pixels (i,j), (i+1,j), (i,j+1) and (i+1,j+1). To perform the compression, we consider all 2x2 blocks in the image. Blocks which contain an odd number of black pixels are classified as corners (the corresponding blocks are shown in the image below).

The compression result is the list of corners - all pairs of indices (i, j) that define a 2x2 block which is a corner. The image below shows 3 separate images with all their corners marked.

The set of corners resulting from this process, together with W and H (the dimensions of the padded image), uniquely identify the original image. To prove this, note that the image can be restored using the following process. Start with a HxW grid of pixels and set the color of the boundary pixels to white (these are the pixels of the padding rows and columns). If the rest of pixels are scanned, for example, in row-wise order (each row scanned from left to right), each pixel is the bottom-right pixel of a 2x2 block, with the other three pixels in this block being known (since they have been scanned earlier). Thus, the color of this pixel is uniquely defined by whether this block is a corner, since one color makes this block a corner, and the other doesn't.

You are given the list of corners in int[]s rows and cols. The coordinates of the i-th corner are (rows[i], cols[i]). Return the number of black pixels in the image which could have been compressed to this list of corners. If no finite image exists that could have been compressed to the given set of corners, return -1.

Definition

Class:	CornersDecoding
Method:	blackPixels
Parameters:	int[], int[]
Returns:	long
Method signature:	long blackPixels(int[] rows, int[] cols)
(be sure your method is public)

Notes

-

You are not given the dimensions of the original image (W and H), so the set of corners can be decoded to several images, but all these images will differ only due to extra white rows and columns on the bottom and right sides of the image, so they all will have the same number of black pixels.

Constraints

-

rows will contain between 0 and 50 elements, inclusive.

-

cols will contain the same number of elements as rows.

-

Each element of rows and cols will be between 0 and 100000, inclusive.

-

All corners will be distinct.

Examples

0)

{0, 0, 5, 5}

{0, 5, 0, 5}

Returns: 25

This example represents the first image from the problem statement - a solid 5x5 square of black cells.

1)

{0, 0, 0, 0, 4, 4, 5, 5}

{0, 1, 4, 5, 1, 4, 0, 5}

Returns: 13

This example represents the second image from the problem statement. Note that several corner blocks can overlap, i.e., have common pixels.

2)

{1, 1, 3, 3, 5, 5}

{1, 3, 1, 5, 3, 5}

Returns: 8

This example represents the third image from the problem statement.

3)

{0, 0, 1, 2}

{0, 2, 3, 4}

Returns: -1

No finite image could have been compressed to the given set of corners.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BouncingDiceGame

Dynamic Programming, Math, Simulation

Used in:

Member SRM 465

Used as:

Division I Level Three

Writer:

vexorian

Testers:

timmac , ivan_metelsky , gojira_tc , boba5551 , keshav_57

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10780

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14182&pm=10780

Problem Statement

The formerly celebrated general Archibald Waving has retired after losing the fifth army. His new peaceful lifestyle made him fond of board games. A particular one is a two player game in which each player has to take a checker across a sequence of cells on the board until reaching the final cell. There are n cells in the board and they are numbered from 1 to n. The dice in use has d faces and each number between 1 and d has the same probability of being the result of a dice throw. For fun purposes, Waving may play with insanely multi-faced dices. In each turn, a player throws a dice and then moves his piece up for as many positions as the face of the dice indicates. A player wins when he reaches the cell n.

Waving has been playing against his wife, Esther, who has added a new rule to the game called 'bouncing'. This rule comes into action when a player whose position is on the last cells of the board gets a dice value that is larger than necessary to reach the n-th cell. In that case, instead of winning the game, the player will bounce back to the previous cells.

Formally, if a is the current cell number in which the player's checker is located and b is the result of the dice throw then the following rules are used:

If a + b is less than n, the player moves the checker to cell (a + b).
If a + b is exactly n, the player moves the checker to cell n and hence wins the game.
If a + b is higher than n, the player moves the checker to cell (n - (a + b - n)).

Archibald has been wondering how does this rule affect the odds of winning the game at different states. You are given the number of cells n, the number of faces in the dice d, the cell on which Archibald's checker is currently located x and the cell on which Esther's checker is located y. Archibald is the next player to move. Return the probability of Archibald winning the game.

Definition

Class:	BouncingDiceGame
Method:	winProbability
Parameters:	int, int, int, int
Returns:	double
Method signature:	double winProbability(int n, int d, int x, int y)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

n will be between 10 and 5000, inclusive.

-

d, x and y will be between 1 and n-1, inclusive.

Examples

0)

Returns: 0.5417251215862328

1)

Returns: 0.6090494791666666

With a two faces dice, the bouncing aspect of the game has less of an effect and thus the probability for the first player to win is larger.

2)

Returns: 0.49158887163174947

3)

Returns: 0.6943018666666667

Even though Waving is one cell away from the goal cell, the probability is still far from 100% due to the bouncing rule.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheFansAndMeetingsDivOne

Dynamic Programming, Simple Math

Used in:

SRM 460

Used as:

Division I Level Two

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , connect4 , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10771

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14146&pm=10771

Problem Statement

John and Brus have become very famous people all over the world, especially in Bolivia. Stories written about them by a Bolivian man have become very popular in that country. John and Brus have decided to visit their fans in Bolivia, but unfortunately, they only have time to visit k cities each.

John will randomly choose k distinct cities. Each set of k cities has the same probability of being chosen. If he chooses the i-th city, he will meet between minJ[i] and maxJ[i] fans there, inclusive. Each possible number of fans is equally likely. Brus will go through the exact same process, but in his case, the number of fans he would meet in the i-th city is between minB[i] and maxB[i], inclusive. Return the probability that John and Brus will each meet the same total number of fans.

Definition

Class:	TheFansAndMeetingsDivOne
Method:	find
Parameters:	int[], int[], int[], int[], int
Returns:	double
Method signature:	double find(int[] minJ, int[] maxJ, int[] minB, int[] maxB, int k)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

minJ will contain between 1 and 40 elements, inclusive.

-

minJ, maxJ, minB and maxB will contain the same number of elements.

-

Each element of minJ, maxJ, minB and maxB will be between 1 and 40, inclusive.

-

The i-th element of minJ will be less than or equal to the i-th element of maxJ.

-

The i-th element of minB will be less than or equal to the i-th element of maxB.

-

k will be between 1 and the number of elements in minJ, inclusive.

Examples

0)

{1}

{9}

{5}

{5}

Returns: 0.1111111111111111

Brus will definitely meet five fans, and the probability of John meeting five fans as well is 1/9.

1)

{5, 2, 5, 1, 1, 2, 4, 1}

{7, 6, 7, 3, 4, 3, 5, 1}

{8, 9, 7, 11, 12, 7, 8, 40}

{9, 10, 9, 33, 14, 7, 11, 40}

Returns: 4.724111866969009E-5

The only possible same total number of fans that John and Brus can meet is 14. In order for them to meet 14 fans, John must visit cities 0 and 2 and Brus must visit cities 2 and 5. In each of these cities they must meet exactly 7 fans.

2)

{4, 7, 4}

{7, 7, 7}

{40, 40, 40}

{40, 40, 40}

Returns: 0.0

No chance to meet the same number of fans.

3)

{3, 6, 2, 1, 1, 10, 3}

{6, 9, 5, 6, 5, 10, 9}

{1, 1, 1, 1, 8, 3, 1}

{3, 9, 7, 3, 10, 6, 5}

Returns: 0.047082056525158976

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheQuestionsAndAnswersDivTwo

Simple Math

Used in:

SRM 460

Used as:

Division II Level One

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , connect4 , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10769

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14146&pm=10769

Problem Statement

John and Brus have become very famous people all over the world, especially in Bolivia. A man in Bolivia decided to write a story about them. To make the story more truthful, he set up an interview with John. He prepared a list of distinct simple "Yes" or "No" questions and he enlisted the help of two friends to transcribe the interview. Each time he asked a question, one friend wrote down the question while the other friend wrote down the answer. He was very nervous when conducting the interview, so he might have asked some of the questions multiple times. However, John's answers always remained the same for the same questions.

Unfortunately, the friend who was writing down John's answers lost his list. You are given a String[] questions, where the i-th element is the i-th question asked. In a desperate attempt to remember the answers, the Bolivian has decided to write down all the possible ways that John might have answered the questions. By doing this, he hopes that he will be able to recognize the correct combination of answers. Return the total number of combinations that he will have to write down.

Definition

Class:	TheQuestionsAndAnswersDivTwo
Method:	find
Parameters:	String[]
Returns:	int
Method signature:	int find(String[] questions)
(be sure your method is public)

Notes

-

Two questions are considered to be the same if corresponding elements of questions are absolutely the same Strings.

-

All questions are case-sensitive, i.e., lowercase and uppercase equivalents of the same letter are considered to be different characters.

Constraints

-

questions will contain between 1 and 10 elements, inclusive.

-

Each element of questions will contain between 1 and 50 characters, inclusive.

-

Each character in questions will be a lowercase letter ('a'-'z'), uppercase letter ('A'-'Z'), question mark ('?') or underscore ('_').

Examples

0)

{"How_are_you_doing?", "How_do_you_like_our_country?", "How_are_you_doing?"}

Returns: 4

There are four ways to answer this sequence of questions:

"Yes", "Yes", "Yes";
"Yes", "No", "Yes";
"No", "Yes", "No";
"No", "No", "No".

1)

{"Whazzup?"}

Returns: 2

Just a single question.

2)

{"Are_you_ready?", "Are_you_ready?", "Are_you_ready?", "Are_you_ready?"}

Returns: 2

All these questions are the same.

3)

{"Do_you_like_my_story?", "Do_you_like_my_story", "DO_YOU_LIKE_MY_STORY?", "Do__you__like__my__story?"}

Returns: 16

All these questions are distinct.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PythTriplets

Graph Theory, Simple Math

Used in:

SRM 477

Used as:

Division I Level Two

Writer:

keshav_57

Testers:

PabloGilberto , ivan_metelsky , mohamedafattah

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10766

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14157&pm=10766

Problem Statement

The prince has just been introduced to primitive pythagorean triplets.

A primitive pythagorean triplet (a, b, c) is a triplet satisfying the following properties:

a, b and c are integers
a^2 + b^2 = c^2
The greatest common divisor of a and b is 1

The prince is not very fond of mathematics. The king is trying to make mathematics fun for his son (the prince). So, the king decides to make as many toys as possible which are triangular in shape having sides (a, b, c) where (a, b, c) form a primitive pythogorean triplet. The wooden framework of the two shorter legs of the toy give the toy its shape and prevent it from breaking, hence each toy with sides of length (a, b, c) must have one wooden stick of length a and one of length b. The third side of length c is not made of wood, and therefore the king does not need a wooden stick for it.

You are given a String[] stick. Concatenate the elements of stick to get a single-space separated list of the lengths of available sticks. The king is a very loving father and would like to make the toys with his own hands. However, he is not skilled enough to cut the sticks, so he must use them in the sizes they are available. Return the maximum possible number of toys the king can make using these sticks.

Definition

Class:	PythTriplets
Method:	findMax
Parameters:	String[]
Returns:	int
Method signature:	int findMax(String[] stick)
(be sure your method is public)

Notes

-

An integer may be listed multiple times in the String formed by the concatenation of stick . If an integer n is listed k times, then the king has exactly k sticks of length n available with him.

Constraints

-

stick will contain between 1 and 50 elements, inclusive.

-

Each element of stick will contain between 1 and 50 characters, inclusive.

-

When concatenated, stick will represent a single-space separated list of N integers, where N is between 1 and 200 inclusive.

-

Each listed integer will be between 1 and 999999, inclusive.

-

Listed integers will not have leading zeroes.

Examples

0)

{"3 4 4 3 11 5 12 9 4"}

Returns: 3

(3, 4, 5) and (5, 12, 13) are primitive pythagorean triplets. Hence, there are three disjoint pairs (a, b) - (3, 4), (3, 4) and (5, 12).

1)

{"20 21 3021 220"}

Returns: 2

Possible pairs (a, b) are (20, 21), (21, 220) and (220, 3021). The maximum number of disjoint pairs is 2. Namely, (20, 21) and (220, 3021).

2)

{"28 19", "5 1035 21412 37995"}

Returns: 2

Make sure you concatenate the elements of stick.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SimpleGuess

Simple Math, Simple Search, Iteration

Used in:

SRM 499

Used as:

Division II Level One

Writer:

lyrically

Testers:

PabloGilberto , ivan_metelsky , nika

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10763

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14428&pm=10763

Problem Statement

A cat and a rabbit are playing a simple number guessing game. The cat chose two different positive integers X and Y. He then told the rabbit several numbers. One of those numbers was X + Y and another was X - Y. The others were simply made up.

The rabbit thinks the cat prefers large numbers. Given a int[] hints containing the numbers the cat told the rabbit, return the largest possible value of X * Y.

Definition

Class:	SimpleGuess
Method:	getMaximum
Parameters:	int[]
Returns:	int
Method signature:	int getMaximum(int[] hints)
(be sure your method is public)

Constraints

-

hints will contain between 2 and 50 elements, inclusive.

-

Each element of hints will be between 1 and 100, inclusive.

-

All elements of hints will be distinct.

-

There will exist at least one pair of positive integers (X, Y) such that both X + Y and X - Y are elements of hints.

Examples

0)

{ 1, 4, 5 }

Returns: 6

The rabbit can determine that (X, Y) = (3, 2).

1)

{ 1, 4, 5, 8 }

Returns: 12

Possible pairs (X, Y) are (3, 2) and (6, 2). The values of X * Y are 6 and 12, respectively, and the largest is 12.

2)

{ 9, 8, 7, 6, 5, 4, 3, 2, 1 }

Returns: 20

3)

{ 2, 100 }

Returns: 2499

4)

{ 50, 58, 47, 57, 40 }

Returns: 441

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Nisoku

Greedy, Math

Used in:

SRM 463

Used as:

Division I Level Two , Division II Level Three

Writer:

rng_58

Testers:

PabloGilberto , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10760

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14148&pm=10760

Problem Statement

Taro and Hanako are playing a game called Nisoku, which is played as follows. Initially, there is a pile of cards. Each card contains a real number between 1.5 and 10.0, inclusive. You are given a double[] cards, the i-th element of which is the number written on the i-th card.

Repeat the following step until there is only one card left in the pile: Remove any two cards from the pile, and add one new card to the pile. Write either a+b or a*b on the new card, where a and b are the numbers written on the two cards that were removed.

Return the maximal possible number written on the final card in the pile.

Definition

Class:	Nisoku
Method:	theMax
Parameters:	double[]
Returns:	double
Method signature:	double theMax(double[] cards)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

cards will contain between 2 and 50 elements, inclusive.

-

Each element of cards will be between 1.5 and 10.0, inclusive.

Examples

0)

{5, 8}

Returns: 40.0

5 * 8 = 40.

1)

{1.5, 1.8}

Returns: 3.3

1.5 + 1.8 = 3.3.

2)

{8.26, 7.54, 3.2567}

Returns: 202.82857868

3)

{1.5, 1.7, 1.6, 1.5}

Returns: 9.920000000000002

4)

{10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 
10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 
10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 
10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 
10, 10, 10, 10, 10, 10, 10, 10, 10, 10}

Returns: 1.0E50

The answer can be extremely big.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PotatoGame

Math

Used in:

SRM 472

Used as:

Division I Level One , Division II Level Two

Writer:

rng_58

Testers:

PabloGilberto , ivan_metelsky , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10759

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14154&pm=10759

Problem Statement

Taro and Hanako like potatoes very much. Today they decided to play Potato Game.

Initially there is a box containing n potatoes. Taro and Hanako alternate turns, and Taro goes first. In each turn, the player must eat some potatoes from the box. The number of eaten potatoes must be a power of four, i.e., 1, 4, 16, 64 and so on. The first player who cannot eat a valid number of potatoes loses. Return the name of the winner assuming that they both play optimally.

Definition

Class:	PotatoGame
Method:	theWinner
Parameters:	int
Returns:	String
Method signature:	String theWinner(int n)
(be sure your method is public)

Constraints

-

n will be between 1 and 1,000,000,000 (10^9), inclusive.

Examples

0)

Returns: "Taro"

Taro will win if he eats 1 potato in the first turn.

1)

Returns: "Hanako"

Taro must eat exactly 1 potato in the first turn. In the second turn, Hanako will eat 1 potato and she will win.

2)

Returns: "Taro"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ColorfulTiles

Dynamic Programming, Math

Used in:

SRM 472

Used as:

Division I Level Three

Writer:

rng_58

Testers:

PabloGilberto , ivan_metelsky , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10758

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14154&pm=10758

Problem Statement

Taro likes colorful things, especially colorful tiles.

Taro's room is an H x W rectangle divided into 1 x 1 tiles. Each tile is one of the following four colors: red, green, blue or yellow. You are given a String[] room. If the j-th character of the i-th element is 'R', 'G', 'B' or 'Y', the color of the tile in the j-th column of the i-th row is red, green, blue or yellow, respectively.

He decided to change the color of some tiles so that no two adjacent tiles have the same color. Two tiles are adjacent if they share a side or a corner (so a tile has at most 8 adjacent tiles). He is allowed to change at most K tiles.

Return the number of ways to change tiles that satisfies the above conditions, modulo 1,000,000,007. Two ways are considered to be different if there is at least one tile of distinct color.

Definition

Class:	ColorfulTiles
Method:	theCount
Parameters:	String[], int
Returns:	int
Method signature:	int theCount(String[] room, int K)
(be sure your method is public)

Constraints

-

room will contain between 1 and 50 elements, inclusive.

-

Each element of room will contain the same number of characters.

-

Each element of room will contain between 1 and 50 characters, inclusive.

-

Each character in room will be 'R', 'G', 'B' or 'Y'.

-

K will be between 0 and the number of characters in room, inclusive.

Examples

0)

{"RG"}

Returns: 5

If he doesn't change any tiles, he can make "RG".

If he changes the first tile, he can make "BG" or "YG".

If he changes the second tile, he can make "RB" or "RY".

1)

{"BY"}

Returns: 12

All pairs of different colors are possible.

2)

{"RG",
 "GR"}

Returns: 8

The eight ways are:

RG  RG  BY  YB  BG  YG  RB  RY
BY  YB  GR  GR  YR  BR  GY  GB

3)

{"BRYBGYRB"
,"GRYGYBBG"
,"RGBGYBYG"
,"YRBRGBYG"
,"RBGRBRGG"
,"RBGYRYBY"}

Returns: 489

4)

{"BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB"
,"BBBBBBYYYBBBBBBBBBBBBBBBBBBBBBBBBBYYYYYBBBBBBBBBBB"
,"BBBBBBYYYBBBBBBBBBBBBBBBBBBBBBBYYYYYYYYYYYBBBBBBBB"
,"BBBBBBYYYYYYYYYYYYYYYYBBBBBBBBYYYYBBBBBYYYYBBBBBBB"
,"BBBBBBYYYYYYYYYYYYYYYYBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBYYYBBBBBBBBBBBBBBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBYYYBBBBBBBBBBBBBBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBYYYBBBBBBBBBBBBBBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBYYYBBBBBBBBBBBBBBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBYYYBBBBBBBBBBBBBBBBBBBBBYYYYBBBBBYYYYBBBBBBB"
,"BBBBBBYYYBBBBBBBBBBBBBBBBBBBBBBBYYYYYYYYYBBBBBBBBB"
,"BBBBBBYYYYYYYYYYYYBBBBBBBBBBBBBBYYYYYYYYYBBBBBBBBB"
,"BBBBBBYYYYYYYYYYYYYYBBBBBBBBBBYYYYBBBBBYYYYBBBBBBB"
,"BBBBBBBBBBBBBBBBYYYYYBBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBBBBBBBBBBBBBYYYBBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBBBBBBBBBBBBBYYYBBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBYYYBBBBBBBBBYYYBBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBYYYBBBBBBBBBYYYBBBBBBBBYYYBBBBBBBBBYYYBBBBBB"
,"BBBBBBBYYYYBBBBBYYYYBBBBBBBBBBYYYYBBBBBYYYYBBBBBBB"
,"BBBBBBBBYYYYYYYYYYYBBBBBBBBBBBBYYYYYYYYYYYBBBBBBBB"
,"BBBBBBBBBBBYYYYYBBBBBBBBBBBBBBBBBBYYYYYBBBBBBBBBBB"
,"BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB"}

Returns: 404506540

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CandyBox

Dynamic Programming, Math

Used in:

SRM 462

Used as:

Division I Level Two

Writer:

Nickolas

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10744

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14147&pm=10744

Problem Statement

You have a box containing N kinds of candy. There are exactly C pieces of each kind. Every piece of candy looks the same, but each kind tastes different, so each kind is placed in a separate section of the box. You have assigned a score to each kind of candy indicating how much you like it. The i-th element of the int[] score is your score for the i-th kind of candy.

Your friend's idea of a practical joke is to mix up all the candies in the box, so that each time you choose a candy, you get a surprise. He sneaks into the box and starts swapping random pairs of candies. For each swap, he chooses two distinct candies (independently from previously chosen pairs) and swaps them. All pairs of candies have the same probability of being chosen, and the two candies are not necessarily chosen from different sections of the box. Fortunately, you catch him after he has done only S swaps. Now you want to know how much on average you'll like a piece of candy chosen at random from each section of the box. Return a double[] containing exactly N elements, where the i-th element is the expected score of one candy chosen randomly from the section of the box that originally contained only candies of the i-th kind.

Definition

Class:	CandyBox
Method:	expectedScore
Parameters:	int, int[], int
Returns:	double[]
Method signature:	double[] expectedScore(int C, int[] score, int S)
(be sure your method is public)

Notes

-

Each element of the return must have an absolute or relative error less than 1e-9.

Constraints

-

C will be between 1 and 100, inclusive.

-

score will contain between 1 and 50 elements, inclusive.

-

Each element of score will be between 1 and 100, inclusive.

-

S will be between 0 and 10000, inclusive.

-

The total number of candies C*(number of elements in score) will be strictly greater than 1.

Examples

0)

{1, 10}

Returns: {1.0, 10.0 }

No swaps were done, so all candies stay in their original sections.

1)

{1, 10}

Returns: {4.0, 7.000000000000001 }

Six pairs of candies can be chosen for the swap. Two of the swaps swap candies of the same type, and all the candies stay in their original sections, and the expected scores of sections are {1, 10}. Four of the swaps swap candies of different types, so in each section there is one candy of each kind, and the expected scores are {5.5, 5.5}. The answer is 1/3 * {1, 10} + 2/3 * {5.5, 5.5} = {4, 7}.

2)

{1, 4, 10}

Returns: {5.0, 5.0, 5.0 }

The swap can turn this box into one of the following: {1, 10, 4}, {4, 1, 10} or {10, 4, 1}. For each section, the probability of finding a candy of a certain kind is 1/3.

3)

{13, 82, 74, 78, 12, 71, 81, 80, 30}

Returns: 
{26.25622829378155, 74.87969915903301, 69.24219529059805, 72.06094722481552, 25.551540310227182, 67.12813133993495, 74.17501117547864, 73.47032319192427, 38.23592401420582 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ColorfulBoxesAndBalls

Simple Math, Simple Search, Iteration

Used in:

SRM 464

Used as:

Division II Level One

Writer:

lyrically

Testers:

PabloGilberto , ivan_metelsky , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10743

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14149&pm=10743

Problem Statement

You are playing a game where you have numRed red boxes, numBlue blue boxes, numRed red balls, and numBlue blue balls.

You must place a single ball into each box. Each box is then scored as follows:

If the box is red and it contains a red ball, you get onlyRed points.
If the box is blue and it contains a blue ball, you get onlyBlue points.
In all other cases, you get bothColors points.

Your total score is the sum of the scores of all the boxes.

Return the maximum possible total score you can get.

Definition

Class:	ColorfulBoxesAndBalls
Method:	getMaximum
Parameters:	int, int, int, int, int
Returns:	int
Method signature:	int getMaximum(int numRed, int numBlue, int onlyRed, int onlyBlue, int bothColors)
(be sure your method is public)

Constraints

-

numRed and numBlue will each be between 1 and 100, inclusive.

-

onlyRed, onlyBlue, and bothColors will each be between -1000 and 1000, inclusive.

Examples

0)

Returns: 1400

In this example, you should put two red balls into red boxes, and three blue balls into blue boxes.

Then you can get 100 * 2 + 400 * 3 = 1400 points in total.

1)

Returns: 1600

bothColors is a larger value here than it was in the previous example.

You should put two blue balls into red boxes, and two red balls and one blue ball into blue boxes.

Then you can get 300 * 4 + 400 * 1 = 1600 points.

2)

Returns: 4640

No matter how you place the balls, your score will always be the same.

3)

-30

-10

Returns: -100

The maximum total score may be less than zero.

4)

-1

-10

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DrawingLines

Math

Used in:

SRM 470

Used as:

Division I Level Two

Writer:

dolphinigle

Testers:

PabloGilberto , ivan_metelsky , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10735

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14153&pm=10735

Problem Statement

NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.

Little John has drawn a rectangle. On the top edge, he draws n dots at different places and numbers them 1 through n from left to right. On the bottom edge, he also draws n dots at different places and numbers them 1 through n from left to right.

John will then draw n straight line segments. For each segment, he will first choose a dot on the top edge that has not been chosen earlier. Then, he will choose a dot on the bottom edge that has not been chosen earlier. Finally, he will connect those two dots to form a straight line segment.

John has drawn several of the n segments so far. You are given int[]s startDot and endDot. startDot[i] is the number of the top dot chosen for the i-th segment which has already been drawn, and endDot[i] is the number of the bottom dot chosen for that segment. For each remaining segment, John will randomly choose an available top dot and an available bottom dot (each available top dot has an equal probability of being chosen, and each available bottom dot has an equal probability of being chosen). Return the expected number of distinct pairs of line segments that cross each other in the final drawing.

Definition

Class:	DrawingLines
Method:	countLineCrossings
Parameters:	int, int[], int[]
Returns:	double
Method signature:	double countLineCrossings(int n, int[] startDot, int[] endDot)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

n will be between 2 and 10000, inclusive.

-

startDot and endDot will each contain between 1 and 50 elements, inclusive.

-

startDot and endDot will contain the same number of elements.

-

startDot and endDot will each contain less than n elements.

-

Each element of startDot will be between 1 and n, inclusive.

-

Each element of endDot will be between 1 and n, inclusive.

-

All elements of startDot will be distinct.

-

All elements of endDot will be distinct.

Examples

0)

{2}

{3}

Returns: 1.5

There are four possible ways for Little John to pick the dots :

[Top 1]-[Bottom 1] [Top 3]-[Bottom 2]
[Top 1]-[Bottom 2] [Top 3]-[Bottom 1]
[Top 3]-[Bottom 1] [Top 1]-[Bottom 2]
[Top 3]-[Bottom 2] [Top 1]-[Bottom 1]

The first and the fourth ways correspond to the left picture, while the second and the third ways correspond to the right picture. The blue line is the line initially drawn by Little John.

In the left configuration, there is 1 pair of segments that cross each other. In the right configuration, there are 2 pairs of segments that cross each other. Hence, the expected number of crossed pairs is 1.5.

1)

{1,4}

{3,1}

Returns: 5.5

2)

{4,1}

{4,1}

Returns: 0.5

3)

{1,4,3,6,7}

{1,3,2,4,5}

Returns: 7.5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FencingGarden

Search, Simple Math

Used in:

Member SRM 461

Used as:

Division I Level Three

Writer:

dolphinigle

Testers:

Rustyoldman , timmac , ivan_metelsky , mohamedafattah , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10733

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14181&pm=10733

Problem Statement

There is an empty grass field with an infinitely long straight wall. You are going to create a rectangular garden against the wall. Three sides of the garden will be enclosed with a fence. The fourth side of the garden is formed by part of the wall.

You currently have some fence segments. Each side of your fence can be created by connecting some of these segments. The length of a side of the fence is equal to the sum of the lengths of the fence segments that form it. The length of each side of the fence must be exactly equal to the length of the corresponding side of the rectangular garden. As in real life, each fence segment may only be used at most once.

Fortunately, you have a saw that can cut at most one of these segments into two shorter segments. The saw will break after being used one time. You may cut the one segment into two shorter segments at any point between its endpoints (non-integer length is allowed). Note that the total length of the two shorter segments created must be equal to the length of the original segment.

You are given int[] segment. The i-th element of segment represents the length of the i-th fence segment. Using these segments construct the garden fence (as described above) enclosing the maximum area possible and return the length of the garden's side parallel to the wall. If the maximum area can be formed in more than one way then return the largest parallel-to-the-wall length that gives the maximum area.

Definition

Class:	FencingGarden
Method:	computeWidth
Parameters:	int[]
Returns:	long
Method signature:	long computeWidth(int[] segment)
(be sure your method is public)

Constraints

-

segment will contain between 2 and 40 elements, inclusive.

-

Each element of segment will be between 1 and 100,000,000, inclusive.

Examples

0)

{1,1,1,1,10}

Returns: 8

Cut the segment with length 10 into segments with lengths 2 and 8. Make two sides with length 3 and one side with length 8 using these segments. This gives a 3x8 rectangular garden.

Note that a 4x6 rectangular garden can also be constructed. It has the same maximum area of 24. But the correct answer is 8 since you should return the largest parallel-to-the-wall length that gives the maximum area and 8 is larger than 6.

1)

{50,25,25}

Returns: 50

Sometimes it is not necessary to cut any segment.

2)

{5,7,9,13,21,581,1848,1058,57172,58281,612,528}

Returns: 60078

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RabbitPuzzle

Dynamic Programming, Graph Theory, Math

Used in:

SRM 463

Used as:

Division I Level Three

Writer:

rng_58

Testers:

PabloGilberto , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10727

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14148&pm=10727

Problem Statement

NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.

Taro and Hanako are playing Rabbit Puzzle. There are three rabbits and three nests on a line. You are given a long[] rabbits, where each element is the initial position of a single rabbit, and a long[] nests, where each element is the position of a single nest.

They must perform the following routine exactly K times:

Choose two different rabbits A and B, located at points a and b, respectively.
A jumps over B and lands at point 2*b-a.

The jump is not allowed if another rabbit is already at point 2*b-a.

The jump is also not allowed if A jumps over more than one rabbit.

The goal of the puzzle is to have every rabbit be in a nest after the K routines. Note that the i-th rabbit doesn't necessarily have to be in the i-th nest. Return the number of ways to solve this puzzle, modulo 1,000,000,007. Two ways are considered different if at least one jump is different.

Definition

Class:	RabbitPuzzle
Method:	theCount
Parameters:	long[], long[], int
Returns:	int
Method signature:	int theCount(long[] rabbits, long[] nests, int K)
(be sure your method is public)

Constraints

-

rabbits will contain exactly 3 elements.

-

Each element of rabbits will be between -10^18 and 10^18, inclusive.

-

rabbits will be sorted in strictly ascending order.

-

nests will contain exactly 3 elements.

-

Each element of nests will be between -10^18 and 10^18, inclusive.

-

nests will be sorted in strictly ascending order.

-

K will be between 1 and 100, inclusive.

Examples

0)

{0, 5, 8}

{0, 8, 11}

Returns: 1

The only solution is moving a rabbit from 5 to 11.

1)

{0, 5, 8}

{0, 8, 11}

Returns: 5

2)

{0, 5, 8}

{0, 8, 11}

Returns: 0

They must use exactly 2 jumps. It's impossible to solve this puzzle.

3)

{5, 8, 58}

{13, 22, 64}

Returns: 0

This puzzle is also impossible.

4)

{0, 1, 2}

{1, 2, 3}

Returns: 0

This puzzle is also impossible.

5)

{5, 8, 58}

{20, 26, 61}

Returns: 537851168

6)

{67, 281, 2348}

{235, 1394, 3293}

Returns: 167142023

7)

{-1000000000000000000, 999999999999999998, 999999999999999999}

{-1000000000000000000, 999999999999999999, 1000000000000000000}

Returns: 29

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BouncingBalls

Math

Used in:

Member SRM 458

Used as:

Division I Level One , Division II Level Two

Writer:

rng_58

Testers:

Rustyoldman , timmac , ivan_metelsky , mohamedafattah , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10726

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14180&pm=10726

Problem Statement

John is playing with balls. All of the balls are identical in weight and considered to have a zero radius. All balls are located on the same straight line and can move only along this line. If a ball rolling to the right and a ball rolling to the left at the same speed collide, they do not change speed, but they change direction.

You are given int[] x. x[i] is the initial position of the i-th ball. John decides the direction for each ball (right or left) with equal probability. At time 0, he rolls the balls in the chosen directions simultaneously at a speed of one unit per second. Return the expected number of bounces between all balls during T seconds (including those collisions that happen exactly at T seconds).

Definition

Class:	BouncingBalls
Method:	expectedBounces
Parameters:	int[], int
Returns:	double
Method signature:	double expectedBounces(int[] x, int T)
(be sure your method is public)

Notes

-

There is no friction. Each ball continues rolling at the same speed forever.

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

x will contain between 1 and 12 elements, inclusive.

-

Each element of x will be between 0 and 100,000,000, inclusive.

-

All elements of x will be distinct.

-

T will be between 1 and 100,000,000, inclusive.

Examples

0)

{5, 8}

Returns: 0.25

If he rolls the left ball to the right and right ball to the left, they collide at time 1.5. Otherwise, they don't collide.

1)

{5, 8}

Returns: 0.0

x is the same as in example 0, but T is too small.

2)

{91, 857, 692, 54, 8679, 83, 792, 86, 9537, 913, 64, 592}

Returns: 11.5

3)

{75432}

Returns: 0.0

4)

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Returns: 12.75

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ParkAmusement

Dynamic Programming, Graph Theory, Math

Used in:

SRM 459

Used as:

Division II Level Three

Writer:

gojira_tc

Testers:

PabloGilberto , legakis , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10723

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14145&pm=10723

Problem Statement

A new ride is opened in an amusement park. It consists of N landings numbered from 0 to N-1. Some of the landings are connected with pipes. All of the landings are at different heights, so the pipes are all inclined and can only be traversed downwards.

A ride-taker begins his ride at some landing. The pipes are long enough that he cannot see where they lead before entering them. Therefore, at each landing, any descending pipe adjacent to it has an equal probability of being used by a ride-taker who reached this landing.

A ride is finished when a ride-taker reaches a landing which has no adjacent descending pipes. There are two types of such landings: exits and crocodile ponds. If the ride-taker reaches the exit landing, his ride is over and he safely returns home. If one reaches the crocodile pond, his trip is also over, but he never returns home.

You're given a String[] landings describing the ride. Element i of landings describes the i-th landing. If the landing is an exit, the i-th character of landings[i] will be 'E' and the rest of the characters will be '0's (zeroes). If it is a crocodile pond, the i-th character will be 'P' and the rest will be '0's. If the landing has at least one adjacent descending pipe, the j-th character of landings[i] will be '1' (one) if a pipe descends from the i-th landing to the j-th, and '0' (zero) otherwise.

A ride-taker began his ride at a randomly chosen landing, used a total of K pipes throughout his descent and safely returned home afterwards. Each of the landings has the same probability of being chosen as the initial landing of the ride. Compute the probability that he started the ride at landing startLanding.

Definition

Class:	ParkAmusement
Method:	getProbability
Parameters:	String[], int, int
Returns:	double
Method signature:	double getProbability(String[] landings, int startLanding, int K)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

landings will contain exactly N elements, where N is between 2 and 50, inclusive.

-

Each element of landings will contain exactly N characters.

-

Each character in landings will be '0' (zero), '1' (one), 'E', or 'P'.

-

If the i-th element of landings contains an 'E', it will contain only one 'E' as its i-th character, and all other characters in that element will be '0'.

-

If the i-th element of landings contains a 'P', it will contain only one 'P' as its i-th character, and all other characters in that element will be '0'.

-

If the i-th element of landings doesn't contain an 'E' or a 'P', it will contain at least one '1' character. The i-th character of such element will always be '0'.

-

K will be between 1 and N-1, inclusive.

-

startLanding will be between 0 and N-1, inclusive.

-

There will be no cycles in landings, i.e. it's never possible to return to the same landing after descending through several pipes.

-

There will be at least one landing from which it is possible to reach an exit using exactly K pipes.

Examples

0)

{"E000",
 "1000",
 "1000",
 "1000"}

Returns: 0.3333333333333333

The ride contains 4 landings, one of which is an exit. Each of the other landings has a single pipe descending to the exit landing. Therefore, each of them could be the starting landing with equal probability of 1/3.

1)

{"E000",
 "1000",
 "1001",
 "000P"}

Returns: 0.6666666666666666

This time, there is an exit landing and a crocodile pond. Of the other two landings, the first has a descending pipe only to the exit, while the second is connected both to the exit and to the pond. So, the probability of reaching an exit starting from landing 2 is lower and the chances of ground 1 being the start of the journey increase.

2)

{"01000100",
 "00111000",
 "00001010",
 "000E0000",
 "0000E000",
 "00000P00",
 "000000P0",
 "01000000"}

Returns: 0.14285714285714288

Analyzing the graph above, we can see that landings 0, 1 and 7 could be the starting landings. One can reach an exit from landing 0 using 2 pipes with probability 2/6, from landing 1 with probability 1/6 and from landing 7 with probability 2/3. Therefore, the probability that the ride-taker began from landing 1 is equal to (1/6)/(2/3+2/6+1/6)=1/7.

3)

{"0100",
 "0010",
 "0001",
 "000E"}

Returns: 0.0

Obviously, the only way to get to the exit landing using 2 pipes is from ground 1. Therefore there is no chance that landing 0 was the initial ground.

4)

{"E00",
 "0E0",
 "010"}

Returns: 0.0

Note that some sections of the ride might be disconnected.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ConvexHexagons

Dynamic Programming, Math

Used in:

Member SRM 455

Used as:

Division I Level Two

Writer:

Seyaua

Testers:

Rustyoldman , timmac , StevieT , maksay , K.A.D.R , Seyaua

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10715

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14179&pm=10715

Problem Statement

Petya likes triangles. He draws a trianglar grid using the following process: He starts off with an equilateral triangle. He then draws points on the edges of this triangle, dividing each edge up into N equal-length segments. Next, he connects each pair of points that is at equal distance from some vertex of the triangle with a straight line, ending up with N*N smaller equilateral triangles. An example of this figure with N = 4 is shown below.

However, he likes hexagons more than he likes triangles. How many non-degenerate convex hexagons can be formed using the line segments in his figure? This number can be very big, so return it modulo 1000000007.

Definition

Class:	ConvexHexagons
Method:	find
Parameters:	int
Returns:	int
Method signature:	int find(int N)
(be sure your method is public)

Notes

-

The length of each edge of every hexagon must be greater than zero.

Constraints

-

N will be between 1 and 500000, inclusive.

Examples

0)

Returns: 7

There are 7 hexagons:

1)

Returns: 232

2)

Returns: 635471838

3)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MegaSum

Math

Used in:

SRM 454

Used as:

Division I Level Three

Writer:

Gluk

Testers:

PabloGilberto , kalinov , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10710

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13908&pm=10710

Problem Statement

Let us define an infinite table of integers as follows:

Each cell is uniquely identified by the value it contains. Let us define S(X) as the sum of all the values in the rectangle with cell 1 as its upper-left corner and cell X as its lower-right corner. For example, S(12) is the sum of all the values in the green rectangle shown above.

You are given a long N. First, find the rectangle with cell 1 as its upper-left corner and cell N as its lower-right corner. Then, calculate the sum of S(X) for all values X inside this rectangle. Return this sum modulo 1,000,000,007.

For example, if N is 8, you would first find the 3 x 2 rectangle with 1 in its upper-left corner and 8 in its lower-right corner. You would then calculate S(X) for each value X in this rectangle: S(1) = 1, S(2) = 3, S(9) = 12, S(4) = 5, S(3) = 10, and S(8) = 27. You would them sum these values to get 1 + 3 + 12 + 5 + 10 + 27 = 58.

Definition

Class:	MegaSum
Method:	calculate
Parameters:	long
Returns:	int
Method signature:	int calculate(long N)
(be sure your method is public)

Constraints

-

N will be between 1 and 10^10, inclusive.

Examples

0)

Returns: 58

This is the example from the problem statement.

1)

Returns: 282

2)

Returns: 128

3)

Returns: 50

4)

Returns: 437909839

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SilverDistance

Math

Used in:

SRM 456

Used as:

Division I Level One , Division II Level Two

Writer:

rng_58

Testers:

PabloGilberto , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10699

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13909&pm=10699

Problem Statement

In Japanese Chess, there is a piece called Silver. A Silver piece located in cell (x,y) can move to any of the following cells in one step: (x-1,y+1), (x,y+1), (x+1,y+1), (x-1,y-1), (x+1,y-1). In other words, it can move one cell in any of the four diagonal directions, or it can move one cell vertically in the positive y direction.

Initially, there's a Silver piece in cell (sx,sy) of an infinitely large board. Return the minimal number of steps required to move to cell (gx,gy).

Definition

Class:	SilverDistance
Method:	minSteps
Parameters:	int, int, int, int
Returns:	int
Method signature:	int minSteps(int sx, int sy, int gx, int gy)
(be sure your method is public)

Constraints

-

sx, sy, gx and gy will each be between -1,000,000 and 1,000,000 inclusive.

Examples

0)

Returns: 9

Move up vertically in the positive y direction 9 times.

1)

-4

Returns: 5

Follow the path : (0,0) -> (-1,1) -> (-1,2) -> (-2,3) -> (-3,2) -> (-4,3)

2)

Returns: 8

Move up vertically in the postive y direction 3 times, then move diagonally up and to the right 5 times.

3)

-487617

-918045

Returns: 1744571

4)

-27857

-27857

Returns: 0

The Silver is already in the goal.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ProductTriplet

Brute Force, Math

Used in:

Member SRM 458

Used as:

Division II Level Three

Writer:

rng_58

Testers:

Rustyoldman , timmac , ivan_metelsky , mohamedafattah , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10698

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14180&pm=10698

Problem Statement

You are given six integers, minx, maxx, miny, maxy, minz and maxz. Return the number of triplets of integers (x,y,z) that satisfy the following three conditions:

x is between minx and maxx, inclusive.
y is between miny and maxy, inclusive.
z is between minz and maxz, inclusive.
x * y = z

Definition

Class:	ProductTriplet
Method:	countTriplets
Parameters:	int, int, int, int, int, int
Returns:	long
Method signature:	long countTriplets(int minx, int maxx, int miny, int maxy, int minz, int maxz)
(be sure your method is public)

Constraints

-

maxx will be between 1 and 1,000,000,000, inclusive.

-

maxy will be between 1 and 1,000,000,000, inclusive.

-

maxz will be between 1 and 1,000,000,000, inclusive.

-

minx will be between 1 and maxx, inclusive.

-

miny will be between 1 and maxy, inclusive.

-

minz will be between 1 and maxz, inclusive.

Examples

0)

Returns: 1

2 * 3 = 6.

1)

Returns: 0

2 * 3 is not 7.

2)

Returns: 4

(x,y,z) = (6,5,30), (7,4,28), (7,5,35) and (8,4,32) satisfy all conditions.

3)

Returns: 2877

4)

45814517

957843164

Returns: 2365846085

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RabbitNumbering

Math

Used in:

SRM 463

Used as:

Division I Level One , Division II Level Two

Writer:

rng_58

Testers:

PabloGilberto , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10697

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14148&pm=10697

Problem Statement

Taro and Hanako have rabbits, and they want to assign a distinct integer to each rabbit so they can easily identify them.

The rabbits have expressed their preferences to Taro and Hanako. The i-th rabbit wants an integer between 1 and maxNumber[i], inclusive. Taro and Hanako must obey the preferences of all their rabbits.

Return the number of ways they can assign numbers to their rabbits, modulo 1,000,000,007. If it's impossible to assign distinct integers to the rabbits, return 0.

Definition

Class:	RabbitNumbering
Method:	theCount
Parameters:	int[]
Returns:	int
Method signature:	int theCount(int[] maxNumber)
(be sure your method is public)

Constraints

-

maxNumber will contain between 1 and 50 elements, inclusive.

-

Each element of maxNumber will be between 1 and 1,000, inclusive.

Examples

0)

{5}

Returns: 5

They can assign any number between 1 and 5, inclusive, to the only rabbit.

1)

{4, 4, 4, 4}

Returns: 24

All permutations of {1, 2, 3, 4} are possible.

2)

{5, 8}

Returns: 35

3)

{2, 1, 2}

Returns: 0

4)

{25, 489, 76, 98, 704, 98, 768, 39, 697, 8, 56, 74, 36, 95, 87, 2, 968, 4, 920, 54, 873, 90}

Returns: 676780400

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheHexagonsDivTwo

Brute Force, Math

Used in:

SRM 457

Used as:

Division II Level Three

Writer:

vexorian

Testers:

PabloGilberto , ivan_metelsky , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10694

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14144&pm=10694

Problem Statement

John and Brus are interested in a new game called "Hexagon Flower". The rules are simple. You are given a flower formed by seven hexagons arranged as follows:

The objective of the game is to place a number in each hexagon of the flower such that all of the following conditions are satisfied:

Each number is an integer between 1 and n, inclusive.
Each number is distinct.
For every pair of adjacent hexagons, if the numbers placed in them are a and b, then a%k != b%k.

Given n and k, return the total number of distinct solutions. Two solutions are considered the same if you can rotate one to form the other.

For example, if n = 8 and k = 4, then:

The top three placements are not valid. The other three placements are valid, but the first two among them are considered equal since one can be rotated to become the other.

Definition

Class:	TheHexagonsDivTwo
Method:	count
Parameters:	int, int
Returns:	long
Method signature:	long count(int n, int k)
(be sure your method is public)

Constraints

-

n will be between 1 and 300, inclusive.

-

k will be between between 1 and 9, inclusive.

Examples

0)

Returns: 0

There is no way to place all 7 numbers (1 through 7, inclusive) such that no two adjacent numbers are equal modulo 3.

1)

Returns: 24

2)

Returns: 256

3)

Returns: 4692480

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheTournamentDivTwo

Simple Math, Simple Search, Iteration

Used in:

SRM 453

Used as:

Division II Level One

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , ivan_metelsky , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10686

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13907&pm=10686

Problem Statement

John and Brus have an interest in team sports tournaments. They are currently investigating the intermediate standings of a tournament. They don't know which games have been played so far. They only know that the tournament is played using the following rules:

Each game is played between two teams and results in either a victory for one team or a draw. If a team wins a game, it gains two points and its opponent gains no points. In case of a draw, each team gains one point. The score of a team is the sum of all the points it has gained from all its games. There are no restrictions on which teams can play against each other, and each pair of teams can play against each other any number of times (possibly zero).

You are given a int[] points representing the intermediate standings of the tournament. The i-th element of points is the score of the i-th team. Return the minimum number of games that could have been played to achieve those standings. If points doesn't represent a valid state, return -1 instead.

Definition

Class:	TheTournamentDivTwo
Method:	find
Parameters:	int[]
Returns:	int
Method signature:	int find(int[] points)
(be sure your method is public)

Constraints

-

points will contain between 2 and 50 elements, inclusive.

-

Each element of points will be between 0 and 1,000,000, inclusive.

Examples

0)

{10, 1, 1}

Returns: 6

Here the first team has five wins or four wins and two draws. The second and the third team each has one draw.

1)

{1, 1, 1}

Returns: -1

These standings are impossible. For each of the three teams to have one point, each one must have played in a game that resulted in a draw. There is no way for three teams to have each played in exactly one game.

2)

{0, 0, 0, 0, 0, 0, 0}

Returns: 0

There are no points, which means no games have been played yet.

3)

{13, 8, 7}

Returns: 14

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheTournamentDivOne

Simple Math, Simple Search, Iteration

Used in:

SRM 453

Used as:

Division I Level Two

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , ivan_metelsky , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10685

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13907&pm=10685

Problem Statement

John and Brus have an interest in team sports tournaments. They are currently investigating the intermediate standings of a tournament. They don't know which games have been played so far. They only know that the tournament is played using the following rules:

Each game is played between two teams and results in either a victory for one team or a draw. If a team wins a game, it gains w points and its opponent gains no points. In case of a draw, each team gains d points. The score of a team is the sum of all the points it has gained from all its games. There are no restrictions on which teams can play against each other, and each pair of teams can play against each other any number of times (possibly zero).

You are given a int[] points representing the intermediate standings of the tournament. The i-th element of points is the score of the i-th team. Return the minimum number of games that could have been played to achieve those standings. If points doesn't represent a valid state, return -1 instead.

Definition

Class:	TheTournamentDivOne
Method:	find
Parameters:	int[], int, int
Returns:	int
Method signature:	int find(int[] points, int w, int d)
(be sure your method is public)

Constraints

-

points will contain between 2 and 50 elements, inclusive.

-

Each element of points will be between 0 and 10,000, inclusive.

-

w will be between 1 and 10,000, inclusive.

-

d will be between 1 and w, inclusive.

Examples

0)

{10, 1, 1}

Returns: 6

The first team has five wins or four wins and two draws. The second and the third teams each has one draw.

1)

{1, 1, 1}

Returns: -1

These standings are impossible. For each of the three teams to have one point, each one must have played in a game that resulted in a draw. There is no way for three teams to have each played in exactly one game.

2)

{1, 4, 0, 2}

Returns: 3

The only win goes to the second team.

3)

{8, 3, 8, 5, 9, 2, 7, 11}

Returns: 15

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumberPyramids

Dynamic Programming, Math

Used in:

SRM 459

Used as:

Division I Level Two

Writer:

gojira_tc

Testers:

PabloGilberto , legakis , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10683

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14145&pm=10683

Problem Statement

Suppose that there are N numbers written in a row. A row above this one consists of N-1 numbers, the i-th of which is the sum of the i-th and (i+1)-th elements of the first row. Every next row contains one number less than the previous one and every element is the sum of the two corresponding elements in the row below. The N-th row contains a single number. For example, if the initial numbers are {2,1,2,4}, the whole structure will look like this:

We shall refer to such a structure as a number pyramid. Two number pyramids are equal if all the numbers at corresponding positions are equal.

Given ints baseLength and top, compute the total number of different number pyramids consisting of positive integers, having baseLength elements in the first row and the value at the top equal to top. Since the number of such pyramids might be enormous, return the result modulo 1,000,000,009.

Definition

Class:	NumberPyramids
Method:	count
Parameters:	int, int
Returns:	int
Method signature:	int count(int baseLength, int top)
(be sure your method is public)

Constraints

-

baseLength will be between 2 and 1,000,000, inclusive.

-

top will be between 1 and 1,000,000, inclusive.

Examples

0)

Returns: 2

The following are two possible pyramids with 3 numbers in the base and the number 5 at the top:

1)

Returns: 1

The only number pyramid with base of size 5 and 16 at the top looks like this:

2)

Returns: 24

3)

Returns: 74280915

4)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Inequalities

Simple Math, Simple Search, Iteration

Used in:

SRM 459

Used as:

Division I Level One , Division II Level Two

Writer:

gojira_tc

Testers:

PabloGilberto , legakis , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10682

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14145&pm=10682

Problem Statement

You're given a set of inequalities. Each of the inequalities refers to the variable X. Determine the maximum subset of the given set which has a solution.

To make your task easier, the inequalities in the given set are always reduced to one of the following five forms:

	X < C
	X <= C
	X = C
	X > C
	X >= C

Here, C indicates some non-negative integer constant.

The inequalities are given in the String[] inequalities, where each element is a single inequality formatted as shown above. Return the maximal number of inequalities of the set which can be satisfied simultaneously.

Definition

Class:	Inequalities
Method:	maximumSubset
Parameters:	String[]
Returns:	int
Method signature:	int maximumSubset(String[] inequalities)
(be sure your method is public)

Notes

-

Note that X doesn't have to be an integer or positive number.

Constraints

-

inequalities will contain between 1 and 50 elements, inclusive.

-

Each element of inequalities will be formatted "X <E> <C>", where 'X' is uppercase, <E> is one of "<", "<=", "=", ">=" or ">", and <C> is an integer between 0 and 1000, inclusive, with no extra leading zeroes (all quotes for clarity).

-

No two elements of inequalities will be equal.

Examples

0)

{"X <= 12","X = 13","X > 9","X < 10","X >= 14"}

Returns: 3

Any value between 9 and 10 will satisfy the first, third and fourth inequalities.

1)

{"X < 0","X <= 0"}

Returns: 2

The solution to the whole set is any negative number.

2)

{"X = 1","X = 2","X = 3","X > 0"}

Returns: 2

Obviously, you can choose no more than one equality in addition to the fourth inequality.

3)

{"X <= 521","X >= 521","X = 521","X > 902","X > 12","X <= 1000"}

Returns: 5

The best choice is number 521.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EnclosingCircles

Geometry, Simple Math

Used in:

Marathon Match 56

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10655

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13964&pm=10655

Problem Statement

You are given N points on a two-dimensional plane. You have to enclose these points with at most M circles so that each point is inside of at least one circle. Your task is to minimize the sum of areas of the circles you use.

Implementation Details

Your code should implement one method placeCircles. int[]s pointX and pointY give you the coordinates of the points on the plane, and M is the maximal number of circles you can use.

You must return the list of the circles you'll use to enclose these points. Each element of your return describes one circle and should be formatted as "CENTERX CENTERY RADIUS" (quotes for clarity only). CENTERX and CENTERY specify x- and y-coordinates of the circle's center, and RADIUS specifies its radius. RADIUS must be strictly greater than 0.1. All values are double precision.

Scoring

Your score for an individual test case will be the sum of the areas of the circles you used. Note that the score is NOT equal to the area on the plane covered with the circles; if the returned circles overlap, the area of the overlap is counted for each overlapping circle. If at least one of the given points is outside of all circles, your score for this test case will be zero. An invalid return of any kind will result in zero absolute score for that test case.

Your overall score will be the sum over all test cases of max(0, 400000 - AREA) / 1000, where AREA is the area you used.

Test Case Generation

The number of points N is chosen between 50 and 1000, inclusive.

The maximal number of circles M is chosen between 10 and max(10, floor(N / 10)), inclusive.

x- and y-coordinates of each point are chosen between 0 and 511, inclusive.

You will have the opportunity to submit four test cases during the first week of the contest. Of the four, one will be selected at random for provisional testing, while the others will be used for final testing. After the first week, the submitted test cases will be locked. Your code should implement a method generateTestCase that takes one int argument and returns a int[] that contains the information about the test case that you want to submit. The first element must contain M. The second element must contain N. The next N elements should contain the values for pointX, following that another N elements that contain the values for pointY. This solution will be called four times on some tests -- you should not count on it being called every time. The test case will be validated and only valid test cases will be accepted.

Visualizer

A visualizer is available for offline testing.

Definition

Class:	EnclosingCircles
Method:	placeCircles
Parameters:	int[], int[], int
Returns:	String[]
Method signature:	String[] placeCircles(int[] pointX, int[] pointY, int M)

Method:	generateTestCase
Parameters:	int
Returns:	int[]
Method signature:	int[] generateTestCase(int testNumber)
(be sure your methods are public)

Notes

-

All variables are chosen randomly, independently and uniformly.

-

For more implementation details see the visualizer source.

-

The memory limit is 1024 MB and the time limit for placeCircles() is 20 seconds (which includes only time spent in your code). The time limit for generateTestCase() is 5 seconds per call.

-

There are 10 example test cases and 200 full submission test cases. The number of test cases will remain constant. The user generated tests will replace the randomly generated ones over the course of the first week.

-

A point (px, py) is considered to be inside a circle (cx, cy) with radius (R) if ((cx-px)*(cx-px) + (cy-py)*(cy-py)) <= R*R.

-

Your submission will only be tested against the test suite at the time that you submit it. This means that as new tests arrive, the scores may become somewhat stale.

-

You must implement the generateTestCase() method, but is not obliged to return a valid case. Returning an empty array is ok, but we encourage you to generate some test cases.

Examples

0)

"1"

Returns: "seed = 1
N = 321
M = 17
"

1)

"2"

Returns: "seed = 2
N = 344
M = 25
"

2)

"3"

Returns: "seed = 3
N = 558
M = 54
"

3)

"4"

Returns: "seed = 4
N = 170
M = 13
"

4)

"5"

Returns: "seed = 5
N = 205
M = 20
"

5)

"6"

Returns: "seed = 6
N = 872
M = 49
"

6)

"7"

Returns: "seed = 7
N = 509
M = 28
"

7)

"8"

Returns: "seed = 8
N = 165
M = 16
"

8)

"9"

Returns: "seed = 9
N = 219
M = 19
"

9)

"10"

Returns: "seed = 10
N = 396
M = 20
"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CUDAPermute

Advanced Math

Used in:

CUDA Beta

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10639

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13956&pm=10639

Problem Statement

For 0 <= i,j < N, you will be given w_i,j. You should find a permutation of 0..N-1: {p₀, p₁, ..., p_N-1}, such that the sum over i < j of w_{p_i,p_j} is maximized.

Each of the weights will be selected randomly from a normal distribution with mean 0 and variance 1. The weights will be given to you as an array w, where w[i*N+j] gives w_i,j (you may deduce N as sqrt(length(w))). You should return an array with N elements, specifying the permutation p.

Your score for each test case will be the sum mentioned above, divided by N*sqrt(N*log(N)-N)/100. Your overall final score will simply be the average of your individual scores.

Definition

Class:	CUDAPermute
Method:	findOrder
Parameters:	double[]
Returns:	int[]
Method signature:	int[] findOrder(double[] w)
(be sure your method is public)

Notes

- There are 20 system tests.

- If your sum is less than 0, it will be increased to 0.

Constraints

- N will be between 100 and 1000, with the exception of some of the examples.

- The elements representing w_i,i will be 0.

- The time limit is 30 seconds, and the memory limit is 1024M.

Examples

0)

"1"

Returns: "N=3<br><a href=/contest/problem/Permute/1.txt>download</a>"

1)

"2"

Returns: "N=5<br><a href=/contest/problem/Permute/2.txt>download</a>"

2)

"3"

Returns: "N=10<br><a href=/contest/problem/Permute/3.txt>download</a>"

3)

"4"

Returns: "N=20<br><a href=/contest/problem/Permute/4.txt>download</a>"

4)

"5"

Returns: "N=50<br><a href=/contest/problem/Permute/5.txt>download</a>"

5)

"6"

Returns: "N=159<br><a href=/contest/problem/Permute/6.txt>download</a>"

6)

"7"

Returns: "N=992<br><a href=/contest/problem/Permute/7.txt>download</a>"

7)

"8"

Returns: "N=290<br><a href=/contest/problem/Permute/8.txt>download</a>"

8)

"9"

Returns: "N=352<br><a href=/contest/problem/Permute/9.txt>download</a>"

9)

"10"

Returns: "N=1000<br><a href=/contest/problem/Permute/10.txt>download</a>"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MagicalSource

Math, Simple Math, Simple Search, Iteration

Used in:

SRM 451

Used as:

Division I Level One

Writer:

vexorian

Testers:

PabloGilberto , bmerry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10635

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13905&pm=10635

Problem Statement

Rick firmly believes that there are magical patterns related to some numbers. This belief is the result of his own tendency to find odd patterns everywhere. He has recently thought that some numbers have a "magical source". For example, the number 1371110974 has a magical source equal to 1234 because of the following process:

        1234
+      12340
+     123400
+    1234000
+   12340000
+  123400000
+ 1234000000
------------
  1371110974

Formally, 1234 is a magical source of 1371110974 because there exists a number n such that the sum of a sequence of n numbers, where the i-th number (0-indexed) is 1234 multipled by 10^i, is equal to 1371110974. Note that by this definition, a positive number is a magical source of itself.

Given a positive long x, return its minimum positive magical source.

Definition

Class:	MagicalSource
Method:	calculate
Parameters:	long
Returns:	long
Method signature:	long calculate(long x)
(be sure your method is public)

Constraints

-

x will be between 1 and 1000000000000 (10^12), inclusive.

Examples

0)

1371110974

Returns: 1234

This is the example from the statement.

1)

Returns: 1

2)

Returns: 99

3)

Returns: 120

Note that a number is always a magical source of itself.

4)

109999999989

Returns: 99

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AgeEncoding

Search, Simple Math

Used in:

SRM 462

Used as:

Division I Level One , Division II Level Two

Writer:

Nickolas

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10589

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14147&pm=10589

Problem Statement

NOTE: This problem statement contains superscripts that may not display properly if viewed outside of the applet.

Your friend's birthday is approaching, and he wants his age to be written in candles on his cake. In fact, he has already placed several candles on the cake. The candles are arranged in a single row, and there are two different colors of candles. One color represents the digit '0' and the other color represents the digit '1'. You don't want to relayout the candles from scratch, so you have to determine if there's a base for which the existing candles spell out your friend's age. To simplify the task, you can choose any strictly positive base, not necessarily an integer one.

For example, if the candles are "00010" and your friend's age is 10, then the candles spell out 10 in base 10 (decimal). If the candles are "10101" and your friend's age is 21, then you can say that "10101" is 21 in base 2 (binary). If the candles are "10100" and your friend's age is 6, then the candles spell out 6 in base sqrt(2)=1.41421356237.... Note that you are not allowed to rotate the cake, so "10" cannot be read as "01".

You are given a String candlesLine, where the i-th character is the digit ('0' or '1') represented by the i-th candle in the row of candles on the cake. You are also given an int age, which is your friend's age. Return the positive base for which the candles represent your friend's age. If there is no such base, return -1, and if there are multiple such bases, return -2.

Definition

Class:	AgeEncoding
Method:	getRadix
Parameters:	int, String
Returns:	double
Method signature:	double getRadix(int age, String candlesLine)
(be sure your method is public)

Notes

-

The number a_na_n-1...a₁a₀ in base B is equal to a_n*Bⁿ + a_n-1*B^n-1 + ... + a₁*B + a₀.

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

age will be between 1 and 100, inclusive.

-

candlesLine will contain between 1 and 50 characters, inclusive.

-

Each character in candlesLine will be '0' (zero) or '1' (one).

Examples

0)

"00010"

Returns: 10.0

This is the first example from the statement: simply a decimal notation of the given age. Note that notation can have leading zeroes.

1)

"10101"

Returns: 2.0

This is the second example from the statement: "10101" is a binary notation of the given age.

2)

"10100"

Returns: 1.414213562373095

This is the third example from the statement.

3)

"10111111110111101111111100111111110111111111111100"

Returns: 0.9685012944510603

4)

"1"

Returns: -1.0

In any base, "1" represents the age of 1, so it's impossible to get the age of 16.

5)

"1"

Returns: -2.0

In any base, "1" represents the age of 1.

6)

"001000"

Returns: 1.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CantorDustEasy

Simple Math, String Manipulation

Used in:

Member Beta

Used as:

Division II Level Three

Writer:

Nickolas

Testers:

Rustyoldman , timmac , StevieT , vexorian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10588

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13935&pm=10588

Problem Statement

Cantor dust is a 2-dimensional fractal constructed in the following way. Initially the fractal is a black square. At each iteration, each square of the fractal is divided into a 3x3 subgrid of equal subsquares. Any black subsquares which belong to the middle row or to the middle column of a subgrid (or to both of them) are painted white.

You are given a String[] pattern which represents a rectangular pattern of black and white squares (represented by 'X' and '.' characters, respectively). Return the number of occurrences of this pattern in Cantor dust at iteration time. Overlapping occurrences are allowed.

Definition

Class:	CantorDustEasy
Method:	occurrencesNumber
Parameters:	String[], int
Returns:	int
Method signature:	int occurrencesNumber(String[] pattern, int time)
(be sure your method is public)

Constraints

-

time will be between 1 and 9, inclusive.

-

pattern will contain between 1 and min(50, 3^time) elements, inclusive.

-

Each element of pattern will contain between 1 and min(50, 3^time) characters, inclusive.

-

All elements of pattern will contain the same number of characters.

-

Each character in each element of pattern will be '.' or 'X'.

-

pattern will contain at least one 'X' character.

Examples

0)

{".X",".."}

Returns: 1

1)

{"X"}

Returns: 16

2)

{"X...X"}

Returns: 4

3)

{"XX"}

Returns: 0

4)

{"X.X","...","X.."}

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TriFibonacci

Brute Force, Math, Simple Search, Iteration

Used in:

Member Beta

Used as:

Division II Level One

Writer:

vexorian

Testers:

Rustyoldman , timmac , Nickolas , StevieT

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10587

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13935&pm=10587

Problem Statement

A TriFibonacci sequence begins by defining the first three elements A[0], A[1] and A[2]. The remaining elements are calculated using the following recurrence:

A[i] = A[i-1] + A[i-2] + A[i-3]

You are given a int[] A which contains exactly one element that is equal to -1, you must replace this element with a positive number in a way that the sequence becomes a TriFibonacci sequence. Return this number. If no such positive number exists, return -1.

Definition

Class:	TriFibonacci
Method:	complete
Parameters:	int[]
Returns:	int
Method signature:	int complete(int[] A)
(be sure your method is public)

Notes

-

The constraints for the elements of the input int[] A do not necessarily apply for the replacement to the missing element.

Constraints

-

A will contain between 4 and 20 elements, inclusive.

-

Each element of A will be -1 or between 1 and 1000000, inclusive.

-

Exactly one element of A will be -1.

Examples

0)

{1,2,3,-1}

Returns: 6

1)

{10, 20, 30, 60, -1 , 200}

Returns: 110

2)

{1, 2, 3, 5, -1}

Returns: -1

No replacement can make this sequence TriFibonacci as 5 is not equal to 1+2+3.

3)

{1, 1, -1, 2, 3}

Returns: -1

The missing element must be 0 for this sequence to be TriFibonacci. Since this is not a positive integer, return -1.

4)

{-1, 7, 8, 1000000}

Returns: 999985

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Archery

Geometry, Simple Math

Used in:

SRM 462

Used as:

Division II Level One

Writer:

Nickolas

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10586

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14147&pm=10586

Problem Statement

In archery, you shoot an arrow at a target and you get some number of points depending on where the arrow hits the target. In this problem, the target is a circle divided into N concentric rings and a central circle. The width of each ring and the radius of the central circle are equal. The point values assigned to each section of the target are given in the int[] ringPoints. The values are given in order, from innermost to outermost section, so ringPoints[0] is the number of points you get for hitting the central circle, and ringPoints[N] is the number of points you get for hitting the outermost ring.

You are a beginning archer. Whenever you take a shot, the arrow always lands somewhere on the target, but it hits a random point, and all points on the target have an equal probability of being hit. Return the expected point value of your shot.

Definition

Class:	Archery
Method:	expectedPoints
Parameters:	int, int[]
Returns:	double
Method signature:	double expectedPoints(int N, int[] ringPoints)
(be sure your method is public)

Notes

-

The probability of hitting a specific section of the target is defined as the area of the section divided by the total area of the target.

-

The expected point value of a shot is calculated as follows. For each section of the target, multiply its point value by the probability of hitting that section. The expected point value is the sum of all these values.

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

N will be between 1 and 49, inclusive.

-

ringPoints will contain exactly N+1 elements.

-

Each element of ringPoints will be between 0 and 100, inclusive.

Examples

0)

{10, 0}

Returns: 2.5

You score 10 if you hit the central circle, and 0 otherwise. The area of the central circle is 0.25 of the total target area.

1)

{1, 1, 1, 1}

Returns: 1.0

Regardless of what part of the target you hit, you get 1 point.

2)

{100, 0, 100, 0, 100}

Returns: 60.0

Only even rings of the target give you points.

3)

{69, 50, 79, 16, 52, 71, 17, 96, 56, 32}

Returns: 51.96

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CellScores

Math, Search

Used in:

SRM 447

Used as:

Division I Level Three

Writer:

Gluk

Testers:

PabloGilberto , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10581

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13901&pm=10581

Problem Statement

You are given a square board of size NxN, where each 1x1 cell is either black or white. A rectangle on the board is called good if it contains only white cells. The score of each cell is equal to the number of distinct good rectangles that contain that cell.

Use the following instructions to determine the coloring of the board. You are given ints M, K, X0, Y0, A, B, C and D. Generate two lists, X and Y, each of length M+K, using the following recursive definitions:

X[0] = X0 MOD N

X[i] = (X[i-1]*A+B) MOD N

Y[0] = Y0 MOD N

Y[i] = (Y[i-1]*C+D) MOD N

For each i between 0 and M-1, inclusive, the cell at column X[i], row Y[i] is black. The remaining cells are white.

Let's denote the score for the cell at column i, row j as score(i, j). Return the sum of score(X[i], Y[i]) for all i between M and M+K-1, inclusive.

Definition

Class:	CellScores
Method:	countScores
Parameters:	int, int, int, int, int, int, int, int, int
Returns:	long
Method signature:	long countScores(int N, int M, int K, int X0, int A, int B, int Y0, int C, int D)
(be sure your method is public)

Constraints

-

N will be between 1 and 1,500, inclusive.

-

M and K will each be between 0 and 1,000,000, inclusive.

-

X0,Y0,A,B,C,D will each be between 0 and 1,500, inclusive.

Examples

0)

10
0
1
0
1
1
0
1
1

Returns: 100

The whole board is white. You are interested in cell (0,0). The score for this cell is 100.

1)

10
1
1
5
1
5
5
1
5

Returns: 75

Only the cell (5,5) is black. You are interested in cell (0,0). The score for this cell is 75.

2)

7
4
3
0
1
1
0
1
1

Returns: 194

The first 4 cells on the diagonal are black, and you are interested in the other 3 cells on the diagonal.

3)

23
10
30
26
48
76
231
463
707

Returns: 8088

4)

211
30
12
3
35
82
0
43
15

Returns: 18196443

5)

3
0
100
0
0
0
0
0
0

Returns: 900

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SoldierLabeling

Math

Used in:

SRM 446

Used as:

Division II Level One

Writer:

crazyb0y

Testers:

PabloGilberto , ivan_metelsky , Chmel_Tolstiy , MThorn

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10574

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13900&pm=10574

Problem Statement

Tom is a little boy who likes to collect toys. On his birthday, his mom bought him a box of toy soldiers as a gift. There are n soldiers in the box, labeled 1 to n on their uniforms. The numbers are written with no leading zeroes. Tom starts counting the soldiers, but he soon finds that it's difficult to count them all. He decides to count only the soldiers with labels that have length between lowerBound and upperBound, inclusive. Return the number of soldiers that Tom will count.

Definition

Class:	SoldierLabeling
Method:	count
Parameters:	int, int, int
Returns:	int
Method signature:	int count(int n, int lowerBound, int upperBound)
(be sure your method is public)

Constraints

-

n will be between 1 and 10,000,000, inclusive.

-

lowerBound will be between 1 and 8, inclusive.

-

upperBound will be between lowerBound and 8, inclusive.

Examples

0)

Returns: 90

Here there are 100 soldiers and they're labeled 1 to 100. The labels between 10 and 99, inclusive, are of length 2.

1)

Returns: 22

Here there are 31 soldiers and we're looking for labels of length between 2 and 3, inclusive. There are no labels of length 3. Labels between 10 and 31, inclusive, are of length 2.

2)

Returns: 0

Here there is only one soldier and it is labeled 1. We're looking for labels of length between 2 and 8, inclusive, and there are none.

3)

10000000

Returns: 1

Label 10000000 is the only one here of length 8.

4)

Returns: 2718218

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HamiltonPath

Graph Theory, Math

Used in:

SRM 452

Used as:

Division II Level Three

Writer:

rng_58

Testers:

PabloGilberto , connect4 , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10572

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13906&pm=10572

Problem Statement

There are N cities in a country, numbered 0 to N-1. Each pair of cities is connected by a bidirectional road.

John plans to travel through the country using the following rules:

He must start in one city and end in another city after travelling exactly N-1 roads.
He must visit each city exactly once.
You are given a String[] roads. If the j-th character of the i-th element of roads is 'Y', he must travel the road that connects city i and city j.

For example, if there are three cities, and he wants to travel the road between city 0 and city 1, there are 4 possible paths: 0->1->2, 1->0->2, 2->0->1, 2->1->0. Paths 0->2->1 and 1->2->0 are not allowed because they do not allow him to travel the road between city 0 and city 1.

Return the number of paths he can choose, modulo 1,000,000,007.

Definition

Class:	HamiltonPath
Method:	countPaths
Parameters:	String[]
Returns:	int
Method signature:	int countPaths(String[] roads)
(be sure your method is public)

Constraints

-

roads will contain between 2 and 50 elements, inclusive.

-

Each element of roads will contain n characters, where n is the number of elements in roads.

-

Each character in roads will be 'Y' or 'N'.

-

The i-th character in the i-th element of roads will be 'N'.

-

The j-th character in the i-th element of roads and the i-th character in the j-th element of roads will be equal.

Examples

0)

{"NYN",
 "YNN",
 "NNN"}

Returns: 4

The example from the problem statement.

1)

{"NYYY",
 "YNNN",
 "YNNN",
 "YNNN"}

Returns: 0

It's impossible to travel all these roads while obeying the other rules.

2)

{"NYY",
 "YNY",
 "YYN"}

Returns: 0

This is also impossible.

3)

{"NNNNNY",
 "NNNNYN",
 "NNNNYN",
 "NNNNNN",
 "NYYNNN",
 "YNNNNN"}

Returns: 24

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ModuloFourDivisor

Math

Used in:

Member SRM 458

Used as:

Division I Level Three

Writer:

rng_58

Testers:

Rustyoldman , timmac , ivan_metelsky , mohamedafattah , it4.kp

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10571

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14180&pm=10571

Problem Statement

A quadruplet of non-negative integers (a,b,c,d) is called a divisor quadruplet if there exists at least one positive integer N that satisfies the following four conditions:

N has exactly a divisors x such that x ≡ 0 (mod 4).
N has exactly b divisors x such that x ≡ 1 (mod 4).
N has exactly c divisors x such that x ≡ 2 (mod 4).
N has exactly d divisors x such that x ≡ 3 (mod 4).

You are given long[]s A, B, C and D. Return the number of divisor quadruplets (a,b,c,d) such that A contains a, B contains b, C contains c and D contains d.

Definition

Class:	ModuloFourDivisor
Method:	countQuadruplets
Parameters:	long[], long[], long[], long[]
Returns:	int
Method signature:	int countQuadruplets(long[] A, long[] B, long[] C, long[] D)
(be sure your method is public)

Notes

-

x ≡ k (mod 4) means (x - k) is divisible by 4.

Constraints

-

A, B, C and D will contain between 1 and 50 integers, inclusive.

-

Each element of A, B, C and D will be between 0 and 1,000,000,000,000,000,000 (10^18), inclusive.

-

A, B, C and D will contain no duplicate elements.

Examples

0)

{1}

{1}

{1}

{0}

Returns: 1

(1, 1, 1, 0) is a divisor quadruplet because N = 4 satisfies the conditions.

1)

{0}

{0}

{0}

{0}

Returns: 0

All integers have at least one divisor.

2)

{0}

{0,1}

{0}

{0}

Returns: 1

(0, 0, 0, 0) is not a divisor quadruplet. (0, 1, 0, 0) is a divisor quadruplet.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FunctionalEquation

Graph Theory, Math

Used in:

SRM 456

Used as:

Division I Level Three

Writer:

rng_58

Testers:

PabloGilberto , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10570

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13909&pm=10570

Problem Statement

f is a function from integers to integers. In other words, f is defined over integers, and f(x) is an integer for all integers x. You are given an integer C. f is called C-beautiful if the following equality is satisfied for all integers x:

Return the minimal possible value of the following formula when f is C-beautiful:

Use the following recursive definitions to generate the sequences x and y:

x[0] = xzero
For all integer i between 1 and N-1, inclusive, x[i] = (x[i-1] * xprod + xadd) % xmod
y[0] = yzero
For all integer i between 1 and N-1, inclusive, y[i] = (y[i-1] * yprod + yadd) % ymod

Definition

Class:	FunctionalEquation
Method:	minAbsSum
Parameters:	int, int, int, int, int, int, int, int, int, int
Returns:	long
Method signature:	long minAbsSum(int C, int N, int xzero, int xprod, int xadd, int xmod, int yzero, int yprod, int yadd, int ymod)
(be sure your method is public)

Notes

-

64-bit integers should be used to generate the sequences x and y to avoid overflow.

Constraints

-

C will be between 1 and 16, inclusive.

-

N will be between 1 and 10,000, inclusive.

-

xmod and ymod will each be between 1 and 1,000,000,000, inclusive.

-

xzero, xprod and xadd will each be between 0 and xmod - 1, inclusive.

-

yzero, yprod and yadd will each be between 0 and ymod - 1, inclusive.

Examples

0)

3
10
0
1
1
456
1
1
1
456

Returns: 0

f(x) = x + 1 is a 3-beautiful function.

Since x = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} and y = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, the sum of |f(x[i]) - y[i]| is 0.

1)

4
10
0
1
1
456
1
1
1
456

Returns: 5

x and y are the same as in example 0, but f(x) = x + 1 is not a 4-beautiful function.

2)

16
10000
654816386
163457813
165911619
987654321
817645381
871564816
614735118
876543210

Returns: 3150803357206

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IncreasingNumber

Dynamic Programming, Math

Used in:

SRM 452

Used as:

Division I Level Three

Writer:

rng_58

Testers:

PabloGilberto , connect4 , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10566

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13906&pm=10566

Problem Statement

A positive integer is called Increasing Number if its digits are in non-descending order from left to right in decimal notation. For example, 1234, 111, 58 and 8899 are Increasing Numbers, while 314, 7654 and 2009 are not.

You are given a long digits and an int divisor. Calculate the number of Increasing Numbers that satisfy both of the following conditions and return this number modulo 1,000,000,007.

The number contains exactly digits digits in the decimal notation with no leading zeroes.
The number is divisible by divisor.

Definition

Class:	IncreasingNumber
Method:	countNumbers
Parameters:	long, int
Returns:	int
Method signature:	int countNumbers(long digits, int divisor)
(be sure your method is public)

Constraints

-

digits will be between 1 and 1,000,000,000,000,000,000 (10^18), inclusive.

-

divisor will be between 1 and 500, inclusive.

Examples

0)

Returns: 4

12, 24, 36, and 48 satisfy the conditions.

1)

Returns: 9

All 3-digits numbers divisible by 111 are Increasing Numbers.

2)

Returns: 0

There is no Increasing Number divisible by 10.

3)

Returns: 38

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IOIString

Math

Used in:

SRM 452

Used as:

Division I Level Two

Writer:

rng_58

Testers:

PabloGilberto , connect4 , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10564

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13906&pm=10564

Problem Statement

A string s is called an IOI string if it satisfies the following two conditions:

s contains only uppercase 'I' and uppercase 'O' letters.
There is at least one pair of non-negative integers (a,b) such that the a-th (0-indexed) character of s is 'I', the (a+b)-th character is 'O', and the (a+2*b)-th character is 'I'.

You are given a String[] mask. Concatenate the elements of mask to get one string. Each '?' character in mask can be replaced with either 'I' or 'O'.

Return the number of different IOI strings that can be formed, modulo 1,000,000,007 (1E9+7).

Definition

Class:	IOIString
Method:	countIOIs
Parameters:	String[]
Returns:	int
Method signature:	int countIOIs(String[] mask)
(be sure your method is public)

Constraints

-

mask will contain between 1 and 50 elements, inclusive.

-

Each element of mask will contain between 1 and 50 characters, inclusive.

-

Each character in mask will be uppercase 'I' or uppercase 'O' or '?'.

Examples

0)

{"IO?"}

Returns: 1

Two strings can be formed here : "IOI" and "IOO". Only "IOI" is an IOI string.

1)

{"????"}

Returns: 4

There are four IOI strings of length 4 : "IIOI", "IOII", "IOIO", and "OIOI".

2)

{"?II"}

Returns: 0

No IOI string can be formed from "?II".

3)

{"I??O??I"}

Returns: 16

Character 0 is 'I', character 3 is 'O', and character 6 is 'I'.

Therefore, all possible strings are IOI strings here.

4)

{"???I???????O???","???????????O??IO????????I???"}

Returns: 438952513

Don't forget to concatenate strings.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CutSticks

Greedy, Math

Used in:

SRM 456

Used as:

Division I Level Two , Division II Level Three

Writer:

rng_58

Testers:

PabloGilberto , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10563

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13909&pm=10563

Problem Statement

John has some sticks of various lengths. You are given a int[] sticks, where each element is the length of a single stick.

He is allowed to perform at most C cuts. With each cut, he chooses one of his sticks and divides it into exactly two sticks of arbitrary positive lengths (the sum of their lengths must equal the length of the original stick). Each of these sticks can then be chosen again when making subsequent cuts.

After he performs all his cuts, he sorts the sticks in non-increasing order by length and chooses the K-th (1-based) stick. Return the maximal possible length of the stick he chooses. Note that he must perform at least as many cuts as are required to end up with K or more sticks.

Definition

Class:	CutSticks
Method:	maxKth
Parameters:	int[], int, int
Returns:	double
Method signature:	double maxKth(int[] sticks, int C, int K)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

sticks will contain between 1 and 50 elements, inclusive.

-

Each element of sticks will be between 1 and 1,000,000,000, inclusive.

-

C will be between 1 and 1,000,000,000, inclusive.

-

K will be between 1 and n + C, inclusive, where n is the number of elements in sticks.

Examples

0)

{5, 8}

Returns: 8.0

John can make at most one cut. He should either cut the stick of length 5 (it doesn't matter where) or not make any cuts at all. If he makes no cuts, then after he sorts the sticks, they will be in the following order: {8, 5}. He chooses the 1st stick, which has length 8.

1)

{5, 8}

Returns: 5.0

Again, the easiest thing to do here is not make any cuts.

2)

{5, 8}

Returns: 4.0

John has 2 sticks and he can make at most one cut. In this case, since K is 3, he is required to make a cut so he can end up with 3 sticks. He should cut the longest stick into two equal sticks of length 4. After he sorts the sticks, they will be in the following order: {5, 4, 4}. He will choose the 3rd stick, which has length 4.

3)

{1000000000, 1000000000, 1}

Returns: 1.0

4)

{76, 594, 17, 6984, 26, 57, 9, 876, 5816, 73, 969, 527, 49}

Returns: 34.92

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NotTwo

Math

Used in:

SRM 452

Used as:

Division I Level One , Division II Level Two

Writer:

rng_58

Testers:

PabloGilberto , connect4 , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10561

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13906&pm=10561

Problem Statement

Bob has a width x height rectangular board divided into 1 x 1 cells. Rows of the board are numbered 0 to height-1 and columns are numbered 0 to width-1.

Each cell can contain at most one stone, and the Euclidean distance between each pair of stones must not equal 2. The Euclidean distance between cell in row x1, column y1 and cell in row x2, column y2 is defined as the square root from (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2).

Return the maximal number of stones he can place on the board.

Definition

Class:	NotTwo
Method:	maxStones
Parameters:	int, int
Returns:	int
Method signature:	int maxStones(int width, int height)
(be sure your method is public)

Constraints

-

width will be between 1 and 1000, inclusive.

-

height will be between 1 and 1000, inclusive.

Examples

0)

Returns: 4

He can place four stones on the board. Here is one possible arrangement:

- * *
* * -

1)

Returns: 5

* - -
* * -
- * *

2)

Returns: 20

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StairsColoring

Advanced Math, Simple Search, Iteration

Used in:

SRM 449

Used as:

Division I Level Three

Writer:

dzhulgakov

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10551

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13903&pm=10551

Problem Statement

A very rich sultan built an enormous luxurious two-story palace containing several staircases. According to an old tradition, each staircase must:

contain exactly N steps
have a right angle in its base
be built using exactly N rectangular blocks of arbitrary size

Staircases can be built using many different arrangements of blocks. For example, there are 5 ways to build a staircase with 3 steps:

To ensure that his palace is really the most luxurious in the world, the sultan decided to build one staircase for each possible arrangement of blocks.

The sultan is now preparing for a staircase coloring festival. He wants to paint each of the staircases in the palace in one of K different colors. Multiple staircases can be painted the same color, and it is not necessary to use all K colors. Help the sultan by calculating the total number of different ways he can color his staircases. The answer can be large, so return the count modulo 1000000123.

Definition

Class:	StairsColoring
Method:	coloringCount
Parameters:	int, int
Returns:	int
Method signature:	int coloringCount(int N, int K)
(be sure your method is public)

Constraints

-

N will be between 1 and 1000000000, inclusive.

-

K will be between 1 and 1000000000, inclusive.

Examples

0)

Returns: 32

As shown in the picture above, there are exactly 5 different ways to build a staircase with 3 steps. Each staircase can be painted in one of 2 different colors, for a total of 32 possible color combinations.

1)

Returns: 4

2)

Returns: 1

Here, there is only one staircase and one color to paint it.

3)

Returns: 103514887

4)

Returns: 747707397

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OddDivisors

Recursion, Simple Math

Used in:

SRM 449

Used as:

Division II Level Two

Writer:

dzhulgakov

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10547

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13903&pm=10547

Problem Statement

Let f(x) be the greatest odd divisor of x, where x is a positive integer. You are given a positive integer N. Return f(1)+f(2)+?+f(N).

Definition

Class:	OddDivisors
Method:	findSum
Parameters:	int
Returns:	long
Method signature:	long findSum(int N)
(be sure your method is public)

Constraints

-

N will be between 1 and 1000000000, inclusive.

Examples

0)

Returns: 21

f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)=1+1+3+1+5+3+7=21

1)

Returns: 1

2)

Returns: 201537

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MountainRoad

Simple Math, Simple Search, Iteration

Used in:

SRM 449

Used as:

Division II Level One

Writer:

dzhulgakov

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10546

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13903&pm=10546

Problem Statement

Your friend is going to the mountains on vacation. He will climb up and down several mountains, and he has asked you to calculate his total walking distance.

To simplify this task, everything will be represented on a 2-dimensional cartesian plane. The ground is represented as the x-axis, and the mountains are represented as the union of several isosceles triangles. You are given int[]s start and finish. For each index i, construct an isosceles right triangle with its hypotenuse lying on the ground from point start[i] to point finish[i].

The mountains are guaranteed to form a single connected non-degenerate polygon, where the height is positive everywhere between the start and end points. The path your friend will walk is defined as the upper part of this mountain, shown in bold in the figure above. Return the length of this path.

Definition

Class:	MountainRoad
Method:	findDistance
Parameters:	int[], int[]
Returns:	double
Method signature:	double findDistance(int[] start, int[] finish)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

-

An isosceles right triangle is a triangle with angles 90, 45 and 45 degrees. The hypotenuse of such a triangle is the side opposite the 90 degree angle.

Constraints

-

start will contain between 1 and 50 elements, inclusive.

-

start and finish will contain the same number of elements.

-

Each element of start and finish will be between -1000 and 1000, inclusive.

-

For every i start[i] will be strictly less than finish[i].

-

The union of the isosceles triangles described in start and finish will be a single connected nondegenerate polygon.

Examples

0)

{1}

{7}

Returns: 8.485281374238571

In this case there is only one mountain.

1)

{0,3,4}

{5,9,6}

Returns: 12.727922061357857

This situation with three mountains is shown in the figure above.

2)

{1,4,5,6,-10}

{101,102,101,100,99}

Returns: 158.39191898578665

3)

{-5,-3}

{-2,-2}

Returns: 4.242640687119286

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BrickPuzzle

Dynamic Programming, Math, Search

Used in:

SRM 451

Used as:

Division I Level Three

Writer:

vexorian

Testers:

PabloGilberto , bmerry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10524

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13905&pm=10524

Problem Statement

NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.

Howard Benson loves puzzles and is always eager to invent new ones. He has recently invented a new puzzle based on the old puzzles that involved placing various tetrominoes inside a rectangle. For this puzzle, Howard picked four kinds of tetrominoes and made pieces with their shapes. The player can use as many pieces of each kind as necessary. The pieces he made available are shown in the following image:

Another component of the puzzle is the board, which is a square grid composed of white and black cells. The objective of the game is to cover all the white cells by placing a minimum number of pieces on the board. There are many rules regarding the placement of the pieces:

The pieces may not overlap.
Every piece must lie completely inside the board.
The pieces must be aligned to the grid.
The orientation of each piece must be the same as the orientation in the picture above.
Black cells in the board may be covered if necessary.

For example, the following picture shows a board configuration and a solution using a minimum number of pieces:

You are given the board as a String[] board. The j-th character of the i-th element of board is 'X' if the cell at column j, row i is black and '.' if the cell is white. Return the minimum number of shapes that are required to cover all the white cells by following the aforementioned rules. If it is impossible to cover all the white cells following the rules, return -1.

Definition

Class:	BrickPuzzle
Method:	leastShapes
Parameters:	String[]
Returns:	int
Method signature:	int leastShapes(String[] board)
(be sure your method is public)

Constraints

-

board will contain between 1 and 22 elements, inclusive.

-

Each element of board will contain between 1 and 22 characters, inclusive.

-

All elements of board will contain the same number of characters.

-

Each element of board will contain only the characters '.' and uppercase 'X'.

Examples

0)

{"..X....",
 "..XXXXX"}

Returns: 2

1)

{".X",
 "..",
 "X."}

Returns: -1

Note that the pieces cannot be rotated.

2)

{"..XX....",
 "....X..X",
 "XX..XXXX"}

Returns: 4

3)

{"X..XXXX",
 "X.....X",
 "....XX.",
 "X......"}

Returns: 5

This is the example from the statement.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheLockDivOne

Math, Recursion

Used in:

SRM 445

Used as:

Division I Level Two

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10514

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13899&pm=10514

Problem Statement

John is obsessed with security. Recently he bought a new electronic lock. It is protected by a password containing n digits, where each digit is either zero or one. John decides to change the password every day. On the first day, the password is all zeroes. On each day that follows, he will select one or more digits that all have the same value and change their values (so zeroes become ones, and ones become zeroes). He must select the digits according to the following rules:

During the first 2^n days, he must never use the same password twice.
Each new password must come as early as possible alphabetically while not violating rule 1.

For example, if n is 2, the password on the first day is "00". The next day, he can change one or both 0's to get "01", "10" or "11". Of these possibilities, "01" comes earliest alphabetically. The next day, he can change either the 0 or the 1 to get "11" or "00". He can't choose "00" because it was already used, so he chooses "11". The next day, he can change one or both 1's to get "10", "01" or "00". He has already used "01" and "00", so he must choose "10".

Given ints n and k, return the password that comes latest alphabetically during the first k days.

Definition

Class:	TheLockDivOne
Method:	password
Parameters:	int, long
Returns:	String
Method signature:	String password(int n, long k)
(be sure your method is public)

Notes

-

If A and B are two Strings of the same length, then A comes earlier alphabetically than B if it contains a smaller character at the first position where the Strings differ.

Constraints

-

n will be between 1 and 50, inclusive.

-

k will be between 1 and 2^n, inclusive.

Examples

0)

Returns: "11"

This is the example from the statement. The password sequence is the following - "00", "01", "11", "10".

1)

Returns: "111"

"000", "001", "011", "010", "110", "100", "101", "111".

2)

Returns: "0110"

3)

Returns: "0000000000"

4)

Returns: "1111110"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheLockDivTwo

Math, Simulation

Used in:

SRM 445

Used as:

Division II Level Three

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10513

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13899&pm=10513

Problem Statement

John is obsessed with security. Recently he bought a new electronic lock. It is protected by a password containing n digits, where each digit is either zero or one. John decides to change the password every day. On the first day, the password is all zeroes. On each day that follows, he will select one or more digits that all have the same value and change their values (so zeroes become ones, and ones become zeroes). He must select the digits according to the following rules:

During the first 2^n days, he must never use the same password twice.
Each new password must come as early as possible alphabetically while not violating rule 1.

For example, if n is 2, the password on the first day is "00". The next day, he can change one or both 0's to get "01", "10" or "11". Of these possibilities, "01" comes earliest alphabetically. The next day, he can change either the 0 or the 1 to get "11" or "00". He can't choose "00" because it was already used, so he chooses "11". The next day, he can change one or both 1's to get "10", "01" or "00". He has already used "01" and "00", so he must choose "10".

Given ints n and k, return the password that John will choose on the k-th day (where k is a 1-based index).

Definition

Class:	TheLockDivTwo
Method:	password
Parameters:	int, int
Returns:	String
Method signature:	String password(int n, int k)
(be sure your method is public)

Notes

-

If A and B are two Strings of the same length, then A comes earlier alphabetically than B if it contains a smaller character at the first position where the Strings differ.

Constraints

-

n will be between 1 and 10, inclusive.

-

k will be between 1 and 2^n, inclusive.

Examples

0)

Returns: "10"

This is the example from the statement. The password sequence is the following - "00", "01", "11", "10".

1)

Returns: "0100"

"0000", "0001", "0011", "0010", "0110", "0100", ...

2)

Returns: "0000000000"

The password always consists of all zeroes on the first day.

3)

Returns: "1100001"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ShuffledPlaylist

Dynamic Programming, Math

Used in:

SRM 443

Used as:

Division I Level Three

Writer:

gojira_tc

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10486

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13751&pm=10486

Problem Statement

I love music and listen to it all the time. I have a huge amount of songs and often it's easy just to listen to them shuffled rather than to choose a song every time. But I listen to different genres of music and some of them are incompatible (for example, it's quite uncomfortable if some calm classic track is succeeded by a loud noisy song). So I wrote a program which performs the shuffled playback according to some rules.

Speaking formally, I have defined several genres and ascribed each of the songs to one specific genre. I have also defined which genres are compatible, i.e. can be listened to in immediate succession and which are not. The j-th character of the i-th element of String[] transitions is 'Y' if a song of genre i can be succeeded by a song of genre j, and is 'N' otherwise. My program works in the following way: it randomly chooses the first song to play. When the track finishes, the next song is chosen from the set of all songs of compatible genre(s), and so on. The same song may be played several times and it might even happen that the same song is played several times in a row.

You're given String[] songs. Concatenate the elements of songs to obtain a list of the songs. The list will be formatted as a comma-separated list of space-separated pairs of integers, the first of them denoting the genre of the song and the second one denoting its length in minutes. Count the number of different song sequences which might be played using my program and are between minLength and maxLength (both inclusive) minutes long, and return it modulo 600,921,647.

Definition

Class:	ShuffledPlaylist
Method:	count
Parameters:	String[], String[], int, int
Returns:	int
Method signature:	int count(String[] songs, String[] transitions, int minLength, int maxLength)
(be sure your method is public)

Constraints

-

transitions will contain exactly n elements, where n is between 1 and 9, inclusive.

-

Each element of transitions will contain exactly n characters.

-

transitions will contain only 'N' and 'Y' characters.

-

For each i between 0 and n-1, the i-th character of the i-th element of transitions will be 'Y'.

-

songs will contain between 1 and 50 elements, inclusive.

-

Each element of songs will contain between 1 and 50 characters, inclusive.

-

The concatenation of the elements of songs will be a comma-separated list of space-separated pairs of integers.

-

The first integer of each pair will be between 0 and n-1, inclusive, with no extra leading zeroes.

-

The second integer of each pair will be between 1 and 9, inclusive, with no leading zeroes.

-

minLength will be between 1 and 1,000,000,000, inclusive.

-

maxLength will be between minLength and 1,000,000,000, inclusive.

Examples

0)

{"0 3,1 2,0 2"}

{"YY","YY"}

Returns: 7

If we enumerate the songs from 0 to 2, then the 7 possible song sequences are: {0},{1},{2},{1,1},{1,2},{2,1},{2,2}.

1)

{"0 3,1 2,0 2"}

{"YN","NY"}

Returns: 5

This time, the genres are incompatible, so the sequences {1,2} and {2,1} are not allowed any more.

2)

{"0 9",",1 8,","2 3,2 5"}

{"YYY","NYY","NNY"}

Returns: 7

The sequences are: {0},{1},{2,2},{2,2,2},{3},{2,3},{3,2}.

3)

{"0 8,","5 6,2"," 2,2 3,6 8,5 8,5 3,0 6,0 7,6 5,3 2",
",0 9,2 3,3 4,5 4,3 3,3 3,2 8,2 9,5 7,2 8,0 1,5 9,1",
" 8,2 9,1 6,3 6,2 6,0 4,6 3,1 5,2 7,4 5,3 3,0",
" 5,6 1,5 6,4 8,5 9,1 4,2 9,5 6,5 6,0 8,3 5,4 6,0 3",
",4 2,5 6,6 2,4 3,1 3,6 3,0 8,2 8,3 7,4 2,0 7,0 2,1",
" 3,4 7,6 3,6 4,3 9,0 2,0 7,0 8,6 4,1 3,2 5,0 6,5 4",
",3 2,3 2,1 5,2 1,5 2,4 8,0 5,1"," ","7,2 6,5 7",",",
"6 9,5 5,","4 2",",4"," 9,0 5,4 8,6 5,5 9,5 8,3 ","2",
",5 ","6,2 3,0 7,1 7,","2 1,0 4",",2 9",",","3"," ","4"}

{"YYYYYYY","YYYYYYY","YYYYYYY","YYYYYYY","YYYYYYY","YYYYYYY","YYYYYYY"}

Returns: 348387817

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OverlappingConcatenation

Dynamic Programming, Math

Used in:

TCO10 Round 5

Used as:

Division I Level Three

Writer:

StevieT

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10477

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14283&pm=10477

Problem Statement

An overlapping concatenation of an ordered pair of Strings (A, B) is a String S such that A is a prefix of S and B is a suffix of S. A shortest overlapping concatenation (SOC) of (A, B) is an overlapping concatenation whose length is as small as possible. For example, if A is "cabab" and B is "ababc", the shortest overlapping concatenation is "cababc" (all quotes for clarity). You are given two Strings A and B, in which some of the characters are known and some are unknown. Each character in A and B will be a lowercase letter ('a' - 'z') if it is known or '*' if it is unknown.

Assuming that each unknown character will be selected uniformly at random from the characters contained in alphabet, return the expected length of the shortest overlapping concatenation of A and B.

Definition

Class:	OverlappingConcatenation
Method:	shortestExpected
Parameters:	String, String, String
Returns:	double
Method signature:	double shortestExpected(String A, String B, String alphabet)
(be sure your method is public)

Constraints

-

alphabet will contain between 1 and 26 lowercase letters ('a' - 'z'), inclusive.

-

The characters in alphabet will be distinct.

-

A and B will contain between 1 and 32 characters, inclusive.

-

A and B will contain the same number of characters.

-

Each character in A and B will either be contained in alphabet or it will be '*'.

Examples

0)

"aa*aa"

"a*aaa"

"ab"

Returns: 7.0

The 4 equal-probability possibilities for the shortest overlapping concatenation (SOC) are as follows:

A     | B     | SOC
aaaaa | aaaaa | aaaaa
aabaa | aaaaa | aabaaaaa
aaaaa | abaaa | aaaaabaaa
aabaa | abaaa | aabaaa

The result is therefore (5 + 8 + 9 + 6) / 4 = 7.

1)

"**"

"**"

"ab"

Returns: 3.125

There are 16 possibilities for A and B. Of these, 4 give a SOC of length 2; 6 give a SOC of length 3; and 6 give a SOC of length 4. The answer is therefore (4*2 + 6*3 + 6*4) / 16 = 3.125.

2)

"**a*cd"

"cde***"

"abcdefghijklmnopqrstuvwxyz"

Returns: 10.0

It makes no difference what the unknown characters are; the SOC is always the same length.

3)

"h*phz*"

"hzph*p"

"zph"

Returns: 10.555555555555557

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PerfectPermutationHard

Greedy, Simple Math, Simple Search, Iteration

Used in:

SRM 441

Used as:

Division II Level Three

Writer:

giolekva

Testers:

PabloGilberto , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10469

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13749&pm=10469

Problem Statement

A permutation A[0], A[1], ..., A[N-1] is a sequence containing each integer between 0 and N-1, inclusive, exactly once. Each permutation A of length N has a corresponding child array B of the same length, where B is defined as follows:

B[0] = 0
B[i] = A[B[i-1]], for every i between 1 and N-1, inclusive.

A permutation is considered perfect if its child array is also a permutation.

Below are given all permutations for N=3 with their child arrays. Note that for two of these permutations ({1, 2, 0} and {2, 0, 1}) the child array is also a permutation, so these two permutations are perfect.

Permutation		Child array
{0, 1, 2}		{0, 0, 0}
{0, 2, 1}		{0, 0, 0}
{1, 0, 2}		{0, 1, 0}
{1, 2, 0}		{0, 1, 2}
{2, 0, 1}		{0, 2, 1}
{2, 1, 0}		{0, 2, 0}

You are given a int[] P containing a permutation of length N. Find a perfect permutation Q of the same length such that the difference between P and Q is as small as possible. The difference between P and Q is the number of indices i for which P[i] and Q[i] are different. If there are several such permutations Q, return the one among them that has the lexicographically smallest child array.

Definition

Class:	PerfectPermutationHard
Method:	reorder
Parameters:	int[]
Returns:	int[]
Method signature:	int[] reorder(int[] P)
(be sure your method is public)

Notes

-

int[] A comes before int[] B (with the same length) lexicographically if A has a smaller integer at the first position where the arrays differ.

Constraints

-

P will contain between 1 and 50 elements, inclusive.

-

P will contain each integer between 0 and N-1, inclusive, exactly once, where N is the number of elements in P.

Examples

0)

{2, 0, 1}

Returns: {2, 0, 1 }

This permutation is already perfect.

1)

{4, 0, 5, 2, 1, 3}

Returns: {2, 0, 5, 4, 1, 3 }

Here the smallest possible difference between P and Q is 2. There are 9 possible choices for Q: {2,0,5,4,1,3}, {3,0,5,2,1,4}, {4,0,1,2,5,3}, {4,0,5,1,2,3}, {4,0,5,2,3,1}, {4,2,5,0,1,3}, {4,3,5,2,1,0}, {4,5,0,2,1,3} and {5,0,4,2,1,3}. Among them, {2,0,5,4,1,3} has the lexicographically smallest child array (this array is {0,2,5,3,4,1}).

2)

{2, 7, 3, 0, 6, 4, 5, 1}

Returns: {1, 7, 3, 0, 6, 2, 5, 4 }

3)

{11, 8, 10, 1, 5, 4, 0, 7, 3, 9, 12, 6, 2}

Returns: {1, 8, 10, 2, 5, 7, 0, 9, 3, 11, 12, 6, 4 }

4)

{0, 1, 4, 2, 3, 5}

Returns: {1, 2, 4, 5, 3, 0 }

5)

{0, 2, 6, 5, 7, 3, 1, 4}

Returns: {1, 2, 6, 5, 7, 4, 3, 0 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PaperAndPaintEasy

Brute Force, Simple Math

Used in:

SRM 441

Used as:

Division II Level Two

Writer:

giolekva

Testers:

PabloGilberto , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10468

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13749&pm=10468

Problem Statement

Onise likes to play with paper and paint. He has a piece of paper with dimensions width x height. He does the following steps with the paper:

Fold the paper along the line x = xfold (the left side of the paper is folded over the right side).
Divide the paper vertically into cnt+1 equal sections. Then, cnt times, take the topmost section and fold it over the section below it.
Paint a rectangle with the lower-left corner at (x1, y1) and the upper-right corner at (x2, y2). Note that (0, 0) is now the lower-left corner of the paper in its current folded state, not its original state. The paint will seep through all the layers of the folded paper. See the image below for clarification.
Unfold the paper.

For example, let's say Onise has a piece of paper that is 5 x 6. He performs the described steps where xfold is 2, cnt is 2, and the coordinates of the painted rectangle's corners are (1, 1) and (3, 2). The following will happen (note that the paper starts out blue in the images and gets painted white):

You are given ints width and height, and ints xfold, cnt, x1, y1, x2 and y2. Return the total area of of the paper that is not covered in paint after Onise is done.

Definition

Class:	PaperAndPaintEasy
Method:	computeArea
Parameters:	int, int, int, int, int, int, int, int
Returns:	long
Method signature:	long computeArea(int width, int height, int xfold, int cnt, int x1, int y1, int x2, int y2)
(be sure your method is public)

Constraints

-

width and height will be between 1 and 10^9, inclusive.

-

xfold will be between 0 and width, inclusive.

-

cnt will be between 0 and 1000, inclusive.

-

cnt+1 will be a divisor of height.

-

0 <= x1 < x2 <= max(xfold, width-xfold) and 0 <= y1 < y2 <= height/(cnt+1).

Examples

0)

5
6
2
2
1
1
3
2

Returns: 21

The example from the problem statement.

1)

3
13
1
0
1
8
2
12

Returns: 35

2)

12
12
7
3
3
1
6
2

Returns: 124

3)

4
5
4
0
0
0
1
1

Returns: 19

4)

4
8
4
3
0
1
2
2

Returns: 24

5)

4
8
3
0
1
1
3
2

Returns: 30

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PerfectPermutation

Brute Force, Greedy, Simple Math

Used in:

SRM 441

Used as:

Division I Level One

Writer:

giolekva

Testers:

PabloGilberto , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10463

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13749&pm=10463

Problem Statement

A permutation A[0], A[1], ..., A[N-1] is a sequence containing each integer between 0 and N-1, inclusive, exactly once. Each permutation A of length N has a corresponding child array B of the same length, where B is defined as follows:

B[0] = 0
B[i] = A[B[i-1]], for every i between 1 and N-1, inclusive.

A permutation is considered perfect if its child array is also a permutation.

Below are given all permutations for N=3 with their child arrays. Note that for two of these permutations ({1, 2, 0} and {2, 0, 1}) the child array is also a permutation, so these two permutations are perfect.

Permutation		Child array
{0, 1, 2}		{0, 0, 0}
{0, 2, 1}		{0, 0, 0}
{1, 0, 2}		{0, 1, 0}
{1, 2, 0}		{0, 1, 2}
{2, 0, 1}		{0, 2, 1}
{2, 1, 0}		{0, 2, 0}

You are given a int[] P containing a permutation of length N. Find a perfect permutation Q of the same length such that the difference between P and Q is as small as possible, and return this difference. The difference between P and Q is the number of indices i for which P[i] and Q[i] are different.

Definition

Class:	PerfectPermutation
Method:	reorder
Parameters:	int[]
Returns:	int
Method signature:	int reorder(int[] P)
(be sure your method is public)

Constraints

-

P will contain between 1 and 50 elements, inclusive.

-

P will contain each integer between 0 and N-1, inclusive, exactly once, where N is the number of elements in P.

Examples

0)

{2, 0, 1}

Returns: 0

P is a perfect permutation, so we can use the same permutation for Q. The difference is then 0 because P and Q are the same.

1)

{2, 0, 1, 4, 3}

Returns: 2

Q might be {2, 0, 3, 4, 1}.

2)

{2, 3, 0, 1}

Returns: 2

Q might be {1, 3, 0, 2}.

3)

{0, 5, 3, 2, 1, 4}

Returns: 3

4)

{4, 2, 6, 0, 3, 5, 9, 7, 8, 1}

Returns: 5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumericalPerfectionLevel

Math

Used in:

SRM 444

Used as:

Division II Level Two

Writer:

vexorian

Testers:

PabloGilberto , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10457

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13898&pm=10457

Problem Statement

It is a well known fact that of all numbers, the number 4 is the most relevant. Patterns related to the number 4 tend to appear everywhere. For example, the numerical perfection level is closely related to the number 4.

We define the perfection level of a positive integer N as k if N can be expressed as a product of 4 positive integers, each with a perfection level of at least (k-1), and cannot be expressed as a product of 4 positive integers, each with a perfection level greater than (k-1). There is one exception - if it is not possible to express N as a product of 4 positive integers all greater than 1, then the perfection level of N is 0.

Given a long N, return its perfection level.

Definition

Class:	NumericalPerfectionLevel
Method:	getLevel
Parameters:	long
Returns:	int
Method signature:	int getLevel(long N)
(be sure your method is public)

Constraints

-

N will be between 1 and 10000000000000 (10^13), inclusive.

Examples

0)

Returns: 0

4 cannot be expressed as a product of 4 numbers all greater than 1.

1)

Returns: 1

144 = 4 x 2 x 3 x 6

The level of 4, 2, 3 and 6 is 0.

2)

Returns: 1

One of many possible ways to express 1152 is:

1152 = 144 x 2 x 2 x 2

Although 144's level is 1, the remaining factors are of level 0. There is no way to express 1152 as a product of four level 1 numbers.

3)

Returns: 2

1679616 = 36 x 36 x 36 x 36

36 = 2 x 2 x 3 x 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheBoredJohn

Dynamic Programming, Simple Math

Used in:

TCO09 Championship

Used as:

Division I Level Three

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10422

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13765&pm=10422

Problem Statement

John is flying to Las Vegas for the TopCoder finals. The flight is several hours long, and he can't sleep, so he decides to play his favorite mobile phone game. The game is played on a n x n 2-dimensional plane, where (0, 0) is the lower-left corner. There is a single monster at each point with integer coordinates except at (0, 0). At (0, 0), there's a laser gun that John can use to kill monsters. He can take at most k shots. On each shot, he can aim the gun in any direction and press a button that releases an infinite laser ray that kills all monsters in its path. The monsters are quite small so we can treat them as points.

Some monsters were so afraid of John that they decided to escape before the game starts, and they are now missing from the battlefield. You are given ints n and k, and a String[] missing. Concatenate the elements of missing to obtain a comma separated list of the points where monsters are missing. Each point is formatted as "row column" (quotes for clarity), where rows are numbered from bottom to top starting at 0 and columns are numbered from left to right starting at 0. Return the maximum number of monsters that John can kill using no more than k shots.

Definition

Class:	TheBoredJohn
Method:	killMonsters
Parameters:	int, long, String[]
Returns:	long
Method signature:	long killMonsters(int n, long k, String[] missing)
(be sure your method is public)

Constraints

-

n will be between 2 and 4,000,000, inclusive.

-

k will be between 1 and 16,000,000,000,000, inclusive.

-

missing will contain between 1 and 50 elements, inclusive.

-

Each element of missing will consist of between 1 and 50 characters, inclusive.

-

missing, when concatenated, will contain a comma separated list of points.

-

missing will contain between 1 and n*n-1 points.

-

Each point in missing will be formatted "row column" (quotes for clarity), where each row and column is an integer between 0 and n-1, inclusive, with no extra leading zeroes.

-

All points in missing will be distinct.

-

missing will not contain the point "0 0".

Examples

0)

{"1 1,0 1,1 0"}

Returns: 4

Here, John can't kill more than one monster with a single shot.

1)

1000000000

{"1 1,0 1,1 0"}

Returns: 0

2)

{"8 2,0 1,7 6,6 8,3 3,0 5,3 4"}

Returns: 8

Just a single shot.

3)

{"0 3,2"," 4,3 3",",4 2,2 0"}

Returns: 18

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheProduct

Greedy, Simple Math, Sorting

Used in:

SRM 453.5

Used as:

Division II Level Three

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , ivan_metelsky , Xixas

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10421

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14174&pm=10421

Problem Statement

You are given an int k and a int[] numbers containing exactly N elements. Choose exactly k distinct integers between 0 and N-1, inclusive, and arrange them in ascending order. The difference between each pair of consecutive elements in this sequence must be less than or equal to maxDist. Each element in this sequence represents a zero-based index into the int[] numbers. Multiply the corresponding elements of numbers together to obtain a product. Return the maximal possible product you can get.

Definition

Class:	TheProduct
Method:	maxProduct
Parameters:	int[], int, int
Returns:	long
Method signature:	long maxProduct(int[] numbers, int k, int maxDist)
(be sure your method is public)

Constraints

-

numbers will contain between 1 and 50 elements, inclusive.

-

Each element of numbers will be between -50 and 50, inclusive.

-

k will be between 1 and 10, inclusive.

-

k will be less than or equal to the number of elements in numbers.

-

maxDist will be between 1 and 50, inclusive.

Examples

0)

{7, 4, 7}

Returns: 28

The maximal distance is 1, so we can't choose both 7's.

1)

{7, 4, 7}

Returns: 49

And now it's possible.

2)

{-3, -5, -8, -9, -1, -2}

Returns: -10

Here, the product will always be negative, so we need to find the product with the smallest absolute value.

3)

{3, 0, -2, 10, 0, 0, 3, -8, 0, 2}

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CantorDust

Simple Math, String Manipulation

Used in:

Member Beta

Used as:

Division I Level Two

Writer:

Nickolas

Testers:

Rustyoldman , timmac , StevieT , vexorian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10418

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13935&pm=10418

Problem Statement

Cantor dust is a 2-dimensional fractal constructed in the following way. Initially the fractal is a black square. At each iteration, each square of the fractal is divided into a 3x3 subgrid of equal subsquares. Any black subsquares which belong to the middle row or to the middle column of a subgrid (or to both of them) are painted white.

You are given a String[] pattern which represents a rectangular pattern of black and white squares (represented by 'X' and '.' characters, respectively). Return the number of occurrences of this pattern in Cantor dust at iteration time. Overlapping occurrences are allowed.

Definition

Class:	CantorDust
Method:	occurrencesNumber
Parameters:	String[], int
Returns:	int
Method signature:	int occurrencesNumber(String[] pattern, int time)
(be sure your method is public)

Constraints

-

time will be between 1 and 9, inclusive.

-

pattern will contain between 1 and min(50, 3^time) elements, inclusive.

-

Each element of pattern will contain between 1 and min(50, 3^time) characters, inclusive.

-

All elements of pattern will contain the same number of characters.

-

Each character in each element of pattern will be '.' or 'X'.

Examples

0)

{".X",".."}

Returns: 1

1)

{".."}

Returns: 2

2)

{"."}

Returns: 65

3)

{"X...X"}

Returns: 4

4)

{"X"}

Returns: 262144

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PouringWater

Brute Force, Math, Search

Used in:

SRM 439

Used as:

Division I Level One , Division II Level Two

Writer:

it4.kp

Testers:

PabloGilberto , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10408

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13747&pm=10408

Problem Statement

You have N bottles, each with unlimited capacity. Initially, each bottle contains exactly 1 liter of water. You want to carry these bottles to another location, but you can only carry K bottles at a time. You don't want to waste any water and you don't want to make more than one trip, so you decide to redistribute the contents of the bottles until you end up with no more than K non-empty bottles.

You are only allowed to redistribute your water using the following method. First, pick two bottles that contain an equal amount of water. Then, pour the entire content of one of those bottles into the other. Repeat this process as many times as necessary.

Because of this restriction, it may be impossible to end up with no more than K non-empty bottles using only the N bottles that you have initially. Fortunately, you can also buy more bottles. Each bottle that you buy will contain exactly 1 liter of water and have unlimited capacity. For example, consider the case where N is 3 and K is 1. It's impossible to get from 3 bottles to 1. If you pour one bottle into another, you end up with one 2 liter bottle and one 1 liter bottle. At that point, you're stuck. However, if you then buy another bottle, you can pour that bottle into the 1 liter bottle, and pour the resulting 2 liter bottle into the other 2 liter bottle to end up with just one 4 liter bottle.

Return the minimum number of additional bottles you must buy in order to achieve your goal. If it's impossible, return -1 instead.

Definition

Class:	PouringWater
Method:	getMinBottles
Parameters:	int, int
Returns:	int
Method signature:	int getMinBottles(int N, int K)
(be sure your method is public)

Constraints

-

N will be between 1 and 10^7, inclusive.

-

K will be between 1 and 1000, inclusive.

Examples

0)

Returns: 1

The example from the problem statement.

1)

Returns: 3

If you have 13, 14, or 15 bottles, you can't end up with one or two bottles. With 16 bottles, you can end up with one bottle.

2)

Returns: 15808

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Automaton

Math, String Manipulation

Used in:

TCO09 Semifinal

Used as:

Division I Level Two

Writer:

griffon

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10401

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13764&pm=10401

Problem Statement

A finite automaton is a mathematical object that consists of the following components:

Alphabet A. This is simply a set of characters.
Set of states S. One of the states is called starting and some of the states are called accepting.
Transition function F. For each state i from S and for each character j from A the result of this function is some state F(i, j) from S.

For each string composed of alphabet characters, an automaton either accepts or rejects it. This is done as follows. First, the automaton is set to its starting state. Then it subsequently reads all the characters from the given string. For each character c it reads, the automaton's state is changed to F(cur, c), where cur is the automaton's state immediately before reading this character. After all characters are read, the automaton checks its final state. If it is accepting, then the string is accepted, otherwise it is rejected.

You are given a String[] transitions describing a finite automaton. The number of elements in transitions is the number of states in the automaton. States are denoted by consecutive uppercase letters starting from 'A'. The first state is the starting state and the last state is the only accepting state. The input alphabet consists of consecutive lowercase letters starting from 'a', and the size of the alphabet is equal to the length of transitions[0].

The transition function is defined as follows. From the i-th state (where state 0 is 'A'), the j-th symbol (where symbol 0 is 'a') will lead to the X-th state, where X = transitions[i][j].

First, the automaton is given an input string of length stringLength consisting entirely of 'a' symbols. The automaton either accepts or rejects the string. Then, the following happens modifications times. One of the symbols in the input string is modified, the automaton is reset to its starting state, and it is then given the new input string, which it either accepts or rejects.

To generate the sequence of modifications you should generate arrays x and c using the following code:

int initElements = length(x0);
int letters = length(transitions[0]);

for (int i = 0; i < initElements; i++) {
	x[i] = x0[i] mod stringLength;
	c[i] = c0[i] mod letters;
}

for (int i = initElements; i < modifications; i++) {
	x[i] = 0;
	c[i] = 0;	
	for (int j = i - initElements; j < i; j++) {
		x[i] = (x[i] + xa[j - i + initElements] * x[j]) mod stringLength;
		c[i] = (c[i] + ca[j - i + initElements] * c[j]) mod letters;
	}
}

The i-th element of the array x is the position where the i-th modification occurs. The symbol at position x[i] of the string should be modified to the c[i]-th symbol of the alphabet (where symbol 0 is 'a'). All indices are 0-based.

Return the number of times the automaton accepts a string.

Definition

Class:	Automaton
Method:	numberOfMatchings
Parameters:	String[], int, int[], int[], int[], int[], int
Returns:	int
Method signature:	int numberOfMatchings(String[] transitions, int stringLength, int[] x0, int[] xa, int[] c0, int[] ca, int modifications)
(be sure your method is public)

Constraints

-

transitions will contain between 1 and 10 elements, inclusive.

-

Each element of transitions will contain between 1 and 10 charactes, inclusive.

-

All elements of transitions will contain the same number of characters.

-

transitions will only contain uppercase letters between 'A' and 'A' + n - 1, inclusive, where n is the number of elements in transitions.

-

stringLength and modifications will each be between 1 and 125000, inclusive.

-

ca will contain between 1 and 50 elements, inclusive.

-

ca will contain at most modifications elements.

-

ca, xa, x0 and c0 will each contain the same number of elements.

-

Each element of ca, xa, x0 and c0 will be between 0 and 10000, inclusive.

Examples

0)

{"AA"}

{0, 0, 0, 0, 0}

{0, 0, 0, 0, 0}

{1, 0, 1, 0, 1}

{0, 0, 0, 0, 0}

Returns: 6

An automaton with only one state accepts all strings, so the answer is 6.

1)

{"BA", "AB"}

{0, 0, 0, 0, 0}

{0, 0, 0, 0, 0}

{1, 0, 1, 0, 1}

{0, 0, 0, 0, 0}

Returns: 3

This automaton has 2 states. It changes state on the symbol 'a' and does nothing on the symbol 'b', so it only accepts strings containing an odd number of 'a's. Of the 6 given strings ("a", "b", "a", "b", "a" and "b"), it accepts only 3.

2)

{"BC", "CA", "AB"}

{0, 1, 2, 3, 4}

{0, 0, 0, 0, 0}

{1, 1, 1, 1, 1}

{0, 0, 0, 0, 0}

Returns: 2

The automaton is consecutively given 6 strings: "aaaaa", "baaaa", "bbaaa", "bbbaa", "bbbba" and "bbbbb". Two of them ("aaaaa" and "bbbaa") are accepted.

3)

{"ABB", "BAA"}

{0, 1}

{1, 1}

{0, 1}

{1, 1}

Returns: 5

The automaton is consecutively given 11 strings: "aa", "aa", "ab", "ab", "cb", "ca", "cc", "cc", "cb", "ca", "ba". Five of them ("ab", "ab", "ca", "ca", "ba") are accepted.

4)

{"BA", "AB"}

{0, 3, 5}

{10, 9, 7}

{1, 2, 4}

{5, 1, 3}

Returns: 1601

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

UnluckyNumbers

Math, Simple Search, Iteration, Sorting

Used in:

SRM 438

Used as:

Division II Level One

Writer:

vexorian

Testers:

PabloGilberto , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10396

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13803&pm=10396

Problem Statement

You are given a set of integers called luckySet. An interval [A,B], where B is greater than A, and A and B are positive integers, is considered unlucky if none of the integers between A and B, inclusive, belongs to luckySet.

Given a int[] luckySet and a int n that is not greater than the maximum element in luckySet. Return the total number of unlucky intervals that contain n.

Definition

Class:	UnluckyNumbers
Method:	getCount
Parameters:	int[], int
Returns:	int
Method signature:	int getCount(int[] luckySet, int n)
(be sure your method is public)

Constraints

-

luckySet will contain between 2 and 50 elements, inclusive.

-

Each element of luckySet will be between 1 and 1000, inclusive.

-

Each element of luckySet will be distinct.

-

n will be between 1 and the largest element in luckySet, inclusive.

Examples

0)

{1, 7, 14, 10}

Returns: 4

4 unlucky intervals in total contain 2:

[2,3], [2,4], [2,5] and [2, 6].

1)

{4, 8, 13, 24, 30}

Returns: 5

The five unlucky intervals that contain 10 are:

[9, 10], [9, 11], [9, 12], [10, 11] and [10, 12].

2)

{10, 20, 30, 40, 50}

Returns: 0

By definition, no unlucky interval can contain 30.

3)

{3, 7, 12, 18, 25, 100, 33, 1000}

Returns: 1065

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BinaryFlips

Greedy, Simple Math

Used in:

SRM 443

Used as:

Division I Level Two

Writer:

gojira_tc

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10387

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13751&pm=10387

Problem Statement

You are playing a game where you initially have A zeros and B ones. Your goal is to end up with all ones. In each move, you must choose exactly K of the numbers and flip their values (zeros change to ones, and vice-versa). You can choose any K numbers each time, regardless of their current values or whether you have flipped them before. Return the minimal number of moves required to win the game, or -1 if it is impossible.

Definition

Class:	BinaryFlips
Method:	minimalMoves
Parameters:	int, int, int
Returns:	int
Method signature:	int minimalMoves(int A, int B, int K)
(be sure your method is public)

Constraints

-

A will be between 0 and 100,000, inclusive.

-

B will be between 0 and 100,000, inclusive.

-

K will be between 1 and 100,000, inclusive.

Examples

0)

Returns: 1

You initially have 3 zeros and 0 ones, and you must flip 3 numbers in each move. Your only possible move is to flip every number. After the first move, you end up with all ones and win the game.

1)

Returns: 4

This is similar to the previous example, but this time, you have 4 zeros. Here's one minimal sequence of moves that will lead to a win:

0. 0000 (the initial state)

1. 1110 (first three numbers flipped)

2. 1001 (last three numbers flipped)

3. 0100 (first, second and fourth numbers flipped)

4. 1111 (first, third and fourth numbers flipped)

2)

Returns: 2

3)

Returns: -1

4)

Returns: 174

5)

Returns: 0

6)

Returns: -1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SquareFreeSets

Dynamic Programming, Math

Used in:

SRM 440

Used as:

Division I Level Three

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , Vasyl[alphacom]

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10386

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13748&pm=10386

Problem Statement

A square-free number is an integer that is not divisible by the square of any integer except 1. A set containing only square-free numbers is called a square-free set. The product of such a set is the product of all its elements. If the product of a square-free set is a square-free number itself, that set is called a perfect set.

You are given two ints N and K. Determine the number of perfect square-free sets that contain between 1 and K elements, inclusive, where each element is between 2 and N, inclusive. Return this number modulo 1,000,000,007.

Definition

Class:	SquareFreeSets
Method:	countPerfect
Parameters:	int, int
Returns:	int
Method signature:	int countPerfect(int N, int K)
(be sure your method is public)

Constraints

-

N will be between 2 and 500, inclusive.

-

K will be between 1 and 500, inclusive.

Examples

0)

Returns: 3

The possible sets are: {2}, {3}, {5}.

1)

Returns: 6

Here, {2,3}, {2,5} and {3,5} are also possible.

2)

Returns: 7

The set {2,3,5} is added to the previous ones.

3)

Returns: 9

Here, the sets are: {2}, {3}, {5}, {6}, {2,3}, {2,5}, {3,5}, {5,6}, {2,3,5}.

4)

Returns: 1599

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DigitsSwap

Simple Math, Simple Search, Iteration

Used in:

SRM 436

Used as:

Division II Level Three

Writer:

Gluk

Testers:

PabloGilberto , ivan_metelsky , ged , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10342

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13698&pm=10342

Problem Statement

You are given two positive integers, x and y, whose decimal representations contain the same number of digits. A digit-swap operation for an index i swaps the digits at the i-th positions in x and y. After exactly swaps digit-swap operations, what is the maximal possible value of x*y? Return the String representation of this maximal product with no leading zeroes.

Definition

Class:	DigitsSwap
Method:	maximalProduct
Parameters:	String, String, int
Returns:	String
Method signature:	String maximalProduct(String x, String y, int swaps)
(be sure your method is public)

Constraints

-

x and y will each contain between 1 and 50 characters, inclusive.

-

x and y will contain only decimal digits ('0' to '9'), and will not start with a '0'.

-

x and y will contain the same number of characters.

-

swaps will be between 0 and 1,000,000,000, inclusive.

Examples

0)

"123"

"321"

Returns: "39483"

You can transform the numbers to "123", "321" (making two swaps at the same position) or to "321", "123" (making swaps at positions 0 and 2) to produce the product 39483.

1)

"4531"

"1332"

Returns: "6035292"

You are not allowed to make swaps, so the answer is just x * y.

2)

"13425"

"87694"

Returns: "1476187680"

The optimal answer is 17695 * 83424.

3)

"2872876342876443222"

"2309482482304823423"

Returns: "6669566046086333877050194232995188906"

4)

"940948"

"124551"

Returns: "133434353148"

5)

"56710852"

"18058360"

Returns: "1050671725722720"

6)

"9"

"1"

1000000000

Returns: "9"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BestView

Math

Used in:

SRM 436

Used as:

Division I Level One , Division II Level Two

Writer:

Gluk

Testers:

PabloGilberto , ivan_metelsky , ged , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10341

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13698&pm=10341

Problem Statement

There are several skyscrapers arranged in a row. You're interested in finding the one from which the maximal number of other skyscrapers can be seen. The i-th skyscraper can be represented as a line segment on a plane with endpoints (i, 0) and (i, heights[i]). A skyscraper can be seen from the roof of another skyscraper if a line segment connecting their roofs does not intersect with or touch any other skyscraper. Return the maximal number of other skyscrapers that can be seen from the roof of some skyscraper.

Definition

Class:	BestView
Method:	numberOfBuildings
Parameters:	int[]
Returns:	int
Method signature:	int numberOfBuildings(int[] heights)
(be sure your method is public)

Constraints

-

heights will contain between 1 and 50 elements, inclusive.

-

Each element of heights will be between 1 and 1,000,000,000, inclusive.

Examples

0)

{10}

Returns: 0

There's only a single skyscraper, so you can see no other skyscrapers from its roof.

1)

{5,5,5,5}

Returns: 2

From each skyscraper, you can only see its adjacent neighbors.

2)

{1,2,7,3,2}

Returns: 4

You can see all the other skyscrapers from the central one.

3)

{1,5,3,2,6,3,2,6,4,2,5,7,3,1,5}

Returns: 7

You can see seven skyscrapers from the skyscraper with height 7:

4)

{1000000000,999999999,999999998,999999997,999999996,1,2,3,4,5}

Returns: 6

You can see 6 skyscrapers from the skyscraper with height 999999996 - the nearest one to the left and all 5 skyscrapers to the right.

5)

{244645169,956664793,752259473,577152868,605440232,569378507,111664772,653430457,454612157,397154317}

Returns: 7

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CircularShifts

Math

Used in:

SRM 436

Used as:

Division I Level Three

Writer:

Gluk

Testers:

PabloGilberto , ivan_metelsky , ged , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10336

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13698&pm=10336

Problem Statement

You have two lists of numbers, X and Y, each containing exactly N elements. You can optionally apply any number of circular shifts to each list. A circular shift means removing the last element from a list and re-inserting it before the first element. For example, {1, 2, 3} would become {3, 1, 2}, and {3, 1, 2} would become {2, 3, 1}. After you apply any circular shifts, the final score is calculated as:

X[0]*Y[0] + X[1]*Y[1] + ... + X[N-1]*Y[N-1]

You are given ints Z0, A, B and M. Generate a list Z of length 2*N, using the following recursive definition:

Z[0] = Z0 MOD M

Z[i] = (Z[i-1]*A+B) MOD M (note that Z[i-1]*A+B may overflow a 32-bit integer)

Then, generate lists X and Y, each of length N, using the following definitions:

X[i] = Z[i] MOD 100

Y[i] = Z[i+N] MOD 100

Return the maximal final score you can achieve.

Definition

Class:	CircularShifts
Method:	maxScore
Parameters:	int, int, int, int, int
Returns:	int
Method signature:	int maxScore(int N, int Z0, int A, int B, int M)
(be sure your method is public)

Notes

-

In the statement, "A MOD B" represents the remainder of integer division of A by B. For example, 14 MOD 5 = 4 and 20 MOD 4 = 0.

-

The author's solution does not depend on any properties of the pseudorandom generator. It would solve any input of allowed size within the given limits.

Constraints

-

N will be between 1 and 60,000, inclusive.

-

Z0, A and B will each be between 0 and 1,000,000,000, inclusive.

-

M will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 5

Both lists contain only ones, so no matter how many shifts you perform, the score will always be 5.

1)

Returns: 70

The lists are {1, 2, 3, 4} and {5, 6, 7, 8}. The maximal score is achieved by not making any shifts.

2)

Returns: 28886

The lists are (23, 4, 95, 20, 17, 94, 63, 44, 13, 96) and (87, 54, 13, 18, 61, 24, 17, 94, 53, 2).

3)

111111111

Returns: 2585408

4)

Returns: 419992

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KthProbableElement

Dynamic Programming, Math

Used in:

TCO09 Round 1

Used as:

Division I Level Two

Writer:

Nickolas

Testers:

PabloGilberto , Jan_Kuipers , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10335

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13759&pm=10335

Problem Statement

M integers are randomly independently chosen from the interval lowerBound...upperBound, inclusive. Return the probability that the K-th smallest element of the generated set is equal to N. K=1 refers to the smallest element, K=2 refers to the second smallest element, and so on.

Definition

Class:	KthProbableElement
Method:	probability
Parameters:	int, int, int, int, int
Returns:	double
Method signature:	double probability(int M, int lowerBound, int upperBound, int N, int K)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

M will be between 1 and 100, inclusive.

-

lowerBound will be between 1 and 1000, inclusive.

-

upperBound will be between lowerBound and 1000, inclusive.

-

N will be between lowerBound and upperBound, inclusive.

-

K will be between 1 and M, inclusive.

Examples

0)

Returns: 0.1

The probability that the only chosen number will be equal to 3 is 0.1.

1)

Returns: 0.5

There are 8 ways to choose 3 numbers from the interval 1..2:

Numbers | 2nd smallest element
 1 1 1  |  1
 1 1 2  |  1
 1 2 1  |  1
 1 2 2  |  2
 2 1 1  |  1
 2 1 2  |  2
 2 2 1  |  2
 2 2 2  |  2

Exactly 4 of the ways have the 2nd smallest element equal to 2.

2)

Returns: 0.48148148148148145

There are 27 ways to choose 3 numbers from the interval 1..3, 13 of them have the 2nd smallest element equal to 2.

3)

Returns: 1.0000000000000003E-10

Only one of 10¹⁰ ways to choose 10 numbers from the interval 1..10 has 1 as the 10th smallest element.

4)

Returns: 0.15200000000000002

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PlaneFractal

Brute Force, Simple Math

Used in:

TCO09 Round 2

Used as:

Division I Level One

Writer:

Nickolas

Testers:

PabloGilberto , marian , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10333

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13760&pm=10333

Problem Statement

A plane fractal grows in the following way. At time 0, the fractal is a single white square. During each unit of time, each square in the fractal is divided into an NxN grid of equal subsquares. If the square was white, then the center KxK subsquares will become black (N and K will have the same parity).

For example, if N = 3 and K = 1, then at time 1, there are 3x3 squares, the middle square is black and the rest are white. At time 2, there are 9x9 squares, 17 are black and the rest are white.

Return a String[] representing the content of the fractal at time s between rows r1 and r2, inclusive, and columns c1 and c2, inclusive (all indices are 0-based). White squares should be represented by '0' (zero) and black squares should be represented by '1'.

Definition

Class:	PlaneFractal
Method:	getPattern
Parameters:	int, int, int, int, int, int, int
Returns:	String[]
Method signature:	String[] getPattern(int s, int N, int K, int r1, int r2, int c1, int c2)
(be sure your method is public)

Constraints

-

s will be between 0 and 10, inclusive.

-

N will be between 3 and 8, inclusive.

-

K will be between 1 and N-2, inclusive.

-

N and K will have the same parity, i.e., N-K will be divisible by 2.

-

r1, r2, c1 and c2 will each be between 0 and N^s-1, inclusive.

-

r2 will be between r1 and r1+49, inclusive.

-

c2 will be between c1 and c1+49, inclusive.

Examples

0)

Returns: {"00000", "01110", "01110", "01110", "00000" }

At time 1, there are 5x5 squares, the middle 3x3 of them are black.

1)

Returns: 
{"000000000",
"010010010",
"000000000",
"000111000",
"010111010",
"000111000",
"000000000",
"010010010",
"000000000" }

The example from the problem statement.

2)

Returns: 
{"101001",
"100000",
"000000",
"001001",
"000000",
"000011",
"001011",
"000011" }

At time 3, the fractal looks like this (the area that needs to be returned is shown in red):

3)

Returns: 
{"000000000000000000000000",
"000000000000000000000000",
"011110000111100001111000",
"011110000111100001111000",
"011110000111100001111000",
"011110000111100001111000" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PageNumbers

Brute Force, Recursion, Simple Math, Simple Search, Iteration

Used in:

TCO09 Qual 2

Used as:

Division I Level Two

Writer:

misof

Testers:

PabloGilberto , marian , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10329

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13757&pm=10329

Problem Statement

We have a book with N pages, numbered 1 to N. How many times does each digit occur in the page numbers?

You are given an int N. Return a int[] with 10 elements, where for all i between 0 and 9, inclusive, the element i will be the number of times digit i occurs when we write down all the numbers between 1 and N, inclusive.

Definition

Class:	PageNumbers
Method:	getCounts
Parameters:	int
Returns:	int[]
Method signature:	int[] getCounts(int N)
(be sure your method is public)

Notes

-

You may assume that for any valid input each of the output values fits into an int.

Constraints

-

N will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: {0, 1, 1, 1, 1, 1, 1, 1, 0, 0 }

The page numbers in this case are simply 1, 2, 3, 4, 5, 6, and 7.

1)

Returns: {1, 4, 1, 1, 1, 1, 1, 1, 1, 1 }

In comparison to the previous case, we added the pages 8, 9, 10, and 11. Now we have each digit exactly once, except for the digit 1 that occurs four times: once in 1 and 10, and twice in 11.

2)

Returns: {1, 12, 2, 2, 2, 2, 2, 2, 2, 2 }

Digits 2 to 9 now occur twice each, and we have plenty of occurrences of the digit 1.

3)

Returns: {189, 300, 300, 300, 300, 300, 300, 300, 300, 300 }

Due to symmetry, each of the digits 1 to 9 occurs equally many times in the sequence 1,2,...,999.

4)

543212345

Returns: 
{429904664, 541008121, 540917467, 540117067, 533117017, 473117011, 429904664, 429904664, 429904664, 429904664 }

Watch out for the time limit.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumberGraph

Graph Theory, Math

Used in:

TCO09 Round 5

Used as:

Division I Level Three

Writer:

StevieT

Testers:

PabloGilberto , legakis , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10319

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13763&pm=10319

Problem Statement

Two integers X and Y are joined by a positive integer P if the magnitude of their difference |X-Y| = P. X and Y are joined by a set of integers if they are joined by one of the numbers in that set. You are given a set of positive integers joiningSet, with the property that the number of trailing zeros in the binary representation of each integer in joiningSet is the same. You are also given a set of integers in a String[] graphSet. Concatenate the elements of graphSet to obtain a space-separated list of these integers. Consider the graph G with an edge joining each pair of numbers in graphSet that is joined by joiningSet. Determine the size of the largest subgraph of G, such that no pair of vertices in the subgraph is separated by a distance greater than 2.

Definition

Class:	NumberGraph
Method:	largestSet
Parameters:	String[], int[]
Returns:	int
Method signature:	int largestSet(String[] graphSet, int[] joiningSet)
(be sure your method is public)

Notes

-

In this problem, the size of a graph is equal to the number of vertices it contains.

-

The distance between two vertices is the length of the shortest path joining them, and can be considered infinite if the vertices are not connected.

-

The distance is measured within the taken subgraph, not within the whole graph.

Constraints

-

graphSet and joiningSet will each contain between 1 and 50 elements, inclusive.

-

Each element of joiningSet will be between 1 and 1000000 (10^6), inclusive.

-

Each element of graphSet will contain between 1 and 50 characters, inclusive.

-

The concatenation of the elements of graphSet will be a single-space-delimited list of integers, formatted without extra leading zeros.

-

graphSet will contain between 1 and 80 integers, inclusive.

-

Each integer in graphSet will be between 0 and 1000000 (10^6), inclusive.

-

The integers within each of graphSet and joiningSet will be distinct.

-

The lowest set bit in the binary representation of each element of joiningSet will be the same.

Examples

0)

{"1 2 3 4 6 9 13 15 16 18 21 26"}

{2,6,10}

Returns: 4

The subgraph induced by {3,9,13,15} is optimal in this case. 3 and 15 are both joined to 9 and 13, so any distance in this subgraph is no greater than 2.

1)

{"4 11 12 10 9 6 2 7 1 8 5"}

{3,5,1,7}

Returns: 9

The subgraph induced by {4, 12, 10, 9, 6, 2, 7, 8, 5} is optimal here.

2)

{"100 260 164 244 84 340 52 2"
,"12 388 4 308 180 228 484"}

{16,176,208,48,240,80}

Returns: 8

The number "212" has been separated into two parts "2" and "12". Make sure you concatenate the Strings before splitting into numbers.

3)

{"10 6 130 162 164 39 73 27 72 167 41"}

{3,63,95,123,57,91,35,137
,135,125,33,121,17,5,31
,45,67,29,157}

Returns: 8

4)

{"2136 2108 876 8"
,"6 348 8 1784 1146 1596 608 446 14"
,"64"
," 344 1452 1938 692 376 1482 860 1870"}

{644,844,348,604,1260,516,868,2100,260
,1492,316,1076,268,852,12,1500,4,772
,1108,188,1444,1764,84,1732,532,332
,1588,500,700,1116,252,1060,68,1092
,724,132,484,340,684,1276,28,1788,588}

Returns: 12

5)

{"1000000"}

{1}

Returns: 1

6)

{"1 2 3 4 5 6 7 8"}

{1}

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CubeOfDice

Greedy, Math, Sorting

Used in:

TCO09 Round 4

Used as:

Division I Level One

Writer:

misof

Testers:

PabloGilberto , legakis , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10316

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13762&pm=10316

Problem Statement

    +---+
    | D |
+---+---+---+---+
| E | A | B | F |
+---+---+---+---+
    | C |
    +---+

The ASCII art above shows the net of a general 6-sided die. There is a number written on each of the six sides. In the picture, these numbers are denoted A to F. (The net is folded so that the numbers are on the outside, but this information is not necessary to solve the following problem.)

The numbers A to F will be given to you as a int[] values, where A will be values[0], B will be values[1], and so on.

You have N^3 identical dice, each one matching the net shown above. You want to take all the dice, rotate some of them, and assemble a N×N×N cube. The cube will be standing on a table, hence only 5 of its sides will be visible.

You are given the int N, and the int[] values. Write a method that will return the smallest possible sum of the 5N^2 visible faces of the dice.

Definition

Class:	CubeOfDice
Method:	minimumSum
Parameters:	int, int[]
Returns:	long
Method signature:	long minimumSum(int N, int[] values)
(be sure your method is public)

Constraints

-

N will be between 1 and 1,000,000, inclusive.

-

values will contain exactly 6 elements.

-

Each element of values will be between 1 and 50, inclusive.

Examples

0)

{1,2,3,4,5,6}

Returns: 36

This input corresponds to 8 classical dice.

1)

{1,2,3,4,5,6}

Returns: 69

Now we have 27 classical dice.

2)

{50,50,50,50,50,50}

Returns: 250000000000000

The largest possible output. Note that all numbers are equal, hence in this case there is only one possible way to arrange the dice.

3)

{1,1,1,1,50,1}

Returns: 500

It is possible to rotate and arrange the dice so that no side with the 50 will be visible.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IncredibleMachine

Math, Search

Used in:

SRM 440

Used as:

Division I Level One

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , Vasyl[alphacom]

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10310

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13748&pm=10310

Problem Statement

You may remember an old computer game called "The Incredible Machine". It was a game where you could simulate simple processes like balls falling, lasers shooting, or cats pursuing mice. Moreover, you were able to perform these observations with different values for gravitational acceleration.

We are observing a system with some unknown acceleration of gravity. There is a slope which has the form of a polyline with N vertices. Each vertex of the polyline is positioned lower and to the right of the previous one. At time 0, a ball is placed at the first vertex. The ball is small enough to be considered a single point. Assume that there's no friction between the slope and the ball, the ball is absolutely nonelastic, and the direction of its velocity changes instantly at the polyline's vertices. Under these conditions, the ball will follow the polyline without ever losing contact with it. The ball reaches the final vertex at time T.

You are given int[]s x and y, where (x[i], y[i]) are the coordinates of the i-th vertex. Return the gravitational acceleration in this system. A body rolling down an inclined plane of angle alpha (measured between the plane and horizontal direction) under gravitational acceleration g has a constant acceleration of a = g * sin(alpha). The distance d travelled by an object during time t moving with initial velocity v0 and with constant acceleration a is equal to d = v0 * t + 0.5 * a * t^2. The velocity v1 of the object after time t has passed is equal to v1 = v0 + a * t.

Definition

Class:	IncredibleMachine
Method:	gravitationalAcceleration
Parameters:	int[], int[], int
Returns:	double
Method signature:	double gravitationalAcceleration(int[] x, int[] y, int T)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

x will contain between 2 and 50 elements, inclusive.

-

Elements of x will be strictly ascending.

-

Elements of x will be between 0 and 100, inclusive.

-

x and y will contain the same number of elements.

-

Elements of y will be strictly descending.

-

Elements of y will be between 0 and 100, inclusive.

-

T will be between 1 and 100, inclusive.

Examples

0)

{0,6}

{100,22}

Returns: 9.807692307692307

That's an acceleration of gravity that might be somewhere on Earth's surface.

1)

{0,26,100}

{50,26,24}

Returns: 26.743031720603582

And this is likely on Jupiter.

2)

{0,7,8}

{10,6,0}

Returns: 1.1076837407708007

Note that in spite of the angle at vertex (7,6), the body won't fly off the slope and will follow the segment (7,6)-(8,0).

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IncredibleMachineEasy

Math

Used in:

SRM 440

Used as:

Division II Level One

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , Vasyl[alphacom]

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10309

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13748&pm=10309

Problem Statement

You may remember an old computer game called "The Incredible Machine". It was a game where you could simulate simple processes like balls falling, lasers shooting, or cats pursuing mice. Moreover, you were able to perform these observations with different values for gravitational acceleration.

Imagine a system with some unknown acceleration of gravity. There are N balls, each fixed initially at some height above the ground. You are given a int[] height, where the i-th element is the height of the i-th ball above the ground. At time 0, the first ball is set loose and it starts falling. When it reaches the ground, the second ball is instantly set loose, and so on. This continues until the last ball reaches the ground at time T.

Return the acceleration of gravity in this system. Neglect air resistance and any other resisting factors. The distance d travelled by an object falling for time t with no initial velocity in a system with gravitational acceleration g and no resisting factors is equal to d = 0.5 * g * t^2.

Definition

Class:	IncredibleMachineEasy
Method:	gravitationalAcceleration
Parameters:	int[], int
Returns:	double
Method signature:	double gravitationalAcceleration(int[] height, int T)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

height will contain between 1 and 50 elements, inclusive.

-

Each element of height will be between 1 and 100, inclusive.

-

T will be between 1 and 100, inclusive.

Examples

0)

{16,23,85,3,35,72,96,88,2,14,63}

Returns: 9.803799620759717

That's an acceleration of gravity that might be somewhere on Earth's surface.

1)

{6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,5}

Returns: 26.73924541044107

And this is likely on Jupiter.

2)

{8,8}

Returns: 7.111111111111111

That's a light one.

3)

{3,1,3,1,3}

Returns: 0.7192306901503684

You could nearly fly under such conditions.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WickedTeacher

Dynamic Programming, Math

Used in:

SRM 440

Used as:

Division II Level Three

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , Vasyl[alphacom]

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10289

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13748&pm=10289

Problem Statement

A wicked teacher is trying to fail one of his students. He gives him the following problem:

You are given a String[] numbers containing a set of distinct integers. You can concatenate some permutation of these integers to obtain one large integer. For example, the permutation {5221, 40, 1, 58, 9} can be concatenated to form 5221401589. Find a permutation of the given numbers such that its concatenation is divisible by the integer K.

The student doesn't have a clue how to solve this problem, so he just answers with some random permutation. There may be multiple correct answers, and maybe the student has chosen one of them by chance. Return the probability that the student has chosen one of the correct answers and return it as a String in the form of an irreducible fraction "p/q" (quotes for clarity), where p is the fraction's numerator and q is its denominator. Assume that each permutation has the same probability of being chosen.

Definition

Class:	WickedTeacher
Method:	cheatProbability
Parameters:	String[], int
Returns:	String
Method signature:	String cheatProbability(String[] numbers, int K)
(be sure your method is public)

Constraints

-

numbers will contain between 1 and 15 elements, inclusive.

-

Each element of numbers will contain between 1 and 50 characters, inclusive.

-

Each element of numbers will contain digits ('0'-'9') only.

-

Each element of numbers will begin with a non-zero digit.

-

Elements of numbers will be distinct.

-

K will be between 1 and 100, inclusive.

Examples

0)

{"3","2","1"}

Returns: "1/3"

If the student chooses a permutation where the number 2 is the last element, the concatenation will be divisible by 2.

1)

{"10","100","1000","10000","100000"}

Returns: "1/1"

No matter which permutation the student chooses, its concatenation will be divisible by 10.

2)

{"11","101","1001","10001","100001"}

Returns: "0/1"

It's possible that the teacher is cheating, and no correct answer is possible.

3)

{"13","10129414190271203","102","102666818896","1216","1217","1218","101278001","1000021412678412681"}

Returns: "5183/36288"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Parallelograms

Geometry, Simple Math

Used in:

TCHS09 Round 3

Used as:

Division I Level One

Writer:

misof

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10284

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13730&pm=10284

Problem Statement

A parallelogram is a quadrilateral with two sets of parallel sides.

You are given three distinct points A(xA,yA), B(xB,yB) and C(xC,yC) in the plane.

Consider all non-degenerate parallelograms such that A, B, and C are three of its vertices. Your method should return the difference between the largest and the smallest possible perimeter of such a parallelogram. If there is no such parallelogram, return -1 instead.

Definition

Class:	Parallelograms
Method:	getDifference
Parameters:	int, int, int, int, int, int
Returns:	double
Method signature:	double getDifference(int xA, int yA, int xB, int yB, int xC, int yC)
(be sure your method is public)

Constraints

-

xA, yA, xB, yB, xC and yC will be between -5,000 and 5,000, inclusive.

-

A, B, and C will be three different points.

Examples

0)

Returns: 0.8284271247461898

For this input there are three possible parallelograms, with the fourth vertex at (1,1), (1,-1), or (-1,1). In the first case, we get a 1 by 1 square with a perimeter of 4. In both the second and third cases, we get a parallelogram with side lengths 1 and sqrt(2), with a perimeter of approximately 4.828427.

1)

Returns: 4.0

In this case the largest possible perimeter is 18 and the smallest possible perimeter is 14.

2)

Returns: -1.0

No parallelogram can have three vertices on the same line. Therefore, the answer for this test case is -1.

3)

Returns: 11.547796284592874

4)

-1

-7

-1

Returns: -1.0

One more example of three points on the same line.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Underprimes

Math, Simple Search, Iteration

Used in:

SRM 442

Used as:

Division I Level One , Division II Level Two

Writer:

mateuszek

Testers:

PabloGilberto , kalinov , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10274

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13750&pm=10274

Problem Statement

The prime factorization of a number X is the list of prime numbers that multiply together to form X. For example, the prime factorization of 12 is 2 * 2 * 3. Note that 1 is not a prime number.

An underprime is a number whose prime factorization contains a prime number of elements. For example, 12 is an underprime because its prime factorization contains 3 elements, and 3 is a prime number. Given ints A and B, return the number of underprimes between A and B, inclusive.

Definition

Class:	Underprimes
Method:	howMany
Parameters:	int, int
Returns:	int
Method signature:	int howMany(int A, int B)
(be sure your method is public)

Notes

-

A positive integer number is called prime if it has exactly two divisors - 1 and itself. For example, 2, 3, 5 and 7 are prime numbers, and 4, 6, 8 and 9 are not prime. By convention, 1 is not considered to be a prime number.

-

All prime factorizations of the same integer always contain the same prime numbers and can only differ by the order of primes within them.

Constraints

-

A will be between 2 and 100000, inclusive.

-

B will be between A and 100000, inclusive.

Examples

0)

Returns: 5

The underprimes in this interval are: 4, 6, 8, 9, 10.

1)

Returns: 2

The underprimes in this interval are 102 = 2 * 3 * 17 and 105 = 3 * 5 * 7.

2)

Returns: 0

17 is a prime number, so its prime factorization contains one element. 1 is not a prime, so 17 is not an underprime.

3)

Returns: 217

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FindingSquareInTable

Search, Simple Math

Used in:

SRM 434

Used as:

Division I Level One , Division II Level Two

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10268

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13696&pm=10268

Problem Statement

You are given a String[] table representing a rectangular grid where each cell contains a digit. The j-th character of the i-th element of table is the digit in the cell at row i, column j of the grid.

Consider a sequence of distinct cells in this table where the row numbers of the cells (in the order they appear in the sequence) form an arithmetic progression, and the column numbers also form an arithmetic progression. Concatenate the digits in the cells of this sequence to obtain a number.

Among all numbers that can be obtained in this manner, find and return the largest perfect square (a square of an integer). If there are no perfect squares, return -1 instead.

Definition

Class:	FindingSquareInTable
Method:	findMaximalSquare
Parameters:	String[]
Returns:	int
Method signature:	int findMaximalSquare(String[] table)
(be sure your method is public)

Notes

-

An arithmetic progression is a sequence of numbers where the difference between each number and the previous number is constant.

Constraints

-

table will contain between 1 and 9 elements, inclusive.

-

Each element of table will contain between 1 and 9 characters, inclusive.

-

All elements of table will be of the same length.

-

Each element of table will contain only digits ('0'-'9').

Examples

0)

{"123",
 "456"}

Returns: 64

Several three-digit numbers can be obtained: 123, 321, 456, and 654, but none of them is a perfect square. The largest obtainable perfect square is 64.

1)

{"00000",
 "00000",
 "00200",
 "00000",
 "00000"}

Returns: 0

0 is a perfect square. It is the largest one that can be obtained in this table.

2)

{"3791178",
 "1283252",
 "4103617",
 "8233494",
 "8725572",
 "2937261"}

Returns: 320356

Take the i-th digit of each row i, and you'll get 320356 = 566 × 566.

3)

{"135791357",
 "357913579",
 "579135791",
 "791357913",
 "913579135"}

Returns: 9

It is known that a perfect square can't end with two odd digits. Therefore, the largest perfect square that contains only odd digits is 9.

4)

{"553333733",
 "775337775",
 "777537775",
 "777357333",
 "755553557",
 "355533335",
 "373773573",
 "337373777",
 "775557777"}

Returns: -1

There exists no perfect square that contains only digits 3, 5, and 7.

5)

{"257240281",
 "197510846",
 "014345401",
 "035562575",
 "974935632",
 "865865933",
 "684684987",
 "768934659",
 "287493867"}

Returns: 95481

The sequence of digits that forms 95481 is shown in bold:

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LeastMajorityMultiple

Search, Simple Math

Used in:

SRM 434

Used as:

Division II Level One

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10267

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13696&pm=10267

Problem Statement

Given five positive integers, their least majority multiple is the smallest positive integer that is divisible by at least three of them.

Given distinct ints a, b, c, d and e, return their least majority multiple.

Definition

Class:	LeastMajorityMultiple
Method:	leastMajorityMultiple
Parameters:	int, int, int, int, int
Returns:	int
Method signature:	int leastMajorityMultiple(int a, int b, int c, int d, int e)
(be sure your method is public)

Constraints

-

a, b, c, d and e will each be between 1 and 100, inclusive.

-

a, b, c, d and e will be distinct.

Examples

0)

Returns: 4

4 is divisible by 1, 2, and 4 - the majority of the given five numbers.

1)

Returns: 210

210 is divisible by 30, 42, 70, and 35 - four out of five numbers, which is a majority.

2)

Returns: 1170

3)

Returns: 195

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HexatridecimalSum

Simple Math, Sorting, String Manipulation

Used in:

SRM 434

Used as:

Division I Level Two , Division II Level Three

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10266

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13696&pm=10266

Problem Statement

Hexatridecimal notation is base 36 notation. The digits are '0' to '9' (with values 0 to 9) and 'A' to 'Z' (with values 10 to 35).

You are given a String[] numbers, where each element represents a positive integer in hexatridecimal notation. You must select exactly k digits (from the set of all digits - '0' to '9' and 'A' to 'Z') and replace all of their occurrences in all of the numbers with 'Z'. Then, calculate the sum of all the numbers.

Return the maximal possible sum you can get. The return value must be in hexatridecimal format with no leading zeroes.

Definition

Class:	HexatridecimalSum
Method:	maximizeSum
Parameters:	String[], int
Returns:	String
Method signature:	String maximizeSum(String[] numbers, int k)
(be sure your method is public)

Constraints

-

numbers will contain between 1 and 50 elements, inclusive.

-

Each element of numbers will contain between 1 and 50 characters, inclusive.

-

Each element of numbers will contain only characters '0' to '9' and 'A' to 'Z'.

-

Each element of numbers will not start with '0'.

-

k will be between 0 and 36, inclusive.

Examples

0)

{"HELLO"}

Returns: "ZZLLO"

It is optimal to change the two most significant digits in the given number.

1)

{"500", "POINTS", "FOR", "THIS", "PROBLEM"}

Returns: "1100TC85"

2)

{"TO", "BE", "OR", "NOT", "TO", "BE"}

Returns: "QNO"

k = 0 means that you're not allowed to change any digits, so the answer is the sum of the given numbers.

3)

{"KEQUALS36"}

Returns: "ZZZZZZZZZ"

k = 36 means that you have to replace all the letters with 'Z'.

4)

{"GOOD", "LUCK", "AND", "HAVE", "FUN"}

Returns: "31YUB"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FallingPoints

Simple Math

Used in:

SRM 431

Used as:

Division II Level Two

Writer:

Gluk

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10261

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13522&pm=10261

Problem Statement

You are given a int[] X containing the x-coordinates of several points. Each point starts at an infinitely high y-coordinate. Starting with the first point, each point falls down until it is either a distance of R away from a previously fallen point or it reaches y = 0. Each point (after the first point) will start falling only when the previous one stops. Return a double[], where the i-th element is the final y-coordinate of the i-th point.

Definition

Class:	FallingPoints
Method:	getHeights
Parameters:	int[], int
Returns:	double[]
Method signature:	double[] getHeights(int[] X, int R)
(be sure your method is public)

Notes

-

Each element of your return value must have an absolute or relative error less than 1e-9.

Constraints

-

X will contain between 1 and 50 elements, inclusive.

-

All elements of X will be between 0 and 1,000, inclusive.

-

R will be between 1 and 1,000, inclusive.

Examples

0)

{0}

Returns: {0.0 }

There is only one point and it will just fall down.

1)

{1,100}

Returns: {0.0, 0.0 }

Both points will fall down.

2)

{0,9}

Returns: {0.0, 4.358898943540674 }

The first point falls down. The second point stops at a distance of 10 away from the first point.

3)

{0,9,19}

Returns: {0.0, 4.358898943540674, 4.358898943540674 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SumAndProduct

Math

Used in:

SRM 431

Used as:

Division II Level Three

Writer:

Gluk

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10257

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13522&pm=10257

Problem Statement

A list of non-negative numbers is called satisfactory if the sum of the numbers in the list is equal to S and the product of the numbers is equal to P. Find a satisfactory list with the least possible number of elements, and return its size. If no such list exists, return -1 instead. Please note that the list may contain non-integer numbers.

Definition

Class:	SumAndProduct
Method:	smallestSet
Parameters:	int, int
Returns:	int
Method signature:	int smallestSet(int S, int P)
(be sure your method is public)

Constraints

-

S and P will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 1

The list contains only one element: 10.

1)

Returns: 2

The list contains two elements: 2 and 3.

2)

Returns: -1

No such list exists.

3)

1000000000

Returns: 9

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WizardsAppointments

Math

Used in:

TCHS09 Round 2

Used as:

Division I Level Three

Writer:

Nickolas

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10255

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13729&pm=10255

Problem Statement

Several wizards have scheduled appointments to meet with non-wizards. Each wizard will have exactly one meeting with a non-wizard. Unfortunately, some of the wizards have just realized that they will not be able to arrive at their meetings on time. They will show up either too early or too late.

In an attempt to minimize the total waiting time, the wizards have decided to reschedule all of the meetings by shifting each one by the same amount of time. The total waiting time includes the time spent by wizards waiting for non-wizards to show up and the time spent by non-wizards waiting for wizards to show up. The non-wizards will all arrive exactly on time to the rescheduled meetings.

You are given int[]s scheduledTimes and arrivalTimes. The i-th element of scheduledTimes is the original scheduled starting time for the i-th wizard's meeting. The i-th element of arrivalTimes is the time when the i-th wizard will show up to his meeting. All times are given in hours. If you shift all the meetings by T hours, the total waiting time can be calculated as the sum of abs(scheduledTimes[i] + T - arrivalTimes[i]) over all the meetings. Return the number of distinct integer shifts which allow to minimize the total waiting time.

Definition

Class:	WizardsAppointments
Method:	scheduleAdjustment
Parameters:	int[], int[]
Returns:	int
Method signature:	int scheduleAdjustment(int[] scheduledTimes, int[] arrivalTimes)
(be sure your method is public)

Constraints

-

scheduledTimes will contain between 1 and 50 elements, inclusive.

-

arrivalTimes will contain the same number of elements as scheduledTimes.

-

Each element of scheduledTimes will be between 1 and 10⁹, inclusive.

-

Each element of arrivalTimes will be between 1 and 10⁹, inclusive.

Examples

0)

{10}

{9}

Returns: 1

The wizard will arrive at his meeting 1 hour earlier than the scheduled time. If the meeting is shifted 1 hour earlier, the total waiting time will be 0.

1)

{20, 30}

{18, 25}

Returns: 4

Both wizards arrive too early, one of them being 2 hours early and the second one being 5 hours early. Every shift between -5 and -2 hours makes the total waiting time equal to 3 hours.

2)

{10, 20}

{11, 17}

Returns: 5

This time, one wizard is late by 1 hour and the other is early by 3 hours. Every shift between -3 hours and 1 hour makes the total waiting time equal to 4 hours.

3)

{10, 20, 30}

{13, 15, 34}

Returns: 1

Of the three wizards, one is 5 hours early and two are 3 and 4 hours late. After a 3 hour shift, one wizard comes in time, one is 8 hours early, and one is 1 hour late.

4)

{10, 20, 30, 40}

{14, 24, 39, 37}

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SubwayTrip

Math

Used in:

TCHS09 Round 1

Used as:

Division I Level One

Writer:

Nickolas

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10254

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13728&pm=10254

Problem Statement

You are walking down the escalator to catch a subway train. The escalator itself moves at a speed of Ve meters per minute. You can walk down the escalator at a relative speed of Vy meters per minute. The length of the escalator is L meters. Trains arrive T minutes apart.

Let t be the time between your arrival to the station if you stand still on the escalator and the arrival of the last train before your arrival. Assume that t is a random variable uniformly distributed between 0 and T.

Return the probability of catching an earlier train if you choose to walk down the escalator instead of standing still on it.

Definition

Class:	SubwayTrip
Method:	earlierTrain
Parameters:	int, int, int, int
Returns:	double
Method signature:	double earlierTrain(int Ve, int Vy, int L, int T)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

Ve will be between 10 and 60, inclusive.

-

Vy will be between 1 and 10, inclusive.

-

L will be between 10 and 100, inclusive.

-

T will be between 2 and 20, inclusive.

Examples

0)

Returns: 0.5

If you stand still, it'll take you 20/10 = 2 minutes to reach the bottom of the escalator. If you choose to walk, it'll make you 20/(10+10) = 1 minute. In the second case you save 1 minute and in 50% of the cases it'll allow you to catch an earlier train.

1)

Returns: 0.005000000000000004

2)

Returns: 0.028957528957528934

3)

Returns: 1.0

Here, if you choose to walk instead of stand still, you will save 5 minutes and you will certainly be guaranteed to catch an earlier train.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SubrectanglesOfTable

Simple Math, Simple Search, Iteration

Used in:

SRM 429

Used as:

Division I Level One , Division II Level Two

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10246

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13520&pm=10246

Problem Statement

Tanya has a rectangular table filled with letters.

First, she makes four copies of this table, and arranges the copies as a 2×2 rectangle.

Then she lists all subrectangles of the resulting table.

For example, for the following original table:

OK

she will arrange the copies like this:

OKOK
OKOK

and then she will list the following 30 subrectangles (dots for clarity only):

OKOK .... OKOK OKO. .... OKO. .KOK .... .KOK
OKOK OKOK .... OKO. OKO. .... .KOK .KOK ....

OK.. .... OK.. .KO. .... .KO. ..OK .... ..OK 
OK.. OK.. .... .KO. .KO. .... ..OK ..OK .... 

O... .... O... .K.. .... .K.. ..O. .... ..O. ...K .... ...K 
O... O... .... .K.. .K.. .... ..O. ..O. .... ...K ...K ....

(Note that she is considering all subrectangles based on their positions rather than their content, so the same subrectangle might appear multiple times in the list. In this case, subrectangle "K" appears four times because it occurs at four different positions.)

Tanya wonders how frequently each letter of the alphabet occurs among all these subrectangles. You are given a String[] table, where the j-th character of the i-th element is the letter at row i, column j of the original table. Return a long[] containing exactly 26 elements, where the i-th element is the number of occurrences of the i-th letter in the alphabet among all of Tanya's subrectangles. 'A' is the 0-th letter, 'B' is the 1-st letter, etc.

Definition

Class:	SubrectanglesOfTable
Method:	getQuantity
Parameters:	String[]
Returns:	long[]
Method signature:	long[] getQuantity(String[] table)
(be sure your method is public)

Constraints

-

table will contain between 1 and 50 elements, inclusive.

-

Each element of table will contain between 1 and 50 characters, inclusive.

-

Each element of table will contain the same number of characters.

-

Each element of table will contain only uppercase letters ('A'-'Z').

Examples

0)

{"OK"}

Returns: 
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 40, 0, 0, 0, 40, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 }

The 30 Tanya's rectangles are listed above. There is a total of 40 Ks and 40 Os in these rectangles.

1)

{"GOOD", "LUCK"}

Returns: 
{0, 0, 320, 280, 0, 0, 280, 0, 0, 0, 280, 280, 0, 0, 640, 0, 0, 0, 0, 0, 320, 0, 0, 0, 0, 0 }

The four copies form the following table:

GOODGOOD
LUCKLUCK
GOODGOOD
LUCKLUCK

Tanya lists 360 rectangles that contain a total of 320 Cs, 280 Ds, 280 Gs, 280 Ks, 280 Ls, 640 Os, and 320 Us.

2)

{"TANYA",
 "HAPPY",
 "BIRTH",
 "DAYYY"}

Returns: 
{5168, 1280, 0, 1120, 0, 0, 0, 2560, 1472, 0, 0, 0, 0, 1344, 0, 3008, 0, 1536, 0, 2592, 0, 0, 0, 0, 6320, 0 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BirdsCounting

Dynamic Programming, Math

Used in:

SRM 435

Used as:

Division II Level Three

Writer:

almelv

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10243

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13697&pm=10243

Problem Statement

In ecology, there are several ways of estimating the size of a population in a given area. We are interested in estimating the size of a population of birds. To do this, we will use the following procedure.

First, there will be a data collection phase that lasts exactly daysNumber days. Initially, all the birds are unmarked. During each day of data collection, we will catch exactly caughtPerDay birds. At the end of each day, we will examine each of the birds we have caught. If a bird is unmarked, we will mark it. If a bird is already marked, we will leave it alone (and it will remain marked). We will then release all of them back into the wild before the next day begins.

After the data collection phase is complete, we can use the number of unmarked birds caught each day to estimate the size of the population.

To help our fellow ecologists in analyzing the collected data, we must compute the probability that after daysNumber days of data collection, there will be exactly birdsMarked marked birds assuming that there are birdsNumber birds in this area. Assume that the probability of being caught is exactly the same for every bird on every day.

Definition

Class:	BirdsCounting
Method:	computeProbability
Parameters:	int, int, int, int
Returns:	double
Method signature:	double computeProbability(int birdsNumber, int caughtPerDay, int daysNumber, int birdsMarked)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

birdsNumber will be between 1 and 20, inclusive.

-

caughtPerDay will be between 1 and birdsNumber, inclusive.

-

daysNumber will be between 1 and 5, inclusive.

-

birdsMarked will be between 0 and birdsNumber, inclusive.

Examples

0)

Returns: 0.6666666666666666

After the first day, there will be exactly one marked bird. During the second day, there is a 1/3 chance that we will catch this marked bird (which means we will have 1 marked bird after 2 days), and a 2/3 chance that we will catch an unmarked bird (in which case, we will mark it and have 2 marked birds after 2 days).

1)

Returns: 0.012345679012345678

2)

Returns: 0.2582908163265306

3)

Returns: 0.6

4)

Returns: 0.30035494805367574

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SequenceSums

Math, Simple Search, Iteration

Used in:

TCO09 Round 1

Used as:

Division I Level One

Writer:

legakis

Testers:

PabloGilberto , Jan_Kuipers , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10241

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13759&pm=10241

Problem Statement

Given a number N and a length L, find the shortest list of at least L consecutive non-negative integers whose sum is N. If the length of that list is 100 or smaller, return the sequence as a int[] in ascending order. If there is no such sequence or its length is larger than 100, return { }.

Definition

Class:	SequenceSums
Method:	sequence
Parameters:	int, int
Returns:	int[]
Method signature:	int[] sequence(int N, int L)
(be sure your method is public)

Constraints

-

N will be between 1 and 1000000000, inclusive.

-

L will be between 2 and 100, inclusive.

Examples

0)

Returns: {5, 6, 7 }

18 can be expressed as 5 + 6 + 7 or 3 + 4 + 5 + 6. Both of these lists contain more than 2 elements, so you should return the shortest among them.

1)

Returns: {3, 4, 5, 6 }

Now the correct answer is 3 + 4 + 5 + 6 because 5 + 6 + 7 contains less than 4 elements.

2)

Returns: { }

Both possible presentations of 18 contain less than 5 elements, so there's no answer for this case.

3)

Returns: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }

4)

1000000000

Returns: {199999998, 199999999, 200000000, 200000001, 200000002 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ShorterSuperSum

Dynamic Programming, Math

Used in:

SRM 467

Used as:

Division II Level One

Writer:

vexorian

Testers:

PabloGilberto , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10240

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14151&pm=10240

Problem Statement

SuperSum is a function defined as:

SuperSum(0 , n) = n, for all positive n.
SuperSum(k , n) = SuperSum(k-1 , 1) + SuperSum(k-1 , 2) + ... + SuperSum(k-1 , n), for all positive k, n.

Given k and n, return the value for SuperSum(k , n).

Definition

Class:	ShorterSuperSum
Method:	calculate
Parameters:	int, int
Returns:	int
Method signature:	int calculate(int k, int n)
(be sure your method is public)

Constraints

-

k will be between 1 and 14, inclusive.

-

n will be between 1 and 14, inclusive.

Examples

0)

Returns: 6

When k = 1, SuperSum is equal to the sum of the first n = 3 numbers: 1 + 2 + 3 = 6.

1)

Returns: 10

SuperSum(2 , 3) = SuperSum(1 , 1) + SuperSum(1 , 2) + SuperSum(1 , 3) = 1 + 3 + 6 = 10.

2)

Returns: 2002

3)

Returns: 167960

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SuperSum

Advanced Math

Used in:

SRM 467

Used as:

Division I Level Two

Writer:

vexorian

Testers:

PabloGilberto , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10239

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14151&pm=10239

Problem Statement

SuperSum is a function defined as:

SuperSum(0 , n) = n, for all positive n.
SuperSum(k , n) = SuperSum(k-1 , 1) + SuperSum(k-1 , 2) + ... + SuperSum(k-1 , n), for all positive k, n.

Given k and n, return the value for SuperSum(k , n) modulo 1000000007.

Definition

Class:	SuperSum
Method:	calculate
Parameters:	int, int
Returns:	int
Method signature:	int calculate(int k, int n)
(be sure your method is public)

Constraints

-

k will be between 1 and 50, inclusive.

-

n will be between 1 and 1000000000, inclusive.

Examples

0)

Returns: 6

When k = 1, SuperSum is equal to the sum of the first n = 3 numbers: 1 + 2 + 3 = 6.

1)

Returns: 10

SuperSum(2 , 3) = SuperSum(1 , 1) + SuperSum(1 , 2) + SuperSum(1 , 3) = 1 + 3 + 6 = 10.

2)

Returns: 2002

3)

Returns: 150595840

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AvoidFour

Advanced Math, Dynamic Programming

Used in:

SRM 444

Used as:

Division I Level Three

Writer:

vexorian

Testers:

PabloGilberto , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10238

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13898&pm=10238

Problem Statement

It is a known fact that of all numbers, 4 is the one that brings the worst luck. It is for this reason that when generating number sequences, we need to avoid patterns related to the number 4 as much as possible.

You are given a long n. Count the number of positive integers that satisfy all of the following conditions:

The number contains at most n digits.
The number does not contain four consecutive '4' digits. For example, 43444124 is allowed, but 45444474 is not.
The number of digits in the number is not a multiple of any of the integers greater than 10 that contain only '4' in their decimal representations (44, 444, 4444, 44444, ...).

Return the total count of these numbers modulo 1000000007.

Definition

Class:	AvoidFour
Method:	count
Parameters:	long
Returns:	int
Method signature:	int count(long n)
(be sure your method is public)

Constraints

-

n will be between 1 and 40000000000 (4e10), inclusive.

Examples

0)

Returns: 9998

Of all the 9999 positive integers containing 1, 2, 3 or 4 digits, 4444 is the only one that contains four consecutive '4' digits.

1)

Returns: 99980

The numbers to ignore are: 4444, 44440, 44441, 44442, ..., 44449, 14444, 24444, 34444, 54444, ... , 94444.

2)

Returns: 576334228

3)

Returns: 576334228

88 is a multiple of 44, so all numbers with 88 digits are ignored.

4)

Returns: 547731225

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Deanonymize

Advanced Math

Used in:

MM 45

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10227

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13570&pm=10227

Problem Statement

A company has recently released a large database. Each record in the database corresponds to one user. There are N public fields which do not contain sensitive information, and M private fields which do. The company claims that it has added noise to anonymize the database and that there is no way to recover accurate private values from unperturbed public information. You're not so sure...

You will be given the perturbed database and unperturbed public information for a number of users (but not everyone). Your task is to return your best guess as to the unperturbed private values of the users whose public information you know.

The data will be generated by first picking N and M. Then, C gaussian distributions will be generated in N+M dimensional space. The mean and standard deviation of each dimension of each gaussian will be selected independently and uniformly from [-1,1] and [0,1]. To generate each of U users, one of the C gaussians will be selected at random, and a sample will be pulled from it. Finally, the data will be perturbed by adding gaussian noise to every value, sampled from a distribution with mean 0 and standard deviation SD. You will then be given the unperturbed public information about Q users (selected randomly from the U) and are to return your best guess as to their unperturbed private information.

Your raw score will be the mean squared error of your return. This will be compared to a baseline measure which, for every user whose unperturbed public information is given, takes the expected value of the private information (given the C distributions used to generate the data). Your score will be your improvement over this baseline (in mean squared error). Your overall score will simply be the sum of these scores, with any negative values increased to 0.

You must implement a method deanonymize. Your method will take N, M and SD as described above. The parameter database will give you U records, where field j of record i is given by database[i*(N+M)+j] and the first N fields are the public ones. users will give you the unperturbed users whose data we are interested in, where public field j of user i is given by users[i*N+j]. You should return an array with Q*M elements, grouped by user in the same way that the users array is.

An offline tester is also available.

Definition

Class:	Deanonymize
Method:	deanonymize
Parameters:	int, int, double[], double[], double
Returns:	double[]
Method signature:	double[] deanonymize(int N, int M, double[] database, double[] users, double SD)
(be sure your method is public)

Notes

- The memory limit is 2048MB, however you may experience performance degradation due to swapping when using more than 1024MB.

- The time limit is 20 seconds.

- There are 100 provisional test cases.

Constraints

- In generating the parameters, rand() is a uniform random variable in [0,1], and floor is used for rounding to integers when necessary.

- N will be 100^rand()

- M will be 100^rand()

- C will be 1000^rand()

- U will be 100+100000^rand()

- Q will be U/10

- SD will be (rand()+0.5)*min(0.5,U^-1/N)

Examples

0)

"1"

Returns: "Seed = 1
N = 15
M = 6
SD = 0.6794676326705618
U = 146
Q = 14
"

1)

"2"

Returns: "Seed = 2
N = 7
M = 1
SD = 0.335403841291766
U = 682
Q = 68
"

2)

"3"

Returns: "Seed = 3
N = 43
M = 1
SD = 0.6342912229585391
U = 653
Q = 65
"

3)

"4"

Returns: "Seed = 4
N = 55
M = 2
SD = 0.7483313334749946
U = 947
Q = 94
"

4)

"5"

Returns: "Seed = 5
N = 7
M = 1
SD = 0.34758487121050863
U = 9770
Q = 977
"

5)

"6"

Returns: "Seed = 6
N = 92
M = 17
SD = 0.3416127850569974
U = 146
Q = 14
"

6)

"7"

Returns: "Seed = 7
N = 5
M = 4
SD = 0.20131294912571285
U = 697
Q = 69
"

7)

"8"

Returns: "Seed = 8
N = 6
M = 10
SD = 0.44062796822464706
U = 111
Q = 11
"

8)

"9"

Returns: "Seed = 9
N = 22
M = 46
SD = 0.533073548894668
U = 27926
Q = 2792
"

9)

"10"

Returns: "Seed = 10
N = 3
M = 1
SD = 0.038548775274140114
U = 18476
Q = 1847
"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SoccerFan

Brute Force, Simple Math, Simple Search, Iteration, Simulation

Used in:

TCHS SRM 63

Used as:

Division I Level Three

Writer:

DStepanenko

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10206

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13532&pm=10206

Problem Statement

You are tracking the results of a soccer tournament. For each match that has been played so far, you have written down the names of the two opposing teams, along with the number of goals scored by each team. However, you suspect that for one of the matches, you may have written down the wrong number of goals scored by one of the teams.

Fortunately, you know which team is the current tournament leader. The tournament is scored as follows. For each game, the winning team (the team that scored more goals) gets 3 points and the losing team gets 0 points. If there is no winner (both teams scored the same number of goals), each team gets 1 point. The tournament leader is the team that has strictly more points than any other team.

You are given a String[] results, where the i-th element is what you have written down as the result of the i-th match. Each element is formatted as "team1 team2 a:b" (quotes for clarity), where team1 is the name of the first team, team2 is the name of the second team, a is the number of goals scored by the first team, and b is the number of goals scored by the second team. You are also given a String winner, the name of the current tournament leader according to the real results.

If, according to your written results, the tournament leader is winner, return -2. Otherwise, if there exists exactly one match in your written results where you can change the number of goals scored by one of the teams, and the tournament leader would then be winner according to the changed written results, return the index of that match. If there exist several such matches, return the index of the earliest of those matches. If no such match exists, return -1. All indices are 0-based.

Definition

Class:	SoccerFan
Method:	whereIsMistake
Parameters:	String[], String
Returns:	int
Method signature:	int whereIsMistake(String[] results, String winner)
(be sure your method is public)

Constraints

-

results will contain between 1 and 50 elements, inclusive.

-

Each element of results will contain between 7 and 50 characters, inclusive.

-

Each element of results will be formatted as "team1 team2 a:b" (quotes for clarity).

-

In each element of results, team1 and team2 will each contain between 1 and 43 lowercase letters ('a'-'z'), inclusive.

-

In each element of results, a and b will each be a single digit ('0'-'9').

-

In each element of results, team1 and team2 will be distinct.

-

winner will contain between 1 and 50 lowercase letters ('a'-'z'), inclusive.

Examples

0)

{"real bayer 2:2"}

"bayer"

Returns: 0

According to your written results, the one match resulted in a draw. This means there is no tournament leader (both teams have 1 point). To make "bayer" the tournament leader, we can change the number of goals scored by "bayer" in that match to 3.

1)

{"breda ajax 2:2", "breda psv 0:0", "psv ajax 1:1"}

"ajax"

Returns: 0

Here, every match has resulted in a draw according to your written results, so there is no tournament leader (each team has 2 points). To make "ajax" the leader, we can change either match 0 or match 2. We return the smallest among these two matches.

2)

{"borussia shalke 4:2", "bayer herta 3:2","bayer bavaria 5:2"}

"borussia"

Returns: -1

According to your written results, "bayer" has 6 points, "borussia" has 3 points, and "shalke", "herta" and "bavaria" have 0 points. You cannot increase the score for "borussia" by changing 1 match. You can decrease the score for "bayer" to 3 points, but that is not enough to make "borussia" the leader.

3)

{"spartak real 2:1", "real spartak 3:2"}

"spartak"

Returns: 1

Both "real" and "spartak" have 3 points. Changing match 0 can't increase the score for "spartak", so we need to change match 1.

4)

{"xy yx 3:2", "xx yy 1:1"}

"yx"

Returns: 0

We can, for example, change match 0 to 1:2.

5)

{"borussia shalke 4:2", "bayer herta 3:2","bayer bavaria 5:2", "borussia verder 1:1"}

"borussia"

Returns: 1

Even though "borussia" didn't play in match 1, we can change its result to decrease the final score for "bayer" and thus make "borussia" the leader.

6)

{"spartak dinamo 3:2","dinamo rubin 2:2"}

"spartak"

Returns: -2

"spartak" has 3 points, and "dinamo" and "rubin" have 1 point each. "spartak" is the leader without any changes.

7)

{"a b 9:0"}

"c"

Returns: -1

8)

{"a b 0:0", "a c 1:1", "g d 3:1"}

"a"

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LaggedGenerator

Advanced Math

Used in:

MM 44

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10201

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13569&pm=10201

Problem Statement

In this problem your task is to break a pseudorandom number generator given its last K outputs. Each `random' number will be generated as a function of the previous M `random' numbers, for some M. After the function is evaluated, the result is taken modulo a prime P, and that is the output. For instance, a simple generator function would be S_n = S_n-1+S_n-2 (mod P). A more complicated one is S_n = S_n-11*S_n-2 + S_n-1 + 1 (mod P). In general we will consider polynomials functions of the last M numbers. Your task is to write a method crack that takes a int[] S, a int, M, an int P, and returns your best guess for the next M numbers output by the generator.

The prime, P will be between 101 and 40000, inclusive. M will be chosen as floor(rand()*rand()*996)+5, where rand() is a uniform random number in [0,1]. The polynomial will be generated by first picking D, the maximum degree as 1, 2, or 3. The number of terms will then be chosen in [2,min(200,1+M+(D>1?M(M+1)/2)+(D>2?M(M+1)(M+2)/6)], and each term will be generated with a degree in [0,D]. After the degree d is chosen, d (not necessarily distinct) previous random numbers (offsets) are selected as the components of the term. If this generates a term which has already been generated, the process is repeated (so, degree 0 will only occur once, for instance). After the variables are chosen, the coefficient is chosen in [0,P-1]. You will be given the K sequential random numbers for K in [M,min(1000000,3*M^D)]. The random number generator will be initialized with M random values, and then run for K+100*M iterations, of which you will be given the final K. All random choices are uniform and independent.

Your score will be the number of the M entries that are correct. Your overall score will simply be the sum of your individual scores.

You can download the source code and class files to generate a sequence of random numbers. To run, simply enter 'java LaggedGenerator <seed>'. The output will be the M initial values, followed by an asterisk, followed by 100M random values, followed by an asterisk, followed by K random values, followed by an asterisk, and finally the M values to predict. The seeds for the examples are 1-9 and 18, in order.

Definition

Class:	LaggedGenerator
Method:	crack
Parameters:	int[], int, int
Returns:	int[]
Method signature:	int[] crack(int[] S, int P, int M)
(be sure your method is public)

Notes

- The time limit is 30 seconds.

- The memory limit is 1024M.

- In the examples, N is the number of terms in the polynomial.

- There are 100 non-example test cases.

Examples

0)

"1"

Returns: ""

P = 101

N = 4

D = 2

M = 5

K = 50

1)

"2"

Returns: ""

P = 36299

N = 7

D = 1

M = 16

K = 44

2)

"3"

Returns: ""

P = 23789

N = 177

D = 3

M = 102

K = 668069

3)

"4"

Returns: ""

P = 13687

N = 62

D = 2

M = 155

K = 4147

4)

"5"

Returns: ""

P = 28403

N = 26

D = 1

M = 25

K = 40

5)

"6"

Returns: ""

P = 17257

N = 19

D = 3

M = 611

K = 682883

6)

"7"

Returns: ""

P = 21481

N = 51

D = 1

M = 115

K = 193

7)

"8"

Returns: ""

P = 24281

N = 180

D = 2

M = 211

K = 125395

8)

"9"

Returns: ""

P = 27847

N = 127

D = 1

M = 565

K = 928

9)

"18"

Returns: ""

P = 39317

N = 169

D = 2

M = 26

K = 1485

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ThirtyRocks

Greedy, Math, Simple Search, Iteration

Used in:

TCHS SRM 64

Used as:

Division I Level Two

Writer:

vexorian

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10199

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13533&pm=10199

Problem Statement

You have 30 rocks and n boxes in which you wish to place them. Each box can hold some minimum and maximum number of rocks. The i-th element of boxMinimum is the minimum number of rocks you can place in box i, and the i-th element of boxMaximum is the maximum number of rocks you can place in box i.

If you can put all 30 rocks into the boxes, return a int[] containing exactly n elements, where the i-th element is the number of rocks in box i. If there are multiple ways to do this, return the one that comes first lexicographically. If it is not possible to put all 30 rocks into boxes, return an empty int[] instead.

Definition

Class:	ThirtyRocks
Method:	assign
Parameters:	int[], int[]
Returns:	int[]
Method signature:	int[] assign(int[] boxMinimum, int[] boxMaximum)
(be sure your method is public)

Notes

-

int[] A comes before int[] B lexicographically if A contains the lesser number in the first position in which A and B differ.

Constraints

-

boxMinimum will contain between 1 and 50 elements, inclusive.

-

boxMaximum will contain the same number of elements as boxMinimum.

-

Each element of boxMinimum will be between 0 and 30, inclusive.

-

Each element i of boxMaximum will be between boxMinimum[i] and 30, inclusive.

Examples

0)

{0,0}

{20,10}

Returns: {20, 10 }

The only possible way to distribute the 30 rocks is by placing 20 rocks in the first box and the remaining 10 in the second box. If we moved any of the rocks to another box we would be breaking the specified limits.

1)

{15,15,15}

{25,24,16}

Returns: { }

This time, there are three boxes but each of them requires a minimum of 15 rocks, which is impossible to achieve since we only have 30.

2)

{0,0}

{20,11}

Returns: {19, 11 }

This is similar to the first example. However, we are now allowed to place 11 rocks in the second box. This allows two possible answers: {20,10} and {19,11} . We pick the second one since it comes first lexicographically.

3)

{10,0,0}

{10,2,15}

Returns: { }

The first box requires 10 rocks, but you cannot place the remaining rocks in the other boxes since they allow a maximum of 17 rocks. It is not possible to comply with all the rules.

4)

{0,0,0,0,0}

{30,30,30,30,30}

Returns: {0, 0, 0, 0, 30 }

Of all the many possible solutions for this case, {0,0,0,0,30} comes first lexicographically.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CommanderIdol

Graph Theory, Simple Math

Used in:

TCHS SRM 64

Used as:

Division I Level Three

Writer:

vexorian

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10197

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13533&pm=10197

Problem Statement

You are the commander of a group of soldiers on a battlefield. There are several forts on that battlefield, and you and your soldiers are currently at fort 0. Your task is to send a soldier to each of the other forts to deliver some secret prototypes.

Your mission is considered complete when there is exactly one solider at each of the other forts. You want to complete the mission as soon as possible, but you also want to maintain your high popularity among your soldiers. You have noticed that allowing soldiers to sleep a couple of hours before beginning their missions will make you more popular with them. Specifically, if you let one soldier sleep for X hours before beginning his mission, you will gain X popularity points.

You are given a String[] roads, where the j-th character of the i-th element is '-' if no road exists between forts i and j, or a digit between '0' and '9' representing the number of hours it would take a soldier to travel between forts i and j. Return the maximum total number of popularity points you can gain while still completing the mission as quickly as possible. Return -1 if it is impossible to complete the mission.

Definition

Class:	CommanderIdol
Method:	getMaxPopularity
Parameters:	String[]
Returns:	int
Method signature:	int getMaxPopularity(String[] roads)
(be sure your method is public)

Constraints

-

roads will contain n elements, where n is between 2 and 50, inclusive.

-

Each element of roads will contain exactly n characters.

-

Each character in roads will be '-' or a digit between '0' and '9', inclusive.

-

Character i in element i of roads will be '-'.

-

Character i in element j of roads will be the same as character j in element i of roads.

Examples

0)

{"-1-","1-2","-2-"}

Returns: 2

The mission will require at least 3 hours to be finished. You can allow the soldier assigned to fort 1 to sleep 2 more hours without delaying the mission completion.

1)

{"-1--","1-2-","-2--","----"}

Returns: -1

There is no way for your soldiers to reach fort 3, so this mission cannot be accomplished.

2)

{"--7-6",
 "----8",
 "7--51",
 "--5-7",
 "6817-"}

Returns: 17

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ShufflingMachine

Brute Force, Simple Math, Simulation

Used in:

SRM 426

Used as:

Division I Level One , Division II Level Two

Writer:

StevieT

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10196

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13517&pm=10196

Problem Statement

A card shuffling machine is a device designed to randomize the order of a deck of cards. A particularly poor (but unfortunately relatively common) design of machine works as follows: an integer N is selected uniformly at random between 1 and maxShuffles, inclusive, and a series of N exactly similar deterministic shuffles are performed. A deterministic shuffle is a fixed permutation of the cards. The randomness of the resulting ordering is clearly therefore only dependent on the number of shuffles chosen. After the deck has been shuffled N times, the cards are distributed to the players.

A particularly dishonest player has decided that he wishes to cheat. He has identified K cards in the deck that he wants to receive when the cards are distributed. He has managed to figure out both the fixed shuffle that the machine uses and also the maximum number of shuffles chosen. The fixed shuffle is given in a int[] shuffle, in which element i gives the position after the shuffle of the card that was initially in position i (both 0-based). The positions in the deck of the cards the player will receive after they have been shuffled are given in cardsReceived (0-based). Before the cards are shuffled, the player can order them in any way he wishes. Determine the initial ordering that will maximize the expected number of the K desired cards that he will receive and return this expected number.

Definition

Class:	ShufflingMachine
Method:	stackDeck
Parameters:	int[], int, int[], int
Returns:	double
Method signature:	double stackDeck(int[] shuffle, int maxShuffles, int[] cardsReceived, int K)
(be sure your method is public)

Notes

-

Your return value must be accurate to an absolute or relative tolerance of 1e-9.

Constraints

-

shuffle will contain between 1 and 50 elements, inclusive.

-

shuffle will be a permutation of the numbers between 0 and M-1, inclusive, where M is the number of elements in shuffle.

-

maxShuffles will be between 1 and 100, inclusive.

-

cardsReceived will contain between 1 and M elements, inclusive.

-

Each element of cardsReceived will be between 0 and M-1.

-

The elements of cardsReceived will be distinct.

-

K will be between 1 and M, inclusive.

Examples

0)

{1,0}

{0}

Returns: 0.6666666666666666

This deck contains only 2 cards and they swap positions after each shuffle. The cheating player receives first card in the deck after the shuffling is completed and he wants to receive 1 of the cards in the deck. If the deck is shuffled 1 or 3 times, he will receive the card that was initially in position 1. If the deck is shuffled 2 times, he will receive the card in position 0. It is therefore optimal to put the card that he wants in position 1 and he will receive it 2 times out of 3.

1)

{1,2,0}

{0}

Returns: 0.8

If he puts the cards he wants in positions 1 and 2, he will receive one of them 4 times out of 5.

2)

{1,2,0,4,3}

{0,3}

Returns: 1.0

If he puts the cards in positions 3 and 4, he will receive exactly one of them, regardless of how many shuffles are chosen.

3)

{0,4,3,5,2,6,1}

{1,3,5}

Returns: 1.0526315789473684

4)

{3,4,7,2,8,5,6,1,0,9}

{6,3,5,2,8,7,4}

Returns: 6.297872340425532

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OrderedNim

Simple Math

Used in:

SRM 450

Used as:

Division I Level One , Division II Level Two

Writer:

Rydberg

Testers:

PabloGilberto , Andrew_Lazarev , ivan_metelsky , Smylic

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10190

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13904&pm=10190

Problem Statement

Nim is a game in which two players take turns removing stones from heaps. On each turn, a player must choose a single heap and remove one or more stones from that heap. The player who takes the last stone wins.

Alice and Bob are bored with playing Nim over and over again, so they've decided to create a new variation called Ordered Nim. Ordered Nim differs from regular Nim in the following way. The heaps are numbered 0 through n-1 (where n is the number of heaps), and a player can only remove stones from a heap if all the lower-numbered heaps are empty.

You are given a int[] layout, where the i-th element (0-indexed) is the number of stones in heap i at the beginning of the game. Alice will take the first turn. Determine who will win the game, assuming both players play optimally. Return "Alice" if Alice will win, or "Bob" if Bob will win (all quotes for clarity).

Definition

Class:	OrderedNim
Method:	winner
Parameters:	int[]
Returns:	String
Method signature:	String winner(int[] layout)
(be sure your method is public)

Constraints

-

layout will contain between 1 and 50 elements, inclusive.

-

Each element of layout will be between 1 and 1000000000, inclusive.

Examples

0)

{5}

Returns: "Alice"

Alice takes all 5 stones and wins.

1)

{1,2}

Returns: "Bob"

According to the rules of the game, Alice is not allowed to take stones from heap 1 because heap 0 is not empty. Her only option is to take the one stone from heap 0. Heap 0 will then be empty, so Bob can take both stones from heap 1 to win the game.

2)

{2,1}

Returns: "Alice"

3)

{10,9,8,7,6,5,4,3,2,1}

Returns: "Alice"

4)

{1,1,1,1}

Returns: "Bob"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CampaignTrail

Dynamic Programming, Simple Math

Used in:

TCO09 Round 3

Used as:

Division I Level Two

Writer:

legakis

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10188

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13761&pm=10188

Problem Statement

Your are running for president of a country that uses an electoral college to select its leader. The country is comprised of states, each having a set number of electors. All electors support the presidential candidate who wins the popular vote in their state. The candidate supported by the greatest number of electors wins the election.

National election laws permit you to campaign in a limited number of states, given as an int visits. You are given the number of electors in each state as a int[] electors. Your estimates of the probabilies you have for winning the popular vote in each state with and without visiting it are given as int[]s winCurrent and winIfVisited, respectively, both expressed as percents.

The states hold their elections one at a time (in the order they are represented in electors, winCurrent, and winIfVisited). You get to see the result of each election before deciding if you wish to visit the next state to hold an election.

Compute your chance of winning the election, assuming that you make optimal choices regarding which state(s) to visit.

Definition

Class:	CampaignTrail
Method:	probWin
Parameters:	int[], int[], int[], int
Returns:	double
Method signature:	double probWin(int[] electors, int[] winCurrent, int[] winIfVisited, int visits)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1e-9.

-

You want to win the election. A tie results in a drawn-out legal battle, which as far as you are concerned is just as bad as losing.

Constraints

-

electors will contain between 1 and 50 elements, inclusive.

-

electors, winCurrent, and winIfVisited will each have the same number of elements.

-

Each element of electors will be between 1 and 50, inclusive.

-

Each element of winCurrent and winIfVisited will be between 0 and 100, inclusive.

-

visits will be between 0 and the number of elements in electors, inclusive.

Examples

0)

{ 5, 1, 5 }

{ 0, 50, 0 }

{ 50, 100, 50 }

Returns: 0.625

You should definitely visit the first state. If you win the first state, then you can guarantee yourself the support of 6 electors by visiting the second state. If you lose the first state, your only chance is to visit the third state instead.

1)

{ 4, 9, 5 }

{ 0, 50, 50 }

{ 100, 100, 0 }

Returns: 0.5

If you visit the second state, you will win the election if and only if you win the third state, so your chances are 50%.

2)

{ 5, 9, 4 }

{ 50, 50, 0 }

{ 0, 100, 100 }

Returns: 0.75

The same data as in the previous example, but in the reverse order. Here the following strategy guarantees you winning the election with 75% probability. Wait for the results in the first state. If you win there, then you can guarantee winning the election by visiting the second state. Otherwise, it's better to visit the third state to obtain 50% probability of winning the election.

3)

{ 1, 1, 1, 1, 3 }

{ 0, 0, 0, 0, 49 }

{ 100, 100, 100, 100, 51 }

Returns: 0.49

There are 4 states with 1 elector each. You will win each of those states that you visit with 100% probability, and will lose each that you do not. If you visit the fifth state (with 3 electors) you will increase your chance from 49% to 51%.

With only time to visit 1 state, your best option is to visit one of the first 4. Then you will win the election if and only if you win the 5th state. If instead you chose to visit the 5th state, you would have a 0% chance of winning the election.

4)

{ 1, 1, 1, 1, 3 }

{ 0, 0, 0, 0, 49 }

{ 100, 100, 100, 100, 51 }

Returns: 0.51

With time to visit 2 states, you can now visit the 5th state and increase your chance of winning to 51%.

5)

{ 1, 1, 1, 1, 3 }

{ 0, 0, 0, 0, 49 }

{ 100, 100, 100, 100, 51 }

Returns: 1.0

With time to visit 4 states, you can change your strategy and visit all the single-elector states and ignore the 5th state.

6)

{ 1, 1, 1 }

{ 25, 50, 25 }

{ 50, 25, 50 }

Returns: 0.5

You better stay away from the second state, as campaigning there will decrease your chance of winning.

7)

{ 1, 1 }

{ 0, 0 }

{ 0, 100 }

Returns: 0.0

It is impossible to win the election outright.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DistinctDigits

Brute Force, Math, Search

Used in:

SRM 426

Used as:

Division II Level Three

Writer:

StevieT

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10186

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13517&pm=10186

Problem Statement

Consider the set of numbers formed by taking every number between low and high, inclusive, and sorting the digits of each number in non-increasing order (the numbers are initially written without any extra leading zeros). Return the number of distinct numbers in this new set.

Definition

Class:	DistinctDigits
Method:	count
Parameters:	int, int
Returns:	int
Method signature:	int count(int low, int high)
(be sure your method is public)

Constraints

-

high will be between 1 and 100,000,000 (10^8), inclusive.

-

low will be between 1 and high, inclusive.

Examples

0)

Returns: 20

All of the integers between 1 and 20 have distincts sets of digits.

1)

Returns: 29

"21" has the same digits as "12" when sorted. All the rest are still distinct.

2)

Returns: 98

3)

Returns: 1641

4)

Returns: 318

5)

10000000

Returns: 19159

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ProductOfDigits

Simple Math

Used in:

SRM 424

Used as:

Division I Level One , Division II Level Two

Writer:

Gluk

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10177

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13515&pm=10177

Problem Statement

You are given an int N. Find the smallest positive integer X such that the product of its digits (in decimal notation) is equal to N. Return the number of digits in X, or return -1 if such a number does not exist.

Definition

Class:	ProductOfDigits
Method:	smallestNumber
Parameters:	int
Returns:	int
Method signature:	int smallestNumber(int N)
(be sure your method is public)

Constraints

-

N will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 1

Just take X = 1. It contains 1 digit.

1)

Returns: 2

Here the smallest possible X is 25.

2)

Returns: -1

3)

Returns: 3

The number 455 has 3 digits and the product of its digits is 4 * 5 * 5 = 100.

4)

Returns: 4

5)

Returns: 4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ProductOfPrices

Geometry, Search, Simple Math

Used in:

SRM 424

Used as:

Division I Level Three

Writer:

Gluk

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10170

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13515&pm=10170

Problem Statement

There are N trees numbered 0 to N-1, and you must plant them along a straight line. Tree i will be planted at coordinate X[i], where X is constructed using the following recursive definition:

X[0] = X0 MOD L

X[i] = (X[i-1]*A+B) MOD L (note that X[i-1]*A+B may overflow a 32-bit integer)

The price of planting tree i is the sum of the distances between tree i and each tree numbered less than i. Calculate the product of the prices of all the trees (except tree 0), and return this number modulo 1,000,000,007.

Definition

Class:	ProductOfPrices
Method:	product
Parameters:	int, int, int, int, int
Returns:	int
Method signature:	int product(int N, int L, int X0, int A, int B)
(be sure your method is public)

Constraints

-

N will be between 2 and 200,000, inclusive.

-

L will be between 1 and 200,000, inclusive.

-

X0,A,B will each be between 0 and 1,000,000,000, inclusive.

Examples

0)

Returns: 180

The trees are planted at positions: 3, 4, 5, 6, 7. Their prices are (starting from tree 1): 1, 3, 6, 10. The product of prices is 1 * 3 * 6 * 10 = 180.

1)

Returns: 64

2)

Returns: 3087

3)

Returns: 591860767

4)

999999999

123456789

987654321

Returns: 499739175

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DesignCalendar

Math

Used in:

SRM 427

Used as:

Division I Level One , Division II Level Two

Writer:

StevieT

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10155

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13518&pm=10155

Problem Statement

An alien civilization has advanced to the point where it needs to start keeping track of time. Its leaders have therefore decided to design a calendar. Like many Earthly calendars, this calendar is going to be based on the motion of celestial bodies: in particular the calendar must include period of rotation of their planet (a day) and the period of orbit of the planet around the sun (a real year). Unfortunately, just as is the case on Earth, a real year is not necessarily a convenient integer number of days. Their solution to this problem is to define a calendar year, which is an integer number of days long, and periodically insert an extra day into some calendar years (leap years) in order to correct the discrepancy and resychronize the start of the calendar year with the start of the real year.

The formal requirements for the calendar are as follows:

A normal calendar year is a length of time that is some integer number N days long.
A leap calendar year is exactly one day longer than a normal calendar year (N+1 days long).
Each calendar year is either a normal year or a leap year.
The calendar must have some positive integer period P, such that every P whole consecutive calendar years sum to exactly the same length of time as P real years.

The leaders wish to design the calendar to make the period P as short as possible. A day is dayLength time units long and a real year is yearLength time units long. Return the smallest achievable positive integer value of P.

Definition

Class:	DesignCalendar
Method:	shortestPeriod
Parameters:	int, int
Returns:	int
Method signature:	int shortestPeriod(int dayLength, int yearLength)
(be sure your method is public)

Constraints

-

yearLength will be between 1 and 1000000000 (10^9), inclusive.

-

dayLength will be between 1 and yearLength, inclusive.

Examples

0)

Returns: 4

These are the values for the Earth to the nearest quarter day. A days here is 4 quarter days long and a year is 365 * 4 + 1 = 1461 quarter days long. A single leap year every 4 years keeps the calendar synchronized.

1)

31558150

Returns: 1728

These are the values for the Earth to the nearest second. A calendar with a period of 1728 years would be aligned to the start of the solar year to within a second after the first period.

2)

Returns: 49

3)

50000100

Returns: 10

4)

28565335

Returns: 5673

5)

Returns: 1111

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KnockoutTourney

Math

Used in:

SRM 426

Used as:

Division II Level One

Writer:

StevieT

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10146

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13517&pm=10146

Problem Statement

You have just entered a knockout tournament with N competitors. The tournament is structured as follows: at the start, the competitors are written down in a list. Adjacent competitors in the list are then paired off, starting from the first competitor on the list, and each pair plays a match (competitor 1 plays against 2, 3 plays against 4, etc.). The losers of each match are eliminated and their names are crossed off the list, while the winners progress to the next round. If there are an odd number of competitors in a round, then the last competitor in the list advances to the next round automatically, without having to play a match. This process then repeats with the new list of competitors, until only a single competitor remains, who is declared the winner. Note that the ordering of the competitors is preserved between rounds.

Your arch-rival has also entered the tournament and you want to know when you might end up playing against him. Your position in the list for the first round is you and your rival's position is rival (both indexed from 1). Assuming that both you and your rival win all the matches before you play each other, return the number of the round in which you will meet (counting the rounds from 1).

Definition

Class:	KnockoutTourney
Method:	meetRival
Parameters:	int, int, int
Returns:	int
Method signature:	int meetRival(int N, int you, int rival)
(be sure your method is public)

Constraints

-

N will be between 2 and 100000, inclusive.

-

you and rival will each be between 1 and N, inclusive.

-

you and rival will be distinct.

Examples

0)

Returns: 1

This is a 4 round tournament, with 16 players, so every player plays a match in every round. You are paired with your rival in the first round.

1)

Returns: 4

Despite being adjacent in the list, you are not paired with your rival until the final round.

2)

Returns: 4

3)

Returns: 16

4)

Returns: 10

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CavePassage

Graph Theory, Search, Simple Math

Used in:

SRM 422

Used as:

Division I Level Two

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10123

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13513&pm=10123

Problem Statement

Several travelers are standing at the entrance of a dark cave. The travelers must all pass through the cave and stand together at the exit. Unfortunately, a variety of circumstances can make it impossible for them to all pass through the cave together at the same time. Therefore, they may have to take turns going through the cave in smaller groups. There is only one map though, and it is impossible to navigate the cave without it, so whenever a group of travelers is inside the cave, one member of that group must be holding the map.

When a group of travelers walks through the cave, either from the entrance or the exit, they must traverse an old bridge to get to the other side of the cave. The entire group inside the cave must cross the bridge together at the same time. The bridge cannot hold more than bridgeStrength kilograms, or it will collapse. You are given a int[] travelersWeights, where the i-th element is the weight of the i-th traveler in kilograms.

Travelers may walk through the cave alone. Although, when travelers walk through the cave in a group of two or more, each traveler must trust at least one of the other travelers in the group. You are given a String[] trustTable, where the j-th character of the i-th element is 'Y' if traveler i trusts traveler j, and 'N' otherwise. Note that the trust relation is not necessarily symmetric.

Travelers walk at different speeds, but when they go through the cave, they must stick together and walk at the same speed. Therefore, when a group of travelers walks through the cave, they must walk at the speed of the slowest traveler in the group. You are given a int[] travelersTimes, where the i-th element is the amount of time it takes the i-th traveler to walk through the cave in any direction.

Return the minimal total time required for all the travelers to end up together at the exit of the cave. If it is impossible, return -1 instead.

Definition

Class:	CavePassage
Method:	minimalTime
Parameters:	int[], int[], String[], int
Returns:	int
Method signature:	int minimalTime(int[] travelersWeights, int[] travelersTimes, String[] trustTable, int bridgeStrength)
(be sure your method is public)

Constraints

-

travelersWeights will contain between 1 and 13 elements, inclusive.

-

Each element of travelersWeights will be between 1 and 1000, inclusive.

-

travelersTimes will contain the same number of elements as travelersWeights.

-

Each element of travelersTimes will be between 1 and 1000, inclusive.

-

trustTable will contain the same number of elements as travelersWeights.

-

Each element of trustTable will contain exactly n characters, where n is the number of elements in trustTable.

-

Each element of trustTable will contain only uppercase letters 'Y' and 'N'.

-

The i-th character of the i-th element of trustTable will always be 'Y'.

-

bridgeStrength will be between 1 and 5000, inclusive.

Examples

0)

{ 1, 1, 1 }

{ 2, 3, 4 }

{ "YYY", "YYY", "YYY" }

Returns: 9

The travelers can achieve the goal as follows. First, traveler 0 and traveler 2 go through the cave together. It normally takes 2 time units for traveler 0 to go through the cave, and it takes 4 time units for traveler 2. Since they are traveling together in a group, they must walk at the speed of the slower traveler. So, after 4 time units, both travelers are at the exit. Then, traveler 0 takes the map and goes back through the cave to the entrance. This time, it only takes 2 time units because he is alone. Finally, traveler 0 and traveler 1 go through the cave together in 3 time units and all the travelers end up together at the exit. The total time is 4 + 2 + 3 = 9.

1)

{ 1, 1, 1 }

{ 2, 3, 4 }

{ "YYY", "YYY", "NYY" }

Returns: 10

Here things become a little bit more complicated, because traveler 2 doesn't trust traveler 0.

2)

{ 1, 1, 1 }

{ 7, 13, 19 }

{ "YYN", "NYY", "YNY" }

Returns: 19

3)

{ 43 }

{ 23 }

{ "Y" }

Returns: -1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

InverseFactoring

Simple Math

Used in:

SRM 425

Used as:

Division II Level One

Writer:

crazyb0y

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10118

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13516&pm=10118

Problem Statement

A positive integer a is a proper factor of n if and only if n is a multiple of a and a does not equal 1 or n. You are given a int[] factors containing all the proper factors of some integer n. Return n.

Definition

Class:	InverseFactoring
Method:	getTheNumber
Parameters:	int[]
Returns:	int
Method signature:	int getTheNumber(int[] factors)
(be sure your method is public)

Constraints

-

factors will contain between 1 and 50 elements, inclusive.

-

factors will be a valid set of proper factors of some number n, where n is between 2 and 1,000,000, inclusive.

-

All elements in factors will be distinct.

Examples

0)

{2}

Returns: 4

The factors of 4 are 1, 2 and 4. Among them, only 2 is a proper factor.

1)

{4,2}

Returns: 8

The factors of 8 are 1, 2, 4, and 8. Among them, 2 and 4 are proper factors.

2)

{3,4,2,12,6,8}

Returns: 24

The proper factors of 24 are 2, 3, 4, 6, 8 and 12.

3)

{14,26456,2,28,13228,3307,7,23149,8,6614,46298,56,4,92596}

Returns: 185192

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EquilibriumPoints

Search, Simple Math

Used in:

SRM 421

Used as:

Division I Level One , Division II Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10104

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13512&pm=10104

Problem Statement

There are N points situated on a straight line. The i-th point is located at coordinate x[i] and has a mass of m[i]. The locat?on of each point is strongly fixed and cannot be changed by any forces. Coordinates of all points are distinct.

When another point P is added on the line and its position is not fixed, the point falls under the impact of gravitational forces from each of the given N points. Points located to the left of P force it to the left, and points located to the right of P force it to the right. When two points are located a distance of d apart and have masses m1 and m2, the value of gravitational force between them is F = G * m1 * m2 / d^2, where G is some positive constant.

Point P is said to be an equilibrium point if the vector sum of gravitational forces from all points on P equals zero. In other words, the sum of the values of gravitational forces between P and all the points located to the left of P must be the same as the sum of the values of gravitational forces between P and all the points located to the right of P.

It is known that there always exist exactly N-1 equilibrium points. Return a double[] containing their coordinates sorted in ascending order.

Definition

Class:	EquilibriumPoints
Method:	getPoints
Parameters:	int[], int[]
Returns:	double[]
Method signature:	double[] getPoints(int[] x, int[] m)
(be sure your method is public)

Notes

-

Each element of your return value must have an absolute or relative error less than 1e-9.

-

You don't need to know the mass of point P and the value of constant G to solve the problem.

Constraints

-

x will contain between 2 and 50 elements, inclusive.

-

m will contain the same number of elements as x.

-

Each element of x will be between 1 and 1000, inclusive.

-

Each element of m will be between 1 and 1000, inclusive.

-

x will be sorted in strictly ascending order.

Examples

0)

{1, 2}

{1, 1}

Returns: {1.5 }

When two points have the same mass, the equilibrium point is located exactly halfway between them.

1)

{1, 2}

{1, 1000}

Returns: {1.0306534300317156 }

When two points have distinct masses, the equlibrium point is located closer to the point with lesser mass.

2)

{1, 2, 3}

{1, 2, 1}

Returns: {1.4060952084922507, 2.5939047915077493 }

There are two equilibrium points located symmetrically with respect to the middle point of the input points.

3)

{2, 3, 5, 7}

{3, 2, 7, 5}

Returns: {2.532859446114924, 3.7271944335152813, 6.099953640852538 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MultiNumber

Math

Used in:

SRM 422

Used as:

Division II Level One

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10072

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13513&pm=10072

Problem Statement

A number is a multi number if its decimal representation can be split into two numbers, such that the product of all the digits in the first number is equal to the product of all the digits in the second number. For example, 1221 is a multi number because it can be split into 12 and 21, and 1 * 2 = 2 * 1. 1236 is also a multi number, but 1234 is not. Note that you can only split a number into two sequences of consecutive digits, where each sequence contains at least one digit. So, for example, we can only split 12345 in four different ways: 1-2345, 12-345, 123-45, 1234-5. You will be given an int number. Return "YES" if it is a multi number, or "NO" otherwise (all quotes for clarity).

Definition

Class:	MultiNumber
Method:	check
Parameters:	int
Returns:	String
Method signature:	String check(int number)
(be sure your method is public)

Constraints

-

number will be between 1 and 2,147,483,647, inclusive.

Examples

0)

Returns: "NO"

Note that all single-digit numbers are not multi numbers. That's because they cannot be split into two non-empty parts.

1)

Returns: "YES"

Example from the problem statement.

2)

Returns: "YES"

3)

Returns: "NO"

4)

42393338

Returns: "YES"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TwoLotteryGames

Math, Simple Math

Used in:

SRM 418

Used as:

Division I Level One , Division II Level Two

Writer:

ltdtl

Testers:

PabloGilberto , Olexiy , Mike Mirzayanov , ivan_metelsky , darnley

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10071

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13509&pm=10071

Problem Statement

Yesterday, when you were passing by the newsstand near your home, you saw an advertisement for lottery games. The advertisement said "Choose m different numbers between 1 and n, inclusive. We will also randomly pick m different numbers between 1 and n, inclusive, and if you have at least k numbers in common with us, you win!".

You want to know the probability of winning this lottery game. You are given three integers n, m, and k as described above. Return the probability of winning the game.

Definition

Class:	TwoLotteryGames
Method:	getHigherChanceGame
Parameters:	int, int, int
Returns:	double
Method signature:	double getHigherChanceGame(int n, int m, int k)
(be sure your method is public)

Notes

-

Your return must have relative or absolute error less than 1E-9.

Constraints

-

n will be between 2 and 8, inclusive.

-

m will be between 1 and n-1, inclusive.

-

k will be between 1 and m, inclusive.

Examples

0)

Returns: 1.0

Here you and the organizers will choose 2 numbers among 3. It will be 4 numbers in total, so at least 1 number in your and their sets will repeat for sure.

1)

Returns: 0.3333333333333333

Now you and the organizers will choose 1 number. These numbers will be the same with probability 1/3.

2)

Returns: 0.4642857142857143

3)

Returns: 0.7571428571428571

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

YearProgressbar

Simple Math, Simple Search, Iteration, String Manipulation, String Parsing

Used in:

SRM 420

Used as:

Division II Level Two

Writer:

misof

Testers:

PabloGilberto , Olexiy , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10058

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13511&pm=10058

Problem Statement

You are a big fan of New Year's Eve parties. The next one is not too far away, and you are already looking forward to it.

Then, one day, you wake up with a question: "Wait a moment, exactly how far away is it?"

To answer this question, you decided to implement a simple application: a year progress bar that will always show how much of the current year has already passed.

In this problem, your goal is to implement the most important part of this application: a function that gets a String currentDate, and returns the elapsed part of the year, as a percentage.

The variable currentDate will be of the form "Month DD, YYYY HH:MM" (quotes for clarity). Here, "Month" is the name of the current month, "YYYY" is a four-digit number representing the current year, and "DD", "HH", and "MM" are two-digit numbers (possibly with a leading zero) that represent the current day, hour and minute.

Definition

Class:	YearProgressbar
Method:	percentage
Parameters:	String
Returns:	double
Method signature:	double percentage(String currentDate)
(be sure your method is public)

Notes

- The months of a normal year have 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, and 31 days.

- In leap years, the second month (February) has 29 days.

- A year is a leap year if (it is divisible by 400) or (it is divisible by 4, but not by 100).

- Ignore location-dependent changes to time flow such as daylight saving time.

- Your return value must have a relative or absolute error less than 1e-9.

Constraints

- currentDate will be of the form given in the problem statement.

- Month will be one of January, February, March, April, May, June, July, August, September, October, November, and December.

- YYYY will be between 1800 and 2600, inclusive.

- DD will be between 01 and the number of days in the given month (in the given year), inclusive.

- HH will be between 00 and 23, inclusive.

- MM will be between 00 and 59, inclusive.

Examples

0)

"January 01, 2008 00:00"

Returns: 0.0

This is the exact beginning of the year 2008; no time has elapsed yet.

1)

"December 31, 2007 23:59"

Returns: 99.99980974124807

One last minute of the year 2007 is remaining.

2)

"July 02, 2007 12:00"

Returns: 50.0

The exact half of a normal year is at noon on the second day of July.

3)

"July 02, 2008 00:00"

Returns: 50.0

On a leap year, the exact half of the year is the midnight between the first and the second of July.

4)

"May 10, 1981 00:31"

Returns: 35.348363774733635

The date and time when the problem setter was born :-)

5)

"January 31, 1900 00:47"

Returns: 8.228120243531203

Note that 1900 is not a leap year.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CactusAutomorphisms

Graph Theory, Math

Used in:

SRM 419

Used as:

Division I Level Three

Writer:

andrewzta

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10055

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13510&pm=10055

Problem Statement

A vertex cactus is a connected graph such that each vertex belongs to at most one simple cycle. A simple cycle is a cycle that doesn't pass through any vertex more than once. For example, the graph in the picture below is a vertex cactus:

Given a graph G with vertices numbered from 1 to n, its automorphism is a permutation p[1], p[2], ..., p[n] such that there is an edge i-j in G if and only if there is an edge p[i]-p[j].

You are given an int n - the number of vertices in a vertex cactus. The vertices are numbered 1 to n. The edges of the graph are given to you in the String[] edges. Concatenate the elements of edges to get a comma-separated list of integer pairs. The integers in each pair are separated by a space. The pair "i j" (quotes for clarity) means that there is an edge between vertices i and j in the given graph. Return the number of automorphisms that exist for the given vertex cactus, modulo 10^9+3.

Definition

Class:	CactusAutomorphisms
Method:	count
Parameters:	int, String[]
Returns:	int
Method signature:	int count(int n, String[] edges)
(be sure your method is public)

Constraints

-

n will be between 1 and 200, inclusive.

-

edges will contain between 0 and 50 elements, inclusive.

-

Each element of edges will contain between 1 and 50 characters, inclusive.

-

When concatenated edges will contain a comma separated list of pairs of integers.

-

Each integer pair will contain two distinct integers between 1 and n, inclusive, separated by a space.

-

The given graph will be a vertex cactus - it will be connected and each vertex will belong to at most one simple cycle.

-

Every pair of vertices in the graph will be connected by at most one edge.

Examples

0)

{"1 2,1 3,1 4"}

Returns: 6

We can arbitrarily permute vertices 2, 3 and 4.

1)

{"1 2,2 3,3 4,4 1"}

Returns: 8

The permutation can either perform a circular shift of the vertices along the cycle, or flip the cycle, or both.

2)

{"1 2,2 3,3 1,4 5,5 6,6 4,1 4"}

Returns: 8

The permutation can swap triangles. Also, in each triangle, the permutation can swap the two vertices that are not incident to another triangle.

3)

{"1 2,2 3,3 4,2 4,1 5,1 10,5 10,5 6,6 7",
 ",7 8,7 16,7 17,7 9,6 9,10 18,18 ",
 "12,12 11,11 18,12 13,12 14,12 15"}

Returns: 144

This is the graph in the picture in the problem statement.

4)

{}

Returns: 1

5)

{"1 2,2 3,3 4,4 5,5 6,6 7,7 8,8 9,9 10,10 11,11 2,1 ",
 "12,12 13,13 14,14 15,15 16,16 17,17 18,18 19,19 20",
 ",20 21,21 12,1 22,22 23,23 24,24 25,25 26,26 27,27",
 " 28,28 29,29 30,30 31,31 22,1 32,32 33,32 34,34 35",
 ",35 36,36 32,1 37,37 38,37 39,39 40,40 41,41 37,1 ",
 "42,42 43,42 44,44 45,45 46,46 42,1 47,47 48,47 49,",
 "49 50,50 51,51 47,1 52,52 53,52 54,54 55,55 56,56 ",
 "52,1 57,57 58,57 59,59 60,60 61,61 57,1 62,62 63,6",
 "2 64,64 65,65 66,66 62,1 67,67 68,67 69,69 70,70 7",
 "1,71 67,1 72,72 73,72 74,74 75,75 76,76 72,1 77,77",
 " 78,78 79,79 80,80 81,81 77,1 82,82 83,83 84,84 85",
 ",85 86,86 82,1 87,87 88,88 89,89 90,90 91,91 87,1 ",
 "92,92 93,93 94,94 95,95 96,96 92,1 97,97 98,98 99,",
 "99 100,100 101,101 97,1 102,102 103,103 104,104 10",
 "5,105 106,106 102,1 107,107 108,108 109,109 110,11",
 "0 111,111 107,1 112,112 113,113 114,114 115,115 11",
 "6,116 112,1 117,117 118,118 119,119 120,120 121,12",
 "1 117,1 122,122 123,123 124,124 125,125 126,126 12",
 "2,1 127,127 128,128 129,129 130,130 131,131 127,1 ",
 "132,132 133,133 134,134 135,135 136,136 132,1 137,",
 "137 138,138 139,139 140,140 141,141 137,1 142,142 ",
 "143,142 144,142 145,1 146,146 147,146 148,146 149,",
 "1 150,150 151,150 152,150 153,1 154,154 155,154 15",
 "6,154 157,1 158,158 159,158 160,158 161,1 162,162 ",
 "163,162 164,162 165,1 166,166 167,167 168,166 169,",
 "166 170,166 171,166 172,1 173,173 174,174 175,173 ",
 "176,173 177,173 178,173 179,1 180,180 181,181 182,",
 "180 183,180 184,180 185,180 186,1 187,187 188,188 ",
 "189,187 190,187 191,187 192,187 193,1 194,194 195,",
 "195 196,194 197,194 198,194 199,194 200"}

Returns: 886565533

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StreetSales

Math, Simulation

Used in:

Marathon Match 64

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10034

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14354&pm=10034

Problem Statement

You work as a retail dealer at a certain district, and you sell goods of several types. Each morning you buy goods from the warehouse, set your prices for each type of goods and start your journey to the customers. You visit houses in the district at most once per day, and customers of each house you visit might want to buy some of your goods.

The preferences of customers of one house are described as a list of elements (GOODS_TYPE, STOP_PROB, MAX_PRICE), and their behavior is modeled as follows:

starting with the first element of the list, the customer decides whether he wants to buy goods of type GOODS_TYPE;
he stops without buying anything (not proceeding to next elements of the list) with probability STOP_PROB, otherwise he tries to buy one unit of goods of type GOODS_TYPE;
if you carry at least one unit of goods of this type and your price for it is not greater than MAX_PRICE, he buys it and stops, otherwise he proceeds to the next element of preferences;
if the list of preferences is over, nothing is bought.

The problem is, you don't know anything about the preferences of your customers. Your task is to maximize your average daily profit over the time of your work.

Implementation

Your code should implement the following methods:

init method is called once per test case to give you:
- the map of the district districtMap; 'X' marks a house and '.' marks a piece of street. You can walk on the streets, and you can trade at the house only if you stand at a street cell which is horizontally or vertically adjacent to it.
- warehouse prices per unit of goods of each type warehousePrices. You can figure out the number of distinct goods you can trade G as the number of elements in warehousePrices;
- the number of units of goods you can carry C;
- the number of steps you can perform per day S;
dayTrade method is called at the start of each day to get your decision about this day's actions. It gives you the results of the previous day as int[] visitedHouses. Element i*W+j of visitedHouses will describe the result of visiting the house in row i and column j and will be -2 if no trade was attempted (or there is no house at this cell), -1 if customers of this house bought nothing, or the index of the type of goods (0..G-1) they bought otherwise.

You must return a String[], formatted as follows:
- first G elements must be formatted as "QUANTITY PRICE" and give the (integer) quantity of units of each type of goods (in order) that you want to purchase from the warehouse for this day and the (integer) price you are setting for one unit of this type of goods for this day.
- the rest of the elements (at most S+1) must be formatted as "ROW COL" and describe the sequence of movements and trade actions. First element gives coordinates of the cell you want to start your day with. Next elements denote either moving to street cell (ROW, COL) or trading at house cell (ROW, COL). Each next cell must be adjacent to previous one. Trading at a house doesn't change your position. You can move only on street cells. You can trade at each house at most once.

Scoring

Your score for a test case will be your balance after 3000 days. Your overall score will be the sum of your individual scores, divided by the greatest score achieved by anyone for that test case. Negative individual scores are replaced with 0 when calculating the overall score.

Test Case Generation

The main part of generating test case is putting the houses on the map. This is done by choosing the type of housing - long parallel streets one house wide or small blocks of houses with houses along their borders. The chosen type of housing fills a random rectangular part of the area. The rest of the area is filled randomly with isolated houses, i.e., houses which don't have neighbors. Note that isolated houses are considered to be 'rich' when generating the customers' preferences, so their inhabitants get a bonus to MAX_PRICE.

For the details of test case generation process see visualizer source code.

Tools

A visualization tool is provided for offline testing.

Definition

Class:	StreetSales
Method:	dayTrade
Parameters:	int[]
Returns:	String[]
Method signature:	String[] dayTrade(int[] visitedHouses)

Method:	init
Parameters:	String[], int[], int, int
Returns:	int
Method signature:	int init(String[] districtMap, int[] warehousePrices, int C, int S)
(be sure your methods are public)

Notes

-

You can return any integer from init, it will be ignored.

-

Invalid parameters returned from dayTrade result in a score of 0.

-

The goods you trade are good for one day only, so if you haven't sold them the day you bought them, you can't sell them later.

-

Your starting balance is 0, and you can have negative balance during the simulation as well as at the end of the simulation (note that only positive balance will contribute to your score).

-

Your return must contain between G+1 and G+1+S elements.

-

The memory limit is 1024 MB and the time limit is 10 seconds per test case (which includes only time spent in your code). There is no explicit code size limit.

-

There are 10 example test cases and 100 full submission test cases.

Constraints

-

The numbers of rows H and columns W in the area will be between 20 and 100, inclusive (except for seed=1).

-

The number of types of goods G will be between 2 and 10, inclusive.

-

The warehouse price for each type of goods will be between 70 and 100, inclusive.

-

The number of elements in preferences of each house will be between 1 and G, inclusive.

-

GOODS_TYPEs of one house will be chosen as the first elements of a random permutation of 0..G-1, so they all will be distinct.

-

STOP_PROB will be between 0 and 10, inclusive (in percent).

-

MAX_PRICE will be calculated as warehouse price for this type of goods plus random bonus 10..25. Isolated houses will get an extra bonus of 5..15.

-

C will be approximately from 0.5 to 1.0 of the number of houses in the area.

-

S will be approximately from 0.125 to 0.25 of the number of cells in the area.

Examples

0)

"1"

Returns: "seed = 1
H = 15
W = 15
G = 10
C = 45
S = 34"

1)

"2"

Returns: "seed = 2
H = 74
W = 86
G = 7
C = 1031
S = 925"

2)

"3"

Returns: "seed = 3
H = 78
W = 74
G = 10
C = 545
S = 1379"

3)

"4"

Returns: "seed = 4
H = 41
W = 65
G = 10
C = 384
S = 603"

4)

"5"

Returns: "seed = 5
H = 43
W = 68
G = 8
C = 294
S = 468"

5)

"6"

Returns: "seed = 6
H = 71
W = 77
G = 9
C = 728
S = 829"

6)

"7"

Returns: "seed = 7
H = 80
W = 28
G = 10
C = 370
S = 364"

7)

"8"

Returns: "seed = 8
H = 24
W = 35
G = 7
C = 196
S = 168"

8)

"9"

Returns: "seed = 9
H = 84
W = 44
G = 4
C = 435
S = 816"

9)

"10"

Returns: "seed = 10
H = 87
W = 33
G = 2
C = 580
S = 546"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PrimeSoccer

Dynamic Programming, Math

Used in:

SRM 422

Used as:

Division I Level One , Division II Level Two

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10033

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13513&pm=10033

Problem Statement

You are watching a soccer match, and you wonder what the probability is that at least one of the two teams will score a prime number of goals. The game lasts 90 minutes, and to simplify the analysis, we will split the match into five-minute intervals. The first interval is the first five minutes, the second interval is the next five minutes, and so on. During each interval, there is a skillOfTeamA percent probability that team A will score a goal, and a skillOfTeamB percent probability that teamB will score a goal. Assume that each team will score at most one goal within each interval. Return the probability that at least one team will have a prime number as its final score.

Definition

Class:	PrimeSoccer
Method:	getProbability
Parameters:	int, int
Returns:	double
Method signature:	double getProbability(int skillOfTeamA, int skillOfTeamB)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

-

A prime number is a number that has exactly two divisors, 1 and itself. Note that 0 and 1 are not prime.

Constraints

-

skillOfTeamA will be between 0 and 100, inclusive.

-

skillOfTeamB will be between 0 and 100, inclusive.

Examples

0)

Returns: 0.5265618908306351

1)

Returns: 0.0

Both teams will score a goal in each interval, so the final result will be 18 to 18.

2)

Returns: 0.6772047168840167

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RoyalTreasurer

Simple Search, Iteration, Sorting

Used in:

SRM 433

Used as:

Division II Level One

Writer:

gojira_tc

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10007

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13695&pm=10007

Problem Statement

Once upon a time, there was a kingdom where math was always a big problem. When the post of the royal treasurer needed to be filled, applicants were presented with the following problem:

"We have two arrays of integers, A and B. A and B each contain exactly N elements. Let's define a function S over A and B:


	S = A₀*B₀ + ? + A_N-1*B_N-1

Rearrange the numbers in A in such a way that the value of S is as small as possible. You are not allowed to rearrange the numbers in B.?

The problem writers need a program to check the correctness of the applicants' answers. Given int[]s A and B, return the smallest possible value for S.

Definition

Class:	RoyalTreasurer
Method:	minimalArrangement
Parameters:	int[], int[]
Returns:	int
Method signature:	int minimalArrangement(int[] A, int[] B)
(be sure your method is public)

Constraints

-

A will contain between 1 and 50 elements, inclusive.

-

A and B will contain the same number of elements.

-

Each element of A will be between 0 and 100, inclusive.

-

Each element of B will be between 0 and 100, inclusive.

Examples

0)

{1,1,3}

{10,30,20}

Returns: 80

If you move the number 3 to the beginning of A, you get the minimal possible sum.

1)

{1,1,1,6,0}

{2,7,8,3,1}

Returns: 18

The best option would be to rearrange the numbers in A this way: {1,1,0,1,6}.

2)

{5,15,100,31,39,0,0,3,26}

{11,12,13,2,3,4,5,9,1}

Returns: 528

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MazeWandering

Graph Theory, Math, Recursion

Used in:

SRM 440

Used as:

Division I Level Two

Writer:

gojira_tc

Testers:

PabloGilberto , ivan_metelsky , Vasyl[alphacom]

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10005

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13748&pm=10005

Problem Statement

According to research conducted recently, listening to classical music increases one's mental abilities, while listening to metal decreases them. Now, yet another experiment is being conducted to try to prove or disprove this statement.

In this new experiment, a mouse is placed in a rectangular maze consisting of NxM squares. Each square either contains a wall or is empty. The maze is structured in such a way that for any two empty squares, there exists exactly one path between them. A path is a sequence of pairwise distinct empty squares such that every two consecutive squares are neighboring. Two squares are considered neighboring if they share a common edge.

One of the empty squares in the maze contains a piece of cheese, and the mouse's goal is to reach that square. The mouse can only move between neighboring empty squares. The mouse has been listening to metal for a week, so his mental abilities have become absolutely dull. Not only can he not smell the cheese, he can't even remember where he was heading a moment ago, so he is just wandering randomly. More precisely, from each square, the mouse will randomly choose one of the neighboring empty squares and move there. The probability of choosing each of the squares is equal. Each move takes one second.

You are given a String[] maze representing the maze. It contains N elements, each containing M characters. Empty squares are denoted by '.', walls are denoted by uppercase 'X', and the square containing the cheese is denoted by '*'. For each empty square, calculate the expected time required for the mouse to reach the cheese starting from that square. Return the arithmetical mean of all the expected times.

Definition

Class:	MazeWandering
Method:	expectedTime
Parameters:	String[]
Returns:	double
Method signature:	double expectedTime(String[] maze)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

maze will contain between 1 and 50 elements, inclusive.

-

Each element of maze will contain between 1 and 50 characters, inclusive.

-

Elements of maze will be of the same length.

-

maze will contain only '.', 'X', or '*' characters.

-

There will be exactly one '*' character in maze.

-

For every pair of empty squares in the maze, there will exist exactly one path between them.

Examples

0)

{"*",
 "."}

Returns: 0.5

The mouse will need 0 seconds to find the cheese if it is put in the cheese-square and 1 second otherwise.

1)

{"*.."}

Returns: 2.3333333333333335

The expectations for each square are 0.0, 3.0 and 4.0.

2)

{"...",
 "X*X",
 "..."}

Returns: 4.857142857142857

3)

{".*.",
 ".XX",
 "..."}

Returns: 13.714285714285714

4)

{"*........",
 "XXX.XXXX.",
 ".XX.X....",
 ".....XX.X"}

Returns: 167.2608695652174

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Polygons2

Dynamic Programming, Simple Math

Used in:

SRM 443

Used as:

Division II Level Three

Writer:

gojira_tc

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9995

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13751&pm=9995

Problem Statement

You are given N line segments numbered 1 to N. The lengths of these segments are given in the int[] segments. Compose a convex K-sided polygon, where each side is one of the given segments. Each segment can only be used once in the polygon.

Return the number of different polygons you can compose. Two polygons are considered different if there exists a segment i such that one of the polygons contains segment i but the other polygon does not.

Definition

Class:	Polygons2
Method:	number
Parameters:	int[], int
Returns:	long
Method signature:	long number(int[] segments, int K)
(be sure your method is public)

Notes

-

A convex polygon can be constructed from a set of segments if the length of each segment from this set is strictly less than the sum of lengths of the remaining segments.

Constraints

-

segments will contain between 1 and 50 elements, inclusive.

-

K will be between 3 and 10, inclusive.

-

Each element of segments will be between 1 and 50,000, inclusive.

Examples

0)

{1,1,1,1}

Returns: 4

A nondegenerate triangle can be built using any triple from the given segments.

1)

{2,3,4,5}

Returns: 3

Any triple except {2,3,5} will do.

2)

{4,4,4,2,2,2}

Returns: 11

You can a make nondegenerate triangle using three segments of length 2, or three segments of length 4, or any two segments of length 4 with any segment of length 2.

3)

{10,1,4,9,20}

Returns: 2

One can build a convex quadrangle using segments {10,1,4,9} or {10,4,9,20}.

4)

{3310,1660,211,1260,160,213,884,539,17212,2025,105,120,5510}

Returns: 532

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LocateTreasure

Dynamic Programming, Math

Used in:

SRM 427

Used as:

Division I Level Two

Writer:

rasto6sk

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9984

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13518&pm=9984

Problem Statement

First of all we define a function dig for all nonnegative integers:

dig(x) := x                          if 0 <= x <= 9
dig(x) := dig(sum of digits of x)    if x >= 10

For example: dig(49) = dig(13) = dig(4) = 4.

Your crew of treasure hunters have recently found a very old map with instructions on how to find the treasure of an old civilization. There is a variable named Gold number, and it is initially assigned a value of 1. You are currently standing at position (0, 0), facing north.

Repeat the following instructions K times:

1. Take dig(Gold number) steps forward, and then turn 90 degrees right.

2. Multiply Gold number by multi.

Each step forward moves you one unit in your current direction. Moving north changes your location by (0, 1), south changes your location by (0, -1), west changes your location by (-1, 0) and east changes your location by (1, 0). After you perform all the instructions, you can start digging. Return the coordinates (X, Y) of your final location as a String in the form "X Y" (quotes for clarity), where X and Y contain no extra leading zeroes.

Definition

Class:	LocateTreasure
Method:	location
Parameters:	int, int
Returns:	String
Method signature:	String location(int K, int multi)
(be sure your method is public)

Constraints

-

K will be between 1 and 10^9, inclusive.

-

multi will be between 1 and 1000, inclusive.

Examples

0)

Returns: "-6 4"

You will go 1 step north, 2 steps east, 4 steps south, 8 steps west and 7 steps north.

1)

Returns: "1 0"

You will do exactly 1 step in every iteration.

2)

Returns: "9 1"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheBeautifulBoard

Math

Used in:

SRM 423

Used as:

Division I Level Three

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , bmerry , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9975

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13514&pm=9975

Problem Statement

You have a n x n board and several checkers of different colors. The i-th element of checkers is the number of checkers you have of color i. You want to place all of the checkers on the board in such a way that no cell contains more than one checker.

Return the number of different possible placements modulo 1234567891. Two placements are equal if you can get one from the other by rotating the board. Note that checkers of the same color are indistinguishable. If you have more checkers than the number of cells on the board, there are no possible placements, so you should return 0.

Definition

Class:	TheBeautifulBoard
Method:	count
Parameters:	int, int[]
Returns:	int
Method signature:	int count(int n, int[] checkers)
(be sure your method is public)

Notes

-

You are not allowed to flip the board.

Constraints

-

n will be between 1 and 100,000, inclusive.

-

checkers will contain between 1 and 50 elements, inclusive.

-

Each element of checkers will be between 1 and 100,000, inclusive.

Examples

0)

{1}

Returns: 1

It's simple.

1)

{1, 2}

Returns: 3

There are only 3 different placements. Do not forget that you can't flip the board.

2)

{1, 1}

Returns: 18

3)

{4, 2, 1, 3}

Returns: 0

Too many checkers.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheSimpleGame

Simple Math

Used in:

SRM 423

Used as:

Division II Level One

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , bmerry , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9966

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13514&pm=9966

Problem Statement

You have a n x n board and several checkers placed on it. The i-th checker is in the cell at row x[i], column y[i]. All coordinates are 1-based. There can be more than one checker in the same cell. A move consists of taking one checker and moving it one cell up, down, left or right.

You want to put each checker in one of the four corners of the board. Return the minimum number of moves necessary to achieve the goal.

Definition

Class:	TheSimpleGame
Method:	count
Parameters:	int, int[], int[]
Returns:	int
Method signature:	int count(int n, int[] x, int[] y)
(be sure your method is public)

Constraints

-

n will be between 1 and 100, inclusive.

-

x will contain between 1 and 50 elements, inclusive.

-

y will contain the same number of elements as x.

-

Each element of x will be between 1 and n, inclusive.

-

Each element of y will be between 1 and n, inclusive.

Examples

0)

{2}

{3}

Returns: 2

You need two moves to put the only checker to cell (1, 4).

1)

{2, 2, 1, 3}

{2, 2, 3, 1}

Returns: 4

For the first two checkers you can choose any of the four corners.

2)

{7, 1, 7, 7, 1, 7, 1}

{7, 1, 1, 1, 1, 7, 7}

Returns: 0

All checkers are already in the corners.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ChangeOMatic

Dynamic Programming, Greedy, Simple Math

Used in:

SRM 420

Used as:

Division I Level Three

Writer:

misof

Testers:

PabloGilberto , Olexiy , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9963

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13511&pm=9963

Problem Statement

The Change-O-Matic is a deterministic machine with a single goal: to provide change. That is, you throw in a banknote or a coin, and the machine throws out a bunch of smaller coins with the same total value.

More precisely, the Change-O-Matic operates as follows:

The machine contains several large stacks of coins. The values of these coins are given as a int[] outputValues. For the purpose of this problem we may assume that the machine contains an infinite number of coins of each of these values. One of the available values is always 1.

The customer may throw in any coin or banknote with value greater than 1. The machine will output a set of at least two coins with the same total value. If there are multiple ways to satisfy this requirement, the machine prefers the one where the total number of output coins is minimized. If there are still multiple ways, the machine prefers the one that is lexicographically maximal (see Notes for a precise definition).

You have a single banknote, and its value is given as a long inputValue. You would like to change it into coins of value 1 each. Return the number of times you have to throw something into the machine.

Definition

Class:	ChangeOMatic
Method:	howManyRounds
Parameters:	int[], long
Returns:	long
Method signature:	long howManyRounds(int[] outputValues, long inputValue)
(be sure your method is public)

Notes

-

Let A=(a₁,...,a_N) and B=(b₁,...,b_N) be two different but equally large sets of coins, with a₁ >= a₂ >= ... >= a_N and b₁ >= b₂ >= ... >= b_N. Let x be the smallest index such that a_x != b_x. If a_x > b_x, we say that the set A is lexicographically larger than the set B.

-

Given a collection of different but equally large sets of coins, the lexicographically maximal set is the one that is lexicographically larger than each of the other sets. (Note that there is always exactly one such set.)

Constraints

-

outputValues will contain between 1 and 50 elements, inclusive.

-

outputValues will be sorted in strictly ascending order. That is, for each i, outputValues[i] < outputValues[i+1].

-

Each element of outputValues will be between 1 and 1,000, inclusive.

-

Element 0 of outputValues will be equal to 1.

-

inputValue will be between 2 and 10^15, inclusive.

Examples

0)

{1,5,10}

Returns: 7

The process of changing your money may look as follows:

You insert:    You get:      You then have:
21             10+10+1       10+10+1
10             5+5           10+5+5+1
5              1+1+1+1+1     10+5+1+1+1+1+1+1
10             5+5           5+5+5+1+1+1+1+1+1
5              1+1+1+1+1     5+5+(eleven times 1)
5              1+1+1+1+1     5+(sixteen times 1)
5              1+1+1+1+1     twenty-one coins worth 1 each

1)

{1,33,90,91,92,93,94,95,96,97,98}

Returns: 12

In each step, the machine minimizes the number of coins it throws out, not the number of steps you need to accomplish your task. In the first step it will output a coin worth 98 and a coin worth 1.

2)

{1,30,60}

Returns: 2

The value of the banknote may be less than the values of some coin types.

3)

{1,30,60,90}

Returns: 3

The value of the banknote may even be equal to the value of some coin type. Note that for any input the machine must always output at least two coins. Therefore if you throw in the banknote worth 60, you will get two coins worth 30 each.

4)

{1,8,9,11,12,100}

Returns: 37

In the first step the machine would output 100+12+8. (The combination 100+11+9 has the same number of coins, but 100+12+8 is lexicographically larger.)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

VeryInterestingMovie

Simple Math

Used in:

TCHS SRM 55

Used as:

Division I Level One

Writer:

Gluk

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9955

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13524&pm=9955

Problem Statement

A teacher wants to take his students to see a movie at the theater. The only problem is that the students talk a lot, so the teacher doesn't want any two students in the same row to sit in adjacent seats.

You are given a String[] seats which contains information about which seats are available for purchase. Character j of element i of seats is 'Y' if the j-th seat in row i is available, or 'N' otherwise. Return the maximum number of students who can watch the movie.

Definition

Class:	VeryInterestingMovie
Method:	maximumPupils
Parameters:	String[]
Returns:	int
Method signature:	int maximumPupils(String[] seats)
(be sure your method is public)

Constraints

-

seats will contain between 1 and 50 elements, inclusive.

-

Each element of seats will contain between 1 and 50 characters, inclusive.

-

All elements of seats will be of equal length.

-

Each element of seats will contain only 'Y' or 'N' characters.

Examples

0)

{"YY","YY","YY"}

Returns: 3

Only one student can sit in each row.

1)

{"NNNNN","NNNNN","NNNNN","NNNNN","NNNNN"}

Returns: 0

No places are available.

2)

{"YYYYYYN","YYYYNYY","NYYYNYY","NYYYYYN","YYYYYYN","NYYNYNY","YYYYYYY"}

Returns: 22

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TripleJump

Math

Used in:

SRM 417

Used as:

Division II Level Three

Writer:

Pawa

Testers:

PabloGilberto , Olexiy , ivan_metelsky , Xixas

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9944

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13508&pm=9944

Problem Statement

The triple jump works as follows. The athlete runs down a runway until he reaches a designated mark. He then makes three consecutive jumps and lands in a sand-filled box. The length of the triple jump is the sum of the lengths of the three consecutive jumps. The winner of the competition is the athlete with the longest triple jump.

You are taking part in the competition and jumping after all your opponents. Since you are the last to jump, you already know all your opponents' results. They are given in the int[] opponents, where opponents[i] is the length of the i-th opponent's triple jump in centimeters.

You have already made the first of your three jumps, and it was first centimeters long. You ask yourself a question: "What is the probability that I will take first place? Second place? And all the other places?". You know that each of your two remaining jumps will be between lower and upper centimeters, inclusive, in length. The lengths will not necessarily be integers, and all possible lengths between lower and upper will be equally likely. Return a double[] containing exactly N + 1 elements (N is the number of opponents you have) such that the i-th element (0-indexed) is the probability of you taking (i+1)-th place. Note that your place number is equal to one plus the number of opponents who had longer triple jumps than you.

Definition

Class:	TripleJump
Method:	getProbabilities
Parameters:	int, int, int, int[]
Returns:	double[]
Method signature:	double[] getProbabilities(int lower, int upper, int first, int[] opponents)
(be sure your method is public)

Notes

-

Each element of your return value must have an absolute or relative error less than 1e-9.

Constraints

-

lower will be between 1 and 1000, inclusive.

-

upper will be between lower and 1000, inclusive.

-

first will be between lower and upper, inclusive.

-

opponents will contain between 1 and 50 elements, inclusive.

-

Each element of opponents will be between 1 and 3000, inclusive.

Examples

0)

{1,2,3,4}

Returns: {0.5, 0.5, 0.0, 0.0, 0.0 }

Your first jump has length 1, and the two subsequent jumps - any lengths between 1 and 2. So your triple jump will have a total length between 3 and 5. This guarantees you at least the second place with an equal chance of getting the first one.

1)

{9,9,19,19,19}

Returns: {0.0, 0.0, 0.0, 1.0, 0.0, 0.0 }

Now the length of your triple jump will be between 11 and 19, and thus you are inevitably fourth. Note that the probability to have a triple jump with length exactly 19 in this case is zero.

2)

{5}

Returns: {0.9753086419753086, 0.024691358024691357 }

3)

{1,2,3,5,10,11,12,19}

Returns: 
{0.22222222222222227, 0.6234567901234567, 0.05555555555555558, 0.043209876543209846, 0.05555555555555558, 0.0, 0.0, 0.0, 0.0 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CubeNets

Math, Simulation

Used in:

SRM 417

Used as:

Division I Level Two

Writer:

Pawa

Testers:

PabloGilberto , Olexiy , ivan_metelsky , Xixas

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9942

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13508&pm=9942

Problem Statement

In geometry a cube net is an arrangement of identical edge-joined squares in the plane which can be folded (along the edges) to become the faces of a cube.

In this problem you need to check if the given figure is a cube net. The given figure will be a union of six identical squares lying in the same plane and will be given to you as a String[] figure. Each element of figure will consist of '.' (dot) and '#' (sharp) characters only. A sharp represents one of the six squares, whereas a dot represents an empty space. Return "YES" if figure represents a cube net, or "NO" otherwise (all quotes for clarity).

Definition

Class:	CubeNets
Method:	isCubeNet
Parameters:	String[]
Returns:	String
Method signature:	String isCubeNet(String[] figure)
(be sure your method is public)

Constraints

-

figure will contain between 1 and 6 elements, inclusive.

-

Each element of figure will contain between 1 and 6 characters, inclusive.

-

Each element of figure will contain '.' (dot) and '#' (sharp) characters only.

-

All elements of figure will contain the same number of characters.

-

There will be exactly 6 '#' (sharp) characters among all the elements of figure.

Examples

0)

{"..#.",
 "####",
 "..#."}

Returns: "YES"

Here you can first fold across all the vertical edges to make the middle four squares become the down, right, up and left faces of the cube-to-be. One then finishes off the construction by folding across the remaining two edges to make the other two squares become the front and back faces of the cube.

1)

{"###",
 "###"}

Returns: "NO"

This is not a cube net.

2)

{"..#.",
"####",
".#.."}

Returns: "YES"

3)

{"##..",
 ".##.",
 "..##"}

Returns: "YES"

4)

{"####",
 "...#",
 "...#"}

Returns: "NO"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BankLoans

Math, String Parsing

Used in:

TCHS09 Round 1

Used as:

Division I Level Two

Writer:

Nickolas

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9929

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13728&pm=9929

Problem Statement

You are working as an analyst in the credit department of a bank. The bank has just issued several loans, each to be repaid with interest. Unfortunately, some debtors are unreliable and will not pay any money back to the bank. Your task is to estimate the expected profit the bank will get from this set of loans.

You are given a String[] loans, each element of which represents a single loan and is formatted as "AMOUNT INTEREST CLASS" (quotes for clarity only). AMOUNT is the base amount of the loan, INTEREST is the amount of interest the debtor must pay, and CLASS is the name of the debtor's risk class. You are also given a String[] riskClasses, each element of which represents a single risk class and is formatted as "CLASS PROB" (quotes for clarity only). CLASS is the name of the risk class, and PROB is the percent probability of a debtor in that risk class turning out to be unreliable.

An unreliable debtor will pay no money back to the bank. A reliable debtor will pay back the entire amount of the loan plus all of the interest. The bank's profit is the total amount of money (including interest) the bank will get back from its debtors minus the total amount of money it loaned out. Return the expected profit for the described set of loans.

Definition

Class:	BankLoans
Method:	expectedProfit
Parameters:	String[], String[]
Returns:	double
Method signature:	double expectedProfit(String[] loans, String[] riskClasses)
(be sure your method is public)

Notes

-

For the purposes of this problem we assume that debtors make their decisions on returning the loans independently.

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

loans will contain between 1 and 50 elements, inclusive.

-

Each element of loans will contain between 8 and 28 characters, inclusive.

-

Each element of loans will be formatted as "AMOUNT INTEREST CLASS" (quotes for clarity only), where AMOUNT is an integer between 100 and 100000, inclusive, without leading zeroes, INTEREST is an integer between 10 and 20000, inclusive, without leading zeroes, and CLASS is a non-empty sequence of lowercase letters ('a'-'z').

-

riskClasses will contain between 1 and 50 elements, inclusive.

-

Each element of riskClasses will contain between 3 and 19 characters, inclusive.

-

Each element of riskClasses will be formatted as "CLASS PROB" (quotes for clarity only), where CLASS is a non-empty sequence of lowercase letters ('a'-'z'), and PROB is an integer between 0 and 100, inclusive, without extra leading zeroes.

-

Each CLASS will contain between 1 and 15 characters, inclusive.

-

All CLASSes in riskClasses will be distinct.

-

Each CLASS in loans will be described in riskClasses.

Examples

0)

{"1000 100 a", "500 80 b", "600 120 c"}

{"a 0", "b 5", "c 10"}

Returns: 199.0

The profit from the first loan is 100, since the debitor is reliable with probability 1.0. For the second loan the bank receives a profit of 80 with probability 0.95 and loses the initial amount of 500 with probability 0.05, so the expected profit is 80*0.95-500*0.05=51. For the third loan the expected profit is 48.

1)

{"1000 150 beta", "1500 200 beta", "2000 250 beta"}

{"alpha 0", "beta 10", "gamma 20"}

Returns: 90.0

It is possible to have no debtors of a certain risk class.

2)

{"1000 400 hopeless", "1000 400 bad", "1000 400 weak"}

{"weak 50", "bad 75", "hopeless 100"}

Returns: -1950.0

The expected profit can be negative despite a high interest rate.

3)

{"500 55 ok", "1500 170 fine"}

{"ok 10", "fine 10"}

Returns: 2.5

4)

{"8132 19387 s",
 "20219 1791 iarkhyvewuqo",
 "19219 4464 s",
 "6947 18098 s",
 "28985 7338 iarkhyvewuqo",
 "21878 7894 iarkhyvewuqo",
 "21495 8307 s"}

{"s 13","iarkhyvewuqo 16"}

Returns: 39395.83

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TournamentWinner

Math, Simulation

Used in:

TCHS09 Round 2

Used as:

Division I Level Two

Writer:

Nickolas

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9928

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13729&pm=9928

Problem Statement

You are running a local tournament with 8 competitors. The tournament will consist of 3 rounds and will be organized as follows.

In round 1 game i is played between competitors 2*i and 2*i+1 (0<=i<=3). 4 winning competitors advance to round 2.

In round 2 game i is played between the winners of games 2*i and 2*i+1 (0<=i<=1). 2 winning competitors advance to round 3.

Finally, the winners of round 2 games play one game in round 3 to determine the winner of the tournament.

You are given a int[] P describing the percent probabilities of each competitor winning a game against another competitor. The first 7 elements of P are the probabilities of competitor 0 winning a game against competitors 1 through 7, the next 6 elements are the probabilities of competitor 1 winning a game against competitors 2 through 7, etc.

Return a double[] containing exactly 8 elements, where the i-th element is the probability of competitor i winning the tournament.

Definition

Class:	TournamentWinner
Method:	winningProbabilities
Parameters:	int[]
Returns:	double[]
Method signature:	double[] winningProbabilities(int[] P)
(be sure your method is public)

Notes

-

The games played in the tournament will not end in a tie.

-

Each element of your return must have an absolute or relative error less than 1e-9.

Constraints

-

P will contain exactly 28 elements.

-

Each element of P will be between 0 and 100, inclusive.

Examples

0)

{5,   0,  10,  15,  20,  25,  30,
      0,  35,  40,  45,  50,  55,
         100, 100, 100, 100, 100,
               60,  65,  70,  75,
                    80,  85,  90,
                         95,  50,
                              50}

Returns: {0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0 }

Competitor 2 wins a game against any other competitor with probability 1.0, so he will win the tournament, leaving no chances to other competitors.

1)

{100,  25,   0,  25,  25,  25,  25,
       25,  25,  25,  25,  25,  25,
             0,  25,  25,  25,  25,
                 50,  25,  25,  25,
                     100,  25, 100,
                           25,  25,
                                 0}

Returns: {0.0, 0.0, 0.0, 0.5, 0.5, 0.0, 0.0, 0.0 }

In round 1, players 0, 3, 4 and 7 win against players 1, 2, 5 and 6, respectively. In round 2, 3 wins against 0 and 4 wins against 7. Finally, both 3 and 4 have a 50% chance to win against the opponent in round 3 and to win the tourney.

2)

{50,  50,  50,  50,  50,  50,  50,
      50,  50,  50,  50,  50,  50,
           50,  50,  50,  50,  50,
                50,  50,  50,  50,
                     50,  50,  50,
                          50,  50,
                               50}

Returns: {0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125 }

All competitors have equal chances.

3)

{100, 50,  50,  50,  50,  50,  50,
       0,  50,  50,  50,  50,  50,
          100,  50,  50,  50,  50,
                 0,  50,  50,  50,
                    100,  50,  50,
                           0,  50,
                              100}

Returns: {0.25, 0.0, 0.25, 0.0, 0.25, 0.0, 0.25, 0.0 }

Competitors 0, 2, 4 and 6 win their games in round 1 and have equal chances in later rounds.

4)

{ 50, 50,  50,  50,  50,  50,  50,
      50,  50,  50,  50,  50,  50,
           50,  50,  50,  50,  50,
                50,  50,  50,  50,
                    100, 100, 100,
                          10,  20,
                               30}

Returns: {0.125, 0.125, 0.125, 0.125, 0.5, 0.0, 0.0, 0.0 }

Competitor 4 will get to round 3 for sure, while competitors 0, 1, 2 and 3 have equal chances to get to round 3.

5)

{  1,  2,   4,   7,  11,  16,  22,
       3,   5,   8,  12,  17,  23,
            6,   9,  13,  18,  24,
                10,  14,  19,  25,
                     15,  20,  26,
                          21,  27,
                               28}

Returns: 
{6.88919608E-5, 0.009061234459199999, 0.011498979459599998, 0.1853675541204, 0.0328889066112, 0.18542493028680002, 0.17985791390280004, 0.3958315891991999 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ReversedSum

Simple Math

Used in:

SRM 417

Used as:

Division II Level One

Writer:

Pawa

Testers:

PabloGilberto , Olexiy , ivan_metelsky , Xixas

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9925

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13508&pm=9925

Problem Statement

For a given positive integer X we can obtain the reversed positive integer Rev(X) by reversing the order of X's digits and removing leading zeroes. For example, if X = 123 then Rev(X) = 321; and if X = 100, then Rev(X) = 1.

You will be given two positive integers x and y. Return their reversed sum, which is defined as Rev(Rev(x) + Rev(y)).

Definition

Class:	ReversedSum
Method:	getReversedSum
Parameters:	int, int
Returns:	int
Method signature:	int getReversedSum(int x, int y)
(be sure your method is public)

Constraints

-

x and y will each be between 1 and 1000, inclusive.

Examples

0)

Returns: 223

As mentioned in the problem statement, Rev(123) = 321 and Rev(100) = 1. So, the reversed sum is equal to Rev(322) = 223.

1)

Returns: 222

2)

Returns: 1

3)

Returns: 2

4)

Returns: 1461

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WalkingDistance

Geometry, Graph Theory, Math

Used in:

SRM 417

Used as:

Division I Level Three

Writer:

Pawa

Testers:

PabloGilberto , Olexiy , ivan_metelsky , Xixas

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9924

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13508&pm=9924

Problem Statement

A map of the city consists of a number of streets connecting several junctions. All the streets are straight line segments connecting two junctions, organized in such a way that starting at any junction and walking along the streets one can reach any other junction. The walking distance between two points (each either a junction or some intermediate point of a street) in the city is the shortest path from the first point to the second, if you are allowed to walk only along the streets. The length of the street is the Cartesian distance between its ends. Streets never intersect outside the junctions. Tunnels and overpasses are used whenever necessary to achieve this (see example 1 for further clarification).

Given a map of the city, your goal is to find the maximal walking distance among any two points in the city. The map of the city is provided as follows. You are given two int[]s x and y, each of the same length N. These two int[]s represent N junctions with Cartesian coordinates (x[i], y[i]) for i = 0..N-1. You are also given a String[] streets, where the j-th element of streets[i] is 'Y' if the junctions i and j are connected by a street, and 'N' otherwise.

Definition

Class:	WalkingDistance
Method:	getLongestShortest
Parameters:	int[], int[], String[]
Returns:	double
Method signature:	double getLongestShortest(int[] x, int[] y, String[] streets)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

x and y and streets will each contain between 2 and 50 elements, inclusive.

-

x, y and streets will have the same number of elements.

-

Each element of x and y will be between -1000 and 1000, inclusive.

-

Each element of streets will contain exactly n characters, where n is the number of elements in streets.

-

Each element of streets will contain only 'N' and 'Y' characters.

-

The i-th character of the i-th element of streets will always be 'N'.

-

The i-th character of the j-th element of streets will always be equal to the j-th character of the i-th element of streets.

-

All junctions represented by x and y will be distinct.

-

There will be a path between every pair of junctions.

Examples

0)

{0,1}

{0,1}

{"NY","YN"}

Returns: 1.4142135623730951

There are just two junctions conntected by a road. So the answer is the length of the street, which is the square root of 2.

1)

{0,2,2,0}

{0,0,2,2}

{"NNYY","NNYY","YYNN","YYNN"}

Returns: 4.82842712474619

Both points on which this maximal shortest distance is achieved have coordinates (1, 1), but they are located on different streets.

2)

{0,1,0}

{0,0,1}

{"NYY","YNY", "YYN"}

Returns: 1.7071067811865475

The three junctions form a right isosceles triangle. Two points for which the maximal walking distance is achieved are (0,0) and (1/2, 1/2).

3)

{0, 1, 2}

{0, 1, 2}

{"NYY", "YNN", "YNN"}

Returns: 4.242640687119286

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BitwiseEquations

Simple Math

Used in:

SRM 430

Used as:

Division I Level One , Division II Level Two

Writer:

Janq

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9921

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13521&pm=9921

Problem Statement

You are given two positive integers x and k. Return the k-th smallest positive integer y (where k is 1-based) for which the following equation holds:

x + y = x | y

where '|' denotes the bitwise OR operator.

Definition

Class:	BitwiseEquations
Method:	kthPlusOrSolution
Parameters:	int, int
Returns:	long
Method signature:	long kthPlusOrSolution(int x, int k)
(be sure your method is public)

Constraints

-

x will be between 1 and 2,000,000,000, inclusive.

-

k will be between 1 and 2,000,000,000, inclusive.

Examples

0)

Returns: 2

The first positive integer for which the equation holds is 2. You can check that 5+2=7 as well as 5|2=7. Both plus and bitwise OR look like the following:

 101
+ 10
 ---
 111

1)

Returns: 18

The fifth number for which the equation 5 + y = 5 | y holds is 18. The first four solutions are 2,8,10,16. The binary sum for 18 looks like the following:

   101
+10010
 -----
 10111

2)

Returns: 5

The third solution is 5. The first two solutions are 1 and 4.

3)

1000000000

Returns: 2000000000

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PrettyPrintingProduct

Math

Used in:

SRM 420

Used as:

Division II Level Three

Writer:

misof

Testers:

PabloGilberto , Olexiy , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9916

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13511&pm=9916

Problem Statement

You will be given two positive ints A and B.

Let C be the product of all integers between A and B, inclusive.

The number C has a unique representation of the form C = D * 10^E, where D and E are non-negative integers and the last digit of D is non-zero.

Write a method that will return the value of C formatted as a String of the form "D * 10^E" (quotes for clarity only). Substitute the actual values of D and E into the output. If D has more than 10 digits, only output the first five and the last five digits of D, and separate them by three periods.

Definition

Class:	PrettyPrintingProduct
Method:	prettyPrint
Parameters:	int, int
Returns:	String
Method signature:	String prettyPrint(int A, int B)
(be sure your method is public)

Notes

- The purpose of the last constraint is to disallow inputs where precision problems could arise.

Constraints

- A will be between 1 and 1,000,000, inclusive.

- B will be between A and 1,000,000, inclusive.

- If C has more than 10 digits, then the sixth most significant digit of C will be neither 0 nor 9.

Examples

0)

Returns: "36288 * 10^2"

1 * 2 * ... * 10 = 3628800 = 36288 * 10^2

1)

Returns: "7 * 10^0"

The product of all numbers between 7 and 7, inclusive, is obviously 7.

2)

Returns: "2038974024 * 10^0"

For this input D has 10 digits.

3)

Returns: "28952...24024 * 10^0"

For this input D has 11 digits. Note that we output three dots even if just one digit is missing in the output.

4)

Returns: "2923450236 * 10^1"

The actual value of C is larger than in the previous example. However, C ends in a zero and therefore D only has 10 digits.

5)

Returns: "14806...28928 * 10^1163"

6)

Returns: "12164...08832 * 10^3"

Note that the last five digits of D can start with a zero.

7)

Returns: "32382...26624 * 10^4"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RedIsGood

Dynamic Programming, Math

Used in:

SRM 420

Used as:

Division I Level Two

Writer:

misof

Testers:

PabloGilberto , Olexiy , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9915

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13511&pm=9915

Problem Statement

You have a deck that contains R red and B black cards.

You are playing the following game: You shuffle the deck, and then begin dealing the cards one by one. For each red card you flip you get a dollar, and for each black card you flip you have to pay a dollar. At any moment (including the beginning of the game) you are allowed to stop and keep the money you have.

Write a method that will take the ints R and B, and return the expected amount you will gain if you play this game optimally.

Definition

Class:	RedIsGood
Method:	getProfit
Parameters:	int, int
Returns:	double
Method signature:	double getProfit(int R, int B)
(be sure your method is public)

Notes

-

During the game, your balance may be negative.

-

We assume that each permutation of the cards in the deck is equally likely.

-

Your return value must have a relative or absolute error less than 1e-9.

Constraints

-

R will be between 0 and 5,000, inclusive.

-

B will be between 0 and 5,000, inclusive.

Examples

0)

Returns: 0.0

If all cards are black, the best strategy is not to play at all.

1)

Returns: 4.0

If all cards are red, the best strategy is to flip them all.

2)

Returns: 4.166666666666667

The strategy "flip all cards" is guaranteed to earn $4. However, we can do better. If we flipped 5 cards and all of them are red, it makes no sense to flip the final, black card. Therefore if we play optimally the expected gain is more than $4.

3)

Returns: 0.6666666666666666

An optimal strategy for this case: Flip the first card. If it is red, stop. If it is black, flip the second and the third card. If both are red, stop, otherwise flip the fourth card.

4)

Returns: 8.324175824175823

This is a game I would surely like to play often.

5)

Returns: 1.075642825339958

Surprisingly, sometimes there is a good strategy even if the number of red cards is smaller than the number of black cards.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FloorIndicator

Simple Math, Simple Search, Iteration, String Parsing

Used in:

SRM 421

Used as:

Division II Level Three

Writer:

Alexus

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9871

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13512&pm=9871

Problem Statement

Imagine a skyscraper with 10^N floors, numbered 0 to 10^N-1. The floor indicator in the elevator shows the floor number using exactly N digits, padding it with leading zeroes if necessary. Each digit is shown as a 5x3 field of small lamps, some of which are lit and some of which are unlit. Here is a representation of all the digits from 0 to 9 ('#' represents lit lamps and '.' represents unlit lamps) :

###...#.###.###.#.#.###.###.###.###.### #.#...#...#...#.#.#.#...#.....#.#.#.#.# #.#...#.###.###.###.###.###...#.###.### #.#...#.#.....#...#...#.#.#...#.#.#...# ###...#.###.###...#.###.###...#.###.###

Here, as in the actual floor indicator, consecutive digits are separated by a single column of unlit lamps. Some of the lamps in the floor indicator are malfunctioning and always remain unlit. Imagine that you are stuck in this elevator and you want to know the current floor number. You decide to calculate it as the average value of all floor numbers that could possibly be represented by the current state of the indicator, assuming that any number of the unlit lamps might be malfunctioning. You are given the state of the indicator as a String[] where each element represents a row of lamps, and rows are given from top to bottom. Return the average that you calculate, or -1 if no valid floor number could possibly be represented by the indicator.

Definition

Class:	FloorIndicator
Method:	averageFloor
Parameters:	int, String[]
Returns:	double
Method signature:	double averageFloor(int N, String[] indicator)
(be sure your method is public)

Notes

- The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

- N will be between 1 and 9, inclusive.

- indicator will contain exactly 5 elements.

- Each element of indicator will contain exactly 4*N - 1 characters.

- Each element of indicator will be either '#' or '.' (dot).

- All characters corresponding to lamps in separating columns will be '.' (dots).

Examples

0)

{"###",
 "#.#",
 "###",
 "#.#",
 "###"}

Returns: 8.0

This digit is clearly "8", so it is the only possible floor.

1)

{"###.###",
 "#.#.#.#",
 "#.#.###",
 "#.#...#",
 "###.###"}

Returns: 48.5

Although the indicator shows "09", both digits can also be partially lit "8", so the possible floor numbers are: 08,09,88,89. This results in average floor number (8+9+88+89)/4 = 48.5.

2)

{".......",
 ".......",
 ".......",
 ".......",
 "......."}

Returns: 49.5

This indicator is completely broken, so any floor number between 0 and 99 is possible.

3)

{"...",
 ".#.",
 "...",
 "...",
 "..."}

Returns: -1.0

No digit fits here.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ColoringRectangles

Geometry, Greedy, Simple Math

Used in:

TCHS SRM 60

Used as:

Division I Level Three

Writer:

boba5551

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9858

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13529&pm=9858

Problem Statement

You are given several rectangles in the Cartesian plane with sides parallel to the axes. They are represented by the int[]s x1, y1, x2 and y2, where (x1[i], y1[i]) are the coordinates of the lower-left corner and (x2[i], y2[i]) are the coordinates of the upper-right corner of the i-th rectangle.

Your task is to color exactly K rectangles in such a way that the visible colored area is as large as possible. If some area is covered by more than one rectangle, only the part of the rectangle with the highest index is visible (see example 0). Return a int[] containing exactly K elements - the 0-based indices of the colored rectangles. If there are several possible return values, return the one that comes earliest lexicographically. A int[] a1 comes before a int[] a2 lexicographically if a1 has a smaller element at the first index where they differ.

Definition

Class:	ColoringRectangles
Method:	maxColoredArea
Parameters:	int[], int[], int[], int[], int
Returns:	int[]
Method signature:	int[] maxColoredArea(int[] x1, int[] y1, int[] x2, int[] y2, int K)
(be sure your method is public)

Constraints

-

x1 will contain between 1 and 50 elements, inclusive.

-

x1, y1, x2 and y2 will all contain same number of elements.

-

Each element of x1, x2, y1 and y2 will be between -10000 and 10000, inclusive.

-

x1[i] will be strictly less than x2[i] for all i.

-

y1[i] will be strictly less than y2[i] for all i.

-

K will be between 1 and number of elements in x1, inclusive.

Examples

0)

{1, 3, 2}

{1, 2, 5}

{5, 7, 9}

{3, 4, 7}

Returns: {1, 2 }

If you color rectangles with indices 0 and 1, the visible colored area will be 6 + 8 = 14.

If you color rectangles with indices 0 and 2, the visible colored area will be 6 + 14 = 20.

If you color rectangles with indices 1 and 2, the visible colored area will be 8 + 14 = 22.

1)

{1, 2, 4, 7, 1, 6, 2}

{1, 2, 0, 1, 5, 5, 5}

{5, 4, 6, 9, 4, 9, 8}

{4, 3, 2, 4, 7, 7, 6}

Returns: {0, 2, 3, 6 }

2)

{-5646, -5814, -1459, 6522, -6564, 1450, -2132, 6911, -9062}

{1463, 2872, -5496, 5163, -8549, -7835, 4725, 2420, 6350}

{471, -626, -1110, 7374, 5856, 3365, 1934, 7775, 3495}

{5776, 4869, 7008, 8802, -1730, -7161, 8571, 8905, 7573}

Returns: {4, 8 }

3)

{-3591, 1138, -4086, -9022, 4306, -5936, 8559, -6010, 9427, 3327, -4508, 6444, -4004, 
-3183, -7990, -1338, -4241, -5417, 1057, -8444, -9621, 4001, -4373, -6506, -1068, -5504}

{347, -1456, 117, -5894, -9053, -762, 6132, -9380, 3501, -8102, -2173, -271, -6271, 
-7546, -4792, -4591, -9430, 1185, -914, -5802, -1424, -9786, -3138, 1433, -9060, 2509}

{7239, 4410, 7929, -2195, 6088, 8953, 8700, -1599, 9886, 8966, -3672, 7583, -1242, 
1923, 9511, 3815, -3549, 7758, 1323, 1730, -1868, 5412, 727, 8930, 6211, -4513}

{6643, 7598, 4989, 3169, 1833, 4242, 8541, 8428, 5596, -2838, 2957, 1326, -5883, 
1850, 7082, 9761, -6129, 4223, 8920, -5237, 992, -5976, 2830, 4338, -8927, 6236}

Returns: {3, 7, 9, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25 }

4)

{-1, 2, -2, 2}

{-5, 2, 3, -4}

{1, 5, 1, 6}

{1, 6, 7, -1}

Returns: {0, 1, 2 }

All rectangles are of equal size and no two of them are overlapping.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Subway2

Simple Math

Used in:

SRM 413

Used as:

Division II Level One

Writer:

yuhch123

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9840

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13504&pm=9840

Problem Statement

Subway trains can move people quickly from one station to the next. It is known that the distance between two consecutive stations is length meters. For safety, the train can't move faster than maxVelocity meters/sec. For comfort, the absolute acceleration can't be larger than maxAcceleration meters/sec^2. The train starts with velocity 0 meters/sec, and it must stop at the next station (i.e., arrive there with a velocity of 0 meters/sec). Return the minimal possible time to get to the next station.

Definition

Class:	Subway2
Method:	minTime
Parameters:	int, int, int
Returns:	double
Method signature:	double minTime(int length, int maxAcceleration, int maxVelocity)
(be sure your method is public)

Notes

-

Your return value must be accurate to within an absolute or relative tolerance of 1E-9.

-

If the train's speed at time 0 is v0 and the acceleration is always a, then at time t the speed will be (v0 + t * a) and the train will be (v0 * t + 0.5 * a * t^2) away.

Constraints

-

length, maxAcceleration and maxVelocity will each be between 1 and 1000, inclusive.

Examples

0)

Returns: 1.4142135623730951

maxVelocity is very large. So the train can keep speeding up until it reaches position 0.5.

1)

Returns: 2.0

2)

Returns: 11.0

The train reaches its maximum velocity after 1 second, while traveling 0.5 meters. It then travels the next 9 meters in 9 seconds, and takes 1 second to decelerate to 0 m/s while covering the final 0.5 meters.

3)

Returns: 1.1

4)

Returns: 2.458961621570838

5)

Returns: 1.301036207838119

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ArithmeticProgression

Math

Used in:

SRM 413

Used as:

Division I Level One , Division II Level Two

Writer:

yuhch123

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9839

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13504&pm=9839

Problem Statement

NOTE: This problem statement contains subscripts that may not display properly if viewed outside of the applet.

In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant. For instance, the sequence 3, 5, 7, 9, 11, 13... is an arithmetic progression with common difference 2. An arithmetic sequence can always be represented as a_n=a0+n*d.

You will be given a sequence seq, where seq_i = [a_i+1] for some nondecreasing arithmetic sequence a (both indices are 0-based). [x] denotes the floor function (see Notes). The sequence a is defined as a0+i*d. Return the minimal possible value for d. If no possible value exists for d, return -1 instead.

Definition

Class:	ArithmeticProgression
Method:	minCommonDifference
Parameters:	int, int[]
Returns:	double
Method signature:	double minCommonDifference(int a0, int[] seq)
(be sure your method is public)

Notes

-

[x] denotes the floor function of x which returns the highest integer less than or equal to x. For example, [3.4] = 3, [0.6] = 0, [-1.2] = -2 and [-0.6] = -1.

-

Your return value must be accurate to within an absolute or relative tolerance of 1E-9.

Constraints

-

seq will contain between 0 and 50 elements, inclusive.

-

Each element of seq will be between -10^6 and 10^6, inclusive.

-

a0 will be between -10^6 and 10^6, inclusive.

Examples

0)

{6, 13, 20, 27}

Returns: 6.75

1)

{2, 3, 4, 5, 6}

Returns: 1.0

2)

{}

Returns: 0.0

Since the sequence a is nondecreasing, d must be at least 0.

3)

{3, 3, 3, 3, 4}

Returns: 0.2

4)

{-3}

Returns: -1.0

5)

{6, 14}

Returns: -1.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RoadsOfKingdom

Graph Theory, Math

Used in:

SRM 425

Used as:

Division I Level Three

Writer:

crazyb0y

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9834

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13516&pm=9834

Problem Statement

Long long ago, there was a kingdom named Kingdom C. There were n cities in Kingdom C, and every pair of cities was connected by a two-way road. Unfortunately, some of those roads may have been destroyed in a heavy rain.

You are given a String[] roads. The probability that the road connecting city i and city j is still available after the heavy rain is d/8, where d is the j-th digit of the i-th element of roads.

The king of Kingdom C is very sad, and he wants to know the probability of the following scenario: Every city is reachable from the capital (city 0), but if you were to destroy any one of the remaining roads, there would be at least one city that is not reachable from the capital. Return the probability of this scenario as a double.

Definition

Class:	RoadsOfKingdom
Method:	getProbability
Parameters:	String[]
Returns:	double
Method signature:	double getProbability(String[] roads)
(be sure your method is public)

Notes

-

Your return must have relative or absolute error less than 1E-9.

Constraints

-

roads will contain exactly n elements, where n is between 2 and 16, inclusive.

-

Each element of roads will contain exactly n characters.

-

All characters in roads will be between '0' and '8', inclusive.

-

Character i in element i of roads will be '0'.

-

Character i in element j of roads will be the same as character j in element i of roads.

Examples

0)

{"04",
 "40"}

Returns: 0.5

There is exactly one road connecting the capital and city 1. The answer is equal to the probability that the road is available after the rain.

1)

{"08",
 "80"}

Returns: 1.0

The same example as above, but this time the road is always available.

2)

{"00",
 "00"}

Returns: 0.0

In this case, all roads have been destroyed.

3)

{"088",
 "808",
 "880"}

Returns: 0.0

Here all three roads 0-1, 0-2 and 1-2 are definitely not destroyed. These roads form a cycle, so you can always remove a road in such way that all cities are reachable from the capital.

4)

{"044",
 "404",
 "440"}

Returns: 0.375

Exactly two of three roads should be available, so the probability is C(3,2) * 0.5^3 = 0.375.

5)

{"0701",
 "7071",
 "0708",
 "1180"}

Returns: 0.622314453125

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MagicalSpheres

Brute Force, Math

Used in:

SRM 409

Used as:

Division I Level Two

Writer:

slex

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9828

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12181&pm=9828

Problem Statement

Once upon a time, there lived a powerful wizard who created spheresCount magical spheres. These spheres, when connected together, were a source of unimaginable power. To prevent anyone else from using them, the wizard created fakeSpheresCount spheres that are indistinguishable from the real ones, but don't hold any magical power.

You are determined to find out which spheres are real, and use them to rule the world. To accomplish this, you want to gather a team of gnomes to try every combination of spheresCount spheres out of (spheresCount + fakeSpheresCount) spheres, even if it takes centuries. You will assign combinations to each gnome beforehand, and you will not test any combination more than once. Unfortunately, the gnomes have a labor union that won't allow some gnomes to have more work than others. Therefore, you must select a team size that will allow you to assign an equal number of combinations to each gnome.

Return the maximum possible team size less than or equal to gnomesAvailable that allows even distribution of the work.

Definition

Class:	MagicalSpheres
Method:	divideWork
Parameters:	int, int, int
Returns:	int
Method signature:	int divideWork(int spheresCount, int fakeSpheresCount, int gnomesAvailable)
(be sure your method is public)

Constraints

-

spheresCount will be between 1 and 1,000,000,000, inclusive.

-

fakeSpheresCount will be between 1 and 1,000,000,000, inclusive.

-

availableGnomes will be between 1 and 100000, inclusive.

Examples

0)

Returns: 2

We have a total of four spheres, lets call them {a,b,c,d}. We need to check all triplets to find which of them are real. The different triplets are: {a,b,c}, {a,b,d}, {a,c,d}, {b,c,d}. Since there are four possibilities to check, we can divide it between two gnomes, by assigning two to each of them.

1)

Returns: 20

With three fake spheres, there are 20 triplets to check. You can use 20 gnomes and assign one of the triplets to each of them.

2)

Returns: 1

3)

Returns: 4990

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TournamentJudging

Simple Math

Used in:

SRM 408

Used as:

Division II Level One

Writer:

connect4

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9822

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12180&pm=9822

Problem Statement

You have just been hired to be a judge in the Thought Challenge Olympics. Your task is to calculate an overall score for a competitor based on his performance in a series of events. For each event, you have given him a raw score. The overall score is the sum of the adjusted scores for each event.

To calculate the adjusted score for an event, divide the raw score by the conversion factor for that event, and round the result to the nearest integer (.5 rounds up). You are given int[]s rawScores and conversionFactors. Element i of rawScores is the raw score you have given for the i-th event, and element i of conversionFactors is the conversion factor for the i-th event. Return the competitor's overall score.

Definition

Class:	TournamentJudging
Method:	getPoints
Parameters:	int[], int[]
Returns:	int
Method signature:	int getPoints(int[] rawScores, int[] conversionFactor)
(be sure your method is public)

Constraints

-

rawScores will contain between 1 and 50 elements, inclusive.

-

Each element of rawScores will be between 0 and 1,000,000, inclusive.

-

conversionFactor will contain the same number of elements as rawScores.

-

Each element of conversionFactors will be between 1 and 1,000,000, inclusive.

Examples

0)

{10, 20, 30}

{10, 10, 5}

Returns: 9

The competitor receives 1, 2, and 6 points, respectively.

1)

{8, 16, 32}

{10, 10, 5}

Returns: 9

Due to rounding, the competitor again gets 1, 2, and 6 points.

2)

{60, 59}

{24, 24}

Returns: 5

Be careful to correctly round to the nearest integer (0.5 rounds up).

3)

{47, 42, 37, 30, 27, 21, 18}

{1, 2, 3, 4, 5, 6, 7}

Returns: 100

4)

{0, 1000000, 5000, 1000000}

{1, 2, 1000000, 4}

Returns: 750000

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DNAConstruction

Simple Math

Used in:

TCHS SRM 53

Used as:

Division I Level One

Writer:

Nickolas

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9818

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13486&pm=9818

Problem Statement

A DNA molecule is formed by two nucleotide chains of equal length. Each nucleotide in the first chain must form a bond with the nucleotide at the same position in the second chain. There are four types of nucleotides: A, C, G and T. Each type of nucleotide can only form a bond with one other type: A can only bond with T, and G can only bond with C. These pairs, AT and CG, are called complementary pairs. No other bonds are allowed.

You are given a String nucleotides, where each character is an available nucleotide. Return the length of the longest DNA molecule that can be created using only the available nucleotides. The length of a DNA molecule is the number of nucleotides in either one of its chains. If no DNA molecule can be created, return 0.

Definition

Class:	DNAConstruction
Method:	maxLength
Parameters:	String
Returns:	int
Method signature:	int maxLength(String nucleotides)
(be sure your method is public)

Notes

-

For the purposes of this problem we assume that there is no restriction for the set of nucleotides in each DNA chain.

Constraints

-

nucleotides will contain between 1 and 50 characters, inclusive.

-

Each character in nucleotides will be 'A','C','G' or 'T'.

Examples

0)

"AGGCA"

Returns: 1

The set of nucleotides contains only one complementary pair CG.

1)

"GGTACAGTTT"

Returns: 3

The set of nucleotides contains one CG pair and two AT pairs.

2)

"ACCACCAACCA"

Returns: 0

The set of nucleotides contains only A and C nucleotides, which aren't complementary.

3)

"AAAAAAAAAAAAAAAAACCCCCCCCGGGGGGGGTTTTTTTTTTTTTTTTT"

Returns: 25

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Stick

Simple Math, Simulation

Used in:

SRM 409

Used as:

Division II Level One

Writer:

slex

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9810

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12181&pm=9810

Problem Statement

Little Johnny has a stick that is 64 centimeters long, but he thinks it would be more fun to play with a stick that is x centimeters long. He decides to break the original stick into a number of smaller sticks, and then glue them together to get a stick that is exactly x centimeters long.

The easiest way to break a stick is to break it in half, so Johnny will use the following procedure:

Sum the lengths of all the sticks (initially, there is just one 64 centimeter stick). While this sum is greater than x, repeat the following:
- Take one of the sticks with the shortest length and break it in half.
- If discarding one of the halves would not make the sum of the remaining sticks' lengths less than x, throw that half away.
Finally, glue the remaining sticks together to form a stick that is x centimeters long.

Return the number of sticks Johnny would have to glue together in the final step if he follows the above procedure. If he has only one stick when he gets to the final step, return 1 (see example 0).

Definition

Class:	Stick
Method:	pieces
Parameters:	int
Returns:	int
Method signature:	int pieces(int x)
(be sure your method is public)

Notes

-

The algorithm described in the problem statement guarantees that you will always end up with a total length of exactly x in the final step.

Constraints

-

x will be between 1 and 64, inclusive.

Examples

0)

Returns: 1

After the first break Johnny gets a stick 32cm long.

1)

Returns: 2

First, he breaks the stick into two 32cm long sticks. Then, he breaks one of the 32cm sticks in half and discards one of the halves. The remaining two sticks have a total length of 48cm when glued together.

2)

Returns: 4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AnomalousCancellation

Brute Force, Simple Math, String Manipulation

Used in:

TCHS SRM 53

Used as:

Division I Level Two

Writer:

Nickolas

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9804

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13486&pm=9804

Problem Statement

Given a fraction, you can divide its numerator and denominator by one of their common divisors to get a fraction with the same value. For example, 8/16 can become 4/8 if you divide the numerator and denominator by 2. With some fractions, you can get a similar result by removing digits that are common to both the numerator and denominator. The removed digits must occur in the same relative order in both the numerator and denominator of the original fraction.

For example, consider 4784/7475. We can remove the 7 in the numerator and the first 7 in the denominator, and then remove the second 4 in the numerator and the 4 in the denominator to get 48/75, which has the same value as the original fraction.

You are given the numerator and denominator of a fraction. Use the procedure described above to get a fraction with the smallest possible numerator. Return the resulting fraction formatted as "NUMERATOR/DENOMINATOR" (quotes for clarity only), where both the numerator and denominator are written without leading zeroes. If the procedure cannot be applied, return the original fraction.

Definition

Class:	AnomalousCancellation
Method:	reducedFraction
Parameters:	int, int
Returns:	String
Method signature:	String reducedFraction(int numerator, int denominator)
(be sure your method is public)

Constraints

-

numerator and denominator will each be between 10 and 9999, inclusive.

Examples

0)

Returns: "1/4"

We can cancel the 6's to get 16/64=1/4.

1)

Returns: "48/75"

This is the example from the problem statement.

2)

Returns: "2/2"

The fraction can be reduced to 2/2 or 5/5. We choose 2/2 since it has the smallest numerator.

3)

Returns: "5/1"

We can cancel the 9's to get 95/19=5/1.

4)

Returns: "1/10"

We can cancel two 0's to get 100/1000=1/10.

5)

Returns: "123/456"

The numerator and denominator have no digits in common, so the cancellation procedure can't be applied.

6)

Returns: "1/7"

After cancelling the 1's and the 5's we get 151/1057=1/07, and we write the denominator without the leading zero.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DigitPrime

Brute Force, Simple Math, Simple Search, Iteration

Used in:

TC China 08 - Finals

Used as:

Division I Level One

Writer:

boba5551

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9800

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13678&pm=9800

Problem Statement

A number is called 2-digit-prime if using each of its digits at most once, we can make a prime number containing exactly 2 digits (with no leading zeros). For example, 153 is 2-digit-prime because we can use its digits to make 13, which is a prime number with 2 digits (note that we can also make 53 and 31). Given ints a and b, return the number of 2-digit-prime numbers between a and b, inclusive. See examples for further clarification.

Definition

Class:	DigitPrime
Method:	countNumbers
Parameters:	int, int
Returns:	int
Method signature:	int countNumbers(int a, int b)
(be sure your method is public)

Constraints

-

b will be between 10 and 100000, inclusive.

-

a will be between 10 and b, inclusive.

Examples

0)

Returns: 6

2-digit-prime numbers are:

11 (note that we can use some digit twice if it appears twice in the number), 13, 14 (using its digits we can make 41), 16 (we can make 61), 17 and 19.

1)

Returns: 21

2)

Returns: 0

Note that we are looking for 2 digit prime numbers with no leading zeros, so 03 is not considered a 2 digit prime number.

3)

Returns: 8777

4)

Returns: 2436

5)

Returns: 40

The only number in this interval that is not 2-digit-prime is 33600.

6)

Returns: 1000

Each number in this interval is 2-digit-prime.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

XORPlusEncryption

Encryption/Compression, Math

Used in:

MM 36

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9798

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12202&pm=9798

Problem Statement

You are given a ciphertext which is an output of a known encryption method. Your task is to decrypt this ciphertext.

The encryption method uses the message M and the key K as an input and generates the ciphertext C using the following procedure:

The alphabet of the plaintext P and the key K consists of characters 'a'-'z' (codes 1-26), 'A'-'Z' (codes 27-52) and '0'-'9' (codes 53-62). To form the plaintext, all other characters are removed from message M.

Plaintext P is converted to ciphertext C using the following algorithm:

   for i = 0 .. P.length
       C[i] = P[i] XOR K[i%k];
       K[i%k] = ( K[i%k] + P[i] ) mod 64;

k denotes the length of the key K.

You must return your guess for the plaintext. Your score will be the number of correct letters in your return, divided by the length of the return. If you fail to return a string of the correct length in the allotted time, you will get a 0. Letter i of return R is considered to be correct if it is the same as letter i of the plaintext P (this includes having the right capitalization).

Your overall score will be a sum of scores for individual test cases.

Each test case will be generated using a random article from Wikipedia as the message, and a random word as the key.

The random page feature on Wikipedia is used to fetch a random page. Only those sections of the page enclosed by tags are used. All non-alphanumeric characters and all tags are then stripped. If the result is less than 2000 bytes (roughly), the page is discarded. The source of the program used to get the content is available for download: WikiDownload.java. After compiling, run "java WikiDownload <number of pages>".

The key is chosen as a random word of at least 4 characters from the TWL word list. A random number between 0 and 999 is appended to the end of the chosen word. With probability 0.5 the first character is capitalized. Lowercase 'o' is then converted to '0' (zero) with probability 0.5 for each 'o'. Similarly, each lowercase 'l' (ell) is converted to '1' (one), each 'e' to '3', each 's' to '5', and each 't' to '7', all with probability 0.5.

Definition

Class:	XORPlusEncryption
Method:	getMessage
Parameters:	int[]
Returns:	String
Method signature:	String getMessage(int[] cipherText)
(be sure your method is public)

Notes

-

The memory limit is 1 GB and the time limit is 10 seconds (which includes only time spent in your code).

-

There are 9 example test cases and 500 full submission test cases.

-

The downloads below have some characters other than 'a'-'z', 'A'-'Z' and '0'-'9'. These are all removed when testing.

-

You can access the word list be calling a static method getWords in class Words. This method will return a String[] with the TWL word list.

-

Your code must be under 300K.

Examples

0)

"San_Carlos_Seminary.txt oracularly588"

Returns: 
"Article = San_Carlos_Seminary.txt
Key = oracularly588
<a href=http://www.topcoder.com/contest/problem/XORPlusEncryption/San_Carlos_Seminary.txt>Download</a>
"

1)

"Vermonster.txt M0rtali7ie5606"

Returns: 
"Article = Vermonster.txt
Key = M0rtali7ie5606
<a href=http://www.topcoder.com/contest/problem/XORPlusEncryption/Vermonster.txt>Download</a>
"

2)

"Shep_Messing.txt Ru7henic592"

Returns: 
"Article = Shep_Messing.txt
Key = Ru7henic592
<a href=http://www.topcoder.com/contest/problem/XORPlusEncryption/Shep_Messing.txt>Download</a>
"

3)

"Modular_building.txt cornhusk332"

Returns: 
"Article = Modular_building.txt
Key = cornhusk332
<a href=http://www.topcoder.com/contest/problem/XORPlusEncryption/Modular_building.txt>Download</a>
"

4)

"Frankenstein%27s_Monster_%28Toho%29.txt Coxcombic854"

Returns: 
"Article = Frankenstein%27s_Monster_%28Toho%29.txt
Key = Coxcombic854
<a href=http://www.topcoder.com/contest/problem/XORPlusEncryption/Frankenstein%27s_Monster_%28Toho%29.txt>Download</a>
"

5)

"Out_of_My_Mind_%28Buffy_episode%29.txt Pyxidium689"

Returns: 
"Article = Out_of_My_Mind_%28Buffy_episode%29.txt
Key = Pyxidium689
<a href=http://www.topcoder.com/contest/problem/XORPlusEncryption/Out_of_My_Mind_%28Buffy_episode%29.txt>Download</a>
"

6)

"Eurovision_Song_Contest_1973.txt Picom0le834"

Returns: 
"Article = Eurovision_Song_Contest_1973.txt
Key = Picom0le834
<a href=http://www.topcoder.com/contest/problem/XORPlusEncryption/Eurovision_Song_Contest_1973.txt>Download</a>
"

7)

"Duamutef.txt dup3r5220"

Returns: 
"Article = Duamutef.txt
Key = dup3r5220
<a href=http://www.topcoder.com/contest/problem/XORPlusEncryption/Duamutef.txt>Download</a>
"

8)

"House_of_Savoy.txt ski773ring333"

Returns: 
"Article = House_of_Savoy.txt
Key = ski773ring333
<a href=http://www.topcoder.com/contest/problem/XORPlusEncryption/House_of_Savoy.txt>Download</a>
"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SquareCovering

Simple Math

Used in:

TCHS SRM 50

Used as:

Division I Level Two

Writer:

it4.kp

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9772

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13483&pm=9772

Problem Statement

A square covers a point on a plane if this point lies on the border of this square.

You will be given int[]s px and py, with the i-th elements of px and py representing x and y coordinates of a point on a plane. Find the smallest square with its sides parallel to coordinate axes, which can cover all points from the input and return the length of its side. If no such square exists, return -1.

Definition

Class:	SquareCovering
Method:	getMinimalSide
Parameters:	int[], int[]
Returns:	int
Method signature:	int getMinimalSide(int[] px, int[] py)
(be sure your method is public)

Constraints

-

px will contain between 2 and 50 elements, inclusive.

-

px and py will contain the same number of elements.

-

All elements of px and py will be between -1000 and 1000, inclusive.

-

All points specified by px and py will be different.

Examples

0)

{0,1}

{0,1}

Returns: 1

Both points can be covered with a square with vertices (0,0), (1,0), (1, 1) and (0, 1).

1)

{0,1,2}

{0,1,2}

Returns: -1

These points can not be covered by a square.

2)

{1,-3, 2}

{1, 0, -4}

Returns: 5

3)

{-10, 0, 3, -1}

{0, -1, 3, 4}

Returns: -1

These points can be covered by a rectangle, but not by a square.

4)

{1,2,3,4,5,6,7,8,9,10}

{1000,1000,1000,1000,1000,1000,1000,1000,1000,1000}

Returns: 9

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PositiveArray

Brute Force, Simple Math

Used in:

TCHS SRM 50

Used as:

Division I Level Three

Writer:

it4.kp

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9771

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13483&pm=9771

Problem Statement

A two-dimensional array of integers is positive if the sum of all elements in each row and each column is strictly greater than zero.

For example, the following array is positive:

 2  1 -1
-1  2  2

, while the next one is not:

 1  1 -1
-1  2  2

(the sum of the elements in the first column is 0).

You will be given a String[] data, representing a 2-d array. The j-th character of the i-th element of data represents the j-th number in the i-th row of the array. Digits ('0'-'9') denote numbers between 0 and 9, lowercase letters ('a'-'z') denote numbers between 10 and 35, respectively, and uppercase letters ('A'-'Z') denote negative numbers between -1 and -26, respectively. For example, 'a' represents 10, 'c' represents 12, 'A' represents -1 and 'Z' represents -26.

In one move you are allowed to change the signs of all numbers in some row or column (i.e., multiply all numbers in a row or in a column by -1). Return the minimal number of moves you'll need to get a positive array, or -1 if this is impossible.

Definition

Class:	PositiveArray
Method:	countMoves
Parameters:	String[]
Returns:	int
Method signature:	int countMoves(String[] data)
(be sure your method is public)

Constraints

-

data will contain between 1 and 18 elements, inclusive.

-

Each element of data will contain between 1 and 18 characters, inclusive.

-

Each element of data will contain only digits ('0'-'9') or letters ('a'-'z', 'A'-'Z').

-

All elements of data will have the same length.

Examples

0)

{"12"}

Returns: 0

The input array is already positive.

1)

{"aB"}

Returns: 1

We change signs in the last column and get a positive array.

2)

{"Z2","21"}

Returns: 2

We can not succeed with less than 2 moves. One of the possible solutions is to reverse the first row and the last column.

3)

{"Z9",
 "99"}

Returns: -1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FallingFactorialPower

Simple Math

Used in:

SRM 405

Used as:

Division II Level One

Writer:

Petr

Testers:

PabloGilberto , Olexiy , Jan_Kuipers , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9761

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12177&pm=9761

Problem Statement

A number n taken to the falling factorial power k is defined as n*(n-1)*...*(n-k+1). We will denote it by n^^k. For example, 7^^3=7*6*5=210. By definition, n^^1=n.

We will now continue this definition to the non-positive values of k using the following fact: (n-k)*(n^^k)=n^^(k+1), or, in other words, n^^k=(n^^(k+1))/(n-k). It is directly derived from the above definition.

By using it, we find:

n^^0=n^^1/(n-0)=1,
n^^(-1)=n^^0/(n+1)=1/(n+1),
n^^(-2)=1/(n+1)/(n+2),
and, in general, n^^(-k)=1/(n+1)/(n+2)/.../(n+k).

For example, 3^^(-1)=1/4=0.25, 2^^(-3)=1/3/4/5=1/60=0.016666...

Given a positive int n and an int k, return a double containing the value of n taken to the falling factorial power of k.

Definition

Class:	FallingFactorialPower
Method:	compute
Parameters:	int, int
Returns:	double
Method signature:	double compute(int n, int k)
(be sure your method is public)

Notes

-

Your return must have relative or absolute error less than 1E-9.

Constraints

-

n will be between 1 and 10, inclusive.

-

k will be between -5 and 5, inclusive.

Examples

0)

Returns: 210.0

7^^3=7*6*5=210.

1)

Returns: 10.0

2)

Returns: 1.0

3)

-1

Returns: 0.25

4)

-3

Returns: 0.016666666666666666

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IdealString

Greedy, Simple Math, String Manipulation

Used in:

SRM 405

Used as:

Division II Level Three

Writer:

Petr

Testers:

PabloGilberto , Olexiy , Jan_Kuipers , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9757

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12177&pm=9757

Problem Statement

An ideal string is a string where the 1-based index of the first occurrence of each letter is equal to the number of occurrences of that letter in the string. For example, the "BAOOOA" is an ideal string (quotes for clarity only). The letter 'B' appears 1 time, and its index is 1. The letter 'A' occurs 2 times and its first index is 2. The letter 'O' occurs 3 times and its first index is 3.

Given an int length, return the lexicographically smallest ideal string of that length containing only uppercase letters ('A'-'Z'). If there are no such ideal strings of that length, return an empty String instead.

Definition

Class:	IdealString
Method:	construct
Parameters:	int
Returns:	String
Method signature:	String construct(int length)
(be sure your method is public)

Notes

-

String A is lexicographically smaller than string B of the same length if it contains a smaller letter at the first position they differ. Letter X is smaller than letter Y if it comes earlier in the alphabet.

Constraints

-

length will be between 1 and 100, inclusive.

Examples

0)

Returns: "A"

1)

Returns: "ABB"

2)

Returns: ""

There's no way we can construct an ideal string of length 2 - if both its characters are equal, then the number of occurrences (2) and the position of its first occurrence (1) do not match; if they are distinct, then for the second character the number of occurrences (1) and the position of its first occurrence (2) do not match as well.

3)

Returns: "ABCBCC"

We can permute the last 3 characters in any way, but this way gets us the lexicographically smallest answer.

4)

Returns: "ABBCCCC"

5)

Returns: ""

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GetToTheTop

Dynamic Programming, Geometry, Simple Math

Used in:

SRM 404

Used as:

Division II Level Three

Writer:

boba5551

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9755

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12176&pm=9755

Problem Statement

Little John has found a set of stairs where each stair might contain a number of sweets. He wants to collect as many of these sweets as possible. Each stair can be described as a line segment in the Cartesian plane parallel to the x-axis and having a positive y-coordinate. These segments don't overlap and don't have common endpoints. When John is on a stair, he can move freely between its two endpoints and can collect all sweets on it. He can jump from a point on one stair to a point on another stair (including endpoints of stairs) if the Euclidean distance between them is less than or equal to K. He can only jump to stairs where the y-coordinate is greater than or equal to his current y-coordinate.

You are given a int[] sweets, the i-th element of which is the number of sweets on the i-th stair. You are also given int[]s x, y and stairLength. The coordinates of the leftmost point of the i-th stair are (x[i], y[i]) and the horizontal length of that stair is stairLength[i]. John starts at point (0, 0) and can move wherever he wants along the x-axis before making his first jump. He can first jump to any point on any stair (including endpoints of stairs) as long as the Euclidean distance between the initial and the final points of the jump does not exceed K. Return the maximum possible number of sweets he can collect.

Definition

Class:	GetToTheTop
Method:	collectSweets
Parameters:	int, int[], int[], int[], int[]
Returns:	int
Method signature:	int collectSweets(int K, int[] sweets, int[] x, int[] y, int[] stairLength)
(be sure your method is public)

Notes

-

The Euclidean distance between points (x1, y1) and (x2, y2) is equal to the square root of (x1 - x2)^2 + (y1 - y2)^2.

Constraints

-

K will be between 1 and 10000, inclusive.

-

sweets will contain between 1 and 50 elements, inclusive.

-

sweets, x, y and stairLength will all contain the same number of elements.

-

Each element of sweets will be between 0 and 9999, inclusive.

-

Each element of x will be between 1 and 10000, inclusive.

-

Each element of y will be between 1 and 10000, inclusive.

-

Each element of stairLength will be between 1 and 1000, inclusive.

-

No stairs will overlap or share endpoints. More formally, for each i and j, where y[i] is equal to y[j], either x[i] + stairLength[i] will be less than x[j] or x[j] + stairLength[j] will be less than x[i].

Examples

0)

{1, 2, 3, 4, 3, 5}

{1, 1, 1, 4, 5, 5}

{1, 3, 4, 1, 2, 3}

{2, 1, 1, 2, 1, 1}

Returns: 13

From the start position (0, 0) John can jump on stair 0 (all stair indices are 0-based) and collect 1 sweet. Then he can move to the rightmost point of this stair and jump on stair 3 (the one with the leftmost coordinate (4, 1)). There he collects 4 sweets. Now he has two options:

go back to stair 0, jump on stair 1 to collect 2 sweets and then jump on stair 2 to collect 3 sweets;
jump from stair 3 to stair 4 to collect 3 sweets and then to stair 5 to collect 5 sweets.

Obviously the second option gives more sweets, so he will choose it and collect 1+4+3+5=13 sweets.

1)

{2, 8, 7, 4, 1, 4, 7, 5, 11, 4}

{2, 9, 4, 6, 10, 5, 2, 8, 1, 10}

{1, 1, 3, 3, 3, 5, 6, 6, 8, 9}

{2, 2, 1, 2, 2, 2, 4, 3, 2, 2}

Returns: 47

John can make his first jump on stair 0 or on stair 1 (all stair indices are 0-based). Both choices allow him to visit the same set of stairs afterwards. It is better to jump on stair 1, because it contains 8 sweets. Then he can visit stairs 2, 3, ..., 7 collecting 1+4+7+4+7+5=28 sweets. Finally, he should choose between stairs 8 and 9. Stair 8 contains more sweets, so he will jump on it and collect 11 more sweets.

2)

{1, 3, 5, 7}

{1, 6, 2, 8}

{2, 4, 1, 2}

{4, 1, 7, 4}

Returns: 16

3)

{80, 20, 15, 13, 10, 7, 8, 9, 1, 4, 3, 15, 14, 19, 22, 12, 6, 15, 10, 30, 1, 1}

{2, 8, 11, 17, 20, 14, 10, 16, 8, 14, 19, 6, 6, 6, 6, 15, 15, 15, 14, 20, 20, 20}

{1, 2, 3, 2, 1, 4, 6, 7, 8, 8, 8, 9, 10, 11, 12, 9, 10, 11, 12, 9, 10, 11}

{2, 2, 2, 2, 2, 2, 3, 2, 3, 2, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1}

Returns: 129

4)

{0, 10, 11, 2, 0}

{1, 26, 29, 22, 3}

{1, 83, 88, 22, 5}

{11, 1, 23, 15, 8}

Returns: 0

John can not collect any sweets.

5)

{2, 0, 5}

{1, 8, 9}

{6, 6, 1}

{3, 6, 3}

Returns: 7

6)

{2, 9, 9, 1, 9, 9, 8}

{10, 8, 6, 6, 8, 7, 3}

{6, 7, 5, 4, 5, 2, 5}

{1, 1, 1, 1, 1, 1, 1}

Returns: 47

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MaximumScoredNumber

Simple Search, Iteration

Used in:

SRM 411

Used as:

Division II Level One

Writer:

hken

Testers:

PabloGilberto , Olexiy , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9753

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12183&pm=9753

Problem Statement

In her favorite Math class, Little Bonnie learned that some non-negative integers can be represented as the sum of the squares of two non-negative integers. For example, 13 can be represented as 2*2 + 3*3.

Bonnie later discovered that some of those integers can even be represented by more than one possible pair. For example, 25 can be represented as 0*0 + 5*5, and it can also be represented as 3*3 + 4*4.

She has defined the score of an integer as the number of different ways it can be represented as the sum of the squares of two non-negative integers. The order of the two squared integers is not important. In other words, a*a + b*b is equivalent to b*b + a*a, so they should only count once in the score. So, 25 has a score of 2, 2 has a score of 1 (2 = 1*1 + 1*1), 1 also has a score of 1 (1 = 0*0 + 1*1) and 3 has a score of 0.

Bonnie needs your help in solving the following problem. She wants to find the integer between lowerBound and upperBound, inclusive, with the maximum score. If multiple integers have the same highest score, return the largest among them.

Definition

Class:	MaximumScoredNumber
Method:	getNumber
Parameters:	int, int
Returns:	int
Method signature:	int getNumber(int lowerBound, int upperBound)
(be sure your method is public)

Constraints

-

upperBound will be between 0 and 10000, inclusive.

-

lowerBound will be between 0 and upperBound, inclusive.

Examples

0)

Returns: 2

In the range 0 to 2, the numbers have the following scores:

0 has a score of 1: 0 = 0*0 + 0*0
1 has a score of 1: 1 = 0*0 + 1*1
2 has a score of 1: 2 = 1*1 + 1*1

All of them have the same score. Number 2 is the biggest so it is returned.

1)

Returns: 25

25 is the only number between 0 and 30 having a score of 2.

2)

Returns: 0

3)

Returns: 85

4)

Returns: 9425

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HoleCakeCuts

Geometry, Simple Math

Used in:

SRM 411

Used as:

Division I Level Two , Division II Level Three

Writer:

hken

Testers:

PabloGilberto , Olexiy , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9752

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12183&pm=9752

Problem Statement

Little Bonnie has been given a special cake as a reward for her good performance in her Math class. When viewed from above, the cake is a square, with an empty square hole inside. Both squares are centered at (0, 0) and their sides are parallel to the x- and y-axes.

Bonnie is going to cut the cake using several horizontal and vertical cuts. These cuts are given in the int[]s horizontalCuts and verticalCuts. The i-th horizontal cut is a line parallel to the x-axis which goes through the point (0, horizontalCuts[i]). Likewise, the i-th vertical cut is a line parallel to the y-axis which goes through the point (verticalCuts[i], 0). All cuts have infinite lengths.

You are given an int cakeLength, half of the side length of the outer square, and an int holeLength, half of the side length of the inner square hole. Note that both of these numbers are halves of the sides of the corresponding squares. Return the number of pieces of cake that will exist after all the cuts are performed.

Definition

Class:	HoleCakeCuts
Method:	cutTheCake
Parameters:	int, int, int[], int[]
Returns:	int
Method signature:	int cutTheCake(int cakeLength, int holeLength, int[] horizontalCuts, int[] verticalCuts)
(be sure your method is public)

Notes

-

A piece is a region of the cake with non-zero area.

Constraints

-

cakeLength will be between 2 and 100, inclusive.

-

holeLength will be between 1 and (cakeLength-1), inclusive.

-

horizontalCuts and verticalCuts will each contain between 0 and 50 elements, inclusive.

-

Each element of horizontalCuts and verticalCuts will be between (-cakeLength+1) and (cakeLength-1), inclusive.

-

Elements of horizontalCuts will be distinct.

-

Elements of verticalCuts will be distinct.

Examples

0)

{1, -4}

{1}

Returns: 6

The cake has the side length of 10, and the side of the hole is 6. Two horizontal and one vertical cuts divide the cake into 6 pieces. Those pieces are colored differently in the following picture:

1)

{}

{-2, 2}

Returns: 4

There may be no horizontal cuts.

2)

{1}

{-5, 5}

Returns: 6

3)

{40, -40}

{20, 0, -20}

Returns: 12

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumberPartition

Dynamic Programming, Math, Search

Used in:

TCHS SRM 54

Used as:

Division I Level Three

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9750

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13523&pm=9750

Problem Statement

A partition of the number n is the set of numbers that all sum up to n. For example, we have 5 different partitions of 4: {1, 1, 1, 1}, {1, 1, 2}, {1, 3}, {2, 2}, {4}. If we sort all the numbers within each set, we can treat each partition as a sorted list of numbers and so introduce a lexicographic order on all partitions. For example, the partitions of 4 mentioned before are given in order. You are given ints n and k. Determine all the partitions of n, sort them in lexicographical order, and return a int[] containing the k-th one (k is a 1-based index). If there are not enough partitions of n, return an empty int[].

Definition

Class:	NumberPartition
Method:	kthPartition
Parameters:	int, int
Returns:	int[]
Method signature:	int[] kthPartition(int n, int k)
(be sure your method is public)

Notes

-

The lexicographical order is exactly the same as in a dictionary. A int[] A is lexicographically before a int[] B if there exists an integer i such that A[i] < B[i] and A[j] = B[j] for all j < i or if A is a proper prefix of B.

Constraints

-

n will be between 1 and 50, inclusive.

-

k will be between 1 and 1000000, inclusive.

Examples

0)

Returns: {1, 1, 1, 1 }

Example from the problem statement.

1)

Returns: {1, 3 }

2)

Returns: {1, 1, 1, 3, 3, 3, 5 }

3)

Returns: { }

There are less then 1234 partitions of 12.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ReasonableOdds

Math, Simulation

Used in:

SRM 405

Used as:

Division I Level Three

Writer:

Petr

Testers:

PabloGilberto , Olexiy , Jan_Kuipers , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9744

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12177&pm=9744

Problem Statement

When it's impossible to determine a winner after normal soccer play between two teams, a penalty shoot-out is used. During a penalty shoot-out, each of the teams takes k shots (each of those can either result in scoring a goal or not), and the team who scores the most goals is declared the winner. If both teams score an equal number of goals, we will assume in this problem that the game ends in a draw.

We will also assume that for each team there exists a number between 0 and 1, inclusive, denoting the skill level of that team, such that each penalty shot taken by that team results in a goal with probability equal to that number. You can assume that all shots are independent.

Your friend, an eager sports better, tells you that he knows that team 1 will win with probability p1%, team 2 will win with probability p2%, and the probability of a draw is pDraw%. You need to check if such a probability distribution is possible. In other words, can there exist two teams with valid skill levels such that those three outcomes would happen with the given probabilities?

Given ints p1, pDraw, p2 and k, return "YES" if such a distribution is possible, and "NO" otherwise (quotes for clarity only).

Definition

Class:	ReasonableOdds
Method:	check
Parameters:	int, int, int, int
Returns:	String
Method signature:	String check(int p1, int pDraw, int p2, int k)
(be sure your method is public)

Constraints

-

p1, pDraw and p2 will be between 0 and 100, inclusive.

-

p1, pDraw and p2 will sum up to 100.

-

k will be between 1 and 5, inclusive.

Examples

0)

Returns: "YES"

When both teams have a skill level of 0, a draw is unavoidable.

1)

Returns: "NO"

When both teams can win, a draw is also a possibility.

2)

Returns: "NO"

3)

Returns: "NO"

Moreover, a draw is a significant possibility.

4)

Returns: "YES"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WifiPlanet

Geometry, Math

Used in:

SRM 410

Used as:

Division I Level Three

Writer:

bmerry

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=9733

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12182&pm=9733

Problem Statement

Dissatisfied with the inconvenient spherical shape of the Earth, a group of map-makers have gone to Magrathea to obtain a custom-built planet. They decided to design their new planet to be flat and in the shape of a polygon. All coordinates will be in the Cartesian (x, y) plane.

In order to provide everyone on the planet with internet access, a wireless router will be placed at every lattice point that is inside the polygon (a lattice point is a point with integer coordinates). The map-makers decided to keep their job simple by choosing a polygon with no lattice points on its boundary.

Because the map-makers are highly rational people, they decided that the coordinates of all the vertices of the polygon would be fractions with a common denominator. The vertices of the polygon (in order), are given by the int[]s x and y, and by the common denominator denom. The ith vertex is (x[i]/denom, y[i]/denom).

Calculate and return the number of routers required.

Definition

Class:	WifiPlanet
Method:	routersNeeded
Parameters:	int[], int[], int
Returns:	long
Method signature:	long routersNeeded(int[] x, int[] y, int denom)
(be sure your method is public)

Constraints

-

x and y will contain the same number of elements.

-

x and y will each contain between 3 and 50 elements, inclusive.

-

Each element of x and y will be between 1 and 10^9, inclusive.

-

No two vertices of the polygon will be the same.

-

No two edges of the polygon (including their end-points) will intersect, with the exception that adjacent edges will intersect at their common end-point.

-

No lattice point will lie on the boundary of the polygon.

-

denom will be between 2 and 10^9, inclusive.

Examples

0)

{1,7,3,3}

{1,1,3,5}

Returns: 2

This is illustrated in the image below:

1)

{3,3,4,4,5,6,10,10,11,11,10,10,9,9}

{1,2,2,6,3,8,8,9,9,3,3,2,2,1}

Returns: 4

2)

{50,1000050,1000049}

{2,1000002,1000003}

Returns: 0

3)

{32,32,64,8,15,1000,999}

{1,10,10,48,48,47,1}

Returns: 120

4)

{1,1000000000,1000000000,1}

{1,1,1000000000,1000000000}

Returns: 111111110888888889

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EvilRobot

Greedy, Simple Math

Used in:

College Tour West China

Used as:

Division I Level Two

Writer:

slex

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8821

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12240&pm=8821

Problem Statement

An evil robot has been tormenting your land for years. You decided to get rid of him by creating a deadly trap. The trap is now ready, and the only problem left is to make the robot walk inside it. Luckily, you managed to hack into the robot's movement system, and you can reprogram it to move the way you want.

The land is represented by an infinite grid of cells. The robot is currently standing in cell (robotX, robotY), and the trap is set in cell (trapX, trapY). The robot's program is very simple and consists of N commands, where each command is one of:

'U': the robot moves from coordinates (x, y) to coordinates (x, y + 1).
'R': the robot moves from coordinates (x, y) to coordinates (x + 1, y).

The commands are executed in order, starting from the first one, and the program is cyclical (i.e., after the last command is executed, it will start over from the first command).

As soon as the robot walks into the trap, the program will stop executing. Write a program with exactly N commands that will make the robot walk into the trap. Return this program as a String, where the i-th character is the i-th command. If there are multiple possible programs, return the one among them that comes first alphabetically. If no such program exists, return "I'LL GET YOU NEXT TIME" (quotes for clarity) instead.

Definition

Class:	EvilRobot
Method:	createProgram
Parameters:	int, int, int, int, int
Returns:	String
Method signature:	String createProgram(int N, int robotX, int robotY, int trapX, int trapY)
(be sure your method is public)

Constraints

-

N will be between 1 and 50, inclusive.

-

robotX will be between 0 and 1000000000, inclusive.

-

robotY will be between 0 and 1000000000, inclusive.

-

trapX will be between 0 and 1000000000, inclusive.

-

trapY will be between 0 and 1000000000, inclusive.

Examples

0)

Returns: "RUU"

The robot starts at point (1,1). After executing the commands RUURU, he steps into the trap at (3,4). There is one more program that leads to the trap (URU), but RUU comes earlier alphabetically.

1)

Returns: "UUURRRRRRR"

Here the trap is straight above the robot, so the first three of his moves must be U.

2)

Returns: "I'LL GET YOU NEXT TIME"

The robot is already to the right of the trap. This time there is nothing you can do.

3)

Returns: "I'LL GET YOU NEXT TIME"

Even though the robot hasn't passed the trap yet, it's not possible to create a program with 5 commands that leads into it.

4)

Returns: "RRRRRRRRRUUUUUUUUUUUUUUUUUUUURRRRRRRRRUUUUUUUUUU"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OptimalPlay

Math

Used in:

TCO08 Wildcard

Used as:

Division I Level One

Writer:

lars2520

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8820

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12018&pm=8820

Problem Statement

We're going to play a very simple game of poker. As in regular poker, there is a pot, and the winner of the hand wins the money in the pot. In this game, each of two players will be given a single card, numbered between 0 and N-1, inclusive. The pot initially contains $1, and the size of each bet is also $1. The player who goes first may either check (put nothing in the pot) or bet (put $1 in the pot). If the first player checked, the second player may either check or bet. If he bets the first player must then either fold (concede the pot to the second player) or call (put $1 in). If, on the other hand, the first player bets, the second player must decide whether to fold or call. If one player folds, then the other player wins the pot automatically. If neither player folds, then the player with the higher card wins the pot (ties split the pot). Thus, there will only be five possible outcomes to the betting:

Player 1 bets, player 2 folds; player 1 wins the pot
Player 1 bets, player 2 calls; the player with the higher card wins, a tie results in the pot being evenly divided
Player 1 checks, player 2 checks; the player with the higher card wins, a tie results in the pot being evenly divided
Player 1 checks, player 2 bets, player 1 folds; player 2 wins the pot
Player 1 checks, player 2 bets, player 1 calls; the player with the higher card wins, a tie results in the pot being evenly divided

You will be given a complete description of a probabilistic strategy played by player 1. You, as player two, want to maximize your expected value, and must play accordingly, given player one's strategy.

A double[] betProb gives the probability that player one will bet with each of the N cards. betProb[i] gives the probability that player one will bet given that his card is i. Similarly, callProb[i] gives the probability that player one will first check, and then call if you bet, given that his card is i. Therefore, 1-betProb[i]-callProb[i] gives the probability that player one will check and then fold to your bet.

You should return your expected profit (including the initial $1 in the pot) given that you play optimally (knowing player one's strategy), and that each player's card is assigned independently and uniformly at random.

Definition

Class:	OptimalPlay
Method:	winnings
Parameters:	double[], double[]
Returns:	double
Method signature:	double winnings(double[] betProb, double[] callProb)
(be sure your method is public)

Notes

- The players do not know each other's cards.

- The call probability is not conditional on not betting. It gives the joint probability of checking and then calling.

- The profit is the amount you get from the pot that you didn't put in. Thus, if you tie your profit is $0.5, half of the original $1. If you call a bet and win your profit is $2. If you call a bet and lose, your profit is -$1.

- Your return must have relative or absolute error less than 1E-9.

Constraints

- N will be between 2 and 50, inclusive.

- betProb and callProb will each contain exactly N elements between 0 and 1, inclusive.

- The sum of corresponding elements of betProb and callProb will be at most 1.

Examples

0)

{0,0}

{0,0}

Returns: 1.0

You can win every time -- just bet and your opponent will fold, giving you the initial $1.

1)

{1,1,1}

{0,0,0}

Returns: 0.6666666666666666

Your opponent bets no matter what. You should call if your card is a 1 or a 2. When it is a one, you will lose $1 when your opponent has a 2, win $2 when your opponent has a 0, and win $0.5 when your opponent also has a 1.

2)

{0.5,0,1}

{0,1,0}

Returns: 0.5833333333333334

We can describe your optimal strategy one card at a time (this is not the unique optimal strategy):

If you have a 0, you should fold to a bet, and check if player one checks.
If you have a 1, you should fold to a bet, and check if player one checks.
If you have a 2, you should call a bet, and bet if player one checks.

Using this strategy you will win 0.083 when you have card 0, 0.333 when you have card 1, and 1.333 when you have card 2. Thus 1.75/3=0.583 overall.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SequentialT

Dynamic Programming, Simple Math

Used in:

TCO08 Semifinal 3

Used as:

Division I Level Three

Writer:

SnapDragon

Testers:

PabloGilberto , lbackstrom , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8818

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12017&pm=8818

Problem Statement

You have written a complicated multi-threaded program, and you would like to analyze its expected runtime.

The program consists of n threads in a specific order, indexed from 0 to n-1. Each thread has a task to execute which is divided into up to 10 subtasks. Each subtask requires one time slice to process, and they must be processed in order. In every thread (except the first), one of the subtasks will be a special "synchronization" subtask; the thread may not process this subtask until all the threads with lower indices have finished. The thread's task is described as a String with a character for each subtask. A normal subtask is denoted by a '.'; the "synchronization" subtask is denoted by 'S'.

The processor executes your program in a simple way. For each time slice it picks a thread uniformly at random and allows it to process one subtask. If the chosen thread has already finished, the unfinished thread with the lowest index is picked instead. However, if the chosen thread is blocked on a "synchronization" subtask, that time slice is wasted. (Yes, this is a silly way to implement multithreading!)

Return the expected (average) number of time slices the entire program will take to execute.

Definition

Class:	SequentialT
Method:	expectedExecutionTime
Parameters:	String[]
Returns:	double
Method signature:	double expectedExecutionTime(String[] threads)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

threads will contain between 1 and 10 elements, inclusive.

-

Each element of threads will contain between 1 and 10 characters, inclusive.

-

Each element of threads will contain only the characters '.' and 'S'.

-

Each element of threads, except the first, will have exactly one 'S'.

-

The first element of threads will not contain an uppercase 'S'.

Examples

0)

{"....."}

Returns: 5.0

No multithreading; just 5 subtasks to perform.

1)

{".","S"}

Returns: 2.9999999999999996

There's a 1/2 chance of 0 wasted time slices, a 1/4 chance of 1, a 1/8 of 2, and so on. An average of 1 time slice is wasted.

2)

{"..","S"}

Returns: 4.999999999999999

Now there is a (k+1)/2^k+2 chance of wasting k time slices.

3)

{".","...S.",".........S"}

Returns: 16.144458312987712

These threads will most likely not have to wait.

4)

{".....","...S...","S......","......S..","...S.","..S"}

Returns: 65.45700302526924

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CarRace

Simulation

Used in:

TCO08 MM Finals

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8816

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12020&pm=8816

Problem Statement

You need to write a program to race a car. The car will drive along a track, as defined by a sequence of waypoints (you don't actually have to stay on the track, you just have to hit the waypoints).

You will first be given a number of parameters relating to the performance of the car, in a method init, along with the locations of the waypoints. Your car starts out at (0,0), facing in the +x direction. A number of calls will then be made to a method step, reminding you of your current location and direction. You should return a double[] from this method, where consecutive elements of the return indicate first how much to accelerate or break, and then how much to turn the car (in radians), with the acceleration element coming first. Each turning element must have absolute value no more than 0.005, and each accelerating element must have absolute value no more than maxacc. The car's motion will be simulated in a number of discrete timesteps, corresponding to your return. Thus, a return with 6 elements, would result in the simulation running for 3 steps.

The physics of our car's motion are fairly simple (and perhaps not too realistic). The current state of the car is (mostly) defined by five values: it's x and y positions, it's x and y velocities, and the angle it is facing. It should be noted that the car may be facing in a different direction from the one it is moving in, as it might skid around a turn, or even roll backwards.

In a particular time step, you apply a forward force of up to maxacc to the car, propeling it in the direction it is facing. Air resistance works to counter that force, and the net forward force is given by the force you apply minus the forward air resistance (which is proportional to velocity squared). If the car is not moving in the same direction it is facing, there is also a cross force, which can be as large as the car's velocity in this cross direction. Finally, you can apply the breaks, slowing the car down up to maxacc in the forward direction, by returning a negative value for acceleration.

The friction of the tires can only provide a limited amount of force, which must be distributed between the cross force and the forward force. If the magnitude of the overall force vector is larger than the force of friction, then the car is said to be skidding. In this case, the force of friction is divided between the forward and cross directions. At the end of each time step, after all the forces have been computed, the car's velocity is first adjusted, and then the car's position is adjusted according to this new velocity. Finally, if the car was skidding in the previous timestep, it builds some angular momentum, and the change in it's angle will be set to whatever change you impart, plus half of the change from the previous timestep.

All this adds up to fairly intuitive motion. If you don't turn too sharply and you don't accelerate too much, the force of friction is large enough to entirely adjust the cars velocity so that it is moving in the direction it is facing, and no skidding occurs. If you turn too sharply, there isn't enough friction on the tires, and you will start to skid. In this case, the car will still turn, but it won't be moving in the direction it is facing. In extreme cases, you could turn the car all the way around, and end up rolling backwards. The amount of acceleration you can apply without exceeding the force of friction increases with your speed (so its more like power than acceleration), as air resistance is removed from forward acceleration before checking if there is enough friction.

To complete the race, you must come within 1000 units of each of the waypoints, in order. The simulation will be run for at most 100,000 steps and you will be allowed a total of 30 seconds for each test case.

Test Case Generation

The friction parameter will be uniformly chosen in [0.002,0.03]. The air resistance will be chosen in [0.0001,0.001], and the maximum acceleration will be chosen in [0.01,0.1]. The waypoints will be generated by starting at (0,0), facing in the +x direction. A sequence of moves and turns will then be made, placing a waypoint after each:

        S = nextInt(91)+10;
        double alpha = 0;
        double cx = 0, cy = 0;
        wx[0] = wy[0] = 0;
        for(int i = 1; i<S; i++){
            alpha += nextGaussian()/2;
            double d = pow(nextDouble(),2) * 5000;
            wx[i] = cx += Math.cos(alpha)*d;
            wy[i] = cy += Math.sin(alpha)*d;
        }

Scoring

Your raw score will be the timestep at which you hit the last of all the waypoints that you hit, plus the number of waypoints hit divided by 1000. Competitors will be ranked primarily by the number of waypoints hit (you should be able to always hit all of them), with ties broken by the speed with which you hit them. The highest rank is 1, and each competitor will get (12-rank)² points. Thus, the winner will get 121 points. In the event of a tie, the points for the tied places will be divided evenly. Thus, if there were a tie for first, the top two would each get (121+100)/2 points, while third would still get 81.

Resources

You can see the source code and a more detailed explanation of the physics at http://www.topcoder.com/contest/problem/CarRace/physics.html.

There is also a visualizer, described at http://www.topcoder.com/contest/problem/CarRace/vis.html.

Definition

Class:	CarRace
Method:	init
Parameters:	double, double, double, double[], double[]
Returns:	int
Method signature:	int init(double friction, double air, double maxacc, double[] wx, double[] wy)

Method:	step
Parameters:	double, double, double, double, double, int
Returns:	double[]
Method signature:	double[] step(double x, double y, double dx, double dy, double alpha, int wp)
(be sure your methods are public)

Notes

-

Breaking while going backwards still makes you stop -- it doesn't accelerate you in reverse.

-

The time limit is 30 seconds and the memory limit is 512M.

-

You will have at most 100,000 steps to finish. If you don't finish all waypoints, your score will be as described in the problem, and you will be ranked behind everyone who hit more waypoints than you.

-

The direction you are facing will be between -PI and PI. You will start facing in the +x direction, with alpha = 0. Turning clockwise corresponds to increasing alpha.

Constraints

-

In each step you may turn any amount between -0.005 and 0.005.

-

In each step you may accelerate an amount between -maxacc and maxacc

Examples

0)

"1"

Returns: 
"friction = 0.025353231925443906<br>
air = 4.965840810810231E-4<br>
maxacc = 0.010020588605228068<br>
N = 85<br>
"

1)

"2"

Returns: 
"friction = 0.026415714551864464<br>
air = 1.4666721060721836E-4<br>
maxacc = 0.01893924570669956<br>
N = 92<br>
"

2)

"3"

Returns: 
"friction = 0.004844682646896966<br>
air = 4.746660802103152E-4<br>
maxacc = 0.06236285385761371<br>
N = 10<br>
"

3)

"4"

Returns: 
"friction = 0.02815367095844578<br>
air = 1.8501805598421562E-4<br>
maxacc = 0.09508318371791942<br>
N = 97<br>
"

4)

"5"

Returns: 
"friction = 0.014431617598556953<br>
air = 7.673181465344457E-4<br>
maxacc = 0.04720944775523275<br>
N = 26<br>
"

5)

"6"

Returns: 
"friction = 0.02400016822715227<br>
air = 6.975636481665687E-4<br>
maxacc = 0.06782124248871851<br>
N = 89<br>
"

6)

"7"

Returns: 
"friction = 0.0062732643115944176<br>
air = 6.03853832499194E-4<br>
maxacc = 0.08891366051327443<br>
N = 33<br>
"

7)

"8"

Returns: 
"friction = 0.022912046591109785<br>
air = 9.433731971918565E-4<br>
maxacc = 0.07645501697340658<br>
N = 18<br>
"

8)

"9"

Returns: 
"friction = 0.0025809528661937535<br>
air = 1.0337427216509109E-4<br>
maxacc = 0.09923919367667183<br>
N = 32<br>
"

9)

"10"

Returns: 
"friction = 0.017193956023422358<br>
air = 1.3735350430489604E-4<br>
maxacc = 0.034056681729733335<br>
N = 38<br>
"

10)

"11"

Returns: 
"friction = 0.012095102876343383<br>
air = 1.350554326067197E-4<br>
maxacc = 0.09337933523810507<br>
N = 23<br>
"

11)

"12"

Returns: 
"friction = 0.01063311914214325<br>
air = 5.320894448422347E-4<br>
maxacc = 0.057396703337113456<br>
N = 13<br>
"

12)

"13"

Returns: 
"friction = 0.017551334976223812<br>
air = 5.275741890291596E-4<br>
maxacc = 0.06837013496585978<br>
N = 35<br>
"

13)

"14"

Returns: 
"friction = 0.002780827021052145<br>
air = 5.916970900662024E-4<br>
maxacc = 0.07667698326331136<br>
N = 38<br>
"

14)

"15"

Returns: 
"friction = 0.02153379082007357<br>
air = 4.2201266203282357E-4<br>
maxacc = 0.019785379399535032<br>
N = 38<br>
"

15)

"16"

Returns: 
"friction = 0.014504300422171476<br>
air = 1.4169402429845034E-4<br>
maxacc = 0.019126261838502728<br>
N = 78<br>
"

16)

"17"

Returns: 
"friction = 0.018501240274952514<br>
air = 1.5505615534243216E-4<br>
maxacc = 0.04447374141309209<br>
N = 55<br>
"

17)

"18"

Returns: 
"friction = 0.010420957638070267<br>
air = 1.098160773416636E-4<br>
maxacc = 0.07814826571569722<br>
N = 56<br>
"

18)

"19"

Returns: 
"friction = 0.007461881907706251<br>
air = 5.702494936263828E-4<br>
maxacc = 0.05444883456395739<br>
N = 62<br>
"

19)

"20"

Returns: 
"friction = 0.006935324539288438<br>
air = 8.158847041045977E-4<br>
maxacc = 0.08047553123971915<br>
N = 19<br>
"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PolygonColors

Dynamic Programming, Math

Used in:

SRM 406

Used as:

Division II Level Three

Writer:

eleusive

Testers:

PabloGilberto , Olexiy , gawry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8801

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12178&pm=8801

Problem Statement

Consider a regular polygon with N sides. A diagonal is defined to be a line segment drawn that connects two non-adjacent vertices of the polygon (with the two vertices as its endpoints). A set of diagonals is said to be safe if no two diagonals cross one another, except for possibly at the polygon's vertices.

A coloring of a polygon is a mapping of the non-negative integers, or colors, to the vertices of the polygon. Given a set of safe diagonals, a valid coloring of a polygon is a coloring of the polygon such that no two vertices which are connected by a diagonal or share a side have the same color.

Two diagonals are distinct if at least one of their endpoints is different, and two sets of diagonals are distinct if one set contains some diagonal not contained in the other.

You're given a coloring of a polygon with N sides, where the coloring is given by a int[] colors and N is described by a int. Here, the ith element of colors is the color of the ith vertex. Return how many distinct sets of safe diagonals may be assigned to the polygon such that the coloring is valid. As this result may be very large, return the answer modulo 100000007.

Definition

Class:	PolygonColors
Method:	getWays
Parameters:	int, int[]
Returns:	int
Method signature:	int getWays(int N, int[] colors)
(be sure your method is public)

Constraints

-

N will be between 3 and 50, inclusive.

-

colors will have exactly N elements.

-

Each element of colors will be between 0 and N-1, inclusive.

Examples

0)

{1, 2, 0}

Returns: 1

There are no diagonals we can add to a triangle, so the empty set is the only possibility.

1)

{1, 2, 3, 0}

Returns: 3

We can either add 0 or 1 diagonals, and there are two ways to add a diagonal.

2)

{0, 1, 1, 1, 1}

Returns: 0

Here we have vertices that share sides, but have the same color. Even if we choose not to add any diagonals, there are no safe sets here.

3)

{0,1,2,6,4,5,6,7,1,9,10,11,12,13,14,10}

Returns: 96791474

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ShortPaths

Dynamic Programming, Graph Theory, Math, Search

Used in:

SRM 406

Used as:

Division I Level Three

Writer:

eleusive

Testers:

PabloGilberto , Olexiy , gawry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8791

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12178&pm=8791

Problem Statement

You're given a weighted, directed graph that satisfies two conditions: each vertex is contained in at most one simple cycle, and for any two vertices u and v, there exists at most one simple path from u to v (see the notes section for definitions).

The graph is described by a String[] graph, where the jth character of the ith element of graph is either '0' if there is no edge from vertex i to j, or a digit between '1' and '9', inclusive, which is the weight of the edge from vertex i to j.

Given such a graph, return the length of the kth shortest path from start to finish. If there are fewer than k paths, you should return -1. Note that all paths of the same length should be counted (see example 3 for clarification).

Definition

Class:	ShortPaths
Method:	getPath
Parameters:	String[], long, int, int
Returns:	long
Method signature:	long getPath(String[] graph, long k, int start, int finish)
(be sure your method is public)

Notes

-

A simple path is an ordered sequence of distinct vertices such that for each vertex in the sequence, there is an edge to the next vertex in the sequence (except for the last vertex).

-

A simple cycle is an ordered sequence of vertices such that for each vertex in the sequence, there is an edge to the next vertex in the sequence (except the last vertex). In addition, the sequence must contain no repeated vertices, except for the first and last vertices which must be the same.

Constraints

-

k will be between 1 and 10^12, inclusive.

-

The graph represented by graph will satisfy the constraints described in the problem statement.

-

graph will contain between 2 and 50 elements, inclusive.

-

Each element of graph will contain exactly N characters, where N is the number of elements in graph.

-

Each character in graph will be a digit between '0' and '9', inclusive.

-

The ith character of the ith element of graph will always be '0'.

-

start and finish will be distinct integers between 0 and N-1, inclusive, where N is the number of elements in graph.

Examples

0)

{
"0100",
"0020",
"0003",
"4000"
}

Returns: 3

The direct path between nodes 0 and 2 is 0->1->2.

1)

{
"0100",
"0020",
"0003",
"4000"
}

Returns: 13

The same graph as above, but the second shortest path is 0->1->2->3->0->1->2.

2)

{
"011",
"000",
"000"
}

Returns: -1

There is no path from vertex 1 to vertex 2.

3)

{
"010000",
"001010",
"000101",
"000000",
"010000",
"001000"
}

Returns: 5

The shortest path is of length 3. The next two shortest paths are both of length 5, and since all paths of length 5 must be counted, the third shortest path is of length 5.

4)

{
"010000",
"001010",
"000103",
"000000",
"010000",
"002000"
}

Returns: 14

5)

{
"010000000",
"001002000",
"000100000",
"000010900",
"000000006",
"030000000",
"007000000",
"000040000",
"000000070"
}

Returns: 363

6)

{
"09000000000000000000000002000000000000000000000000",
"00900000000000000000000000000000000000000000000000",
"00090000000000000000000000000000000000000000000000",
"00009000000000000000000000000000000000000000000000",
"00000900000000000000000000000000000000000000000000",
"00000090000000000000000000000000000000000000000000",
"00000009000000000000000000000000000000000000000000",
"00000000900000000000000000000000000000000000000000",
"00000000090000000000000000000000000000000000000000",
"00000000009000000000000000000000000000000000000000",
"00000000000900000000000000000000000000000000000000",
"00000000000090000000000000000000000000000000000000",
"00000000000009000000000000000000000000000000000000",
"00000000000000900000000000000000000000000000000000",
"00000000000000090000000000000000000000000000000000",
"00000000000000009000000000000000000000000000000000",
"00000000000000000900000000000000000000000000000000",
"00000000000000000090000000000000000000000000000000",
"00000000000000000009000000000000000000000000000000",
"00000000000000000000900000000000000000000000000000",
"00000000000000000000090000000000000000000000000000",
"00000000000000000000009000000000000000000000000000",
"00000000000000000000000900000000000000000000000000",
"00000000000000000000000090000000000000000000000000",
"40000000000000000000000000000000000000000000000000",
"00000000000000000000000000900000000000000000000000",
"00000000000000000000000000090000000000000000000000",
"00000000000000000000000000009000000000000000000000",
"00000000000000000000000000000900000000000000000000",
"00000000000000000000000000000090000000000000000000",
"00000000000000000000000000000009000000000000000000",
"00000000000000000000000000000000900000000000000000",
"00000000000000000000000000000000090000000000000000",
"00000000000000000000000000000000009000000000000000",
"00000000000000000000000000000000000900000000000000",
"00000000000000000000000000000000000090000000000000",
"00000000000000000000000000000000000009000000000000",
"00000000000000000000000000000000000000900000000000",
"00000000000000000000000000000000000000090000000000",
"00000000000000000000000000000000000000009000000000",
"00000000000000000000000000000000000000000900000000",
"00000000000000000000000000000000000000000090000000",
"00000000000000000000000000000000000000000009000000",
"00000000000000000000000000000000000000000000900000",
"00000000000000000000000000000000000000000000090000",
"00000000000000000000000000000000000000000000009000",
"00000000000000000000000000000000000000000000000900",
"00000000000000000000000000000000000000000000000090",
"00000000000000000000000000000000000000000000000009",
"00000000000000000000000004000000000000000000000000"
}

10000000000

Returns: 31112618

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BestResult

Geometry, Simple Math, Simulation, Sorting, String Parsing

Used in:

East China Round 1

Used as:

Division I Level Three

Writer:

DStepanenko

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8789

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12226&pm=8789

Problem Statement

The Olympic Games are over and now you need to rank the teams. You must pick three integers Pg, Ps and Pb, representing the number of points awarded to each team for each gold, silver and bronze medal they won, respectively, where 1000 >= Pg >= Ps >= Pb >= 1. The teams will be ranked according to the total number of points they have (teams with more points will be ranked higher). You want to select Pg, Ps and Pb so that your team gets ranked as high as possible.

You will be given a String[] teams, the i-th element of which represents the medal counts of the i-th team. Each element will be formatted as "G S B" (quotes for clarity), where G, S and B are integers representing the total number of gold, silver and bronze medals won by that team, respectively. Your team is the 0-th team. The highest possible rank is 1, the second highest rank is 2, and so on. If your team has the same number of total points as some other teams, your team will be ranked higher than those other teams. In other words, your final ranking will be equal to 1 plus the number of teams that have a strictly greater number of points than your team.

Return a int[] containing exactly three elements - the values of Pg, Ps and Pb (in that order) that will give your team the highest ranking. If there are multiple possible return values, return the one with the smallest value for Pg. If there are still multiple return values, return the one with the smallest value for Ps. If there are still multiple return values, return the one with the smallest value for Pb.

Definition

Class:	BestResult
Method:	findBestResult
Parameters:	String[]
Returns:	int[]
Method signature:	int[] findBestResult(String[] teams)
(be sure your method is public)

Constraints

-

Each element of teams will be formatted as "G S B" (quotes for clarity), where G, S and B are integers between 0 and 100000, inclusive, with no extra leading zeroes.

-

teams will contain between 2 and 15 elements, inclusive.

Examples

0)

{"1 1 1", "0 1 2", "2 1 0"}

Returns: {1, 1, 1 }

In this example, your team has won 1 gold, 1 silver and 1 bronze. There are multiple ways to get your team ranked number 1, but the best way is to assign 1 to Pg, Ps and Pb. Every team gets 3 points, and your team gets ranked the highest.

1)

{"0 0 0", "1 1 1"}

Returns: {1, 1, 1 }

In this example, no matter what values you choose, your team will always be ranked second.

2)

{"0 1 2", "1 0 0", "0 0 4"}

Returns: {2, 2, 1 }

3)

{"0 3 0", "0 0 4", "3 0 0"}

Returns: {2, 2, 1 }

4)

{"24 0 0", "5 6 7", "5 45 5", "4 4 64"}

Returns: {4, 1, 1 }

5)

{ "1 2 0", "5 4 0", "3 0 1", "0 4 5", "2 3 4" }

Returns: {7, 1, 1 }

6)

{ "6 4 8", "2 0 4", "3 8 1", "0 6 5", "3 6 10", "5 6 7", "8 2 7" }

Returns: {3, 2, 2 }

7)

{ "7 8 5", "8 2 7", "3 10 0", "10 8 0", "5 2 7", "1 10 10", "9 7 1", "5 8 0" }

Returns: {3, 2, 2 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ColorfulBalls

Dynamic Programming, Math

Used in:

TCO08 Semifinal 2

Used as:

Division I Level Three

Writer:

misof

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8782

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12016&pm=8782

Problem Statement

We have a bag that contains N balls of different colors. In each turn we pick two balls from the bag, one after another, and paint the second one with the first one's color. After the paint dries, we put both balls back into the bag and shuffle its contents.

You are given a String colors describing the initial colors. More precisely, each character in colors corresponds to a single ball. Balls represented by equal characters have the same color.

Return the expected number of turns until all the balls have the same color.

Definition

Class:	ColorfulBalls
Method:	expectedStepCount
Parameters:	String
Returns:	double
Method signature:	double expectedStepCount(String colors)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

colors will contain between 1 and 24 characters, inclusive.

-

Each character in colors will be an uppercase letter ('A'-'Z').

Examples

0)

"AB"

Returns: 1.0

In the first turn we will paint one ball with the other's color, and we are done.

1)

"Q"

Returns: 0.0

If there is just a single ball, all balls already have the same color, and thus the correct answer is zero.

2)

"AAAAAAA"

Returns: 0.0

All balls already have the same color.

3)

"ZCZ"

Returns: 3.0

4)

"KLM"

Returns: 4.0

After the first turn we are sure to get a situation that's similar to the one in the previous example.

5)

"AAABB"

Returns: 11.666666666666668

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FIELDDiagrams

Simple Math

Used in:

SRM 401

Used as:

Division I Level One , Division II Level Two

Writer:

griffon

Testers:

PabloGilberto , Olexiy , gawry

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8776

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12173&pm=8776

Problem Statement

A Ferrers diagram of the partition of positive number n = a₁ + a₂ + ... + a_k, for a list a₁, a₂, ..., a_k of k positive integers with a₁ ≥ a₂ ≥ ... ≥ a_k is an arrangement of n boxes in k rows, such that the boxes are left-justified, the first row is of length a₁, the second row is of length a₂, and so on, with the kth row of length a_k. Let's call a FIELD diagram of order fieldOrder a Ferrers diagram with a₁ ≤ fieldOrder, a₂ ≤ fieldOrder - 1, ..., a_k ≤ fieldOrder - k + 1, so a FIELD diagram can have a number of rows which is less than or equal to fieldOrder. Your method will be given fieldOrder, it should return the total number of FIELD diagrams of order fieldOrder.

Definition

Class:	FIELDDiagrams
Method:	countDiagrams
Parameters:	int
Returns:	long
Method signature:	long countDiagrams(int fieldOrder)
(be sure your method is public)

Constraints

-

fieldOrder will be between 1 and 30, inclusive

Examples

0)

Returns: 4

There are four possible FIELD diagrams for fieldOrder equal to 2, corresponding to partitions: (1), (2), (1, 1), (2,1). They are shown in the picture below. There white stands for unused space in a row and red for boxes, corresponding to FIELD diagrams.

1)

Returns: 13

2)

Returns: 131

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PerfectPowers

Search, Simple Math, Sorting

Used in:

TCO09 Semifinal

Used as:

Division I Level One

Writer:

mohamedafattah

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8774

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13764&pm=8774

Problem Statement

A number is called a perfect power if it can be written in the form m^k, where m and k are positive integers, and k > 1.

Given two positive integers A and B, find the two perfect powers between A and B, inclusive, that are closest to each other, and return the absolute difference between them. If less than two perfect powers exist in the interval, return -1 instead.

Definition

Class:	PerfectPowers
Method:	nearestCouple
Parameters:	long, long
Returns:	long
Method signature:	long nearestCouple(long A, long B)
(be sure your method is public)

Notes

-

1 is a perfect power.

Constraints

-

A will be between 1 and 10^18, inclusive.

-

B will be between A+1 and 10^18, inclusive.

Examples

0)

Returns: 3

1 and 4 are the first pair of perfect powers.

1)

Returns: 1

8 and 9 are the closest pair of perfect powers.

2)

Returns: -1

No pair of perfect powers is present in the interval.

3)

1000000000000000000

Returns: 1

This is the largest possible range, and 8 and 9 are the closest pair of perfect powers.

4)

Returns: 80

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FairDiceGame

Greedy, Simple Math

Used in:

TCO08 Semifinal 2

Used as:

Division I Level One

Writer:

misof

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8769

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12016&pm=8769

Problem Statement

Several people play with a 6-sided die and take alternating turns. In each turn the player starts by throwing the die, and the player who throws a '6' wins immediately. Obviously, each turn entails a one in six chance of winning. As soon as one player wins, the game ends and all other players lose the game.

The game is not fair. For example, in a two-player version, the first player is expected to win 6 out of 11 games.

In our problem playerCount mathematicians decided to play a fair version of the game. After a while, they came up with a solution -- they will not take alternating turns. Instead, they will find and follow a different sequence of turns that will make the game fair. (See notes for a precise definition.)

For simplicity, assume that the players are assigned the first playerCount letters of the alphabet. Then the sequence of turns can be represented as an infinite string of letters. Out of all fair sequences we will be interested in the lexicographically smallest one.

You are given an int playerCount, and an int turnNumber. Your method should find the lexicographically smallest fair sequence of moves for playerCount players, and return a one-character String containing the player that has to play in the turn turnNumber. Turns are numbered starting from 1. If there is no fair sequence of moves for playerCount players, return an empty string instead.

Definition

Class:	FairDiceGame
Method:	getPlayer
Parameters:	int, int
Returns:	String
Method signature:	String getPlayer(int playerCount, int turnNumber)
(be sure your method is public)

Notes

-

Given two different sequences of turns X and Y, sequence X is lexicographically smaller than Y if and only if at the first place where they differ the character in X is earlier in the alphabet than the one in Y.

-

An infinite sequence of turns S is fair if for any player P and for any number of turns T the following sentence is true: If the players take turns according to the sequence, then the probability that player P wins in one of the first T turns is at most equal to 1/playerCount.

Constraints

-

playerCount will be between 2 and 26, inclusive.

-

turnNumber will be between 1 and 20, inclusive.

Examples

0)

Returns: "A"

For two players, there are many fair sequences of turns. In the lexicographically smallest one, the first player must obviously be A.

1)

Returns: "A"

There is at least one fair sequence such that A takes the second turn as well.

2)

Returns: "B"

In the lexicographically smallest fair sequence for two players the player A takes the first three turns, and B takes the fourth one.

3)

Returns: ""

There is no fair sequence of turns for 17 players.

4)

Returns: "B"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CollectingBonuses

Math

Used in:

SRM 400

Used as:

Division I Level Three

Writer:

ymatsu

Testers:

PabloGilberto , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8764

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12172&pm=8764

Problem Statement

A juice company is running a promotion where each juice bottle they sell contains a code that you can redeem for a prize. There are n different codes, each corresponding to a different type of prize. The codes are evenly distributed, so the probability of winning a certain type of prize is 1/n for each bottle. The codes are written underneath the bottle caps, so you can't read them until you buy the bottles. Your goal is to collect k different types of prizes. Return the expected number of bottles you must buy to achieve this goal.

Definition

Class:	CollectingBonuses
Method:	expectedBuy
Parameters:	String, String
Returns:	double
Method signature:	double expectedBuy(String n, String k)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

n and k will contain digits ('0' - '9') only.

-

n and k will represent positive integers without leading zeros.

-

n will represent an integer between 1 and 10^18, inclusive.

-

k will represent an integer between 1 and the integer n represents, inclusive.

Examples

0)

"1"

"1"

Returns: 1.0

With only 1 type of prizes you just need to buy 1 bottle.

1)

"2"

"1"

Returns: 1.0

Now there are 2 types of prizes, but any one will satisfy you, so you again need only 1 bottle.

2)

"2"

"2"

Returns: 3.0

First you buy 1 bottle and collect some type of prizes. After this, you need to collect another type of prizes. Only half of bottles contains it, so in average you must buy 2 more bottles to achieve your goal.

3)

"4"

"3"

Returns: 4.333333333333333

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StrongPrimePower

Simple Math, Simple Search, Iteration

Used in:

SRM 400

Used as:

Division I Level One , Division II Level Two

Writer:

ymatsu

Testers:

PabloGilberto , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8763

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12172&pm=8763

Problem Statement

NOTE: This problem statement contains superscripts that may not display properly if viewed outside of the applet.

A number which can be represented as p^q, where p is a prime number and q is an integer greater than 0, is called a prime power. If q is larger than 1, we call the number a strong prime power. You are given an integer n. If n is a strong prime power, return an int[] containing exactly two elements. The first element is p and the second element is q. If n is not a strong prime power, return an empty int[].

Definition

Class:	StrongPrimePower
Method:	baseAndExponent
Parameters:	String
Returns:	int[]
Method signature:	int[] baseAndExponent(String n)
(be sure your method is public)

Constraints

-

n will contain digits ('0' - '9') only.

-

n will represent an integer between 2 and 10^18, inclusive.

-

n will have no leading zeros.

Examples

0)

"27"

Returns: {3, 3 }

27 = 3³. This is a strong prime power.

1)

"10"

Returns: { }

10 = 2 * 5. This is not a strong prime power.

2)

"7"

Returns: { }

A prime number is not a strong prime power.

3)

"1296"

Returns: { }

4)

"576460752303423488"

Returns: {2, 59 }

5)

"999999874000003969"

Returns: {999999937, 2 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HouseProtection

Geometry, Graph Theory, Search, Simple Math

Used in:

SRM 397

Used as:

Division I Level Three

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8762

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12169&pm=8762

Problem Statement

You have recently started to feel unsafe in your own house, so you decided to place surveillance radars in the garden. When a radar with range r is placed at point S, it totally covers the area of the circle with radius r centered at point S. The maximum allowable range is R, and all your radars must be set to the same range.

There are two types of radars - blue and red. You can buy as many of each as you like, but they can only be placed at certain points in the garden. You are given two int[]s possibleXForBlue and possibleYForBlue, where (possibleXForBlue[i], possibleYForBlue[i]) is the i-th point where you are allowed to place a blue radar. Similarly, you are given two int[]s possibleXForRed and possibleYForRed describing the allowable points for red radars. You cannot place more than one radar at a single point. Also, the area covered by blue radars cannot overlap with the area covered by red radars. Otherwise, the whole system will malfunction.

Your goal is to place the radars in such a way that maximizes the safety factor. The safety factor is the sum of all the areas covered by the radars. Note that if an area is covered by multiple radars, it will count multiple times toward the sum. Return the maximal safety factor you can achieve.

Definition

Class:	HouseProtection
Method:	safetyFactor
Parameters:	int[], int[], int[], int[], int
Returns:	double
Method signature:	double safetyFactor(int[] possibleXForBlue, int[] possibleYForBlue, int[] possibleXForRed, int[] possibleYForRed, int R)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

possibleXForBlue will contain between 1 and 50 elements, inclusive.

-

possibleXForBlue and possibleYForBlue will both contain the same number of elements.

-

Each element of possibleXForBlue will be between -1000 and 1000, inclusive.

-

Each element of possibleYForBlue will be between -1000 and 1000, inclusive.

-

All points represented by possibleXForBlue and possibleYForBlue will be distinct.

-

possibleXForRed will contain between 1 and 50 elements, inclusive.

-

possibleXForRed and possibleYForRed will both contain the same number of elements.

-

Each element of possibleXForRed will be between -1000 and 1000, inclusive.

-

Each element of possibleYForRed will be between -1000 and 1000, inclusive.

-

All points represented by possibleXForRed and possibleYForRed will be distinct.

-

R will be between 1 and 1000, inclusive.

Examples

0)

{ 0, 4 }

{ 0, 0 }

{ 2, 1 }

{ 2, -1 }

Returns: 9.42477796076938

We can place two blue radars at points (0,0) and (4,0) and one red radar at point (2,2). Setting their ranges to 1 will give us the safety factor of about 3.14 * 3 = 9.42.

1)

{ 1 }

{ 1 }

{ 1 }

{ 1 }

Returns: 78.53981633974483

Note that there may be overlap between the allowable points for blue radars and the allowable points for red radars.

2)

{ 0 }

{ 0 }

{ 100 }

{ 0 }

Returns: 15707.963267948966

3)

{ 23, 29, 29, 35 }

{ 77, 79, 75, 77 }

{ 26, 26, 32 }

{ 78, 76, 76 }

Returns: 113.09733552923255

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MaximalProduct

Math

Used in:

SRM 399

Used as:

Division II Level Two

Writer:

andrewzta

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8760

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12171&pm=8760

Problem Statement

You are given an integer s and an integer k. Find k positive integers a₁, a₂, ..., a_k such that their sum is equal to s and their product is the maximal possible. Return their product.

Definition

Class:	MaximalProduct
Method:	maximalProduct
Parameters:	int, int
Returns:	long
Method signature:	long maximalProduct(int s, int k)
(be sure your method is public)

Notes

-

For all valid inputs, the return value will fit in a long.

Constraints

-

k will be between 1 and 20, inclusive.

-

s will be between k and 100, inclusive.

Examples

0)

Returns: 36

The 3 positive integers are 3, 3, 4.

1)

Returns: 10

2)

Returns: 1

3)

Returns: 32

4)

Returns: 12

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AvoidingProduct

Math, Search

Used in:

SRM 399

Used as:

Division I Level One , Division II Level Three

Writer:

andrewzta

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8758

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12171&pm=8758

Problem Statement

You are given a set A of integers and a positive integer n. You must find positive integers x, y and z such that their product is as close to n as possible (minimize |n - x * y * z|), and none of them belongs to A. If there are several such triples, find the one with the smallest x. If there are still several such triples, minimize y. If there is still a tie, minimize z.

You are given the elements of A as a int[] a. Return a int[] with exactly three elements: x, y and z, in this order.

Definition

Class:	AvoidingProduct
Method:	getTriple
Parameters:	int[], int
Returns:	int[]
Method signature:	int[] getTriple(int[] a, int n)
(be sure your method is public)

Constraints

-

a will contain between 0 and 50 elements, inclusive.

-

Each element of a will be between 1 and 1000, inclusive.

-

All elements of a will be distinct.

-

n will be between 1 and 1000, inclusive.

Examples

0)

{2,4}

Returns: {1, 1, 3 }

You can get 3=1*1*3 and 5=1*1*5. 3 is better.

1)

{1}

Returns: {2, 2, 2 }

2)

{1,2}

Returns: {3, 3, 3 }

3)

{1,3}

Returns: {2, 2, 2 }

4)

{1,3}

Returns: {2, 2, 4 }

5)

{1,15}

Returns: {2, 5, 9 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KnightsOut

Math

Used in:

Member SRM 494

Used as:

Division I Level Three

Writer:

ivan_metelsky

Testers:

SnapDragon , Olexiy , Mike Mirzayanov , eleusive , gojira_tc

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8744

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14423&pm=8744

Problem Statement

Mr. Purple is a very imaginative and creative person. In his spare time he invents different puzzles and games. Recently he has come up with a new puzzle called "Knights Out". Mr. Purple likes his new idea very much, but he is somewhat afraid that it may appear to be too easy or too hard. Therefore, Mr. Purple would like to know how many solutions these puzzles have before he presents the idea to puzzle-producing companies.

"Knights Out" is a one-player game played on a NxM rectangular board divided into 1x1 squares. Each square on the board can be white or black. Initially all the squares are white.

A knight is a chess piece that moves by simultaneously shifting one square horizontally and two squares vertically, or one square vertically and two squares horizontally. Two squares A and B on the board are called neighboring if it's possible to make a single knight's move to reach B from A.

In one move the player can choose a square on the board and simultaneously change colors of the chosen square and all its neighboring squares (white becomes black and vice versa). The game is finished when all the squares are colored black.

A sequence of moves is called a solution if it transforms the white board into a black one, and there's no cell which is chosen in more than one move. Note that when a cell is chosen, its neighbors which get changed do not also count as being "chosen" in that step. It's not hard to see that the order of moves doesn't matter, so any solution can be viewed as a set of moves. Two solutions are considered distinct if the corresponding sets are distinct. Return the number of distinct solutions modulo 123,456,789.

Definition

Class:	KnightsOut
Method:	count
Parameters:	int, int
Returns:	int
Method signature:	int count(int N, int M)
(be sure your method is public)

Constraints

-

N and M will each be between 1 and 150, inclusive.

Examples

0)

Returns: 4

4 possible solutions are listed below ('X' means a square should be chosen and '.' means it shouldn't):

XX.	.X.	XXX	.XX
XX.	XXX	.X.	.XX

1)

Returns: 1

The only solution is to choose each square on the board.

2)

Returns: 16

3)

Returns: 1

4)

Returns: 77502052

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ModuleSequence

Brute Force, Math

Used in:

SRM 497

Used as:

Division I Level Three

Writer:

stone

Testers:

PabloGilberto , Yarin , ivan_metelsky , Chmel_Tolstiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8741

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14426&pm=8741

Problem Statement

You are given four longs K, N, A and B. Generate an integer list X of length B-A+1 using the following recursive definition:

        X[0]=(K*A) MOD N
	(note that K*A may overflow a 64-bit integer variable)

        X[i]=(X[i-1]+K) MOD N

Given another two longs lower and upper, return the number of elements in the list which are between lower and upper, inclusive.

Definition

Class:	ModuleSequence
Method:	countElements
Parameters:	long, long, long, long, long, long
Returns:	long
Method signature:	long countElements(long K, long N, long A, long B, long lower, long upper)
(be sure your method is public)

Constraints

-

K will be between 0 and 10,000,000,000, inclusive.

-

N will be between 1 and 10,000,000,000, inclusive.

-

A will be between 0 and 10,000,000,000, inclusive.

-

B will be between A and 10,000,000,000, inclusive.

-

lower will be between 0 and N-1, inclusive.

-

upper will be between lower and N-1, inclusive.

Examples

0)

Returns: 3

The generated list is: 2, 4, 6, 1, 3.

1)

Returns: 8

2)

Returns: 6

Note that K, A and B may be greater than N.

3)

Returns: 9

4)

Returns: 4770

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Textures

Math

Used in:

MM 37

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8737

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12203&pm=8737

Problem Statement

You are given a square black-and-white image divided into two parts, each part filled with its own texture. Your task is to separate the parts and return the corresponding marking of the image.

Implementation

You will implement one method recognize. image is a square image SxS pixels (S can be determined as number of elements in image), character j of image[i] representing the color of the pixel in row i and column j, '0' for black and '1' for white. You must return a marking of the image in the same format, '0' for a pixel that belongs to one texture, and '1' for a pixel that belongs to the other texture. It doesn't matter which texture you mark with '0's, the marking which results in higher percentage of correctly marked pixels is used.

Image generation

To generate a texture, the number of axes is chosen between 2 and 4, inclusive, each being vertical (dx=0, dy=1), horizontal (dx=1, dy=0) or diagonal (dx=dy=1 or dx=-dy=1). Several axes of the set can have the same direction. For each axis, its "weight" is chosen between 1 and 5.

The neighborhood of a pixel (x,y) for a chosen set of axes is generated as follows:

    pixel (x,y) is added to the neighborhood
    for each axis
        for k = 1 .. weight
            pixels ((x+dx*k+S)%S,(y+dy*k+S)%S) and ((x-dx*k+S)%S,(y-dy*k+S)%S) are added to the neighborhood

Note that the neighborhood of a pixel is a multiset and can contain each pixel more than once.

The initial state of the texture is generated randomly by assigning each pixel color '0' or '1'.

The procedure of adjusting a pixel's color is as follows:

    if the number of '1's in its neighborhood is strictly greater than the number of '0's
         set the color of the pixel to '1'
    else 
         set the color of the pixel to '0'

The image is then modified iteratively:

    for k = 1 .. 2*S*S
        pick random pixel
        adjust its color
    for i = 1 .. S
        for j = 1 .. S
            pick pixel (i,j)
            adjust its color

Finally, the image is inverted with a probability of 1/3.

To generate an image with two textures, two images are generated independently, as above. We then use a stochastic flood fill algorithm to determine which pixels of the final image are colored according to which texture. Four (unique) pixels out of an SxS pixel image are chosen randomly. Two of these are colored black, and two are colored blue. We then perform the following to color the rest of the image, where neighbor means adjacent in one of the four cardinal directions:

    while(there is an uncolored pixel)
        pick a colored pixel (i,j) with an uncolored neighbor (ii,jj) 
        color the (ii,jj) with the color of (i,j)

If this procedure produces more than two colored regions (a colored region is a connected component of all the same color), it is repeated from scratch.

Finally, the black pixels are replaced with the pixel values from one texture, and the blue pixels are replaced with the pixel values from the second texture.

Scoring

Your score for an individual test case will be the number of pixels you marked correctly multiplied by 100/(S*S). Invalid return (wrong number of elements in return, or characters other than '0' or '1') will result in 0 score for that test case.

Your overall score will be the sum of your individual scores.

Tools

A visualization tool is provided at http://www.topcoder.com/contest/problem/Textures/vis.html

Definition

Class:	Textures
Method:	recognize
Parameters:	String[]
Returns:	String[]
Method signature:	String[] recognize(String[] image)
(be sure your method is public)

Notes

-

The time limit is 10 seconds and the memory limit is 1024M.

-

There are 10 example test cases and 500 full submission test cases.

-

For more details on the image generation, see the visualizer source.

Constraints

-

S will be between 100 and 300, inclusive, and will be divisible by 10.

Examples

0)

"1"

Returns: 
"Seed = 1
S = 260
Texture:<br/>
dx = 1, dy = 0, w = 1<br/>
dx = 1, dy = 0, w = 2<br/>
Texture:<br/>
dx = 0, dy = 1, w = 5<br/>
dx = 1, dy = -1, w = 2<br/>
"

1)

"2"

Returns: 
"Seed = 2
S = 160
Texture:<br/>
dx = 0, dy = 1, w = 1<br/>
dx = 1, dy = 1, w = 5<br/>
Texture:<br/>
dx = 1, dy = -1, w = 2<br/>
dx = 0, dy = 1, w = 4<br/>
dx = 1, dy = -1, w = 4<br/>
dx = 1, dy = 0, w = 4<br/>
"

2)

"3"

Returns: 
"Seed = 3
S = 290
Texture:<br/>
dx = 0, dy = 1, w = 4<br/>
dx = 1, dy = 1, w = 5<br/>
Texture:<br/>
dx = 1, dy = 1, w = 4<br/>
dx = 1, dy = -1, w = 5<br/>
dx = 0, dy = 1, w = 3<br/>
"

3)

"4"

Returns: 
"Seed = 4
S = 100
Texture:<br/>
dx = 0, dy = 1, w = 3<br/>
dx = 1, dy = 1, w = 1<br/>
Texture:<br/>
dx = 1, dy = -1, w = 4<br/>
dx = 1, dy = -1, w = 1<br/>
"

4)

"5"

Returns: 
"Seed = 5
S = 270
Texture:<br/>
dx = 0, dy = 1, w = 3<br/>
dx = 1, dy = -1, w = 5<br/>
Texture:<br/>
dx = 1, dy = -1, w = 1<br/>
dx = 1, dy = 1, w = 2<br/>
dx = 1, dy = 1, w = 3<br/>
dx = 0, dy = 1, w = 5<br/>
"

5)

"6"

Returns: 
"Seed = 6
S = 130
Texture:<br/>
dx = 1, dy = 1, w = 1<br/>
dx = 1, dy = 0, w = 1<br/>
Texture:<br/>
dx = 1, dy = 0, w = 1<br/>
dx = 0, dy = 1, w = 1<br/>
dx = 0, dy = 1, w = 5<br/>
"

6)

"7"

Returns: 
"Seed = 7
S = 280
Texture:<br/>
dx = 1, dy = 0, w = 2<br/>
dx = 1, dy = 1, w = 5<br/>
dx = 1, dy = 1, w = 2<br/>
dx = 0, dy = 1, w = 1<br/>
Texture:<br/>
dx = 0, dy = 1, w = 3<br/>
dx = 0, dy = 1, w = 2<br/>
"

7)

"8"

Returns: 
"Seed = 8
S = 140
Texture:<br/>
dx = 1, dy = 1, w = 4<br/>
dx = 0, dy = 1, w = 4<br/>
Texture:<br/>
dx = 1, dy = 0, w = 2<br/>
dx = 1, dy = 1, w = 1<br/>
dx = 1, dy = 1, w = 4<br/>
"

8)

"9"

Returns: 
"Seed = 9
S = 200
Texture:<br/>
dx = 1, dy = -1, w = 3<br/>
dx = 1, dy = -1, w = 4<br/>
Texture:<br/>
dx = 0, dy = 1, w = 3<br/>
dx = 0, dy = 1, w = 2<br/>
"

9)

"10"

Returns: 
"Seed = 10
S = 140
Texture:<br/>
dx = 0, dy = 1, w = 2<br/>
dx = 1, dy = -1, w = 4<br/>
dx = 1, dy = -1, w = 4<br/>
Texture:<br/>
dx = 1, dy = 0, w = 2<br/>
dx = 1, dy = 1, w = 2<br/>
dx = 0, dy = 1, w = 4<br/>
dx = 1, dy = 1, w = 2<br/>
"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RollingLetters

Math, Simulation

Used in:

College Tour West China

Used as:

Division I Level Three

Writer:

slex

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8731

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12240&pm=8731

Problem Statement

A display mechanism is built from several spinning reels arranged in a line, from left to right. Each reel has a number of distinct letters on its perimeter, and only one of them is visible at a time. The visible letter changes every second. Each reel may have a different number of letters.

You are given a String[] reels, where reels[k] represents the letters on the k-th reel.

At time 0, each reel shows the letter at index 0 from the corresponding element of reels. At every second, the visible letter changes from the letter at index i to the letter at index i+1. Since reels are circular, the first letter shows up again after the last one.

Return the first second when the text displayed is equal to requiredText, or -1 if this will never happen.

Definition

Class:	RollingLetters
Method:	getTime
Parameters:	String[], String
Returns:	long
Method signature:	long getTime(String[] reels, String requiredText)
(be sure your method is public)

Notes

-

The return value will fit in a signed 64 bit integer.

Constraints

-

reels will contain between 1 and 50 elements, inclusive.

-

Each element of reels will contain between 2 and 26 uppercase letters ('A'-'Z'), inclusive.

-

Characters in each element of reels will be distinct.

-

requiredText will contain exactly N uppercase letters ('A'-'Z'), where N is the number of elements in reels.

Examples

0)

{"XYZ", "DEF", "OPRS"}

"YES"

Returns: 7

The message displayed at each second is:

0: XDO
1: YEP
2: ZFR
3: XDS
4: YEO
5: ZFP
6: XDR
7: YES

1)

{"ABC","ABC"}

"AB"

Returns: -1

The only possible messages are "AA", "BB", "CC".

2)

{"ABC"}

"X"

Returns: -1

There is no 'X' on the reel.

3)

{"CPKHFQEYXVMODNRTSGUBLJ", "TJLSURVHFQPAXGCEI", "JXNSGADPEWICKLFMVOQ", "UOFVKGQIJRECMWXADTPNL",
"OREWASJFLY", "HBEC", "ESDRVXCNQUFWKGTOLH", "CPLTAMBHYSQDVJIORNW", "CG"}

"CAIIEHLQC"

Returns: 4088392

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

VariableSpeedLimit

Search, Simple Math, Simulation

Used in:

SRM 393

Used as:

Division II Level One

Writer:

StevieT

Testers:

PabloGilberto , Olexiy , gawry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8730

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11127&pm=8730

Problem Statement

In order to make its roads safer, the government of a particular country has decided to introduce a speed limit that varies throughout the day. At busy times, the speed limit will decrease to reduce the risk of a dangerous accident. You need to drive a distance of journeyLength units and want to know how long it will take you.

You are given details of the speed limit in a int[] speedLimit. Element i (zero-based) gives the speed limit in DISTANCE UNITS/TIME UNITS that is in force between times T = i and T = i + 1. speedLimit describes the speed limit for a full day, so after this the pattern repeats (i.e., if N is the number of elements in speedLimit, the speed limit between times N and N+1 is given by speedLimit[0], etc.). You start your journey at time T = 0 and should assume that you travel exactly at the speed limit for your entire journey. Return a double containing the amount of time it takes to complete your journey.

Definition

Class:	VariableSpeedLimit
Method:	journeyTime
Parameters:	int, int[]
Returns:	double
Method signature:	double journeyTime(int journeyLength, int[] speedLimit)
(be sure your method is public)

Notes

-

Your return value must be accurate to an absolute or relative tolerance of 1E-9.

Constraints

-

journeyLength will be between 1 and 100000 (10^5), inclusive.

-

speedLimit will contain between 1 and 50 elements, inclusive.

-

Each element of speedLimit will be between 1 and 100, inclusive.

Examples

0)

{50}

Returns: 2.0

Here the speed limit doesn't change. The journey therefore takes a time of DISTANCE/SPEED = 100/50 = 2 time units.

1)

{50,25}

Returns: 2.5

Now the speed limit drops to 25 every other time unit. You drive 50 units in the first time unit and 25 in the second. You reach the end of your journey halfway through the third time unit.

2)

{50,40,30,40,50}

Returns: 24.0

3)

{80,43,57,23,28,45,60,75,73,80}

Returns: 37.4

4)

{26,30,62,55,51,56,58,4,60,23,31}

Returns: 415.03333333333336

5)

{45,90,13,4,81,50,81,10,64,86,69}

Returns: 182.8395061728395

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IngredientProportions

Graph Theory, Simple Math, String Parsing

Used in:

SRM 429

Used as:

Division I Level Two , Division II Level Three

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8729

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13520&pm=8729

Problem Statement

Your friend has invented a splendid cocktail consisting of N ingredients. However, she has forgotten the amount of each ingredient that goes into the recipe.

For N-1 pairs of ingredients, she remembers the proportion in which the ingredients within each pair should be added to the cocktail. Fortunately, these N-1 proportions are sufficient to restore the recipe of the entire cocktail.

You are given a String[] proportions containing the N-1 proportions. Each element is formatted "#<a> and # as :<q>" (quotes for clarity), which means that the mass of ingredient <a> divided by the mass of ingredient in the cocktail must be equal to /<q> (all ingredients are 0-indexed). Return a int[] containing exactly N elements, where the i-th element is the mass of ingredient i, such that all the given proportions are satisfied and the total mass is as small as possible. The total mass must be greater than 0.

Definition

Class:	IngredientProportions
Method:	getMasses
Parameters:	String[]
Returns:	int[]
Method signature:	int[] getMasses(String[] proportions)
(be sure your method is public)

Constraints

-

proportions will contain between 1 and 9 elements, inclusive.

-

proportions will contain exactly N-1 elements, where N is the number of ingredients in the cocktail.

-

Each element of proportions will contain exactly 16 characters.

-

Each element of proportions will be formatted as described in the statement.

-

Each <a> will be between 0 and N-1, inclusive.

-

Each will be between 0 and N-1, inclusive.

-

Each will be between 1 and 9, inclusive.

-

Each <q> will be between 1 and 9, inclusive.

-

The information given in proportions will be sufficient to restore the recipe of the cocktail uniquely up to a constant factor.

Examples

0)

{"#0 and #1 as 6:4"}

Returns: {3, 2 }

Taking 6 units of ingredient #0 and 4 units of ingredient #1 would satisfy the proportion, but it wouldn't give the smallest possible total mass. To minimize the total mass, divide the masses by 2.

1)

{"#0 and #1 as 9:8","#1 and #2 as 9:8"}

Returns: {81, 72, 64 }

2)

{"#4 and #0 as 1:1", "#4 and #1 as 3:1", "#4 and #2 as 5:1", "#4 and #3 as 7:1"}

Returns: {105, 35, 21, 15, 105 }

The mass of ingredient #4 should be divisible by 3, 5 and 7. The smallest such number is 105.

3)

{"#2 and #3 as 6:8", "#0 and #1 as 9:3", "#3 and #0 as 7:5"}

Returns: {60, 20, 63, 84 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SumOfPowers

Advanced Math

Used in:

SRM 397

Used as:

Division I Level Two

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8725

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12169&pm=8725

Problem Statement

NOTE: This problem statement contains superscripts that may not display properly if viewed outside of the applet.

You are given ints n and k. Return the value of the sum 1^k + 2^k + 3^k + ... + n^k modulo 1000000007.

Definition

Class:	SumOfPowers
Method:	value
Parameters:	int, int
Returns:	int
Method signature:	int value(int n, int k)
(be sure your method is public)

Constraints

-

n will be between 1 and 10⁹, inclusive.

-

k will be between 1 and 50, inclusive.

Examples

0)

Returns: 15

Here, we have arithmethic progression: 1 + 2 + 3 + 4 + 5 = 15.

1)

Returns: 30

Just a little bit more complicated example here: 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16 = 30.

2)

Returns: 1002001

This one would be harder to check by hand.

3)

123456789

Returns: 383478132

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ReversingPrefixes

Dynamic Programming, Math, String Manipulation

Used in:

TCHS08 Finals

Used as:

Division I Level Two

Writer:

andrewzta

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8713

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12046&pm=8713

Problem Statement

You are given a String s. In increasing order, consider each integer i between 1 and the length of s, inclusive. For each value of i, you can choose whether or not to perform the following operation: Take the prefix of length i of the current string and reverse it. Your ultimate goal is to end up with the alphabetically earliest string possible.

For example, if s = "BCDAF", you should reverse the prefix of length 3 to get "DCBAF", and then reverse the prefix of length 4 to get "ABCDF".

Return the alphabetically earliest string possible.

Definition

Class:	ReversingPrefixes
Method:	getMinimal
Parameters:	String
Returns:	String
Method signature:	String getMinimal(String s)
(be sure your method is public)

Notes

-

A String A comes before a String B alphabetically if A is a proper prefix of B, or if A has a smaller character at the first position where the strings differ.

Constraints

-

s will contain between 1 and 50 characters, inclusive.

-

s will contain only uppercase letters ('A'-'Z').

Examples

0)

"BCDAF"

Returns: "ABCDF"

The example from the problem statement.

1)

"ABBA"

Returns: "AABB"

2)

"ACAB"

Returns: "AACB"

Here, you cannot get "AABC". The best you can get is "AACB" by reversing prefixes of length 2 and 3.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PredictionCardGame

Dynamic Programming, Math

Used in:

TCHS08 Finals

Used as:

Division I Level Three

Writer:

andrewzta

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8712

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12046&pm=8712

Problem Statement

You have a deck of cards containing n red and m black cards. Initially, you have c chips. The cards are shuffled and then dealt one after another. Before each card is dealt, you place a bet of B chips (where B is between 0 and the number of chips you have left, inclusive) and predict whether that card will be red or black. If your prediction is correct, you receive back the B chips that you bet and win an additional B chips. If your prediction is incorrect, you lose the B chips that you bet.

You are a cautious player, so your strategy is to play in such a way that maximizes the number of chips you have at the end of the game in the worst possible case. In other words, your strategy must guarantee that you end the game with at least X chips, regardless of the order of cards in the deck, where X is as large as possible. Return this value of X.

For example, let n = 1, m = 2 and c = 3. The following optimal strategy will guarantee that you end the game with at least 8 chips: Bet 1 chip that the first card is black. If it is, you will then have 4 chips. Skip the next card, and bet all 4 chips on the last card. You will know the color of that last card because you will have already seen the other two cards. If you lose your first bet, you will have 2 chips left, and the two remaining cards will be black. Bet all your chips on each of the remaining cards, and you will double your chips twice, for a total of 8 chips. No other strategy can guarantee more than 8 chips in the worst case.

Definition

Class:	PredictionCardGame
Method:	winnings
Parameters:	int, int, int
Returns:	int
Method signature:	int winnings(int n, int m, int c)
(be sure your method is public)

Constraints

-

n and m will each be between 0 and 10, inclusive.

-

c will be between 1 and 30, inclusive.

Examples

0)

Returns: 8

The example from the problem statement.

1)

Returns: 30720

This time all cards are red, so you must bet each time.

2)

Returns: 2

Do not bet on the first card (or you can lose everything).

3)

Returns: 2

You cannot split your chip, so you must wait until all the remaining cards are of the same color. In the worst case, this will not happen until there is only one card left.

4)

Returns: 20

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AverageCandyLifetime

Simple Math

Used in:

SRM 392

Used as:

Division II Level One

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8707

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11126&pm=8707

Problem Statement

On January 1, 2007, a confectioner made several candies.

On the last day of each month she allows her children to eat several of those candies.

The lifetime of a candy is the number of days between January 1 and the day the candy is eaten, inclusive. For example, the lifetime of a candy eaten on January 31 is 31, and the lifetime of a candy eaten on December 31 is 365 (note that 2007 wasn't a leap year).

You are given a int[] eatenCandies, the i-th element of which is the number of candies eaten on the last day of the i-th month of 2007 (January is month 0, February is month 1, etc.). Return the average lifetime of the candies.

Definition

Class:	AverageCandyLifetime
Method:	getAverage
Parameters:	int[]
Returns:	double
Method signature:	double getAverage(int[] eatenCandies)
(be sure your method is public)

Notes

-

The year 2007 was not a leap year.

-

The number of days in the months of 2007, in order, were 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30 and 31.

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

eatenCandies will contain exactly 12 elements.

-

Each element of eatenCandies will be between 0 and 1000, inclusive.

-

The sum of all the elements in eatenCandies will be greater than 0.

Examples

0)

{1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0}

Returns: 60.5

One candy was eaten on January 31 and the other was eaten on March 31. The lifetimes of the candies are 31 and 31+28+31=90. The average lifetime is (31+90)/2=60.5.

1)

{0, 1000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}

Returns: 59.0

All candies were eaten on February 28. The lifetime of each candy is 31+28=59, so the average candy lifetime is 59.0.

2)

{0, 0, 0, 0, 0, 1, 0, 0, 0, 50, 0, 0}

Returns: 301.5882352941176

Most of the candies were eaten on October 31 (Halloween), and the lifetime of each of those candies is 304. The average lifetime is smaller than 304, because of a candy with lifetime 181, eaten on June 30.

3)

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Returns: 252.80769230769232

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

JohnnysCannon

Math

Used in:

TC China 08 - 1E

Used as:

Division I Level One

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , Mike Mirzayanov , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8704

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13677&pm=8704

Problem Statement

Johnny has recently constructed a cannon, and he wants to a hit a ground target that is distance units away. The cannon shoots bullets at velocity units per second. When a bullet is in the air, its flight follows the standard laws of physics. This means that if he shoots a bullet at angle alpha from the ground, it will travel a distance of

( 2 * velocity^2 * sin(alpha) * cos(alpha) ) / g ,

where g is the acceleration of gravity on Earth. In this problem, we will use 10 as the value of g.

The cannon can only be set at the angles given in the int[] angles (all angles are given in degrees). Johnny must pick the angle that will land the bullet as close as possible to the target. Return this closest possible distance between the landing point and the target as a double.

Definition

Class:	JohnnysCannon
Method:	getDistance
Parameters:	int, int, int[]
Returns:	double
Method signature:	double getDistance(int velocity, int distance, int[] angles)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1e-9.

Constraints

-

velocity will be between 1 and 1000, inclusive.

-

distance will be between 0 and 100000, inclusive.

-

angles will contain between 1 and 50 elements, inclusive.

-

Each element of angles will be between 0 and 90, inclusive.

Examples

0)

{ 0, 45, 90 }

Returns: 37.5

Here we can choose 0, 45 or 90 degrees. The first and the last options are not very clever as we will shoot ourselves rather than hitting any target. So, the best possibility is 45 degrees.

1)

{ 23, 76, 33, 12, 45 }

Returns: 0.30528437214108894

Here are the distances the bullet will travel using the given angles:

     23 degrees: 7.193...

     76 degrees: 4.694...

     33 degrees: 9.135...

     12 degrees: 4.067...

     45 degrees: 10.0

We will be closest to hitting the target if we choose 76 degrees.

2)

{ 4, 55, 22, 13, 7, 88, 90 }

Returns: 14.999999999999877

3)

{ 4, 55, 22, 13, 7, 88, 90 }

Returns: 19013.842626068294

4)

{ 45 }

Returns: 90000.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PrettyPrintASpiral

Brute Force, Simple Math

Used in:

TCO09 Qual 3

Used as:

Division I Level Two

Writer:

misof

Testers:

PabloGilberto , vorthys , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8693

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13758&pm=8693

Problem Statement

Consider an infinite square grid. Each square in the grid can be represented by a pair of integer coordinates that specify its row and column.

We will fill the entire grid with a spiral of positive integers. We will start by writing the number 1 into the square in row 0, column 0. Then we will write the number 2 into the square in row 0, column 1. From there, the spiral will continue in a counter-clockwise direction. The next few numbers are placed as shown in the scheme below:

                columns
         -3 -2 -1  0  1  2  3
         --------------------
    -3 | 37 36 35 34 33 32 31
    -2 | 38 17 16 15 14 13 30
    -1 | 39 18  5  4  3 12 29
rows 0 | 40 19  6  1  2 11 28
     1 | 41 20  7  8  9 10 27
     2 | 42 21 22 23 24 25 26
     3 | 43 44 45 46 .. .. ..

Your task will be to return a String[] containing a pretty-printed version of a rectangular part of the filled grid.

More precisely, you will be given four ints row1, col1, row2, and col2. Here, row1,col1 will be the coordinates of the top left cell, and row2,col2 the coordinates of the bottom right cell to be displayed.

The returned String[] must be formatted according to the following rules:

The String[] contains one element for each row of the displayed rectangle. The elements are ordered by the row coordinate they describe.
Each element is a concatenation of space-separated tokens, each describing a cell in the corresponding row. The tokens are ordered by the column coordinates of cells they describe.
All tokens in the entire output have the same length.
The length of a token is minimal, i.e., equal to the number of digits in the largest number displayed.
Tokens that contain numbers with fewer digits are padded from the left using spaces.

Definition

Class:	PrettyPrintASpiral
Method:	getWindow
Parameters:	int, int, int, int
Returns:	String[]
Method signature:	String[] getWindow(int row1, int col1, int row2, int col2)
(be sure your method is public)

Notes

-

The constraints guarantee that the returned String[] will have at most 50 elements, and the length of each element will be at most 50.

Constraints

-

row1 will be between -5,000 and 5,000, inclusive.

-

col1 will be between -5,000 and 5,000, inclusive.

-

row2 will be between -5,000 and 5,000, inclusive.

-

col2 will be between -5,000 and 5,000, inclusive.

-

row2-row1 will be between 0 and 49, inclusive.

-

col2-col1 will be between 0 and 4, inclusive.

Examples

0)

Returns: {"1" }

The spiral starts at coordinates (0,0).

1)

-1

-2

-1

Returns: {"18  5  4  3" }

Note that the single-digit values are now padded with spaces.

2)

-2

Returns: {"13 30", "12 29", "11 28" }

3)

-3

-3

Returns: 
{"37 36 35 34",
"38 17 16 15",
"39 18  5  4",
"40 19  6  1",
"41 20  7  8",
"42 21 22 23" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MagicLabeling

Graph Theory, Simple Math

Used in:

TCO08 Round 4

Used as:

Division I Level One

Writer:

ivan_metelsky

Testers:

PabloGilberto , legakis , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8676

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12014&pm=8676

Problem Statement

You are given a String[] graph, containing N elements and representing an undirected graph on N vertices. The j-th character in the i-th element of graph (which is the same as the i-th character in the j-th element of graph) is 'Y' if the i-th and j-th vertices of the graph are connected by an edge, and is 'N' otherwise.

You should label each vertex of the graph with an integer between 1 and M, inclusive, and then label each edge with the sum of its end vertices' labels. The labeling of vertices is called magic if each edge is labeled with the same integer. Two labelings of vertices are considered distinct if there's at least one vertex which has different labels in these labelings. Calculate the total count of distinct magic labelings of the given graph. Return this number modulo 1,000,003.

Definition

Class:	MagicLabeling
Method:	count
Parameters:	String[], int
Returns:	int
Method signature:	int count(String[] graph, int M)
(be sure your method is public)

Constraints

-

graph will contain between 1 and 50 elements, inclusive.

-

Each element of graph will contain the same number of characters as the number of elements in graph.

-

Each character in each element of graph will be 'Y' or 'N'.

-

The i-th character in the i-th element of graph will be 'N' for all possible i.

-

The i-th character in the j-th element of graph will be the same as the j-th character in the i-th element of graph for all possible i and j.

-

M will be between 1 and 100, inclusive.

Examples

0)

{"NNNNN",
 "NNNNN",
 "NNNNN",
 "NNNNN",
 "NNNNN"}

Returns: 970003

Here we have 5 isolated vertices. As there are no edges at all, any labeling is magic. So the answer is 100^5 % 1000003 = 970003.

1)

{"NNNNN",
 "NNNNN",
 "NNNNY",
 "NNNNN",
 "NNYNN"}

Returns: 970003

An edge and 3 isolated vertices. With a single edge, any labeling is still valid.

2)

{"NYY",
 "YNN",
 "YNN"}

Returns: 100

Two edges joined at vertex 0. The labeling is magic if and only if vertices 1 and 2 have the same labels.

3)

{"NYNN",
 "YNNN",
 "NNNY",
 "NNYN"}

Returns: 19

Two separate edges. You can obtain the following sums on a single edge: 2 (1+1), 3 (1+2, 2+1), 4 (1+3, 2+2, 3+1), 5 (2+3, 3+2) and 6 (3+3). The number of ways to have the same sum on both edges is 1*1 + 2*2 + 3*3 + 2*2 + 1*1 = 19.

4)

{"NYY",
 "YNY",
 "YYN"}

Returns: 15

A triangle. The labeling is magic if and only if all vertices have the same labels.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KPlanetaryAlignment

Math, Search

Used in:

SRM 414

Used as:

Division I Level Three

Writer:

StevieT

Testers:

PabloGilberto , Olexiy , gawry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8673

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13505&pm=8673

Problem Statement

A particular star system consists of a single star, with N planets orbiting it. Each planetary orbit is a perfect circle of distinct radius centered on the star and all orbits lie in the same 2-D plane. The planets move along their circular paths with constant speed and planet i completes 1 full orbit in the time given by the absolute value of periods[i]. periods[i] will be positive if planet i orbits clockwise and negative if it orbits counter-clockwise. A k-planetary alignment occurs when an infinite straight line exists, passing through the center of the star and through the centers of at least k of the planets. A N-planetary alignment occurs at time T = 0, i.e., all the planets lie in a line at this time (see notes for clarification). Return the number of distinct times between T1 and T2, inclusive, when a k-planetary alignment occurs.

Definition

Class:	KPlanetaryAlignment
Method:	number
Parameters:	int[], int, int, int
Returns:	int
Method signature:	int number(int[] periods, int k, int T1, int T2)
(be sure your method is public)

Notes

- The constraints ensure the return value will fit in a signed 32-bit integer.

- Alignments can occur with the planets either on the same side of the star or diametrically opposite each other.

- The configuration of the planets at T = 0 (i.e., whether the planets are all on the same side, or some are diametrically opposite) makes no difference to the answer.

Constraints

- periods will contain between 2 and 5 elements, inclusive.

- Each element of periods will be a non-zero integer between -100 and 100, inclusive.

- The elements of periods will be distinct.

- k will be between 2 and the number of elements in periods, inclusive.

- T2 will be between 0 and 50,000,000 (5 * 10^7), inclusive.

- T1 will be between 0 and T2, inclusive.

Examples

0)

{8,40}

Returns: 5

Here, the first planet is rotating 5 times as quickly as the second. Ater 5 seconds, the first will have completed 5/8 of an orbit, while the second will have completed 5/40 = 1/8 of an orbit. They are therefore diametrically opposite and this is the first 2-alignment after time 0. Further 2-alignments happen at T = 10, 15 and 20.

1)

{8,24,40}

Returns: 8

With an additional planet, 2-alignments happen at T = 0, 5, 6, 10, 12, 15, 18, 20.

2)

{8,24,40}

Returns: 4

3-alignments of the same set of planets happen at T = 0, 30, 60, 90.

3)

{-10,10}

Returns: 10

Now that the planets are rotating in opposite directions, 2-alignments occur every 2 1/2 seconds.

4)

{-1,2,3,4,5}

Returns: 53333

5)

{-1,1}

Returns: 200001

6)

{-2,91,87,77,71}

50000000

Returns: 1471

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DiscountCombination

Greedy, Simple Math, Simple Search, Iteration

Used in:

TCO08 Round 1

Used as:

Division I Level One

Writer:

ivan_metelsky

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8641

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12011&pm=8641

Problem Statement

There's a shoe store in which some models are popular, and some are not. In order to sell more unpopular models, the store introduced a system of discounts. Each discount works in the following way: if you buy an unpopular model for a cost of COST, then you can buy a popular model with a PERCENT% discount. However, the owner of the store is greedy, and therefore only discounts with PERCENTs equal to 1, 2 and 3 were introduced.

After it became obvious that such low discounts didn't work well, the store allowed people to apply more than one discount to the same pair of shoes. For example, you can buy three unpopular models, obtain three discounts and use all three to reduce the cost of the same popular model. When many discounts are applied to the same model, they are applied one after another. For example, if you apply 2% and 3% discounts to a model with cost 100, it's cost will be 0.98 * 0.97 * 100 = 95.06.

The available discounts are given in a String[] discounts, each element of which is formatted "COST PERCENT" (quotes for clarity). Different elements of discounts correspond to different unpopular models. You want to buy a popular model, which costs price. In order to reduce the model's cost, you can buy some unpopular models and obtain discounts from them, but you don't wish to buy the same unpopular model more than once. Return the minimum amount of money you need to spend in order to buy the desired popular model.

Definition

Class:	DiscountCombination
Method:	minimumPrice
Parameters:	String[], int
Returns:	double
Method signature:	double minimumPrice(String[] discounts, int price)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

discounts will contain between 1 and 50 elements, inclusive.

-

Each element of discounts will be formatted "COST PERCENT" (quotes for clarity), where COST and PERCENT are integers with no leading zeros.

-

Each COST will be between 1 and 10,000,000, inclusive.

-

Each PERCENT will be between 1 and 3, inclusive.

-

price will be between 1 and 1,000,000,000, inclusive.

Examples

0)

{"1 1", "1 2", "1 3"}

Returns: 97.06

The best choice is to take 3% and 2% discounts. You pay 2 for unpopular models and reduce the cost of the popular model to 95.06.

1)

{"1000 1", "100 2", "10 3"}

Returns: 33.0

It doesn't make sense to use any discounts.

2)

{"10 2", "2 3", "6 2", "3 2", "3 1",
 "2 3", "9 3", "4 3", "2 3", "10 1"}

1000000000

Returns: 7.921497975738132E8

price is very large and discounts are cheap, so we use all of them.

3)

{"8667276 2",
 "3833771 1",
 "9208836 1",
 "5081823 3",
 "3367749 1",
 "4393655 2",
 "552508 1",
 "8648685 2",
 "3798496 2",
 "8104796 1"}

246918635

Returns: 2.415526549689562E8

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PreciousStones

Greedy, Math, Search

Used in:

TCO08 Round 2

Used as:

Division I Level Three

Writer:

legakis

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8605

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12012&pm=8605

Problem Statement

Dr. Agnew and Dr. Austin have acquired a bag of stones, each containing some amount of silver and gold. Dr. Agnew is only interested in the silver contained in the stones, while Dr. Austin is only interested in the gold. Using their sophisticated instruments, they have measured the value of the silver and gold in each stone. They want to divide the stones between them, cutting some if necessary, in such a way that they each get the same value of the element they are interested in, and that that value is as high as possible.

Given the value of silver and gold in each stone, determine the highest value that both Dr. Agnew and Dr. Austin can receive of the element they want. Assume that each element is distributed uniformly within each stone, so that if they cut a stone in two parts, each part will have the same ratio of elements as did the whole stone. Between them they must take all of the stones, without throwing any out.

The value of the precious elements in each stone will be given as two int[]s, silver and gold, where silver[i] and gold[i] give the value of the silver and gold, respectively, in stone i.

Definition

Class:	PreciousStones
Method:	value
Parameters:	int[], int[]
Returns:	double
Method signature:	double value(int[] silver, int[] gold)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1e-9.

Constraints

-

silver and gold will each contain between 1 and 50 elements, inclusive.

-

silver and gold will contain the same number of elements.

-

Each element of silver and gold will be between 0 and 100, inclusive.

Examples

0)

{ 10, 6 }

{ 3, 10 }

Returns: 10.0

If Dr. Agnew takes the first stone and Dr. Austin takes the second, they can each get a value of 10.

1)

{ 30 }

{ 15 }

Returns: 10.0

They cut the stone into pieces of size 1/3 and 2/3. Dr. Agnew takes the smaller piece (value = 30*1/3 = 10) and Dr. Austin takes the larger piece (value = 15*2/3 = 10).

2)

{ 0, 0 }

{ 10, 11 }

Returns: 0.0

There is no silver. The only way for each person to get an equal value is for Dr. Agnew to take both stones.

3)

{ 3, 5, 4 }

{ 3, 5, 4 }

Returns: 6.0

There are multiple ways for each doctor to get a value of 6. One way is for both of them to take half of each stone.

4)

{ 1, 2, 3 }

{ 2, 2, 2 }

Returns: 3.5

5)

{ 11, 9, 13, 10 }

{ 8, 14, 17, 21 }

Returns: 28.304347826086957

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BoxFilling

Brute Force, Recursion, Simple Math, Simple Search, Iteration, Simulation

Used in:

TCO08 Round 1

Used as:

Division I Level Three

Writer:

misof

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8598

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12011&pm=8598

Problem Statement

We have a box that consists of (sizeX x sizeY x sizeZ) = N unit cubes. These cubes have coordinates ranging from (1,1,1) to (sizeX,sizeY,sizeZ).

We want to number the unit cubes, using integers from 1 to N. We will do this algorithmically.

We will call a box "1-dimensional (1D)" if at least two of its dimensions are 1, "2-dimensional (2D)" if exactly one of its dimensions is 1, and "3-dimensional (3D)" otherwise.

The algorithm used to number a 1-dimensional box is simple: order the cubes according to the sums of their coordinates (in ascending order), and number them in this order.

To number a 2-dimensional box, we follow this algorithm:

If X size is greater than 1, consider all cubes with both Y and Z coordinates minimal, number them as a 1D box, and throw them away.
If we still have a 2D box, if Y size is greater than 1, consider all cubes with both X and Z coordinates minimal, number them as a 1D box, and throw them away.
If we still have a 2D box, if Z size is greater than 1, consider all cubes with both X and Y coordinates minimal, number them as a 1D box, and throw them away.
Recursively number the rest of the box.

For example, a 4x5x1 box filled using this algorithm looks as follows:

z=1
   x:1  2  3  4
 y:+--+--+--+--+
  1| 1| 2| 3| 4|
   +--+--+--+--+
  2| 5| 9|10|11|
   +--+--+--+--+
  3| 6|12|15|16|
   +--+--+--+--+
  4| 7|13|17|19|
   +--+--+--+--+
  5| 8|14|18|20|
   +--+--+--+--+

To number a 3-dimensional box, we follow this algorithm:

Consider all cubes with the Z coordinate minimal, number them as a 2D box, and throw them away.
If we still have a 3D box, consider all cubes with the Y coordinate minimal, number them as a 2D box, and throw them away.
If we still have a 3D box, consider all cubes with the X coordinate minimal, number them as a 2D box, and throw them away.
Recursively number the rest of the box.

For example, a 4x3x3 box filled using this algorithm looks as follows:

z=1
   x:1  2  3  4
 y:+--+--+--+--+
  1| 1| 2| 3| 4|
   +--+--+--+--+
  2| 5| 7| 8| 9|
   +--+--+--+--+
  3| 6|10|11|12|
   +--+--+--+--+

z=2
   x:1  2  3  4
 y:+--+--+--+--+
  1|13|14|15|16|
   +--+--+--+--+
  2|21|25|26|27|
   +--+--+--+--+
  3|22|28|29|30|
   +--+--+--+--+

z=3
   x:1  2  3  4
 y:+--+--+--+--+
  1|17|18|19|20|
   +--+--+--+--+
  2|23|31|32|33|
   +--+--+--+--+
  3|24|34|35|36|
   +--+--+--+--+

You will be given the box dimensions sizeX, sizeY, and sizeZ, and the coordinates of a single cube (cubeX,cubeY,cubeZ). Write a method that will compute the number assigned to the cube at the given coordinates, when using the algorithm described above.

Definition

Class:	BoxFilling
Method:	getNumber
Parameters:	int, int, int, int, int, int
Returns:	long
Method signature:	long getNumber(int sizeX, int sizeY, int sizeZ, int cubeX, int cubeY, int cubeZ)
(be sure your method is public)

Notes

-

Note that the box described by sizeX, sizeY, and sizeZ is not necessarily a 3D box.

Constraints

-

sizeX, sizeY and sizeZ will be between 1 and 10⁹, inclusive.

-

The volume of the box will not exceed 10¹⁸.

-

cubeX will be between 1 and sizeX, inclusive.

-

cubeY will be between 1 and sizeY, inclusive.

-

cubeZ will be between 1 and sizeZ, inclusive.

Examples

0)

Returns: 13

This is the box from the first example in the problem statement.

1)

Returns: 25

This is the box from the second example in the problem statement.

2)

Returns: 9

Same box, different cube coordinates.

3)

Returns: 1

4)

Returns: 9416237809215

5)

Returns: 14

6)

Returns: 28

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PrimeSums

Dynamic Programming, Simple Math

Used in:

TCO08 Qual 1

Used as:

Division I Level Two

Writer:

misof

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8596

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12007&pm=8596

Problem Statement

The int[] bag describes a bag of non-negative integers. A bag is the same thing as a set, only it may contain repeated elements. The order of elements in a bag does not matter.

Given two bags A and B, we say that A is a sub-bag of B if A can be obtained by erasing zero or more elements from B.

The weight of a bag is the sum of its elements.

Examples:

The bags (1,2,1,3,1) and (3,1,1,1,2) are the same, but different from the bag (1,2,3,3).

Bags (1,2) and (3,1,1) are sub-bags of the bag (1,2,1,3,1), but bag (1,2,2) is not.

The weight of the bag (1,2,1,3,1) is 1+2+1+3+1=8.

Write a method that will compute how many sub-bags of bag have a prime weight.

Definition

Class:	PrimeSums
Method:	getCount
Parameters:	int[]
Returns:	long
Method signature:	long getCount(int[] bag)
(be sure your method is public)

Notes

-

A prime number is a positive integer with exactly two positive integer divisors.

-

Zero (0) and one (1) are not prime numbers.

Constraints

-

bag will contain between 1 and 50 elements, inclusive.

-

Each element in bag will be between 0 and 10,000, inclusive.

Examples

0)

{1,1,2,7}

Returns: 5

This bag has 12 different sub-bags: (1,1,2,7), (1,2,7), (2,7), (1,1,7), (1,7), (7), (1,1,2), (1,2), (2), (1,1), (1), and ().

Out of these 12, 5 have prime weights: (1,1,2,7) has weight 11, (7) has weight 7, (1,2) has weight 3, and both (2) and (1,1) have weight 2.

1)

{1,1,1,1,1,1,1,1,1,1}

Returns: 4

This bag has eleven different sub-bags. Out of them four have prime weights (2, 3, 5, and 7).

2)

{4,6,8,10,12,14}

Returns: 0

The empty sub-bag has weight zero, and any other sub-bag has an even weight greater than 2.

3)

{1,2,4,8,16,32,64,128}

Returns: 54

4)

{1234,5678,9012,3456,7890,2345,6789,123,4567,8901}

Returns: 97

5)

{0,0,7}

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MonstersAndBunnies

Dynamic Programming, Simple Math

Used in:

TCO08 Qual 1

Used as:

Division I Level One

Writer:

misof

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8595

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12007&pm=8595

Problem Statement

You just entered a strange town. The town is currently inhabited by M monsters and B bunnies.

The inhabitants interact in the following way: Whenever two bunnies meet, nothing happens. Whenever a monster meets a bunny, the monster eats the bunny. Whenever two monsters meet, they start fighting and they both die in the fight.

Whenever you meet a bunny, you can decide whether you kill it or not. A bunny will never kill you. You can not kill a monster. However, if you meet a monster, it will kill you without hesitation.

All the town's inhabitants roam the town at random. More precisely, we will make the following assumptions.

Meetings will occur at different moments in time.
Each time exactly two beings will meet.
Those two beings are always chosen uniformly at random from the set of all living beings in town, including you.

You win if at some moment you can not be killed anymore. You are not allowed to leave the town until you either win or get killed.

Write a method that will calculate the expected probability that you will win.

Definition

Class:	MonstersAndBunnies
Method:	survivalProbability
Parameters:	int, int
Returns:	double
Method signature:	double survivalProbability(int M, int B)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

-

When deciding whether to kill a bunny you just met, your only goal is to maximize your winning probability.

Constraints

-

M will be between 0 and 1,000, inclusive.

-

B will be between 0 and 1,000, inclusive.

Examples

0)

Returns: 1.0

This town is empty. As soon as you enter it, you win.

1)

Returns: 1.0

Peaceful bunny pastures, you will not get killed here.

2)

Returns: 0.0

Sooner or later the monster will find you and kill you.

3)

Returns: 0.0

The bunnies won't help you. Sooner or later the monster will find you and kill you.

4)

Returns: 0.3333333333333333

In 1/3 of all cases the two monsters meet first, kill each other and you win. In the other 2/3 cases, one of the two monsters meets you first and kills you.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PseudoRandomKingdom

Dynamic Programming, Simple Math

Used in:

SRM 394

Used as:

Division I Level Three

Writer:

Xixas

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8593

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11128&pm=8593

Problem Statement

There are n cities in a kingdom, numbered 0 through n-1. Some pairs of cities are connected by bidirectional roads in such a way that one can traverse all the cities in the kingdom by following these roads. There are exactly n-1 roads. The configuration of the roads is given as a String[] g, where the i-th element is a single-space separated list of the cities connected to city i by direct roads.

A spendthrift king devised the following scheme for taxing the roads: Each road is assigned a random integer between 0 and cost, inclusive, where each such integer is equally likely. This integer is the cost in dollars of traversing the road. John lives in one of the cities in the kingdom, and he is not happy to learn about these taxes. His fiancee Mary lives in another city, and he wants to go visit her. However, he only has savings dollars to spend on taxes. Return the probability that John will be able to reach Mary, regardless of where they each live. In other words, return the probability that the cost of travel between any two cities in the kingdom will not be greater than savings.

Definition

Class:	PseudoRandomKingdom
Method:	probabilityOfHappiness
Parameters:	String[], int, int
Returns:	double
Method signature:	double probabilityOfHappiness(String[] g, int cost, int savings)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

g will contain n elements, where n is between 2 and 50, inclusive.

-

Each element of g will contain between 0 and 50 characters, inclusive.

-

Each element of g will be a single-space seperated list of distinct integers with no leading zeroes, each of which will be between 0 and n - 1, inclusive.

-

i will not appear in the list g[i].

-

i will appear in the list g[j] if and only if the number j will appear in the list g[i].

-

g will represent a graph with the properties described in the problem statement.

-

cost will be between 1 and 10, inclusive.

-

savings will be between 0 and 500, inclusive.

Examples

0)

{"1 2",
 "0",
 "0 3",
 "2"}

Returns: 0.875

This is a path of length 3 so no more than two roads can have cost 1. We have 8 possible graphs in all and only the one where every road has a cost of 1 does not suit us. Thus the answer is 7/8.

1)

{"1 2 3 4 5 6",
 "0",
 "0",
 "0",
 "0",
 "0",
 "0"}

Returns: 0.903158288086044

Almost all graphs satisfy us.

2)

{"1 2 3 4 5 6",
 "0",
 "0",
 "0",
 "0",
 "0",
 "0"}

Returns: 5.644739300537775E-7

Now John does not have any savings at all.

3)

{"1",
 "0"}

Returns: 1.0000000000000002

4)

{"9 6",
 "6 4",
 "8",
 "5",
 "7 1",
 "8 3",
 "1 0 8",
 "4",
 "2 5 6",
 "0"}

Returns: 0.350862063

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RandomSort

Dynamic Programming, Simple Math

Used in:

SRM 402

Used as:

Division I Level One , Division II Level Three

Writer:

srbga

Testers:

PabloGilberto , Olexiy , ivan_metelsky , Gassa

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8590

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12174&pm=8590

Problem Statement

You are given a int[] permutation containing a permutation of the first n positive integers (1 through n), and you want to sort them in ascending order. To do this, you will perform a series of swaps. For each swap, you consider all pairs (i, j) such that i < j and permutation[i] > permutation[j]. Among all those pairs, you choose one randomly and swap permutation[i] and permutation[j]. Each pair has the same probability of being chosen. Return the expected number of swaps needed to sort permutation in ascending order.

Definition

Class:	RandomSort
Method:	getExpected
Parameters:	int[]
Returns:	double
Method signature:	double getExpected(int[] permutation)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

permutation will contain between 1 and 8 elements, inclusive.

-

permutation will contain each integer between 1 and n, inclusive, exactly once, where n is the number of elements in permutation.

Examples

0)

{1,3,2}

Returns: 1.0

Exactly one swap is needed.

1)

{4,3,2,1}

Returns: 4.066666666666666

In the first step, any two elements can be swapped.

2)

{1}

Returns: 0.0

This permutation is already sorted, so there's no need to perform any swaps.

3)

{2,5,1,6,3,4}

Returns: 5.666666666666666

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ConcatenateNumber

Brute Force, Math, Simple Math

Used in:

SRM 390

Used as:

Division I Level One , Division II Level Two

Writer:

srbga

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8589

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11124&pm=8589

Problem Statement

Given a positive integer number, concatenate one or more copies of number to create an integer that is divisible by k. Do not add any leading zeroes. Return the least number of copies needed, or -1 if it is impossible.

Definition

Class:	ConcatenateNumber
Method:	getSmallest
Parameters:	int, int
Returns:	int
Method signature:	int getSmallest(int number, int k)
(be sure your method is public)

Constraints

-

number will be between 1 and 1,000,000,000, inclusive.

-

k will be between 1 and 100,000, inclusive.

Examples

0)

Returns: 9

At least 9 copies are needed, since 222222222 is divisible by 9.

1)

Returns: 1

121 is divisible by 11.

2)

Returns: -1

You can never get an even number by concatenating only 1's.

3)

Returns: 9876

The resulting integer could be really big.

4)

1000000000

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MoreNim

Greedy, Math

Used in:

SRM 396

Used as:

Division I Level Three

Writer:

asal1

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8587

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12168&pm=8587

Problem Statement

Nim is a game in which players take turns removing objects from distinct heaps. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap. The player to remove the last object is the winner.

You and your friend got tired of the same old game so you decided to try something different. The modified game consists of two phases. In the first phase you first take a turn removing as many entire heaps as you want. Your opponent then takes a turn removing as many heaps as he wants. Both you and your opponent are allowed to take no heaps, but are not allowed to take all the remaining heaps. After this the second phase starts in which the game continues as a normal Nim game.

You are given a String[] where each element represents the number of objects in a single heap at the beginning of the game. Return the minimum total number of objects you must remove in the first phase to ensure your victory even if your friend plays optimally.

Definition

Class:	MoreNim
Method:	bestSet
Parameters:	String[]
Returns:	long
Method signature:	long bestSet(String[] heaps)
(be sure your method is public)

Constraints

-

heaps will contain between 1 and 50 elements, inclusive.

-

Each element of heaps will contain digits ('0' - '9') only.

-

Each element of heaps will represent a positive integer without leading zeros.

-

Each element of heaps will contain between 1 and 16 characters, inclusive.

Examples

0)

{"5","5","6","6","5","5"}

Returns: 21

If you're left with two equal piles at the end of the first phase, you will lose the game. In each turn, however many objects you remove from a heap, your opponent will remove the same number of objects from the other heap, and you will eventually lose. To prevent this from happening, remove three of the heaps containing 5 objects and one of the heaps containing 6 objects (for a total of 21 objects).

1)

{"1","2","3"}

Returns: 1

Here, the piles are distinct, but if you are presented with them at the beginning of the second phase, you will lose the game. No matter how many objects you remove during your turn, your opponent will be able to make a move that leaves you with two equal piles in your next turn. Removing the heap of size 1 during the first phase will guarantee your victory.

2)

{"1","2","3","4","5","6","7","8","9"}

Returns: 16

3)

{"1","2","4","8","16","32","64","128","256"}

Returns: 0

4)

{"12","13","16","121","13","14","52","23","1","29"}

Returns: 27

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TriangularSubsequence

Simple Math, Simple Search, Iteration

Used in:

TCHS08 Round 2

Used as:

Division I Level Two

Writer:

andrewzta

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8580

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11151&pm=8580

Problem Statement

Three numbers x, y and z are said to satisfy the triangle inequality if x + y > z, x + z > y, and y + z > x.

The sequence of integers b[0], b[1], ..., b[n-1] is said to be triangular if b[i], b[j] and b[k] satisfy the triangle inequality for all distinct values of i, j and k.

You are given an integer sequence as a int[] a. Return the length of the longest subsequence of a that is triangular. A subsequence of a sequence is obtained by removing zero or more elements from the sequence.

Definition

Class:	TriangularSubsequence
Method:	longest
Parameters:	int[]
Returns:	int
Method signature:	int longest(int[] a)
(be sure your method is public)

Constraints

-

a will contain between 1 and 50 elements, inclusive.

-

Each element of a will be between 1 and 10^9, inclusive.

Examples

0)

{2,3,4,1,3,4,5}

Returns: 5

The subsequence {2,3,4,3,4} is the longest triangular subsequence.

1)

{1,2,3}

Returns: 2

Note that a sequence of length 2 is always triangular.

2)

{1,1,1,1,1,1,1,1}

Returns: 8

The whole sequence is triangular.

3)

{1,1,1,1000000000,1000000000,1000000000}

Returns: 4

4)

{1000000000}

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NextNumber

Simple Math

Used in:

SRM 416

Used as:

Division I Level One , Division II Level Two

Writer:

xOberon

Testers:

PabloGilberto , Olexiy , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8576

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13507&pm=8576

Problem Statement

The binary weight of a positive integer is the number of 1's in its binary representation. For example, the decimal number 1 has a binary weight of 1, and the decimal number 1717 (which is 11010110101 in binary) has a binary weight of 7.

Given a positive integer N, return the smallest integer greater than N that has the same binary weight as N.

Definition

Class:	NextNumber
Method:	getNextNumber
Parameters:	int
Returns:	int
Method signature:	int getNextNumber(int N)
(be sure your method is public)

Notes

-

The result is guaranteed to fit in a signed 32-bit integer.

Constraints

-

N will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 1718

Example from the problem statement.

1)

Returns: 8

4 is 100 in its binary representation and weighs 1. The next number is 1000(in binary) which represents 8.

2)

Returns: 11

The decimal 7 is binary 111, so it has binary weight of 3. The next number with the same binary weight is 11, which is 1011 in binary.

3)

Returns: 17

12 in decimal is 1100 in binary. The next number with the same binary weight is 10001 in binary, which is 17.

4)

Returns: 555557

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SmoothNumbersHard

Math

Used in:

SRM 388

Used as:

Division II Level Three

Writer:

bmerry

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8565

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11122&pm=8565

Problem Statement

A positive integer is said to be k-smooth if its largest prime factor is no greater than k. Compute how many positive integers less than or equal to N are k-smooth.

Definition

Class:	SmoothNumbersHard
Method:	countSmoothNumbers
Parameters:	int, int
Returns:	int
Method signature:	int countSmoothNumbers(int N, int k)
(be sure your method is public)

Constraints

-

N will be between 1 and 5,000,000, inclusive.

-

k will be between 1 and 1,000, inclusive.

Examples

0)

Returns: 7

Of the first ten positive integers, only 5, 7 and 10 have prime factors greater than 3; the rest are 3-smooth.

1)

Returns: 7

4 is not prime, so 4-smooth numbers are the same as 3-smooth numbers.

2)

Returns: 8

3)

Returns: 5

4)

Returns: 23855

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BoxesOfBooks

Greedy, Simple Math

Used in:

SRM 389

Used as:

Division II Level One

Writer:

legakis

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8559

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11123&pm=8559

Problem Statement

You are packing a stack of books into some boxes, packing as many books as you can into each box without exceeding a given weight limit. Once you have packed as many books into a box as you can, you close and seal that box, and then begin filling the next one. You take the books off the stack in order, packing each one before picking up the next.

The weights of the books will be given as a int[] weights, where the first element is the weight of the book on top of the stack and the last element is the weight of the book on the bottom of the stack. The maximum weight that can fit into each box will be given as an int maxWeight. Return the minimum number of boxes you will need.

Definition

Class:	BoxesOfBooks
Method:	boxes
Parameters:	int[], int
Returns:	int
Method signature:	int boxes(int[] weights, int maxWeight)
(be sure your method is public)

Constraints

-

weights will contain between 0 and 50 elements, inclusive.

-

maxWeight will be between 1 and 1000, inclusive.

-

Each element of weights will be between 1 and maxWeight, inclusive.

Examples

0)

{ 5, 5, 5, 5, 5, 5 }

Returns: 3

You have 6 books that weigh 5 kilograms each. Each box can hold 10 kilograms (2 books). Therefore, you need 3 boxes.

1)

{ 51, 51, 51, 51, 51 }

Returns: 5

Each box can hold 100 kg, but since the books weigh 51 kg each, you can only put one in each box.

2)

{ 1, 1, 1, 7, 7, 7 }

Returns: 4

You would like to put one 1 kg book and one 7 kg book in each of 3 boxes. But, since you must pack the books in order, you end up putting the three 1 kg books in one box and each of the three 7 kg books in its own box, for a total of 4 boxes.

3)

{ 12, 1, 11, 2, 10, 3, 4, 5, 6, 6, 1 }

Returns: 6

4)

{ }

Returns: 0

5)

{ 20, 20, 20, 20, 20, 20, 20, 20, 20, 20,
  20, 20, 20, 20, 20, 20, 20, 20, 20, 20,
  20, 20, 20, 20, 20, 20, 20, 20, 20, 20,
  20, 20, 20, 20, 20, 20, 20, 20, 20, 20,
  20, 20, 20, 20, 20, 20, 20, 20, 20, 20 }

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

UnfixedArrangements

Dynamic Programming, Math

Used in:

TCHS08 Round 2

Used as:

Division I Level Three

Writer:

andrewzta

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8553

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11151&pm=8553

Problem Statement

There are k slots numbered 1 through k, and you must assign a distinct integer between 1 and n, inclusive, to each slot. The resulting configuration is called an arrangement of k from n. An example of an arrangement of 3 from 5 is (2, 4, 3).

An arrangement is called unfixed if no integer is equal to the number of its slot. For example, the arrangement (2, 4, 3) is not unfixed because the integer 3 is in slot number 3. The arrangement (2, 4, 5), on the other hand, is unfixed.

Given ints n and k, return the number of unfixed arrangements of k from n.

Definition

Class:	UnfixedArrangements
Method:	count
Parameters:	int, int
Returns:	long
Method signature:	long count(int n, int k)
(be sure your method is public)

Constraints

-

n will be betwen 1 and 20, inclusive.

-

k will be between 1 and n, inclusive.

Examples

0)

Returns: 3

The unfixed arrangements of 2 from 3 are (2,1), (2,3) and (3,1).

1)

Returns: 0

The only arrangement of 1 from 1 is not unfixed.

2)

Returns: 1

The arrangement (2,1) is unfixed.

3)

Returns: 32

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ProperDivisors

Math, Simple Search, Iteration

Used in:

SRM 394

Used as:

Division II Level Three

Writer:

Xixas

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8547

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11128&pm=8547

Problem Statement

An integer k greater than 0 is called a cool divisor of m if it is less than m and divides m, but k^n does not divide m. Let d(m) denote the number of cool divisors that exist for an integer m. Given two integers a and b return the sum d(a) + d(a + 1) + ... + d(a + b).

Definition

Class:	ProperDivisors
Method:	analyzeInterval
Parameters:	int, int, int
Returns:	int
Method signature:	int analyzeInterval(int a, int b, int n)
(be sure your method is public)

Notes

-

The result will always fit into a signed 32-bit integer.

Constraints

-

a will be between 1 and 1000000 (10^6), inclusive.

-

b will be between 1 and 10000000 (10^7), inclusive.

-

n will be between 2 and 10, inclusive.

Examples

0)

Returns: 5

The cool divisors of 32 are 4, 8 and 16 so d(32) = 3; the cool divisors of 33 are 3 and 11 so d(33) = 2. Hence the desired sum d(32) + d(33) = 3 + 2 = 5.

1)

Returns: 8

2)

10000000

Returns: 146066338

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CentersOfSymmetry

Geometry, Math

Used in:

SRM 394

Used as:

Division I Level Two

Writer:

Xixas

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8546

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11128&pm=8546

Problem Statement

We have n straight lines drawn in the Cartesian plane each described by two distinct points (x1[i], y1[i]) and (x2[i], y2[i]) lying on it. A center of symmetry is such a point that under a symmetry centered at this point the given configuration of lines goes into itself (i.e., the image of every given line under this symmetry is again one of the given lines). Return the number of centers of symmetry that the given system of lines has. Return -1 if there are infinitely many centers of symmetry.

Definition

Class:	CentersOfSymmetry
Method:	lineConfigurations
Parameters:	int[], int[], int[], int[]
Returns:	int
Method signature:	int lineConfigurations(int[] x1, int[] y1, int[] x2, int[] y2)
(be sure your method is public)

Notes

-

A symmetry centered at point X works as follows. The image of a point A is such a point B that X is the midpoint of the line segment AB (note that if A = X, then also B = X). The image of a line is the union of images of all points on this line.

Constraints

-

x1 will contain between 1 and 50 elements, inclusive.

-

x1, y1, x2, y2 will all contain the same number of elements.

-

All the elements of x1, y1, x2 and y2 will be between -50 and 50, inclusive.

-

For each i either x1[i] and x2[i] or y1[i] and y2[i] will be distinct (i.e., two points defining a line will be distinct).

-

All the lines defined by (x1[i], y1[i]) and (x2[i], y2[i]) will be distinct.

Examples

0)

{0, 0}

{0, 0}

{1, -1}

{1, 1}

Returns: 1

A configuration of two intersecting lines has a single center of symmetry - their intersection point.

1)

{0, 0, 0, 0, 0, 0, 0, 0, 0}

{0, 0, 0, 0, 0, 0, 0, 0, 0}

{1, 1, 1, 1, 1, 1, 1, 1, 1}

{1, 2, 3, 4, 5, 6, 7, 8, 9}

Returns: 1

All the lines pass through the origin.

2)

{0, 1, 2}

{0, 1, -1}

{1, 2, 0}

{1, -1, 0}

Returns: 0

3)

{-10, 10}

{10, -10}

{-10, 10}

{-10, 10}

Returns: -1

Two parallel lines produce infinitely many centers of symmetry.

4)

{-50, -50, -50, -50}

{-50, -49, -48, -46}

{50, 49, 48, 46}

{50, 50, 50, 50}

Returns: 0

4 parallel lines with no centers of symmetry.

5)

{10, -35, -8, 7, -5, -8, -9, -50, -17, -18, -17, -26, -5, 23, 18, -7, -8, -6,
 -8, -12, 22, -7, 17, -48, -6, -16, -12, -14, 13, 30, 11, 17, -3, -5, -27, -30}

{-27, -25, -17, -26, -3, -19, -20, -33, -22, -21, -23, -38, -2, -32, -27, -8, -2, -5,
 -21, -7, -15, -15, -5, -27, 0, -19, -25, 1, -22, -11, -13, -38, -1, -6, -17, -32}

{16, -32, -11, 11, -3, -9, -8, -45, -16, -15, -19, -29, -2, 20, 24, -1, 4, -7,
 -5, -13, 16, -9, 29, -43, 2, -17, -15, -15, 17, 24, 23, 14, -7, -3, -24, -33}

{-35, -23, -26, -32, -3, -21, -18, -30, -20, -15, -27, -42, -5, -28, -35, 2, -5, -6,
 -15, -7, -13, -19, -9, -24, -12, -21, -34, 1, -28, -9, -17, -34, -9, 0, -15, -36}

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EquiDigitNumbers

Search, Simple Math

Used in:

SRM 392

Used as:

Division I Level Three

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8536

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11126&pm=8536

Problem Statement

A number x is called equidigit if each digit that appears in the decimal notation of x appears the same number of times. (x must be written with no leading zeroes.)

For example, the numbers 5, 239, 333888 and 566353 are equidigit.

Given a string representing a number n, return the smallest equidigit number that is greater than or equal to n.

Definition

Class:	EquiDigitNumbers
Method:	findNext
Parameters:	String
Returns:	long
Method signature:	long findNext(String n)
(be sure your method is public)

Notes

-

The answer always fits into a 64-bit signed integer.

Constraints

-

n will contain only digits, and will represent an integer between 1 and 10^18, inclusive, with no leading zeros.

Examples

0)

"42"

Returns: 42

When given an equidigit number, you should return that same number.

1)

"2008"

Returns: 2013

The numbers 2008, 2009, 2010, 2011 and 2012 are not equidigit, and the number 2013 is.

2)

"987654322"

Returns: 987778899

3)

"12345678910"

Returns: 22222222222

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SmoothNumbers

Brute Force, Simple Math

Used in:

SRM 388

Used as:

Division I Level One

Writer:

bmerry

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8519

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11122&pm=8519

Problem Statement

A positive integer is said to be k-smooth if its largest prime factor is no greater than k. Compute how many positive integers less than or equal to N are k-smooth.

Definition

Class:	SmoothNumbers
Method:	countSmoothNumbers
Parameters:	int, int
Returns:	int
Method signature:	int countSmoothNumbers(int N, int k)
(be sure your method is public)

Constraints

-

N will be between 1 and 100,000, inclusive.

-

k will be between 1 and 100, inclusive.

Examples

0)

Returns: 7

Of the first ten integers, only 5, 7 and 10 have prime factors greater than 3.

1)

Returns: 7

4 is not prime, so 4-smooth numbers are the same as 3-smooth numbers.

2)

Returns: 8

3)

Returns: 5

4)

Returns: 17442

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BuildCircuit

Brute Force, Math

Used in:

SRM 390

Used as:

Division I Level Three

Writer:

srbga

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8510

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11124&pm=8510

Problem Statement

A serial-parallel resistor circuit is either

a single resistor. The resistance of such circuit is equal to the resistance of the resistor. Or
several circuits R₁,R₂,...,R_n combined in serial. The resistance is equal to R₁+R₂+...+R_n. Or
several circuits R₁,R₂,...,R_n combined in parallel. The resistance is equal to 1/((1/R₁)+(1/R₂)+...+(1/R_n)).

Given two positive integers a and b, your task is to build a serial-parallel resistor circuit that has resistance equal to a/b. You are only allowed to use two kinds of resistors: R=1 and R=2. Return the minimal number of resistors needed. If the circuit cannot be built with 16 or less resistors, return -1.

Definition

Class:	BuildCircuit
Method:	minimalCount
Parameters:	int, int
Returns:	int
Method signature:	int minimalCount(int a, int b)
(be sure your method is public)

Constraints

-

a and b will each be between 1 and 50000, inclusive.

Examples

0)

Returns: 1

One unit resistor is enough.

1)

Returns: 2

Combine R=1 and R=2 in parallel.

2)

Returns: 3

Combine R=1 and R=2 in serial, then with R=2 in parallel.

3)

Returns: 7

4)

Returns: -1

5)

Returns: 10

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BirthdayReminders

Simple Math, Simple Search, Iteration

Used in:

SRM 412

Used as:

Division II Level Two

Writer:

Eryx

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8481

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13503&pm=8481

Problem Statement

You are a geek with so many geeky friends that you sometimes forget about their birthdays. So, you've decided to write a program that will remind you about such recurring events. Since your friends are geeks, they may celebrate occasions other than their actual birthdays. For example, they might celebrate whenever their age in days becomes divisible by 1000.

You are given a String[] friendNames and a int[] birthDates. Your i-th friend is named friendNames[i] and was born on birthDates[i]. All dates in this problem are non-negative integers representing the number of days that have elapsed since day 0.

The occasions celebrated by all your friends are given in the String[] occasions and int[] days. Occasion i is named occasions[i]. Each of your friends celebrates that occasion on each date b+n*day[i], where b is that friend's birth date and n is an integer greater than or equal to 1. For example, if a friend was born on day 10, and there's an occasion that is celebrated every 4 days, that friend would celebrate it on day 14, day 18, day 22, etc.

Today's date is given as an int currentDate. Your task is to generate the next k occasions that will be celebrated by your friends (starting from today). Return these occasions in a String[] where each element represents a single occasion formatted as "DATE. FRIEND OCCASION (NUMBER)" (quotes for clarity). Each DATE is the date of the occasion with no extra leading zeroes, FRIEND is the name of the friend, OCCASION is the name of the occasion, and NUMBER is the number of the occasion (1 is the first time the occasion has happened since that person's birth date, 2 is the second time, etc.). The String[] should be sorted in chronological order from earliest to latest. If multiple occasions happen on the same day, order them by occasion (occasions that appear earlier in occasions and days should be listed earlier), breaking ties by friend (friends that appear earlier in friendNames and birthDates should be listed earlier).

Definition

Class:	BirthdayReminders
Method:	remind
Parameters:	String[], int[], int, String[], int[], int
Returns:	String[]
Method signature:	String[] remind(String[] friendNames, int[] birthDates, int currentDate, String[] occasions, int[] days, int k)
(be sure your method is public)

Constraints

-

currentDate will be between 1 and 1000000, inclusive.

-

friendNames will contain the same number of elements as birthDates.

-

friendNames and birthDates will contain between 1 and 50 elements, inclusive.

-

Each element of birthDates will be between 0 and currentDate-1, inclusive.

-

occasions will contain the same number of elements as days.

-

occasions and days will contain between 1 and 50 elements, inclusive.

-

Each element of days will be between 1 and 1000000, inclusive.

-

k will be between 1 and 100, inclusive.

-

Each element of friendNames will contain only uppercase letters ('A' - 'Z'), lowercase letters ('a' - 'z'), and spaces.

-

Each element of occasions will contain only uppercase letters ('A' - 'Z'), lowercase letters ('a' - 'z'), and spaces.

Examples

0)

{"John", "Jack", "Bill"}

{50, 100, 150}

{"birthday", "decimal birthday", "binary birthday"}

{365, 1000, 512}

Returns: 
{"515. Bill birthday (1)",
"562. John binary birthday (1)",
"612. Jack binary birthday (1)",
"662. Bill binary birthday (1)",
"780. John birthday (2)",
"830. Jack birthday (2)",
"880. Bill birthday (2)",
"1050. John decimal birthday (1)",
"1074. John binary birthday (2)",
"1100. Jack decimal birthday (1)" }

1)

{"Zero", "Two", "Three"}

{0, 2, 3}

{"threeday", "twoday"}

{3,2}

Returns: 
{"24. Zero threeday (8)",
"24. Three threeday (7)",
"24. Zero twoday (12)",
"24. Two twoday (11)",
"25. Three twoday (11)",
"26. Two threeday (8)",
"26. Zero twoday (13)",
"26. Two twoday (12)",
"27. Zero threeday (9)",
"27. Three threeday (8)" }

This demonstrates the sorting rules used.

2)

{"Jessica Alba", "Angelina Jolie", "Paris Hilton", "Britney Spears"}

{4135, 1980, 4065, 4353}

{"Venus year", "Earth year", "Mars year", "Jupiter year", "Saturn year"}

{225, 365, 687, 4332, 10760}

Returns: 
{"14130. Angelina Jolie Venus year (54)",
"14190. Paris Hilton Venus year (45)",
"14208. Britney Spears Earth year (27)",
"14253. Britney Spears Venus year (44)",
"14260. Jessica Alba Venus year (45)",
"14285. Paris Hilton Earth year (28)",
"14346. Angelina Jolie Mars year (18)",
"14355. Angelina Jolie Venus year (55)",
"14355. Jessica Alba Earth year (28)",
"14370. Paris Hilton Mars year (15)",
"14390. Angelina Jolie Earth year (34)",
"14415. Paris Hilton Venus year (46)",
"14440. Jessica Alba Mars year (15)",
"14478. Britney Spears Venus year (45)",
"14485. Jessica Alba Venus year (46)",
"14573. Britney Spears Earth year (28)",
"14580. Angelina Jolie Venus year (56)",
"14640. Paris Hilton Venus year (47)",
"14650. Paris Hilton Earth year (29)",
"14658. Britney Spears Mars year (15)" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ForbiddenStrings

Dynamic Programming, Math

Used in:

SRM 412

Used as:

Division I Level One

Writer:

Eryx

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8480

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13503&pm=8480

Problem Statement

A string of letters A, B, C is forbidden if there are three consecutive letters from which one is A, one is B, and one is C. For example, BAACAACCBAAA is forbidden, while AABBCCAABB is not.

Your task is to calculate how many such strings of length n are not forbidden.

Definition

Class:	ForbiddenStrings
Method:	countNotForbidden
Parameters:	int
Returns:	long
Method signature:	long countNotForbidden(int n)
(be sure your method is public)

Constraints

- n will be between 1 and 30, inclusive.

Examples

0)

Returns: 9

All 9 strings of length 2 are not forbidden.

1)

Returns: 21

There are 27 strings of length 3. Of these, 6 contain one occurrence of each letter. Those 6 strings are forbidden, so you should return 21.

2)

Returns: 51

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TrueSpace

Simple Math

Used in:

SRM 412

Used as:

Division II Level One

Writer:

Eryx

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8477

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13503&pm=8477

Problem Statement

In some filesystems, the disk space used by a file is not always equal to the file's size. This is because the disk is divided into clusters of equal size, and each cluster can only be used by a single file. For example, if the cluster size is 512 bytes, and we have a file of size 600 bytes, it would have to be stored in two clusters. Those two clusters cannot be shared with any other files, so the file ends up using 1024 bytes of disk space.

You are given a int[] sizes, where each element is the size of a single file, and an int clusterSize, the cluster size of the filesystem. Return the total disk space used by the given files.

Definition

Class:	TrueSpace
Method:	calculateSpace
Parameters:	int[], int
Returns:	long
Method signature:	long calculateSpace(int[] sizes, int clusterSize)
(be sure your method is public)

Constraints

-

sizes will contain between 1 and 50 elements, inclusive.

-

clusterSize will be between 1 and 1,048,576, inclusive.

-

Each element of sizes will be between 0 and 1,000,000,000, inclusive.

Examples

0)

{600}

Returns: 1024

From the problem statement.

1)

{16,32,128,128,0}

Returns: 131072

We waste a lot of space here. (Note that we don't need any clusters for a file of size 0.)

2)

{4096, 33792, 76800}

Returns: 114688

We don't waste any space here.

3)

{1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000, 1000000000, 1000000000,
 1000000000, 1000000000}

Returns: 50017075200

4)

{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SummingArithmeticProgressions

Simple Math

Used in:

SRM 385

Used as:

Division II Level Three

Writer:

Petr

Testers:

PabloGilberto , Olexiy , gawry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8474

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10810&pm=8474

Problem Statement

A magic arithmetic progression with k elements is a sequence of the form x, x+d, x+2*d, ..., x+(k-1)*d for some positive integers x and d. How many integers between left and right, inclusive, can be represented as the sum of some magic arithmetic progression with exactly k elements?

Definition

Class:	SummingArithmeticProgressions
Method:	howMany
Parameters:	int, int, int
Returns:	int
Method signature:	int howMany(int left, int right, int k)
(be sure your method is public)

Constraints

-

left will be between 1 and 1000000000, inclusive.

-

right will be between left and 1000000000, inclusive.

-

k will be between 2 and 5, inclusive.

Examples

0)

Returns: 3

The representable numbers are: 6=1+2+3, 9=2+3+4=1+3+5, 12=3+4+5=2+4+6=1+4+7. Note that there can be several possible representations for a number.

1)

Returns: 8

Every number except 1 and 2 is representable: 3=1+2, 4=1+3, 5=1+4, etc.

2)

Returns: 6

The representable numbers are 20, 22, 24, 26, 28 and 30.

3)

Returns: 0

The minimal possible sum is 1+2+3+4=10.

4)

Returns: 1

And the next possible sum is 2+3+4+5=14.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SquareDigitNumbers

Brute Force, Simple Math

Used in:

SRM 395

Used as:

Division II Level One

Writer:

connect4

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8469

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11129&pm=8469

Problem Statement

You enjoy working with numbers that contain only square digits (namely, 0, 1, 4 and 9). The sequence containing only these digits is 0, 1, 4, 9, 10, 11, 14... Return the n-th term (indexed from 0) in this sequence.

Definition

Class:	SquareDigitNumbers
Method:	getNumber
Parameters:	int
Returns:	int
Method signature:	int getNumber(int n)
(be sure your method is public)

Constraints

-

n will be between 0 and 1000, inclusive.

Examples

0)

Returns: 0

The first square digit number is 0.

1)

Returns: 11

2)

Returns: 100

3)

Returns: 1941

4)

Returns: 1949

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StreetWalking

Greedy, Simple Math

Used in:

SRM 395

Used as:

Division I Level One , Division II Level Two

Writer:

connect4

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8464

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11129&pm=8464

Problem Statement

You are walking home from school through the city. The city is infinite in size, with vertical streets located at every integer X value and horizontal streets located at every Y value. You are currently located at (0,0) and are trying to get to your home, located at (X, Y). You have two methods of travel available to you: you can walk along the street to proceed to a horizontally or vertically adjacent intersection (which takes walkTime seconds), or you can sneak across the block diagonally to the opposite corner (taking sneakTime seconds). You can walk or sneak in any of the eight directions shown in the image (see example 2).

Return the least amount of time that it will take you to return home. See the examples for clarification.

Definition

Class:	StreetWalking
Method:	minTime
Parameters:	int, int, int, int
Returns:	long
Method signature:	long minTime(int X, int Y, int walkTime, int sneakTime)
(be sure your method is public)

Constraints

-

X will be between 0 and 1,000,000,000, inclusive.

-

Y will be between 0 and 1,000,000,000, inclusive.

-

walkTime will be between 1 and 10000, inclusive.

-

sneakTime will be between 1 and 10000, inclusive.

Examples

0)

Returns: 18

The fastest way to your home is to not sneak at all.

1)

Returns: 16

In this case, it is faster to sneak across twice, following the path (0,0)->(1,0)->(2,1)->(3,1)->(4,2). This takes 10 seconds for the sneaking, and 6 seconds for the walking.

2)

Returns: 20

One possible path is (0,0)->(1,1)->(2,0).

3)

Returns: 247

4)

Returns: 240

5)

10000000

50000000

Returns: 41010000000

6)

Returns: 3929

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

InfiniteAddition

Math, Sorting, String Manipulation

Used in:

SRM 385

Used as:

Division I Level Three

Writer:

Petr

Testers:

PabloGilberto , Olexiy , gawry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8458

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10810&pm=8458

Problem Statement

An infinite periodic string is a string consisting of a non-periodic string S repeated infinitely, and is denoted as (S). For example, (ABC)=ABCABCABCA... Note that S must not be a repetition itself, so (ABAB)=ABABABAB... is not legal, and should be written as (AB)=ABABABAB... instead. S must contain only uppercase letters ('A'-'Z').

The sum of two infinite periodic strings is the string where each character is the sum of the corresponding characters in the two strings. Two characters are added as follows. Adding A to a character means changing it to the next character in the alphabet (where A is the next character after Z): A+A=B, A+B=C, A+C=D, ..., A+Y=Z, A+Z=A. Adding B to a character means changing it to the next character twice: B+A=C, B+B=D, B+C=E, ..., B+Z=B. All the other characters behave in the same manner (C means changing to the next character 3 times, D means 4, ..., Z means 26, so adding Z doesn't change a character).

The sum of two infinite periodic strings is itself an infinite periodic string. For example, (YAAZZB)=(AB)+(XYZ).

Given three integers, sum, op1 and op2, return an example of such an addition formatted as "(S)=(P)+(Q)" (quotes for clarity only), where S contains exactly sum characters, P contains exactly op1 characters, and Q contains exactly op2 characters. Remember that S, P and Q each need to be non-periodic.

If there are several possible answers, return the one among them where S comes earliest alphabetically. If there is a tie, return the answer among the ties where P comes earliest alphabetically. If there is no solution, return "NO SOLUTION" (quotes for clarity only).

Definition

Class:	InfiniteAddition
Method:	giveExample
Parameters:	int, int, int
Returns:	String
Method signature:	String giveExample(int sum, int op1, int op2)
(be sure your method is public)

Constraints

-

sum, op1 and op2 will each be between 1 and 20, inclusive.

Examples

0)

Returns: "(AAABZB)=(AB)+(ZYZ)"

The more 'A's you have in the beginning, the better. However, you can't make it just "(AAAAAA)=(AA)+(ZZZ)", as the strings inside parentheses need to be non-periodic.

1)

Returns: "NO SOLUTION"

No matter what the added strings are, the period of the sum can't be more than 5 in this case.

2)

Returns: "(AAAAB)=(AAAAC)+(ZZZZY)"

3)

Returns: "(A)=(AAAAB)+(ZZZZY)"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GoodHours

Brute Force, Simple Math

Used in:

TC China 08 - 1E

Used as:

Division I Level Two

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , Mike Mirzayanov , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8448

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13677&pm=8448

Problem Statement

Johnny likes to watch the clock. He likes some moments more than others. The time "HH:MM" is good if you can split the four digits into two adjacent groups such that the products of the digits within each group are equal. Each group must contain at least one digit, so there are totally 3 possible ways to do the split: "H" and "H:MM", "HH" and "MM", or "HH:M" and "M". For example, "22:28" is good because you can split it into "22:2" and "8", and 2 * 2 * 2 = 8. "23:32" and "10:00" are also good, while "23:45" and "12:42" are not.

You are given two Strings, beforeTime and afterTime, each formatted as "HH:MM" (quotes for clarity). The two times are less than 24 hours apart. Return the number of good times between beforeTime and afterTime, inclusive.

Definition

Class:	GoodHours
Method:	howMany
Parameters:	String, String
Returns:	int
Method signature:	int howMany(String beforeTime, String afterTime)
(be sure your method is public)

Constraints

-

beforeTime and afterTime will both be formatted as "HH:MM" (quotes for clarity), where HH is a two digit integer between 00 and 23, inclusive, and MM is a two digit integer between 00 and 59, inclusive.

Examples

0)

"11:11"

"11:11"

Returns: 1

Of course, 11:11 is good.

1)

"00:56"

"12:32"

Returns: 164

2)

"00:00"

"00:59"

Returns: 60

3)

"10:10"

"10:20"

Returns: 2

Only 10:10 and 10:20 are good here.

4)

"23:10"

"01:23"

Returns: 75

Good times here are 23:16, 23:23, 23:32, 00:00 ... 01:10, 01:20.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OneTwoThree

Brute Force, Math, Simple Search, Iteration

Used in:

TCHS08 Round 3

Used as:

Division I Level Two

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8445

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11150&pm=8445

Problem Statement

Find the smallest number that is divisible by all the integers between 1 and n, inclusive, and return it modulo 987654321.

Definition

Class:	OneTwoThree
Method:	minimalNumber
Parameters:	int
Returns:	int
Method signature:	int minimalNumber(int n)
(be sure your method is public)

Constraints

-

n will be between 1 and 100000, inclusive.

Examples

0)

Returns: 1

1)

Returns: 6

The smallest number divisible by 1, 2 and 3 is just 1 * 2 * 3.

2)

Returns: 2520

3)

Returns: 411860547

4)

Returns: 528039414

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FillBox

Greedy, Simple Math

Used in:

SRM 379

Used as:

Division I Level Two

Writer:

asal1

Testers:

PabloGilberto , Olexiy , gawry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8442

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10800&pm=8442

Problem Statement

You have a length x width x height box, and you want to fill it with cubes. The cubes have sides that are powers of 2 (1x1x1, 2x2x2, 4x4x4, 8x8x8, etc.). You are given a int[] cubes, the i-th element of which is the number of 2^i x 2^i x 2^i cubes you have (i is a 0-based index). Return the minimum number of cubes necessary to fill the box, or -1 if it is impossible to do so.

Definition

Class:	FillBox
Method:	minCubes
Parameters:	int, int, int, int[]
Returns:	int
Method signature:	int minCubes(int length, int width, int height, int[] cubes)
(be sure your method is public)

Constraints

-

length, width and height will each be between 1 and 10^6, inclusive.

-

cubes will contain between 1 and 20 elements, inclusive.

-

Each element of cubes will be between 0 and 10^6, inclusive.

Examples

0)

{10,10,10}

Returns: 2

In order to cover the 4x4x8 box we need two 4x4x4 cubes.

1)

{10,10,1}

Returns: 9

Same case as before but we have only one 4x4x4 cube so we will use eight 2x2x2 cubes

2)

{2000}

Returns: 1100

We have only 1x1x1 cubes. We will need 1100 of those cubes to cover the whole box.

3)

{1099}

Returns: -1

We don't have enough 1x1x1 cubes.

4)

{143821,14382,1438,143,14,1}

Returns: 5061

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MaxwellDemon

Geometry, Simulation

Used in:

MM 27

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8433

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10933&pm=8433

Problem Statement

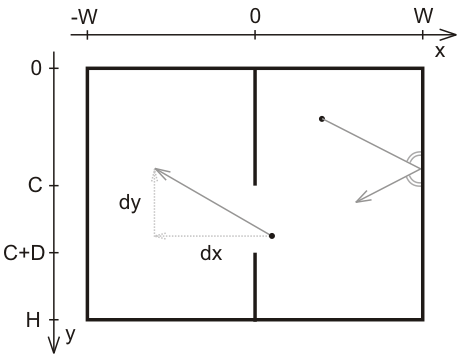
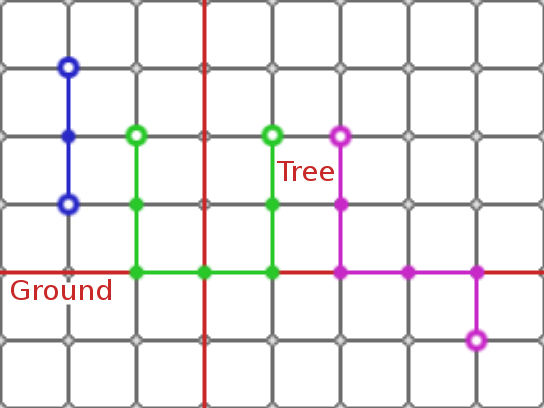
A rectangular vessel is divided in two equal parts with a vertical partition. The vessel contains particles which are randomly distributed between two parts and move in different directions. Particles don't interact with each other. Particles bounce off the walls of the vessel and the partition obeying the law of reflection (angle of incidence equals angle of reflection).

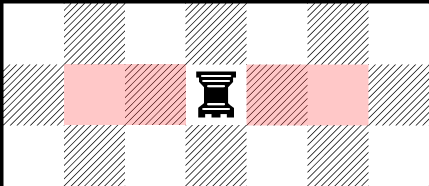
You move a mobile opening of fixed width D in the partition. If the particle was to bounce off the partition within the opening, it will move through the opening to another part of the vessel instead.

Your goal is to separate red and blue particles into different parts of the vessel.

Input Format

You will be given the width W and height H of the vessel, the width of the opening D and the list of the particles' parameters particles. Element i of particles will be formatted as "C X Y DX DY", where

C will be "R" or "B" for red or blue,
X and Y will be the x and y coordinates of the particle at time 0, in units,
DX and DY will be the x and y components of the particle's velocity at time 0, in units per second. During one second the particle's coordinates change by (DX, DY), unless it hits a wall or the partition and changes direction.

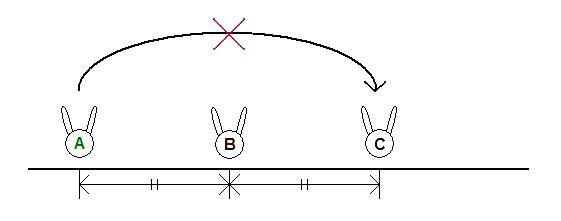
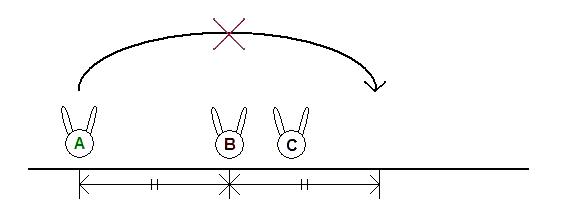
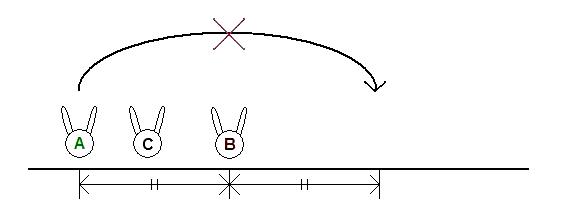
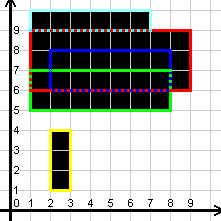
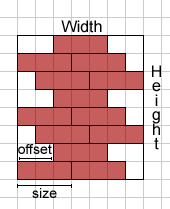
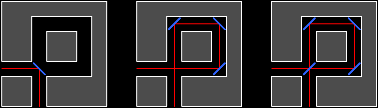
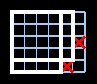
See the picture for clarification of coordinates used in input and output. The partition starts at the very top, from Y = 0 to D.

Output Format

Your method will return a list of moves to perform. You may slide the opening in the partition up or down at a rate of speed. If you try to slide the opening outside of the vessel, it will simply stop when it reaches an edge. You may also close the opening, ending the simulation. Each element of your return should be formatted as one of

UP <duration>
DOWN <duration>
STAY <duration>
CLOSE

The moves you return will be executed in the order you specify them. Thus, a return of {"DOWN 10", "STAY 2", "UP 4.3"} with speed = 5 will result in the partion first sliding down to leave a gap from 50 to 50+D, then staying there for 2 seconds, and finally sliding up to leave an opening from 28.5 to 28.5+D. The partition slides continuously, so at time 5, for instance, it will span from 25 to 25+D. The simulation will be run till time=1000 or a CLOSE command, at which point you will be scored. If you do not specify moves through time=1000 and do not issue a CLOSE command, the gap will simply stay in the last position you move it to.

Scoring

Your score for a test case will be based on how well you separate the red particles from the blues ones. If LR and LB are the number of red and blue particles in the left side of the vessel, while RR and RB are the numbers for the ride side, your score will be the entropy of the particles:

1 + (LR lg (LR / (LR + LB)) + LB lg (LB / (LR + LB)) + RR lg (RR / (RR + RB)) + RB lg (RB / (RR + RB)))/(LR+LB+RR+RB)

where lg(x) is the logarithm of x with base 2. Note also that we treat 0 lg (0) as evaluating to 0 (which it does if you take the limit). Thus a perfect separation will score a 1, while complete disorder (LR=LB=RR=RB) will score a 0.

Your final score will be computed by taking the sum over all test cases of YOU/BEST, where YOU is your score for that test case, and best is the best score anyone was able to achieve for that test case.

Test case generation

All parameters are chosen uniformly at random.

Visualizer

A visualizer, which includes manual play, is available at http://www.topcoder.com/contest/problem/MaxwellDemon/vis.html.

Definition

Class:	MaxwellDemon
Method:	moveOpening
Parameters:	int, int, int, int, String[]
Returns:	String[]
Method signature:	String[] moveOpening(int W, int H, int D, int speed, String[] particles)
(be sure your method is public)

Notes

- Invalid return results in a score of 0. This includes returns with negative durations, or improper formatting. You may also not have more than 100,000 elements in your return.

- The behavior of particles that bounce extremely close to the edge of the opening is undefined -- they may bounce or they may not, depending on the details of the floating point math being done. More specifically, a particle which would hit exactly on the edge of the opening should pass through the openning. However, if you move the opening for non-integral durations, it may end up off by a small amount from where you expect it, causing the particle to bounce instead of pass through.

- The memory limit is 1024 MB and the time limit is 20 seconds (which includes only time spent in your code).

- There are 10 example test cases and 100 full submission test cases.

- Your score will be evaluated a moment after the end of the simulation. Thus a particle which ends with X=0 will move slightly to one side or the other.

Constraints

- W will be between 10 and 100, inclusive.

- H will be between 40 and 200, inclusive.

- D will be between 10 and floor(H/4), inclusive.

- speed will be between 1 and 10, inclusive.

- The number of particles will be between 10 and 200, inclusive.

- For each particle: X will be between -W+1 and -1 or between 1 and W-1, inclusive; Y will be between 1 and H-1, inclusive; DX and DY will be between -5 and 5, inclusive, though no DX will be 0.

Examples

0)

"1"

Returns: 
"seed = 1
W = 89, H = 70, D = 13, speed=6
179 particles:
  R 4 36 -5 2,
  B -30 61 3 -3,
  R -43 53 -3 -2,
  R -51 48 4 3,
  R -33 54 -5 5,
  B 26 13 2 -2,
  R -30 31 5 0,
  B -39 61 -3 -5,
  R -25 67 -2 -3,
  B 38 16 1 -4,
  B -43 26 -4 4,
  R 72 5 5 -4,
  B -68 56 -3 5,
  B -63 58 2 3,
  B -13 45 -3 -5,
  R -30 27 -4 1,
  B 6 10 2 -4,
  R -50 23 -4 -3,
  R -19 47 -3 2,
  R 45 53 2 -5,
  B 56 35 3 -5,
  R -49 47 -5 -2,
  B -8 58 2 -4,
  B -53 5 -3 -2,
  B -6 3 -4 -5,
  R 7 21 5 2,
  B 14 44 -2 0,
  B -47 31 1 -5,
  B 25 29 -3 2,
  B -54 60 -1 4,
  R -54 2 -1 0,
  B -26 27 3 4,
  B 81 36 5 5,
  R 84 11 1 0,
  R 28 31 3 5,
  R -35 66 5 -2,
  R 81 65 1 -3,
  B 64 16 2 3,
  R -17 48 -4 -2,
  B -24 67 1 -5,
  B -47 47 5 -1,
  B 88 32 -4 3,
  R 87 9 2 5,
  R 63 40 -1 0,
  B 2 36 -5 -4,
  R -12 12 -5 -4,
  R 39 40 -3 -4,
  R -83 33 -2 5,
  B -39 20 5 -3,
  R -72 59 5 -5,
  R -38 11 2 3,
  R 35 28 -5 0,
  R -53 50 4 2,
  B -52 4 4 -4,
  B 87 27 1 3,
  B -1 33 -5 -1,
  R 16 43 -4 3,
  B 81 28 -5 4,
  B -32 45 4 -3,
  R 63 49 -2 2,
  R -12 21 5 2,
  B 57 32 -4 1,
  R 51 9 -5 2,
  R -50 12 -4 4,
  B -40 60 -2 -4,
  R -50 66 3 4,
  B 2 60 1 2,
  B -60 41 2 0,
  B -67 14 2 2,
  B -25 55 -4 0,
  B -54 45 -4 -5,
  B 59 10 1 3,
  B 46 21 2 0,
  R -67 13 1 -5,
  R -84 25 -2 3,
  R 17 5 3 2,
  B -73 47 -2 5,
  B 12 16 -4 -2,
  R 74 34 4 2,
  R 34 67 -4 -2,
  B 69 5 -5 -5,
  B -70 20 3 2,
  R 2 61 2 3,
  R -50 16 -1 -2,
  R -69 42 -1 -1,
  B -39 27 5 -2,
  R -8 15 4 -3,
  B -88 30 -5 0,
  R 40 52 3 -1,
  B -22 45 -4 4,
  B 38 2 4 -2,
  B 22 60 -4 5,
  R -49 30 -5 3,
  R 66 61 1 5,
  B -66 30 -3 0,
  B 38 1 1 2,
  B 52 28 -2 -5,
  B -74 56 -1 -2,
  B -53 29 5 -3,
  B 46 32 3 0,
  B -61 20 2 3,
  B 1 60 -2 0,
  B -28 23 -1 1,
  R -34 32 -3 5,
  R -43 34 -4 2,
  R 65 15 4 -3,
  R -71 16 2 1,
  R -21 49 4 -5,
  R 66 68 -3 -2,
  B -88 65 -1 -5,
  B -83 32 1 1,
  R -79 18 5 -5,
  R -36 64 3 -1,
  B -53 48 -3 3,
  B 79 15 3 3,
  B -49 64 3 -5,
  B -16 1 5 3,
  B -51 32 -3 2,
  R -8 52 -1 5,
  R 44 31 3 1,
  B 8 16 3 -2,
  R 63 67 -5 -4,
  B 56 16 -1 -1,
  R -25 3 1 -1,
  R 82 27 1 0,
  R -21 30 5 -2,
  B -13 59 4 4,
  R 27 63 2 2,
  R 69 21 2 3,
  B -15 36 -2 5,
  R -43 49 -2 -2,
  B 35 30 2 -5,
  B 82 45 5 -4,
  B 14 38 3 -2,
  R -65 52 3 2,
  B 39 46 5 -4,
  B -25 46 2 -2,
  B -27 26 2 1,
  B 7 23 -2 2,
  B 83 49 3 2,
  R 46 4 2 4,
  R -1 59 4 3,
  R 54 39 2 4,
  B 21 20 -3 2,
  R 85 35 4 2,
  R 31 58 4 4,
  B -32 47 5 3,
  B 75 67 4 2,
  B 18 66 2 4,
  R 50 40 1 -3,
  R -52 42 -1 1,
  R -51 64 4 3,
  R -7 33 -3 3,
  B 60 52 -1 -1,
  R -64 38 5 -3,
  R 83 27 -1 -3,
  R 39 13 3 2,
  R 15 32 -5 3,
  R -77 49 5 -4,
  B -9 34 1 0,
  R -17 53 -2 1,
  B 70 51 -3 -3,
  B 2 32 -1 0,
  B -74 62 -3 3,
  B 44 53 2 -1,
  B 31 69 4 5,
  R 15 1 5 -4,
  R 31 7 1 5,
  R -78 61 -5 -5,
  R -22 28 -4 2,
  R -19 46 -5 2,
  B 2 49 1 -5,
  B -75 26 1 2,
  R 27 4 4 -2,
  R 75 65 -1 -5,
  B 11 48 -3 -5,
  B -40 32 1 5,
  R 44 41 -3 5,
  B -75 53 3 -3"

1)

"2"

Returns: 
"seed = 2
W = 23, H = 45, D = 10, speed=6
101 particles:
  R 14 25 2 -4,
  B -1 40 -5 4,
  R 21 11 -5 5,
  B -14 16 1 4,
  B 1 3 -5 0,
  B 17 13 -5 0,
  B -17 13 -5 0,
  R 7 33 3 2,
  B 11 35 4 -3,
  B 21 4 -3 3,
  B -22 32 5 -4,
  B -19 23 4 2,
  B -13 25 3 3,
  R 20 40 3 -5,
  R -10 24 4 -4,
  B 9 6 -5 4,
  R -2 20 -3 -3,
  R -18 21 2 2,
  B -19 13 -4 -5,
  B -22 16 -2 -4,
  R -1 30 1 2,
  R 19 16 3 -3,
  R -3 10 5 -2,
  B -4 40 2 1,
  R 15 35 5 4,
  R 3 31 3 4,
  B -14 14 -4 3,
  B 14 11 -4 -4,
  B -3 12 -4 -3,
  R 19 9 1 1,
  B 3 7 4 -5,
  B 5 2 -1 -2,
  B 4 3 4 -1,
  R 11 14 3 4,
  B 3 33 -5 -2,
  R -21 30 3 -4,
  R 3 15 -2 4,
  B 4 9 4 3,
  B -22 14 -2 -1,
  R 17 21 3 -1,
  B 13 1 4 5,
  R 1 32 -3 3,
  B -9 34 -5 -3,
  R 5 37 -3 0,
  B 13 26 1 -2,
  B -3 7 1 -3,
  B 8 43 -3 -4,
  B 5 13 1 3,
  R 18 4 5 -1,
  B 17 30 -3 -3,
  B 7 7 -2 -1,
  B 6 25 3 -2,
  R -2 6 5 1,
  R 6 14 4 -5,
  R -20 44 2 -5,
  B 14 10 2 3,
  R -16 20 -1 3,
  R 19 16 1 3,
  R 7 20 3 -4,
  R 19 26 -4 3,
  B 22 44 -4 2,
  B -10 44 1 3,
  B 2 20 -1 3,
  B -13 44 3 -1,
  B -12 41 2 -5,
  B 22 38 -1 -2,
  B 7 39 -3 3,
  B 14 33 -2 3,
  B 11 22 4 -2,
  B 2 16 -5 2,
  R -2 20 -2 4,
  B -5 3 5 4,
  B 18 34 5 -2,
  R 17 14 4 -4,
  R -4 9 3 -5,
  R 18 2 -3 1,
  B -17 28 -4 -5,
  B -13 16 5 2,
  B -14 39 5 -5,
  B 7 16 1 5,
  R -11 26 4 -5,
  B 22 2 1 5,
  R 1 20 4 3,
  B 2 24 1 0,
  R 1 1 3 -1,
  R 7 11 -4 4,
  B 20 44 1 5,
  B -20 17 5 -5,
  R -3 2 1 -1,
  R -3 13 1 -2,
  R -10 6 3 1,
  R -7 8 -1 -3,
  B -6 8 1 2,
  B 11 24 5 0,
  R -3 33 4 -5,
  R 1 36 -5 4,
  R -14 37 5 -2,
  B 2 30 -2 3,
  B -14 29 1 5,
  R 8 26 2 -4,
  R 14 7 3 -2"

2)

"3"

Returns: 
"seed = 3
W = 99, H = 199, D = 22, speed=9
71 particles:
  R 81 155 -4 -5,
  B 67 23 -5 -1,
  R 16 103 5 -4,
  R 92 55 -1 -1,
  R -51 95 5 4,
  B 58 124 -5 -4,
  R 22 196 3 5,
  B -50 166 1 -1,
  R 79 183 1 1,
  B -74 69 -1 -3,
  R -25 48 3 1,
  B 63 184 -3 -3,
  R -98 190 -3 2,
  R 66 138 -5 -3,
  R 28 24 -3 -3,
  B -60 80 2 2,
  R -57 73 -3 4,
  R -30 46 -1 5,
  B -82 74 -2 2,
  R 22 24 -3 -5,
  B -32 112 -1 -1,
  B 41 81 1 2,
  R -11 75 2 -3,
  B -70 8 -3 -1,
  R -95 170 5 -1,
  R -60 7 2 -3,
  R -2 10 -2 5,
  B -44 173 -2 5,
  R -81 16 3 -3,
  B -22 173 -3 0,
  B 25 14 -4 4,
  B -71 100 -1 3,
  B 31 32 -3 0,
  B 34 124 5 1,
  B 63 133 1 -2,
  R -35 66 -4 1,
  B -3 101 5 1,
  B 11 182 -2 0,
  B -2 33 4 3,
  B 41 51 3 -4,
  R 15 147 -3 -5,
  R -44 150 3 -3,
  B -57 115 -5 3,
  R -65 166 4 5,
  R 90 148 -3 -5,
  B -38 37 -2 -4,
  R -77 56 -1 -1,
  R -70 79 -1 0,
  R -24 39 3 5,
  B -21 7 5 -4,
  B -4 102 -2 4,
  R 77 61 -1 2,
  R 74 51 2 2,
  B 78 56 4 3,
  R -41 29 -4 3,
  R 66 57 3 -4,
  B -84 116 3 -2,
  B 75 71 -1 2,
  R -36 126 -2 3,
  R -87 20 -4 -3,
  R -50 98 -4 -3,
  R 97 183 3 -4,
  R -4 164 3 -4,
  R -70 181 -4 -5,
  R 48 175 -2 -5,
  R 31 51 1 2,
  B 89 64 4 -4,
  B 41 183 2 1,
  R -70 145 -1 0,
  R 88 99 1 -5,
  B -23 154 -5 2"

3)

"4"

Returns: 
"seed = 4
W = 52, H = 169, D = 35, speed=3
193 particles:
  B 34 86 2 5,
  R -1 115 3 0,
  R 39 123 2 0,
  B 33 108 -5 -1,
  R -14 88 -4 5,
  R -48 153 5 -3,
  R 23 69 1 1,
  B 16 166 1 1,
  R 14 47 2 2,
  R -40 77 -5 0,
  R -4 25 -3 -2,
  B -14 67 -1 -5,
  R -44 9 4 -4,
  R 33 22 -5 3,
  R 31 93 -5 -5,
  B -34 8 4 3,
  R -46 30 -1 -5,
  B 46 52 -3 -5,
  R -25 127 4 2,
  R 20 99 4 0,
  R 5 43 1 -1,
  R 43 156 -2 -1,
  B 49 10 -5 3,
  B 9 160 -1 5,
  B -34 6 3 -4,
  B 28 29 3 3,
  R -7 119 -3 -3,
  B -48 121 -1 2,
  R -15 55 -4 4,
  B -47 159 -3 -2,
  B 24 139 5 4,
  R 22 144 -5 -1,
  B -50 4 -5 2,
  B 8 140 5 -5,
  R -41 47 3 -4,
  R 27 109 -4 3,
  B 11 151 1 2,
  R 19 133 5 -2,
  R 49 151 -5 -5,
  R -8 151 2 1,
  R 20 32 5 4,
  B -36 152 -4 -3,
  B -51 38 -4 3,
  R 8 19 -1 4,
  R 8 46 -3 -1,
  B 23 166 -1 0,
  R -17 119 3 0,
  B -26 121 -2 -2,
  R -49 14 -1 1,
  B -46 12 5 -1,
  R -31 17 -1 3,
  R 41 123 4 -3,
  B -45 23 -2 0,
  B -28 103 1 -3,
  B 10 10 -5 -4,
  R 30 166 -4 4,
  R 5 70 -5 5,
  B -2 46 4 5,
  B 6 49 -2 -1,
  R 20 156 -2 3,
  R 26 165 1 -3,
  R 41 28 -4 2,
  R 28 75 1 -3,
  B -6 136 1 -1,
  R -35 28 3 0,
  B -34 44 -1 -1,
  B -5 6 2 4,
  R 13 57 3 -2,
  B -29 168 -1 -2,
  B -11 142 -5 4,
  R -32 130 -1 0,
  B -7 33 2 0,
  R -5 138 -4 5,
  B 35 82 -5 -2,
  R -20 103 -1 1,
  B 10 166 1 3,
  R -5 115 -1 -1,
  R 26 45 -5 5,
  R 10 41 5 4,
  R -12 39 -3 2,
  R -8 2 4 -1,
  R 15 78 -2 0,
  B -34 4 4 -5,
  B -17 17 -4 -4,
  R 3 143 3 4,
  R 7 2 -5 -1,
  R 26 167 5 -5,
  R -21 34 2 -4,
  B -26 98 1 5,
  B -28 115 1 2,
  R -17 109 3 4,
  B -30 104 1 1,
  R 25 163 -5 4,
  B 11 62 -2 -3,
  B -8 99 -2 2,
  R -42 74 2 2,
  R 15 132 2 3,
  R 19 141 4 5,
  B -24 139 2 3,
  B 29 65 5 -3,
  B 45 129 2 0,
  B 8 14 -1 4,
  R -8 123 -5 -3,
  B -45 124 -4 1,
  B 23 59 4 0,
  B 1 50 3 0,
  B 51 61 -3 4,
  R -21 132 -1 1,
  R 27 145 -1 3,
  B 46 129 -2 2,
  R -34 103 -3 -4,
  B 44 1 4 1,
  R -50 10 2 1,
  B -37 103 -3 4,
  B 9 69 -5 1,
  B -25 139 -4 -3,
  R -2 115 -1 1,
  B 3 58 4 1,
  R 44 131 -5 4,
  B 3 131 1 0,
  R 12 56 -2 -3,
  R -20 101 1 -3,
  R 41 120 3 -2,
  B 46 15 -4 -1,
  R 4 97 3 -1,
  B -19 133 4 2,
  B 36 52 4 -5,
  R -2 76 -5 -2,
  B -24 145 3 3,
  R -31 159 -3 0,
  B -5 146 -3 -3,
  B 16 32 3 0,
  R 6 88 4 3,
  B 40 62 -3 4,
  R 10 80 -2 -2,
  R 23 159 -3 -4,
  R 22 62 -2 5,
  B -50 104 2 -1,
  B -20 152 -2 4,
  B -30 66 -5 -2,
  B -1 87 4 -2,
  R -14 80 -3 1,
  R -33 68 1 -1,
  B 15 101 1 3,
  B 4 165 4 4,
  B -5 106 4 -3,
  R -36 24 5 -1,
  B 5 161 -1 4,
  R -29 112 5 -2,
  B -36 3 -3 -4,
  B 38 74 5 -2,
  B 34 135 -5 -3,
  R -8 27 2 -3,
  B 25 80 4 -2,
  R -19 29 -1 0,
  R 1 108 3 3,
  B -51 84 -3 -3,
  B -9 150 -1 -1,
  B -51 45 1 -2,
  R -29 135 5 4,
  B 20 119 1 3,
  B -8 117 1 3,
  B -12 71 2 3,
  R -5 67 -2 -2,
  B 10 80 -4 3,
  B 36 79 4 5,
  B -12 136 3 5,
  R 17 28 2 -2,
  B 28 117 5 0,
  B 2 37 2 -2,
  B -5 34 4 -5,
  R -20 16 -4 3,
  R -42 99 -2 0,
  B -29 32 -5 1,
  R 46 128 4 -2,
  B 14 21 3 3,
  B 8 5 -5 1,
  R -43 107 4 -5,
  R 41 130 3 -4,
  B -5 101 5 -5,
  B 47 57 -1 2,
  R 1 129 -3 0,
  R -5 117 -4 -2,
  R 7 54 -5 0,
  R -36 64 1 4,
  B -30 102 3 5,
  R 42 22 5 3,
  B 40 2 3 3,
  R 20 103 -2 -3,
  R -41 38 4 -5,
  R 41 163 -3 -4,
  B -6 103 -5 -1,
  R -51 29 3 3"

4)

"5"

Returns: 
"seed = 5
W = 83, H = 124, D = 29, speed=8
178 particles:
  R -73 26 -3 -4,
  R -54 88 2 3,
  B 22 77 4 0,
  R 79 29 4 3,
  B -1 69 3 5,
  R 7 1 -5 1,
  B -2 81 -3 1,
  B 59 90 -1 -1,
  B -57 44 4 -1,
  B -78 76 3 -1,
  B -11 81 5 -5,
  B -56 17 5 -1,
  B -28 43 -4 -3,
  R -82 35 2 3,
  B -21 60 -2 0,
  R -41 86 -1 0,
  R 54 77 4 4,
  R -58 29 4 2,
  R -41 67 -1 0,
  R 37 99 5 -2,
  R -54 114 3 0,
  B 50 42 3 0,
  R 73 57 4 1,
  R 73 64 2 -2,
  R 51 64 2 -2,
  B -52 14 5 -2,
  R 10 79 4 0,
  B -81 25 -4 -3,
  B 8 102 2 5,
  R -68 62 -1 2,
  R 61 104 5 1,
  R 8 66 1 0,
  R -81 121 2 2,
  B 54 32 -5 -2,
  B -15 110 5 0,
  R 73 57 -1 3,
  R 6 12 3 3,
  B -14 30 1 -5,
  R 51 14 5 -5,
  B 81 80 -3 4,
  B 47 115 2 -4,
  B 11 18 -2 2,
  R 36 113 4 -3,
  R 63 7 2 2,
  B -8 81 -4 -2,
  B 79 29 -5 -3,
  R -49 5 -5 -3,
  B 18 56 4 5,
  B 67 25 5 -3,
  B -14 96 4 -5,
  R -25 44 1 4,
  B -70 94 -1 -5,
  B 37 83 -4 3,
  B 42 4 2 -2,
  B 26 51 -2 -4,
  R -79 74 -2 -2,
  R -47 59 -1 5,
  B 47 45 -5 -4,
  B 74 71 5 -2,
  B 80 2 1 -4,
  B 26 61 4 4,
  B 72 84 3 -4,
  R 26 94 5 -3,
  B 39 120 -2 -3,
  R -64 82 3 1,
  B -33 74 2 -2,
  B -3 73 -3 -5,
  B 65 116 4 -4,
  R 30 2 1 3,
  B 80 65 -5 -5,
  R 61 100 -4 -1,
  B 82 58 -4 -2,
  B 37 7 -5 -5,
  R -16 72 -4 -4,
  B -31 97 1 -4,
  R 22 41 -4 2,
  B 32 54 -5 -2,
  B -45 5 4 -1,
  B -53 77 4 -2,
  B 26 53 -2 5,
  R 38 56 -2 4,
  R -42 12 -3 -2,
  R 3 115 3 -2,
  B -6 42 -5 -4,
  R 62 19 1 -4,
  B 67 118 -1 -2,
  B -75 31 -5 -1,
  R -17 11 1 -1,
  B -59 18 5 2,
  R 41 87 -3 3,
  R 6 13 2 0,
  R -31 82 1 -2,
  R 16 88 2 -1,
  R 1 115 1 -1,
  B -29 56 -1 2,
  R 74 34 4 1,
  R -5 57 3 2,
  R -72 48 -2 -3,
  B 75 15 4 3,
  B -33 113 -2 -2,
  B -28 20 1 -2,
  B -54 44 -1 2,
  R -9 60 -5 0,
  R 81 69 3 -2,
  B 55 6 -1 5,
  R 9 35 -3 -3,
  R -56 53 4 -4,
  R -61 13 -4 4,
  R 65 101 -5 -3,
  B 50 87 -1 4,
  R -41 98 -3 0,
  R -51 90 4 0,
  R -8 31 5 0,
  B 13 9 -3 -2,
  R 48 105 -2 1,
  R 63 33 4 2,
  R 63 34 -3 -1,
  B -3 69 3 4,
  R 59 106 -3 3,
  R -25 120 5 1,
  B 63 60 -4 5,
  B -26 67 1 0,
  R 61 97 -1 -4,
  B -53 109 5 -1,
  R -11 75 -4 5,
  R 34 9 4 0,
  B -8 16 -2 -5,
  B 56 65 -5 1,
  R 38 55 -1 -3,
  B 26 88 -5 -1,
  B 41 52 1 5,
  B -35 42 2 1,
  R 49 21 -5 -5,
  R 14 26 -5 0,
  R 60 34 2 4,
  R 56 123 1 2,
  B 46 84 -2 4,
  R -67 107 5 -1,
  R 32 46 3 -3,
  B -69 88 1 -1,
  B 38 110 -1 -4,
  R -12 81 5 4,
  R -64 2 4 0,
  R -23 115 2 4,
  R 22 12 3 1,
  B 16 10 -2 -2,
  R 24 12 5 -2,
  R -21 30 2 3,
  B 7 75 -4 -4,
  B -67 51 -5 5,
  B -43 122 2 3,
  B -46 90 5 4,
  R -29 20 3 3,
  B 40 14 -4 -4,
  B -2 31 3 2,
  R 46 54 -2 -2,
  B -79 33 -1 -5,
  B 47 56 4 5,
  R 33 93 4 -4,
  R 26 52 -3 1,
  B -7 38 5 2,
  B -14 109 -1 -1,
  R 65 118 3 5,
  B -63 19 4 3,
  R 19 50 -3 -5,
  R -1 20 -1 -4,
  R -28 55 -3 3,
  B -52 23 -4 4,
  R 12 90 -2 -2,
  B 74 4 -3 4,
  B -48 3 -2 0,
  R 9 46 2 -5,
  B -31 112 4 -1,
  R 81 104 -5 2,
  R 81 59 2 -3,
  B -40 90 5 3,
  R 79 3 -2 4,
  B -56 93 2 -1"

5)

"6"

Returns: 
"seed = 6
W = 34, H = 45, D = 11, speed=6
89 particles:
  R 19 35 -3 -5,
  B 4 10 -3 3,
  B -22 2 4 -1,
  B 15 19 3 5,
  B 20 25 -1 3,
  R 3 38 1 2,
  R 9 6 -5 -3,
  R 7 39 1 3,
  R -26 12 -5 -3,
  R -4 7 1 -3,
  B -11 38 -3 5,
  R -12 44 -2 -5,
  B 3 38 -4 4,
  B -4 26 4 -3,
  R -17 23 1 3,
  R 22 16 2 0,
  R -20 40 -5 -3,
  R -1 3 -1 -2,
  B 29 7 -3 3,
  B -19 39 -3 -5,
  R -7 15 1 2,
  R 3 37 -1 -5,
  R -4 35 5 -4,
  B -7 28 -2 5,
  B -21 29 3 -1,
  B -32 12 -2 5,
  R -24 38 2 2,
  B 31 40 -5 -3,
  B 16 5 -4 -3,
  R -19 15 -3 -1,
  B 33 18 -4 1,
  B -15 18 4 3,
  R 9 41 -5 0,
  R 2 18 1 2,
  R -29 43 4 4,
  B 15 7 4 -3,
  B -2 23 5 0,
  B 25 5 -2 -5,
  R -9 41 -2 -4,
  B 1 31 -2 5,
  B 2 38 -2 5,
  B -29 12 -4 0,
  R -2 39 5 1,
  R 32 2 5 0,
  B 18 8 -3 4,
  B -4 23 1 -2,
  R -26 21 4 -2,
  R -20 14 4 -5,
  R -19 17 -5 -2,
  B 24 36 -1 5,
  B 15 32 3 4,
  R 9 7 3 5,
  B -9 9 -5 -2,
  R 8 20 3 5,
  B -3 2 -3 3,
  R 12 39 2 2,
  B 13 18 5 5,
  B -13 32 -4 -3,
  B -33 32 -4 2,
  B 11 22 1 -1,
  B 27 12 5 3,
  R -33 24 -2 -2,
  R -9 38 2 -5,
  B -6 5 1 -5,
  B 29 13 -2 1,
  R 17 32 -5 3,
  B 23 4 -4 4,
  B 30 26 2 0,
  B 6 32 1 1,
  B 31 5 -1 -5,
  B -14 23 -2 5,
  B -27 13 -3 -5,
  B 18 18 5 -4,
  R -30 24 -4 3,
  B 23 23 -3 -1,
  B -30 37 2 0,
  R -2 8 5 -3,
  R -33 20 3 -3,
  B 8 22 2 -5,
  R -21 10 -3 -2,
  R 20 21 2 0,
  B -6 17 -2 -4,
  B 22 5 -3 2,
  B 20 26 -2 -4,
  B 21 42 -4 -5,
  R 20 38 -1 1,
  R 2 14 -5 -1,
  B -15 24 -5 3,
  R -14 33 5 5"

6)

"7"

Returns: 
"seed = 7
W = 98, H = 77, D = 11, speed=7
61 particles:
  R 25 61 2 -3,
  B 92 26 1 1,
  B 47 40 1 5,
  B -94 52 4 1,
  B -43 76 -1 -1,
  B -63 31 -3 2,
  B -42 62 -3 5,
  B 25 63 5 0,
  R -69 73 -2 -2,
  R 34 65 -1 3,
  R 40 37 -1 5,
  B -77 62 -1 4,
  R 55 19 5 -5,
  R 65 32 3 -4,
  B -17 8 -3 4,
  B -58 46 5 -5,
  R 93 15 -2 -5,
  B 76 26 -5 -3,
  R 65 57 -1 5,
  B -56 64 5 3,
  B -93 3 1 -4,
  B 92 61 -3 2,
  R -79 45 3 -3,
  R -38 56 -3 2,
  R -44 33 -3 5,
  R 69 8 -1 2,
  B 19 70 -2 5,
  R 72 69 -5 -1,
  R 5 54 -4 5,
  B 57 35 3 4,
  B -70 45 -2 -1,
  B -28 26 5 -3,
  B 28 56 -4 -4,
  B -2 6 -5 0,
  R 59 32 -4 -1,
  R 50 41 1 0,
  B -42 50 -2 4,
  B -27 74 2 -4,
  R -93 11 -4 -4,
  B -70 15 -2 -4,
  R 96 37 -1 -1,
  B -57 15 1 2,
  B 50 67 -4 4,
  R 57 35 -1 -2,
  R 59 58 -5 -2,
  R 39 29 -5 0,
  B -14 59 -3 -1,
  R -1 16 4 2,
  R -19 21 3 3,
  R -86 11 -4 0,
  B 30 24 1 -3,
  R -37 62 4 4,
  B 58 23 -5 4,
  R -85 73 5 -4,
  B 83 45 -5 1,
  B 15 29 -3 2,
  B 79 13 3 -1,
  R 26 34 -1 3,
  B 81 50 -4 4,
  R -69 63 -3 -3,
  R 28 31 -5 -4"

7)

"8"

Returns: 
"seed = 8
W = 49, H = 137, D = 17, speed=9
124 particles:
  B -17 27 4 3,
  B -38 23 -3 -2,
  B -19 77 5 5,
  B 33 111 -4 -3,
  R -29 8 1 1,
  R -15 31 4 -4,
  R -4 62 4 4,
  B 23 49 -1 0,
  B 27 133 -1 5,
  B 14 133 -2 -5,
  R -46 136 -4 1,
  R -14 116 -1 -4,
  B 36 52 2 -4,
  R -31 78 5 4,
  R 46 91 5 -3,
  R 37 40 3 0,
  B 21 21 4 0,
  R 40 8 -1 5,
  R -38 101 2 0,
  B -20 20 4 2,
  R -42 71 -1 5,
  R -20 131 3 0,
  R -24 68 -1 3,
  R -34 46 1 4,
  R -37 21 -4 2,
  R 42 11 -5 3,
  B -32 16 -3 2,
  R -43 111 -5 5,
  R -23 109 1 5,
  R 10 23 -4 -5,
  R 3 46 -5 5,
  R 13 70 4 1,
  R -33 85 1 4,
  R -33 116 -3 -5,
  B 40 77 -4 3,
  R -16 80 -3 -1,
  B -41 87 1 3,
  R 28 133 1 -4,
  B -9 56 5 3,
  R -22 39 -5 5,
  R -23 105 1 5,
  R -11 24 -5 -1,
  R -36 86 5 3,
  B 27 30 -1 5,
  B -36 126 -2 5,
  B 3 128 -5 1,
  B -7 32 -1 2,
  R 17 34 1 -2,
  R -31 27 -4 -1,
  R -17 89 1 -3,
  B 41 91 5 -2,
  R 24 13 3 -3,
  R -24 134 -1 3,
  R 25 8 -5 5,
  R 34 98 3 3,
  B -10 7 1 5,
  B -12 71 5 3,
  B 37 81 3 -5,
  R 31 61 3 -5,
  B -15 3 5 -1,
  B 18 77 1 -2,
  R 39 79 2 0,
  B -4 73 3 4,
  R 9 36 2 5,
  B 43 88 4 1,
  R -21 19 1 -4,
  B -40 22 4 -3,
  B -18 27 1 -5,
  B -21 22 -1 1,
  B 23 7 -1 -3,
  R -22 114 2 0,
  R -27 52 5 2,
  R 40 52 -1 -1,
  B 34 92 4 2,
  R -37 85 -1 -1,
  R 7 122 -5 4,
  B -40 133 -5 -2,
  R -30 73 -3 1,
  B -31 66 -1 4,
  R -43 33 5 4,
  R 9 134 1 4,
  B 7 42 5 -4,
  B -46 5 -5 3,
  B 37 109 -1 0,
  R -24 3 -4 4,
  R -45 118 -2 1,
  R -1 57 -4 2,
  B 30 134 5 -4,
  B -47 35 -4 -1,
  R 29 54 4 -5,
  B 16 132 -1 3,
  B 12 2 -5 5,
  B 15 115 1 -1,
  B -32 3 2 -1,
  B 46 5 -3 -2,
  B -24 46 3 0,
  R 15 113 2 -5,
  R 5 104 -2 4,
  B -8 50 -1 5,
  R -15 102 4 4,
  R 45 44 3 1,
  R 3 57 4 5,
  R 28 37 1 2,
  R 38 1 -3 0,
  R -17 40 2 -1,
  R -8 74 -5 0,
  R 4 26 4 -1,
  R 11 39 -1 1,
  R 21 45 -1 -4,
  R 33 47 3 2,
  R 26 78 5 4,
  R 27 48 1 4,
  R 46 74 2 1,
  B 11 1 4 3,
  B -14 78 5 -4,
  B -8 90 -3 -1,
  R 36 133 3 5,
  R 23 70 -5 2,
  B 15 52 -5 -4,
  R 15 68 -3 -5,
  B 35 28 -2 2,
  B -22 106 -4 3,
  R 44 126 3 3,
  B -17 122 -4 -5"

8)

"9"

Returns: 
"seed = 9
W = 55, H = 69, D = 16, speed=3
173 particles:
  R -18 48 2 0,
  R -48 66 -2 1,
  R 26 67 2 1,
  R -18 11 -4 3,
  B -54 28 3 -5,
  B 7 58 1 -5,
  R 1 33 1 -5,
  R 7 32 2 -4,
  B -35 23 2 -3,
  B -54 15 5 -5,
  B 40 61 -2 -4,
  B -32 60 -4 3,
  B 20 18 1 4,
  B 40 23 -4 -2,
  R 50 65 -2 -5,
  B -10 18 -2 5,
  B -43 62 -1 -1,
  B -22 19 -2 -4,
  R -40 28 3 0,
  B 48 32 2 -2,
  R 18 10 -5 2,
  B -40 4 2 -5,
  B 45 67 2 0,
  R 46 30 -4 2,
  R 19 26 3 2,
  R -36 5 -2 3,
  B -29 5 3 0,
  B 19 20 4 0,
  R 45 33 1 1,
  R -49 66 -5 -4,
  R 12 54 1 0,
  R 36 56 -5 -1,
  R -51 53 3 5,
  R -25 61 2 2,
  B -46 65 -4 -4,
  R 44 25 2 -1,
  R 31 33 -3 -2,
  B -8 35 4 4,
  R 20 35 -4 4,
  B 21 44 5 2,
  R 34 30 -2 0,
  B -34 37 -2 3,
  R 34 32 -2 2,
  R -31 55 -3 -3,
  B -15 41 3 -3,
  B -15 2 -2 -3,
  R -42 2 -5 -4,
  R -36 26 1 5,
  R -42 68 2 -2,
  B 49 5 -4 5,
  B -25 57 -5 -5,
  B -2 53 3 -5,
  R 6 59 -1 2,
  B -43 39 -2 0,
  R 9 33 3 2,
  R 2 13 -2 -1,
  B -32 31 -2 -3,
  B -52 45 -2 1,
  R 43 13 3 5,
  R 27 39 5 -5,
  R -41 52 -4 -4,
  B 39 12 -2 -4,
  B 37 24 -3 5,
  R 54 32 3 -4,
  B 15 57 -1 5,
  B -23 37 -5 0,
  R -24 23 3 1,
  R -11 3 2 -3,
  B -48 61 -1 -1,
  R -4 61 4 4,
  R -48 38 -2 4,
  B -4 10 5 -5,
  R -27 32 -4 -5,
  R -48 50 -5 5,
  B -33 44 3 -2,
  R 9 43 1 -4,
  R -45 1 -3 1,
  R 28 10 5 -4,
  R -23 6 -5 3,
  B 46 12 -2 1,
  R -51 20 1 0,
  B -20 44 -2 4,
  B -15 49 5 -3,
  R -19 42 -5 2,
  B 19 41 -2 3,
  B -26 62 2 -2,
  B -44 31 -5 0,
  B -42 11 4 -1,
  R 21 18 2 -5,
  R 6 10 -2 -3,
  R 38 5 3 -4,
  B -29 49 -1 0,
  R -36 12 -5 -3,
  R 41 32 3 -2,
  B 12 44 2 4,
  R -14 55 5 -1,
  B -41 52 4 5,
  B 2 41 3 5,
  R 38 52 2 2,
  R 14 38 5 -4,
  R -45 68 3 1,
  R 33 58 4 3,
  B -18 15 2 -5,
  R 38 44 -3 4,
  R 22 6 1 -2,
  R 12 11 -5 -4,
  B 22 57 4 -3,
  B -24 31 -3 -1,
  R 25 26 -3 0,
  B 32 52 -5 4,
  R 37 25 5 0,
  B 47 22 -5 -2,
  B 41 22 -1 3,
  R -5 46 -2 -5,
  R -24 8 5 2,
  B 39 14 -2 0,
  R 25 34 5 0,
  R -16 26 3 5,
  B -25 61 -3 2,
  B -16 61 -1 5,
  R 3 16 3 -3,
  B -35 47 4 0,
  R -36 24 5 4,
  R 21 8 -5 3,
  B 26 20 -4 -1,
  B 3 48 -5 -1,
  R -3 11 -3 1,
  R -6 18 5 2,
  B 17 26 -2 -3,
  R -37 38 1 -1,
  R 47 50 2 -3,
  R 8 45 -5 -3,
  B -2 46 -2 4,
  R -33 53 1 1,
  B 2 23 -5 -3,
  B -26 45 1 1,
  B -18 29 3 -5,
  B -26 30 -2 3,
  B 7 7 -4 0,
  R -53 10 5 0,
  R -8 52 3 -2,
  R 10 1 -4 0,
  B 18 11 1 0,
  B -16 45 3 -3,
  B 18 12 2 0,
  R 32 1 -5 -5,
  B 53 34 3 -3,
  B -35 60 -1 1,
  B -10 23 3 3,
  B -13 34 -3 4,
  B 41 30 -3 -2,
  R -6 21 3 5,
  B -33 24 2 3,
  B 17 42 1 -2,
  R 39 9 1 -1,
  R -26 12 4 3,
  R 15 46 -4 -2,
  R -48 56 -3 -2,
  R 41 53 1 -2,
  B -14 63 -3 1,
  B -6 39 -1 5,
  R -28 51 -1 2,
  R -15 55 -2 -2,
  R 5 31 -2 -3,
  B -36 14 5 5,
  R -23 44 5 2,
  B 27 52 -2 2,
  B -23 8 -2 4,
  R 22 66 4 0,
  R -31 52 -1 -5,
  B -6 49 1 2,
  B 6 58 1 2,
  R -53 2 -4 4"

9)

"10"

Returns: 
"seed = 10
W = 84, H = 71, D = 10, speed=2
133 particles:
  R 70 1 -2 4,
  B 18 57 1 1,
  B 28 53 -4 3,
  B 69 36 3 -3,
  B -55 46 1 0,
  B -5 26 -1 4,
  B 71 65 4 2,
  R -2 53 1 -4,
  R -61 1 1 -5,
  R -34 32 5 4,
  B -52 22 -3 1,
  B -36 2 3 4,
  B 16 41 1 -4,
  R 36 53 -1 -1,
  B 31 57 -2 5,
  B -8 29 1 2,
  B 66 69 2 -4,
  B 82 40 -2 -5,
  R 28 34 2 0,
  R 4 67 -5 5,
  R 55 9 2 -3,
  R 11 39 -2 -2,
  B 23 36 -2 4,
  R 6 56 -1 -3,
  R -66 50 5 1,
  R -24 57 1 1,
  R 70 52 1 -4,
  B 73 57 1 -5,
  R -10 56 4 -2,
  R -51 18 -2 -4,
  R 22 8 3 -5,
  B 5 25 4 -2,
  B 11 36 -1 -2,
  R 50 31 -1 1,
  B 68 14 -5 -1,
  B 43 6 -3 4,
  R 82 51 -5 -5,
  R -31 66 -1 -2,
  R -17 39 -2 2,
  B -18 13 2 2,
  R 37 18 3 -4,
  B -19 46 -1 -2,
  B 49 19 -5 -1,
  R 75 43 -3 1,
  B 7 14 -5 3,
  B -13 53 -2 -5,
  B -10 36 -3 -5,
  B -7 57 5 3,
  B 28 31 4 0,
  B -32 40 3 -1,
  B 25 24 -5 4,
  R 27 63 2 3,
  B 20 41 -5 -3,
  B 19 16 -3 1,
  R 51 5 -4 4,
  R 51 63 3 3,
  B 33 57 -4 2,
  B 30 5 -5 3,
  B 22 36 2 4,
  B -31 4 -3 -2,
  R -53 17 -5 -1,
  R -3 38 1 -1,
  R -82 12 -2 5,
  R 20 28 4 -4,
  R -12 20 2 5,
  R 79 28 4 0,
  R -56 54 -5 -5,
  B -63 63 -3 -5,
  B -78 56 -1 -4,
  B 34 48 -5 1,
  R 73 44 2 -2,
  B -70 63 1 1,
  B -9 46 -5 -1,
  B 30 55 3 -2,
  B 42 22 5 -4,
  R 32 52 5 1,
  B 36 35 5 -3,
  B -27 25 -5 -4,
  R -81 4 2 -2,
  B -49 52 -2 3,
  B -11 1 1 -1,
  R 3 32 -1 5,
  R -31 31 -2 -4,
  R -49 47 2 1,
  B 79 60 -4 0,
  B -11 3 -4 0,
  R 56 34 4 3,
  R -71 20 -1 2,
  B 20 17 1 4,
  R -36 18 4 -4,
  R -71 17 2 -1,
  B 68 45 4 -2,
  B -13 66 4 -1,
  B 5 4 4 -5,
  R -3 45 1 -1,
  B -33 21 -4 5,
  B -46 17 1 0,
  B 21 51 2 5,
  R -44 69 4 -3,
  B 15 66 -5 0,
  R -82 24 3 -4,
  R 39 60 -1 0,
  R 21 7 -1 -4,
  R -54 3 1 -4,
  B 67 55 -2 -4,
  B -1 21 -4 -4,
  B 13 21 -3 -2,
  B 53 11 4 0,
  B 26 32 5 5,
  B 36 14 4 -4,
  B 52 31 -1 1,
  R -49 37 3 -2,
  B -43 52 -4 -3,
  R 21 49 1 -5,
  R 43 36 4 2,
  R 6 38 4 2,
  R 55 63 3 -2,
  R 39 45 -4 -2,
  R 48 31 -3 -2,
  R -81 42 -1 5,
  B -82 21 -5 -3,
  B -61 42 -3 -2,
  R 27 64 -1 -1,
  R 31 29 -3 5,
  B -10 31 -3 4,
  R -41 66 3 5,
  R 18 6 5 2,
  B 54 64 3 -3,
  B -7 64 3 4,
  B -9 58 -3 -1,
  R -47 68 -4 0,
  B 13 68 -3 -1,
  B 62 6 1 -1"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FactoVisors

Math

Used in:

SRM 406

Used as:

Division II Level Two

Writer:

eleusive

Testers:

PabloGilberto , Olexiy , gawry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8427

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12178&pm=8427

Problem Statement

Return the number of positive integers that are multiples of each number in divisors and divisors of each number in multiples.

Definition

Class:	FactoVisors
Method:	getNum
Parameters:	int[], int[]
Returns:	int
Method signature:	int getNum(int[] divisors, int[] multiples)
(be sure your method is public)

Constraints

-

divisors and multiples will each contain between 1 and 50 elements, inclusive.

-

Each element of divisors and multiples will be between 1 and 10^9, inclusive.

Examples

0)

{1}

{100}

Returns: 9

The working integers are 1, 2, 4, 5, 10, 20, 25, 50, and 100.

1)

{6,9}

{18}

Returns: 1

18 is the only integer that works.

2)

{6,9}

{96,180}

Returns: 0

No integers work.

3)

{2,4}

{256}

Returns: 7

4)

{1000,10000,100000}

{1000000000}

Returns: 25

Beware of overflow.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheDiceGame

Simple Math

Used in:

SRM 381

Used as:

Division I Level One , Division II Level Two

Writer:

Vasyl[alphacom]

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8414

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10804&pm=8414

Problem Statement

Little John has one standard die with numbers one to six on its sides. Each time he throws the die, he gets as many candies from his mom as the number on the top of the die. John?s goal is to collect at least candies candies. Then he will eat them all and became a little fat boy.

Return the expected number of throws needed for John to achieve his goal.

Definition

Class:	TheDiceGame
Method:	expectedThrows
Parameters:	int
Returns:	double
Method signature:	double expectedThrows(int candies)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

candies will be between 1 and 1000000, inclusive.

Examples

0)

Returns: 1.0

John needs only one throw to get at least one candy.

1)

Returns: 1.1666666666666667

After the first throw, there is a probability of 1/6 that John will need an additional throw.

2)

Returns: 2.5216263717421126

3)

Returns: 13.90476189046144

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CreateGroups

Greedy, Simple Math

Used in:

SRM 430

Used as:

Division II Level One

Writer:

Janq

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8376

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13521&pm=8376

Problem Statement

Your language school is starting a new semester, and each student must select a time schedule. You are given a int[] groups, where the i-th element is the number of students who selected the i-th schedule. Your school has a rule stating that the number of students assigned to each schedule must be between minSize and maxSize, inclusive. However, this rule was not enforced properly during the sign up phase. It is your job to reassign students in such a way that the rule is satisfied. A reassignment is defined as removing a student from one time schedule and placing him in a different time schedule. Return the minimal number of students you must reassign, or return -1 if it is impossible to satisfy the rule. Note that you may not create new schedules or delete existing schedules.

Definition

Class:	CreateGroups
Method:	minChanges
Parameters:	int[], int, int
Returns:	int
Method signature:	int minChanges(int[] groups, int minSize, int maxSize)
(be sure your method is public)

Constraints

-

groups will contain between 1 and 50 elements, inclusive.

-

Each element of groups will be between 1 and 1,000,000, inclusive.

-

maxSize will be between 1 and 1,000,000, inclusive.

-

minSize will be between 1 and maxSize, inclusive.

Examples

0)

{10,20}

Returns: 5

We can move 5 students from the second time schedule to the first. Both schedules will then have a size of 15, which is the maximum allowed size.

1)

{20,8,6}

Returns: 6

We can move 2 students from the first schedule to the second, and another 4 students from the first schedule to the third. The sizes of the resulting schedules will be 14, 10 and 10.

2)

{10,20,30}

Returns: -1

There is no solution possible here. We have 60 students in 3 time schedules, so it is impossible to have at most 18 students per schedule.

3)

{50,10,20,20,5}

Returns: 20

4)

{100,200,301}

Returns: -1

5)

{1,10,10}

Returns: -1

6)

{55,33,45,71,27,89,16,14,61}

Returns: 53

7)

{49,60,36,34,36,52,60,43,52,59}

Returns: 31

8)

{5,5,5,5,5}

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NCool

Geometry, Search, Simple Math

Used in:

SRM 401

Used as:

Division I Level Three

Writer:

griffon

Testers:

PabloGilberto , Olexiy , gawry

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8320

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12173&pm=8320

Problem Statement

You are given a convex polygon and you must count the number of N-cool points. A point is N-cool if it is a lattice point covered by the polygon and also an endpoint of some N-cool segment. A line segment is N-cool if it contains at least N lattice points that are covered by the polygon. A point is considered covered by the polygon if it is inside or on the boundary of the polygon. Endpoints of a segment are considered to be inside of it. A lattice point is a point with integer coordinates.

Consider the example in the picture below. Here N is equal to 6, and there are 21 6-cool points, marked green. Also two 6-cool segments, which are colored red, are shown.

You are given int[]s x and y describing the vertices of the polygon (in no particular order). The coordinates of each vertex are specified by corresponding elements of x and y. Return the number of N-cool points.

Definition

Class:	NCool
Method:	nCoolPoints
Parameters:	int[], int[], int
Returns:	int
Method signature:	int nCoolPoints(int[] x, int[] y, int n)
(be sure your method is public)

Notes

-

A polygon is convex if it contains all the line segments connecting any pair of its points.

Constraints

-

x and y will each contain between 3 and 50 elements, inclusive.

-

x and y will contain the same number of elements.

-

All elements of x and y will be between 0 and 10000, inclusive.

-

The number of lattice points inside or on the boundary of the specified polygon will not be greater than 500000.

-

N will be between 2 and 500000, inclusive.

-

The polygon specified by x and y will be convex and will have nonzero area.

Examples

0)

{0, 1, 2, 7, 7}

{3, 1, 6, 1, 5}

Returns: 21

This is the example from the problem statement.

1)

{0, 1, 0}

{0, 0, 1}

Returns: 3

These three points form a triangle, whose sides are 2-cool segments, so all three vertices are 2-cool.

2)

{0, 0, 1, 2, 2, 1, 0, 0, 2}

{0, 1, 2, 2, 1, 0, 0, 0, 2}

Returns: 6

One point can be mentioned in the input two or more times.

3)

{0, 1, 1, 2, 2, 3, 3, 4, 4, 5}

{1, 0, 2, 0, 2, 0, 2, 0, 2, 1}

Returns: 4

There can be 3 points of the polygon, lying on the same line.

4)

{0, 1, 1, 2, 2, 3, 3, 4, 4, 5}

{1, 0, 2, 0, 2, 0, 2, 0, 2, 1}

Returns: 10

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DivisibleByDigits

Simple Math, Simple Search, Iteration

Used in:

SRM 375

Used as:

Division I Level One , Division II Level Three

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8318

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10794&pm=8318

Problem Statement

Given an integer n, find the smallest integer that starts with n and is divisible by every non-zero digit of n (all in decimal notation).

Definition

Class:	DivisibleByDigits
Method:	getContinuation
Parameters:	int
Returns:	long
Method signature:	long getContinuation(int n)
(be sure your method is public)

Notes

-

An integer A starts with an integer B if the string representation of B is a prefix of the string representation of A (both in decimal notation with no leading zeroes).

Constraints

-

n will be between 1 and 1000000000, inclusive.

Examples

0)

Returns: 132

We need a number that starts with 13 and is divisible by 1 (always true) and by 3. The smallest one is 132.

1)

Returns: 648

If n is divisible by all its non-zero digits, the answer to the problem is n itself.

2)

Returns: 56610

The resulting number must be divisible by 5, so it should end either with 0 or with 5. But a number ending with 5 is odd and can't be divisible by 6. So the last digit of the answer must be 0. In order to make the number divisible by 6, we need to put something before this 0, and the smallest appropriate digit is 1.

3)

1000000000

Returns: 1000000000

4)

987654321

Returns: 987654321360

5)

Returns: 8304

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CharmingTickets

Dynamic Programming, Math

Used in:

SRM 382

Used as:

Division I Level Three

Writer:

dkorduban

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8316

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10805&pm=8316

Problem Statement

A ticket number that contains exactly 2*K digits is called charming if and only if at least one of the following conditions is satisfied:

The sum of the first K digits is equal to the sum of the last K digits.
The sum of all the digits at positions with odd indices is equal to the sum of all the digits at positions with even indices.

Also, you think that some digits are better than others, so a charming number must contain only digits that you consider to be good. These digits are given in the String good. Determine the number of different charming numbers containing exactly 2*K digits. Return this number modulo 999983. Remember that ticket numbers may contain leading zeroes.

Definition

Class:	CharmingTickets
Method:	count
Parameters:	int, String
Returns:	int
Method signature:	int count(int K, String good)
(be sure your method is public)

Constraints

-

K will be between 1 and 1000, inclusive.

-

good will contain between 1 and 10 characters, inclusive.

-

good will contain only digits ('0' - '9').

-

All characters in good will be distinct.

Examples

0)

"0123456789"

Returns: 10

Only "XX" numbers are charming.

1)

"21"

Returns: 8

Only 1111, 1122, 1212, 1221, 2112, 2121, 2211, 2222 are charming numbers.

2)

"0987654321"

Returns: 1240

3)

"0123456789"

Returns: 630063

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ParticleCollision

Geometry, Math, String Parsing

Used in:

SRM 401

Used as:

Division I Level Two

Writer:

griffon

Testers:

PabloGilberto , Olexiy , gawry

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8315

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12173&pm=8315

Problem Statement

Particles (which can be considered points in 3D-space for the purposes of the problem) can move in an electro-magnetic field. If a particle is charged, its trajectory can be described as spiral, and if it is uncharged, it is just a straight line. Given two particles (one charged and one uncharged) it should be determined whether they can possibly collide or not. Two particles can possibly collide if and only if their trajectories intersect.

Some steps have already been made by the physicist to simplify the problem, so the coordinates of the charged particle are represented as follows:

x1 = cos(PI * t)

y1 = sin(PI * t)

z1 = t

and for the uncharged particle:

x2 = vx * t + x0

y2 = vy * t + y0

z2 = vz * t + z0

Here t is a parameter which can be chosen arbitrarily and independently for both trajectories.

Your method will be given 6 integers - vx, vy, vz, x0, y0 and z0, describing the trajectory of the uncharged particle. It should determine whether the two given trajectories intersect or not. If they do, it should return a double[] containing exactly 3 elements x, y and z - the coordinates of the point where a collision can happen. If there is more than one such point, it should return a double[] containing exactly three zeroes. If collision of the two particles is impossible it should return an empty double[].

Definition

Class:	ParticleCollision
Method:	collision
Parameters:	int, int, int, int, int, int
Returns:	double[]
Method signature:	double[] collision(int vx, int vy, int vz, int x0, int y0, int z0)
(be sure your method is public)

Notes

-

PI can be considered equal to 3.14159265358979323846.

-

All return values with either an absolute or relative error of less than 1.0E-9 are considered correct.

Constraints

-

vx, vy and vz will each be between -10 and 10, inclusive.

-

x0, y0 and z0 will each be between -10 and 10, inclusive.

Examples

0)

Returns: { }

The second trajectory is a single point (0, 0, 0), which doesn't lie on the first trajectory.

1)

-1

-1

Returns: {0.0, 1.0, 0.5 }

There is a single intersection point with coordinates (0, 1, 0.5).

2)

Returns: {0.0, 0.0, 0.0 }

There are two intersection points.

3)

Returns: {0.0, 0.0, 0.0 }

There are infinitely many intersection points.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DreamingAboutCarrots

Geometry, Simple Math

Used in:

SRM 401

Used as:

Division II Level One

Writer:

griffon

Testers:

PabloGilberto , Olexiy , gawry

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8314

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12173&pm=8314

Problem Statement

John works at a company called "FIELD-Tech", and today, he was so tired after work that he fell asleep as soon as he got home. Unfortunately, even in his sleep, he was unable to forget about his work. In one dream, he was asked to help a carrot producing company deal with the following question: how many carrots grow on a line segment connecting two given carrots? The endpoints of the segment (i.e., the two given carrots) should not be included. It's a rather strange question, and to make it even stranger, the company's representatives (guys who have carrots instead of heads) said that all the carrots grow on an infinite plane, and there is exactly one carrot at each point with integer coordinates. You must help tired John deal with this problem.

The coordinates of the two carrots are (x1, y1) and (x2, y2). Return the number of carrots that lie strictly on the line segment connecting these carrots.

Definition

Class:	DreamingAboutCarrots
Method:	carrotsBetweenCarrots
Parameters:	int, int, int, int
Returns:	int
Method signature:	int carrotsBetweenCarrots(int x1, int y1, int x2, int y2)
(be sure your method is public)

Constraints

-

x1, y1, x2, and y2 will each be between 0 and 50, inclusive.

-

(x1, y1) and (x2, y2) will represent different points.

Examples

0)

Returns: 3

There are three points inside of the segment: (2,2), (3,3) and (4,4).

1)

Returns: 0

2)

Returns: 1

3)

Returns: 5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DepositProfit

Math

Used in:

TCHS SRM 49

Used as:

Division I Level One

Writer:

Nickolas

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8313

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10809&pm=8313

Problem Statement

You've deposited amount dollars into a bank account. The interest rate is annualInterest percent per year, and it is compounded monthly. This means that at the end of each month, the total balance increases by annualInterest/12 percent, and after that the balance is rounded down to the integer number of cents. Return the minimum number of months required to obtain at least profit dollars in profit.

Definition

Class:	DepositProfit
Method:	depositTerm
Parameters:	int, int, int
Returns:	int
Method signature:	int depositTerm(int amount, int annualInterest, int profit)
(be sure your method is public)

Notes

-

The monthly interest is calculated as (current deposit amount) * (annual interest rate in percent) / (100*12).

Constraints

-

amount will be between 10 and 10000, inclusive.

-

annualInterest will be between 4 and 24, inclusive.

-

profit will be between 1 and amount, inclusive.

Examples

0)

Returns: 2

The monthly interest rate is 1%. At the end of the first month, the interest added is 1000*0.01 = 10, for a new total balance of 1010. At the end of the second month, the interest added is 1010*0.01 = 10.10, for a total balance of 1020.10. At this point, the profit is 20.10, which is greater than 20.

1)

Returns: 236

2)

Returns: 30

3)

Returns: 1

The monthly interest rate is 0.5%. At the end of the first month, the interest added is equal to the profit wanted.

4)

Returns: 49

5)

Returns: 34

At the end of the first month, the interest added is approximately 3.33 cents. At the end of the 34-th month, the interest added is approximately 3.67 cents. Both these interests are rounded down to 3 cents.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SetOfPatterns

Advanced Math, Dynamic Programming, String Manipulation

Used in:

SRM 390

Used as:

Division II Level Three

Writer:

srbga

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8307

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11124&pm=8307

Problem Statement

You are given a String[] patterns, each element of which is a single pattern. Each pattern contains only lowercase letters and question marks ('?'). A string matches a pattern if it has the same length as the pattern, and at each position, either the corresponding characters are equal or the character in the pattern is a question mark. For example, "abc" matches "a?c", but not "a?b" or "abc?". Return the number of strings consisting of only lowercase letters that match exactly k of the given patterns, modulo 1,000,003.

Definition

Class:	SetOfPatterns
Method:	howMany
Parameters:	String[], int
Returns:	int
Method signature:	int howMany(String[] patterns, int k)
(be sure your method is public)

Constraints

-

patterns will contain between 1 and 15 elements, inclusive.

-

k will be between 1 and the number of elements in patterns, inclusive.

-

Each element of patterns will contain between 1 and 50 characters, inclusive.

-

Each element of patterns will have the same length.

-

Each element of patterns will contain only lowercase letters ('a' - 'z') and question marks ('?').

Examples

0)

{"?"}

Returns: 26

Every lowercase letter matches this pattern.

1)

{"a","b","c"}

Returns: 3

"a" or "b" or "c".

2)

{"a?","?b"}

Returns: 1

The only possible solution is "ab".

3)

{"?????"}

Returns: 881343

26^5 mod 1000003 = 881343.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FingerCounting

Brute Force, Simple Math, Simple Search, Iteration, Simulation

Used in:

SRM 390

Used as:

Division II Level One

Writer:

srbga

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8300

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11124&pm=8300

Problem Statement

Your little son is counting numbers with his left hand. Starting with his thumb and going toward his pinky, he counts each finger in order. After counting his pinky, he reverses direction and goes back toward his thumb. He repeats this process until he reaches his target number. He never skips a finger. For example, to count to ten, he would count: thumb, index, middle, ring, pinky, ring, middle, index, thumb, index. Sadly, one of his fingers hurts and he can only count on it a limited number of times. His fingers are numbered 1 through 5 from thumb to pinky. You are given an int weakFinger, the finger that hurts, and an int maxCount, the maximum number of times he can use that finger. Return the largest number he can count to. If he cannot even begin counting, return 0.

Definition

Class:	FingerCounting
Method:	maxNumber
Parameters:	int, int
Returns:	int
Method signature:	int maxNumber(int weakFinger, int maxCount)
(be sure your method is public)

Constraints

-

weakFinger will be between 1 and 5, inclusive.

-

maxCount will be between 0 and 100000, inclusive.

Examples

0)

Returns: 15

The first 15 numbers are counted with fingers 1,2,3,4,5,4,3,2,1,2,3,4,5,4,3. He would then have to use finger 2 for the next number, but since he has already used it 3 times, he has to stop.

1)

Returns: 0

He needs to use his thumb when counting the first number, 1, but it's too weak to be used even once.

2)

Returns: 4

Even though his pinky cannot be used at all, he can count 1,2,3,4 with the other fingers.

3)

Returns: 193

4)

Returns: 7788

5)

Returns: 399998

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CardsShuffle

Simple Math

Used in:

TCHS SRM 47

Used as:

Division I Level One

Writer:

stone

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8295

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10803&pm=8295

Problem Statement

You are given a String cards, which represents a sequence of cards. Shuffle the cards by repeatedly performing the specified exchange operation. The exchange operation is specified by the ints first and last, which are both 1-based indices in the sequence. Take all the cards between the first-th card and the last-th card, inclusive, and move them to the beginning of the sequence. Do not change the relative order of the moved cards. For example, if first = 2 and last = 4, an exchange operation on "ABCDEFG" would produce "BCDAEFG".

Perform the specified exchange operation times times on the given sequence and return a String containing the resulting sequence.

Definition

Class:	CardsShuffle
Method:	shuffle
Parameters:	String, int, int, int
Returns:	String
Method signature:	String shuffle(String cards, int first, int last, int times)
(be sure your method is public)

Constraints

-

cards will contain between 1 and 50 characters, inclusive.

-

cards will contain only uppercase letters ('A'-'Z').

-

first will be between 1 and n, inclusive, where n is the number of characters in cards.

-

last will be between first and n, inclusive, where n is the number of characters in cards.

-

times will be between 1 and 100, inclusive.

Examples

0)

"NW"

Returns: "WN"

It always moves the second card to the front.

1)

"BMQ"

Returns: "BMQ"

This operation does not change anything.

2)

"KYHID"

Returns: "YHIDK"

3)

"YGGXXPKLO"

Returns: "YGGXXPKLO"

cards may contain duplicate characters.

4)

"KMCOQHNWNKU"

Returns: "COQHNWNKKMU"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Transformation

Math

Used in:

SRM 391

Used as:

Division I Level Three

Writer:

stone

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8291

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11125&pm=8291

Problem Statement

You are to transform a positive integer vector (A₁,A₂,...,A_n) into another positive integer vector (B₁,B₂,...,B_n) of the same length. The transformation must satisfy the conditions below:

1) For 1 < = i < =n., B_i must evenly divide into A_i.

2) The least common multiple of all A_i should be equal to that of all B_i.

You are given the original integer vector as a String[] A, where the i-th (1-based) element is a positive integer representing A_i. Return a String[] containing the transformed integer vector in the same format. Each element of the return String[] must be a positive integer with no leading zeroes. If there are multiple solutions, return the one where the first number is the smallest. If there are still multiple solutions, return the one with the smallest second number etc.

Definition

Class:	Transformation
Method:	transform
Parameters:	String[]
Returns:	String[]
Method signature:	String[] transform(String[] A)
(be sure your method is public)

Notes

-

The least common multiple of a group of positive integers is the least positive integer which is a multiple of every integer in the group.

Constraints

-

A will contain between 1 and 50 elements, inclusive.

-

Each element of A will contain digits ('0' - '9') only.

-

Each element of A will represent a positive integer without leading zeros.

-

Each element of A will contain between 1 and 18 characters, inclusive.

Examples

0)

{"1","2"}

Returns: {"1", "2" }

1)

{"2","3","6"}

Returns: {"1", "1", "6" }

{1,1,6},{1,3,2},{1,3,6},{2,1,3},{2,1,6},{2,3,1},{2,3,2},{2,3,3},{2,3,6} are all transformation results.

2)

{"210","2","3","5","7"}

Returns: {"1", "2", "3", "5", "7" }

3)

{"6","2","3","4","9"}

Returns: {"1", "1", "1", "4", "9" }

4)

{"6","2","3","4","9","8"}

Returns: {"1", "1", "1", "1", "9", "8" }

5)

{"3637","260","26122993443584","47715564111559878","2","871126696052836","3492829317","83024857214176826"}

Returns: 
{"3637",
"5",
"26122993443584",
"7952594018593313",
"1",
"217781674013209",
"3492829317",
"41512428607088413" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TransformingArray

Simple Math, Simple Search, Iteration

Used in:

TCHS SRM 49

Used as:

Division I Level Two

Writer:

Nickolas

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8279

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10809&pm=8279

Problem Statement

You are given a int[] a. Perform the following transformation operation N times: replace each element a[i] with the product of all the elements of a except a[i]. All products are calculated using the values of a at the beginning of the operation. For example, if a = {1, 2, 3}, a single transformation would result in a = {2*3, 1*3, 1*2}. Return the 0-based index of the smallest element in a after all the transformations.

Definition

Class:	TransformingArray
Method:	minimalElement
Parameters:	int[], int
Returns:	int
Method signature:	int minimalElement(int[] a, int N)
(be sure your method is public)

Constraints

-

N will be between 0 and 100000, inclusive.

-

a will contain between 1 and 50 elements, inclusive.

-

Each element of a will be between 1 and 10000, inclusive.

-

All elements of a will be distinct.

Examples

0)

{1,2,3,4}

Returns: 3

The transformation will result in a = {2*3*4, 1*3*4, 1*2*4, 1*2*3} = {24, 12, 8, 6}. The last element is the smallest.

1)

{3,17,1,10}

Returns: 2

2)

{650,9511,4746,3187}

Returns: 0

3)

{8684,3214}

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SolvePolynomial

Advanced Math

Used in:

SRM 378

Used as:

Division I Level Two

Writer:

bmerry

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8273

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10798&pm=8273

Problem Statement

An integer polynomial of degree n is a function of the form a₀ + a₁x¹ + a₂x² + ... + a_nxⁿ, where each a_i is a constant integer and x is a variable. An integer root of an integer polynomial is an integer value of x for which the expression equals zero.

You will be given the coefficients of an integer polynomial, and must return all the integer roots in increasing order. Roots must appear only once in the output (see example 1 for clarification).

Since the degree may be quite large, the coefficients are presented indirectly. Use the following pseudo-code to generate the coefficients a[0] to a[n]:

lX = length(X)
lY = length(Y)
for i = 0, 1, ..., n:
  p = i mod lX
  q = (i + Y[i mod lY]) mod lX
  a[i] = X[p]
  X[p] = X[q]
  X[q] = a[i]

The array indices are all 0-based and a mod b is the remainder when a is divided by b.

Definition

Class:	SolvePolynomial
Method:	integerRoots
Parameters:	int[], int[], int
Returns:	int[]
Method signature:	int[] integerRoots(int[] X, int[] Y, int n)
(be sure your method is public)

Notes

- The intended solution is independent of the method of generation, and will work for any integer polynomial.

Constraints

- n will be between 0 and 10,000, inclusive.

- X will contain between 1 and 50 elements, inclusive.

- Y will contain between 1 and 50 elements, inclusive.

- Each element of X will be between -10⁹ and 10⁹, inclusive.

- Each element of Y will be between 0 and 50, inclusive.

- At least one element of a will be non-zero.

Examples

0)

{-4, 2, 2}

{0}

Returns: {-2, 1 }

-4 + 2x + 2x² = 2(x - 1)(x + 2).

1)

{1, 2, 0}

{2, 0, 0, 0}

Returns: {-1 }

1 + 2x + x^2 + 0x^3 = (x + 1)(x + 1). Note that a_n may be zero and that roots must appear only once in the output.

2)

{1, 4, 4}

{0}

Returns: { }

3)

{-15, -10, 2, 1}

{0}

Returns: {3 }

4)

{735134400, 1383, 4121, 18875, 10463, 
 13512, 19603, 28679, 13483, 9509, 1701,
 13383, 24425, 7923, 7978, 21702, 30989,
 20676, 18547, 28130, 10944}

{34,23,6,5,3,5,4,34,37,5,6,21,17,9}

Returns: { }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MixtureDensity

Simple Math, String Manipulation

Used in:

SRM 375

Used as:

Division II Level One

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8269

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10794&pm=8269

Problem Statement

A pharmacist is making a mixture of several ingredients. She needs to know the density of the resulting mixture. Density is defined as the mass of the mixture divided by its volume.

You're given a String[] ingredients, each element of which describes a single ingredient and is formatted "<Volume> ml of <Name>, weighing <Mass> g" (quotes for clarity). <Volume> and <Mass> are integers representing the volume in milliliters and mass in grams, respectively. <Name> is the name of the ingredient.

Return the density of the resulting mixture in grams per milliliters.

Definition

Class:	MixtureDensity
Method:	getDensity
Parameters:	String[]
Returns:	double
Method signature:	double getDensity(String[] ingredients)
(be sure your method is public)

Notes

- The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

- ingredients will contain between 1 and 50 elements, inclusive.

- Each element of ingredients will contain between 23 and 50 characters, inclusive.

- Each element of ingredients will be formatted as described in the statement.

- Each <Volume> in ingredients will be an integer between 1 and 1000, inclusive, with no leading zeroes.

- Each <Mass> in ingredients will be an integer between 1 and 1000, inclusive, with no leading zeroes.

- Each <Name> in ingredients will contain only lowercase letters ('a'-'z') and spaces (' ').

- Each <Name> in ingredients will begin and end with a lowercase letter.

Examples

0)

{"200 ml of oil, weighing 180 g"}

Returns: 0.9

The density is mass/volume = 180g/200ml = 0.9g/ml, the answer is 0.9.

1)

{"100 ml of dichloromethane, weighing 130 g", "100 ml of sea water, weighing 103 g"}

Returns: 1.165

The volume of the resulting mixture is 200 ml and the mass is 233 g. Therefore, the density is 233g/200ml = 1.165g/ml.

2)

{"1000 ml of water, weighing 1000 g", "500 ml of orange juice concentrate, weighing 566 g"}

Returns: 1.044

3)

{"1000 ml of something   l i g h t, weighing 1 g"}

Returns: 0.0010

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OddGraph

Advanced Math, Graph Theory

Used in:

TCCC07 Semi 3

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8266

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10958&pm=8266

Problem Statement

We want to design a network consisting of n identical Worker nodes and one Server node. The network must be connected and must not contain any cycles. We also require that each Worker node must be connected to an odd number of other nodes. How many distinct networks are there?

Here is a listing of all the distinct networks containing exactly 5 worker nodes:

                                                       
       W               W     W              W          W  W 
       |                \    |              |          | /   
   W---S----W            S---W          S---W      S---W    
       | \              /    |              |          | \  
       W  W            W     W          W---W---W      W  W

Two configurations G and G' are not distinct if there is a 1-1 mapping between their nodes such that the server in G maps to the server in G', and such that for every pair of nodes in G the pair that they are mapped to in G' is connected if and only if the pair in G is connected. Note that two configurations are not distinct if they have the same connection pattern, even if they are different geometrically as displayed in the plane. For example, these two configurations with 8 worker nodes are not distinct:


   W   W   W          W       W                                      
   |   |   |          |       |  
   W---S---W      W---S-------W                                                 
   |   |   |          |       | 
   W   W   W      W---W---W   W

Given n, return the number of distinct networks that can be constructed with exactly n worker nodes.

Definition

Class:	OddGraph
Method:	count
Parameters:	int
Returns:	int
Method signature:	int count(int n)
(be sure your method is public)

Notes

-

The answer will fit in an int.

Constraints

-

n will be between 1 and 40, inclusive.

Examples

0)

Returns: 4

The 4 networks are listed above.

1)

Returns: 1

S---W is the only network with 1 worker node.

2)

Returns: 929556155

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SpiralRoute

Simple Math

Used in:

SRM 371

Used as:

Division I Level One , Division II Level Two

Writer:

bmerry

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8262

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10787&pm=8262

Problem Statement

The King of Elbonia lives in a palace that is width meters by length meters. Since he makes his subjects live in mud, he is not very popular. He wants the palace partitioned so that visitors have to walk a long way to reach him. His security advisors have settled on a spiral. A visitor enters the palace at the South-West corner and starts walking East. Every time the visitor reaches an outer wall or his own path, he turns left. The corridors in the spiral are 1 meter wide. The diagram below shows an example of a spiral path: the visitor moves from a (the South-West corner) through the alphabet to x, the throne.

nmlkji
oxwvuh
pqrstg
abcdef

The King wants to have his throne correctly placed before all the partitioning is done, so he needs to know where the spiral will end. Write a class SpiralRoute with a method thronePosition that returns two integers, indicating the coordinates of the throne. The South-West corner is (0, 0), the South-East corner is (width - 1, 0) and the North-East corner is (width - 1, length - 1).

Definition

Class:	SpiralRoute
Method:	thronePosition
Parameters:	int, int
Returns:	int[]
Method signature:	int[] thronePosition(int width, int length)
(be sure your method is public)

Constraints

- width and length will both be between 1 and 5000, inclusive.

Examples

0)

Returns: {1, 2 }

This is the example above.

1)

Returns: {3, 2 }

2)

Returns: {0, 10 }

3)

Returns: {5, 6 }

4)

Returns: {2499, 2500 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

JollyJumpers

Math, Simulation

Used in:

SRM 376

Used as:

Division II Level Three

Writer:

jmzero

Testers:

PabloGilberto , Olexiy , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8261

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10796&pm=8261

Problem Statement

You are playing a board game called Jolly Jumpers. The game begins with some number of pawns on a 4x4 board. On each turn, you must either:

Have one pawn jump over another pawn vertically. To do this, the jumping pawn must be vertically adjacent to the pawn it is to jump, with an empty space on the far side. The jumping pawn moves to the empty space, while the jumped pawn is removed from the game. Jumping a pawn scores two points.
Move a pawn one space horizontally. The space it moves to must be empty. Moving a pawn means you lose one point.

You start the game with a score of zero points, and the goal of the game is to score as high as possible. You may stop moving at any time, including before your first move. The layout of the board will be given to you in the String[] layout, the first element of which represents the topmost row of the board. Empty squares will be denoted with the '.' character and pawns will be denoted with '#'.

For the layout given, return the maximum score you can achieve using any number of moves.

Definition

Class:	JollyJumpers
Method:	maxScore
Parameters:	String[]
Returns:	int
Method signature:	int maxScore(String[] layout)
(be sure your method is public)

Constraints

-

layout will contain 4 elements.

-

Each element of layout will contain exactly 4 characters.

-

Elements of layout will contain only '.' and '#' characters.

Examples

0)

{
"....",
".#..",
"..#.",
"...."}

Returns: 1

Move either piece horizontally (-1 point), then jump vertically (+2 points).

1)

{
"....",
"....",
"....",
"...."}

Returns: 0

Not the most exciting layout...

2)

{
".#..",
".#..",
"..#.",
"...#"}

Returns: 4

3)

{
"####",
"####",
"####",
"####"}

Returns: 0

You can't move outside the board, so there's no moves available.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FoodCollecting

Simple Math, Simple Search, Iteration

Used in:

TCHS SRM 46

Used as:

Division I Level Two

Writer:

Rydberg

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8239

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10801&pm=8239

Problem Statement

As a serious strategy-games player, you know how important it is to gather enough food for your army before any invasion. Because of this, you decided to collect at least neededFood units of food for your soldiers.

At the beginning, you have n workers to help you. In a single round, each of your workers gathers one unit of food. At the end of each round, you can trade some of your food for new workers. Hiring a single new worker costs price units of food. You can purchase any amount of new workers as long as you have the food to pay for it.

Return the minimum number of rounds you need to gather at least neededFood units of food.

Definition

Class:	FoodCollecting
Method:	gather
Parameters:	int, int, int
Returns:	int
Method signature:	int gather(int neededFood, int n, int price)
(be sure your method is public)

Constraints

-

neededFood, n and price will each be between 1 and 1000, inclusive.

Examples

0)

Returns: 4

Round 1: Gather 2 units of food. Hire a new worker.

Round 2: Gather 3 units of food. Now you have 4 units.

Round 3: Gather 3 units of food. Now you have 7 units.

Round 4: Gather 3 units of food. Now you have 10 units - enough for your army.

1)

Returns: 4

Round 1: Gather 4 units of food. Hire 4 new workers.

Round 2: Gather 8 units of food. Hire 7 new workers.

Round 3: Gather 15 units of food. Now you have 16 units.

Round 4: Gather 15 units of food. Now you have 31 units - enough for your army.

2)

Returns: 11

3)

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ArithmeticalMean

Brute Force, Search, Simple Math

Used in:

TCHS SRM 43

Used as:

Division I Level Three

Writer:

it4.kp

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8221

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10792&pm=8221

Problem Statement

You are given a int[] elements. If the arithmetic mean of a non-empty subset of elements is between L and H, inclusive, the subset is considered "good". A subset of a int[] is obtained by removing 0 or more elements from the int[]. Return the number of "good" subsets.

Definition

Class:	ArithmeticalMean
Method:	howMany
Parameters:	int[], int, int
Returns:	long
Method signature:	long howMany(int[] elements, int L, int H)
(be sure your method is public)

Constraints

-

elements will contain between 1 and 36 elements, inclusive.

-

Each element of elements will be between -25000000 and 25000000, inclusive.

-

Each element of elements will be distinct.

-

L and H will each be between -25000000 and 25000000, inclusive.

-

L will not be greater than H.

Examples

0)

{10,1,3}

Returns: 4

All possible arithmetic means are: 1, 2, 3, 14/3, 11/2, 13/2, 10.

Four of them (2, 3, 14/2, 11/2) make "good" subsets.

1)

{0}

-1

Returns: 1

There is just one subset and it's "good".

2)

{0}

Returns: 0

Same one subset but it's not "good".

3)

{1,2,3,4,5,6,7,8,9,10}

Returns: 949

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RevealTriangle

Simple Math

Used in:

SRM 404

Used as:

Division I Level One , Division II Level Two

Writer:

boba5551

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8215

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12176&pm=8215

Problem Statement

Suppose there is a triangle of digits like the following:

Each digit, with the exception of those in the top row, is equal to the last digit of the sum of its upper and upper-right neighboring digits.

You will be given a String[] questionMarkTriangle containing a triangle where only one digit in each row is known and all others are represented by '?'s (see example 0 for clarification). Each element of questionMarkTriangle represents a row of the triangle, and the rows are given from top to bottom. Each element contains exactly one digit ('0'-'9') and the remaining characters are all '?'s. Restore the triangle and return it as a String[] without '?'s.

Definition

Class:	RevealTriangle
Method:	calcTriangle
Parameters:	String[]
Returns:	String[]
Method signature:	String[] calcTriangle(String[] questionMarkTriangle)
(be sure your method is public)

Constraints

-

questionMarkTriangle will contain between 1 and 50 elements, inclusive.

-

Element i (0 indexed) of questionMarkTriangle will contain exactly n-i characters, where n is the number of elements in questionMarkTriangle.

-

Each element of questionMarkTriangle will contain exactly one digit ('0'-'9') and all others characters will be '?'s.

Examples

0)

{"4??", 
 "?2", 
 "1"}

Returns: {"457", "92", "1" }

Let's substitute '?'s with unknown variables:

4ab 
c2 
1

Having done that, we start solving for the variables from the bottom to the top. First, we know that the last digit of (c + 2) is 1. Therefore, c must be 9:

4ab 
92 
1

Now we know that the last digit of (4 + a) is 9, which means a is 5:

45b 
92 
1

And, finally, the last digit of (5 + b) is 2, so b is 7.

1)

{"1"}

Returns: {"1" }

2)

{"???2", "??2", "?2", "2"}

Returns: {"0002", "002", "02", "2" }

3)

{"??5?", "??9", "?4", "6"}

Returns: {"7054", "759", "24", "6" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Barracks

Math, Simple Search, Iteration, Simulation

Used in:

SRM 418

Used as:

Division I Level Three

Writer:

Rydberg

Testers:

PabloGilberto , Olexiy , Mike Mirzayanov , ivan_metelsky , darnley

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8211

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13509&pm=8211

Problem Statement

As a serious strategy-games player, you decided to solve one of the most common problems - attacking your opponent's building (barracks), which constantly produces new soldiers.

Before the attack, you've got myUnits soldiers. In a single round, each soldier can either kill one of your opponent's soldiers or inflict 1 hit point of damage to the barracks.

Your opponent doesn't have any soldiers initially. However, his barracks has barHp hit points and produces unitsPerRound soldiers per round.

The course of one round:

1. Each solider from your army either kills one of your opponent's soldiers or inflicts 1 hit point of damage to the barracks. Each soldier can choose to do something different. When the barracks loses all of its hit points, it is destroyed.

2. Your opponent attacks. He will kill k of your soldiers, where k is the number of remaining soldiers he has.

3. If the barracks are not yet destroyed, your opponent will produce unitsPerRound new soldiers.

Your task is to destroy the barracks and kill all your opponent's soldiers. If it is possible, return the minimum number of rounds you need to do this. Otherwise return -1.

Definition

Class:	Barracks
Method:	attack
Parameters:	int, int, int
Returns:	int
Method signature:	int attack(int myUnits, int barHp, int unitsPerRound)
(be sure your method is public)

Constraints

-

myUnits, barHp, unitsPerRound will each be between 1 and 5000, inclusive.

Examples

0)

Returns: 4

Round 1:

- All your soldiers attack the barracks, leaving it with 1 hit point.

- Your opponent has no soldiers, so he cannot kill any of your soldiers.

- Your opponent's army increases from 0 soldiers to 15 soldiers.

Round 2:

- One of your soldiers destroys the barracks. The other nine kill 9 of your opponent's soldiers.

- Your opponent has 6 soldiers, so he kills 6 of your soldiers.

- The barracks have been destroyed, so no new soldiers are produced.

Round 3:

- You have got 4 soldiers, so you decrease your opponent's army to 2 soldiers.

- Your opponent kills 2 of your soldiers.

- The barracks have been destroyed, so no new soldiers are produced.

Round 4:

- You kill 2 remaining soldiers.

1)

Returns: -1

2)

Returns: 1

3)

Returns: 13

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KeysInBoxes

Simple Math

Used in:

SRM 391

Used as:

Division I Level Two

Writer:

stone

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8202

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11125&pm=8202

Problem Statement

There are N boxes numbered from 1 to N and N keys numbered from 1 to N. The i-th key can only be used to open the i-th box. Now, we randomly put exactly one key into each of the boxes. We assume that all configurations of keys in boxes occur with the same probability. Then we lock all the boxes. You have M bombs, each of which can be used to open one locked box. Once you open a locked box, you can get the key in it and perhaps open another locked box with that key. Your strategy is to select a box, open it with a bomb, take the key and open all the boxes you can and then repeat with another bomb.

Return the probability that you can get all the keys. The return value must be a string formatted as "A/B" (quotes for clarity), representing the probability as a fraction. A and B must both be positive integers with no leading zeroes, and the greatest common divisor of A and B must be 1.

Definition

Class:	KeysInBoxes
Method:	getAllKeys
Parameters:	int, int
Returns:	String
Method signature:	String getAllKeys(int N, int M)
(be sure your method is public)

Constraints

-

N will be between 1 and 20, inclusive.

-

M will be between 1 and N, inclusive.

Examples

0)

Returns: "1/2"

When box 1 contains key 2, you can get all the keys.

1)

Returns: "1/1"

When N=M, you can always get all the keys.

2)

Returns: "1/3"

There are 6 possible configurations of keys in boxes. Using 1 bomb, you can open all the boxes in 2 of them:

box 1 - key 2, box 2 - key 3, box 3 - key 1;
box 1 - key 3, box 2 - key 1, box 3 - key 2.

3)

Returns: "5/6"

Now, when you have 2 bombs, you are only unable to get all the keys in the following configuration: box 1 - key 1, box 2 - key 2, box 3 - key 3.

4)

Returns: "17/24"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Prank

Simple Math

Used in:

SRM 384

Used as:

Division II Level One

Writer:

lovro

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8199

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10808&pm=8199

Problem Statement

Jane tries her best to stay fit. Knowing this, her sister decided to play a prank on Jane: after Jane's old scale broke down, her sister got her a new scale that shows the square of a person's weight, instead of the real weight.

Not noticing the change, Jane has been using the scale for a while. One morning she screamed "Oh no! I gained apparentGain pounds!". Given an int apparentGain (the difference between the square of Jane's current weight and the square of her previous weight), return a int[] containing Jane's possible real weights after the latest measurement, sorted in ascending order.

All weights (displayed and real, previous and current) are positive integers.

Definition

Class:	Prank
Method:	realWeight
Parameters:	int
Returns:	int[]
Method signature:	int[] realWeight(int apparentGain)
(be sure your method is public)

Constraints

-

apparentGain will be between 1 and 100000, inclusive.

Examples

0)

Returns: {117 }

If Jane had previously weighed 116 pounds, the scale would have shown 116^2 = 13456. If she gained 1 pound, the scale would show 117^2 = 13689, for an apparent gain of 13689 - 13456 = 233.

1)

Returns: {4, 8 }

Assuming in this example Jane is actually a small animal, she could have gone from 1 to 4 or from 7 to 8.

2)

Returns: {38, 39, 42, 46, 49, 53, 66, 77, 94, 123, 182, 361 }

3)

Returns: {325, 350, 550, 665, 1025, 1270, 2510, 3133, 5005, 6254, 12502, 25001 }

This is the largest input.

4)

Returns: {3595, 46651 }

Watch out for overflow!

5)

Returns: {5 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StudentEnrollment

Brute Force, String Manipulation

Used in:

TCHS08 Round 1

Used as:

Division I Level One

Writer:

vlad_D

Testers:

PabloGilberto , Olexiy , ivan_metelsky , andrewzta

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8195

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11153&pm=8195

Problem Statement

You are working as an intern at Talilulu University. Your task is to make a program that will help people to enroll in classes at the university. You are given a String[] names containing the names of the classes and a int[] spaces containing the number of spaces currently available in each class. The i-th element of names corresponds to the i-th element of spaces. You are also given a String[] queries containing the sequence of enrollment requests. Each element of queries is the name of the class in which a student wants to enroll.

Go through the elements of queries in order, and for each one, enroll the student in the class if there's room, or reject the request if the class does not exist or does not have any space available. Return a String[] containing the responses for each request. The i-th element of the String[] is the response to the i-th query. It should be "GOOD" if the enrollment is accepted, "NOT GOOD" if there is no available space in the requested class, or "DOES NOT EXIST" if the class does not exist (all quotes for clarity).

Definition

Class:	StudentEnrollment
Method:	checkClasses
Parameters:	String[], int[], String[]
Returns:	String[]
Method signature:	String[] checkClasses(String[] names, int[] spaces, String[] queries)
(be sure your method is public)

Constraints

-

names will contain between 0 and 50 elements, inclusive.

-

names and spaces will contain the same number of elements.

-

Each element of names will contain between 1 and 50 characters, inclusive.

-

Each element of names will contain only uppercase letters ('A'-'Z').

-

Each element of spaces will be between 0 and 100, inclusive.

-

queries will contain between 0 and 50 elements, inclusive.

-

Each element of queries will contain only uppercase letters ('A'-'Z').

-

Each element of queries will contain between 1 and 50 characters, inclusive.

-

All elements of names will be distinct.

Examples

0)

{"MATH", "ENGLISH"}

{1, 2}

{"ENGLISH", "MATH", "MATH"}

Returns: {"GOOD", "GOOD", "NOT GOOD" }

There is only one space available in MATH.

1)

{"MATH", "ENGLISH"}

{2, 0}

{"ENGLISH", "MATH", "MATH"}

Returns: {"NOT GOOD", "GOOD", "GOOD" }

2)

{"MATH", "ENGLISH"}

{2, 0}

{"ENGLISH", "FRENCH"}

Returns: {"NOT GOOD", "DOES NOT EXIST" }

3)

{"QCDTBCZICBJGQCCKIWXN",
 "LFAYDMBGLNXWNNDLHARQLYLWYJWMWOZ",
 "KPYATSAMTTKX",
 "HCNJGXTYCLPRENVMJPFEPVOYMTHXACMKTLGPQSEUJONXNZAVMR",
 "QADJYGPJ",
 "WVAGAZUCBG",
 "NHCKOMRNBSYRCKLNLCEOM",
 "SXXHKMNERPHPEQE",
 "JJUOCTOLFRJLJERFIXTCE",
 "SHQHEJGLUEWJIWPTSKTOPZTBVFFL"}

{2, 1, 41, 5, 1, 0, 1, 13, 11, 9}

{"NHCKOMRNBSYRCKLNLCEOM",
 "MTLRHPNKFNEXQQOWYERECRZXT",
 "QADJYGPJ",
 "WVAGAZUCBG",
 "EWWVWQZQNXEJGZJGZEVHKE",
 "QADJYGPJ",
 "IBQEMIBIGLVZLAOAYVPOMWZI",
 "JTFOEIPGOAHSGLYMQSCTVVMDINGURUWEZTHJFWUYAWBLAD",
 "ZRVMTHVAXCXJQPN",
 "QCDTBCZICBJGQCCKIWXN",
 "BVYUCAHSOBCBEFDEXWXFTKURXTIFDXXIDNBUPOPAWCBZHQY",
 "WVAGAZUCBG",
 "RVEJYNRBCOWRJBZHRTNQXROHWQOODMVDMVJDRNKWRGLXWWGPPW",
 "QADJYGPJ",
 "TYOMTKEVXMAVJBFBFDFOWARMZXSBUEMMQUWUNPSW",
 "SXXHKMNERPHPEQE",
 "JJUOCTOLFRJLJERFIXTCE",
 "SXXHKMNERPHPEQE",
 "SHQHEJGLUEWJIWPTSKTOPZTBVFFL",
 "JJUOCTOLFRJLJERFIXTCE",
 "QCDTBCZICBJGQCCKIWXN",
 "SXXHKMNERPHPEQE",
 "JJUOCTOLFRJLJERFIXTCE",
 "NJQBVNXCZZNLWM",
 "JJUOCTOLFRJLJERFIXTCE",
 "QADJYGPJ",
 "LFAYDMBGLNXWNNDLHARQLYLWYJWMWOZ"}

Returns: 
{"GOOD",
"DOES NOT EXIST",
"GOOD",
"NOT GOOD",
"DOES NOT EXIST",
"NOT GOOD",
"DOES NOT EXIST",
"DOES NOT EXIST",
"DOES NOT EXIST",
"GOOD",
"DOES NOT EXIST",
"NOT GOOD",
"DOES NOT EXIST",
"NOT GOOD",
"DOES NOT EXIST",
"GOOD",
"GOOD",
"GOOD",
"GOOD",
"GOOD",
"GOOD",
"GOOD",
"GOOD",
"DOES NOT EXIST",
"GOOD",
"NOT GOOD",
"GOOD" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BeautifulString

Simple Math, Simple Search, Iteration

Used in:

SRM 369

Used as:

Division I Level One , Division II Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8193

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10785&pm=8193

Problem Statement

A string composed of the letters 'A' and 'B' is called beautiful if it satisfies all of the following criteria:

it contains no more than countA occurences of 'A';
it contains no more than countB occurences of 'B';
each substring that contains only 'A's consists of no more than maxA characters;
each substring that contains only 'B's consists of no more than maxB characters.

Given countA, countB, maxA and maxB, return the maximum possible length of a beautiful string.

Definition

Class:	BeautifulString
Method:	maximumLength
Parameters:	int, int, int, int
Returns:	int
Method signature:	int maximumLength(int countA, int countB, int maxA, int maxB)
(be sure your method is public)

Constraints

-

countA will be between 0 and 1000000, inclusive.

-

countB will be between 0 and 1000000, inclusive.

-

maxA will be between 0 and 1000000, inclusive.

-

maxB will be between 0 and 1000000, inclusive.

Examples

0)

Returns: 0

We don't have any available letters as countA=0 and countB=0, so the only beautiful string is the empty one.

1)

Returns: 0

Now we have available letters, but can't include them into the beautiful string as maxA=0 and maxB=0.

2)

Returns: 7

In this case we can't have two consecutive 'A's or 'B's, so letters in the beautiful string should alternate. If we start the string from 'A', the longest one we'll be able to get is "ABABAB". But if we start the string from 'B', we'll be able to get the longer one - "BABABAB".

3)

Returns: 1180102

Here maxA >= countA and maxB >= countB, so we can easily construct a beautiful string using all available countA+countB letters.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ChainOfRectangles

Simple Math

Used in:

SRM 369

Used as:

Division II Level One

Writer:

ivan_metelsky

Testers:

PabloGilberto , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8192

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10785&pm=8192

Problem Statement

A sequence of rectangles is drawn on a plane that is initially completely white. Each rectangle lies strictly inside the previous one. Each rectangle is completely colored in one of three colors - red, green or blue. The colors do not mix, so when a rectangle is drawn inside another rectangle, the new color replaces any existing color in that same area.

The rectangles are described by the int[]s width and height, and the String color. The width and height of the i-th drawn rectangle are width[i] and height[i], respectively, and its color is the i-th character of color. The characters 'R', 'G' and 'B' represent red, green and blue, respectively.

After all the rectangles are drawn, calculate the total area occupied by red, the total area occupied by green, and the total area occupied by blue. Return the maximum of these three areas.

Definition

Class:	ChainOfRectangles
Method:	getMaximalArea
Parameters:	int[], int[], String
Returns:	int
Method signature:	int getMaximalArea(int[] width, int[] height, String color)
(be sure your method is public)

Notes

-

You won't be given the information about the exact location of each rectangle, since it's not needed to solve the problem.

Constraints

-

width will contain between 1 and 50 elements, inclusive.

-

height will contain the same number of elements as width.

-

color will contain the same number of characters as the number of elements in width.

-

Each element of width and height will be between 1 and 10000, inclusive.

-

Elements of width and height will be in strictly descending order.

-

Each character of color will be 'R', 'G' or 'B'.

Examples

0)

{10000}

{10000}

"R"

Returns: 100000000

There is only one 10,000x10,000 rectangle. It's colored red, so the area covered by red is 10,000 * 10,000 = 100,000,000. The areas covered by the other two colors are 0.

1)

{10, 5}

{10, 5}

"GB"

Returns: 75

Here, the area covered by blue is 5 * 5 = 25 and the area, covered by green is 10 * 10 - 5 * 5 = 75. We return max{75, 25} = 75.

2)

{10, 9}

{8, 7}

"GB"

Returns: 63

Now, the area covered by green is 17, and the area covered by blue is 63.

3)

{10, 8, 6, 4, 2}

{9, 7, 5, 3, 1}

"GBRRG"

Returns: 36

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CoolFunction

Simple Math

Used in:

TCO08 Championship

Used as:

Division I Level One

Writer:

ivan_metelsky

Testers:

PabloGilberto , SnapDragon , Olexiy , Mike Mirzayanov

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8180

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12019&pm=8180

Problem Statement

The function f: R -> R is called cool if there are integer numbers a₀ <= a₁ <= ... <= a_k-1 (k >= 1) such that f(x) = |x - a₀| + |x - a₁| + ... + |x - a_k-1| for every real value of x.

You will be given a int[] values, containing n elements. You should find a cool function f such that f(i) = values[i] for every i, where 0 <= i < n. Return a int[], containing the values a₀, a₁, ..., a_k-1 for this function. If there are many possible answers, choose the one with the smallest number of elements. If tie still exists, return the lexicographically smallest int[]. Constraints will guarantee that values corresponds to at least one cool function.

Definition

Class:	CoolFunction
Method:	restore
Parameters:	int[]
Returns:	int[]
Method signature:	int[] restore(int[] values)
(be sure your method is public)

Constraints

-

values will contain between 1 and 50 elements, inclusive.

-

Each element of values will be between 0 and 50, inclusive.

-

values will correspond to at least one cool function.

Examples

0)

{0}

Returns: {0 }

|x| is acceptable here.

1)

{50}

Returns: {-50 }

Here there are two variants with k=1: |x-50| and |x+50|. The second one is lexicographically smaller.

2)

{2, 4}

Returns: {-2, 0 }

3)

{3, 3}

Returns: {-2, 1 }

4)

{5, 1}

Returns: {1, 1, 1, 2 }

The return is not necessarily strictly increasing.

5)

{10, 4, 6}

Returns: {1, 1, 1, 1, 2, 4 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AbsSequence

Math, Simple Search, Iteration

Used in:

SRM 369

Used as:

Division I Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8178

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10785&pm=8178

Problem Statement

Let's consider an infinite sequence S of non-negative integers defined as follows:

S₀ = first;

S₁ = second;

S_i = |S_i-2 - S_i-1| for all i >= 2.

You will be given Strings first and second, representing the 0-th and the 1-st elements of the sequence S, and a String[] indices, each element of which represents a non-negative integer without extra leading zeros. Return a String[] containing as many elements as indices, where the i-th element is equal to the indices[i]-th element of the sequence S (index is 0-based). No element of the return should contain extra leading zeros.

Definition

Class:	AbsSequence
Method:	getElements
Parameters:	String, String, String[]
Returns:	String[]
Method signature:	String[] getElements(String first, String second, String[] indices)
(be sure your method is public)

Constraints

-

first will represent an integer between 0 and 10^18, inclusive, with no extra leading zeros.

-

second will represent an integer between 0 and 10^18, inclusive, with no extra leading zeros.

-

indices will contain between 1 and 50 elements, inclusive.

-

Each element of indices will represent an integer between 0 and 10^18, inclusive, with no extra leading zeros.

Examples

0)

"21"

"12"

{"0", "1", "2", "3", "4"}

Returns: {"21", "12", "9", "3", "6" }

Here S₀=21 and S₁=12. The next three sequence elements are S₂ = |21 - 12| = 9, S₃ = |12 - 9| = 3 and S₄ = |9 - 3| = 6.

1)

"0"

"0"

{"1000000000000000000"}

Returns: {"0" }

Here we get the sequence consisting of only zeros.

2)

"823"

"470"

{"3","1","31","0","8","29","57","75","8","77"}

Returns: {"117", "470", "2", "823", "115", "87", "49", "25", "115", "23" }

3)

"710370"

"177300"

{"5","95","164721","418","3387","710","0","1197","19507","5848"}

Returns: {"178470", "108270", "90", "0", "90", "90", "710370", "90", "0", "0" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TVGame

Advanced Math

Used in:

SRM 379

Used as:

Division I Level Three

Writer:

asal1

Testers:

PabloGilberto , Olexiy , gawry , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8174

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10800&pm=8174

Problem Statement

A domino is a rectangular tile with a number on each end.

On a TV game show, a player is presented with a NxN board containing N^2 dominoes. The domino in row i, column j (both 1-based indices) contains the numbers i and j. The player must choose exactly N dominoes from the board such that no two dominoes are from the same column and no two are from the same row. He is then required to join all pairs of dominoes that contain the same number. For example, if he picks (1,3), (3,2), (2,4) and (4,1), he must join them all together in a cycle.

At this point, there are one or more groups of connected dominoes (a single domino counts as a group). Because the player is not allowed to choose dominoes from the same column or row, there will always be a single way to join the dominoes together.

Each domino has a hidden number on its back. Compute the product of the hidden numbers of all the selected dominoes. If there is an even number of connected domino groups, multiply this product by -1. The final product is the outcome of the game, and if it is positive, the player wins money, and if it's negative, he loses money.

You are given a String[] board containing the hidden numbers of all the dominoes on the board. The j-th character of the i-th element of board is a character representing the hidden number of the domino in row i, column j. Digits '0' to '9' represent the numbers 0 to 9. Letters 'A' to 'I' represent the numbers -1 to -9. Your task is to find the sum of every possible outcome given the hidden numbers of the dominoes. Calculate the sum of every possible outcome of the game, and return this sum modulo 121547.

Definition

Class:	TVGame
Method:	expectedProfit
Parameters:	String[]
Returns:	int
Method signature:	int expectedProfit(String[] board)
(be sure your method is public)

Constraints

-

board will contain between 1 and 50 elements, inclusive.

-

Each element of board will contain exactly n characters, where n is the number of elements in board.

-

board will contain only digits '0'-'9' and uppercase letters 'A'-'I'.

Examples

0)

{"35",
 "44"}

Returns: 8

There are two possible ways to select the dominoes:

1) Select (1,1) and (2,2). You can't join them together, so you have two groups of dominoes (each containing a single domino). The product of their hidden numbers is 3x4 = 12. Since there's an even number of groups, you then multiply by -1 to get -12.

2) Select (1,2) and (2,1). You must join these two together, so you have one connected group of dominoes. The product of their hidden numbers is 4x5 = 20.

The sum of these two possible outcomes is -12+20 = 8.

1)

{"00200",
 "0B000",
 "00020",
 "10000",
 "00001"}

Returns: 121539

Every choice leads to 0 earnings except (1,3), (2,2), (3,4), (4,1), (5,5). When we choose those, we get three groups of connected dominoes:

(1,3) - (3,4) - (4,1)
(2,2)
(5,5)

The outcome here is 2*(-2)*2*1*1 = -8. -8 mod 121547 = 121539.

2)

{"12A",
 "A12",
 "2A1"}

Returns: 14

There are 6 possible ways to select the dominoes, and their outcomes are: -1, 1, 2, 2, 2, 8.

3)

{"AAAA",
 "BBBB",
 "CCCC",
 "DDDD"}

Returns: 0

Here, no matter how we choose the dominoes, the outcome will always be either 24 or -24. It is 24 half the time, and -24 half the time, so the sum is 0.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FlashFlood

Geometry, Math

Used in:

TCCC07 Semi 2

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8169

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10957&pm=8169

Problem Statement

The creek bed is dry. We are given the elevation of the creek bed every 50 feet horizontally along its course, west to east. Our town is located in a valley just to the east of the last elevation. It has just started raining at a rate of r inches per hour over the entire creek bed. (This means that in a volume with straight sides and a flat bottom the water level would rise r inches per hour.)

We can treat this as a 2-dimensional problem by approximating the creek as having a constant width. We will assume that the creek bed is made up of linear segments between the known elevations. We will also treat the water as flowing instantaneously.

Given r, and a int[] ht giving the elevations (in feet) in order from west to east, return the number of hours before the water starts flooding the town.

Definition

Class:	FlashFlood
Method:	hours
Parameters:	int, int[]
Returns:	double
Method signature:	double hours(int r, int[] ht)
(be sure your method is public)

Notes

-

The conversion between feet and inches is 12 inches = 1 foot.

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

r will be between 1 and 100, inclusive.

-

ht will contain between 2 and 50 elements, inclusive.

-

Each element of ht will be between 0 and 5000, inclusive.

-

The elements of ht will have distinct values.

-

At least one element of ht will be greater than its last element.

Examples

0)

{150,140}

Returns: 0.0

All the rain that falls in the creek bed immediately flows into town.

1)

{160,140,150}

Returns: 6.428571428571427

          160     
         /  \         
        /    \       
              \^^^^^^^^^150 
               \^^^^^^^/
                \^^^^/      (Town)
                 140   
      -----+------+------+------

The water will build up in a triangular region until its height reaches 150. The picture shows the water at the crucial moment. The horizontal width of the triangle is (25+50) and its altitude is 10 so its area is 75*10/2 = 375. All the rain that falls on the 100 foot long creek bed goes into this region, so every hour the area of water increases by 100*(7/12) square feet. So the region will be full and start flooding the town in 375 / (700/12) = 45/7 hours.

2)

{110,170,175,155,160,140,150}

Returns: 2.6562500000000018


          175                 
         /  \         
        /     \                
               \         160  
                \     /     \   
                 155         \   
                              \       150
                               \    /     
                               140        (town)
      -----+------+------+------+------+-----

Before the easternmost triangular region fills up, the triangular region just to its west will fill up. So flooding will begin when the water level is 150 in the easternmost region and 160 in the region to its west. The rain falling on the first 100 feet of creek (not shown in the picture) fortunately drains the other way, but all the rain on the remaining 200 foot long creek bed will contribute. So we calculate area/rain = [(62.5*5)/2 + (75*10)/2 ] / (200 * 12 / 12)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CountExpressions

Brute Force, Simple Math

Used in:

SRM 398

Used as:

Division I Level One , Division II Level Two

Writer:

boba5551

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8157

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12170&pm=8157

Problem Statement

You are helping your brother with his homework assignment. His teacher gave him two distinct numbers x and y, and asked him to use those numbers to form as many different expressions as possible. Each expression must satisfy all of the following rules:

The only allowed operators are '+', '-' and '*'.
x and y must each appear exactly twice. No other numbers are allowed.
The result of the expression must be equal to val.

In other words, each expression can be written in the form "a op1 b op2 c op3 d", where each of op1, op2 and op3 is '+', '-' or '*', and among the numbers a, b, c and d, exactly two are equal to x and the other two are equal to y. Please note that the unary minus is not allowed (see example 0). Expressions are calculated from left to right, and there is no operator precedence. For example, to calculate the result of "2 + 2 * 3 + 3", you would first calculate 2 + 2, then multiply the result by 3, and then add 3 to get 15.

Return the total number of different expressions that can be formed. Two expressions are considered different if their string notations (as described in the previous paragraph) are different. For example, the expressions "2 + 3 - 2 - 3", "2 - 2 + 3 - 3" and "2 - 3 - 2 + 3" are all different.

Definition

Class:	CountExpressions
Method:	calcExpressions
Parameters:	int, int, int
Returns:	int
Method signature:	int calcExpressions(int x, int y, int val)
(be sure your method is public)

Constraints

-

x and y will each be between -100 and 100, inclusive.

-

x and y will be different.

-

val will be between -100000000 and 100000000, inclusive.

Examples

0)

Returns: 9

The possible expressions are:

8 + 8 + 7 - 7
8 + 7 + 8 - 7
7 + 8 + 8 - 7
8 + 8 - 7 + 7
8 + 7 - 7 + 8
7 + 8 - 7 + 8
8 - 7 + 8 + 7
8 - 7 + 7 + 8
7 - 7 + 8 + 8

Please note that the unary minus is not allowed, so "-7 + 7 + 8 + 8" is not a valid expression.

1)

Returns: 5

The possible expressions are:

3 * 5 - 3 - 5
5 * 3 - 3 - 5
3 * 5 - 5 - 3
5 * 3 - 5 - 3
5 - 3 * 5 - 3

2)

98010000

Returns: 6

3)

-99

-1764

Returns: 2

-99 - (-99) - 42 * 42
-99 - 42 - (-99) * 42

4)

-100

-100000000

Returns: 0

There are no valid expressions.

5)

Returns: 17

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KSubstring

Greedy, Simple Math, Sorting

Used in:

SRM 404

Used as:

Division I Level Two

Writer:

boba5551

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8154

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12176&pm=8154

Problem Statement

You are given numbers A0, X, Y, M and n. Generate a list A of length n using the following recursive definition:

A[0] = A0

A[i] = (A[i - 1] * X + Y) MOD M (note that A[i - 1] * X + Y may overflow 32-bit integer)

Let s(i, k) be a sum of k consecutive elements of the list A starting with the element at position i (0 indexed). More formally, s(i, k) = A[i] + A[i + 1] + ... + A[i + k - 1].

Your task is to find the smallest difference between s(i, k) and s(j, k) (where difference is defined as abs(s(i, k) - s(j, k))) such that i + k <= j. In other words, you must find the smallest difference between two subsequences of the same length that do not overlap.

Call this smallest difference val, and return a int[] containing exactly two elements. The first element should be k, and the second element should be val. If there are multiple solutions with the same val, return the one among them with the highest k.

Definition

Class:	KSubstring
Method:	maxSubstring
Parameters:	int, int, int, int, int
Returns:	int[]
Method signature:	int[] maxSubstring(int A0, int X, int Y, int M, int n)
(be sure your method is public)

Constraints

-

M will be between 1 and 1,000,000,000, inclusive.

-

A0 will be between 0 and M-1, inclusive.

-

X will be between 0 and M-1, inclusive.

-

Y will be between 0 and M-1, inclusive.

-

n will be between 2 and 3,000, inclusive.

Examples

0)

Returns: {2, 1 }

The elements of the list are {5, 19, 11, 12, 15}. There is no way to find two subsequences that have equal sums and do not overlap, so there is no way to obtain 0 as a difference. |s(0, 2) - s(2, 2)| = 1 and that is the minimal difference. Note that |s(2, 1) - s(3, 1)| is also 1, but we don't choose these subsequences because they have a lower value for k.

1)

Returns: {5, 161 }

The elements of the list are {8, 169, 1135, 652, 1940, 1296, 1618, 1457, 491, 974, 1779, 330}. The smallest difference is |s(1, 5) - s(7, 5)| = 161.

2)

Returns: {244, 0 }

3)

Returns: {35, 4 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MyFriends

Graph Theory, Greedy, Math

Used in:

SRM 398

Used as:

Division I Level Three

Writer:

boba5551

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8144

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12170&pm=8144

Problem Statement

There is a group of n kids, numbered 0 through n-1, where n is an odd number. Each kid has some friends within the group, and each kid knows how many friends each of the other kids has. Friendship is symmetric, so if kid 0 is a friend of kid 1, then kid 1 is a friend of kid 0. Each kid i also supports exactly one other kid (i+k) % n, not necessarily a friend.

You ask each kid to answer the following question: Consider each kid in the group except yourself and the kid you support. What is the sum of the number of friends each of them has? For example, if you ask kid 0 this question, and kid 0 supports kid 1, he should tell you (the number of friends kid 2 has) + (the number of friends kid 3 has) + ... + (the number of friends kid n-1 has).

You are given a int[] sumFriends, where the i-th element (0-indexed) is the answer given to you by kid i. Some of the kids might not be telling the truth (they are just kids, forgive them). Return "IMPOSSIBLE" if it is impossible for all the given answers to be accurate. Otherwise, return "POSSIBLE" (all quotes for clarity).

Definition

Class:	MyFriends
Method:	calcFriends
Parameters:	int[], int
Returns:	String
Method signature:	String calcFriends(int[] sumFriends, int k)
(be sure your method is public)

Constraints

-

sumFriends will contain odd number of elements.

-

sumFriends will contain between 3 and 49 elements, inclusive.

-

Each element of sumFriends will be between 0 and 9999, inclusive.

-

k will be between 1 and (number of elements in sumFriends)-1, inclusive.

Examples

0)

{8, 9, 8, 8, 9}

Returns: "POSSIBLE"

We can get such sums only if kid 1 has 2 friends and all other kids have 3 friends. Such a situation is possible. For example:

Kid             His/her friends
0               1, 3, 4
1               0, 2
2               1, 3, 4
3               0, 2, 4
4               0, 2, 3

1)

{7, 6, 5, 4, 4}

Returns: "IMPOSSIBLE"

2)

{5, 6, 5, 4, 4}

Returns: "POSSIBLE"

3)

{1, 2, 3}

Returns: "IMPOSSIBLE"

Here kid 2 supports kid 0, so he tells us the number of friends of kid 1. But it's obviously impossible for kid 1 to have 3 friends.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BlackWhiteRectangles

Geometry, Simple Math

Used in:

TCO08 Qual 2

Used as:

Division I Level Three

Writer:

ivan_metelsky

Testers:

PabloGilberto , radeye , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8142

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12008&pm=8142

Problem Statement

NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.

There is an infinite sheet of paper which is divided into 1x1 cells. A cartesian coordinate system exists on the sheet, with its origin at the corner of one of the cells. The X-axis goes from left to right in the positive direction and the Y-axis goes from bottom to top in the positive direction. The axes are parallel to the sides of the cells.

Initially, all the cells are white. You are given a String[] rectangles, each element of which represents a rectangular pattern you will draw on the sheet. Each rectangle is formatted "x1 y1 x2 y2 type" (quotes for clarity), where (x1, y1) is the bottom left corner of the rectangle, (x2, y2) is the top right corner of the rectangle, and type is the number of one of the following patterns:

Pattern 1: All cells are colored black.
Pattern 2: All cells in odd-numbered rows are colored black (the rows of the rectangle are numbered from bottom to top, starting from 0).
Pattern 3: All cells in odd-numbered columns are colored black (the columns of the rectangle are numbered from left to right, starting from 0).
Pattern 4: All cells with row and column numbers that are either both odd or both even are colored black.

The pictures below illustrate a rectangle and all the possible patterns:

Return the total number of black cells on the sheet of paper after all the rectangles are drawn.

Definition

Class:	BlackWhiteRectangles
Method:	blackCount
Parameters:	String[]
Returns:	int
Method signature:	int blackCount(String[] rectangles)
(be sure your method is public)

Constraints

-

rectangles will contain between 1 and 50 elements, inclusive.

-

Each element of rectangles will be formatted as "x1 y1 x2 y2 type" (quotes for clarity), where x1, y1, x2, y2 will each be an integer between 1 and 40000, inclusive, without leading zeros, and type will be an integer between 1 and 4, inclusive, without leading zeros.

-

In each element of rectangles, x1 will be strictly less than x2, and y1 will be strictly less than y2.

Examples

0)

{"1 1 6 8 1",
 "11 1 16 8 2",
 "1 11 6 18 3",
 "11 11 16 18 4"}

Returns: 82

Here we have 4 non-overlapping 5x7 rectangles with all possible filling patterns. Therefore the total number of black cells is 35 + 14 + 15 + 18 = 82.

1)

{"1 1 11 11 1",
 "1 1 11 11 2",
 "9 9 19 19 3",
 "9 9 19 19 4"}

Returns: 172

In this case we have 2 equal 10x10 rectangles with filling patterns 1 and 2 (100 black cells) and 2 equal 10x10 rectangles with filling patterns 3 and 4 (75 black cells). Since the first two rectangles and the last two rectangles have 3 black cells in common, the result is 100 + 75 - 3 = 172.

2)

{"1 6 9 9 1",
 "1 9 7 10 1",
 "1 5 8 7 1",
 "2 6 8 8 1",
 "2 1 3 4 1"}

Returns: 40

3)

{"7 5 9 6 4",
 "6 3 9 6 4",
 "8 3 9 8 4",
 "5 9 10 10 4",
 "5 3 8 5 4"}

Returns: 13

4)

{"7 1 10 3 1",
 "8 2 9 7 4",
 "5 3 7 4 3",
 "4 3 9 4 2",
 "3 1 9 2 1"}

Returns: 13

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CommonFactors

Brute Force, Simple Math

Used in:

TCHS SRM 48

Used as:

Division I Level Two

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8140

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10807&pm=8140

Problem Statement

You are given a list of numbers in a int[] n. A number k is a factor of number m if m can be exactly divided into k. Find the factor greater than 1 that is shared by the most elements in n. If there are several such factors, return the largest one among them.

Definition

Class:	CommonFactors
Method:	mostCommon
Parameters:	int[]
Returns:	int
Method signature:	int mostCommon(int[] n)
(be sure your method is public)

Constraints

-

n will contain between 1 and 50 elements, inclusive.

-

Each element of n will be between 2 and 1000000000, inclusive.

Examples

0)

{2, 3, 4, 6}

Returns: 2

2 is a factor of 3 elements of n (2, 4 and 6). 3 is a factor of two elements (3 and 6). 4 and 6 are not factors of any numbers except themselves.

1)

{2, 3, 6}

Returns: 3

Both 2 and 3 are factors of exactly two numbers. Based on the tie-breaker rule, we pick the larger.

2)

{2, 3, 5, 7}

Returns: 7

No factor appears more than once, so again we use the tie-breaker rule.

3)

{2, 3, 5, 6, 7, 9, 11, 12}

Returns: 3

4)

{24, 12, 37, 18, 11}

Returns: 6

5)

{3, 49, 7, 100, 100}

Returns: 100

6)

{123456789, 987654321, 246813579, 975318642}

Returns: 9

7)

{1000000000, 999999999, 999999999}

Returns: 999999999

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MovieRating

Simple Math, Sorting

Used in:

TCCC07 Qual 1

Used as:

Division I Level One

Writer:

ivan_metelsky

Testers:

PabloGilberto , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8118

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10888&pm=8118

Problem Statement

A web site for movie fans assigns a composite rating to each movie. Your task is to calculate the rating of a particular movie. Users of the site rate the movie on a scale of 0 to 100, inclusive. The lowCount lowest ratings and the highCount highest ratings are thrown away, and the composite rating is the average of the remaining individual ratings.

Given the user ratings in a int[] marks, together with lowCount and highCount, return the rating of the movie.

Definition

Class:	MovieRating
Method:	calculate
Parameters:	int[], int, int
Returns:	double
Method signature:	double calculate(int[] marks, int lowCount, int highCount)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

marks will contain between 1 and 50 elements, inclusive.

-

Each element of marks will be between 0 and 100, inclusive.

-

lowCount and highCount will be between 0 and 50, inclusive.

-

lowCount+highCount will be strictly less than the number of elements in marks.

Examples

0)

{70, 99, 96, 0, 30}

Returns: 59.0

With no individual ratings thrown away we should return just (70 + 99 + 96 + 0 + 30) / 5 = 295 / 5 = 59.

1)

{91, 90, 50}

Returns: 90.0

Here the lowest rating (50) and the highest rating (91) are thrown away, so only one individual rating (90) is left.

2)

{23, 23, 23, 23, 23, 23, 23, 23}

Returns: 23.0

There can be repeats in marks.

3)

{31, 52, 20, 86, 47, 76, 82, 27, 42, 29}

Returns: 35.2

4)

{1, 1, 0, 0, 1, 1, 0, 1, 0, 2}

Returns: 0.6666666666666666

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ComplementaryDNAChains

Simple Math

Used in:

TCCC07 Qual 3

Used as:

Division I Level One

Writer:

ivan_metelsky

Testers:

PabloGilberto , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8114

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10889&pm=8114

Problem Statement

A DNA chain is a sequence of proteins of 4 types. The types are encoded using the characters 'A', 'C', 'G', 'T'. Two proteins are called complementary if one is of type 'A' and the other is of type 'T', or if one is of type 'C' and the other is of type 'G'. Two DNA chains are called complementary if they have equal length, and the i-th protein in the first chain and the i-th protein in the second chain are complementary for all possible values of i.

You will be given Strings first and second, representing two DNA chains of equal length. Your goal is to make the two chains complementary. To do this, you can perform a number of replacements, where each replacement involves changing a single protein in either one of the chains to a different type. Return the minimum number of replacements required to achieve your goal.

Definition

Class:	ComplementaryDNAChains
Method:	minReplaces
Parameters:	String, String
Returns:	int
Method signature:	int minReplaces(String first, String second)
(be sure your method is public)

Constraints

-

first will contain between 1 and 50 characters, inclusive.

-

second will contain the same number of characters as first.

-

Each character in first and second will be 'A', 'C', 'G' or 'T'.

Examples

0)

"ACGT"

"TGCA"

Returns: 0

The input DNA chains are already complementary, so no replacements are needed.

1)

"ACGT"

"ACGT"

Returns: 4

We need 4 replacements to transform one of the input DNA chains to "TGCA":

ACGT -> TCGT -> TGGT -> TGCT -> TGCA.

2)

"ATAGTACCAC"

"CTTATTGGGT"

Returns: 6

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RLESum

Math

Used in:

TCCC07 Round 2

Used as:

Division I Level Two

Writer:

andrewzta

Testers:

PabloGilberto , radeye , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8111

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10891&pm=8111

Problem Statement

An RLE compressed number is uncompressed as follows. Replace each occurrence of the substring "[k]c" (quotes for clarity), where k is a positive integer without leading zeroes and c is a single digit, with k consecutive occurrences of c. For example, "12[3]3[2]4[5]1" uncompresses to "123334411111". "123[2]3441[3]11" uncompresses to the same number.

Note that uncompression is not recursive; brackets are not allowed to be nested.

You are given two RLE compressed numbers a and b and String[] k. Uncompress a and b, and add them together. Return a int[], the i-th element of which is the k[i]-th digit of the sum. The 0-th digit is the rightmost digit, the 1-st digit is the next digit to the left, etc. If there are not enough digits, the corresponding element must be equal to 0.

Definition

Class:	RLESum
Method:	getDigits
Parameters:	String, String, String[]
Returns:	int[]
Method signature:	int[] getDigits(String a, String b, String[] k)
(be sure your method is public)

Constraints

-

a and b will contain only digits ('0'-'9') and brackets ('[' and ']').

-

a and b will each contain between 1 and 50 characters, inclusive.

-

a and b will each be an RLE compressed number that uncompresses to a valid positive integer with no extra leading zeroes.

-

a and b, when uncompressed, will each contain no more than 10^18 digits.

-

k will contain between 1 and 50 elements, inclusive.

-

Each element of k will be an integer between 0 and 10^18, inclusive, without extra leading zeroes.

Examples

0)

"[12]3"

"[3]1[3]2[3]3"

{"12", "11", "10", "9", "8","7","6","5","4","3","2","1","0"}

Returns: {0, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6 }

a decompresses to 333333333333, and b decompresses to 111222333. Their sum is 333444555666. We return all of its digits, and also 0 for the 12-th digit which doesn't exist.

1)

"[5]9"

"[5]9"

{"5", "0", "1"}

Returns: {1, 8, 9 }

2)

"123456789"

"987656789"

{"10", "9", "1", "3", "1", "2"}

Returns: {0, 1, 7, 3, 7, 5 }

Note that k need not be sorted, and its elements can be equal to each other.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OptimalGroupMovement

Simple Math, Simple Search, Iteration

Used in:

TCCC07 Qual 1

Used as:

Division I Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8101

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10888&pm=8101

Problem Statement

NOTE: This problem statement contains superscripts that may not display properly if viewed outside of the applet.

There is a horizontal row of N squares, each of which either contains a counter or is empty. A set of counters in this row is called a group if it meets all of the following requirements:

They form a contiguous part of the row.
The square immediately to the left of the leftmost counter in the set is empty, or the leftmost counter in the set is in the leftmost square of the row.
The square immediately to the right of the rightmost counter in the set is empty, or the rightmost counter in the set is in the rightmost square of the row.

In one move, we can take any group and simultaneously move all of its counters one square to the right (only if the rightmost counter in the group is not in the rightmost square of the row), or one square to the left (if the leftmost counter in the group is not in the leftmost square of the row). The cost of such a move is C², where C is the number of counters in the group.

You will be given a String board that represents the initial row from left to right. Each character of board represents the content of a single square and is either uppercase 'X' (counter) or '.' (empty). Your goal is to have all the counters in the row form exactly one group. Return the minimum possible total cost required to achieve this.

Definition

Class:	OptimalGroupMovement
Method:	minimumCost
Parameters:	String
Returns:	int
Method signature:	int minimumCost(String board)
(be sure your method is public)

Constraints

-

board will contain between 1 and 50 characters, inclusive.

-

Each character of board will be '.' or 'X'.

-

At least one character of board will be 'X'.

Examples

0)

".XXX.XXXX."

Returns: 9

Initially, there are two groups of counters: a group of 3 on the left side and a group of 4 on the right side. To form a single group, we can move the group of 3 one square to the right (at a cost of 9), or move the group of 4 one square to the left (at a cost of 16). The first option is cheaper.

1)

"X"

Returns: 0

Here we already have one group of 1 counter.

2)

"XXXXX...X..X.X"

Returns: 14

The leftmost group is large, so we don't move it. We move the other three groups to the left.

3)

".X.X.X..X.X.X.......XX..X.X..X"

Returns: 70

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ColorApproximation

Simple Math, String Manipulation

Used in:

TCCC07 Qual 3

Used as:

Division I Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8099

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10889&pm=8099

Problem Statement

In the RGB color model, colors are encoded as triples (R, G, B), where R, G and B denote the quantity of red, green and blue, respectively, in the color. Each number in the triple is between 0 and 255, inclusive. The distance between two colors (R1, G1, B1) and (R2, G2, B2) is max{|R1-R2|, |G1-G2|, |B1-B2|}. The distance between a color C and a set of colors S is the maximum among the distances between C and each color in S. A best approximation for a set of colors S is a color C such that the distance between C and S is as small as possible.

You will be given a String[] colors, each element of which contains a single space separated list of colors, with no leading or trailing spaces. Each color in the list will be formatted as "RRGGBB" (quotes for clarity), where RR, GG and BB are the color's two-digit red, green and blue quantities, respectively, in hexadecimal notation. All letters will be uppercase. Find the best approximation for this set of colors and return it as a String in the same format as the input colors. If there are multiple possible answers, return the String among them that comes first alphabetically.

Definition

Class:	ColorApproximation
Method:	bestApproximation
Parameters:	String[]
Returns:	String
Method signature:	String bestApproximation(String[] colors)
(be sure your method is public)

Notes

-

Digits come before letters in the alphabetical order. For example, String "A9" is alphabetically less than String "AA".

Constraints

-

colors will contain between 1 and 50 elements, inclusive.

-

Each element of colors will contain between 6 and 48 characters, inclusive.

-

Each element of colors will contain a single space separated list of colors without leading or trailing spaces.

-

Each color in each element of colors will contain exactly 6 hexadecimal digits ('0'-'9', 'A'-'F').

-

All colors will be distinct.

Examples

0)

{"F36F4E"}

Returns: "F36F4E"

If a set contains only one color, that color is the set's best approximation.

1)

{"7A946B","3B6473"}

Returns: "5A7453"

This set contains two colors (122, 148, 107) and (59, 100, 115). Every best approximation for this set will have a distance of 32 from it. The one among them whose hexadecimal representation comes first alphabetically is (90, 116, 83).

2)

{"40FE20", "800040"}

Returns: "017F00"

3)

{"626848 321D3A 60EACA 521A88 9C188F",
 "94F0B3 B55795 B34004 20983C 7A644B"}

Returns: "49845E"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

JoshString

Brute Force, Simple Math, String Parsing

Used in:

TCHS SRM 38

Used as:

Division I Level One

Writer:

vlad_D

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8094

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10779&pm=8094

Problem Statement

Josh said every string with a certain property is his string. The property that Josh is talking about is that the sum of the letters of the string has to be a prime number. The string will contain only lowercase letters ('a'-'z'). For each letter you add to the sum the 1-based position of the letter in the alphabet. For 'a' you add 1, for 'b' you add '2', and so on. For example, the sum of the letters in "bad" is 2 + 1 + 4 = 7, and 7 is prime, so therefore, "bad" is Josh's string. Given a String s, return "YES" if it is Josh's string or "NO" otherwise (all quotes for clarity only).

Definition

Class:	JoshString
Method:	isJoshString
Parameters:	String
Returns:	String
Method signature:	String isJoshString(String s)
(be sure your method is public)

Constraints

-

s will contain only lowercase letters ('a'-'z').

-

s will contain between 2 and 50 characters, inclusive.

Examples

0)

"bad"

Returns: "YES"

The example from the problem statement.

1)

"badbad"

Returns: "NO"

"bad" two times. The sum is 7 * 2 = 14. 14 is not a prime number.

2)

"abcdefghijklmnopqrstuvwxyz"

Returns: "NO"

The whole alphabet. The sum will be 1 + 2 + 3 + .. + 26 = 351. 351 is not a prime number because it is divisible by 3.

3)

"abcdefghijklmnopqrstuvwxyzaa"

Returns: "YES"

Same string but contains 2 extra 'a's. The sum will be 351 + 2 = 353 which is a prime number.

4)

"asdjkhqwaieyajhdjsahjquawyhasdhwauyashjzxdf"

Returns: "YES"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StrangeArray

Math, Recursion

Used in:

SRM 387

Used as:

Division I Level Three

Writer:

Relja

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8086

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11121&pm=8086

Problem Statement

You are given an infinite sequence P, where the i-th member is defined as follows:

  P[i] = (A[i % A.size] ^ (B[i % B.size] + i / B.size)) % 1000000007

where % denotes modulo, ^ denotes exponentiation, / denotes integer division, and X.size represents the number of elements in X.

Alternatively, the following pseudocode can be used to calculate the elements of P successively:

int i = 0;
loop forever
	P[i] = (A[i % A.size] ^ B[i % B.size]) % 1000000007;
	B[i % B.size] = B[i % B.size] + 1;
	i = i + 1;
end of loop

You are given int[]s A and B, and a String N containing an integer. Calculate the sum of the first N elements of the sequence (i.e., P[0] + P[1] + ... + P[N - 1]), and return that sum modulo 1000000007.

Definition

Class:	StrangeArray
Method:	calculateSum
Parameters:	int[], int[], String
Returns:	int
Method signature:	int calculateSum(int[] A, int[] B, String N)
(be sure your method is public)

Constraints

-

A and B will each contain between 1 and 50 elements, inclusive.

-

Each element of A and B will be between 1 and 10^9, inclusive.

-

N will represent an integer between 1 and 10^18, inclusive, with no leading zeros.

Examples

0)

{1,2,3}

{3,4}

"2"

Returns: 17

1^3 + 2^4 = 17.

1)

{2, 3, 4}

{2, 3}

"3"

Returns: 95

2^2 + 3^3 + 4^(2 + 1) = 95.

2)

{2, 3, 4}

{2, 3}

"5"

Returns: 192

2^2 + 3^3 + 4^(2 + 1) + 2^(3 + 1) + 3^(2 + 2) = 192.

3)

{1, 2, 3, 4}

{1}

"1000000000"

Returns: 607570807

1^1 + 2^2 + 3^3 + 4^4 + 1^5 + 2^6 + ... + 4^1000000000 = 607570807 (mod 1000000007).

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

JoshSum

Brute Force, Math

Used in:

TCHS SRM 38

Used as:

Division I Level Two

Writer:

vlad_D

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8070

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10779&pm=8070

Problem Statement

Josh thought he would be cooler if he had his own secret sum. The Josh Sum of an integer n is the sum of the last digit of each of the first n terms of the Fibonacci series. The Fibonacci series is : 1,1,2,3,5,etc. The i-th term of the series is equal to the sum of the (i-1)-th term and (i-2)-th term, and the first and second terms are 1. The Josh Sum for n = 7 is 1 + 1 + 2 + 3 + 5 + 8 + 3 = 23. Given n, return its Josh Sum.

Definition

Class:	JoshSum
Method:	getJoshSum
Parameters:	int
Returns:	int
Method signature:	int getJoshSum(int n)
(be sure your method is public)

Constraints

-

n will be between 1 and 100000, inclusive.

Examples

0)

Returns: 23

The first 7 Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13; therefore the answer is 1 + 1 + 2 + 3 + 5 + 8 + 3 = 23.

1)

Returns: 1

The first Fibonacci number is 1. The answer is 1.

2)

Returns: 1692

3)

Returns: 212

4)

Returns: 460892

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CatchTheMice

Brute Force, Geometry, Math, Search

Used in:

SRM 426

Used as:

Division I Level Two

Writer:

StevieT

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8066

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13517&pm=8066

Problem Statement

A fairground operator has designed a new game, called "Catch the Mice". This consists of a set of electronic "mice" that move around on a large board. The contestant controls a square cage, which is initially suspended above the board. The contestant can position the cage anywhere above the board and then drop it, the aim being to enclose some of the mice in the cage. The contestant wins a prize accoring to how many mice he managed to capture. If the contestant captures all of the mice, then he wins the grand prize, which is a sports car. However the fairground operator is not entirely honest, and wants your help to rig the game so that it is impossible to win the grand prize. He wants to make the cage sufficiently small that at no point in time are the mice close enough for it to capture them all.

Consider the mice as a set of points moving in an infinite 2D cartesian plane. Each mouse starts at a known position at time t = 0, then moves with constant velocity in time t ? 0. Consider the cage as a perfect square of side length L, that can be positioned anywhere in the plane with its sides parallel to the axes (i.e., the contestant can move, but cannot rotate the cage). The cage can be dropped at any time t ? 0 and it will capture a mouse if at that point in time the mouse's position is strictly contained within its boundary (mice exactly on the boundary are not considered to be captured). You should calculate the maximum value of L that doesn't allow all the mice to be captured.

You will be given 4 int[]s xp, yp, xv and yv. The position of the mouse with index i is given by (xp[i], yp[i]) and its velocity by (xv[i], yv[i]). The position of the mouse at time t will therefore be (xp[i] + xv[i]*t, yp[i] + yv[i]*t). Return a double giving the length of the side of the largest cage that cannot capture all the mice at any time t ? 0.

Definition

Class:	CatchTheMice
Method:	largestCage
Parameters:	int[], int[], int[], int[]
Returns:	double
Method signature:	double largestCage(int[] xp, int[] yp, int[] xv, int[] yv)
(be sure your method is public)

Notes

- Your return value must be accurate to an absolute or relative tolerance of 1e-9.

Constraints

- xp, yp, xv and yv will contain between 2 and 50 elements, inclusive.

- xp, yp, xv and yv will contain the same number of elements.

- Each element of xp, yp, xv and yv will be between -1000 and 1000, inclusive.

- At no point in time t ? 0 will any two mice occupy the same point in space.

Examples

0)

{0,10}

{0,10}

{10,-10}

{0,0}

Returns: 10.0

A cage with side length greater than 10 would be able to catch both the mice at any time before t = 1.

1)

{0,10,0}

{0,0,10}

{1,-6,4}

{4,5,-4}

Returns: 3.0

At time t = 1, the mice are at positions (1, 4), (4, 5) and (4, 6). At this point in time any cage with an edge length larger than 3 would be able to catch them. This is the point in time when the mice are closest together.

2)

{50,10,30,15}

{-10,30,20,40}

{-5,-10,-15,-5}

{40,-10,-1,-50}

Returns: 40.526315789473685

3)

{0,10,10,0}

{0,0,10,10}

{1,0,-1,0}

{0,1,0,-1}

Returns: 10.0

4)

{13,50,100,40,-100}

{20,20,-150,-40,63}

{4,50,41,-41,-79}

{1,1,1,3,-1}

Returns: 212.78688524590163

5)

{0,10}

{0,0}

{5,5}

{3,3}

Returns: 10.0

6)

{-49,-463,-212,-204,-557,-67,-374,-335,-590,-4}

{352,491,280,355,129,78,404,597,553,445}

{-82,57,-23,-32,89,-72,27,17,100,-94}

{-9,-58,9,-14,56,75,-32,-98,-81,-43}

Returns: 25.467532467532468

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CrazySequence

Math, Search

Used in:

TCHS SRM 36

Used as:

Division I Level Two

Writer:

mateuszek

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8064

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10774&pm=8064

Problem Statement

Consider the following infinite sequence of numbers: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, ... (number k appears exactly k times in the sequence). You are given a String n representing an integer (without leading zeros). Return the n-th number in that sequence (index will be 1-based).

Definition

Class:	CrazySequence
Method:	nthNumber
Parameters:	String
Returns:	int
Method signature:	int nthNumber(String n)
(be sure your method is public)

Constraints

-

n will represent an integer between 1 and 10¹⁸, inclusive.

-

n will have no leading zeros.

Examples

0)

"1"

Returns: 1

1)

"4"

Returns: 3

2)

"169"

Returns: 18

3)

"25342536783"

Returns: 225133

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MirroredClock

Simple Math, String Parsing

Used in:

SRM 363

Used as:

Division II Level One

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8058

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10777&pm=8058

Problem Statement

You are sitting in front of a mirror and looking at the image of a clock located behind you. You want to know what time it is. The clock is a traditional clock with a 12-hour board (without numbers written on it), a minute and an hour hand (the hour hand is shorter, so that you can distuniguish them). You are given a String time denoting the time as it is seen in the mirror. The time will be formatted as "HH:MM" (quotes for clarity), where HH is the two digit hour and MM is the two digit minute. The hour will be between 00 and 11, inclusive, where 00 represents 12 o' clock. Return a String in the same format denoting the actual time. See examples for further clarification.

Definition

Class:	MirroredClock
Method:	whatTimeIsIt
Parameters:	String
Returns:	String
Method signature:	String whatTimeIsIt(String time)
(be sure your method is public)

Constraints

-

time will be formatted as "HH:MM" (quotes for clarity), where HH is a two digit integer between 00 and 11, inclusive, and MM is a two digit integer between 00 and 59, inclusive.

Examples

0)

"10:00"

Returns: "02:00"

1)

"01:15"

Returns: "10:45"

2)

"03:40"

Returns: "08:20"

3)

"00:00"

Returns: "00:00"

Although it doesn't happen often, sometimes we can see the actual time right in the mirror.

4)

"11:53"

Returns: "00:07"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SignificanceArithmetic

Search, Simple Math, Simulation

Used in:

SRM 362

Used as:

Division II Level Three

Writer:

eleusive

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8056

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10775&pm=8056

Problem Statement

Significance arithmetic is a set of rules used in scientific calculations, and is used extensively in scientific application software. Specifically, significance arithmetic is used to determine the correct number of significant digits, or measured digits, in a calculation. The significant digits in a number are all its digits except for leading zeros that are two or more places to the left of the decimal point. For instance, 00.30, 0.00 and 0.60 each contain three significant digits, while 5 and 00 each only contain one significant digit.

We need to compute the result of the addition of two numbers. The result must be rounded to n significant digits, where n is determined as follows:

First determine the number with the least number of digits to the right of the decimal point (this may be zero). Then the result will not contain any significant digits to the right of this digit, and all other digits are significant (except leading zeros that are two or more places to the left of the decimal point). For example, the result of 1.56 + 1236.1 will have only one significant digit immediately to the right of the decimal point, but all digits to the left of the decimal point will be significant.

There are several cases to consider when rounding a number to n significant digits:

1) If the number has less than n significant digits, the number is padded with trailing zeros. For example, 2.5 rounded to 3 significant digits is 2.50.

2) If the digit immediately to the right of the nth digit is greater than 5, the number is rounded up. For example, 2.56 rounded to 2 significant digits is 2.6.

3) If the digit immediately to the right of the nth digit is less than 5, the number is rounded down. For example, 2.54 rounded to 2 significant digits is 2.5.

4) If the digit immediately to the right of the nth digit is 5 and there are non-zero digits after the 5, the number is rounded up. For example, 2.551 rounded to 2 significant digits is 2.6.

5) If the digit immediately to the right of the nth digit is 5 and there are no subsequent non-zero digits, then the number is rounded whichever way leaves the nth digit even. For example, 2.55 rounded to 2 significant digits is 2.6, but 2.45 rounded to 2 significant digits is 2.4.

You will be given an expression as a String that will contain two numbers that are separated by a '+'. Each number will contain a non-empty integral part, as well as an optional fractional part which, if present, will be preceded by a decimal point. The numbers may contain leading zeros, and will always be positive. Examples of valid numbers are 0.456, 004.0, and 0. However, .025 is invalid because it has no integral part, and 45. is invalid because a fractional part must follow the decimal point.

Your result should be in the same format as described above. However, there should only be a leading zero if the integral part of the number is 0. For example, 0.00450 is a valid result, while 0459.2 is not.

Definition

Class:	SignificanceArithmetic
Method:	evaluate
Parameters:	String
Returns:	String
Method signature:	String evaluate(String expression)
(be sure your method is public)

Notes

-

Numbers in expression may contain leading zeros.

Constraints

-

expression will contain two numbers that are separated by a '+'.

-

Each number in expression will be a real number containing between 1 and 6 digits, inclusive (not including the decimal point).

-

Each number in expression will be formatted exactly as described in the problem statement.

Examples

0)

"2+2"

Returns: "4"

Two has one significant digit, so the result will as well.

1)

"1.234+0.000"

Returns: "1.234"

All digits here are significant.

2)

"1.234+0.006"

Returns: "1.240"

Again, all digits here are significant. Therefore the result will contain the same number of significant digits, and rounding rule #1 is used.

3)

"12.57+2.6"

Returns: "15.2"

12.45 + 2.6 = 15.17. Rounding rule #2 is used.

4)

"5.50005+0"

Returns: "6"

The only significant digit here is the one immediately to the left of the decimal point, and rounding rule #4 is used.

5)

"2.5+2"

Returns: "4"

Again, the only significant digit here is the one immediately to the left of the decimal point. Here, rounding rule #5 is used.

6)

"0.00+000"

Returns: "0"

7)

"983.17+76.8"

Returns: "1060.0"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MarbleMachine

Math, Simulation

Used in:

SRM 376

Used as:

Division I Level Two

Writer:

jmzero

Testers:

PabloGilberto , Olexiy , misof , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8045

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10796&pm=8045

Problem Statement

You have built a moving sculpture containing several devices that move marbles around on a grid. Each device occupies a single square on the grid and repeatedly executes a sequence of actions. The possible actions are:

Digits 0-9: Bring up 0-9 marbles from the central store (which never runs out of marbles) and place them on the square.
N,E,S,W: Move all the marbles on the square one square North, East, South, or West. If this causes the marbles to leave the grid, they will be removed and placed back in the central store.
D: Remove all the marbles from the square and drop them back into the central store.

Each device has its own sequence of actions, and different devices may have sequences of different lengths. At time 0, each device executes its first action, at time 1, each device executes its second action, etc. When a device reaches the end of its sequence, it starts again at the beginning of the sequence.

During each unit of time, all actions happen simultaneously and only operate on marbles on the squares at the beginning of that time unit. For example, suppose there is one marble on square (0, 0) and one on square (1, 0). Now suppose the first square's action is 'E' and the second square's action is 'D'. At the end of this time unit, the first square will have 0 marbles and the second will have 1. The second square drops the marble that it had at the beginning of the time unit, but it does not drop the marble that arrives from the first square during that time unit.

You are given a String[] actions, the i-th element of which is the action sequence for a device of type i (where i is a 0-based index). You are also given a String[] layout, where the j-th character of the i-th element is a digit representing the type of device located in row i, column j of the grid. Rows are numbered in increasing order from North to South, and columns are numbered in increasing order from West to East. Return the maximum number of marbles that exist on a single square after t time units have passed.

Definition

Class:	MarbleMachine
Method:	maxMarbles
Parameters:	String[], String[], int
Returns:	long
Method signature:	long maxMarbles(String[] layout, String[] actions, int t)
(be sure your method is public)

Constraints

-

layout will contain between 1 and 8 elements, inclusive.

-

Each element of layout will contain between 1 and 8 characters, inclusive.

-

Each element of layout will contain the same number of characters.

-

Each element of layout will contain only digits between 0 and n-1, inclusive, where n is the number of elements in actions.

-

actions will contain between 1 and 10 elements, inclusive.

-

Each element of actions will contain between 1 and 6 characters, inclusive.

-

Each element of actions will contain only digits ('0'-'9') and the characters 'N', 'E', 'S', 'W' and 'D'.

-

t will be between 1 and 100,000,000, inclusive.

Examples

0)

{
"0101",
"1010",
"0101"}

{"4","5353"}

Returns: 21

Devices of type 0 are simple; they pull up 4 marbles on each turn. Over 5 cycles, this is 20 marbles. Devices of type 1 will complete just over 1 cycle in this time - pulling up a total of 5+3+5+3+5=21 marbles. So the maximum marbles at any position will be 21 (which occurs at each location with a device of type 1).

1)

{"011112"}

{"1E","E","0"}

Returns: 498

This structure functions as a kind of conveyor belt. At the left, the device of type 0 alternately grabs one marble and pushes it East. The devices of type 1 move the marble along to the East until they reach the device of type 2, which accumulates the marbles. After 1000 cycles, 500 marbles have been brought up. 2 are still on the "conveyor belt", and 498 are on the square at the East end.

2)

{
"01",
"32"}

{"1E","SSDSS","W","00000W"}

Returns: 3

This machine delivers marbles to the Southwest corner, from which they are periodically dumped off the West edge. The Northeast corner also occasionally loses its marbles.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IsoscelesTriangles

Brute Force, Simple Math

Used in:

TCO08 Semifinal 2

Used as:

Division I Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , SnapDragon , Olexiy , Mike Mirzayanov

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8043

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12016&pm=8043

Problem Statement

A triangle is called isosceles if it has two sides of equal length. Two triangles are considered to be different if they have different sets of vertices. You have a grid of N x M square cells. Return the number of different isosceles triangles you can form using only the centers of grid cells as vertices.

Definition

Class:	IsoscelesTriangles
Method:	count
Parameters:	int, int
Returns:	long
Method signature:	long count(int N, int M)
(be sure your method is public)

Constraints

-

N will be between 1 and 200, inclusive.

-

M will be between 1 and 200, inclusive.

Examples

0)

Returns: 0

Any three centers of grid cells will lie on the same straight line, so it's impossible to form a triangle at all.

1)

Returns: 4

We can select 4 triples of centers of grid cells, and all these triples will form isosceles triangles.

2)

Returns: 10

All 10 isosceles triangles for a 2x3 grid are listed below ('X' stands for a triangle vertex):

XX.  XX.  .X.  X..  X.X
X..  .X.  XX.  XX.  .X.

.XX  .XX  ..X  .X.  .X. 
.X.  ..X  .XX  .XX  X.X

3)

Returns: 248

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MountainMap

Brute Force, Dynamic Programming, Simple Math

Used in:

SRM 369

Used as:

Division I Level Three

Writer:

ivan_metelsky

Testers:

PabloGilberto , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8041

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10785&pm=8041

Problem Statement

A mountain map is a NxM rectangular grid where each cell has a height. The heights are positive integers between 1 and N*M, inclusive, and no two distinct cells have equal heights. Two cells are called neighboring if they share a side or a corner. A cell is called locally minimal if its height is less than the heights of all its neighboring cells.

You are given a String[] data. The j-th character of the i-th element of data is 'X' if the j-th cell in the i-th row of the mountain map is locally minimal, and '.' otherwise. Calculate the number of distinct mountain maps that match the data. Return the result modulo 12345678.

Definition

Class:	MountainMap
Method:	count
Parameters:	String[]
Returns:	int
Method signature:	int count(String[] data)
(be sure your method is public)

Constraints

-

data will contain between 1 and 4 elements, inclusive.

-

Each element of data will contain between 1 and 7 characters, inclusive.

-

All elements of data will contain the same number of characters.

-

Each character in each element of data will be '.' or uppercase 'X'.

Examples

0)

{".X."}

Returns: 2

The middle cell is lower than its neighbors, so its height is 1. There are two variants of heights for the other cells: the left cell's height is 2 and the right cell's height is 3, or vice versa.

1)

{"X.",
 ".X"}

Returns: 0

No two neighboring cells can both be locally minimal, so the answer is 0.

2)

{"...",
 "..."}

Returns: 0

Each mountain map contains at least one locally minimal cell.

3)

{"X.",
 "..",
 ".X"}

Returns: 60

4)

{"X.X",
 "...",
 "X.X"}

Returns: 4800

5)

{"..X.."}

Returns: 6

6)

{"....X.",
 "......",
 ".X...X"}

Returns: 869490

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AzimuthMonitoring

Simple Math, String Manipulation

Used in:

SRM 360

Used as:

Division II Level One

Writer:

darnley

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8027

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10772&pm=8027

Problem Statement

A robot is moving in a plane following a set of instructions.

The following instructions are possible (quotes for clarity only):

"LEFT" - turn left 90 degrees

"RIGHT" - turn right 90 degrees

"TURN AROUND" - turn around (a 180 degree turn)

"LEFT X" - turn left X degrees, where X is a positive integer

"RIGHT X" - turn right X degrees, where X is a positive integer

"HALT" - stop executing instructions; further instructions are not executed

You are given a String[] containing the robot's instructions. Initially, the robot is facing north. Return the robot's final azimuth - the angle between north and the direction the robot is facing. Azimuth is always measured clockwise, and is a number between 0, inclusive, and 360, exclusive. For example, west corresponds to azimuth 270.

Definition

Class:	AzimuthMonitoring
Method:	getAzimuth
Parameters:	String[]
Returns:	int
Method signature:	int getAzimuth(String[] instructions)
(be sure your method is public)

Notes

-

Turning right corresponds to turning clockwise, turning left corresponds to turning counterclockwise.

Constraints

-

instructions will contain between 1 and 50 elements, inclusive.

-

Each element of instructions will be a valid instruction, as listed in the problem statement.

-

In an instruction of the form "LEFT X" or "RIGHT X", X will be an integer between 1 and 179, inclusive, with no leading zeroes.

Examples

0)

{"RIGHT"}

Returns: 90

Turning 90 degrees right changes the azimuth from 0 to 90.

1)

{"LEFT", "LEFT", "TURN AROUND"}

Returns: 0

After turning left, the robot is facing west (azimuth 270). After turning left again, the robot is facing south (azimuth 180). Finally, turning around makes the robot face north, azimuth 0.

2)

{"LEFT 5", "RIGHT 10", "LEFT 15", "RIGHT 20", "LEFT 25", "RIGHT 30", "LEFT 35", "RIGHT 40"}

Returns: 20

There are four pairs of instructions, each pair making the robot turn right 5 degrees.

3)

{"RIGHT 59", "RIGHT", "RIGHT", "HALT", "LEFT", "LEFT", "LEFT"}

Returns: 239

The fourth instruction is "HALT", thus none of the following "LEFT" instructions are executed.

4)

{"TURN AROUND", "HALT", "LEFT 5", "HALT", "LEFT 5", "HALT"}

Returns: 180

Note that there might be more then one "HALT" instruction.

5)

{"LEFT", "LEFT", "LEFT", "LEFT", "LEFT", "HALT"}

Returns: 270

After the first 4 turns the robot is facing north again, and the fifth instruction turns him west. The last instruction doesn't change anything.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TakeSubstringGame

Dynamic Programming, Simple Math

Used in:

SRM 360

Used as:

Division II Level Three

Writer:

darnley

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8026

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10772&pm=8026

Problem Statement

A positive integer n is written on a board, and two players take turns making moves.

In each move, the player selects a positive integer m that is a proper substring of the number currently written on the board. The number on the board is then decreased by m. A proper substring is a substring that doesn't equal the whole string.

For example, if a board contains the number 2309, a player can select m = 2, 3, 9, 23, 30, 230 or 309. Thus the possible moves from 2309 are 2000, 2079, 2279, 2286, 2300, 2306 and 2307.

A player who can't make a valid move loses the game.

Return the number m that the first player should select in his first move in order to win the game. If there are several such numbers, return the smallest among them. If the first player cannot win the game, return -1.

Definition

Class:	TakeSubstringGame
Method:	winningMove
Parameters:	int
Returns:	int
Method signature:	int winningMove(int n)
(be sure your method is public)

Constraints

-

n will be between 1 and 1000000, inclusive.

Examples

0)

Returns: -1

A single-digit number doesn't have a proper substring, so there is no valid move for the first player. Thus, the second player wins.

1)

Returns: 1

Subtracting 0 is not a valid move (m must be positive). So the only valid move is to subtract 1. Now the second player receives number 9 and can't make a move, providing victory for the first player.

2)

Returns: -1

Subtracting 7 will leave the second player with number 10, which is favorable for him, as shown in example above. Therefore the first player should subtract 1 and leave 16. Similarly, the second player will move on to 15. Three more such pairs of moves and the first player will be facing number 11. He will then subtract 1 and lose as shown above. Thus the second player wins.

3)

Returns: 9

The optimal first move is to subtract either 9 or 23, leaving 230 or 216. In case of a tie, you should return the smallest subtracted number which is 9.

4)

Returns: 66

Subtract 66 and leave your opponent with 500, which is apparently a losing position.

5)

Returns: -1

No first move is advantageous for the first player.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ImageReconstruction

Brute Force, Math, Search

Used in:

MM 20

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8024

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10860&pm=8024

Problem Statement

Your job is to unscramble a photograph in the fewest number of iterations possible.

The image is divided up into uniformly-sized square pieces and the pieces are shuffled. Your method will be provided with the size of each piece in pixels (the width and height are the same), the number of columns and rows of pieces in the image, and an array of pixel values. Each pixel value is encoded as an integer with eight bits per color component in RGB order, from most significant to least significant. You can decode each pixel with int red = (pixel >> 16), green = (pixel >> 8) & 0xff, blue = pixel & 0xff;.

Pieces are numbered from zero to rows*columns-1. Given a piece n, the image data for that piece can be found in row-major order in the pixels array starting at n*pieceSize*pieceSize. You can extract the pixel value at line y and column x of piece n with the expression pixels[n*pieceSize*pieceSize+y*pieceSize+x].

You are provided with a verify method which tells you which pieces are in the correct places in a guess. You pass it an array containing rows*columns integers, each of which represents a slot in the image in row major order so that the guess for the slot at row r and column c is at r*columns+c. Each slot should contain a piece number as described above. The method returns a corresponding array of integers. If the guess for a particular slot is correct, the corresponding return slot will be 1; otherwise, it will be 0. This means that it is possible to create the correct image without looking at the pixel data.

Your solution must return a guess in the same format as would be passed to the verify method. Your raw score for each case will be 1 plus the number of calls made to verify, or zero if your solution does not return the pieces in the correct order. Your aggregated score will be the sum of the lowest raw score received by any competitor on a case divided by your score on the case, excluding any cases in which you received a raw zero.

Visualizer

As in past contests, we have provided a Java visualization tool .

Definition

Class:	ImageReconstruction
Method:	reconstruct
Parameters:	int, int, int, int[]
Returns:	int[]
Method signature:	int[] reconstruct(int pieceSize, int columns, int rows, int[] pixels)
(be sure your method is public)

Notes

- You have 60 seconds per case.

- You can use a maximum of 512M of memory.

- Test cases are chosen using http://commons.wikimedia.org/wiki/Special:Random/Image . Images which are not primarily photographic or photo-realistic, such as line drawings, are discarded.

- Images are centered and cropped after any scaling to make each image dimension a multiple of the piece size.

- As is customary, row (or line) 0 is the top.

- verify does not require each slot to be filled with a unique piece number. You can pass all zeros, for example.

Constraints

- pieceSize will be 10, 20, or 30, chosen uniformly at random

- neither image dimension will be more than 500 pixels - larger images will be scaled so that the larger dimension becomes 500

Examples

0)

"e1,http://commons.wikimedia.org/wiki/Image:Chemical_Brothers_Live.jpg,20,25,18,23784"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:Chemical_Brothers_Live.jpg
  Piece Size: 20x20
     Columns: 25
        Rows: 18
        Seed: 23784

"

1)

"e2,http://commons.wikimedia.org/wiki/Image:Flickr_hellochris_202508906--In-N-Out_triple_cheeseburger_fries.jpg,30,16,12,27360"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:Flickr_hellochris_202508906--In-N-Out_triple_cheeseburger_fries.jpg
  Piece Size: 30x30
     Columns: 16
        Rows: 12
        Seed: 27360

"

2)

"e3,http://commons.wikimedia.org/wiki/Image:Tienen_Stadhuis.jpg,30,16,11,9981"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:Tienen_Stadhuis.jpg
  Piece Size: 30x30
     Columns: 16
        Rows: 11
        Seed: 9981

"

3)

"e4,http://commons.wikimedia.org/wiki/Image:Todaiji05s3200.jpg,30,11,16,6231"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:Todaiji05s3200.jpg
  Piece Size: 30x30
     Columns: 11
        Rows: 16
        Seed: 6231

"

4)

"e5,http://commons.wikimedia.org/wiki/Image:800px-Kalithea_Achaias.jpg,20,24,15,20710"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:800px-Kalithea_Achaias.jpg
  Piece Size: 20x20
     Columns: 24
        Rows: 15
        Seed: 20710

"

5)

"e6,http://commons.wikimedia.org/wiki/Image:Passower_Kirche.JPG,30,16,12,32464"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:Passower_Kirche.JPG
  Piece Size: 30x30
     Columns: 16
        Rows: 12
        Seed: 32464

"

6)

"e7,http://commons.wikimedia.org/wiki/Image:Wawer.jpg,30,12,16,10059"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:Wawer.jpg
  Piece Size: 30x30
     Columns: 12
        Rows: 16
        Seed: 10059

"

7)

"e8,http://commons.wikimedia.org/wiki/Image:Eisenbahnmarkthalle5_Detail_Berlin.JPG,10,32,50,21813"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:Eisenbahnmarkthalle5_Detail_Berlin.JPG
  Piece Size: 10x10
     Columns: 32
        Rows: 50
        Seed: 21813

"

8)

"e9,http://commons.wikimedia.org/wiki/Image:Teplice%2C_Prosetice%2C_14Tr_III.JPG,20,25,16,23572"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:Teplice%2C_Prosetice%2C_14Tr_III.JPG
  Piece Size: 20x20
     Columns: 25
        Rows: 16
        Seed: 23572

"

9)

"e10,http://commons.wikimedia.org/wiki/Image:Woody_London.jpg,20,24,15,26240"

Returns: 
"   Image URL: http://commons.wikimedia.org/wiki/Image:Woody_London.jpg
  Piece Size: 20x20
     Columns: 24
        Rows: 15
        Seed: 26240

"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MonkeyTreeDistance

Greedy, Math, Search

Used in:

TCHS SRM 42

Used as:

Division I Level Three

Writer:

mohamedafattah

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8020

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10790&pm=8020

Problem Statement

Monkeys live in trees. Their world can be abstracted as a two-dimensional grid with integer coordinates. The ground is the x-axis and trees are planted perpendicular to the x-axis (in both the positive and negative y directions). Monkeys can only move up and down trees, and horizontally on the ground. Therefore, the distance between two monkeys is calculated as follows:

- If the two monkeys have the same x coordinate (meaning that they're in the same tree), the distance between them is the absolute difference between their y coordinates. See the blue pair in the image below.

- Otherwise, the distance is the distance between monkey₁ and the ground + the distance between monkey₂ and the ground + the absolute difference between their x coordinates. See the green and purple pairs in the image below.

The government is about to make a bold decision that will make the lives of the monkeys easier. They will minimize the maximum distance between any pair of monkeys by moving the ground to a horizontal line y = N, where N is an integer. If the ground is already at the optimal position, it will not be moved.

You are given two int[]s x and y, The i^th monkey lives at (x[i], y[i]), where the absolute values of x[i] and y[i] are each less than or equal to 10⁹. Return the maximum distance between any pair of monkeys after the the ground is moved to the optimal position. The distance should be returned as a String with no leading zeros.

Definition

Class:	MonkeyTreeDistance
Method:	minimalMaximumDistance
Parameters:	int[], int[]
Returns:	String
Method signature:	String minimalMaximumDistance(int[] x, int[] y)
(be sure your method is public)

Constraints

-

x and y will each contain between 2 and 50 elements, inclusive.

-

x and y will contain the same number of elements.

-

Neither two monkeys will occupy the same position.

-

The absolute value of each element in x and y will be between 0 and 10^9, inclusive.

Examples

0)

{1, 4, 1}

{4, 1, 1}

Returns: "6"

1)

{-1, -2, -1, 0, 2}

{-1, 3, -3, 0, 3}

Returns: "9"

2)

{1, 1, 1, 1}

{1, 10, 100, 1000}

Returns: "999"

These four monkeys live in the same tree, so moving the ground will not affect any of the distances.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EvenOnes

Simple Math

Used in:

TCO08 Qual 3

Used as:

Division I Level Three

Writer:

ivan_metelsky

Testers:

PabloGilberto , vorthys , Olexiy , misof

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8018

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12058&pm=8018

Problem Statement

You are given a rectangular matrix with odd numbers of rows and columns. Each cell of the matrix contains either 0 or 1. In one move, you can select any one row or column of the matrix and replace all 0's with 1's and all 1's with 0's in that row/column. Your aim is to have an even number of 1's in each row and each column.

The elements of the String[] matrix correspond to the rows of the matrix. Return the minimal number of moves needed to achieve your aim, or -1 if it's impossible.

Definition

Class:	EvenOnes
Method:	minOperations
Parameters:	String[]
Returns:	int
Method signature:	int minOperations(String[] matrix)
(be sure your method is public)

Constraints

-

matrix will contain between 1 and 49 elements, inclusive.

-

Each element of matrix will contain between 1 and 49 characters, inclusive.

-

All elements in matrix will contain the same number of characters.

-

The number of elements in matrix will be odd.

-

The number of characters in each element of matrix will be odd.

-

Each character in each element of matrix will be '0' (zero) or '1' (one).

Examples

0)

{
 "111",
 "011",
 "001"
}

Returns: 2

We can first apply the operation to the middle row of the matrix, and then to the middle column.

1)

{
  "111",
  "111",
  "111",
  "111",
  "111"
}

Returns: 3

We must apply the operations either to all rows or to all columns. As the number of columns is less than the number of rows, we choose the second variant.

2)

{
  "00000",
  "00000",
  "00000"
}

Returns: 0

The matrix initially contains an even number of ones in each row and column, so we don't apply any operations.

3)

{
  "10101",
  "01010",
  "10101",
  "01010",
  "10101"
}

Returns: 5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DrawingMarbles

Math

Used in:

SRM 370

Used as:

Division I Level One , Division II Level Two

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8016

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10786&pm=8016

Problem Statement

A big box contains marbles of one or more colors. You're given a int[] colors, each element of which denotes the number of marbles there are of a particular color. You draw n marbles randomly from the box, leaving each marble outside the box after taking it. Return the probability that all marbles drawn will be the same color.

Definition

Class:	DrawingMarbles
Method:	sameColor
Parameters:	int[], int
Returns:	double
Method signature:	double sameColor(int[] colors, int n)
(be sure your method is public)

Notes

-

Every time we draw a marble, all marbles in the box are equally likely to be chosen.

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

colors will contain between 1 and 50 elements, inclusive.

-

Each element of colors will be between 1 and 50, inclusive.

-

n will be between 1 and the sum of all elements of colors, inclusive.

Examples

0)

{ 13 }

Returns: 1.0

All the marbles are the same color, so obviously all drawn marbles will be the same color too.

1)

{ 5, 7 }

Returns: 1.0

2)

{ 5, 6, 7 }

Returns: 0.3006535947712418

The probability that the first drawn marble will be of the color 0 is 5 / 18 (there are 5 marbles of color 0 out of 18). If the first drawn marble is of the color 0, then the probability that the second drawn marble will be of the color 0 is 4 / 17 (there are 4 marbles of color 0 left out of 17). So the probability that both drawn marbles will be of the color 0 is (5 / 18) * (4 / 17) = 0.0653594771... . Similarly, the probability that both drawn marbles will be of the color 1 is (6 / 18) * (5 / 17) = 0.0980392156..., and that both drawn marbles will be of the color 2 is (7 / 18) * (6 / 17) = 0.1372549019... . The answer is the sum of these 3 probabilities.

3)

{ 12, 2, 34, 13, 17 }

Returns: 0.035028830818304504

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CoolRectangles

Geometry, Graph Theory, Greedy, Math

Used in:

SRM 362

Used as:

Division I Level Three

Writer:

eleusive

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8015

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10775&pm=8015

Problem Statement

You're given several rectangles in the cartesian plane with sides parallel to the coordinate axes. A "cool rectangle" is a rectangle in the plane such that each of its edges completely lies on the edges of some input rectangles (these edges may overlap). You want to "compress" the input rectangles by shrinking them into cool rectangles (this will happen instantaneously).

To compress an input rectangle into a cool rectangle, the interior of the cool rectangle must be completely contained within the input rectangle. The interiors of the chosen cool rectangles must not overlap (though their edges may touch), and each cool rectangle may compress at most one input rectangle. Determine the smallest total area of cool rectangles required to shrink all the input rectangles, or return -1 if it is impossible.

The input rectangles will be described by int[]s x1, y1, x2, and y2, where (x1[i],y1[i]) and (x2[i],y2[i]) are opposite corners of the ith rectangle.

Definition

Class:	CoolRectangles
Method:	compress
Parameters:	int[], int[], int[], int[]
Returns:	int
Method signature:	int compress(int[] x1, int[] y1, int[] x2, int[] y2)
(be sure your method is public)

Constraints

-

x1 will contain between 1 and 30 elements, inclusive.

-

x1, y1, x2, and y2 will contain the same number of elements.

-

Each element of x1, y1, x2, and y2 will be between -10000 and 10000, inclusive.

-

For each rectangle, x1[i] < x2[i], and y1[i] < y2[i].

Examples

0)

{0,1,2}

{0,1,2}

{1,2,3}

{1,2,3}

Returns: 3

We have three non-overlapping squares, so the only cool rectangles are the input rectangles.

1)

{0,1}

{0,1}

{2,3}

{2,3}

Returns: -1

The overlapping squares generate 3 cool rectangles. However, there is no way to choose 2 non-overlapping cool rectangles to use.

2)

{1,0}

{1,2}

{3,4}

{4,3}

Returns: 3

These rectangles intersect in a way that allows for cool rectangles of area 1 and 2 to be used (although there are 11 available cool rectangles).

3)

{0,1,1}

{0,1,1}

{2,3,2}

{2,3,2}

Returns: -1

4)

{0,-1,-2,-3}

{0,1,2,3}

{1,2,3,4}

{7,6,5,4}

Returns: 4

5)

{1011,-647,134,-2009,875,819}

{189,-1504,1830,-1383,-319,825}

{2530,1930,620,-805,1821,1054}

{1419,1224,2476,203,1982,2943}

Returns: 2325650

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GridColoring

Math

Used in:

SRM 409

Used as:

Division I Level Three

Writer:

slex

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8012

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12181&pm=8012

Problem Statement

Given a rectangular grid where all the cells are initially white, you perform the following procedure K times:

Select a cell from the grid at random, and call it A
Select a cell from the grid at random, and call it B
Color all the cells in the rectangle bounded by A and B

Each cell is selected at random, with uniform distribution, and each selection is independent from the other selections. It's possible that A and B correspond to the same cell.

For example, the image below shows a 5x7 grid where the selected pairs could have been (row, column):

(0,1); (3,2)
(3,6); (4,0)
(0,6); (0,5)

Resulting in a grid with 22 colored cells and 13 white cells.

You are given ints rows and cols, the dimensions of the grid. Return the expected number of colored cells after K steps.

Definition

Class:	GridColoring
Method:	area
Parameters:	int, int, int
Returns:	double
Method signature:	double area(int K, int rows, int cols)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

K will be between 0 and 100, inclusive.

-

rows will be between 1 and 1000, inclusive.

-

cols will be between 1 and 1000, inclusive.

Examples

0)

Returns: 1.5

The grid has two cells. The probability that both of them will get colored is 0.5, and the probability that only one of them will get colored is 0.5. So the expected value is 0.5 * 2 + 0.5 * 1 = 1.5.

1)

Returns: 1.875

With the same grid as in the previous example, but two selections, the expected value rises to 1.875.

2)

Returns: 2.25

3)

Returns: 19.11917924647044

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WhiteHats

Brute Force, Simple Math, Simple Search, Iteration

Used in:

SRM 361

Used as:

Division I Level One , Division II Level Two

Writer:

slex

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8010

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10773&pm=8010

Problem Statement

There is a number of people in a room, and each of them wears a hat which is either black or white. Every person counts the number of other people wearing white hats. You are given a int[] count, the i-th element of which is the number counted by the i-th person. Return the total number of people wearing white hats, or -1 if count doesn't correspond to a valid situation.

Definition

Class:	WhiteHats
Method:	whiteNumber
Parameters:	int[]
Returns:	int
Method signature:	int whiteNumber(int[] count)
(be sure your method is public)

Constraints

-

count will contain between 2 and 50 elements, inclusive.

-

Each element of count will be between 0 and 50, inclusive.

Examples

0)

{2,1,1}

Returns: 2

The first person wears a black hat and sees two people wearing white hats. Each person wearing a white hat sees only one other white hat in the room.

1)

{2,2,2}

Returns: 3

Everyone wears a white hat here.

2)

{0,0}

Returns: 0

Black hats only.

3)

{1,1,1,2}

Returns: -1

4)

{10,10}

Returns: -1

Now that's interesting. There are only two people in the room, yet each of them counted 10 others.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ReverseDistance

Greedy, Math, Search

Used in:

SRM 361

Used as:

Division I Level Two

Writer:

slex

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8009

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10773&pm=8009

Problem Statement

To obtain the reverse of a number, write it backwards from right to left. For example, the reverse of 1234 is 4321, and the reverse of 100 is 1 (leading zeroes are always ignored). Return the smallest non-negative number x, such that the difference x - reverse(x) is equal to difference. If no such number exists, return "NONE" (quotes for clarity) instead.

Definition

Class:	ReverseDistance
Method:	find
Parameters:	int
Returns:	String
Method signature:	String find(int difference)
(be sure your method is public)

Constraints

-

difference will be between 1 and 1000000, inclusive.

Examples

0)

Returns: "20"

20 - 2 = 18.

18 can be also achieved in other ways like 42 - 24, but 20 is the smallest possible number.

1)

Returns: "NONE"

It's impossible to find a number with a difference of 15.

2)

Returns: "5080"

5080 - 805 = 4275

3)

Returns: "101001"

101001 - 100101 = 900

4)

Returns: "100990"

100990 - 99001 = 1989

5)

Returns: "860300"

860300 - 3068 = 857232

6)

Returns: "50"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SquareFreeNumbers

Math

Used in:

TCO09 Qual 1

Used as:

Division I Level Two

Writer:

FedorTsarev

Testers:

PabloGilberto , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8004

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13742&pm=8004

Problem Statement

A number is called square-free if it is not divisible by a perfect square which is greater than one. A perfect square is the square of an integer. Return the number of square-free numbers between min and max, inclusive.

Definition

Class:	SquareFreeNumbers
Method:	getCount
Parameters:	long, long
Returns:	int
Method signature:	int getCount(long min, long max)
(be sure your method is public)

Constraints

-

min will be between 1 and 1,000,000,000,000, inclusive.

-

max will be between min and (min + 1,000,000), inclusive.

Examples

0)

Returns: 7

Numbers 4, 8 and 9 are not square-free.

1)

Returns: 1

min and max can be equal.

2)

Returns: 608

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BattleDice

Math, String Parsing

Used in:

TCO08 Round 3

Used as:

Division I Level Two

Writer:

legakis

Testers:

PabloGilberto , vorthys , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7992

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12013&pm=7992

Problem Statement

BattleDice is a two-player game where each person uses his own N-sided die. The two players roll their dice, and whoever's die shows the highest number wins. In the event of a tie, they continue rolling until one player wins. You and your opponent start with a total of 3 dice. Your opponent selects one of the three, and then you select one of the remaining two.

To make the game more interesting, you and your opponent begin with only two of the three dice. Given these two, determine the third die you would like to construct and add to the original two in order to maximize your probability of winning the game. Assume that your opponent will play optimally, making the selection that will give him the highest chance of winning.

The two dice will be given as int[]s die1 and die2. The numbers on each side of the dice will be between 1 and range, inclusive, and the numbers on the third die you are constructing must also be in this range. The two given dice will have the same number of sides, and the die you are constructing must have the same number of sides as the first two. Return your die as a int[], sorted in ascending order.

Neither of the two given dice will have the same number on every side, but your third die may.

There may be more than one third die that will give you the same optimal chance of winning the game. In this case, sort the values on each die in ascending order, find the first pair of corresponding values that differ, and prefer the die with the smaller of those two values.

For example, if range = 6 and the first two dice are:


    die1 = { 2, 2, 5 }
    die2 = { 2, 3, 3 }

you would choose to construct:


    die3 = { 1, 3, 4 }

If your opponent selects die1, you could choose die2 to give yourself a 4/7 chance of winning. If your opponent selects die2, you could choose die3 to give yourself a 4/7 chance of winning. If your opponent selects die3, you could choose die1 to give yourself a 5/9 chance of winning. Given these three choices your opponent will select die3, and you will have a 5/9 chance of winning. No other third die will give you a higher chance of winning. The die { 1, 4, 4 } also guarantees you a 5/9 chance of winning, but according to the tiebreaking rules { 1, 3, 4 } is the correct answer.

Definition

Class:	BattleDice
Method:	die3
Parameters:	int[], int[], int
Returns:	int[]
Method signature:	int[] die3(int[] die1, int[] die2, int range)
(be sure your method is public)

Notes

-

The dice used are fair dice, which means that every roll will result in each side with a 1/N probability.

-

Ignore the practical difficulties of constructing a die with an odd number of sides.

Constraints

-

die1 and die2 will each contain between 2 and 10 elements, inclusive.

-

die1 and die2 will have the same number of elements.

-

range will be betwen 2 and 15, inclusive.

-

Each element of die1 and die2 will be between 1 and range, inclusive.

-

At least two elements of die1 will be distinct.

-

At least two elements of die2 will be distinct.

Examples

0)

{ 2, 2, 5 }

{ 2, 3, 3 }

Returns: {1, 3, 4 }

This is the example from the problem statement.

1)

{ 3, 5, 6 }

{ 6, 3, 5 }

Returns: {1, 1, 1 }

If the first 2 dice are the same, the best you can do is end up with a 50% chance of winning. If you add a die better than the first two, your opponent will select it. Otherwise, both you and your opponent will chose one of the first two. Following the tiebreaking rules, the correct answer is therefore the smallest possible die, with a 1 on each side.

2)

{ 1, 3, 8, 10 }

{ 1, 5, 6, 12 }

Returns: {1, 6, 6, 7 }

3)

{ 2, 3, 4 }

{ 5, 6, 7 }

Returns: {1, 6, 8 }

die2 beats die1 every time. The best you can do is construct a third die that beats die2 50% of the time.

4)

{ 6, 6, 8, 9, 13, 13, 15 }

{ 3, 5, 8, 10, 13, 14, 14 }

Returns: {1, 7, 9, 10, 13, 13, 14 }

5)

{ 1, 6, 5, 1, 5 }

{ 3, 3, 7, 7, 1 }

Returns: {4, 4, 4, 4, 4 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DogAndRabbit

Math

Used in:

TCHS SRM 33

Used as:

Division I Level Two

Writer:

mateuszek

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7968

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10767&pm=7968

Problem Statement

A dog is standing at point (0, 0), and a rabbit is standing at point (distanceToRabbit, 0). The rabbit starts running in a straight line toward his home, which is located at (distanceToHome + distanceToRabbit, 0). At the same time, the dog starts running in a straight line toward the rabbit.

The rabbit runs at a constant speed of rabbitSpeed units per second. This means that in t seconds, he travels rabbitSpeed * t units. The dog starts running at an initial speed of 0 and a constant acceleration of dogAcceleration units per second². This means that in t seconds, he travels dogAcceleration * t² / 2 units.

Return "YES" if the dog can catch the rabbit before the rabbit enters its home, or "NO" otherwise (all quotes for clarity). The dog can catch the rabbit if there exists a point (x, 0) such that x <= distanceToHome + distanceToRabbit, and both the dog and the rabbit are at that same point at the same time.

Definition

Class:	DogAndRabbit
Method:	willCatch
Parameters:	int, int, int, int
Returns:	String
Method signature:	String willCatch(int distanceToRabbit, int distanceToHome, int rabbitSpeed, int dogAcceleration)
(be sure your method is public)

Constraints

-

distanceToRabbit will be between 0 and 1000000, inclusive.

-

distanceToHome will be between 0 and 1000000, inclusive.

-

distanceToRabbit and distanceToHome won't both be equal to 0.

-

rabbitSpeed will be between 0 and 1000000, inclusive.

-

dogAcceleration will be between 0 and 1000000, inclusive.

Examples

0)

Returns: "YES"

The dog will catch the rabbit about 62 units away from the rabbit's home.

1)

Returns: "NO"

Here the dog is not so interested in the rabbit, so it stays in place.

2)

Returns: "YES"

The dog got the rabbit already.

3)

Returns: "YES"

The poor rabbit sleeps in front of his house, not aware of the dog.

4)

Returns: "NO"

The dog is too far away from the rabbit to catch it.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EscapeArtist

Brute Force, Dynamic Programming, Graph Theory, Math, Recursion, Search

Used in:

SRM 386

Used as:

Division I Level Three

Writer:

eleusive

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7953

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11120&pm=7953

Problem Statement

You're trapped inside a facility that contains several rooms connected by corridors. You're currently located in room start and you wish to reach the finish using the least amount of time as possible. Each corridor takes one second to travel through.

Your task is complicated by the fact that there are several agents located in various rooms. These agents wish to capture you, but each one has a particular destination, as they each have different intelligence suggesting that you will head towards their destination. Like yourself, these agents will also reach their target room in the least possible amount of time. The agents begin moving at the same time as you do. If there are multiple shortest paths that an agent may use, you may assume each such path is equally likely as his choice. Once an agent reaches his goal, he will stay there indefinitely. Note that while you are aware of each agent's start and target rooms, you will be unaware of the agent's movements as you move through the facility.

As you wish to dodge capture as well as reach the exit as quickly as possible, you will use the following strategy. Each second you choose the way which allows you to reach the exit as quickly as possible (see example 6 for clarification). If there are multiple ways to do so, you choose the corridor that minimizes the probability of being captured from that point on. As soon as you reach the exit room, you leave the facility and cannot be captured. However, you may be captured the moment that you reach the exit room (see example 7).

There are two ways that you can be captured by an agent.

1) You travel through a corridor at the same time an agent does (you can be traversing the corridor in either the same direction or the opposite direction).

2) You're in a room at the same time as an agent.

The facility is described by a String[] corridors. The jth character of the ith element of corridors will be a '1' if there is a corridor between rooms i and j, and '0' otherwise. Each element of agentStart and agentTarget represents the start and target rooms, respectively, of an agent.

Given this information, return the probability that you will be captured by an agent if you follow the described strategy.

Definition

Class:	EscapeArtist
Method:	bestRoute
Parameters:	String[], int[], int[], int, int
Returns:	double
Method signature:	double bestRoute(String[] corridors, int[] agentStart, int[] agentTarget, int start, int finish)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

corridors will contain between 2 and 25 elements, inclusive.

-

Each element of corridors will contain exactly N characters, where N is the number of elements in corridors.

-

Each character in corridors will be either a '0' (zero) or '1' (one).

-

The jth character of the ith element of corridors will be the same as the ith character of the jth element of corridors.

-

The ith character of the ith element of corridors will be '0'.

-

start and finish will each be between 0 and N-1, inclusive, where N is the number of elements in corridors.

-

start will be different from finish.

-

agentStart and agentTarget will each contain between 1 and 10 elements, inclusive.

-

agentStart and agentTarget will contain the same number of elements.

-

Each agent's starting room will be different from his target room.

-

No agent will start in the same room as you.

-

Each element of agentStart and agentTarget will be between 0 and N-1, inclusive, where N is the number of elements in corridors.

-

There will be at least one path between each pair of rooms in the facility.

Examples

0)

{
"0100",
"1011",
"0100",
"0100"
}

{3}

{1}

Returns: 1.0

    3
    |
    |
0---1---2

The agent will always arrive at room 1 at the same time as you do, so there is no way to avoid capture.

1)

{
"01000",
"10110",
"01000",
"01001",
"00010"
}

{4}

{1}

Returns: 0.0

    2
    |
    |
0---1---3---4

You will reach room 1 before the agent does, so you will avoid capture.

2)

{
"010000",
"101011",
"010111",
"001000",
"011000",
"011000"
}

{4}

{5}

Returns: 0.5

     4
    / \
0--1---2--3
    \ /
     5

Your path must be 0-1-2-3. The agent is equally likely to take the paths 4-1-5 or 4-2-5. If he takes the first path, you will be captured in room 1. However, if he takes the second path, you will escape.

3)

{
"010000",
"101001",
"010110",
"001000",
"001000",
"010000"
}

{4}

{5}

Returns: 1.0

    5   4
    |   |
    |   |
0---1---2---3

You will be travelling through the corridor between rooms 1 and 2 at the same time the agent travels through the same corridor in the opposite direction.

4)

{
"01100",
"10011",
"10010",
"01100",
"01000"
}

{4,3}

{1,0}

Returns: 0.5

Here you can choose between two paths. If you take path 0-1-3, you will always be captured by the first agent at room 1. However, if you take path 0-2-3, there is a 50% chance that you will be captured in room 2, depending on which path the second agent takes.

5)

{
"0100",
"1010",
"0101",
"0010"
}

{3}

{2}

Returns: 1.0

0--1--2--3

The agent reaches room 2 before you, but stays there indefinitely. You will then be captured as soon as you enter room 2.

6)

{"0101", "1010", "0101", "1010"}

{1}

{0}

Returns: 1.0

0 -- 1
|    | 
|    |
3----2

The longer path (0 -> 3 -> 2 -> 1) is absolutely safe, but you must take the shortest one (0 --> 1).

7)

{"011", "101", "110"}

{0}

{1}

Returns: 1.0

You are caught at the moment you enter room 1.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MissingDigits

Brute Force, Math

Used in:

TCHS SRM 51

Used as:

Division I Level One

Writer:

Ishan

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7920

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13484&pm=7920

Problem Statement

You are opening a new hotel and are in the process of numbering the rooms. Being a superstitious person, you don't want to allow certain numbers. You are given an int[] notAllowed containing an encoded list of forbidden sequences. The i^th forbidden sequence (where i is a 0-based index) is the concatenation of decimal representations of i and notAllowed[i] (both with no extra leading zeros). For example, if the 0^th element of notAllowed is 33, then "033" is a forbidden sequence. A room number is not allowed if its decimal string representation, with no extra leading zeroes, contains any of the forbidden sequences as a substring. Given an int roomNumber, return "YES" if the room number is allowed, and "NO" otherwise (all quotes for clarity).

Definition

Class:	MissingDigits
Method:	isAllowed
Parameters:	int[], int
Returns:	String
Method signature:	String isAllowed(int[] notAllowed, int roomNumber)
(be sure your method is public)

Constraints

-

notAllowed will contain between 0 and 50 elements, inclusive.

-

Each element of notAllowed will be between 0 and 10000000, inclusive.

-

roomNumber will be between 0 and 10000000, inclusive.

Examples

0)

{1}

Returns: "NO"

Since element 0 of notAllowed is 1, 01 is forbidden. Hence 101 is not a valid room number.

1)

{1,33,7}

Returns: "NO"

Element 1 of notAllowed is 33, so 133 is forbidden.

2)

{1,32,67}

Returns: "NO"

Element 2 of notAllowed is 67, so 267 is forbidden.

3)

{1,33,7}

Returns: "YES"

4)

{0}

Returns: "YES"

"00" is forbidden, but single 0 is allowed.

5)

{1245,2481,1271,1463,557,1544,1462,1710,988,2167,
 1013,736,1816,702,388,207,333,27,349,1659,1818,
 1227,1893,1916,1430,1630,893,651,2142,987,631,
 2290,1267,656,1912,343,1339,1938,753,2150,576,
 76,801,1270,2266,2415,188,1595,1749,2019}

Returns: "YES"

6)

{1245,2481,1271,1463,557,1544,1462,1710,988,2167,
 1013,736,1816,702,388,207,333,27,349,1659,1818,
 1227,1893,1916,1430,1630,893,651,2142,987,631,
 2290,1267,656,1912,343,1339,1938,753,2150,576,
 76,801,1270,2266,2415,188,1595,1749,2019}

Returns: "NO"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AverageProblem

Brute Force, Simple Math, Simple Search, Iteration

Used in:

SRM 356

Used as:

Division I Level One , Division II Level Two

Writer:

Pawa

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7901

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10765&pm=7901

Problem Statement

You are given the results of a sociological survey containing several questions. Each participant was required to answer each question with an integer between 0 and 10, inclusive. You are given the average answer for each question, but the decimal portion of each average is truncated after the first three digits. For example, if there were three participants and their answers to a particular question were 4, 6 and 10, the average for that question would be given to you as 6.666.

You are given a String[] marks. Each element of marks is a single space delimited list of numbers. Each number in marks is the average answer for a survey question. Return the minimum possible number of participants that could have taken this survey.

Definition

Class:	AverageProblem
Method:	numberOfParticipants
Parameters:	String[]
Returns:	int
Method signature:	int numberOfParticipants(String[] marks)
(be sure your method is public)

Constraints

-

marks will contain between 1 and 50 elements, inclusive.

-

Each element of marks will contain between 5 and 50 characters, inclusive.

-

Each element of marks will be a single space separated list of numbers, where each number is between 0 and 10, inclusive, contains no extra leading zeroes, and contains exactly one decimal point followed by exactly 3 digits.

-

marks will contain between 1 and 50 numbers, inclusive.

Examples

0)

{"0.000"}

Returns: 1

There will always be at least one participant. In this case, the smallest number of participants that could have produced this result is 1.

1)

{"0.500 0.250", "0.125"}

Returns: 8

2)

{"0.500","0.300"}

Returns: 10

3)

{"0.500","0.301"}

Returns: 106

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ValueAddedTax

Simple Math

Used in:

SRM 355

Used as:

Division II Level One

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7894

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10712&pm=7894

Problem Statement

In Russia, the Value Added Tax is 18% for almost all goods, with the exception of certain food items, which have a Value Added Tax of only 10%.

You are given a String product, the name of a product, and an int price, the price of the product before tax. You are also given a String[] food, each element of which is the name of a food product. If the given product is an element in food, it is a food item (and thus subject to 10% tax), and otherwise, it is a non-food item (and thus subject to 18% tax). Return the price of the product after tax has been added.

Definition

Class:	ValueAddedTax
Method:	calculateFinalPrice
Parameters:	String, int, String[]
Returns:	double
Method signature:	double calculateFinalPrice(String product, int price, String[] food)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

product will contain between 1 and 50 characters, inclusive.

-

Each character in product will be a lowercase letter ('a'-'z').

-

price will be between 1 and 1000, inclusive.

-

food will contain between 1 and 50 elements, inclusive.

-

Each element of food will contain between 1 and 50 characters, inclusive.

-

Each character in each element of food will be a lowercase letter ('a'-'z').

-

All elements of food will be distinct.

Examples

0)

"milk"

{"bread", "butter", "milk"}

Returns: 1.1

1)

"car"

{"bread", "butter", "milk"}

Returns: 118.0

2)

"abc"

{"a", "b", "c"}

Returns: 67.25999999999999

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CrazyComponents

Dynamic Programming, Math, String Parsing

Used in:

SRM 363

Used as:

Division II Level Three

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7884

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10777&pm=7884

Problem Statement

We are building an application using different types of components. Each time we want to install a new component, we choose one randomly (yes, it is crazy). Each of the n types of components has an equal probability 1/n of being chosen. There is an infinite number of each type.

Each time we choose a component instance, we first determine if it can be installed. Some components may require one or more other types of components to already be installed. If all the required components are not currently installed, we cannot install the chosen component.

If the chosen component can be installed, we then decide whether or not to actually install it. Each component has an associated income and expense. The expense is the amount of money we must spend to install the component, and the income is the amount of money the installed component is expected to give us. Our goal is to maximize the expected total profit (all our income minus all our expenses). If we decide to install a chosen component, we must install it immediately (i.e., we can't put it aside and use it later).

Multiple instances of the same component type can be installed in the application. Each instance costs the same amount of money and has the same expected income. Note that once all the requirements for a component have been met, we may install multiple instances of that component type. For example, consider the case where component type 5 requires component type 3, and a single instance of component type 3 is currently installed. Every time we choose component type 5 from now on, we are allowed to install an instance of it. We do not require an instance of component type 3 for each instance of component type 5.

You are given an int k, the number of times we randomly choose a new component. You are also given a String[] components, where the i-th element (0-indexed) contains the requirements for component type i. Each element is a single space separated list of the component's required component types. You are given int[]s income and expense, where the i-th elements are the income and expense, respectively, associated with component type i. We will use an optimal strategy and always try to maximize our expected total profit when deciding whether or not to install chosen components (so, if installing a component lowers our expected total profit, we don't install it). Return our expected total profit.

Definition

Class:	CrazyComponents
Method:	expectedProfit
Parameters:	int, String[], int[], int[]
Returns:	double
Method signature:	double expectedProfit(int k, String[] components, int[] income, int[] expense)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

k will be between 1 and 50, inclusive.

-

components will contain between 1 and 15 elements, inclusive.

-

components, income and expense will each contain the same number of elements.

-

Each element of components will be a single space separated list of integers, without leading or trailing spaces.

-

Each integer in each element of components will be between 0 and n-1, inclusive, with no extra leading zeroes, where n is the number of elements in components.

-

The list described by element i of components will not contain i.

-

In each element of components, integers will be distinct.

-

Each element of income will be between 0 and 1000000, inclusive.

-

Each element of expense will be between 0 and 1000000, inclusive.

Examples

0)

{ "", "" }

{ 1, 2 }

{ 0, 0 }

Returns: 1.5

Here, we choose a component only once. If we choose component type 0, our profit is 1 - 0 = 1. If we choose component type 1, our profit is 2 - 0 = 2. Since each type is equally likely to be chosen, the expected profit is 0.5 * 1 + 0.5 * 2.

1)

{ "1", "" }

{ 10, 0 }

{ 0, 2 }

Returns: 1.5

If we pick component 0 in the first turn (1/2 probability), we won't be able to install it. Whichever component we pick after that, it's better not to install it and settle for 0 profit. On the other hand, if we pick component 1 in the first turn (1/2 probability), we should install it even though the net is -2. If on the second try we pick component 1 again (1/4 total probability), we don't install it and end up losing the 2 we already spent. However, if we pick component 0 on the second try (1/4 total probability), we can install it and earn 10 for a total profit of 8. The expected profit is 1/4 * (-2) + 1/4 * 8 = 1.5.

2)

{ "1 2", "", "" }

{ 100, 0, 0 }

{ 0, 0, 0 }

Returns: 7.407407407407408

Component 0 (the only one that makes a profit) requires components 1 and 2 to be already installed, so if we draw it in the first or in the second turn, we won't be able to install it. It is only possible to install it in the 3rd turn, supposing that in the 1st and 2nd turns we drew components 1 and 2. The probability that we will have components 1 and 2 installed after the 2nd turn is 2/3 * 1/3 = 2/9. The probability of then picking component 0 is 1/3, so our expected profit equals 2/9 * 1/3 * 100 = 7.407... .

3)

{ "1", "2", "0", "" }

{ 4, 5, 6, 7 }

{ 0, 0, 0, 8 }

Returns: 0.0

4)

{ "", "", "", "", "", "", "", "", "", "" }

{ 142352, 2342, 34534, 2344, 12346, 7589, 79872, 973453, 96233, 34567 }

{ 12432, 2345, 3678, 456, 345, 457, 56758, 4564, 774, 34567 }

Returns: 1269258.9999999998

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SumOfSelectedCells

Math

Used in:

SRM 360

Used as:

Division I Level One , Division II Level Two

Writer:

darnley

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7875

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10772&pm=7875

Problem Statement

There is a rectangular table with an integer written in each cell.

Later, Jessie will come and select some cells in such a way that each row and each column contains no more than one selected cell. She will always select the maximum possible number of cells. However, there might be several possible selections of that size.

Larry suggested a hypothesis: "No matter what maximum selection Jessie choses, the sum of the numbers in the selected cells will always be the same."

Given a String[] table, check whether Larry's hypothesis is correct and return "CORRECT" or "INCORRECT" (quotes for clarity only).

Definition

Class:	SumOfSelectedCells
Method:	hypothesis
Parameters:	String[]
Returns:	String
Method signature:	String hypothesis(String[] table)
(be sure your method is public)

Constraints

-

table will contain between 1 and 20 elements, inclusive.

-

Each element of table will be contain between 1 and 50 characters, inclusive.

-

Each element of table will be a space-separated list of integers.

-

Each element of table will contain the same number of entries.

-

Each element of table will contain between 1 and 20 entries, inclusive.

-

All numbers in the table will be between 1 and 50, inclusive, with no leading zeroes.

Examples

0)

{"5 6 6"}

Returns: "INCORRECT"

Jessie will select exactly one cell. The sum will be either 5 or 6.

1)

{"11 12 13 14",
 "21 22 23 24",
 "31 32 33 34",
 "41 42 43 44"}

Returns: "CORRECT"

There are 4! = 24 possible selections for Jessie, but it can be shown that each of them gives the sum of 1 + 2 + 3 + 4 + 10 + 20 + 30 + 40 = 110.

2)

{"3 7",
 "3 7",
 "3 7"}

Returns: "CORRECT"

Jessie will select exactly one 3 and exactly one 7 giving a total of 10.

3)

{"1 2 3",
 "4 5 6",
 "9 8 7"}

Returns: "INCORRECT"

Jessie can get 13 (2 + 4 + 7) or 15 (1 + 6 + 8) or 17 (3 + 5 + 9).

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MirrorNumber

Recursion, Search, Simple Math

Used in:

SRM 363

Used as:

Division I Level Two

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7869

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10777&pm=7869

Problem Statement

A number is written on a traditional digital display. If the display looks identical when flipped horizontally (i.e., around a vertical axis), the number is called a "mirror number". On a digital display, the digits 0, 1 and 8 are symmetrical, and the digits 2 and 5 are mirror images of each other. No other digits make sense when flipped horizontally. For example, 0, 101 and 1521 are all mirror numbers, while 1221 and 1010 are not (see images below). Given two Strings A and B, both representing integers with no extra leading zeroes, return the number of mirror numbers between A and B, inclusive.

Mirror numbers (both remain unchanged after mirroring):

Not mirror numbers (1221 mirrors to 1551, and 1010 mirrors to 0101):

Definition

Class:	MirrorNumber
Method:	count
Parameters:	String, String
Returns:	int
Method signature:	int count(String A, String B)
(be sure your method is public)

Constraints

-

A will represent an integer between 0 and 10^18, inclusive.

-

B will represent an integer between A and 10^18, inclusive.

-

Both A and B will have no extra leading zeros.

Examples

0)

"0"

"10"

Returns: 3

There is only 0, 1 and 8 here.

1)

"0"

"100"

Returns: 7

Few more: 11, 25, 52, 88.

2)

"143"

"23543"

Returns: 54

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HandsShaking

Advanced Math, Dynamic Programming

Used in:

SRM 363

Used as:

Division I Level One , Division II Level Two

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7868

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10777&pm=7868

Problem Statement

Consider a meeting of n businessmen sitting around a circular table. To start the meeting, they must shake hands. Each businessman shakes the hand of exactly one other businessman. All handshakes happen simultaneously. We say that the shake is perfect if no arms cross each other. Given an int n, return the number of perfect shakes that exist for n businessmen. See examples for further clarification.

Definition

Class:	HandsShaking
Method:	countPerfect
Parameters:	int
Returns:	long
Method signature:	long countPerfect(int n)
(be sure your method is public)

Notes

-

Businessmen are distinguishable. Rotating a perfect shake can yield a different perfect shake (see example 1).

Constraints

-

n will be between 2 and 50, inclusive.

-

n will be even.

Examples

0)

Returns: 1

Two businessmen have only one possibility - just to shake each other's hand.

1)

Returns: 2

Two out of three possible shakes are perfect.

2)

Returns: 14

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AlmostPrime

Math, Simple Search, Iteration

Used in:

TCHS SRM 33

Used as:

Division I Level Three

Writer:

mateuszek

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7867

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10767&pm=7867

Problem Statement

A number is called "almost prime" if it is a power of a prime number, but is not a prime number itself. Note that 1 is not almost prime. You are given two Strings A and B, both representing integers (without leading zeros). Return the number of integers between A and B, inclusive, that are almost prime.

Definition

Class:	AlmostPrime
Method:	count
Parameters:	String, String
Returns:	int
Method signature:	int count(String A, String B)
(be sure your method is public)

Constraints

-

A will represent an integer between 1 and 10^14, inclusive.

-

B will represent an integer between A and 10^14, inclusive.

-

Both A and B will have no leading zeros.

Examples

0)

"1"

"10"

Returns: 3

4, 8 and 9 are almost prime here.

1)

"1"

"1000"

Returns: 25

2)

"5324"

"894739"

Returns: 183

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumberOfDivisors

Dynamic Programming, Math

Used in:

SRM 370

Used as:

Division I Level Three

Writer:

mateuszek

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7863

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10786&pm=7863

Problem Statement

Return the smallest positive integer that has exactly k divisors. If this number is greater than 10¹⁸, return -1 instead.

Definition

Class:	NumberOfDivisors
Method:	smallestNumber
Parameters:	int
Returns:	long
Method signature:	long smallestNumber(int k)
(be sure your method is public)

Constraints

-

k will be between 1 and 50000, inclusive.

Examples

0)

Returns: 1

1)

Returns: 2

2)

Returns: 12

The 6 divisors of 12 are: 1, 2, 3, 4, 6, 12.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

UTF8Decode

Encryption/Compression, Simple Search, Iteration

Used in:

SRM 359

Used as:

Division II Level Three

Writer:

bmerry

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7862

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10770&pm=7862

Problem Statement

Unicode is a standardized set of characters which includes the alphabets from many languages as well as mathematical and other symbols. UTF-8 is a scheme to encode Unicode characters into a byte stream. It has a number of nice features, most importantly backwards compatibility with ASCII, but the encoding is a little complicated. Each Unicode character is represented by between 1 and 4 bytes, inclusive.

For this problem, you will be given a sequence of byte values representing a UTF-8 encoded string, and must decode it to obtain the Unicode character values. However, the string is transmitted by the very unreliable RFC 1149 protocol, so it may contain some extra bytes. RFC 1149 is also very slow, so you must decide whether to accept or reject each byte as soon as it is received, without knowing what the following bytes are, or even if there are any. You should accept a byte if and only if the accepted bytes would then form the start of some UTF-8 encoded string. If you reach the end of the string and have accepted an incomplete character (e.g., only 2 bytes of a 3-byte character), it should also be discarded.

UTF-8 is used to represent Unicode characters between 0 and 1114111 (10FFFF in hex), inclusive. The following pseudo-code will convert a Unicode character into UTF-8 encoding (the output function appends one byte to the encoded string):

getbits(int value, int firstbit, int numbits):
  return (value SHIFTRIGHT firstbit) MOD (1 SHIFTLEFT numbits)

convert(int character):
  if character <= 0x7F:
    output(character)
  else if character <= 0x7FF:
    output(0xC0 + getbits(character, 6, 5))
    output(0x80 + getbits(character, 0, 6))
  else if character <= 0xFFFF:
    output(0xE0 + getbits(character, 12, 4))
    output(0x80 + getbits(character, 6, 6))
    output(0x80 + getbits(character, 0, 6))
  else if character <= 0x10FFFF:
    output(0xF0 + getbits(character, 18, 3))
    output(0x80 + getbits(character, 12, 6))
    output(0x80 + getbits(character, 6, 6))
    output(0x80 + getbits(character, 0, 6))
  else:
    abort - character is out of range

Write a class that accepts a sequence of bytes, in the order that they are received, and returns the sequence of Unicode character values decoded according to the rules above.

Definition

Class:	UTF8Decode
Method:	decodeString
Parameters:	int[]
Returns:	int[]
Method signature:	int[] decodeString(int[] bytes)
(be sure your method is public)

Notes

-

The UTF-8 representation of a character is never a substring of the UTF-8 representation of any other character.

-

Different implementations of UTF-8 may allow characters to be encoded in more than one way or may allow characters beyond the range specified here. For this problem, you should consider a byte sequence to be legal if and only if it could have been produced by the pseudo-code above.

Constraints

-

bytes will contain between 0 and 50 elements, inclusive.

-

Each element of bytes wil be between 0 and 255, inclusive.

Examples

0)

{10,
 207, 168,
 226, 156, 144,
 240, 152, 154, 160}

Returns: {10, 1000, 10000, 100000 }

One case for each possible encoding length.

1)

{10, 255,
 207, 17, 168, 193,
 226, 156, 144,
 240, 143, 152, 154, 160,
 240, 152, 154}

Returns: {10, 1000, 10000, 100000 }

The same as the previous case, but with some invalid bytes added.

2)

{191, 192, 193, 245, 255, 128, 129, 130, 189, 190, 191, 1}

Returns: {1 }

None of these bytes except the last can start a UTF-8 encoded character.

3)

{76, 95, 228, 250, 1, 100, 167, 59, 165, 27, 87, 32, 49, 22, 100, 236, 1,
 111, 209, 100, 155, 35, 156, 47, 135, 56, 114, 131, 32, 73, 24, 104, 92,
 221, 107, 12, 222, 60, 24, 113, 130, 217, 180, 144, 106, 136, 137, 234, 24, 173}

Returns: 
{76, 95, 18917, 27, 87, 32, 49, 22, 100, 50908, 47, 56, 114, 32, 73, 24, 104, 92, 1858, 1652, 106 }

4)

{240, 1}

Returns: { }

240 is valid as the first byte of a four-byte character, so it must be accepted. Since we don't have enough bytes to complete this character, the output is empty.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ArithmeticProgressions

Math, Search

Used in:

SRM 365

Used as:

Division I Level Two

Writer:

Xixas

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7856

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10780&pm=7856

Problem Statement

You are given a String[] numbers containing a set of distinct non-negative integers (no leading zeroes). Let m be the smallest integer in numbers, and let M be the largest integer in numbers. An arithmetic progression of integers a+id, a+(i+1)d, ..., a+(j-1)d, a+jd is called proper if it satisfies all of the following conditions:

It contains at least 3 distinct integers from numbers.
All of the numbers in the progression are integers between m and M, inclusive.
If it were extended in either direction, condition 2 would no longer be satisfied. In other words, neither a+(i-1)d nor a+(j+1)d are between m and M, inclusive. (See example 0 for further clarification.)

Given a proper arithmetic progression, let a be the number of integers in the progression that are contained in numbers, and let b be the total number of integers in the progression. The aptitude of the progression is defined as a divided by b. Given numbers, return the maximal aptitude of a proper arithmetic progression as a String[] containing exactly 2 elements representing 2 integers (with no leading zeroes), first of which divided by the second equals the maximal aptitude. The first and the second elements of String[] you return must represent non-negative integers which do not have common divisors greater than 1. Return {"0", "1"} if no proper arithmetic progression exists.

Definition

Class:	ArithmeticProgressions
Method:	maxAptitude
Parameters:	String[]
Returns:	String[]
Method signature:	String[] maxAptitude(String[] numbers)
(be sure your method is public)

Constraints

-

numbers will contain between 1 and 50 elements, inclusive.

-

Each element of numbers will contain between 1 and 18 characters, inclusive.

-

Each character of every element of numbers will be a digit ('0'-'9').

-

No element of numbers will contain '0' (zero) as its first character.

-

All elements of numbers will be distinct.

Examples

0)

{"1", "3", "5", "8"}

Returns: {"3", "4" }

We have two proper arithmetic progressions here: 1, 2, 3, 4, 5, 6, 7, 8 and 1, 3, 5, 7. Both of them can not be extended since neither 0, nor 9 lies in [1; 8] in the first case and neither -1, nor 9 lies in [1; 8] in the second case. 4 elements of the first progression belong to numbers and so its aptitude is 4/8 = 1/2. 3 elements of the second progression belong to numbers and so its aptitude is 3/4, which is highest possible in this case.

1)

{"1", "3", "5", "7", "9", "11", "13", "15", "17", "19"}

Returns: {"1", "1" }

The elements of numbers form a proper arithmetic progression, hence its aptitude is 1.

2)

{"1", "999999999999999999"}

Returns: {"0", "1" }

There are not enough elements in numbers to form a proper arithmetic progression.

3)

{"1", "7", "13", "3511", "1053", "10", "5"}

Returns: {"3", "391" }

The elements of numbers are not necessarily sorted.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RepeatingFreeStrings

Advanced Math

Used in:

TCO07 Finals

Used as:

Division I Level Three

Writer:

Mike Mirzayanov

Testers:

PabloGilberto , Yarin , legakis , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7849

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10843&pm=7849

Problem Statement

A binary string s is called "repeating free" if no proper prefix equals a proper suffix of the same lengh. A substring is called "proper" if it differs from the whole string. For example, strings "0101011", "10", "10111100" are repeating free, but the string "01101011" is not.

Return the k-th string among all repeating free strings with length n in lexicographical order (k is a 0-based index). Return an empty string if it doesn't exist.

Definition

Class:	RepeatingFreeStrings
Method:	kthString
Parameters:	int, int
Returns:	String
Method signature:	String kthString(int n, int k)
(be sure your method is public)

Constraints

-

n will be between 1 and 50, inclusive.

-

k will be between 0 and 2000000000, inclusive.

Examples

0)

Returns: "01"

All repeating free strings of length 2 are "01" and "10".

1)

Returns: "10"

2)

Returns: "100"

All repeating strings of length 3 are "001", "011", "100", "110".

3)

Returns: "00101"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PlatformJumper

Dynamic Programming, Search, Simple Math

Used in:

SRM 353

Used as:

Division I Level Two , Division II Level Three

Writer:

xOberon

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7847

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10710&pm=7847

Problem Statement

In an old school arcade video game, you have reached the following bonus level. There are a number of platforms containing coins, and you must jump from platform to platform collecting the coins. You may only jump to lower platforms, so your entire journey will be downward. You can select any platform as your starting platform.

Your jumping behavior is defined as follows. On each jump, your horizontal speed is constant and does not exceed v. Your fall down follows the standard laws of physics: your free fall acceleration is g and initially your speed is 0.

For simplicity, we will represent each platform as a single point. Each element of platforms represents a single platform and is formatted "X Y C" (quotes for clarity), where X and Y are the x and y coordinates of the platform and C is the number of coins on the platform. Greater values of y represent higher locations. Return the greatest number of coins you can collect.

Definition

Class:	PlatformJumper
Method:	maxCoins
Parameters:	String[], int, int
Returns:	int
Method signature:	int maxCoins(String[] platforms, int v, int g)
(be sure your method is public)

Notes

-

A dropped object without starting velocity will fall down g*t²/2 units in time t.

-

Note, that you always can drop to the platform right below you.

Constraints

-

platforms will contain between 1 and 50 elements, inclusive.

-

Each element of platforms will be formatted as "X Y C", where X, Y and C are integers with no extra leading zeroes.

-

In each element of platforms, X and Y will be between 0 and 5000, inclusive.

-

In each element of platforms, C will be between 0 and 10000, inclusive.

-

All platforms will have distinct locations.

-

v and g will each be between 1 and 100, inclusive.

Examples

0)

{"3 10 7", "5 15 7", "8 9 12" }

Returns: 14

It is possible to jump from platform 1 to platform 0, thus we can earn 7+7=14 coins. It is impossible to jump from platform 1 to platform 2.

1)

{"0 0 1", "2 4 1", "4 0 1"}

Returns: 2

2)

{"0 0 1", "5000 5000 10"}

Returns: 10

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BalanceScale

Brute Force, Math

Used in:

SRM 358

Used as:

Division I Level Two

Writer:

icanadi

Testers:

PabloGilberto , brett1479 , Olexiy , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7845

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10768&pm=7845

Problem Statement

You are given a int[] weight, a set of weight values. You must choose the minimum number of weight values from the set such that every element in weight is measurable on a balance scale with the chosen weight values. Weight X is measurable with a set Y of weight values if and only if you can do the following. You place one weight with value X on either the left or right side of the scale. You then place some combination of weights on the scale with values from the set Y so that the left and right sides have the same total value. You may use each value in Y zero or more times to achieve this.

For example, consider the set of weight values { 21, 9, 6 }. You can choose the set { 9, 6 }, and every element in the original set will be measurable with this set. With weight 21, you can do the following. Place the one weight of 21 on the left side of the scale. Then place one weight of value 9 on the left side, and 5 weights of value 6 on the right side, and the scale will be balanced. With weights 9 and 6, you can simply place the weight on one side and a weight of equal value on the opposite side to balance the scale.

Return the minimum number of chosen weight values.

Definition

Class:	BalanceScale
Method:	takeWeights
Parameters:	int[]
Returns:	int
Method signature:	int takeWeights(int[] weight)
(be sure your method is public)

Constraints

-

weight will contain between 1 and 50 elements, inclusive.

-

All elements of weight will be distinct.

-

Each element of weight will be between 1 and 10,000,000, inclusive.

Examples

0)

{ 5, 4, 1, 8 }

Returns: 1

With weight value 1 we can measure all the other elements.

1)

{ 2, 3, 8, 9 }

Returns: 2

We choose weight values 2 and 3. Measure 8 by placing the weight of 8 on the left side, and 4 weights of value 2 on the right side. Measure 9 by placing the weight of 9 on the left side, and 3 weights of value 3 on the right side.

2)

{ 60, 105, 490, 42 }

Returns: 4

We can choose all weight values from the set.

3)

{ 15, 25, 9 }

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EllipseCoverage

Geometry, Simple Math

Used in:

SRM 353

Used as:

Division II Level One

Writer:

xOberon

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7839

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10710&pm=7839

Problem Statement

An ellipse is a figure on a plane where the sum of the distances from any point on its perimeter to two fixed points is constant. The two fixed points are called foci (plural of focus). In this problem we are interested in the number of points with integral coordinates that lie strictly inside of the given ellipse.

The foci are (x1, y1) and (x2, y2), and the fixed sum of distances is d.

Definition

Class:	EllipseCoverage
Method:	calculateCoverage
Parameters:	int, int, int, int, int
Returns:	int
Method signature:	int calculateCoverage(int x1, int y1, int x2, int y2, int d)
(be sure your method is public)

Constraints

-

x1, y1, x2, y2 will be between -100 and 100, inclusive.

-

d will be between 1 and 200, inclusive.

-

The arguments will define a valid ellipse with positive area.

Examples

0)

Returns: 9

This is a circle with radius 2. The points (-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 0), (0, 1), (1, -1), (1, 0) and (-1, 1) lie strictly inside the circle. The points (-2, 0), (0, -2), (0, 2) and (2, 0) are on the perimeter, so they do not lie strictly inside the circle and should not be counted.

1)

-3

Returns: 59

Be careful with (0, 4), (-5, 0), (0, -4) and (5, 0).

2)

Returns: 1941

3)

Returns: 31397

4)

-23

Returns: 25187

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BigWheels

Dynamic Programming, Math

Used in:

TCO07 Semi 2

Used as:

Division I Level Two

Writer:

legakis

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7828

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10840&pm=7828

Problem Statement

At the end of a popular television game show, contestants spin large wheels with various numbers on them to determine who wins the big prize. Adjacent to each wheel is an arrow, used to indicate the resulting value when the wheel stops spinning. Each contestant has their own wheel, possibly with a different set of numbers. Each wheel is "fair", meaning that when a wheel with K numbers is spun, there is a 1/K chance that the wheel will stop on any given value. Successive spins of the same wheel are independent.

Each contestant will spin their own wheel one or two times. If they spin once, their score is simply the value indicated by the arrow. If they choose to spin twice, their score is the sum of the values from their two spins, but if their total score is greater than the largest value on their wheel, they are eliminated. Each contestant can wait to see the result of their first spin before deciding if they want to spin a second time. Whoever ends up with the highest score wins the big prize, and the others go home empty handed. If multiple players have the same highest score, the player who went first among them will be declared the winner.

The contestants complete their turn (one or two spins) in a pre-determined order. This gives the later contestants the advantage of knowing the previous contestants' scores, helping them decide if they want to spin their wheel a second time. You are the first player, and want to optimize your probability of winning the game. Write a method to determine, for each value on your wheel, if you should stop if you got that value on your first spin or if you should spin a second time. Assume that the players following you will also play with a strategy that will optimize their own probability of winning. If a player is guaranteed to lose after their first spin, they will always spin again just for fun.

You will be given the contestants' wheels as a String[] wheels, where each element is a space-separated list of integers giving the various values on one player's wheel. The number of elements in wheel indicates the number of contestants, and the elements are given in the order that the players will take their turns. The first element in wheels is your wheel, and the last element is the last player's wheel. Return all the values on your wheel that you should stop with as a int[], in ascending order without duplicates.

Definition

Class:	BigWheels
Method:	enough
Parameters:	String[]
Returns:	int[]
Method signature:	int[] enough(String[] wheels)
(be sure your method is public)

Constraints

-

wheels will contain between 1 and 50 elements, inclusive.

-

The length of each element of wheels will be between 1 and 50, inclusive.

-

Each element of wheels will be a single-space-separated list of integers, with no leading zeros.

-

Each integer in wheels will be between 0 and 100, inclusive.

-

The probability of a contestant winning in any situation will always be at least 1e-9, unless it is zero.

-

The probabilities of a contestant winning if they decide to stop or spin again will differ by at least 1e-6, unless both probabilities are zero.

Examples

0)

{ "1 100 100",
  "2 100",
  "3 100" }

Returns: {100 }

If you first spin a 1, you are guaranteed to lose, and will spin again just for fun. If you first spin a 100, you are guaranteed to win, and will not spin again.

1)

{ "1 2", "2 1" }

Returns: {2 }

First consider the case when your first spin is a 1. If you do not spin again, your opponent must get a 2 to win. There is a 75% chance that he will be able to do this in one or two spins, so there is a 25% chance that you will win. However, if you spin again, there is a 50% chance that you will have an unbeatable score of 2, and a 50% chance that you will have a score of 3 and be eliminated (because 3 is greater than the maximum value of 2 on your wheel). Therefore you would choose to spin again, because that increases your chance of winning from 25% to 50%.

On the other hand, if your first spin resulted in a 2, you would definitely stop.

2)

{ "8 2 4",
  "0 7 7 7 7" }

Returns: {2, 8 }

If your first spin is a 2, there is no reason to spin again. A 2 or 4 on your second spin cannot help you, and an 8 would cause you to be eliminated. However, if your first spin is a 4, you have a 1/25 chance of winning if you stop, but slightly better than a 1/3 chance of winning if you spin again. Therefore, you should not spin again if your first spin is a 2 or 8.

3)

{ "1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20",
  "1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20",
  "1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20" }

Returns: {14, 15, 16, 17, 18, 19, 20 }

These numbers are proportional to the numbers used in an actual game show, with 3 contestants who all spin the same wheel.

4)

{ "5" }

Returns: {5 }

5)

{ "4 4 4", "7 6" }

Returns: { }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RaceManagement

Math, Recursion

Used in:

SRM 352

Used as:

Division II Level Three

Writer:

Ishan

Testers:

PabloGilberto , brett1479 , Olexiy , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7822

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10709&pm=7822

Problem Statement

Your company runs a horse race betting service. Each person bets on a horse, and if that horse wins outright (i.e., it wins alone and doesn't tie for the win with any other hose), the person will win back their money plus a multiple of the amount they bet. This multiple is called a payout factor. In all other cases your company keeps the money. You are given a int[] probability and a int[] amounts. The i^th element of probability is the percentage chance of the i^th horse winning the race, and the i^th element of amounts is the amount bet on the i^th horse. These probabilities are independent (see example 1 for clarification). Return the highest payout factor such that the expected earnings of the company is minimumMoney or higher. If you can not achieve minimumMoney with a non-negative payout factor, then return -1. If you can achieve minimumMoney with any payout factor, then return -2.

Definition

Class:	RaceManagement
Method:	getPayoutFactor
Parameters:	int[], int[], int
Returns:	double
Method signature:	double getPayoutFactor(int[] probability, int[] amounts, int minimumMoney)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

probability will contain between 1 and 5 elements, inclusive.

-

Each element of probability will be between 0 and 100, inclusive.

-

Each element of amounts will be between 0 and 1000, inclusive.

-

amounts will contain the same number of elements as probability.

-

The sum of all the elements in probability will be at most 100.

-

minimumMoney will be between 0 and 1000, inclusive.

Examples

0)

{30}

{100}

Returns: 2.0

Horse 1 has a 30% chance of winning. If it wins, the company has to pay out 100*P dollars, where P is the payout factor, and if it doesn't win, the company gains 100 dollars. Thus, the expected earnings of the compay is 70-30*P. The highest payout factor that ensures this is at least 10 is 2.

1)

{50,40}

{300,200}

Returns: 2.076923076923077

Horse A has a 50% chance of winning and horse B has a 40% chance of winning. But this also means that there is a 20% chance they tie and a remaining 30% chance neither of them wins.

Thus, in this scenario, 4 cases arise

Horse A wins 30% chance => The company loses 300*P dollars and gains 200 dollars

Horse B wins 20% chance => The company loses 200*P dollars and gains 300 dollars

Horse A & B both win (tie) 20% chance => The company loses 0*P dollars and gains 500 dollars

Neither Horse A nor horse B wins (No result) 30% chance => The company loses 0*P dollars and gains 500 dollars

To ensure the expected earnings are at least 100, the payout factor P can be at most approximately 2.077.

2)

{50}

{100}

Returns: -1.0

Return -1 because the payout factor in this case will be negative.

3)

{0}

{100}

Returns: -2.0

The payout factor is irrelevant. The company always gains 100 dollars.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NestedDiamonds

Math, Search

Used in:

SRM 380

Used as:

Division I Level Three

Writer:

gevak

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7817

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10802&pm=7817

Problem Statement

A diamond is a quadrangle with 4 sides of equal length. In this problem, every diamond must be oriented so that one of its diagonals is strictly horizontal and the other is strictly vertical. For example, the diamonds shown in figures 1a, 1b and 1c below are oriented correctly, but figure 1d is not. The horizontal diagonal is called x and the vertical diagonal is called y. Please note that either x or y can be of length 0 (see example 4 for further clarification). There are two categories of diamonds: tall and wide. A diamond is called tall if y >= x, and a diamond is called wide if x >= y. The diamond in figure 1a is tall, and the diamond in figure 1b is wide. In figure 1c, x is equal to y, so you can choose to call the diamond tall or wide.

You want to nest a set of diamonds one inside another. A diamond A is nested in diamond B if exactly two vertices of A are located strictly inside diamond B, and the other two vertices of A coincide with two different vertices of diamond B. Figures 1a and 1b show correctly nested diamonds, and figures 1c and 1d show incorrectly nested diamonds.

For the purposes of this problem, a diamond A is considered nested in diamond B only if A is immediately nested in B. In other words, there must be no other diamonds between them. For example, if a diamond C is nested in diamond A, and diamond B is nested in diamond C, then B is not nested in A. The nesting of the set of diamonds must satisfy all of the following rules:

Each diamond must be used in the nesting exactly once.
Exactly one of the diamonds must be nested in none of the other diamonds. This diamond is called the outside diamond.
Each diamond, except the outside diamond, must be nested in exactly one other diamond.
Each tall diamond must be nested in a wide diamond.
Each wide diamond, except the outside diamond, must be nested in a tall diamond.
The outside diamond must be wide.

The height of the nesting is equal to the length of the vertical diagonal of the outside diamond. You are given a int[] sides, where each element is the side length of a single diamond in the set. Return the minimum possible height of their nesting. If it is impossible to create a valid nesting, return -1 instead.

Definition

Class:	NestedDiamonds
Method:	minHeight
Parameters:	int[]
Returns:	double
Method signature:	double minHeight(int[] sides)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

sides will contain between 1 and 50 elements, inclusive.

-

Each element of sides will be between 1 and 1,000,000, inclusive.

Examples

0)

{4, 2}

Returns: 2.8284271247461903

1)

{10, 5, 2}

Returns: 9.16515138991168

2)

{1,2,5,3}

Returns: 4.69041575982343

The side lengths of the diamonds in their nested order, starting from the outside diamond, are 5, 3, 2, 1.

3)

{1, 1}

Returns: -1.0

A diamond cannot be nested in another diamond with the same side length.

4)

{1,4,3}

Returns: 5.656854249492381

The height of the innermost diamond is 0.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LineOfDice

Math

Used in:

TCO09 Round 5

Used as:

Division I Level Two

Writer:

gevak

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky , zhuzeyuan

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7814

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13763&pm=7814

Problem Statement

A game die is a cube with the numbers 1 to 6 written on its sides: 1 - on the top, 2 - on the left, 3 - on the front, 4 - on the back, 5 - on the right, 6 - on the bottom. You have thrown n dice, and the numbers on their tops (after they've been thrown) are given in the int[] dice. The i-th element (1-based) of dice is equal to the number of dice that were dropped with the number i on top.

You want to construct a single straight line using one or more of these thrown dice. Each pair of adjacent dice must have the same number on the sides where they touch each other. You may rotate dice as long as the numbers on their tops don't change. Each die may be used at most once.

Determine the number of different ways you can construct a single straight line using the thrown dice. Return this number modulo 10007. Two lines are different if:

1. They have different lengths.

or

2. Orient both lines horizontally and compare them from left to right. If two dice at the same position in each line have different orientations, the lines are different. Note that the lines 1-3-6 and 6-3-1 are considered different under this rule.

Definition

Class:	LineOfDice
Method:	howMany
Parameters:	int[]
Returns:	int
Method signature:	int howMany(int[] dice)
(be sure your method is public)

Constraints

-

dice will contain exactly 6 elements.

-

Each element of dice will be between 0 and 1000, inclusive.

Examples

0)

{1,0,0,0,0,1}

Returns: 16

We have one die with a 1 on top, and one die with a 6 on top. There are 4 different ways to construct a line containing only the die with 1 on top (each of the 4 possible rotations of a single die). Similarly, there are 4 different lines that contain only the die with 6 on top. We can also put both dice into a line. There are 4 possible rotations where the two dice can touch each other (on sides 2, 3, 4 and 5). Then, for each of these, we can reverse the left-right order to create different lines, for a total of 8 different lines containing both dice. Thus there are 4 + 4 + 8 = 16 different lines.

1)

{1,1,0,0,0,0}

Returns: 12

We have one die with a 1 on top, and one die with a 2 on top. There are 4 different lines that contain only the die with 1 on top, and 4 different lines that contain only the die with 2 on top. There are only 2 possible rotations where the dice can touch each other (on sides 3 and 4), and for each of these, we can reverse the left-right order to get different lines.

2)

{0,0,2,0,0,0}

Returns: 8

We have 2 dice, both with 3 on top. Unlike the previous examples, where the dice had different numbers on top, there are only 4 different ways to construct a line containing only one die. There are 4 possible rotations where the dice can touch each other to form a line (on sides 1, 2, 5 and 6). Reversing left-right order doesn't produce different lines in this case because each line is horizontally symmetrical.

3)

{1,1,1,1,1,1}

Returns: 384

4)

{0,2,3,1,7,9}

Returns: 8258

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DeviceProgramming

Dynamic Programming, Simple Math

Used in:

SRM 367

Used as:

Division I Level Two

Writer:

gevak

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7810

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10783&pm=7810

Problem Statement

You work in a company that produces measuring devices. The software for each device is stored in reprogrammable memory. To program a device, you must connect it to a personal computer and transmit data to the device's reprogrammable memory through a serial interface. Your task is to make this process as efficient as possible.

You are given two int[]s offset and size. Each corresponding pair of elements in offset and size describes a piece of data that must be transmitted to the device. The i-th piece of data consists of size[i] consecutive bytes that must be written starting at the address in offset[i]. To successfully program a device, you must write every piece of the given data. Memory addresses that are not referenced in this data are not important - so you can write anything to those addresses, or write nothing at all to them.

Data is transmitted from the computer to the device through packets. Each packet contains a consecutive piece of data that will be written to a specified memory address. Each packet must also include overhead bytes of various overhead information (like a packet header, the destination address, checksum, etc.). The size of one packet (including the overhead information) can not be more than maxPacketSize bytes. Return the minimum possible total number of bytes required to transmit all of the given data to the device.

Definition

Class:	DeviceProgramming
Method:	minBytes
Parameters:	int[], int[], int, int
Returns:	long
Method signature:	long minBytes(int[] offset, int[] size, int maxPacketSize, int overhead)
(be sure your method is public)

Notes

-

Assume that the reprogrammable memory of the measuring device is infinitely large.

Constraints

-

offset will contain between 1 and 50 elements, inclusive.

-

offset and size will contain the same number of elements.

-

Each element of offset will be between 0 and 1,000,000,000, inclusive.

-

Each element of size will be between 1 and 1,000,000,000, inclusive.

-

None of the pieces of data described by offset and size will overlap.

-

overhead will be between 1 and 999, inclusive.

-

maxPacketSize will be between overhead + 1 and 1000, inclusive.

Examples

0)

{0, 42, 60}

{40, 15, 2}

Returns: 78

Send 40 bytes starting from offset 0 in 2 packets (26 * 2 = 52 bytes). Then, send 20 bytes starting from offset 42 in 1 packet (26 bytes). Only 17 of those 20 bytes are meaningful. There are 3 dummy bytes starting from offset 57. A total of 78 bytes are sent.

1)

{0, 42, 60}

{40, 15, 13}

Returns: 92

Send 40 bytes starting from offset 0 in 2 packets (26 * 2 = 52 bytes). Then, send 15 bytes starting from offset 42 in 1 packet (6 + 15 = 21 bytes). Finally, send 13 bytes starting from offset 60 in 1 packet (6 + 13 = 19 bytes). A total of 92 bytes are sent.

2)

{0, 2, 13}

{1, 7, 2}

Returns: 26

3)

{10264, 111, 357, 100066, 714}

{117, 134, 235, 2395, 23}

Returns: 3254

4)

{1, 100000000, 450000000}

{99999999, 315000000, 500000000}

Returns: 943298999

5)

{0, 1000000000}

{1000000000, 1000000000}

Returns: 2000000000000

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PlaneDivision

Advanced Math, Geometry, Graph Theory

Used in:

SRM 350

Used as:

Division I Level Three

Writer:

Xixas

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7788

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10674&pm=7788

Problem Statement

You are given n distinct straight lines in the plane. The i-th line is specified by two distinct lattice points (x1[i], y1[i]) and (x2[i], y2[i]) that lie on it. These lines divide the plane into regions, and your task is to compute and return the number of finite regions among them. By a finite region we mean a convex polygon bounded by the given lines, with no points belonging to any of the given lines in its interior.

Definition

Class:	PlaneDivision
Method:	howManyFiniteParts
Parameters:	int[], int[], int[], int[]
Returns:	int
Method signature:	int howManyFiniteParts(int[] x1, int[] y1, int[] x2, int[] y2)
(be sure your method is public)

Notes

-

By a lattice point (x, y) we mean a point on the Cartesian plane with integer coordinates x and y.

-

Two points are said to be distinct if either their x-coordinates or y-coordinates differ.

Constraints

-

x1, y1, x2 and y2 will contain the same number of elements.

-

x1, y1, x2 and y2 will contain between 1 and 50 elements, inclusive.

-

All the elements of x1, y1, x2 and y2 will be between -10000 and 10000, inclusive.

-

(x1[i], y1[i]) and (x2[i], y2[i]) will be distinct for all i (i.e., every two points defining a given line will be distinct).

-

All the lines defined by (x1[i], y1[i]) and (x2[i], y2[i]) will be distinct.

Examples

0)

{0}

{0}

{1}

{1}

Returns: 0

A single line divides the plane into two infinite regions.

1)

{0, 1, 2}

{0, 1, -1}

{1, 2, 0}

{1, -1, 0}

Returns: 1

The three lines are the sidelines of a triangle which is the only finite region in this case.

2)

{-10000, -9999, 10000, -9999, 0, 500, -500}

{-9999, 10000, 9999, -10000, 0, 0, 0}

{-10000, 9999, 10000, 9999, 0, 500, -500}

{9999, 10000, -9999, -10000, 1, -1, -2}

Returns: 4

The only finite regions are the 4 big rectangles.

3)

{0, 0, 0, 0, 0, 0, 0, 0, 0}

{0, 0, 0, 0, 0, 0, 0, 0, 0}

{1, 1, 1, 1, 1, 1, 1, 1, 1}

{1, 2, 3, 4, 5, 6, 7, 8, 9}

Returns: 0

All the lines pass through the origin.

4)

{-1, -1, -1, -1, 1, 3, -3}

{-1, -2, 0, 0, 10000, 1, -5}

{1, 1, 1, -1, 1, -3, 3}

{1, 0, 2, -10000, 0, -2, 4}

Returns: 7

1 parallelogramm and 6 triangles are the only finite regions in this case.

5)

{-100, -100, -100, -100, -100}

{-100, -99, -98, -97, -96}

{100, 100, 100, 100, 100}

{99, 100, 101, 102, 103}

Returns: 0

5 parallel lines do not produce any finite regions.

6)

{-100, -100, -100, -100, -100, 1}

{-100, -99, -98, -97, -96, -1}

{100, 100, 100, 100, 100, -2}

{99, 100, 101, 102, 103, 2}

Returns: 0

A configuration of 5 parallel lines and a single line crossing all of them again yields no finite regions.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PointsOnCircle

Math, Simple Search, Iteration

Used in:

SRM 365

Used as:

Division I Level One , Division II Level Two

Writer:

Xixas

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7787

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10780&pm=7787

Problem Statement

You are given the radius r of a circle centered at the origin. Your task is to return the number of lattice points (points whose coordinates are both integers) on the circle. The number of pairs of integers (x, y) that satisfy x^2 + y^2 = n is given by the formula 4*(d1(n) - d3(n)), where di(n) denotes the number of divisors of n that leave a remainder of i when divided by 4.

Definition

Class:	PointsOnCircle
Method:	count
Parameters:	int
Returns:	long
Method signature:	long count(int r)
(be sure your method is public)

Constraints

-

r will be between 1 and 2*10^9, inclusive.

Examples

0)

Returns: 4

The only lattice points on the circle are (0, 1), (1, 0), (-1, 0), (0, -1).

1)

2000000000

Returns: 76

2)

Returns: 4

The number of lattice points on the circle of radius 3 is the same as the number of integer solutions of the equation x^2 + y^2 = 9. Using the formula from the problem statement we can calculate this number as 4*(d1(9) - d3(9)). It is easy to see that d1(9) = 2 (divisors 1 and 9) and d3(9) = 3 (divisor 3). So the answer is 4*(2 - 1) = 4.

3)

Returns: 12

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SoccerCommentator

Simple Math

Used in:

TCHS07 Semifinal

Used as:

Division I Level Two

Writer:

VitalyGoldstein

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7770

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10763&pm=7770

Problem Statement

A play-off round between 2 teams in most soccer competitions consists of two games. Each team hosts one of these two games, and the team that scores more total goals advances. If both teams have scored the same total number of goals, the team who have scored more away goals advances. If both teams score the same total number of goals, the team that scored more away goals advances. (An "away" goal is one that is scored in a game hosted by the other team.) If both teams score the same number of away goals, they must go into overtime.

You will be given the score of the first game and the current score of the second game (still in progress). Each score will be a String formatted as "G1:G2" (quotes for clarity), where G1 is the number of goals scored by the first team, and G2 is the number of goals scored by the second team. You will also be given firstGameHost, which is equal to 1 if the first game was hosted by team 1, and 2 otherwise. Return the number of additional goals the first team must score in the second game to advance without going into overtime.

Definition

Class:	SoccerCommentator
Method:	goalsToWin
Parameters:	String, String, int
Returns:	int
Method signature:	int goalsToWin(String score1, String score2, int firstGameHost)
(be sure your method is public)

Constraints

-

score1 and score2 will each be formatted as two digits separated by ':'.

-

All digits in score1 and score2 will be between 0 and 5, inclusive.

-

firstGameHost will be equal to 1 or 2.

Examples

0)

"0:0"

"0:0"

Returns: 1

Now is draw. The first team must score goal to advance without going into overtime.

1)

"0:2"

"0:3"

Returns: 5

5 away goals is enough to advance.

2)

"0:2"

"0:3"

Returns: 6

The first team scores 0 away goals, thats why now it is neccesary to score 6 goals.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RadarFinder

Geometry, Math

Used in:

SRM 349

Used as:

Division I Level One , Division II Level Two

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7766

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10673&pm=7766

Problem Statement

You are the commander of a military operation that is focused on determining the location of an enemy unit. Two radar stations have provided measurements of their calculated distance from the enemy unit. You are given the locations of your radar stations in ints x1, y1 and x2, y2, and the calculated distances in ints r1 and r2, respectively.

You are to return an int indicating the number of possible locations of the enemy unit. If there are an infinite number of possible locations, return -1.

Definition

Class:	RadarFinder
Method:	possibleLocations
Parameters:	int, int, int, int, int, int
Returns:	int
Method signature:	int possibleLocations(int x1, int y1, int r1, int x2, int y2, int r2)
(be sure your method is public)

Constraints

-

x1 will be between -1000000000 and 1000000000, inclusive.

-

y1 will be between -1000000000 and 1000000000, inclusive.

-

r1 will be between 1 and 1000000000, inclusive.

-

x2 will be between -1000000000 and 1000000000, inclusive.

-

y2 will be between -1000000000 and 1000000000, inclusive.

-

r2 will be between 1 and 1000000000, inclusive.

Examples

0)

Returns: 2

The points (5, 12) and (5, -12) are the only points that are consistent with both radar measurements.

1)

Returns: 1

Only one point, (0, 3), is consistent with both measurements.

2)

Returns: 0

Perhaps one of the measurements was incorrect, since no points are consistent.

3)

Returns: -1

Getting two identical readings from the same location still leaves an unlimited number of possible locations.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NoEights

Simple Math

Used in:

SRM 355

Used as:

Division II Level Two

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7759

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10712&pm=7759

Problem Statement

Cyclists don't like the number eight because it symbolizes a broken wheel. Recently, the mayor of Moscow decided to force all cyclists to get an identification number. Vasya was presented with the following choice: he can choose any number between low and high, inclusive. He wants his number to contain as few eights as possible. Return the minimal possible number of eights he can have in his number.

Definition

Class:	NoEights
Method:	smallestAmount
Parameters:	int, int
Returns:	int
Method signature:	int smallestAmount(int low, int high)
(be sure your method is public)

Constraints

-

low will be between 1 and 2000000000, inclusive.

-

high will be between low and 2000000000, inclusive.

Examples

0)

Returns: 0

Any number except 8 will do.

1)

Returns: 2

The only possible number is 88.

2)

Returns: 1

The first 8 is unavoidable.

3)

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NotationLength

Math

Used in:

TCHS SRM 41

Used as:

Division I Level Two

Writer:

Nickolas

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7744

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10788&pm=7744

Problem Statement

NOTE: This problem statement contains superscripts that may not display properly if viewed outside of the applet.

It is known that the binary notation (radix 2) of any integer is at most 4 times as long as the corresponding decimal notation. In this problem, you will examine a similar property for radices other then 2.

You are given an int radix and ints low and high. Calculate the ratio of the length of the radix-based notation to the length of the decimal notation for each integer between low and high, inclusive. Return the average of these ratios.

Definition

Class:	NotationLength
Method:	avgRatio
Parameters:	int, int, int
Returns:	double
Method signature:	double avgRatio(int radix, int low, int high)
(be sure your method is public)

Notes

-

Numbers in radix-based notation are represented using the digits from 0 to radix-1, inclusive (uppercase letters A, B, C, ... are used to represent "digits" 10, 11, 12, ...). The number a_na_n-1...a₁a₀ in radix-based notation corresponds to the number a_n*radixⁿ + a_n-1*radix^n-1 + ... + a₁*radix + a₀ in decimal notation. For example, B7F is the 16-based notation of the decimal number 11 * 16² + 7 * 16 + 15 = 2943.

-

When calculating notation lengths, numbers must be represented with no extra leading zeros.

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

high will be between 1 and 1000000, inclusive.

-

low will be between 1 and high, inclusive.

-

radix will be between 2 and 16, inclusive.

Examples

0)

Returns: 1.0

Both decimal and hexadecimal notations of each integer between 16 and 99 are exactly 2 characters long, and the ratio of these lengths is 1.

1)

Returns: 2.0

|   Decimal notation   |   Ternary notation   |   Lengths ratio  |
|         7            |          21          |        2.0       |
|         8            |          22          |        2.0       |
|         9            |         100          |        3.0       |
|        10            |         101          |        1.5       |
|        11            |         102          |        1.5       |

Average lengths ratio is (2.0+2.0+3.0+1.5+1.5)/5 = 2.0.

2)

Returns: 2.4838709677419355

3)

Returns: 1.0

1313 in decimal notation is 2441 in octal notation.

4)

Returns: 1.4452407023781983

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SortingInIterations

Simple Math, Simple Search, Iteration

Used in:

TCO07 Round 4

Used as:

Division I Level Two

Writer:

Mike Mirzayanov

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7743

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10759&pm=7743

Problem Statement

John is going to sort a sequence of numbers using a special algorithm. First all numbers a[0], a[1], a[2], ..., a[n-1] are written on a blackboard. During the first iteration, John checks all numbers in the order of increasing indices (so, he checks a[0] first, followed by a[1], a[2],..., and ends the first iteration with a[n - 1]). At any moment, he can erase the number he is looking at from the blackboard and write it into his notebook. When looking at number a[i], John erases it from the board and writes into his notebook if and only if it is equal to the smallest unerased number on the blackboard. All other iterations are similar to the first one, but, of course, John checks only the numbers which were not erased from the blackboard. The process is over when all numbers are erased from the board and written into John's notebook in non-descending order.

For example, if John is given a sequence of {3, 5, 1, 4, 2}, the process will go as follows. During the first iteration, John will erase 1 and 2 from the board, writing them to the notebook and changing the sequence to {3, 5, 4}. During the second iteration, 3 and 4 will be written into his notebook, so only 5 will be on the board during the third iteration.

You will be given four ints: a0, X, Y, M, n. The sequence John will need to sort can be generated using the following algorithm:

a[0] = a0;
a[i] = (a[i - 1] * X + Y) mod M, for 0 < i < n (where mod is a remainder operation.).

You will be given two more ints start and finish. Return the sum of all numbers John will erase from the board during all iterations with indices (1-based) between start and finish, inclusive. If John will need less than finish iterations to sort the sequence, return -1.

Definition

Class:	SortingInIterations
Method:	sum
Parameters:	int, int, int, int, int, int, int
Returns:	long
Method signature:	long sum(int a0, int X, int Y, int M, int n, int start, int finish)
(be sure your method is public)

Constraints

-

a0 will be between 0 and M-1, inclusive.

-

X will be between 0 and 4*10^5, inclusive.

-

Y will be between 0 and 4*10^5, inclusive.

-

M will be between 1 and 4*10^5, inclusive.

-

n will be between 1 and 4*10^5, inclusive.

-

start will be between 1 and 4*10^5, inclusive.

-

finish will be between start and 4*10^5, inclusive.

Examples

0)

Returns: 5

The sequence is 4 1 2 4 1 2 4 1 2 4. The bolded elements will be erased during the first iteration.

1)

Returns: 1

The sequence is 1, 0, 0, 0, 0. We need two iterations to erase all numbers.

2)

Returns: 20

3)

Returns: 4999950000

Be careful with overflows.

4)

Returns: -1

John needs only four iterations.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Aircraft

Geometry, Simple Math, Simulation

Used in:

SRM 347

Used as:

Division I Level One , Division II Level Two

Writer:

StevieT

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7741

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10671&pm=7741

Problem Statement

In aviation, a "near miss" occurs if the distance between two aircraft at some point in time is less than or equal to some threshold distance R. At a moment in time, the positions and velocities of two aircraft are known exactly. Assuming that each aircraft continues to fly with constant speed and direction, you need to work out if the aircraft will undergo a near miss now or at some point in the future.

You will be given the threshold distance R and the positions and velocities of the aircraft in 4 int[]s: p1, v1, p2 and v2. The position of the first aircraft in 3-D cartesian space is given by (p1[0] , p1[1] , p1[2]) and its velocity vector by (v1[0] , v1[1] , v1[2]) and similarly the second aircraft's position and velocity are given by (p2[0] , p2[1] , p2[2]) and (v2[0] , v2[1] , v2[2]). So, if an aircraft's initial position is the vector p and its velocity vector is v, the position of this aircraft at some future time t will be p + v * t. You should return a String containing "YES" if the aircraft will undergo a near miss now or in the future or "NO" if they won't (quotes for clarity).

Definition

Class:	Aircraft
Method:	nearMiss
Parameters:	int[], int[], int[], int[], int
Returns:	String
Method signature:	String nearMiss(int[] p1, int[] v1, int[] p2, int[] v2, int R)
(be sure your method is public)

Notes

- The distance between two points (x1, y1, z1) and (x2, y2, z2) is given by sqrt((x1-x2)² + (y1-y2)² + (z1-z2)²).

Constraints

- p1, v1, p2 and v2 will contain exactly 3 elements.

- Each element of p1, v1, p2 and v2 will be between -10000 and 10000, inclusive.

- R will be between 0 and 10000, inclusive.

Examples

0)

{15,50,5}

{25,1,0}

{161,102,9}

{-10,-10,-1}

Returns: "YES"

At time 4, the first aircraft will be at position {115,54,5} and the second at {121,62,5}, which is the first point in time at which they are exactly 10 distance units apart.

1)

{0,0,0}

{2,2,0}

{9,0,5}

{-2,2,0}

Returns: "YES"

At time 2.25, aircraft 1 will be at {4.5, 4.5, 0} and aircraft 2 at {4.5, 4.5, 5}, exactly a distance of 5 units apart.

2)

{0,0,0}

{-2,2,0}

{9,0,5}

{2,2,0}

Returns: "NO"

The aircraft are flying away from each other here, so the distance always increases with time.

3)

{-2838,-7940,-2936}

{1,1,-2}

{532,3850,9590}

{1,0,-3}

Returns: "YES"

The closest approach of the aircraft occurs at time 12,158

4)

{-8509,9560,345}

{-89,-33,62}

{-5185,-1417,2846}

{-58,24,26}

Returns: "YES"

A near miss occurs between times 111 and 112

5)

{-7163,-371,-2459}

{-59,-41,-14}

{-2398,-426,-5487}

{-43,27,67}

Returns: "NO"

The aircraft almost have a near miss between times 15 and 16, but stay just outside the threshold distance.

6)

{1774,-4491,7810}

{-12,19,-24}

{2322,3793,9897}

{-12,19,-24}

Returns: "YES"

The aircraft are here flying with identical velocities, so the distance between them never changes. The distance at time 0 is lower than the threshold, so a near miss is already underway.

7)

{3731,8537,5661}

{-70,71,32}

{8701,-1886,-5115}

{28,-13,7}

Returns: "NO"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MaximizeSquares

Geometry, Greedy, Math

Used in:

SRM 362

Used as:

Division I Level One , Division II Level Two

Writer:

eleusive

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7735

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10775&pm=7735

Problem Statement

Consider an arrangement of N points on the cartesian plane. The "square count" of the points is the total number of distinct squares with sides parallel to the coordinate axes which can be built using 4 different points as vertices. Your task is to return the maximum square count, considering all possible arrangements of N points on the plane.

Definition

Class:	MaximizeSquares
Method:	squareCount
Parameters:	int
Returns:	int
Method signature:	int squareCount(int N)
(be sure your method is public)

Notes

-

Two squares are distinct if at least one of their corners is in a different location.

Constraints

-

N will be between 0 and 1000000, inclusive.

Examples

0)

Returns: 1

Clearly, we can only make one square out of 4 points.

1)

Returns: 1

No matter where we place a fifth point, we can't get any extra squares.

2)

Returns: 2

We can get 2 squares by placing the points in the shape of a rectangle.

3)

Returns: 14

4)

Returns: 340

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PolishNotation

Dynamic Programming, Math, String Manipulation

Used in:

TCO07 Round 4

Used as:

Division I Level One

Writer:

Olexiy

Testers:

PabloGilberto , brett1479 , radeye , Mike Mirzayanov

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7733

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10759&pm=7733

Problem Statement

Prefix notation (also known as Polish notation in reference to the nationality of its inventor, Jan Lukasiewicz) is a notation where operators are placed before their arguments (and arguments themselves are also expressions in prefix notation). Since the arity of arithmetic operations is fixed, an expression written in prefix notation is always unambiguous, and parenthesizing the expression is unnecessary. For example:

 Our usual (infix) notation        Prefix notation
 2 + 3                             + 2 3
 3 + 2                             + 3 2
 4 * (-2 + 3)                      * 4 + -2 3
 (22 + 3) * (55 - 4)               * + 22 3 - 55 4
 1 + 2 + 3 + 44 + (-5)             + + + + 1 2 3 44 -5
 1 + (2 + (3 + (44 + (-5))))       + 1 + 2 + 3 + 44 -5

As you can see from the table, any arithmetic expression can be written unambiguously in prefix notation. Since operators and numbers are separated by spaces, we are always able to distinguish a 2-digit number and a sequence of two 1-digit numbers, as well as distinguish between unary and binary minuses.

More formally, any valid expression in prefix notation can be described by the following rules:

Any integer number is a valid expression.
If S and Q are valid expressions, then "+ S Q", "* S Q", "- S Q" and "/ S Q" are valid expressions (all quotes are for clarity only).

You've got an expression written in prefix notation and you'd like to read it. Unfortunately, all the spaces were removed, possibly making it impossible to determine what the original expression was. For example, "--456" could have originally been "- - 4 5 6", "- -4 56" or "- -45 6". You are to return the number of different valid original prefix notation expressions that could have resulted in the given expression. Note that both positive and negative numbers in the original expression may contain leading zeroes. Unary minuses in the original expression are allowed, but there can be at most one unary minus in a number (so, "12" and "-34" are valid numbers, but "--11" and "----22" are not). Also, the original expression cannot contain any unary pluses. See examples for further clarification.

Definition

Class:	PolishNotation
Method:	waysToDecode
Parameters:	String
Returns:	long
Method signature:	long waysToDecode(String expression)
(be sure your method is public)

Constraints

-

expression will contain between 1 and 50 characters, inclusive.

-

expression will contain only '+', '-', '/', '*' characters and digits ('0' - '9').

Examples

0)

"01234567890123456789"

Returns: 1

This string is already a valid expression in prefix notation, and the only way to keep it valid is to not add any spaces.

1)

"+1234567"

Returns: 6

We must put a space after '+' to split the operator and its operands. We need one more space to split the two operands, and it can be put right after '1', '2', '3', '4', '5' or '6'.

2)

"23/33"

Returns: 0

This string can not be transformed into a valid expression.

3)

"/-010"

Returns: 3

The three ways to transform this into a valid expression are (all quotes for clarity):

"/ -0 10" (the minus is unary)
"/ -01 0" (the minus is unary)
"/ - 0 1 0" (the minus is binary)

4)

"-*123"

Returns: 1

Here the minus is followed by another operation, so it must be binary.

5)

"--1"

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DayTrader

Simple Math

Used in:

TCO07 Finals

Used as:

Division I Level One

Writer:

legakis

Testers:

PabloGilberto , Olexiy , Mike Mirzayanov , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7721

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10843&pm=7721

Problem Statement

The New York Stock Exchange is open for 390 minutes a day, from 9:30am until 4:00pm. During this time, you can buy and sell shares of companies listed on the exchange. Given a graph of how the share prices of two companies fluctuate in one day, calculate the highest amount of money you could possibly earn.

You begin the day with $1000. At any time, you can buy shares of either company at a cost of the number of shares you are buying times the current share price. Similarly, at any time you can sell shares you own of either company for a price of the number of shares you are selling times the current share price. You are not limited to buying or selling whole numbers of shares. You may never spend more money than you have, nor may you sell more shares than you own. Assume you pay no fees or commission on any purchase or sale.

The share price for a company will be given as a pair of int[]s, the first giving a list of times, and the second giving the corresponding share price at each of those times. The times will always be in ascending order, the first time will always be 0, and the last time will always be 390. To compute the stock price between two adjacent times in the arrays, linearly interpolate between the two prices. The times and prices of the first stock ("stock A") are given by timeA and priceA, and the times and prices of the second stock ("stock B") are given by timeB and priceB.

For example, given the following input arrays:

    timeA  = { 0,  60, 150, 270, 390 }
    priceA = { 60, 80, 40,  40,  60 }
    timeB  = { 0,  180, 300, 390 }
    priceB = { 40, 20,  70,  80 }

stock A is shown in red and stock B is shown in blue in the figure below.

In this example, you would make the most money by spending your entire $1000 to buy 16 2/3 shares of stock A for $60 each at time 0. One hour later at time 60, you should sell all your shares at $80 each, receiving 1333 1/3 dollars. You would hold on to your money until time 180, and then spend it all on 66 2/3 shares of stock B. At time 300, you would sell these shares for $70 each (4666 2/3 dollars) and immediately buy as many shares of stock A as you can afford. The price of stock A at time 300 is $45 (1/4 of the way between $40 and $60), so you can afford 103 19/27 shares. You would then sell these at the end of the day for $60, for a total of 6222 2/9 dollars, giving you earnings of about $5222.22 over your initial $1000.

Definition

Class:	DayTrader
Method:	earnings
Parameters:	int[], int[], int[], int[]
Returns:	double
Method signature:	double earnings(int[] timeA, int[] priceA, int[] timeB, int[] priceB)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

timeA, priceA, timeB, and priceB will each contain between 2 and 50 elements, inclusive.

-

timeA and priceA will contain the same number of elements.

-

timeB and priceB will contain the same number of elements.

-

The first element of timeA and timeB will be 0.

-

The last element of timeA and timeB will be 390.

-

The elements of timeA and timeB will be strictly ascending.

-

Each element of priceA and priceB will be between 10 and 100, inclusive.

Examples

0)

{ 0, 390 }

{ 25, 50 }

{ 0, 390 }

{ 10, 30 }

Returns: 2000.0

Stock A doubles in value throughout the day, while stock B triples. If you buy stock B at time 0 and sell at time 390, you can earn $2000.

1)

{ 0, 50, 390 }

{ 80, 65, 20 }

{ 0, 310, 390 }

{ 12, 12, 11 }

Returns: 0.0

Neither stock ever goes up in value, so you cannot earn any money today.

2)

{ 0, 60, 150, 270, 390 }

{ 60, 80, 40, 40, 60 }

{ 0, 180, 300, 390 }

{ 40, 20, 70, 80 }

Returns: 5222.222222222223

This is the example from the problem statement.

3)

{ 0, 390 }

{ 10, 20 }

{ 0, 100, 101, 390 }

{ 100, 10, 100, 10 }

Returns: 18959.266802443988

4)

{0, 100, 200, 300, 390 }

{ 10, 11, 14, 19, 26 }

{ 0, 50, 150, 250, 350, 390 }

{ 10, 10, 12, 16, 22, 29 }

Returns: 2403.157552083335

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BrokenButtons

Brute Force, Simple Math

Used in:

SRM 358

Used as:

Division I Level One , Division II Level Two

Writer:

icanadi

Testers:

PabloGilberto , brett1479 , Olexiy , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7716

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10768&pm=7716

Problem Statement

You want to see some page on the teletext (information service on TV where we refer to pages of information by numbers). Unfortunately, some of the digit buttons on the remote control are broken. But you have an idea! If you can't enter the number of the page you want to see, you could enter some other number and with the buttons '+' and '-' (which are not broken) navigate to the desired page. Button '+' increases the number by 1 and button '-' decreases the number by 1. You are initially at page 100. To go to a different page, you may enter the page number using the digit buttons that aren't broken. Then, press the '+' and '-' buttons to navigate to your desired page.

You will be given an int page, the page you want to see, and a int[] broken, the list of broken digit buttons. Return the minimum number of button presses required to navigate to the page.

Definition

Class:	BrokenButtons
Method:	minPresses
Parameters:	int, int[]
Returns:	int
Method signature:	int minPresses(int page, int[] broken)
(be sure your method is public)

Constraints

-

page will be between 0 and 500,000, inclusive.

-

broken will contain between 0 and 10 elements, inclusive.

-

Each element of broken will be between 0 and 9, inclusive.

-

All elements of broken will be distinct.

Examples

0)

{ 6, 7, 8 }

Returns: 6

You can go to page 5457 either by pressing "5455++" or "5459--".

1)

{ 1, 0, 5 }

Returns: 0

If you don't enter anything you'll get page 100.

2)

{ }

Returns: 5

3)

{1, 2, 3, 4, 5, 6, 7, 8, 9}

Returns: 2

We can enter page 0.

4)

{ 8, 9 }

Returns: 2228

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Factorer

Math, Search

Used in:

TCCC07 Finals

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7708

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10980&pm=7708

Problem Statement

A second degree polynomial ax^2 + bx + c can sometimes be factored into two first degree polynomials with integer coefficients. We want to produce the factorization as a string in the following format:

    (<coef>x<sign><num>)(<opneg><coef>x<sign><num>) 
where 
    '(' ')' and 'x' are literal 
    <coef> is either empty or is a positive integer greater than 1. 
    <num> is a positive integer
    <sign> is a sign character, either '+' or '-'
    <opneg> is an optional '-' character

Neither <coef> nor <num> can be expressed with leading zeroes.

Given a, b, and c, return the factorization as a String. If no factorization is possible, return the 4 uppercase letters "NONE". If more than one factorization is possible, choose the one with the largest coefficient of x in the first factor. If more than one is still possible, choose the one whose first factor is bigger when evaluated at x=0.

Definition

Class:	Factorer
Method:	factor
Parameters:	int, int, int
Returns:	String
Method signature:	String factor(int a, int b, int c)
(be sure your method is public)

Constraints

-

a, b, and c will each be between -1,000,000,000 and 1,000,000,000, inclusive.

-

Neither a nor c will be 0.

Examples

0)

-1

Returns: "(x+1)(x-1)"

This factorization of x^2-1 is preferred to "(x-1)(x+1)" by the second tie breaker.

1)

-4

-1

Returns: "(2x-1)(-2x+1)"

-4x^2 + 4x -1 = (2x-1)(-2x+1)

2)

-4

Returns: "NONE"

3)

-3

Returns: "(x-1)(x-2)"

"(x-1)(x-2)" is preferred to "(x-2)(x-1)" by the second tie-breaking rule (since -1 is greater than -2).

4)

-20

Returns: "(20x+20)(-x+1)"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RaceOrdering

Dynamic Programming, Graph Theory, Simple Math

Used in:

SRM 371

Used as:

Division I Level Three

Writer:

bmerry

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7703

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10787&pm=7703

Problem Statement

You are trying to predict the outcome of a race between n runners, numbered from 0 to n - 1.You are given two int[]s, first and second. It is guaranteed that for all i, the runner numbered first[i] will always beat the runner numbered second[i]. Determine how many final orderings are possible, modulo 1,000,003. If the information is contradictionary, return 0. Runners are never tied.

Definition

Class:	RaceOrdering
Method:	countOrders
Parameters:	int, int[], int[]
Returns:	int
Method signature:	int countOrders(int n, int[] first, int[] second)
(be sure your method is public)

Constraints

-

n will be between 1 and 30, inclusive.

-

first and second will each contain between 0 and 15 elements, inclusive.

-

first and second will contain the same number of elements.

-

Each element of first and second will be between 0 and n - 1, inclusive.

-

first[i] does not equal second[i] for all i between 0 and m - 1, inclusive, where m is the number of elements in first and second.

Examples

0)

{1}

{2}

Returns: 3

Contestant 1 beat contestant 2, so the valid orders are 012, 102 and 120.

1)

{0, 0}

{1, 2}

Returns: 8

Contestant 0 beat contestants 1 and 2, but there is no information on contestant 3. The valid orderings are 3012, 3021, 0312, 0321, 0132, 0231, 0123 and 0213.

2)

{1, 2, 3}

{2, 3, 1}

Returns: 0

There is no way to satisfy this cycle.

3)

{}

{}

Returns: 90317

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AmbiguousWatch

Advanced Math, Geometry

Used in:

TCO07 Round 1B

Used as:

Division I Level Three

Writer:

Mike Mirzayanov

Testers:

PabloGilberto , brett1479 , legakis , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7672

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10742&pm=7672

Problem Statement

You have a watch with only an hour hand and a minute hand. The watch is a round 12-hour watch. Both hands move continuously. Both hands have the same length and are indistinguishable, so at certain moments, the time displayed is ambiguous. A time is considered ambiguous if there exists a different time at which the hands appear to have the same positions. For example, the time moment on the picture is ambiguous. At this moment, you would not be able to tell if it was a little past 00:05, or a little past 01:00.

You are given two times in the form "HH:MM" (quotes for clarity), where 00 <= HH < 12, and 00 <= MM < 60. Return the number of ambiguous moments between startTime and finishTime, inclusive. The times represented by startTime and finishTime are in the same half of the day.

Definition

Class:	AmbiguousWatch
Method:	howMany
Parameters:	String, String
Returns:	int
Method signature:	int howMany(String startTime, String finishTime)
(be sure your method is public)

Constraints

-

startTime and finishTime will have the form "HH:MM" (quotes for clarity), where 00 <= HH < 12, 00 <= MM < 60.

-

startTime must be earlier than or the same as finishTime (in the same half of the day).

Examples

0)

"00:00"

"00:00"

Returns: 0

This moment is not ambiguous.

1)

"00:05"

"00:06"

Returns: 1

There is one ambiguous moment in this time range. At that moment, you would not be able to tell if it was a little past 00:05, or a little past 01:00.

2)

"00:00"

"01:00"

Returns: 11

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AntiPalindrome

Simple Math, Simple Search, Iteration, String Manipulation

Used in:

TCO07 Round 1B

Used as:

Division I Level One

Writer:

Mike Mirzayanov

Testers:

PabloGilberto , brett1479 , legakis , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7671

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10742&pm=7671

Problem Statement

A String p is called anti-palindrome if p[i] doesn't equal to p[n - i - 1] for each 0 <= i < (n-1)/2, where n is the length of p. It means that each character (except the middle in the case of a string of odd length) must be different from its symmetric character. For example, "c", "cpp", "java" are anti-palindrome, but "test", "pp" and "weather" are not.

You are given a String s. Rearrange its letters in such a way that the resulting string is anti-palindrome. If there are several solutions, return the one that comes earliest alphabetically. If it is impossible to do it, return the empty string.

Definition

Class:	AntiPalindrome
Method:	rearrange
Parameters:	String
Returns:	String
Method signature:	String rearrange(String s)
(be sure your method is public)

Constraints

-

s will contain between 1 and 50 characters, inclusive.

-

s will contain only lowercase letters ('a'-'z').

Examples

0)

"test"

Returns: "estt"

1)

"aabbcc"

Returns: "aabcbc"

2)

"reflectionnoitcelfer"

Returns: "cceeeeffiillnnoorrtt"

3)

"hello"

Returns: "ehllo"

4)

"www"

Returns: ""

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SumoTournament

Dynamic Programming, Simple Math, Simple Search, Iteration

Used in:

TCHS SRM 37

Used as:

Division I Level Three

Writer:

Janq

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7660

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10776&pm=7660

Problem Statement

There are several sumo wrestlers registered for the current season. You are given a int[] weight, where the i-th element is the weight of the i-th wrestler. One or more of these wrestlers are registered in this week's tournament. You are given an int averageWeight, which is the exact average weight of the wrestlers registered in the tournament. Return the maximal possible weight of a wrestler who might be in this tournament, or -1 if the average is not possible with the given input.

Definition

Class:	SumoTournament
Method:	maxWeight
Parameters:	int[], int
Returns:	int
Method signature:	int maxWeight(int[] weight, int averageWeight)
(be sure your method is public)

Constraints

-

averageWeight will be between 1 and 200, inclusive.

-

weight will contain between 1 and 50 elements, inclusive.

-

Each element of weight will be between 1 and 200, inclusive.

Examples

0)

{80,90,100}

Returns: 100

There are three possible tournaments with an average weight of 90: {80,90,100}, {80,100}, {90}. Thus, it is possible that the wrestler with weight 100 is in the tournament.

1)

{81,90,150}

Returns: 90

2)

{10,20}

Returns: 20

3)

{40,30,20,10}

Returns: -1

There is no way to achieve an average weight of 27.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SchoolTrip

Dynamic Programming, Math, Recursion

Used in:

SRM 384

Used as:

Division I Level Two

Writer:

rasto6sk

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7657

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10808&pm=7657

Problem Statement

There are n students standing in a circle and playing a game with a ball. The students are numbered from 0 to n-1 in clockwise order. On each turn, a student must take the ball and throw it at another student in the circle. Student i has a probability[i] percent chance of hitting the target student, and if he is successful, the student who is hit must leave the circle. Turns go in clockwise order, and student 0 gets the first turn. They are not allowed to skip turns. The game ends when there is only one student left in the circle.

The students are playing this game against their will, so their common goal is to finish the game in the least number of turns. Return the expected number of turns the game will last.

Definition

Class:	SchoolTrip
Method:	duration
Parameters:	int[]
Returns:	double
Method signature:	double duration(int[] probability)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

-

Each student does not worry about how long he will stay in the circle, only the total game time matters.

Constraints

-

probability will contain between 2 and 6 elements, inclusive.

-

Each element of probability will be between 10 and 100, inclusive.

Examples

0)

{100,23}

Returns: 1.0

The first student will certainly hit the second one, so the game will be finished after 1 turn.

1)

{50,50}

Returns: 2.0

With probability 1/2 the game will be finished after 1 turn, with probability 1/4 after 2 turns, .. with probability 1/2^k after k turns. The infinite sum 1*1/2 + 2*1/4 + 3*1/8 +.. n*1/2^n = 2.

2)

{25,50,75}

Returns: 3.892383478590375

3)

{100,100,100,42,11}

Returns: 4.0

The first two students will start out by hitting the last two students. After that, there will be three students remaining, and all of them always hit their targets, so only two more turns will be required for the game to end.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CarBuyer

Simple Math, Sorting

Used in:

SRM 347

Used as:

Division II Level One

Writer:

StevieT

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7652

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10671&pm=7652

Problem Statement

You wish to buy a new car and would like to get the cheapest option available. However, you recognize that the initial purchase cost is only a part of what you will need to spend on the car and you want to factor tax and fuel costs into your decision. You will be given a String[] cars giving the specifications of various models of car and an int annualDistance containing the distance that you will drive each year. For the car that you choose, the purchase cost only has to be paid once, the tax cost specific to the model has to be paid once per year and the fuel cost should be calculated as FUEL PRICE * DISTANCE DRIVEN / FUEL EFFICIENCY, where the fuel efficiency is specific to the car. You should calculate which car model in cars has the lowest cost on aggregate after years amount of time and return a double containing this cost.

Each element of cars will be formatted "<PURCHASE COST> <TAX> <FUEL EFFICIENCY>" (quotes for clarity).

Definition

Class:	CarBuyer
Method:	lowestCost
Parameters:	String[], int, int, int
Returns:	double
Method signature:	double lowestCost(String[] cars, int fuelPrice, int annualDistance, int years)
(be sure your method is public)

Notes

- The return value must be accurate to within an absolute or relative tolerance of 1e-9.

Constraints

- cars will contain between 1 and 50 elements, inclusive.

- Each element of cars will contain between 5 and 15 characters, inclusive.

- Each element of cars will be formatted "<PURCHASE COST> <TAX> <FUEL EFFICIENCY>".

- Each <PURCHASE COST> will be an integer, without leading zeros, between 1 and 100000, inclusive.

- Each <TAX> will be an integer, without leading zeros, between 1 and 1000, inclusive.

- Each <FUEL EFFICIENCY> will be an integer, without leading zeros, between 1 and 100, inclusive.

- fuelPrice will be between 1 and 100, inclusive.

- annualDistance will be between 1 and 100000, inclusive.

- years will be between 1 and 100, inclusive.

Examples

0)

{"10000 50 50","12000 500 10","15000 100 65","20000 20 80","25000 10 90"}

Returns: 10500.0

Here, fuel is cheap, you have a low annual mileage and you don't want to keep the car very long, so you go with the first model, which has the lowest purchase cost.

1)

{"10000 50 50","12000 500 10","15000 100 65","20000 20 80","25000 10 90"}

Returns: 45200.0

This is the same set of cars, but this time fuel is far more expensive and you're going to keep the car for longer and drive it further. Now the more fuel-efficient fourth model is the cheapest.

2)

{"8426 774 19","29709 325 31","30783 853 68","20796 781 3"
,"27726 4 81","20788 369 69","17554 359 34","12039 502 24"
,"6264 230 69","14151 420 65","25115 528 70","22234 719 55"
,"2050 926 40","18618 714 29","173 358 57"}

Returns: 254122.44444444444

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Pathfinding

Geometry, Simple Math

Used in:

SRM 345

Used as:

Division I Level One , Division II Level Two

Writer:

rusolis

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7649

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10669&pm=7649

Problem Statement

Recently you have been working on the pathfinding module for your AI system. Your objective is to find the shortest path for an agent that wants to travel between two points on a plane. The agent will start at the point (0,0), and travel to the point (x,y). You decided that the agent will move either on horizontal of vertical lines such that, at every moment, at least one coordinate of the agent is an integer.

There is yet another restriction however. Each line will only allow movement in one direction. All horizontal lines with odd y-coordinates will be directed toward decreasing values of x, and all other horizontal lines toward increasing values of x. Similarly, all vertical lines with odd x-coordinates will be directed toward decreasing values of y, and all other vertical lines toward increasing values of y.

Given x and y, return the distance that the agent must travel.

Definition

Class:	Pathfinding
Method:	getDirections
Parameters:	int, int
Returns:	int
Method signature:	int getDirections(int x, int y)
(be sure your method is public)

Constraints

-

x and y will both be between -10^6 and 10^6, inclusive.

Examples

0)

-4

Returns: 8

A possible path from (0,0) to (0,-4) is through the points (1,0), (1,-3), (-1,-3) and (-1,-4).

1)

-4

Returns: 9

2)

Returns: 9

3)

-1

-4

Returns: 7

4)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PacketRepack

Simple Math

Used in:

TCO07 Qual 3

Used as:

Division I Level One

Writer:

legakis

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7642

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10735&pm=7642

Problem Statement

You are writing a function to make two pieces of network equipment from different vendors talk to each other. They send and receive data packets with the same data fields, but arranged in opposite orders. Given a data packet from one piece of equipment, reverse the order of the data fields so the second piece of equipment can read it.

The input data will be packed into N b-bit words, for a total of N*b bits. These words will be given to you as a int[] input. The bit 0 of input[0] is bit 0 of the data packet, and bit b-1 of input[N-1] is bit N*b-1 of the data packet. There will be num_fields fields, each field_size bits long. The first field is packed into bits 0 through field_size-1, the second field is packed into bits field_size through field_size*2-1, etc.

For example, given an input packet of { 22, 37, 3 }, with 6-bit words, and four 4-bit fields, the fields would be extracted as shown below:


     input[2]    input[1]    input[0]
         |           |           |
    ----------- ----------- -----------
    0 0 0 0 1 1 1 0 0 1 0 1 0 1 0 1 1 0
        ------- ------- ------- -------
           |       |       |       |
           D       C       B       A

Where A is the first field, B is the second field, C is the third field, and D is the forth field. These fields have the values 6, 5, 9, and 3, respectively. Reversing the order, the fields would be repacked like this:


     output[2]   output[1]   output[0]
         |           |           |
    ----------- ----------- -----------
    0 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 1 1
        ------- ------- ------- -------
           |       |       |       |
           A       B       C       D

and the correct output is { 19, 22, 6 }.

As shown in the example above, the upper bits of the packet may be unused. These bits will be zero in the input, and must be set to zero in the output as well.

Definition

Class:	PacketRepack
Method:	output
Parameters:	int[], int, int, int
Returns:	int[]
Method signature:	int[] output(int[] input, int b, int num_fields, int field_size)
(be sure your method is public)

Constraints

-

input will contain between 1 and 10 elements, inclusive.

-

Each element of input will be between 0 and 2^b-1, inclusive.

-

b will be between 1 and 31, inclusive.

-

field_size will be between 1 and 31, inclusive.

-

The size of input multipled by b will be greater than or equal to num_fields*field_size.

-

Unused bits in the packet will be zeroes.

Examples

0)

{ 22, 37, 3 }

Returns: {19, 22, 6 }

This is the example from the problem statement.

1)

{ 1, 0 }

Returns: {512, 0 }

This 62-bit input packet has ten 1-bit fields, and 52 leading zeros. The first field (bit 0) is 1, and the other nine are 0.

In the output, the tenth field (bit 9) should be set to 1, and all other bits should be 0.

2)

{ 1, 0, 0, 0 }

Returns: {0, 0, 0, 1 }

3)

{ 15834, 2483, 19423 }

Returns: {53074, 60455, 27516 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BalancingGame

Dynamic Programming, Math

Used in:

TCO07 Qual 3

Used as:

Division I Level Three

Writer:

legakis

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7636

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10735&pm=7636

Problem Statement

NOTE: This problem statement contains subscripts and superscripts that may not appear correct when viewed outside of the contest applet.

You are playing a game with a flat board on top of a thin post. On this board are items of various weights, placed in a such a manner that the board balances on top of the post. You and your opponent take turns removing items from the board. If at any time the board falls off the post, whoever removed the last item causing the board to fall loses. If all objects are removed without the board falling, the player who moved first loses.

The board balances if the magnitude of the total torque due to the weight of all objects upon it does not exceed a given threshold. The torque due to a single object is a vector in the plane of the board, computed as:


    (Tx,Ty) = (-y*w,x*w)

Where x and y are the position of the object, and w is its weight. Assume the board is centered on the post, and that the torque due to its own weight is zero. The total torque is the sum of the torque vectors for each object, and the magnitude is the length of that sum.

The position and weight of the objects will be given by three int[] parameters: x, y, and w. x[i], y[i] gives the position of object i, and w gives its weight. The x,y coordinates are relative to the origin, the point where the board rests on the post. Multiple objects can not have the same position on the board.

Return a list of all the objects that the first player could remove on his first turn in order to win the game, assuming that both players play optimally. The return value should be a int[], where each element corresponds to an entry in the x, y, and w int[]s. The elements should be sorted in ascending order. If there are no possible winning moves, return an empty int[].

If the initial state of the board is unbalanced, it will fall before the first player has a chance to make a move. In this case, return { -1 }.

Definition

Class:	BalancingGame
Method:	winningMoves
Parameters:	int[], int[], int[], int
Returns:	int[]
Method signature:	int[] winningMoves(int[] x, int[] y, int[] w, int threshold)
(be sure your method is public)

Notes

-

(x₁, y₁) + (x₂, y₂) = (x₁ + x₂, y₁ + y₂).

-

The square of the length of (x, y) is x² + y².

Constraints

-

x will contain between 1 and 20 elements, inclusive.

-

x, y, and w will all contain the same number of elements.

-

Each element of x and y will be between -100 and 100, inclusive.

-

Each element of w will be between 1 and 100, inclusive.

-

threshold will be between 0 and 1000000000, inclusive.

-

No two objects will occupy the same position.

Examples

0)

{ -10, 0, 10 }

{ 0, 0, 0 }

{ 5, 5, 5 }

Returns: {1 }

There are three objects, one in the center of the board and two others at equal distances and opposite directions from the center. If the first player removes the center object first, the board will continue to balance perfectly. But, the board will fall if the second player removes either of the remaining objects. Therefore, this is a winning move for the first player.

The other two possible moves for the first player are losing moves, because the board will fall immediatly if either of the other two objects are removed first.

1)

{ 1, -1, 1, -1 }

{ -1, -1, 1, 1 }

{ 2, 3, 4, 5 }

Returns: { }

With such a high threshold, the objects can be removed in any order without the board ever falling. Since all moves lead to an empty board, the first player always loses.

2)

{ 0 }

{ 10 }

{ 50 }

Returns: {-1 }

3)

{ -20, -21, 60 }

{ 0, 0, 0 }

{ 20, 20, 10 }

Returns: {0, 1 }

The initial torque on the board is the sum of the vectors (0,-400) + (0,-420) + (0,600) = (0,-220). The magnitude of the torque, 220, is less than the threshold, so the board initially balances.

If the first player removes either of the objects with a weight of 20, the resulting torque will be (0,180) or (0,200), which also balances. The second player loses, because removing either of the two remaining objects causes the board to fall.

If the first player removes the object with a weight of 10, the resulting torque will be (0,-820), and the board will fall.

4)

{ -3, -30, 0, 0, 3, 30 }

{ -2, 20, 3, -30, -2, 20 }

{ 6, 50, 7, 51, 8, 52 }

Returns: {0, 2, 4 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Candles

Math

Used in:

TCO07 Round 3

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7622

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10751&pm=7622

Problem Statement

In Computer Science we hold weird ceremonies -- at each ceremony we display all our candles but only n of them are lit (yeah, a binary code). Unfortunately we have 2 different types of candles: we have n1 candles that each burn at the rate r1, and n2 candles that each burn at the rate r2. (The rates are in mm/hr.)

Before each ceremony we can choose which n of our candles will be the ones that are lit during the ceremony -- we do this in an attempt to keep our candles approximately the same length. Given n, n1, r1, n2, and r2 return the number of ceremonies required for us to return our candles to uniform length. If we can never achieve uniform length, return -1.

(You may assume that our candles are arbitrarily long or that our ceremonies are arbitrarily short so we won't completely burn up any candles.)

Definition

Class:	Candles
Method:	ceremonies
Parameters:	int, int, int, int, int
Returns:	int
Method signature:	int ceremonies(int n, int n1, int r1, int n2, int r2)
(be sure your method is public)

Constraints

-

n, n1, r1, n2, r2 will all be between 1 and 1000, inclusive.

-

n1+n2 will be greater than n.

Examples

0)

Returns: 2

We have 6 type 1 candles and 4 type 2's and we burn 5 candles at each ceremony. Here they burn at the same rate, so we can burn any 5 of them during the first ceremony and the other five at the next ceremony.

1)

Returns: 8

For the first 6 ceremonies we could burn fresh candles, 2 of type 1 and 1 of type 2. At that point the type 1 candles will be shorter than the type 2 candles. For the last 2 ceremonies burn 3 type 2 candles and then the other 3 type 2 candles -- all the candles will now be the same length.

2)

Returns: -1

We don't have much choice here. In each ceremony we must burn all our candles except for 1. We will never be able to burn enough of the slower burning candles to get them as short as the others.

3)

Returns: 125

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ToolingUp

Math, Search

Used in:

TCO07 Semi 3

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , Cosmin.ro , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7621

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10841&pm=7621

Problem Statement

The least common multiple (lcm) of a set of positive integers is the smallest integer that is divisible by each member of the set. It is frequently desirable to have a collection of numbers whose lcm is large.

We want to manufacture parts in a greater variety of sizes -- specifically our goal is to offer sizes whose lcm is greater than or equal to targetLcm. But every new size s that we manufacture costs us s dollars to tool up to produce.

The int[] sizes contains all the sizes we are currently producing. The String targetLcm represents an integer with no leading zeroes. Return the minimum cost of offering additional sizes that will let us achieve our goal.

Definition

Class:	ToolingUp
Method:	cost
Parameters:	String, int[]
Returns:	int
Method signature:	int cost(String targetLcm, int[] sizes)
(be sure your method is public)

Constraints

-

targetLcm will contain only digits ('0' - '9').

-

targetLcm will represent an integer between 1 and 10¹⁵, inclusive.

-

targetLcm will not contain leading zeroes.

-

sizes will contain between 1 and 50 elements, inclusive.

-

Each element of sizes will be between 1 and 1000, inclusive.

Examples

0)

"193"

{82,13,100}

Returns: 0

Our existing sizes already have a big enough lcm.

1)

"1000000"

{100,92,77}

Returns: 9

We can produce a single new size of 9 to get an lcm greater than 1,000,000. (We could also achieve our goal by adding the two sizes 3 and 8, but that would cost 11.)

2)

"999999"

{124,600,7,8}

Returns: 11

3)

"123456789123"

{31,1,1,6}

Returns: 120

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Defects

Math, Simple Search, Iteration

Used in:

TCO07 Round 2

Used as:

Division I Level One

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7615

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10749&pm=7615

Problem Statement

A rectangular chip has some defects on its perimeter. We want to locate a component on the perimeter of the chip as far as possible from the defects. Specifically, we want to maximize the sum of the distances from the connector to the defects, where the distance between the component and a defect is the distance when travelling along the perimeter. (The distance is the shorter of the counterclockwise or clockwise distances.)

The width of the chip is w and its height is h. Positions are given using a coordinate system in which the corner opposite the corner (0,0) is (w,h). Given w and h and double[]s defectw and defecth, return the maximal sum of distances to our component.

The i-th elements of defectw and defecth give the coordinates of the i-th defect.

Definition

Class:	Defects
Method:	maxSum
Parameters:	int, int, double[], double[]
Returns:	double
Method signature:	double maxSum(int w, int h, double[] defectw, double[] defecth)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

w and h will be between 1 and 100, inclusive.

-

defectw will have between 1 and 30 elements, inclusive.

-

defecth will have the same number of elements as defectw.

-

Each coordinate pair in defectw and defecth will be on the chip perimeter.

Examples

0)

{0.0}

{0.0}

Returns: 2.0

The chip has one defect, located in the corner. Locate the component on the opposite corner. Its distance along the perimeter to the defect is 2.

1)

{0,0,2}

{1,1,0}

Returns: 6.0

There are 3 defects located at (0,1), (0,1), and (2,0). We can place the component at (2,0), right on top of one of the defects. Then the sum of the distances to the defects will be 3+3+0 = 6. If we placed the component elsewhere we could not get a sum of more than 6. For example, if we placed it at (2,1), its sum would be 2+2+1 < 6.

2)

{0,0,35,49,75}

{15,20,0,20,6.2934}

Returns: 277.2934

3)

{8, 0}

{0, 2}

Returns: 18.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SumsOfPerfectPowers

Simple Math, Simple Search, Iteration

Used in:

SRM 350

Used as:

Division I Level One , Division II Level Two

Writer:

Xixas

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7613

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10674&pm=7613

Problem Statement

A non-negative integer n is said to be a sum of two perfect powers if there exist two non-negative integers a and b such that a^m + b^k = n for some positive integers m and k, both greater than 1. Given two non-negative integers lowerBound and upperBound, return the number of integers between lowerBound and upperBound, inclusive, that are sums of two perfect powers.

Definition

Class:	SumsOfPerfectPowers
Method:	howMany
Parameters:	int, int
Returns:	int
Method signature:	int howMany(int lowerBound, int upperBound)
(be sure your method is public)

Constraints

-

lowerBound will be between 0 and 5000000, inclusive.

-

upperBound will be between lowerBound and 5000000, inclusive.

Examples

0)

Returns: 2

0 and 1 are both sums of two perfect powers since 0 = 0 + 0 and 1 = 1² + 0².

1)

Returns: 1

5 is a sum of two perfect powers since 5 = 2² + 1² while 6 is not.

2)

Returns: 5

Only 30 is not a sum of two perfect powers.

3)

Returns: 0

There may be no desired integers in the range.

4)

Returns: 33604

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DistanceBetweenStrings

Simple Math, String Manipulation

Used in:

SRM 350

Used as:

Division II Level One

Writer:

Xixas

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7606

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10674&pm=7606

Problem Statement

The distance between two strings with respect to a letter is defined as (n₁ - n₂)², where n₁ and n₂ are the number of occurrences (both lowercase and uppercase) of that letter in the first and second strings, respectively. The distance between two strings with respect to a third string is the sum of the distances between the two strings with respect to each letter in the third string.

You will be given three Strings a, b and letterSet. All the letters in letterSet will be distinct. Return the distance between a and b with respect to letterSet.

Definition

Class:	DistanceBetweenStrings
Method:	getDistance
Parameters:	String, String, String
Returns:	int
Method signature:	int getDistance(String a, String b, String letterSet)
(be sure your method is public)

Constraints

-

a will contain between 1 and 50 characters, inclusive.

-

a will contain only letters ('a'-'z', 'A'-'Z').

-

b will contain between 1 and 50 characters, inclusive.

-

b will contain only letters ('a'-'z', 'A'-'Z').

-

letterSet will contain between 1 and 26 characters, inclusive.

-

letterSet will contain only lowercase letters ('a'-'z').

-

Each character in letterSet will be distinct.

Examples

0)

"topcoder"

"contest"

"tcp"

Returns: 2

The letter 't' occurs once in the first string and twice in the second; the letter 'c' occurs once in the first string and once in the second; the letter 'p' occurs once in the first string and does not occur in the second one. The total distance is 1+0+1=2.

1)

"abcdef"

"fedcba"

"fed"

Returns: 0

The second string is a permutation of the letters in the first one thus the distance is 0.

2)

"aaaaa"

"bbbbb"

"a"

Returns: 25

The distance with respect to a single character in this case is 5*5=25.

3)

"aaAaB"

"BbaAa"

"ab"

Returns: 2

Lowercase and uppercase letters are regarded the same.

4)

"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"

"bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb"

"ba"

Returns: 5000

These two strings are quite far away.

5)

"ToPcOdEr"

"tOpCoDeR"

"wxyz"

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LumberjackExam

Math, Simulation

Used in:

TCO07 MM 3

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7604

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10747&pm=7604

Problem Statement

You are a lumberjack, and it is your job to inspect the forest before harvesting, to mark any trees that have been infected with a wood rotting disease. You only have a limited amount of daylight left, and therefore must work as efficiently as possible to mark off as many such trees as possible, while still having time to return to your starting point. (Otherwise, you would risk becoming hopelessly lost in the forest under the dark of night.) The trees are all arranged in a rectangular grid, so when standing in the middle of four surrounding trees, it is possible to look in any of the four cardinal directions, and attempt to determine visually if any of the trees are infected. Unfortunately, as trees are further away from you, it becomes more difficult to accurately determine whether or not they are infected.

You start at (0,0), the Northwest corner of the forest. At any given moment, you can move in a series of steps East/West/North/South, or look in any of the same four directions. Moving takes one unit of time per step. Looking in any of the four directions also takes one unit of time. Unfortunately, company policy forbids you from looking while moving, as you might trip as a result of not watching where you are going.

Your code must implement a method examineForest. You are given ints height and width describing the size of the forest, an int time indicating the maximum amount of time available before you run out of daylight, and a double density describing how thick the forest is. Your method should make use of the two available library functions, look and move, in order to move throughout the forest in search of infected trees. Your method should return 0 after you have returned to the point of origin.

Library Methods

look: This method should be called with a single String parameter ("E", "W", "S" or "N") indicating the direction you want to look. The method will return a String[] containing exactly two elements. The first element represents your assessment of the row of trees to your left, and the second element your assessment of the row of trees to your right (where left and right are relative to the direction you are looking, and the row extends away from you). Each character of each element represents your assessment of a single tree, and is either 'Y' or 'N', indicating that the tree does or does not appear to be infected. The first character is the tree directly in front of you, the next character is the tree behind it (relative to the direction you are looking), etc. The two trees directly in front of you are always assessed correctly, and are immediately marked when applicable. The probability of assessing a tree in the distance as being infected is described by: baseline * (1 - (1 - density)^distance) + (1 - density)^distance * I, where I is 0 for uninfected trees and 1 for infected trees, baseline is the proportion of infected trees throughout the whole forest, and distance is 0 for the trees directly in front of you, 1 for the next pair, and so on. If there are no trees in one of the rows (for example, if looking east from (0,0)) that element of the return will be the empty string.

move: This method should be called to move through the forest. The single String parameter should indicate the direction(s) you wish to move (in order), where each character is 'E', 'W', 'N' or 'S'. The return will be a int[], indicating your coordinates after moving. (ret[0] = x, ret[1] = y)

Scoring

Your raw score for each test case will simply be the number of infected trees you mark during your travel through the forest, presuming you make it back out within the given time. Any invalid parameters passed to the library methods will result in scoring a 0 for that test case. Any calls to the move method that would cause you to go outside the region from (0,0) to (width,height) will result in a 0 for that test case. If your method makes too many calls, such that your lumberjack is still in the forest after nightfall, you will score a 0 for that test case.

Your total score will be calculated by adding up your relative score for each test case. The relative score for a test case is given by the formula:

(my score for this test case) / (max score by anyone for this test case)

Test Case Generation

width, height, time, and density will be chosen uniformly at random.

We then select, all uniformly at random, M between 40 and 60, P between 10 and 15, q0 between 0.30 and 0.34, and q between 0.45 and 0.49.

We start with a width * height grid of trees. K = (width * height / 200) of them are chosen at random. Those K are the seeds. Each of those K start spreading disease at a random time -t, where t in [0..M - 1]. When spreading, each tree that is infected has an incubation period of P, after which it starts spreading the disease. That is to say, if a tree is infected at time t, then at time t + P it will infect other trees. A tree that has incubated immediately spreads disease to all other (not yet infected) trees, with probability q0 * q^dist (where dist is the Manhattan distance between the two trees). The disease spreading continues until time 0, when you enter the forest. At this point, the disease spreading process stops, (imagine that the disease spreading timescale is much longer than the timescale used for walking around). In pseudocode:

for K seeds 
	(x,y) = a random, uninfected tree
	t = -Random[0...M - 1]
	Mark(x, y) as infected
	Add (x, y) to incubation list at time t


While incubation list has trees 	
	currentTree = take earliest incubated tree from list
	for each tree in forest
		if tree is not already infected and Random < q0 * q^(man dist) then
			set tree as infected
			if (t + P <= 0) then
				add this tree to incubation list for time t + P

Visualizer

A visualizer is provided to help you develop your solution. The seeds for the examples are 1-10.

Definition

Class:	LumberjackExam
Method:	examineForest
Parameters:	int, int, int, double
Returns:	int
Method signature:	int examineForest(int height, int width, int time, double density)
(be sure your method is public)

Notes

-

The time limit is 20 seconds, and the memory limit is 64M.

-

The trees themselves are in between the coordinate points along which you move. That is to say that you can move between (0, 0) and (width, height), while the trees are located at points from (0.5, 0.5) to (width - 0.5, height - 0.5).

-

If nobody scores higher than a 0 for a given test case, then all relative scores will be 0 for that case.

-

The first four examples have been specially constructed outside of the normal constraints, to facilitate testing. The remaining examples follow the generation described in the problem statement.

-

There are 10 example cases and 40 non-example cases.

Constraints

-

width and height will be between 50 and 100, inclusive.

-

time will be between 200 and 2500, inclusive.

-

density will be between 0.05 and 0.30, inclusive.

Examples

0)

"1"

Returns: 
"20 x 20 grid, density = 0.15186, time = 1026
K = 2
M = 53
P = 12
q = 0.47843
q0 = 0.32635
baseline = 0.085

....................
....................
....................
....................
....................
....................
....................
....................
....................
......X.............
.....X..............
.....XX.............
..XX.X..............
..XXXXX.............
XXXX..X.X.......X...
....X..X............
.....XX.X...........
..X..XXX....XX......
.X..XX..............
...X................
 "

Here, the '.' represents a clean tree, and 'X' an infected tree. Note that you start above and to the left of the upper-leftmost '.'.

1)

"2"

Returns: 
"30 x 30 grid, density = 0.05104, time = 1435
K = 4
M = 55
P = 10
q = 0.48692
q0 = 0.30133
baseline = 0.06778

..............................
..............................
.........................X....
..........................X...
.........................XX...
.........................XX...
.........................X..X.
...........................X..
..............................
..............................
..............................
..............................
..............................
..............................
..............................
..............................
..............................
..............................
..................X.X.........
................X...X.........
.........X.....XX..XXX........
...............X..XX..X.......
.........X.....X.X..X..X......
...........X..X.XXXX.XX.......
.............X.X.XX...........
...........X..XX.X...X........
...........X..X.XXXX..........
...........XX...X.X...........
..........XXX.....X...........
.........X.......X............
 "

2)

"3"

Returns: 
"40 x 40 grid, density = 0.25131, time = 1655
K = 8
M = 55
P = 13
q = 0.48409
q0 = 0.32301
baseline = 0.075

........................................
...X...........X..X.....................
.................X......................
..........X..X.XX.......................
...XX...X.......X...X...................
...............XX.XXX...................
...X............XXXX.X..................
.............XX.XXXXX.X.................
..X..........X..XX.X.X.X................
..............XXX..X..X......X..........
..X.X.........XX.XX.XX..................
.............X.X.X..XX.X................
.........X...X.X........XX.....X..X.....
................X....X..X...........X...
.X......................X...............
......................XX...........X.XX.
.......................XX...........X...
.................................X.....X
......................X.........X....XX.
.....................................X..
......................................X.
.......................................X
........................................
........................................
........................................
........................................
......................................X.
....................................X...
.................................X....X.
...................................X..X.
...................................X....
........................................
........................................
........................................
X..X...............................X....
....X............................X.X....
....X...........................XX.XXX..
..X.X..........................X...XX...
..............................X.XX.XX...
..................................X.X...
 "

3)

"4"

Returns: 
"50 x 50 grid, density = 0.25268, time = 2384
K = 12
M = 52
P = 11
q = 0.46993
q0 = 0.31138
baseline = 0.0328

............X.X...................................
...............................................X..
...X...XX...X.....................................
...XX.............................................
.............................................X....
..................................................
............................................X.....
..................................................
...........................................X..X...
...........................................X.XX...
............................................X.X...
........................X......................XX.
.........................XX...................X...
........................XX........................
........................X.X.......................
..................X..XX...........................
..................X.XXX.X.........................
........................X.X.......................
..................................................
.....................X...XX.......................
........................X.........................
..................................................
.................X................................
.................................X................
.......................X..........................
..................................................
..................................................
..................................................
..................................................
..................................................
........................................X.X.......
.................................X.......X.X......
.....................................XX..X........
.................................XX..X.X..........
................................XX................
..............................XX.X................
..............................X...................
..................................................
..................................................
...X..............................................
..................................................
..................................................
..........XX......................................
..............X...................................
..................................................
.........X......XX................................
.........XXX.X.....X..............................
.........XX.XX....................................
.............X....X...............................
.........X........................................
 "

4)

"5"

Returns: 
"66 x 55 grid, density = 0.20295, time = 304
K = 18
M = 54
P = 14
q = 0.4671
q0 = 0.33305
baseline = 0.04298

..................................................................
..................................X.X.............................
..................................................................
.....X......XX......................X.X......X....................
..........X.X.........................X......X....................
..X.........X.X....................X.......XXX....................
..........X......................X......X...XX....................
.XXX.......X..............................XX.X....................
...........................................X......................
X.XX.XX...........................................................
X.....X.........................................XX................
..X..X............................................................
......X...........................................................
..........................XX.....................X................
........................X.........................................
........................XX........................................
.....................X....X.......................................
.......................XX.X.......................................
...............X..................................................
..................................................................
..................................................................
..........................X.......................................
........................XX.X......................................
..................................................................
..................................................................
.................X...XX...........................................
.....................X................................X.X.........
...............X..................................................
...............X..................................................
...............X..................................................
...............X..................................................
..................................................................
......................XX..X.......................................
...................X..XX..........................................
......................XX..........................................
..............XX..XX..............................................
...............X..X....................................X..........
..............X...................................................
..................................................................
..............X.XX.....................................X...XX.....
......................................................XX..........
.......................XX..............................X....X.....
.......................X...............................X..........
......................XX.X...................X....................
....................X..............................X..XX.X...XX...
.....................X...X..................X.....................
...........................................XX.X...XXX.XX..........
.......................................XXXXX......................
..........................................XX..X..X.X...X..........
..............................................X.X.................
.........................................XX..XX..XX...............
.......................................X.......X.X................
.........................................XX....X..................
.....................X....................X.X.XX..................
...........................................X.X.XX.................
 "

5)

"6"

Returns: 
"68 x 63 grid, density = 0.10213, time = 712
K = 21
M = 54
P = 15
q = 0.4756
q0 = 0.30803
baseline = 0.04505

....................................................X.X.............
...................................................XXXX.............
................................................X..X.X..XX..........
.........X..........................................X...X...........
................................................X..............X....
...........................................................X........
....................................................X.............X.
....................................................................
..................................................XXX..XX...........
.....................................................X...X..........
.....................................................X..X........X..
...................................................XX...X.......XX..
...................................................XX...........XX.X
...................................................X.X...........X.X
.....................................................XX........X.XX.
.....................................................X..........X.XX
..............................................................X.XXX.
...................................................................X
.X...........................................................X......
...X.............................................X..................
.X.X...............................................................X
..................................................X.X...............
......X...........................................XX................
....................................................................
.....................................................XX.X...........
.......................................................X............
....................................................................
....................X...............................................
............X.......................................................
....................................................................
...............XXX..................................................
.............X...X..................................................
...........X..X.....................X...............................
........X..XX.......................................................
.........X.XX.X.X.X.................................................
.......XX..X.X..X..........................X.X......................
.......XXXX.XX.X......................X....X............X...........
.....X.XX..XXXXX......X....................XX..........X.X..........
............X.XX............X.................XX........XX.X........
X.X..X.X..........................XX.......X........................
X.X.X..X....X...............X.....X........XXX...X..................
X.X..........X..X.......................X...XX.X....................
...X......................X.X.......X........X......................
...........................X..........XXX.X.........................
....X......................X........................................
....................................................................
....................................................................
........X.......................................X...................
.........X....................................X.....................
.........X.X........................................................
....................................................................
........X...........................................................
....X...X..X........................................................
...XXXX.X.X.........................................................
....X.X.............................................................
....X.XX............................................................
....XX..............................................................
.....X..............................................................
....................................................................
....................................................................
....................................................................
....................................................................
....................................................................
 "

6)

"7"

Returns: 
"76 x 60 grid, density = 0.05241, time = 398
K = 22
M = 53
P = 14
q = 0.47277
q0 = 0.3297
baseline = 0.08684

..........................X.X...............................................
.............................X.........................................X....
........................X.X..X.........................................X.X..
............................XXX.......................................XXX...
..............................XX.......................................X.X..
.......................................................................X.X..
..................................X.........................................
............................................................................
..................................X.............X......X....................
......................................X.X.................X.................
..................................XX....XX......X...........................
....................................X...X.....X......X.X....................
....................................XX.X.......X............................
..................................X..XX.......X...X..X......................
..................................X.X.X........XX......X....................
..................................XXX........X.XX.XX..X.....................
...................................X.XXX.....XX.XXXXXXXX....................
......................................XX.X...XX.XXXX.X.X....................
..............................................XX.XXX........................
..........................X..............X...XXXXXX...X.....................
.........................X.........X.X.X.............X.............X........
...............X........................X...X...X................X..........
............XXXX............X........X.X.........................X.X........
..........X.XXX......................X.....X..X....................X........
...........XXXX...X........................X..X....X........................
................X.....................................................XX....
......XX.X.X.XXX.................................................XX......X..
.......X..XX..XXX...........................................................
...........XX.X...X.........................................................
............X.X.............................................................
.......................................................................XXXXX
...........X...X...............X....................X.......................
......X........................XX.......................................XX..
..............................X.....................X.X.X...............XX..
..............................X.X..................XXXX................XXXXX
....................................................XXX...............X....X
......X.......................X.X................X......X.X..........X......
...................................................XXX...............X......
.....X.X.X......................XXX..................................XX.X...
.......X.........................X............X.............XX.......XX.....
...............................................X...X.....XXX.........X......
...............................................X...........X.X..............
.......................................................XX.X...XX.XX.........
.................................X.X....................X....XX.............
.................................XX.................X..XX.X....XX...........
..............................X...................X.....XXX..XX.XX..........
....................................................XXXXXXXX.XXXXXXX..XX....
.................................X..................XX.XX.X.XXXX...XXX......
X.X.............................XX..XX...............XXX.X..X.....X.........
X.XX...X...........X............X....X.............X.XX.X.........XXXX......
..XX.X......XX.......................................X.........X.X.XXXX.....
X.X.........XX.X.X.................................................X...X....
..........X.X.XX...................................................XXXX.....
...........XXXXX..................................................X.........
.......X..X.X...XXX................................................XX.......
..........X.XXX...................................................XXX.......
.....XX...XXXX.............................X.....................XXX........
.........XXXX..X............................X......................XXX......
..........XXX...............................X........................X......
..........X.X...............................................................
 "

7)

"8"

Returns: 
"90 x 99 grid, density = 0.05378, time = 1662
K = 44
M = 51
P = 13
q = 0.45861
q0 = 0.31808
baseline = 0.05713

..................X.....................................X.................................
................................................X.........................................
..................X..............................X.XX...X........................X........
...................................................X...X..................................
....................................X.............................................X.......
..................................X......................................X......X.........
..................................X............................................XXX...X....
........................................................................X........XXX......
......................................................................X..X......XXX.X.....
......................................................................X..X.X..............
...........X.........................................................X...XX........X......
........XX.X......................................................................XX......
.........XX.......X..X................................................X...................
.........X................................................................................
....................X.....................................................................
.......X..XX........XX..X.................................................................
.....XX..X.XX....XX..X....................................................................
.........XXXX......XXX.X..................................................................
.....X...XXX......XX......................................X...............................
.....X....XXXXX.....X.....................................................................
....X...XXXXX.X....X..XXX.........................................X.......................
..........XXXX.X......X..........................................X........................
...........X.XX...................................................X.......................
.............X..X.X...X.................................................................X.
.............X........................................................................XX.X
........................................................................................X.
......................................................................................XX..
....................................................................................X.X...
..........................................................................................
............................................X..................................X....X.XX..
....................................................................................XX....
......................................................X.....X....................X..XXXXXX
............................XX.............X.........................................XXXXX
..........................X.XX....................................................X..XX...
.......................X...XX...............................XX.X....................XX....
.........................XX.X.............................................................
.........................XXX..............................X...........................X...
......................X.......X..........................X...........................X....
............................................XX...........X.XXX.......................XXX..
......................X.XX...X..........................X...........................X...X.
.........................X..X.........................XXX.XX..............................
..............................X..............................X............................
.................X.X.X..X.X..X........................X..X.XX.............................
...................X..XXXX.X..X............................X..............................
...................X...X.X....X...........................XX..............................
.................XX.XXX..X................................................................
......................X...X.X.............................................................
....................X.......X.............................................................
..........................XXX.............................................................
............................X......................X.X....................................
..........................X...............................................................
.....................................................X....................................
..........................................................................................
....................................................X..XX.................X...............
........................................................X.X...............................
......................................................X......X............................
.......................................................X.....XX...........................
.X.........................................................XXX............................
..........................................X...............X.XXXX..........................
...............................................................X..........................
...............................................................X..X.......................
......................................................X.....X.............................
......................................................XXXXXXXX............................
.............................................................XX..X........................
.............................X..............................XXX.X.........................
...................................................................X.....................X
.................X.........X.X.........................................................XXX
............................X..........................X..X.X.X........................X..
.......................................................XX.X.X.............................
.................X.X..................................X...X.XXX...........................
.................X.....................................X..XXXXXXX.X.......................
...............X.....................................X.......XXXX.........................
............................X............................X..XXX.X..X......................
............................................X.............X...X.XX......X...............X.
........................................................X.XXXX.XXXX.XX.XXX................
................................................................X...XXX.X.................
.....................................................................X....................
.........................................X...............X..XX............................
......XX.................................X................................................
........X..X............................XX...................X.......X....................
.......................................X.......X..........................................
........................................X.....X...........................................
..........X..............................XX.X..XX.........................................
.........X................................X...........................X...................
.........X.......................................................X..................X.....
.......XXXXXX..X....X.......................X......................XX.....................
.X..........X..........X..................X..........................XXX..................
..X.......X.......X......................XX...................X.X.XX...X............XXXXX.
.XX.X..................X.....................................X..XXX.X...X............XX...
....X..X.X......................................................X............X..X....XX...
.X.X.X.X.X.......................................................XX...................X...
........X.X....................................................X.X.....X.X..........X..XX.
.X......X........................................................X.X...XX......X...X.XXX..
...XXX..................................................................X.........X.......
..XX.X...........................................................XX.................X.X.X.
...X.X...................X....X..................................XX....X.............XXXX.
..............................X......................................X......X.........X...
................................X...................................X.XX.X...........X....
..................................................................X.X.XXX...X.............
 "

8)

"9"

Returns: 
"72 x 96 grid, density = 0.25405, time = 1347
K = 34
M = 52
P = 15
q = 0.45578
q0 = 0.33975
baseline = 0.0515

...................X...X..X................................XXX..........
...................XXX..................................................
......................XX................................................
........................................................................
..........XX............................................................
...........XX...........................................................
...........X.......X....................................................
.........X.X....XXX.X...................................................
.................XX....XX...............................................
.............X....X.X...................................................
..............XX.X.XX...................................................
..................X.....................................................
..................X.....................................................
...............X........................................................
...............................................................X........
........................................................................
...................................................................X....
...............................................................X........
........................................................................
.................................X............................XX.X.X....
..............................XX........................X.X....X..XXX.XX
...............................................................X..X.....
........................................X.......................X.X.....
...............................X........XX...........X.........XX...X...
...........XX..............................X..................XXXX......
......X.......X...........................X.............................
.........X..X..X...........................X....................X.......
........XXXXXX.............................X.X..........................
.....X..XX.XXX...........................X.XXXX.........................
.........XX.XX..X..........................XX.X.........................
.........X.XXX............................XXXXX.........................
.........X...XX...........................XXXX.X........................
..........X..X...........................XXXXX..........................
...........X............................................................
.............X...........................X..............................
..X.....................................................................
........................................................................
........................................................................
........................................................................
........................................................................
........................................................................
........................................................................
........................................................................
......................................................X.................
........................X.............................X.................
........................X.............................XX.XX.............
.......................XX...................X...XXX.X..X..X.XXX.........
........................X........................XX....XX....XXX...X....
.......................................................X.X..XX.X........
........................................................XXX.X..XXXX.....
...........................X.........................X..XX.....XX.X.....
.........................XX.............X.........XX.X..X...............
...................X.....................XX......X.....X.X..............
..................XXX....X..X.............XXX............X..............
...................X.....XXX............X.XX......X.....................
.........................X..............X.X..X......................X...
.........................XXX..............X.....................XX.XX...
..........................X......................X..................X...
...................................................................X..X.
....................X................................................XX.
...............................X...................................XX.X.
.......................................................................X
...........................X............................................
................................X.......................................
.........................X..............................................
........................X.XXXXXX.XX.....................................
.......................XX..XX.XXX.......................................
..X...................X....X..X.........................................
............................XX.X.X......................................
.............................X..........................................
...............................X........................................
..............................X.........................................
........................X....X................................XX........
........................XX....X.............................XXXX........
...................X.....X....................................X.........
...................X....XX.....................................X........
...................X.X..........................X...........XXX.........
.............................XXX.X.............X..X...X......XX.........
..............................X..X.............X.X....X.................
.............................XXXX.X...........XXXX......................
.....X..........................X...........XX...X......................
.....X.....X................X....X........X.............................
....X.......................XXX.X.............X.........................
.............................XX.XX......................................
...............................X........................................
........................................................................
........................................................................
..............................X.........................................
........................X.....XX........................................
........................................................................
..............................X.........X...............................
........................................................................
........................................................................
........................................................................
............XXX.........................X...............................
............X.X.........................XXX.............................
 "

9)

"10"

Returns: 
"74 x 53 grid, density = 0.15323, time = 2291
K = 19
M = 53
P = 11
q = 0.46427
q0 = 0.31473
baseline = 0.06451

......................................................................X..X
.......X.......XX.....................................................XX..
...............X.XX..X.............................................XXXXXXX
.................XXX..X........................................X..XX.XX.X.
..................XXX..............................................X..XXXX
...............X.XX.X.....................X..X......................X..XXX
............X...XX.....X.X................X........................X...X.X
.............X.XX....X.XX...............XXX.........................X....X
............XXXXXX.X.....................XX.........................X..X..
............XXX.X.....X................X...X.........................X....
............XX.XX......................X.X..............................XX
........XX...XXX.........................XX........................X.X..XX
.........XXXXXXX........................X...........................XX....
...........X.XXX.........................X.........................X......
........X..XXXX..........................................................X
.......XX.XXXXXXXX........................XX..............X...............
.......XX..XXX.XX.........................XXXXX...........X...X...........
..........XXX...XX....................X...XX.X............X..XX...........
.........X...X..XX....................XX....X..............X.X............
XX...X..X...X..XXX........................................................
....X.XXX........X........................................................
....XX..........XX........................................................
..........................................................................
.....X................................X.XX................................
..........................................................................
...................................X......................................
..........................................................................
..................X.....................X.................................
..........................................................................
...................................X................................X...X.
..........................................................................
....................................................................XX.X..
..........................................................................
.....................................................................X....
X...................................................................X.....
.X...................................................................X....
...................................................................XXX....
....................................................................XXX...
..................................................................XX......
..................X.X.................................................XX..
...................................................................X......
.X..................X..............X............X..................X..XX.X
......................................X................X..........X...XX..
.X...............................................X.X................XX....
..................X.X........................X......................X.....
..................X.............................X..................XXXX...
..............X........................................................X..
..........................................................................
......................................................................X...
..........................................................................
..........................................................................
..........................................................................
..........................................................................
 "

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BooksNumbering

Simple Math, Simple Search, Iteration

Used in:

TCHS SRM 37

Used as:

Division I Level Two

Writer:

Janq

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7602

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10776&pm=7602

Problem Statement

A new library was founded in our city. The books were labeled 1, 2, 3, 4, etc., with no leading zeroes. A total of usedDigits digits were used to create the labels. Return the total number of books in the library, or -1 if usedDigits does not correspond to a valid solution.

Definition

Class:	BooksNumbering
Method:	numberOfBooks
Parameters:	int
Returns:	int
Method signature:	int numberOfBooks(int usedDigits)
(be sure your method is public)

Constraints

-

usedDigits will be between 1 and 2 * 10⁹, inclusive.

Examples

0)

Returns: 10

Each of the first 9 numbers (1-9) contain one digit. Number 10 contains 2 digits. Therefore, there's a total of 11 digits.

1)

Returns: -1

There is no possible solution. It takes 9 digits to label 9 books, and 11 digits to label 10 books.

2)

Returns: 99

3)

Returns: 100

4)

Returns: 7

5)

1863927342

Returns: 219448716

6)

1863927343

Returns: -1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DiceGames

Dynamic Programming, Math

Used in:

SRM 349

Used as:

Division I Level Two

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7601

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10673&pm=7601

Problem Statement

You are attempting to create a new game that is played by rolling several dice. In order to determine scoring, you need to first know how many different formations can be rolled with those dice. We define a formation as the collection of values that are shown on the dice, without regard to order. Thus, {1, 1, 2}, {1, 2, 1}, and {2, 1, 1} are all the same formation, whereas {1, 1, 2}, {1, 2, 2} and {1, 1, 3} are all different formations. Note that even though two dice may have a different number of sides, for the purpose of counting formations, only the number shown on them matters.

You are given a int[] sides, where the i-th element is the number of sides on the i-th die. The sides of an n-sided die contain all numbers between 1 and n, inclusive. Return the number of different formations that can be made from those dice.

Definition

Class:	DiceGames
Method:	countFormations
Parameters:	int[]
Returns:	long
Method signature:	long countFormations(int[] sides)
(be sure your method is public)

Constraints

-

sides will contain between 1 and 32 elements, inclusive.

-

Each element of sides will be between 1 and 32, inclusive.

Examples

0)

{4}

Returns: 4

A single die with four sides can have four formations.

1)

{2, 2}

Returns: 3

This is essentially the equivalent of flipping two coins. We can get Heads/Heads, Heads/Tails, or Tails/Tails.

2)

{4, 4}

Returns: 10

Here, there are 10 formations we can make:

{1, 1}, {1, 2}, {1, 3}, {1, 4}, {2, 2}, {2, 3}, {2, 4}, {3, 3}, {3, 4}, {4, 4}.

3)

{3, 4}

Returns: 9

Now it is impossible to get {4, 4} because the first die has only 3 sides.

4)

{4, 5, 6}

Returns: 48

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StarsInGraphs

Dynamic Programming, Graph Theory, Math, Search

Used in:

SRM 350

Used as:

Division I Level Two

Writer:

Xixas

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7593

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10674&pm=7593

Problem Statement

You are given the adjacency matrix of a directed graph as a String[] adjacencyMatrix. The j-th character of the i-th element of adjacencyMatrix will be '1' if there is an edge going from the i-th vertex to the j-th, or '0' otherwise. A star in a directed graph is defined as follows: it is comprised of a central vertex and at least three distinct edges emanating from it, which we will call the rays of the star. The number of rays in a star is not bounded; the only restriction is that there must be at least 3 of them. The number of distinct stars for which a vertex V is central will be called the star number of V. For example, if V has 5 edges emanating from it then its star number is 16 = 10 + 5 + 1 since it is central for 10 stars with 3 rays, 5 stars with 4 rays, and 1 star with 5 rays. We will call a path in our graph starry if it satisfies two conditions:

Each vertex belonging to the path has a non-zero star number not exceeding C.
Given two subsequent vertices V_i and V_i+1 in the path the star number of V_i+1 is not less than the star number of V_i.

Given the directed graph in the form of its adjacency matrix return the number of vertices in the longest starry path it contains. If there is a starry path of infinite length in the graph return -1. If there are no starry paths (all vertices have star numbers either 0 or greater than C) return 0.

Definition

Class:	StarsInGraphs
Method:	starryPaths
Parameters:	String[], int
Returns:	int
Method signature:	int starryPaths(String[] adjacencyMatrix, int C)
(be sure your method is public)

Notes

-

Two stars are considered distinct if either their central vertices are distinct or the sets of rays are distinct.

Constraints

-

adjacencyMatrix will contain between 2 and 50 elements, inclusive.

-

The number of characters in each string of the adjacencyMatrix will be equal to the total number of elements in adjacencyMatrix.

-

Every character of each element of adjacencyMatrix will be either '0' (zero) or '1' (one).

-

The i-th character of the i-th element of adjacencyMatrix will be '0'.

-

C will be between 1 and 10⁹, inclusive.

Examples

0)

{"01110",
 "10111",
 "00000",
 "00000",
 "00000"}

Returns: 2

The starry path 0 -> 1 is the longest one. Vertex 0 has star number 1, vertex 1 has star number 5, and all other vertices have star numbers 0.

1)

{"01011",
 "00111",
 "10011",
 "00000",
 "00000"}

Returns: -1

Vertices 0, 1, and 2 have star numbers 1 and form a cycle, thus we have an infinite starry path.

2)

{"0111",
 "0000",
 "0000",
 "0000"}

Returns: 1

This time the longest starry path consists of a single vertex.

3)

{"01111",
 "00000",
 "00000",
 "00000",
 "00000"}

Returns: 0

Vertex 0 has star number 5 and the rest of the vertices have a zero star number, and thus none of them can appear in a starry path.

4)

{"010001100",
 "001001100",
 "000101110",
 "000010111",
 "000001111",
 "010000000",
 "000110000",
 "000100001",
 "100001000"}

Returns: 5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FlightScheduler

Math, Search

Used in:

SRM 347

Used as:

Division I Level Two

Writer:

StevieT

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7584

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10671&pm=7584

Problem Statement

The Breguet range equation tells us how far an aircraft can fly if it has a given mass of fuel on board. It states that the maximum range of an aircraft R is given by:

R = K * ln(take-off mass / empty mass)

where K is a constant for the aircraft and the take-off mass is equal to the empty mass + the mass of fuel on board the aircraft. In addition, taking off and gaining altitude takes a certain, constant amount of fuel.

An airline wishes to minimize the amount of fuel consumed on a given journey by allowing the aircraft to stop at intermediate cities along the way to refuel. Assume that the aircraft can stop an unlimited number of times and can stop at any point of its journey. Also assume that it can carry an unlimited amount of fuel.

You will be given an int distance, the total distance of the journey, the int value K for the aircraft, an int emptyMass containing the empty mass of the aircraft and an int takeoffFuel containing the additional mass of fuel required each time the aircraft takes off. You should return a double containing the minimum amount of fuel required to complete the journey.

Definition

Class:	FlightScheduler
Method:	minimizeFuel
Parameters:	int, int, int, int
Returns:	double
Method signature:	double minimizeFuel(int distance, int K, int emptyMass, int takeoffFuel)
(be sure your method is public)

Notes

- The return value must be accurate to within an absolute or relative tolerance of 1e-9.

Constraints

- distance will be between 1 and 200,000, inclusive.

- K will be between 1 and 200,000, inclusive.

- emptyMass will be between 1 and 200,000, inclusive.

- takeoffFuel will be between 1 and 200,000, inclusive.

Examples

0)

Returns: 76420.82744805096

The optimal schedule here is to make 1 stop right in the middle of the flight.

1)

Returns: 138450.61724934017

K is a measure of the efficiency of the aircraft. With this less efficient aircraft it's best to stop twice.

2)

Returns: 2664.9853821314487

3)

Returns: 24635.869665316768

4)

Returns: 3.6576871282155204E8

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Chessboard

Simple Math

Used in:

SRM 344

Used as:

Division II Level One

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7576

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10668&pm=7576

Problem Statement

A 8x8 chessboard is usually marked as follows: rows are marked by digits, 1 through 8, and columns are marked by letters, 'a' through 'h'. A cell is described by its column mark and then its row mark, like "e4".

While working on a chess program, you need to convert these descriptions into your internal cell numbers and back. Internally, cells are numbered row-by-row from 1 to 64 in your program, i.e., cell "a1" has number 1, cell "b1" has number 2, cell "c1" has number 3, ..., cell "h8" has number 64.

Given a String cell, describing either the cell mark or the cell number, change the notation (i.e., if you're given the mark you need to return the number, and vice versa).

Definition

Class:	Chessboard
Method:	changeNotation
Parameters:	String
Returns:	String
Method signature:	String changeNotation(String cell)
(be sure your method is public)

Constraints

-

cell will contain either a cell mark or a cell number.

-

If cell contains a cell mark, it will contain exactly 2 characters: a lowercase letter between 'a' and 'h', inclusive, followed by a digit between '1' and '8', inclusive.

-

If cell contains a cell number, it will be an integer between 1 and 64, inclusive, without leading zeros.

Examples

0)

"1"

Returns: "a1"

1)

"2"

Returns: "b1"

2)

"26"

Returns: "b4"

3)

"c1"

Returns: "3"

4)

"e4"

Returns: "29"

5)

"h8"

Returns: "64"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HittingPerfectTarget

Brute Force, Geometry, Math, Simple Search, Iteration

Used in:

SRM 365

Used as:

Division II Level Three

Writer:

Xixas

Testers:

PabloGilberto , Yarin , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7575

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10780&pm=7575

Problem Statement

A player is going to throw a dart. It is guaranteed that the dart will hit a lattice point (a point whose coordinates are both integers) within a square whose vertices are (-100, -100), (-100, 100), (100, 100), (100, -100). All such lattice points have the same probability of being hit.

In this problem, a point is considered to be within a convex polygon if it lies in the interior of the polygon or on its boundary. In addition, a convex polygon A is considered to be within a convex polygon B if all the points in A are within polygon B.

You are given two convex polygons, both of which are within the square. A shot is said to be lucky if the dart hits a point that is within both polygons. Return the probability that the player's shot will be lucky.

The coordinates of the vertices of the first polygon will be given as two int[]s x1 and y1. The coordinates of the i-th vertex of the polygon are (x1[i], y1[i]). The vertices will not be given in any specific order (so they are not necessarily in clockwise or counter-clockwise order), but it will be possible to construct a convex polygon using each vertex exactly once. The second polygon will be described in an analogous manner using int[]s x2 and y2.

Definition

Class:	HittingPerfectTarget
Method:	getProbability
Parameters:	int[], int[], int[], int[]
Returns:	double
Method signature:	double getProbability(int[] x1, int[] y1, int[] x2, int[] y2)
(be sure your method is public)

Constraints

-

x1, x2, y1, and y2 will each contain between 3 and 15 elements, inclusive.

-

x1 and y1 will contain the same number of elements.

-

x2 and y2 will contain the same number of elements.

-

Each element of x1, x2, y1, and y2 will be between -100 and 100, inclusive.

-

(x1[i], y1[i]) and (x1[j], y1[j]) will be distinct whenever i and j are distinct, i.e., no two vertices of the first polygon will coincide (have both their x and y coordinates equal).

-

(x2[i], y2[i]) and (x2[j], y2[j]) will be distinct whenever i and j are distinct, i.e., no two vertices of the second polygon will coincide (have both their x and y coordinates equal).

-

It will be possible to construct a convex polygon using each of the points (x1[i], y1[i]) exactly once as its vertices.

-

It will be possible to construct a convex polygon using each of the points (x2[i], y2[i]) exactly once as its vertices.

-

No three vertices of the first polygon will lie on a single line.

-

No three vertices of the second polygon will lie on a single line.

Examples

0)

{-100, -100, 100, 100}

{-100, 100, -100, 100}

{-100, -100, 100, 100}

{-100, 100, -100, 100}

Returns: 1.0

Both polygons are just the big square.

1)

{-99, -98, 0}

{-99, 99, 0}

{99, 98, 0}

{-99, 99, 0}

Returns: 2.475186257765897E-5

Hitting the origin is the only way to make a lucky shot.

2)

{0, 0, 1, 1}

{0, 1, 0, 1}

{-54, -99, -100, -100}

{-54, 99, 100, -100}

Returns: 0.0

These polygons are disjoint so it is impossible for the dart to hit a point that is within both of them.

3)

{-1, 1, -30, 30, 0}

{-1, -1, 30, 30, 50}

{-2, 2, -60, 60, 0}

{-2, -2, 60, 60, 100}

Returns: 0.03895943169723522

The first polygon lies within the second one.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FractionPoints

Advanced Math, Recursion, Sorting

Used in:

TCHS07 Gamma 2

Used as:

Division I Level Two

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7565

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10718&pm=7565

Problem Statement

The statistical term median can be thought of as the "middle point" of a set of data. To determine a median, we first start with an ordered set of data. For an odd number of data points, the median is simply the middle point. For an even number of data points, the median is the average (mean) of the two middle points. Examples:

{1, 2, 3, 5, 7} - median = 3
{1, 2, 3, 6, 7, 8} - median = (3 + 6) / 2 = 4.5

We can think of the median of a set of data as the 1/2 way point which divides our data into a lower and upper half. When there are an odd number of data points, the median point does not belong to either set. If we take the medians of the lower and upper halves of data, we can similarly determine the 1/4 and 3/4 points within our data. (These are also known as "quartiles", see notes section for clarification.) Applying this to the two examples above:

{1, 2, 3, 5, 7} - median = 3
- {1, 2} - 1/4 point = (1 + 2) / 2 = 1.5
- {5, 7} - 3/4 point = (5 + 7) / 2 = 6
{1, 2, 3, 6, 7, 8} - median = (3 + 6) / 2 = 4.5
- {1, 2, 3} - 1/4 point = 2
- {6, 7, 8} - 3/4 point = 7

Similarly, we could expand upon this definition to subdivide at the 1/4 and 3/4 points, and find the 1/8, 3/8, 5/8 and 7/8 points, and so on. You are given a int[] data, your set of data points. You are also given an int numerator and an int denominator, describing the data point (as the numerator and denominator of a fraction) you need to find. Your method should return the required data point, based upon the definitions above.

Definition

Class:	FractionPoints
Method:	findPoint
Parameters:	int[], int, int
Returns:	double
Method signature:	double findPoint(int[] data, int numerator, int denominator)
(be sure your method is public)

Notes

-

Statistical definitions, particularly for quartiles, may vary depending upon the source and implementation. For this problem, we will adhere to the definition given within.

-

The return value must be within 1e-9 absolute or relative error of the actual result.

Constraints

-

data will contain between 1 and 50 elements, inclusive.

-

Each element of data will be between -10000 and 10000, inclusive.

-

denominator will be a power of 2 between 2 and 64, inclusive.

-

numerator will be an odd number between 1 and denominator-1, inclusive.

-

There will be enough data points to subdivide the data to the level required.

Examples

0)

{1, 2, 3, 5, 7}

Returns: 3.0

An example from the problem statement.

1)

{1, 2, 3, 6, 7, 8}

Returns: 7.0

Also from the problem statement.

2)

{7, 3, 1, 5, 2}

Returns: 1.5

Again from the problem statement, but provided in unsorted order.

3)

{7}

Returns: 7.0

The median of 1 point is trivial to calculate.

4)

{983, 126, 1078, -512, 1, 9876, -1234, 2387}

Returns: 63.5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

YahtzeeAdversary

Brute Force, Math

Used in:

TCHS07 Gamma 2

Used as:

Division I Level Three

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7563

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10718&pm=7563

Problem Statement

In the game of Yahtzee, 5 dice (6 sided) are rolled (and then some of them re-rolled) in an attempt to make one of several formations with the dice. We will introduce a new two-player version of the game in which player one first rolls all five dice, and then player two chooses at least two of the five dice, which the first player must then re-roll. The goal of player two is to minimize the expected score of the first player.

In our version of the game, we are only concerned about four possible results:

Yahtzee: All five dice show the same value
Large Straight: All five dice form a straight (1,2,3,4,5 or 2,3,4,5,6)
Small Straight: Four of the five dice form a straight
Full House: Three dice show the same value, and the other two also have the same value (ex. {1, 3, 1, 1, 3} or {2, 2, 2, 2, 2})

You are given a int[] scores indicating how many points each of the four formations is worth. (In order, they are given as Yahtzee, Large Straight, Small Straight, Full House) You are also given a int[] dice, indicating the values shown on each of the five dice after player one has rolled. You should return a int[] indiciating the 0-based indices of the dice that should be selected for re-rolling, to minimize the expected score of player one. If more than one selection of dice produces the same expected score, return the one that comes first lexicographically. (See notes)

Definition

Class:	YahtzeeAdversary
Method:	reRollDice
Parameters:	int[], int[]
Returns:	int[]
Method signature:	int[] reRollDice(int[] scores, int[] dice)
(be sure your method is public)

Notes

-

Although a set of five dice may fit the criteria for more than one formation, it can only be scored for one of the formations. The formation of maximum value will be used as the score. (Ex. 1,2,3,4,5 can only count as a small or large straight, but not both at once.)

-

A set of five like values, such as {1, 1, 1, 1, 1} is both a Yahtzee and a Full House. The higher score of the two is counted.

-

int[] A1 comes before int[] A2 lexicographically if A1 has a lower value in the first position at which they differ.

-

To calculate the expected score, multiply the score of each possible outcome by the probability of that outcome, and sum those values together.

Constraints

-

scores will contain exactly four elements.

-

Each element of scores will be between 0 and 10000, inclusive.

-

dice will contain exactly five elements.

-

Each element of dice will be between 1 and 6, inclusive.

Examples

0)

{50, 40, 30, 25}

{1, 1, 1, 1, 1}

Returns: {0, 1, 2 }

This is standard Yahtzee scoring. Rerolling four dice instead of just three increases the likelihood of getting a full house or straight. Rerolling three is the best bet. Picking any three of the five (since they are all showing the same value), we choose the three that come first lexicographically.

1)

{50, 40, 30, 25}

{1, 2, 3, 4, 5}

Returns: {2, 3 }

Notice that any possible straight we could form (small or large) would contain 3 and 4 in it. Forcing these two to be rerolled is a good move.

2)

{50, 40, 30, 25}

{5, 4, 3, 2, 1}

Returns: {1, 2 }

Notice that for this same example (in a different order) it is still those same two values.

3)

{10000, 0, 0, 0}

{1, 1, 1, 1, 1}

Returns: {0, 1, 2, 3 }

A Yahtzee is the only thing that can score us any points. Either rerolling all five dice or only four leaves the same odds of landing the Yahtzee, so we choose the lexicographically first possibility.

4)

{0, 0, 10000, 0}

{4, 2, 3, 4, 4}

Returns: {1, 2 }

Here, only a straight will be worth any points. Leaving the opponent with three like dice makes it impossible to end up with four dice in a straight. Please note that we must reroll at least 2 dice.

5)

{0, 0, 0, 1}

{3, 3, 3, 3, 3}

Returns: {0, 1, 2, 3 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AlmostPerfectNumber

Simple Math, Simple Search, Iteration

Used in:

TCCC07 Qual 2

Used as:

Division I Level One

Writer:

andrewzta

Testers:

PabloGilberto , vorthys , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7557

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10881&pm=7557

Problem Statement

An integer x is called a proper divisor of an integer y if x is a divisor of y and 1 <= x < y.

Let us denote as s(a) the sum of all proper divisors of a. An integer a is called almost perfect by k if |a-s(a)| <= k.

You are given ints left, right and k. Return the number of integers between left and right, inclusive, that are almost perfect by k.

Definition

Class:	AlmostPerfectNumber
Method:	count
Parameters:	int, int, int
Returns:	int
Method signature:	int count(int left, int right, int k)
(be sure your method is public)

Constraints

-

left will be between 2 and 1000, inclusive.

-

right will be between left and 1000, inclusive.

-

k will be between 0 and 1000, inclusive.

Examples

0)

Returns: 4

The following numbers between 2 and 10 are almost perfect by 1: 2 (s(2) = 1), 4 (s(4) = 3), 6 (s(6) = 6) and 8 (s(8) = 7).

1)

Returns: 1

2)

Returns: 10

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PowerOfInteger

Math, Search, Simple Math

Used in:

TCCC07 Round 2

Used as:

Division I Level One

Writer:

andrewzta

Testers:

PabloGilberto , radeye , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7554

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10891&pm=7554

Problem Statement

A number y is said to be the k-th power of a number x if y = x^k, i.e., y is the product of k copies of x.

You are given two Strings left and right. Return the greatest k such that there is an integer y (left <= y <= right) such that y is the k-th power of some integer x.

Definition

Class:	PowerOfInteger
Method:	greatestPower
Parameters:	String, String
Returns:	int
Method signature:	int greatestPower(String left, String right)
(be sure your method is public)

Constraints

-

left will be an integer between 2 and 10^12, inclusive, without extra leading zeroes.

-

right will be an integer between left and 10^12, inclusive, without extra leading zeroes.

Examples

0)

"5"

"20"

Returns: 4

The greatest power between 5 and 20 is 16=2^4.

1)

"10"

"12"

Returns: 1

No nontrivial power of integer between 10 and 12, so return 1.

2)

"2"

"100"

Returns: 6

3)

"1000000000000"

"1000000000000"

Returns: 12

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CellularPhoneTarif

Simple Math

Used in:

TCHS07 Alpha 2

Used as:

Division I Level One

Writer:

Mike Mirzayanov

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7546

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10716&pm=7546

Problem Statement

You have spoken seconds seconds by phone and you'd like to calculate the cost of the call. Starting a call always costs you 5 cents, regardless of the call's duration. Additionally, you need to pay for every minute you've been talking. Any fractional minute is charged at full price, so if you've talked for 65 seconds, you'll be charged for 2 minutes. Also, the timer for a new minute starts when your 60-th, 120-th, 180-th, ... second ends (if you talk for 120 seconds, you'll be charged for 3 minutes).

The payment for the call itself is a bit complicated. During the first 5 minutes of the call, you must pay 10 cents for each minute that you've talked. After the first 5 minutes of the call, each additional minute will cost you only 3 cents. Given the duration of your call in seconds, return the cost of the call.

Definition

Class:	CellularPhoneTarif
Method:	calculatePrice
Parameters:	int
Returns:	int
Method signature:	int calculatePrice(int seconds)
(be sure your method is public)

Constraints

-

seconds will be between 0 and 10000, inclusive.

Examples

0)

Returns: 25

1)

Returns: 58

2)

Returns: 25

3)

Returns: 15

4)

Returns: 58

5)

Returns: 55

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SortMaterials

Simple Math, String Parsing

Used in:

TCO07 Round 3

Used as:

Division I Level One

Writer:

Olexiy

Testers:

PabloGilberto , brett1479 , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7544

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10751&pm=7544

Problem Statement

Your shipping company has just delivered some materials to you, and you'd like to find out how many of these materials are useful. All materials are packed into cubical boxes. The information about each box will be given to you in a String[] data, with the i-th element representing the i-th box. Each element of data will be formatted as "EDGE QUALITY COLOR" (quotes for clarity), where EDGE and QUALITY are positive integers representing the length of an edge of the box and the quality of the material (higher is better), respectively. COLOR will be a sequence of lowercase letters representing the color of the material.

A String[] requirements will represent the specifications for your project. Each element of requirements will follow one of the following templates (all quotes for clarity only):

"EDGE=X" (where X is a positive integer), which means that you can use only materials from boxes with edge length equal to X.
"QUALITY=X" (where X is a positive integer), which means that you can use only materials with the quality greater than or equal to X.
"COLOR=s" (where s is a sequence of lowercase letters), which means that you can use only materials of color s.

Given all this information, you are to return the total volume of the materials you can use.

Definition

Class:	SortMaterials
Method:	totalVolume
Parameters:	String[], String[]
Returns:	int
Method signature:	int totalVolume(String[] data, String[] requirements)
(be sure your method is public)

Notes

-

The volume of a box with edge length of X is equal to X*X*X.

Constraints

-

data will contain between 1 and 50 elements, inclusive.

-

Each element of data will contain between 5 and 50 characters, inclusive.

-

Each element of data will be formatted as "EDGE QUALITY COLOR" (quotes for clarity), where EDGE and QUALITY are integers between 1 and 99, inclusive, with no leading zeroes, and COLOR is a non-empty sequence of lowercase letters ('a'-'z').

-

requirements will contain between 0 and 50 elements, inclusive.

-

Each element of requirements will contain between 6 and 50 characters, inclusive.

-

Each element of requirements will be formatted as "EDGE=X" (where X is an integer between 1 and 99, inclusive, with no leading zeroes), "QUALITY=X" (where X is an integer between 1 and 99, inclusive, with no leading zeroes), or "COLOR=s" (where s is a non-empty sequence of lowercase letters ('a'-'z'). All quotes for clarity only.

Examples

0)

{"1 20 red", "2 30 blue", "10 1 green"}

{}

Returns: 1009

With no special requirements, you can use all the materials you get. The sum of the volumes is 1*1*1 + 2*2*2 + 10*10*10 = 1009.

1)

{"1 20 red", "2 30 blue", "10 1 green"}

{"QUALITY=20"}

Returns: 9

Now you must choose materials with QUALITY of at least 20, so you can not use the third box.

2)

{"1 20 red", "2 30 blue", "10 1 green", "5 5 red", "5 6 red"}

{"COLOR=red", "EDGE=5"}

Returns: 250

3)

{"1 20 red", "2 30 blue", "10 1 green", "5 5 red", "5 6 red"}

{"EDGE=1", "EDGE=5"}

Returns: 0

Obviously, no box can have an edge length of 1 and 5 simultaneously.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Tetrahedron

Geometry, Math

Used in:

SRM 355

Used as:

Division I Level Two

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7539

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10712&pm=7539

Problem Statement

You are given pairwise distances between four hypothetical points. You need to return "YES" if there exist four points in space with such distances between them, and "NO" otherwise (all quotes for clarity only).

The distances are given as a String[] d, each element of which is a single-space separated list of integers. The j-th integer of the i-th element of d gives the distance between the i-th and j-th points.

Definition

Class:	Tetrahedron
Method:	exists
Parameters:	String[]
Returns:	String
Method signature:	String exists(String[] d)
(be sure your method is public)

Constraints

-

d will contain exactly 4 elements.

-

Each element of d will contain exactly 4 integers, separated by single spaces.

-

Each integer in d will be between 0 and 10, inclusive, and contain no extra leading zeroes.

-

The i-th integer of the i-th element of d will be 0.

-

The j-th integer of the i-th element of d will be equal to the i-th integer of the j-th element of d.

-

The j-th integer of the i-th element of d will be between 1 and 10, inclusive, when i is not equal to j.

Examples

0)

{"0 1 1 1",
 "1 0 1 1",
 "1 1 0 1",
 "1 1 1 0"}

Returns: "YES"

Just a regular tetrahedron.

1)

{"0 1 2 3",
 "1 0 1 2",
 "2 1 0 1",
 "3 2 1 0"}

Returns: "YES"

Four points on a single line.

2)

{"0 1 2 4",
 "1 0 1 2",
 "2 1 0 1",
 "4 2 1 0"}

Returns: "NO"

The first and last points are too far away.

3)

{"0 6 6 3",
 "6 0 4 5",
 "6 4 0 4",
 "3 5 4 0"}

Returns: "YES"

4)

{"0 6 6 2",
 "6 0 4 5",
 "6 4 0 4",
 "2 5 4 0"}

Returns: "NO"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BasketballStandings

Math

Used in:

TCO07 Qual 2

Used as:

Division I Level Two

Writer:

Olexiy

Testers:

PabloGilberto , brett1479 , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7538

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10731&pm=7538

Problem Statement

Since the rules of basketball do not allow games to result in ties, comparing two teams during a tournament is usually done by comparing the number of games they've won. When comparing two teams that have played a different number of games, the team that played k games less than the other gets k/2 added to its win total. For further clarification, please see the following table (the notation 7/15 means that a team played 15 games and won 7 of them):

Team A   Team B    Difference
7 / 15   8 / 20    Team A played 5 games less than team B, so we assume it will win 2.5 games more.
		   Therefore Team A is (7 + 2.5) - 8 = 1.5 games ahead of team B.
8 / 8    18 / 18   Though both teams have won all their games, team A played 10 games less. 
                   We assume it wins 5 of those 10 games, so it is 5 games behind team B.
20 / 40  10 / 20   Team B played 20 games less, so we assume it will have 10 more wins.
                   Therefore, the gap between the teams is 0.

Since this comparison is transitive (if team A is better than team B, and team B is better than team C, then team A is better than team C), the teams can be placed into the standings table according to this order. If the gap between two teams is 0, the team whose name comes earlier alphabetically is given the better rank.

You will be given a String[] teams, with the i-th element of teams representing the i-th team. Each element of teams will be formatted as "NAME WINS LOSSES" (quotes for clarity), where NAME is a sequence of uppercase letters representing the name of the team, and WINS and LOSSES are integers representing the number of games the team won and lost respectively. You are to sort teams from the best to worst according to the comparison method defined above, and return the standings as a String[]. Each element of the result must be formatted as "NAME GAP" (quotes for clarity), where NAME is the team's name and GAP is the gap between this team and the top team in the standings. GAP must consist of one or more digits, followed by a decimal point, followed by exactly one digit. There must be no extra leading zeroes. For example, "0.0", "0.5" and "1.0" are valid, but ".5", "0", "05.0" and "5." are not.

Definition

Class:	BasketballStandings
Method:	constructTable
Parameters:	String[]
Returns:	String[]
Method signature:	String[] constructTable(String[] teams)
(be sure your method is public)

Constraints

-

teams will contain between 1 and 50 elements, inclusive.

-

Each element of teams will contain between 5 and 16 characters, inclusive.

-

Each element of teams will be formatted as "NAME WINS LOSSES" (quotes for clarity).

-

In each element of teams, NAME will contain between 1 and 10 uppercase letters ('A'-'Z'), inclusive.

-

In each element of teams, WINS will be an integer between 0 and 99, with no extra leading zeroes.

-

In each element of teams, LOSSES will be an integer between 0 and 99, with no extra leading zeroes.

Examples

0)

{"A 1 1", "A 8 8","D 0 0", "B 7 7", "C 99 99", "BAA 13 13"}

Returns: {"A 0.0", "A 0.0", "B 0.0", "BAA 0.0", "C 0.0", "D 0.0" }

All teams win 50% of their games. They are all tied in the standings and sorted in alphabetical order. Please note that multiple teams may have the same name.

1)

{"B 11 10", "A 10 10", "C 10 11", "D 20 5"}

Returns: {"D 0.0", "B 7.0", "A 7.5", "C 8.0" }

D is a clear favorite here.

Team B played 1 game more than team A, therefore A is supposed to get 0.5 wins out of this game. Since B has 1 win more, it is 0.5 wins ahead of team A.

Team B and team C played the same number of games. Team B get 1 win more, therefore it is 1 win ahead.

2)

{"MAVS 54 11", "SUNS 50 16", "SPURS 46 20", "JAZZ 43 23"}

Returns: {"MAVS 0.0", "SUNS 4.5", "SPURS 8.5", "JAZZ 11.5" }

Top 4 NBA team as of March 20, 2007.

3)

{"TEAMA 17 15", "TEAMB 14 11", "TEAMC 3 0",
 "TEAMD 99 94", "LOSER 10 85", "WINNER 76 34"}

Returns: 
{"WINNER 0.0",
"TEAMD 18.5",
"TEAMB 19.5",
"TEAMC 19.5",
"TEAMA 20.0",
"LOSER 58.5" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TriangleConstruction

Simple Math, Simple Search, Iteration

Used in:

TCHS07 Gamma 1

Used as:

Division I Level One

Writer:

andrewzta

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7523

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10703&pm=7523

Problem Statement

The perimeter of a triangle with edge lengths a, b and c is a + b + c.

You have several sticks of various lengths. The int[] lengths contains the length of each stick. Return the maximum possible perimeter of a triangle that can be constructed with your sticks. Each edge of the triangle must be constructed using exactly one stick. You are not allowed to break sticks into smaller pieces. Return -1 if no triangle can be constructed.

Definition

Class:	TriangleConstruction
Method:	greatestPerimeter
Parameters:	int[]
Returns:	int
Method signature:	int greatestPerimeter(int[] lengths)
(be sure your method is public)

Notes

-

You can construct a triangle with edge lengths x <= y <= z if and only if x + y > z.

Constraints

-

lengths will contain between 3 and 50 elements, inclusive.

-

Each element of lengths will be between 1 and 1000, inclusive.

Examples

0)

{1,2,2}

Returns: 5

In this case there is only one possible triangle, and its perimeter is 1+2+2=5.

1)

{2,3,2,3,2,4}

Returns: 10

2)

{1,2,3}

Returns: -1

No triangle can be constructed from these sticks.

3)

{4, 5, 6, 7, 20}

Returns: 18

4)

{214, 108, 273, 467, 991, 434, 767, 659}

Returns: 2417

5)

{116, 373, 471, 540, 350, 318, 804, 561, 428, 915, 64, 853, 498, 600, 439, 732, 139, 497, 512, 510, 796}

Returns: 2572

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RoadCrossing

Simple Math, Simulation

Used in:

SRM 373

Used as:

Division I Level Two

Writer:

Vedensky

Testers:

PabloGilberto , gawry , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7521

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10791&pm=7521

Problem Statement

Some pedestrians are crossing a road. A car arrives at the crosswalk and wants to pass through, but can only get by if there's an empty gap of at least carWidth centimeters. The road is roadWidth centimeters wide. All the pedestrians are walking in the same direction.

You are given a String[] pedestrians, each element of which is formatted as "T V" (quotes for clarity), where T is the time that one pedestrian starts crossing the road (in seconds), and V is his walking speed (in centimeters per second). The car arrives at time carArrival seconds. The car can pass through at any time after its arrival (including the moment of arrival), when there is sufficient free space to pass through. Return a double indicating the earliest time (in seconds) the car can pass through.

Definition

Class:	RoadCrossing
Method:	passTime
Parameters:	String[], int, int, int
Returns:	double
Method signature:	double passTime(String[] pedestrians, int roadWidth, int carWidth, int carArrival)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

-

The car passes through instantly, i.e., it takes no time for the car to pass through.

Constraints

-

pedestrians will contain between 0 and 50 elements, inclusive.

-

Each element of pedestrians will be formatted as "T V" (quotes for clarity), where T and V are integers with no extra leading zeros.

-

Each T will be between 0 and 1000, inclusive.

-

Each V will be between 1 and 1000, inclusive.

-

roadWidth will be between 1 and 1000, inclusive.

-

carWidth will be between 1 and roadWidth, inclusive.

-

carArrival will be between 1 and 1000, inclusive.

Examples

0)

{"0 1", "2 5"}

Returns: 3.5

At time 3.5, the pedestrians are 3.5 and 7.5 centimeters from the side of the road. The car can pass through the 4 centimeter gap between the pedestrians. This is the earliest time it can pass through.

1)

{"40 1"}

Returns: 140.0

The pedestrian starts crossing the road at time 40. At time 41, the car arrives, and the pedestrian is 1 cm from the side of the road. The car needs the entire width of the road to pass through, and therefore, it must wait until the pedestrian finishes crossing. The pedestrian reaches the other side of the road at time 140.

2)

{"0 1", "0 2", "0 4", "0 8", "0 16", "0 32", "0 64", "0 128", "0 256"}

Returns: 3.125

3)

{"0 1", "0 2", "0 4", "0 8", "0 16", "0 32", "0 64", "0 128", "0 256"}

Returns: 51.0

4)

{"1000 1", "100 1"}

Returns: 2000.0

Maximal possible answer.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MultiprocessorProgramming

Math

Used in:

TCHS07 Gamma 1

Used as:

Division I Level Three

Writer:

andrewzta

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7502

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10703&pm=7502

Problem Statement

As multiprocessor computers become more widespread in our lives, it becomes more and more important to write parallel programs that can solve tasks using several processors.

However, designing parallel programs is difficult for many reasons. Let us consider two of them. First, some amount of work cannot be parallelized and must therefore be executed on a single processor. Besides that, when increasing the number of processors, the amount of work needed for synchronization increases. We will assume that there is one special processor that controls the execution and executes the unparallelizable part, and that the increase in time due to synchronization is linear in the number of processors.

You are given ints t0, tp, and ts. t0 is the number of seconds needed for the execution of the unparallelizable part. tp is the number of seconds needed for execution of the parallelizable part on a single processor. ts is the number of seconds added to the synchronization time for each additional processor.

The time needed to execute the whole task on one processor is t0+tp. The time needed to execute the whole task on n > 1 processors is max(t0, tp/(n-1) + ts*(n-1)). Here tp/(n-1) is a floating point number. Return the number of processors needed to execute the task in minimal time. If there are multiple solutions, return the smallest among them.

Definition

Class:	MultiprocessorProgramming
Method:	optimalNumberOfProcessors
Parameters:	int, int, int
Returns:	long
Method signature:	long optimalNumberOfProcessors(int t0, int tp, int ts)
(be sure your method is public)

Constraints

-

t0 will be between 1 and 10⁹, inclusive.

-

tp will be between 1 and 10⁹, inclusive.

-

ts will be between 1 and 10⁹, inclusive.

Examples

0)

Returns: 4

In this case the optimal number of processors is 4. The time needed to complete the task is max(1,10/3+1*3)=19/3.

1)

Returns: 3

In this case the unparallelizable part is too large, so the optimal number of processors is 3. The time needed to complete the task is max(8,10/2+1*2)=8.

2)

Returns: 1

In this case synchronization is too difficult, so parallelization is unreasonable.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FibonacciKnapsack

Dynamic Programming, Math

Used in:

SRM 352

Used as:

Division I Level Two

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7481

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10709&pm=7481

Problem Statement

We have n items, each with a specified weight and cost, and a bag that can carry a specified maximum weight. We want to place a subset of these items into the bag such that the total cost is maximized.

Unfortunately, this problem cannot be solved effectively in the general case. However, there are pretty good solutions for some special cases. In this problem, you are required to solve it for the special case where the weights of the items are all Fibonacci numbers.

The first two Fibonacci numbers are 1 and 2. Each successive number is obtained by adding together the two previous numbers. Thus, the first Fibonacci numbers are 1, 2, 3, 5, 8, 13...

You will be given String[] items and a String C. Each element of items describes a single item and is formatted "W P" (quotes for clarity only), where W is the weight of the item and P is the cost. C is the maximum weight that the bag can carry. Return the maximum total cost of the subset of items that can fit into the bag.

Definition

Class:	FibonacciKnapsack
Method:	maximalCost
Parameters:	String[], String
Returns:	long
Method signature:	long maximalCost(String[] items, String C)
(be sure your method is public)

Constraints

-

items will contain between 1 and 50 elements, inclusive.

-

Each element of items will be formatted "W P" (quotes for clarity only).

-

In each element of items, W and P will be integers between 1 and 10¹⁶, inclusive, with no leading zeroes.

-

Each W will be a Fibonacci number.

-

C will represent an integer between 1 and 10¹⁶, inclusive, with no leading zeroes.

Examples

0)

{"5 555", "8 195", "13 651"}

"15"

Returns: 750

We should take the first and the second items. Their total weight is 5+8=13, which does not exceed the maximum capacity of 15, and their total cost is 555+195=750.

1)

{"5 555", "8 195", "13 751"}

"15"

Returns: 751

Now it is more profitable to take only the last item with the 751 cost.

2)

{"55 1562", "5 814", "55 1962", "8 996", "2 716", "34 1792"}

"94"

Returns: 4568

3)

{"13 89"}

"1"

Returns: 0

4)

{"27777890035288 9419696870097445", 
 "53316291173 6312623457097563", 
 "165580141 8848283653257131"}

"27777900000000"

Returns: 15160907110354694

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AdPlacement

Math

Used in:

MM 12

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7478

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10704&pm=7478

Problem Statement

Introduction

You are running a website that uses online advertising as its main support. You have K slots available to place a different ad in each of them, numbered from 0 to K-1, ordered by visibility, from high to low. The problem is that you have N ads available, numbered from 0 to N-1, and at each moment you need to decide which ones to place in each slot. Each of the advertisers offers some money M_i for his ad, that is paid each time the ad is clicked (the famous pay-per-click).

Even when you only know their prizes, each ad has the following hidden parameters:

P_i: Probability of click
D_i: Visibility decay value
V_i: Variability through time

When you place the i^th ad on slot number x, it has P_i*(D_i^x) probability of being clicked if none of the above ads was clicked first. See below for details on this.

After each minute, each ad changes its P_i value by adding a random variable X with N(0,V_i) distribution (normal distribution with mean equal to 0 and standard deviation equal to V_i). So, after each minute passes, this operation is performed:

method timeAction()
for i = 0 to N-1
	P_i := P_i + N(0, V_i)
	if (P_i > 1) P_i := 1
	if (P_i < 0) P_i := 0

where N(a,b) is a function that gives a random normal number with mean equal to a and standard deviation equal to b.

When a user shows up it is presented the list of K ads and then he/she acts in the following way:

method userAction()
for x := 0 to K-1
	let i be the number of the ad placed on slot x
	if (random boolean value with probability P_i*(D_i^x))
		click the ad and finish action (your total income is increased by M_i)

Note that at most 1 ad is clicked per user, and with probability equal to the product of each (1-P_i*(D_i^x)), no ad will be clicked and therefore you get no income for this user.

The system will be simulated in the following way:

You are asked to place the ads for the next 20 minutes
totalT := totalT + 20, if totalT > 50000 finish test case
for t := 1 to 20: call timeAction and then userAction

Protocol

At the beginning a method init will be called with an int[] M describing the M_is and an int K, the number of slots you have. That method may return any int, but not crash. After that, a method placeAds will be called at most 2500 times with two parameters:

timeLeft: an int that indicates the time left for execution, in milliseconds. This parameter is only provided for your convenience, and is always a positive number.
prevClicks: a String that is empty on the first call and in the following calls it has exactly 20 characters: The i^th character of it will be a digit representing the slot number that was clicked on the i^th minute of the last interval or 'X' if no ad was clicked during that minute.

placeAds must return an int[] with exactly K elements, the x^th element of the return must be the 0-based index of the ad you want to place at slot number x.

Scoring

You will receive a 0 for a test case if your program crashes, uses more than 64 MB of memory, or exceeds 30 seconds of total execution time. You will also receive a 0 if placeAds returns a null result, a result that does not contain exactly K elements or one that contains a repeated element or an element less than 0 or greater than N-1. Otherwise, your score will be the amount of money you earned at the end of time. Your total score will be the sum of your normalized scores for each test case. A normalized score is your score divided by the best score in that test case.

Input Generation

All inputs will be generated with this constraints and generation method:

N will be an integer uniformly chosen between 10 and 30, inclusive.
K will be an integer uniformly chosen between 2 and 5, inclusive.
Each M_i will be an integer chosen uniformly between 1 and 100, inclusive.
Each initial P_i will be chosen following a power law distribution with exponent equal to -1/2 in [0 ; 0.25]. This means that P_i will be assigned the value X² where X is a real number uniformly chosen in [0 ; 0.5].
Each D_i will be a real number uniformly chosen in [0.7 ; 1.0].
Each V_i will be assigned the value 2^X/10000 where X is a real number uniformly chosen in [0 ; 5].

There are 10 example test cases and 100 system test cases, so your score will be between 0 and 100 when you submit.

Definition

Class:	AdPlacement
Method:	init
Parameters:	int[], int
Returns:	int
Method signature:	int init(int[] M, int K)

Method:	placeAds
Parameters:	int, String
Returns:	int[]
Method signature:	int[] placeAds(int timeLeft, String prevClicks)
(be sure your methods are public)

Notes

- To avoid exceeding time limit, a line like "if (timeLeft<50) return {0,1,..,K-1}" at the beginning of placeAds would be a good idea.

- The way the P_is evolve is a Wiener Process, in case you want to read more about that.

- Notice that, while the initial value of each P_i isno more than 0.25, it may end up being greater than 0.25 by the end of the process.

Examples

0)

"4"

Returns: 
"N=10
K=3
M={
    50,49,15,19,20,
    26,91,9,24,14}
P={
    0.1409,0.0012,0.0375,0.0321,0.0104,
    0.0077,0.1438,0.0269,0.2361,0.0117}
D={
    0.7533,0.8280,0.8739,0.9127,0.9550,
    0.7974,0.7482,0.9848,0.8941,0.9659}
V={
    0.0002,0.0006,0.0004,0.0002,0.0014,
    0.0009,0.0031,0.0003,0.0001,0.0011}
"

If an oracle told you the values of the hidden variables (each P and each D) before you decided on the order in each iteration, the best expected profit you could make would be a little under two million.

1)

"564"

Returns: 
"N=15
K=5
M={
    63,79,25,57,41,
    61,18,48,16,22,
    16,9,12,40,39}
P={
    0.0002,0.0008,0.0900,0.0015,0.0643,
    0.0970,0.1348,0.1755,0.0020,0.1974,
    0.0066,0.0193,0.0256,0.0112,0.0000}
D={
    0.8898,0.9298,0.7114,0.8124,0.8147,
    0.7252,0.9838,0.7928,0.9419,0.7765,
    0.9206,0.8749,0.8901,0.9974,0.7960}
V={
    0.0001,0.0012,0.0001,0.0007,0.0012,
    0.0001,0.0002,0.0002,0.0016,0.0004,
    0.0001,0.0004,0.0008,0.0005,0.0008}
"

Here the best you could hope for, knowing the hidden variables is about 1.14 million.

2)

"5"

Returns: 
"N=27
K=2
M={
    42,41,63,9,77,
    53,68,72,23,71,
    27,90,63,71,39,
    98,27,54,94,12,
    92,28,84,90,44,
    40,24}
P={
    0.2362,0.0507,0.0895,0.1330,0.1867,
    0.0043,0.0772,0.0713,0.0222,0.2080,
    0.1857,0.0843,0.0111,0.1929,0.0505,
    0.0133,0.0735,0.1875,0.2176,0.1510,
    0.0694,0.0289,0.0002,0.1016,0.0273,
    0.0219,0.0005}
D={
    0.7300,0.8590,0.8073,0.9994,0.8464,
    0.7727,0.8610,0.7151,0.7430,0.9208,
    0.7951,0.8956,0.9590,0.8743,0.7723,
    0.7005,0.8881,0.8968,0.8337,0.9046,
    0.8318,0.8995,0.9950,0.8137,0.7077,
    0.9720,0.8664}
V={
    0.0011,0.0011,0.0019,0.0007,0.0015,
    0.0008,0.0001,0.0005,0.0029,0.0003,
    0.0004,0.0029,0.0008,0.0005,0.0012,
    0.0015,0.0022,0.0020,0.0001,0.0006,
    0.0007,0.0023,0.0005,0.0003,0.0004,
    0.0009,0.0017}
"

Best expected is about 2.28 million.

3)

"8"

Returns: 
"N=14
K=4
M={
    58,24,45,93,42,
    59,56,49,24,56,
    40,32,57,28}
P={
    0.1535,0.0690,0.1694,0.0305,0.2202,
    0.0305,0.1151,0.2252,0.1957,0.0722,
    0.2483,0.1819,0.1829,0.0930}
D={
    0.8561,0.9637,0.7928,0.9529,0.9494,
    0.9928,0.8391,0.8044,0.7179,0.8028,
    0.8255,0.7496,0.7314,0.9299}
V={
    0.0005,0.0005,0.0002,0.0001,0.0025,
    0.0007,0.0004,0.0003,0.0010,0.0002,
    0.0020,0.0006,0.0029,0.0004}
"

Best expected is about 1.74 million.

4)

"9091"

Returns: 
"N=22
K=5
M={
    53,68,78,27,13,
    26,53,52,53,33,
    64,7,16,63,69,
    53,9,94,29,98,
    60,68}
P={
    0.0212,0.0033,0.0385,0.2287,0.0747,
    0.0210,0.0656,0.0797,0.0058,0.0067,
    0.1298,0.0683,0.0205,0.1231,0.0590,
    0.1308,0.0133,0.1894,0.1083,0.0217,
    0.0398,0.0408}
D={
    0.7993,0.9238,0.7239,0.7923,0.9390,
    0.9632,0.8225,0.7353,0.8612,0.9692,
    0.7220,0.7481,0.8686,0.8693,0.7585,
    0.9019,0.9381,0.7528,0.8767,0.8491,
    0.9080,0.9543}
V={
    0.0010,0.0012,0.0001,0.0010,0.0002,
    0.0011,0.0002,0.0030,0.0001,0.0011,
    0.0001,0.0020,0.0006,0.0014,0.0009,
    0.0001,0.0016,0.0031,0.0010,0.0002,
    0.0002,0.0004}
"

Best expected is about 2.25 million.

5)

"467"

Returns: 
"N=18
K=4
M={
    85,44,98,61,16,
    18,12,3,84,88,
    6,93,7,95,43,
    99,95,96}
P={
    0.1286,0.0629,0.0208,0.1423,0.1756,
    0.0956,0.1056,0.0343,0.0154,0.0052,
    0.0477,0.0084,0.0199,0.0890,0.0942,
    0.1573,0.0460,0.1294}
D={
    0.7937,0.7580,0.9455,0.9000,0.9903,
    0.8390,0.8380,0.7986,0.7243,0.8809,
    0.7086,0.7400,0.8422,0.7552,0.9542,
    0.9015,0.8238,0.9858}
V={
    0.0016,0.0007,0.0001,0.0011,0.0002,
    0.0002,0.0007,0.0003,0.0003,0.0002,
    0.0007,0.0007,0.0006,0.0011,0.0001,
    0.0003,0.0016,0.0007}
"

Best expected is about 2.05 million.

6)

"9809"

Returns: 
"N=21
K=2
M={
    76,23,41,85,31,
    23,81,12,94,61,
    88,52,52,6,48,
    77,97,26,59,83,
    54}
P={
    0.0001,0.0453,0.0025,0.0059,0.0001,
    0.0155,0.0788,0.0021,0.0977,0.0260,
    0.1285,0.0336,0.0073,0.0752,0.1066,
    0.1341,0.1778,0.0069,0.0632,0.2056,
    0.0069}
D={
    0.8480,0.9871,0.8328,0.8807,0.8779,
    0.9265,0.9865,0.9336,0.7813,0.7395,
    0.7311,0.8926,0.8497,0.8661,0.9665,
    0.8520,0.7816,0.8657,0.7427,0.8445,
    0.7030}
V={
    0.0012,0.0003,0.0002,0.0002,0.0002,
    0.0027,0.0002,0.0015,0.0003,0.0011,
    0.0001,0.0030,0.0007,0.0015,0.0029,
    0.0003,0.0003,0.0005,0.0003,0.0004,
    0.0006}
"

Best expected is about 2.02 million.

7)

"1093"

Returns: 
"N=10
K=4
M={
    67,7,24,34,95,
    63,86,33,69,25}
P={
    0.1426,0.0782,0.0337,0.0787,0.0921,
    0.0802,0.1099,0.0523,0.0034,0.0041}
D={
    0.9681,0.8808,0.8480,0.8514,0.7773,
    0.9400,0.9328,0.9123,0.7418,0.9097}
V={
    0.0010,0.0016,0.0001,0.0002,0.0005,
    0.0006,0.0006,0.0022,0.0002,0.0010}
"

Best expected is about 1.64 million.

8)

"7610"

Returns: 
"N=22
K=3
M={
    86,50,31,4,88,
    79,20,37,29,2,
    29,8,66,41,62,
    33,29,42,61,29,
    44,3}
P={
    0.0241,0.0087,0.0046,0.0782,0.0395,
    0.2401,0.0801,0.0188,0.2470,0.0630,
    0.0286,0.0557,0.1913,0.0285,0.0557,
    0.0653,0.1282,0.0012,0.0017,0.1340,
    0.1603,0.0004}
D={
    0.7790,0.8386,0.8902,0.7090,0.8549,
    0.7993,0.9393,0.7331,0.8225,0.7523,
    0.8205,0.9757,0.9604,0.9495,0.7399,
    0.9487,0.9342,0.7095,0.9518,0.9129,
    0.7205,0.8979}
V={
    0.0021,0.0001,0.0013,0.0004,0.0001,
    0.0002,0.0004,0.0001,0.0011,0.0021,
    0.0001,0.0008,0.0003,0.0003,0.0020,
    0.0004,0.0016,0.0006,0.0003,0.0013,
    0.0005,0.0012}
"

Best expected is about 2.68 million.

9)

"490"

Returns: 
"N=16
K=4
M={
    62,95,1,38,74,
    71,97,99,86,39,
    18,74,41,45,24,
    86}
P={
    0.2130,0.1697,0.0148,0.0456,0.0477,
    0.2360,0.0079,0.2356,0.0155,0.0553,
    0.1163,0.0059,0.0144,0.0194,0.0285,
    0.1431}
D={
    0.7305,0.7016,0.8318,0.7431,0.9564,
    0.7601,0.9144,0.7235,0.9610,0.9638,
    0.9911,0.7158,0.8764,0.9255,0.9550,
    0.7956}
V={
    0.0002,0.0004,0.0004,0.0008,0.0009,
    0.0001,0.0017,0.0014,0.0009,0.0005,
    0.0015,0.0011,0.0005,0.0025,0.0003,
    0.0022}
"

Best expected is about 2.50 million.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CakeParty

Greedy, Math

Used in:

SRM 338

Used as:

Division I Level Three

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7424

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10662&pm=7424

Problem Statement

Julianne invited her two friends Michael and Jane to a cake party. When Michael and Jane arrived, they saw that their host had prepared several tables. On each table there was a plate with one of the cakes. Each cake was cut into several pieces.

Not knowing where to start, Michael and Jane decided to play the following game: Players take alternating turns. In each turn the player selects one cake, and takes and eats several pieces of the cake. The player must take and eat at least one piece. The player who eats the last piece of the last cake wins.

However, the host would be really offended if she had the impression that the guests didn't like some of her cakes. Therefore Michael and Jane agreed on one additional rule: Each time a player selects a cake, he or she may only select one of those cakes that have the most pieces remaining.

Michael starts the game and plays optimally. In other words, if there is a strategy that will ensure his win (no matter how Jane plays), he will follow one such strategy. If he finds himself in a position where no strategy can guarantee him winning the game he just makes a valid move. In addition, whenever Michael has more than one move to choose from, he picks the lexicographically smallest one (explained below).

You are given a int[] pieces. The i-th element of pieces is the initial number of pieces of the i-th cake. Return Michael's first move as a String formatted as follows: "CAKE C PIECES P", where C is the zero-based index of the cake he should select and P is the number of pieces he should eat. The numbers C and P must not contain unnecessary leading zeroes. In case there are multiple valid answers return the one where the resulting String is lexicographically smallest.

Definition

Class:	CakeParty
Method:	makeMove
Parameters:	int[]
Returns:	String
Method signature:	String makeMove(int[] pieces)
(be sure your method is public)

Notes

- Ignore the appetite and eating speed of both players. In other words, assume that each of them is able to eat all the cakes in a short amount of time.

- When selecting the correct output, standard string comparison rules apply:

The string A is lexicograpically smaller than the string B if and only if (A is a proper prefix of B) or (there is an integer X such that first X-1 characters of A and B are equal, and the X-th character of A has a smaller ASCII value than the X-th character of B).

- Valid characters ordered by their ASCII values (smallest to largest): space, digits '0'-'9' in this order, letters 'A'-'Z' in this order.

Constraints

- pieces will contain between 1 and 50 elements, inclusive.

- Each element of pieces will be between 1 and 2,000,000,000, inclusive.

Examples

0)

{47}

Returns: "CAKE 0 PIECES 47"

With one cake the game is simple: just take everything.

1)

{3,3}

Returns: "CAKE 0 PIECES 1"

Two equally big cakes. This is clearly a losing position for the player to move. Thus we return the lexicographically smallest possible move.

2)

{3,5}

Returns: "CAKE 1 PIECES 2"

The winning move is to create the position from the previous example.

3)

{1,1,1,1,1,1,1,1,1,1,1,1,1,1}

Returns: "CAKE 0 PIECES 1"

This is an almost deterministic game. The players can not influence the result at all.

4)

{3,3,112}

Returns: "CAKE 2 PIECES 110"

This is a winning position, as we can eat the entire last cake and thus create the position from Example 1. However, this is not the only winning move, and there is a lexicographically smaller winning move than the one we described.

5)

{3,3,1}

Returns: "CAKE 0 PIECES 1"

Note that we can not eat the last cake now, as it is not one of the largest ones.

6)

{4,7,4,7,4,7,4,7,47,47,47,47}

Returns: "CAKE 10 PIECES 1"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TestBettingStrategy

Dynamic Programming, Recursion, Simple Math

Used in:

SRM 339

Used as:

Division I Level Two

Writer:

_efer_

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7422

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10663&pm=7422

Problem Statement

You are thinking of using the following betting strategy: in the first round, you bet one dollar. If you win the bet, you win the dollar and bet another dollar in the next round. Otherwise you lose the dollar and bet two dollars in the second round (provided you still have at least two dollars in your account). If you win, you get the two dollars and bet one dollar in the third round, otherwise you lose the two dollars and bet four dollars in the third round (provided you have at least that amount in your account) and so on. In other words, whenever you lose a bet, you double the value of the bet for the next round. If you don't have enough money to cover your bet, you have to stop betting. Whenever you win, the bet for the next round will be one dollar.

For example, if you start with 10 dollars, and you win the bet in the first round, lose the bet in the next two rounds and then win the bet in the fourth round, you will end up with 10+1-1-2+4 = 12 dollars.

You will be given four ints initSum, the amount of money you initially have, goalSum, the sum you wish to achieve, rounds, the maximum number of rounds you wish to play, and prob, the percent probability of winning one round. Return the probability that you will reach your goal within the maximum number of rounds you wish to play. Note that if you manage to get to goalSum or more, you stop betting.

Definition

Class:	TestBettingStrategy
Method:	winProbability
Parameters:	int, int, int, int
Returns:	double
Method signature:	double winProbability(int initSum, int goalSum, int rounds, int prob)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

initSum will be between 1 and 1,000, inclusive.

-

goalSum will be between (initSum + 1) and 1,000, inclusive.

-

rounds will be between 1 and 50, inclusive.

-

prob will be between 0 and 100, inclusive.

Examples

0)

Returns: 0.875

You have a 50% chance of reaching 11 dollars in the first round. You could also win by losing the first round and winning the second, with a 25% chance, or losing the first two rounds and winning the third one, with a 12.5% chance. Note that the fourth round is never needed. If you lose the first three rounds, you can't cover your fourth bet. In any other case, you will have already reached 11 dollars and stopped.

1)

Returns: 0.3441343307495117

2)

Returns: 0.34867844010000015

You have to win every round. Since the probability of winning a round is pretty high, you have a decent chance of doing this.

3)

Returns: 0.5940784635646947

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ReverseUnnaturalBaseConversion

Math

Used in:

SRM 342

Used as:

Division II Level Three

Writer:

Kawigi

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7413

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10666&pm=7413

Problem Statement

It is common in modern written languages to express numbers in base 10, where the digits 0-9 are used to express values as sums of powers of 10. For instance, the number written as 12345 in base 10 refers to the sum 1*10⁴ + 2*10³ + 3*10² + 4*10¹ + 5*10⁰. It is also common in various applications to represent numbers in other number bases (such as base 2, which is how computers represent numbers). Additionally, a '-' character preceding a number denotes that it is negative.

Consider for a minute what it would mean to express a number in base -10. The number written as 12345 in base -10 refers to the sum 1*(-10)⁴ + 2*(-10)³ + 3*(-10)² + 4*(-10)¹ + 5*(-10)⁰. Note that the odd powers of ten are negative, and the value of that sum is 10000 - 2000 + 300 - 40 + 5, which comes out to 8265 in base +10. It turns out that there is a unique way of representing any integer in negative bases (as long as the absolute value of the base is at least 2). The really interesting thing about using negative number bases is that the '-' sign isn't needed to represent negative numbers - -1 can be expressed as 19 in base -10, -2 is 18, and so on.

For this problem, write a program that converts a number x to base b, and returns this representation as a String. The '-' character should be used to denote negative numbers in positive bases, but shouldn't ever be present in numbers in negative bases. The return value should have no unnecessary leading zeros.

Definition

Class:	ReverseUnnaturalBaseConversion
Method:	convertToBase
Parameters:	int, int
Returns:	String
Method signature:	String convertToBase(int x, int b)
(be sure your method is public)

Notes

- There will always be a unique answer for any valid input.

Constraints

- The absolute value of b will be between 2 and 10, inclusive.

- x will be between -1000000000 and 1000000000, inclusive.

Examples

0)

Returns: "12345"

Conversion into base 10 should look natural.

1)

-10

Returns: "12345"

The other example from the problem statement.

2)

-2

Returns: "10000111001"

3)

-52

-2

Returns: "11011100"

4)

-38

Returns: "-212"

5)

-123456789

-7

Returns: "3031330536"

6)

Returns: "0"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DegreesToRadians

Simple Math

Used in:

SRM 342

Used as:

Division II Level One

Writer:

Kawigi

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7410

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10666&pm=7410

Problem Statement

In some forms of geometry, like the kind used in geographical longitude/latitude measurements, angles are measured in base-60. The base unit is the degree. One degree contains 60 minutes, and one minute contains 60 seconds.

You will be given the measurement of an angle in degrees, minutes, and seconds. Return the given angle in radians. Note that n degrees is equal to n*PI/180 radians.

Definition

Class:	DegreesToRadians
Method:	convertToRadians
Parameters:	int, int, int
Returns:	double
Method signature:	double convertToRadians(int degrees, int minutes, int seconds)
(be sure your method is public)

Notes

-

The return value must have an absolute or relative error less than 1e-9.

Constraints

-

degrees will be between 0 and 359, inclusive.

-

minutes will be between 0 and 59, inclusive.

-

seconds will be between 0 and 59, inclusive.

Examples

0)

Returns: 0.0

Zero is zero, in either measurement system.

1)

Returns: 3.141592653589793

180 degrees is PI radians.

2)

Returns: 6.283180459042776

This is as close to a full circle as it gets.

3)

Returns: 0.41017661490272295

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CommonMultiples

Simple Math

Used in:

SRM 346

Used as:

Division I Level One , Division II Level Two

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7408

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10670&pm=7408

Problem Statement

You will be given a int[] a and two ints lower and upper. Return the number of integers between lower and upper, inclusive, that are multiples of all members of a.

Definition

Class:	CommonMultiples
Method:	countCommMult
Parameters:	int[], int, int
Returns:	int
Method signature:	int countCommMult(int[] a, int lower, int upper)
(be sure your method is public)

Constraints

-

a will contain between 1 and 50 elements, inclusive.

-

Each element of a will be between 1 and 100, inclusive.

-

upper will be between 1 and 2000000000 (2*10⁹), inclusive.

-

lower will be between 1 and upper, inclusive.

Examples

0)

{1,2,3}

Returns: 2

The only numbers between 5 and 15 that are multiples of 1, 2 and 3 are 6 and 12.

1)

{1,2,4,8,16,32,64}

Returns: 1

128 is a multiple of all smaller powers of 2.

2)

{2,3,5,7,11,13,17,19,23,29,31,37,41,43,49}

2000000000

Returns: 0

3)

{1,1,1}

2000000000

Returns: 2000000000

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AnagramList

Math, Recursion

Used in:

SRM 337

Used as:

Division II Level Three

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Olexiy , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7407

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10661&pm=7407

Problem Statement

An anagram of a string is any string that contains the same characters in any order. For example, the anagrams of "tree" are, in alphabetical order: "eert", "eetr", "eret", "erte", "eter", "etre", "reet", "rete", "rtee", "teer", "tere" and "tree".

You will be given a String s and an int i. Return the i^th (0-based) anagram of s when listed in alphabetical order. If there is no such anagram, return an empty String.

Definition

Class:	AnagramList
Method:	getAnagram
Parameters:	String, int
Returns:	String
Method signature:	String getAnagram(String s, int i)
(be sure your method is public)

Constraints

-

s will contain between 1 and 20 characters, inclusive.

-

Each character of s will be a lowercase letter ('a'-'z').

-

i will be between 0 and 2000000000 (2*10⁹), inclusive.

Examples

0)

"tree"

Returns: "eetr"

An example from the problem statement.

1)

"tree"

Returns: "reet"

Another example from the problem statement.

2)

"tree"

Returns: ""

As you can see in the problem statement, the list of anagrams of "tree" only has 12 elements, so none of them has index 12.

3)

"abcabfebda"

Returns: "aadfcabbbe"

4)

"sdoijgfasdkhaiw"

2000000000

Returns: "adsdghwiiokfjas"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KLastNonZeroDigits

Simple Math

Used in:

SRM 341

Used as:

Division I Level One , Division II Level Two

Writer:

pure_

Testers:

PabloGilberto , brett1479 , Olexiy , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7397

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10665&pm=7397

Problem Statement

You are given an int N. The factorial of N is defined as N*(N-1)*(N-2)*...*1. Compute the factorial of N and remove all of its rightmost zero digits. If the result is more than K digits long, return the last K digits as a string. Otherwise, return the entire result as a string.

Definition

Class:	KLastNonZeroDigits
Method:	getKDigits
Parameters:	int, int
Returns:	String
Method signature:	String getKDigits(int N, int K)
(be sure your method is public)

Constraints

-

N will be between 1 and 20, inclusive.

-

K will be between 1 and 9, inclusive.

Examples

0)

Returns: "288"

You would first compute the factorial of 10, which is 10*9*8*7*6*5*4*3*2*1=3628800. You would then remove all rightmost zeros to get 36288. Finally, you would return the last 3 digits as a string: "288".

1)

Returns: "2"

The factorial of 6 is 720.

2)

Returns: "72"

3)

Returns: "04"

The factorial of 7 is 5040. We remove the last zero to get "504". The last 2 digits of "504" are "04".

4)

Returns: "200817664"

5)

Returns: "1"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ImprovingStatistics

Brute Force, Simple Math, Simple Search, Iteration

Used in:

SRM 338

Used as:

Division I Level One , Division II Level Two

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7386

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10662&pm=7386

Problem Statement

Several years ago I was playing Spider Solitaire on my computer all the time. Sometimes I won, sometimes I lost. Then I stopped playing Spider Solitaire and started participating in programming competitions. After a few years I happened to start my old solitaire program again. I was pleased to discover that with the skill I gained during the years I am now able to win each and every game of Spider Solitaire. However, the program still remembers some of my previous games and thus the statistics don't necessarily reflect my current perfect skills.

The program displays the statistics in the following way:

Games played: X

Games won: Y (Z %)

The number Z is the percentage of games I won, rounded down to the nearest integer. For example, if X=53 and Y=47, then Z=88.

(The value Y/X is roughly equal to 0.8868, which means that I won roughly 88.68% of the games I played. 88.68% rounded down to an integer is 88%.)

You will be given two ints played and won - the number of games I played so far, and the number of games I won so far. Return the smallest positive integer G such that if I now win G games in a row the displayed value of Z will increase. If this is impossible, return -1 instead.

Definition

Class:	ImprovingStatistics
Method:	howManyGames
Parameters:	int, int
Returns:	int
Method signature:	int howManyGames(int played, int won)
(be sure your method is public)

Notes

- You may assume that the return value will always be less than 2,000,000,000.

Constraints

- played will be between 1 and 1,000,000,000, inclusive.

- won will be between 0 and played, inclusive.

Examples

0)

Returns: 1

So far I won 8 games out of 10, and thus the displayed success percentage is 80%. After I win the next game the percentage will increase to 81%.

1)

Returns: 6

Again, the currently displayed value is 80%. However, now I need to win at least 6 more games to bring it to 81%.

2)

Returns: -1

Nothing left to improve.

3)

Returns: 1000

4)

1000000000

470000000

Returns: 19230770

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BinaryIncrementation

Simple Math, String Manipulation

Used in:

SRM 338

Used as:

Division II Level One

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7385

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10662&pm=7385

Problem Statement

The binary numeral system (base 2 numerals) represents numeric values using two symbols: 0 and 1. Counting in binary is similar to counting in any other number system. If you want to increase a number by 1, try to increase its last digit by 1. If this fails, set the last digit to zero, and try to increase the previous digit, and so on, until you succeed.

For example, the decimal sequence:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...

converted to binary looks as follows:

1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, ...

You are given a String x that contains the binary representation of a positive integer X. Write a method that will return a String containing the binary representation of (X+1). The returned String must not contain leading zeroes.

Definition

Class:	BinaryIncrementation
Method:	plusOne
Parameters:	String
Returns:	String
Method signature:	String plusOne(String x)
(be sure your method is public)

Constraints

-

x will contain between 1 and 30 characters, inclusive.

-

Each character in x will be a one ('1') or a zero ('0').

-

The first character in x will be a one ('1').

Examples

0)

"10011"

Returns: "10100"

"10011" is binary for 16+2+1 = 19. The next integer is 20 = 16+4, which is "10100" in binary.

1)

"10000"

Returns: "10001"

2)

"1111"

Returns: "10000"

Be careful not to miss the case when the result is a power of two.

3)

"1"

Returns: "10"

4)

"101010101010101010101010101010"

Returns: "101010101010101010101010101011"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RandomFights

Math, Sorting

Used in:

SRM 335

Used as:

Division I Level Three

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7384

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10659&pm=7384

Problem Statement

There are two teams A and B, each with exactly n members, that will compete in a contest to decide which team is better. The contest consists of n one-on-one fights, where a member of team A fights a member of team B. A valid fight arrangement of the teams assigns each member of team A to a distinct member of team B. All valid pairings are equally likely to be chosen. For example, if each team has 2 fighters (A1, A2 and B1, B2), there are two possible assignments: (A1 vs. B2, A2 vs. B1) and (A1 vs. B1, A2 vs. B2). Each of those assignments has a 50% chance of being chosen.

Each fighter has a non-negative integer strength. If fighters with strengths X and Y are matched in a fight, the team of the fighter with the greater strength is awarded (X-Y)² points. If both have equal strength, the fight ends in a tie and no team is awarded any points. After all the fights are finished, each team adds up their points. The winning margin of team A is their point total minus team B's point total. You must calculate and return the expected value of that number.

To keep the input small, it will be codified in the following way. You will be given two int[]s A and B representing team A and B, respectively. Use the following pseudo-code on each of the int[]s to generate the strengths of that team's members (array indices are 0-based):

input array: X
output array: R (of size n)
j := 0
m := size of X
for i := 0 to n-1
	R[i] := X[j]
	s := (j+1)%m
	X[j] := ( ( X[j] ^ X[s] ) + 13 ) % 49999
	j := s

This code, along with the constraints, ensures that each member's strength is between 0 and 49998, inclusive. In the above code, % is the modulo operator and ^ is the bitwise XOR binary operator. See the notes section for information on performing XOR in your language.

Definition

Class:	RandomFights
Method:	expectedNrOfPoints
Parameters:	int[], int[], int
Returns:	double
Method signature:	double expectedNrOfPoints(int[] A, int[] B, int n)
(be sure your method is public)

Notes

-

The input is only coded for convenience. The intended solution does not rely at all in a property of the way it is generated, it just generates both arrays and works on them.

-

The returned value must have an absolute or relative error less than 1e-9.

-

If x and y are ints, (x^y) represents the bitwise XOR operation on them in C++, Java, C# and Python. In VB.Net (x BitXor y) does it.

Constraints

-

A and B will each contain between 1 and 50 elements, inclusive.

-

Each element of A and B will be between 0 and 49998, inclusive.

-

n will be between 1 and 50000, inclusive.

Examples

0)

{6}

{4}

Returns: 4.0

The winning margin of A is always (6-4)²=4.

1)

{1,7}

{3,5}

Returns: 0.0

There are two possible assignments here: (1 vs. 3) and (7 vs. 5), or (1 vs. 5) and (7 vs. 3). In the first case, each team gets 4 points, so the winning margin of A is 0. In the second case, each team gets 16 points, so the winning margin is also 0. Since the winning margin is 0 in every case, the expected value is, of course, 0.

2)

{3,7}

{1,5}

Returns: 20.0

The two possible assignments in this case are: (3 vs. 1) and (7 vs. 5), or (3 vs. 5) and (7 vs. 1). The winning margin in the first case is 4+4=8, and in the second case, it is 36-4=32. Since both assignments are equally likely to be chosen, the expected value is the average of the two margins.

3)

{45,35,236,2342,5543,21,32,2,6,23,24,23,41,1}

{2345,45,2345,345}

Returns: 1.2721986164E8

A and B can have different lengths. Each one is generated separately.

4)

{34,3245,2534,53,53,46,346,246,346,2,624,624,6,245,6324,6542,624,6}

{345,234,523,4624,6,2456,345,634,634,7,3457,376,34,6234,62,523,52,35,32}

Returns: -9713701.714285715

You can have extra unused elements in the input.

5)

{1,2,3,4}

{1,2,3,4}

Returns: 0.0

If both teams are that even, neither of them can take advantage.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MinimumVariancePartition

Dynamic Programming, Math, Sorting

Used in:

SRM 335

Used as:

Division II Level Three

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7363

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10659&pm=7363

Problem Statement

In this problem a sample will be a collection of numbers. The mean of a sample is the average of all the numbers it contains. The variance of a sample is the sum of the squares of the distances from each number in the collection to its mean, divided by its number of elements. For example, if the sample is {3,4,7,10} the mean is 6 and the variance is (3²+2²+1²+4²)/4=7.5

We have k samples that have been combined into one collection and we need to split them up. The only thing we remember about the samples is that none of them were empty, but they could potentially each have a different number of elements. What you need to do for us is find the partition of mixedSamples, the collection, that minimizes the sum of the variances of the obtained samples. See examples for further clarification.

Definition

Class:	MinimumVariancePartition
Method:	minDev
Parameters:	int[], int
Returns:	double
Method signature:	double minDev(int[] mixedSamples, int k)
(be sure your method is public)

Constraints

-

mixedSamples will contain between 1 and 50 elements, inclusive.

-

Each element of mixedSamples will be between 1 and 1000, inclusive.

-

k will be between 1 and the number of elements in mixedSamples, inclusive.

Examples

0)

{3,4,7,10}

Returns: 7.5

Since all elements are part of the same sample, the result is simply the variance as it was shown in the problem statement.

1)

{1000,500,1,500}

Returns: 0.0

You need to partition the sample into 3 non empty sets. The partition that minimizes the sum of the variances is {1000},{1},{500,500}. The variance of each of these samples is equal to 0.

2)

{54,653,876,2,75}

Returns: 0.0

Each sample must contain a single element, and therefore the resulting variance is 0.

3)

{42,234,10,1,123,545,436,453,74,85,34,999}

Returns: 1700.7397959183672

4)

{923,456,12,12,542,234,11,12,10,9}

Returns: 1850.3333333333333

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EscapeTheJail

Math

Used in:

SRM 356

Used as:

Division I Level Three

Writer:

Pawa

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7353

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10765&pm=7353

Problem Statement

You are a prisoner and you want to escape from your jail. The jail is a grid where each square is either free or impassible. There are one or more exits located in free squares. You are initially standing in a free square and your goal is to reach one of the exits. Unfortunately, your eyes are covered, so you cannot see where you're going. Each time you move, you check up, down, left and right to see which of those four adjacent squares are free, and you randomly walk to one of the free squares. You continue to do this until you land on a square containing an exit. If there is no adjacent free cell, you stay at your current position.

You are given a String[] jail, where your start location is marked by the '@' character, impassible squares are marked with '#', exits are marked with '$' and all other free squares are '.'. Return a double representing the expected number of moves required to escape. If it is impossible to escape, return -1.

Definition

Class:	EscapeTheJail
Method:	findExit
Parameters:	String[]
Returns:	double
Method signature:	double findExit(String[] jail)
(be sure your method is public)

Constraints

-

jail will contain between 1 and 15 elements, inclusive.

-

Each element of jail will contain between 1 and 15 characters, inclusive.

-

All elements in jail will contain the same number of characters.

-

Each character in each element of jail will be '.', '#', '$' or '@'.

-

jail will contain exactly one '@' character.

-

jail will contain at least one '$' character.

Examples

0)

{"@$"}

Returns: 1.0

You have only one possible move, and it leads you to the exit. So, the answer is 1.

1)

{"$.",
 ".@"}

Returns: 4.0

2)

{"@..$"}

Returns: 9.0

3)

{"@#",
 "#$"}

Returns: -1.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Neaten

Math, Search, String Manipulation

Used in:

TCO07 Round 2

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7352

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10749&pm=7352

Problem Statement

We have a real number that we want to approximate with as few characters as possible. We require that either the absolute error or the relative error must be strictly less than 10^-k. The absolute error is the absolute difference between the values of the shortened version and the original. The relative error is the absolute error divided by the absolute value of the original (or is taken to be infinity if the original is 0).

We want the shortened version expressed as a string of digits, possibly with a decimal point. The original number is given to us in that form. Given k and number, return the number of characters in the shortest approximation.

Definition

Class:	Neaten
Method:	shortest
Parameters:	int, String
Returns:	int
Method signature:	int shortest(int k, String number)
(be sure your method is public)

Constraints

-

k will be between 1 and 50, inclusive.

-

number will contain between 1 and 50 characters, inclusive.

-

number will contain at most one decimal point ('.').

-

Other than '.', number will contain only digits ('0'-'9').

-

number will contain at least one digit.

Examples

0)

 "00."

Returns: 1

The approximation "0" has 1 character and has an absolute error of 0.

1)

".20050"

Returns: 2

The approximation ".2" has 2 characters and has an absolute error of .0005 (which is less than .01).

2)

"10000"

Returns: 4

The approximation "9995" has a relative error of 5/10000 (which is less than .001).

3)

"0.90"

Returns: 2

Please note that the error must be strictly less than 10^-k.

4)

"91.909"

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LikelyWord

Math, Search, Sorting

Used in:

SRM 336

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7351

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10660&pm=7351

Problem Statement

Given a dictionary of words, where will a newly coined word be most likely to fit?

We are given k, the length of the new word, and dictionary, a String[] of words in ascending alphabetical order. Suppose that the new word is equally likely to be any k-letter word that is not already in the dictionary. Return the most likely 0-based index for the new word. If there is more than one most likely index, return -1.

Definition

Class:	LikelyWord
Method:	likely
Parameters:	String[], int
Returns:	int
Method signature:	int likely(String[] dictionary, int k)
(be sure your method is public)

Constraints

-

dictionary will contain between 1 and 50 elements, inclusive.

-

Each element of dictionary will contain between 1 and 50 characters, inclusive.

-

Each character in each element of dictionary will be a lowercase letter ('a'-'z').

-

The elements of dictionary will be distinct and in ascending alphabetical order.

-

k will be between 1 and 10, inclusive.

-

There will be at least one k-letter word that is not in dictionary.

Examples

0)

{"time","zoology"}

Returns: 0

There are many more 1 letter words before "time" than either between "time" and "zoology" or after "zoology".

1)

{"az","ma","xz"}

Returns: 1

12 words ("b", "c", ..., "m") would have index 1, while 11 ("n", ... , "x") would have index 2.

2)

{"az","ma","xz"}

Returns: 2

With the same dictionary but a longer new word, it becomes most likely that the new word will go between "ma" and "xz".

3)

{"a","m","y"}

Returns: -1

There are 23 equally likely 1-letter words (since 3 are already in the dictionary). 0 would have index 0, 11 would have index 1, 11 would have index 2, and 1 would have index 3. So no index is most likely.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MostLikely

Simple Math, Simple Search, Iteration

Used in:

SRM 336

Used as:

Division II Level Three

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7350

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10660&pm=7350

Problem Statement

In a contest, we know the scores of all our competitors, and we estimate that our own score is equally likely to be any integer value between low and high, inclusive. We want to know what our rank will most likely be. We define our rank to be 1 + the number of competitors that beat us, so our rank will be number 1 if no one beats us (even if several tie us).

Given a int[] scores, the scores of our competitors, and ints low and high, return our most likely rank. If there is more than one most likely rank, return -1.

Definition

Class:	MostLikely
Method:	likelyRank
Parameters:	int[], int, int
Returns:	int
Method signature:	int likelyRank(int[] sc, int low, int high)
(be sure your method is public)

Constraints

-

scores will contain between 1 and 50 elements, inclusive.

-

Each element of scores will be between 0 and 1,000,000,000, inclusive.

-

low will be between 0 and 1,000,000,000, inclusive.

-

high will be between low and 1,000,000,000, inclusive.

Examples

0)

{3,12,4}

Returns: 2

It is certain that only the 12 will beat us, giving us a rank of 2.

1)

 {3,4,5}

Returns: 1

Our score is equally likely to be 3 or 4 or 5 or 6 or 7. One of those scores (the 3) gives us a rank of 3. Similarly, one of those scores gives us a rank of 2. And the remaining 3 scores all give us a rank of 1 which is thus the most likely.

2)

 {3,4,5}

Returns: -1

Each of our possible scores gives us a different rank, so all those ranks are tied for most likely.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ZenoDivision

Math, Simple Search, Iteration

Used in:

TCO08 Round 3

Used as:

Division I Level One

Writer:

legakis

Testers:

PabloGilberto , vorthys , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7343

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12013&pm=7343

Problem Statement

You and a friend are sharing a piece of cake. First you eat half of the piece, and then your friend eats half of what remains. You continue in this fashion until the two of you have finished the cake (after an infinite number of iterations). If you write the sum of the fractions each of you eat like this:

    you     him
    -----   -----
    1/2   + 1/4   +
    1/8   + 1/16  +
    1/32  + 1/64  +
    1/128 + 1/256 +
    ...

with each fraction you eat in the first column and each fraction your friend eats in the second column, you can clearly see that you eat twice as much cake as your friend does, because in each row the fraction you eat is twice the fraction your friend eats. Since the total amount of cake is 1, you therefore have eaten 2/3 of the cake and your friend has eaten 1/3.

If, instead of simply taking turns eating half of the remaining cake, you and your friend repeat a different pattern, you can each get a different total amount. For example, if you repeat the pattern "you, him, you", you will end up eating 5/7 and your friend will end up eating 2/7. This can be seen by writing the fractions as such:


    you     him     you
    -----   -----   -----
    1/2   + 1/4   + 1/8   +
    1/16  + 1/32  + 1/64  +
    1/128 + 1/256 + 1/512 +
    ...

The first and third fraction in each row sum to 5/2 of the middle fraction, so you each eat cake in the ratio of 5 to 2. Therefore, you end up eating 5/7 of the whole.

Given a fraction a/b, determine the shortest pattern of taking half of the remaining cake that can be repeated infinitely such that you will get a/b of the piece of cake. Return the pattern as a String, made up of the characters '*' (indicating that you take the next half) or '-' (indicating that your friend takes the next half). If it is impossible to achieve with a pattern of length 60 or smaller, return "impossible" (quotes for clarity only).

Definition

Class:	ZenoDivision
Method:	cycle
Parameters:	String, String
Returns:	String
Method signature:	String cycle(String a, String b)
(be sure your method is public)

Constraints

-

b will contain only digits, and will represent a number between 1 and 2^63-1, inclusive, with no unnecessary leading zeros.

-

a will contain only digits, and will represent a number between 0 and b, inclusive, with no unnecessary leading zeros.

-

The integers represented by a and b will not have any common factors (the fraction a/b will be in reduced form).

Examples

0)

"2"

"3"

Returns: "*-"

This is the first example in the problem statement.

1)

"5"

"7"

Returns: "*-*"

This is the second example in the problem statement.

2)

"0"

"1"

Returns: "-"

3)

"5"

"9"

Returns: "*---**"

4)

"1"

"2"

Returns: "impossible"

There is no way for you to each have half of the piece of cake.

5)

"76861433640456464"

"76861433640456465"

Returns: "********************************************************----"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BadExam

Simple Math, Simulation

Used in:

TCHS07 Beta 1

Used as:

Division I Level One

Writer:

tywok

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7342

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10705&pm=7342

Problem Statement

A teacher has just corrected a set of exams, and the marks are terrible! He wants to make them higher, so he uses the following procedure to adjust the grades. Let mmax be the highest mark. Each mark m will be changed to m/mmax*100. For example, if the highest mark was 70 points, and you scored 50 points, your mark would become 50/70*100, which is approximately 71.43.

You will be given a int[] marks.The ith element of marks is the mark received by the ith student. Compute the new marks for the students and return the average.

Definition

Class:	BadExam
Method:	newAverage
Parameters:	int[]
Returns:	double
Method signature:	double newAverage(int[] marks)
(be sure your method is public)

Notes

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

marks will contain between 1 and 50 elements, inclusive.

-

Each element of marks will be an integer between 0 and 100, inclusive.

-

At least one element of marks will be greater than zero.

Examples

0)

{40,80,60}

Returns: 75.0

The new marks are 50, 100 and 75. The average is (50 + 100 + 75) / 3 = 225 / 3 = 75.

1)

{10, 20, 0, 100}

Returns: 32.5

Since the maximum mark is 100, the marks are not changed.

2)

{50}

Returns: 100.0

3)

{10, 20, 30, 40, 50, 60, 70, 80, 90}

Returns: 55.55555555555556

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Squares

Search, Simple Math

Used in:

SRM 332

Used as:

Division II Level Three

Writer:

andrewzta

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7323

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10012&pm=7323

Problem Statement

You are given a rectangular field divided into square cells. Each cell contains a letter. A square with vertices in the centers of four cells is called valid if those four cells are distinct and all contain the same letter. For example, the following field contains two valid squares:

ABA
BAB
ABA

One has vertices in the centers of the following squares:

A.A
...
A.A

Another has vertices in the centers of the following cells:

.B.
B.B
.B.

You are given a String[] field. The j-th character of the i-th element of field is the letter contained in the cell at row i, column j. Return the number of distinct valid squares in the field. Two squares are distinct if one has a vertex in a cell where the other does not.

Definition

Class:	Squares
Method:	countSquares
Parameters:	String[]
Returns:	int
Method signature:	int countSquares(String[] field)
(be sure your method is public)

Constraints

-

field will contain between 1 and 50 elements, inclusive.

-

Each element of field will contain between 1 and 50 characters, inclusive.

-

All elements of field will contain the same number of characters.

-

Each element of field will contain only uppercase letters ('A'-'Z').

Examples

0)

{"ABA", "BAB", "ABA"}

Returns: 2

Example from the problem statement.

1)

{"AA", "AA"}

Returns: 1

2)

{"ABC", "DEF", "GHI"}

Returns: 0

There are no valid squares here.

3)

{"AABCA", "AAAAA", "BAAAB", "AAAEA", "ADBFA"}

Returns: 11

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ProdCalc

Simple Math, Simulation

Used in:

TCHS SRM 28

Used as:

Division I Level Two

Writer:

supernova

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7318

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10652&pm=7318

Problem Statement

You have a calculator that can only handle numbers with up to d digits. Initially, the number shown on the screen is 1. You must perform exactly op multiplication operations. Each operation multiplies the number on the screen by a digit between 2 and 9, inclusive. The result of each operation must be a number with d or less digits. Return the largest number that can be displayed on the screen after op operations. If there is no way to perform op operations without overflowing the calculator, return -1.

Definition

Class:	ProdCalc
Method:	highest
Parameters:	int, int
Returns:	long
Method signature:	long highest(int d, int op)
(be sure your method is public)

Constraints

-

d will be between 2 and 8, inclusive.

-

op will be between 0 and 30, inclusive.

Examples

0)

Returns: 729

The calculator can store up to 4 digits. With 3 multiplications, we can obtain at most 729, by using digit 9 every time: 1 * 9 * 9 * 9 = 729.

1)

Returns: 1

No multiplications can be performed.

2)

Returns: 98

The storage is limited to 2 digits. The highest number that can be shown on screen after 3 multiplications is 98 (2 * 7 * 7).

3)

Returns: 99574272

4)

Returns: 99532800

5)

Returns: -1

Even if we would only use digit 2 every time, 2^30 has more than 8 digits and overflows the calculator.

6)

Returns: 96

7)

Returns: 9

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Destruction

Dynamic Programming, Math

Used in:

TCO07 Round 1A

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7316

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10738&pm=7316

Problem Statement

We must determine whether or not a certain type of container can withstand a pressure of 100.0, and if not determine as closely as possible the "critcal pressure", the greatest pressure that it can withstand. (We know that it can withstand a pressure of 0.0.)

We can run multiple tests. Each test can test only a single pressure on a single container, and the result of a test is either that the container survived or was destroyed. If it survived it can be used in successive tests.

We must develop a testing protocol that uses no more than numTests tests and destroys no more than numDestroyed containers. The testing must determine whether or not the container can withstand 100.0, and if it cannot it must also estimate the critical pressure as accurately as possible. Given numTests and numDestroyed return the minimum absolute error we can guarantee in our estimate of critical pressure.

Definition

Class:	Destruction
Method:	minError
Parameters:	int, int
Returns:	double
Method signature:	double minError(int numTests, int numDestroyed)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

numTests will be between 1 and 50, inclusive.

-

numDestroyed will be between 1 and numTests, inclusive.

Examples

0)

Returns: 50.0

If the one test is at a pressure lower than 100.0 and the container survives, we won't know whether or not the container can survive pressures greater than 100. So the one test must be at a pressure of 100.0. If the container does not survive the test, then we can estimate the critical pressure at 50.0, with a possible error of +- 50.0.

1)

Returns: 16.666666666666664

First test pressure = 33.3333333. If the test container is destroyed, the estimate is 16.66666667 with an error of +-16.6666667. If the container survives the first test, we can run a second test at 66.666667. If the container is destroyed, our estimate is 50.0. Otherwise we run our last test at 100.0 to determine whether to estimate 83.33333 or to report that these containers can survive more than 100.0.

2)

Returns: 0.03703703703704745

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CreatePairs

Greedy, Simple Math, Sorting

Used in:

SRM 332

Used as:

Division I Level One , Division II Level Two

Writer:

andrewzta

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7309

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10012&pm=7309

Problem Statement

You are given a list of integers, and you are allowed to group elements into pairs. Each element must either belong to a single pair or remain unpaired. Sum the products of the pairs with the values of the unpaired elements. Your goal is to maximize this sum.

For example, consider the list {0, 1, 2, 4, 3, 5}. If you make the pairs (2, 3) and (4, 5), the sum is 0 + 1 + (2 * 3) + (4 * 5) = 27.

You are given a int[] data containing the list of integers. Return the maximum possible sum.

Definition

Class:	CreatePairs
Method:	maximalSum
Parameters:	int[]
Returns:	int
Method signature:	int maximalSum(int[] data)
(be sure your method is public)

Constraints

-

data will contain between 1 and 50 elements, inclusive.

-

Each element of data will be between -1000 and 1000, inclusive.

Examples

0)

{0, 1, 2, 4, 3, 5}

Returns: 27

The example from the problem statement.

1)

{-1, 1, 2, 3}

Returns: 6

If we create a pair (2, 3) we get the sum (-1) + 1 + (2 * 3) = 6.

2)

{-1}

Returns: -1

No pairs can be created, so the answer is -1.

3)

{-1, 0, 1}

Returns: 1

In this case we can create a pair (-1, 0) to make the sum equal to (-1) * 0 + 1 = 1.

4)

{1, 1}

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DifDif

Math

Used in:

TCCC07 Round 1C

Used as:

Division I Level One

Writer:

dgoodman

Testers:

PabloGilberto , Olexiy , ivan_metelsky , andrewzta

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7296

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10899&pm=7296

Problem Statement

Given a sequence of integers, s[0],s[1],..,s[n] we can define its difference sequence as the sequence s[1]-s[0], s[2]-s[1], ..., s[n]-s[n-1]. We can similarly generate its second difference sequence as the difference sequence of its difference sequence, and continue generating deeper difference sequences until we get one with length 1.

Here is an example:

seq:         5    -4    12     23
1stdifseq      -9    16    11
2nddifseq         25    -5
3rddifseq            -30

Given a sequence of integers, one useful way to predict the next value in the sequence is by choosing the one that will make the bottom difference of the enlarged sequence be 0. In the example, we would predict -1 as the next value in the sequence -- this would extend the first difference sequence to end with -1 - 23 = -24, the second to end with -35, and the third to end with -30. This would make the single value in the fourth sequence be 0. Given int[] seq, return the predicted value.

Definition

Class:	DifDif
Method:	predict
Parameters:	int[]
Returns:	int
Method signature:	int predict(int[] seq)
(be sure your method is public)

Constraints

-

seq will contain between 1 and 10 elements, inclusive.

-

Each element of seq will be between -1000 and 1000, inclusive.

Examples

0)

{5,-4, 12, 23}

Returns: -1

This is the example given above.

1)

{100}

Returns: 100

The first difference sequence of 100,100 is a sequence consisting of one 0.

2)

{1,4,9,16,25,36}

Returns: 49

3)

{-1000,1000,-1000,1000,-1000,1000,-1000,1000,-1000,1000}

Returns: 1023000

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ThreeBuses

Geometry, Math

Used in:

SRM 333

Used as:

Division I Level Three

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy , Mike Mirzayanov

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7295

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10657&pm=7295

Problem Statement

Little Johnny woke up late. Now he only has timeLeft minutes to get to school.

Sadly, Johnny doesn't have a direct connection to school. He has to use three specific bus lines (one after another) to get there.

The buses in Johnny's town don't have a fixed schedule. Instead, each bus line is assigned some non-negative integer W. If you arrive at a bus stop of a bus line, you know that the time you will have to wait is a random variable drawn from the interval [0,W] with uniform probability. Note that from a passenger's point of view the number W corresponds to the maximum waiting time.

(You can imagine this in a real life setting as follows: If you stand on a bus stop of a line that has a positive W, precisely every W minutes a bus comes by, you just don't know the offset. If you stand on a bus stop of a line that has W=0, there is always a bus ready to take you.)

You are given two int[]s wait and travel, and an int timeLeft. The int[] wait specifies the value W (the maximum waiting time) for each of the bus lines Johnny has to take. The int[] travel specifies how long Johnny rides each of the three buses. Write a method that computes the probability that Johnny will arrive to school on time.

Definition

Class:	ThreeBuses
Method:	getProbability
Parameters:	int[], int[], int
Returns:	double
Method signature:	double getProbability(int[] wait, int[] travel, int timeLeft)
(be sure your method is public)

Notes

-

Time is continuous, e.g., the bus can arrive 0.47 minutes after Johnny comes to a bus stop.

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

wait will contain exactly 3 elements.

-

Each element of wait will be between 0 and 100,000, inclusive.

-

travel will contain exactly 3 elements.

-

Each element of travel will be between 1 and 100,000, inclusive.

-

timeLeft will be between 1 and 600,000, inclusive.

Examples

0)

{0, 0, 0}

{10, 15, 10}

Returns: 1.0

Johnny won't have to wait for the buses. He can be sure his trip will take exactly 35 minutes, and 35 is not more than 47.

1)

{0, 0, 0}

{10, 15, 10}

Returns: 1.0

The same setting as before. With 35 minutes left, Johnny will arrive exactly on time.

2)

{1, 100, 1}

{10, 10, 10}

Returns: 0.21

This time Johnny may get into trouble. It all depends on whether the second bus arrives soon enough. A rough estimate: if the second bus arrives in less then 20 minutes, Johnny will surely make it. Thus the exact probability is slightly over 20/100.

3)

{100, 100, 70}

{1, 1, 1}

Returns: 0.020281904761904737

Johnny must be really lucky to make it.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BirthNumbersValidator

Simple Math

Used in:

SRM 333

Used as:

Division I Level One , Division II Level Two

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy , Mike Mirzayanov

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7291

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10657&pm=7291

Problem Statement

In Slovakia, every person is assigned a unique 10-digit string when he is born. This string is known as the birth number of the respective person.

The birth number has the form "YYMMDDCCCC", where:

YY are the last two digits of the year.
For males, MM is a two-digit number of the month, i.e., a number between 01 and 12, inclusive.

For females, MM is the number of the month increased by 50, i.e., a number between 51 and 62, inclusive.
DD is a two digit number of the day in the month.
CCCC are four arbitrary digits that are used both as a checksum and as a way to distinguish between different people born on the same day.

The checksum property works as follows: the digits CCCC must be chosen in such a way that the entire 10-digit number is divisible by eleven (11).

For example, the strings "8104121234" and "8154121239" represent valid birth numbers.

(The first person is male, the second one female. Both of them are born on April 12th, ??81.)

The strings "8134120005", "8102310007", and "8104121235" are not valid birth numbers.

(In the first case, "34" can not be a valid month. In the second case, the day number is wrong, as the second month has less than 31 days. In the third case, the date is valid but the number is not divisible by 11.)

You will be given a String[] test containing several ten-digit strings. Write a method that will return a String[] with the same number of elements. If the i-th element of test is a valid birth number the i-th element of the return value shall be "YES", otherwise the i-th element of the return value shall be "NO". When checking whether the date is valid, assume that the year when the person was born is between 1907 and 2006, inclusive.

Definition

Class:	BirthNumbersValidator
Method:	validate
Parameters:	String[]
Returns:	String[]
Method signature:	String[] validate(String[] test)
(be sure your method is public)

Notes

- The number of days in each month of a non-leap year (from 1 to 12): 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31.

- Leap years have 29 days in the second month.

- A year is a leap year if either (the year is divisible by 400) or (the year is divisible by 4, but not by 100).

For example, 2000 and 2004 are leap years, 1900 and 1947 are not.

Constraints

- test will contain between 1 and 50 elements, inclusive.

- Each element of test will contain exactly 10 characters.

- Each element of test will contain only digits ('0'-'9').

Examples

0)

{"8104121234"}

Returns: {"YES" }

The first example from the problem statement.

1)

{"8154121239"}

Returns: {"YES" }

The second example from the problem statement.

2)

{"8134120005"}

Returns: {"NO" }

The third example from the problem statement.

3)

{"8102310007","8104121235"}

Returns: {"NO", "NO" }

The last two examples from the problem statement.

4)

{"0411131237"}

Returns: {"YES" }

Note that leading zeros may occur in a valid birth number.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RandomSwaps

Dynamic Programming, Math

Used in:

SRM 338

Used as:

Division I Level Two

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7289

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10662&pm=7289

Problem Statement

Suppose that we have an array with arrayLength distinct elements. A quite common task in programming is to randomly permute this array. Novices who encounter this situation often implement the following algorithm:

Choose a positive integer swapCount.
swapCount times randomly choose two distinct indices and swap the corresponding elements.

This method of permuting an array is bad, because some permutations of the array will be more likely than others. In this problem, you shall compute how bad this method is for a given situation.

You will be given four ints: arrayLength, swapCount, a and b. Consider the element of the array that initially had the index a. Write a method that will compute the probability that this element will have the index b at the end of the process described above.

Definition

Class:	RandomSwaps
Method:	getProbability
Parameters:	int, int, int, int
Returns:	double
Method signature:	double getProbability(int arrayLength, int swapCount, int a, int b)
(be sure your method is public)

Notes

-

The indices of elements that are going to be swapped are generated with a uniform probability distribution, i.e., each pair of indices has got the same probability of being chosen.

-

The indices are zero-based, i.e., the array contains elements with indices 0 to arrayLength-1, inclusive.

-

The returned value must have an absolute or relative error less than 1e-9.

Constraints

-

arrayLength will be between 2 and 1,000, inclusive.

-

swapCount will be between 1 and 100,000, inclusive.

-

a and b will be between 0 and arrayLength-1, inclusive.

Examples

0)

Returns: 0.6

There are ten possible pairs of indices to swap: (0,1), (0,2), (0,3), (0,4), (1,2), (1,3), (1,4), (2,3), (2,4), and (3,4). Out of these ten, the last six leave the element 0 untouched. Thus the probability is 6/10.

1)

Returns: 0.1

Only the swap (0,3) will move the element from position 0 to position 3.

The probability of choosing this swap is 1/10.

2)

Returns: 0.4

Now there are two possibilities: Either the 0-th element stays in its place for the whole time, or it is swapped away and back again. The probability of the first possibility is (6/10)^2, for the second possibility it is (4/10)*(1/10).

3)

Returns: 0.010036635745123007

For 100 elements, even after 500 swaps, the permutation won't be random enough.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TextStatistics

Brute Force, Simple Math

Used in:

SRM 332

Used as:

Division II Level One

Writer:

andrewzta

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7277

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10012&pm=7277

Problem Statement

Most modern text editors are able to give some statistics about the text they are editing. One nice statistic is the average word length in the text.

A word is a maximal continuous sequence of letters ('a'-'z', 'A'-'Z'). Words can be separated by spaces, digits, and punctuation marks.

The average word length is the sum of all the words' lengths divided by the total number of words. For example, in the text "This is div2 easy problem.", there are 5 words: "This", "is", "div", "easy", and "problem". The sum of the word lengths is 4+2+3+4+7=20, so the average word length is 20/5=4.

Given a String text, return the average word length in it. If there are no words in the text, return 0.0.

Definition

Class:	TextStatistics
Method:	averageLength
Parameters:	String
Returns:	double
Method signature:	double averageLength(String text)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

text will contain between 0 and 50 characters, inclusive.

-

text will contain only letters ('a'-'z', 'A'-'Z'), digits ('0'-'9'), spaces, and the following punctuation marks: ',', '.', '?', '!', '-'.

Examples

0)

"This is div2 easy problem."

Returns: 4.0

The example from the problem statement.

1)

"Hello, world!"

Returns: 5.0

In this case all words have the same length.

2)

"Simple"

Returns: 6.0

One word.

3)

""

Returns: 0.0

No words here, so return 0.

4)

"AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA"

Returns: 50.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NextPalindromicNumber

Simple Math, String Manipulation

Used in:

SRM 330

Used as:

Division II Level Three

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Olexiy , misof

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7257

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10010&pm=7257

Problem Statement

A palindromic number is a number that reads the same forward and backward. 101, 4 and 6666 are palindromic numbers while 10, 564 and 15452 are not.

You will be given a String n representing a positive integer. Determine the smallest palindromic integer strictly greater than n, and return it as a String with no leading zeroes.

Definition

Class:	NextPalindromicNumber
Method:	getNext
Parameters:	String
Returns:	String
Method signature:	String getNext(String n)
(be sure your method is public)

Notes

-

No positive multiple of 10 is a palindromic number.

Constraints

-

n will contain between 1 and 50 characters, inclusive.

-

Each character of n will be a digit ('0'-'9').

-

The first character of n will not be zero ('0').

Examples

0)

"12345"

Returns: "12421"

1)

"858"

Returns: "868"

2)

"1999"

Returns: "2002"

3)

"1"

Returns: "2"

4)

"9999"

Returns: "10001"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

VolleyballTournament

Simple Math

Used in:

SRM 344

Used as:

Division I Level One

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7252

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10668&pm=7252

Problem Statement

The common method to print the standings for a volleyball tournament is to print the number of won matches, the number of lost matches, the number of won sets, and the number of lost sets for each team.

Each match consists of three to five sets, where each set is won by one of the teams. The first team to win three sets is declared the winner of the match.

You are given one row of the standings table. That is, you are given an int wonMatches, denoting the number of matches won by a team, an int lostMatches, denoting the number of matches lost by that team, an int wonSets, denoting the total number of sets won by that team, and an int lostSets, denoting the total number of sets lost by that team. These numbers represent a possible tournament outcome for a team, and you are to reconstruct the results of all matches for that team, and return them as a comma-separated list, sorted lexicographically. Each match in the list must be formatted as the number of sets won by the team, followed by a dash ('-'), followed by the number of sets lost by the team. The possible outcomes for a match are "0-3", "1-3", "2-3", "3-0", "3-1", and "3-2" (all quotes for clarity only). If multiple different result sets are possible (sets that are reorderings of each other are not considered different), return "AMBIGUITY" (quotes for clarity) instead.

Definition

Class:	VolleyballTournament
Method:	reconstructResults
Parameters:	int, int, int, int
Returns:	String
Method signature:	String reconstructResults(int wonMatches, int lostMatches, int wonSets, int lostSets)
(be sure your method is public)

Notes

-

The returned string must not contain spaces.

Constraints

-

wonMatches and lostMatches will each be between 0 and 100, inclusive.

-

At least one of wonMatches and lostMatches will be greater than 0.

-

wonSets and lostSets will each be between 0 and 500, inclusive.

-

The numbers given will correspond to at least one possible result set.

Examples

0)

Returns: "0-3,0-3,0-3,3-0,3-0,3-0"

1)

Returns: "2-3,2-3,2-3"

2)

Returns: "AMBIGUITY"

It could have been "3-0,3-1,3-2" or "3-1,3-1,3-1".

3)

Returns: "1-3,3-1"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LightsCube

Brute Force, Simple Math, Simple Search, Iteration, Simulation

Used in:

SRM 328

Used as:

Division I Level One , Division II Level Two

Writer:

_efer_

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7250

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10008&pm=7250

Problem Statement

You have received a nice gift from a friend. It consists of some colored lights arranged in a N x N x N cube, with a light at every slot inside the cube. The position of each light is described by three coordinates (x, y, z) where x, y and z are non-negative integers less than N. The light in position (x, y, z) is adjacent to the lights at positions (x-1, y, z), (x+1, y, z), (x, y-1, z), (x, y+1, z), (x, y, z-1) and (x, y, z+1) (when these lights exist). Initially some lights (at least one) are turned on. During each second, all turned off lights adjacent to a turned on light are switched on and take its color. If a light is adjacent to more than one turned on light, it takes the lower number color. This process continues until all the lights are on.

You are given an int N and a String[] lights. The i-th element of lights is formatted as "x y z" (quotes for clarity only) and describes the position of the light of color i. Return a int[] with the same number of elements as lights, the i-th element of which represents the number of lights of color i after the process described above ends.

Definition

Class:	LightsCube
Method:	count
Parameters:	int, String[]
Returns:	int[]
Method signature:	int[] count(int N, String[] lights)
(be sure your method is public)

Constraints

-

N will be between 1 and 40, inclusive.

-

lights will contain between 1 and 50 elements, inclusive.

-

Each element of lights will be in the form "x y z" (quotes for clarity) where x, y and z are integers between 0 and N-1, inclusive, with no leading zeroes.

-

The positions in lights will be distinct.

Examples

0)

{"0 0 0", "0 0 1", "0 1 0", "0 1 1", "1 0 0", "1 0 1", "1 1 0", "1 1 1"}

Returns: {1, 1, 1, 1, 1, 1, 1, 1 }

Initially all lights are on. Therefore, we end with one light of each color.

1)

{"1 1 1"}

Returns: {27 }

There is only 1 light turned on, so all other 26 lights will take its color. Six lights are turned on during the first second, twelve during the second one and the last eight are turned on during the third second.

2)

{"0 0 0", "3 3 3"}

Returns: {32, 32 }

The lights turned on are at opposite corners. There will never be a turned off light adjacent to lights of different colors, so we end up with an equal number of lights of each color.

3)

{"0 2 4", "2 0 0", "3 4 4", "4 1 2"}

Returns: {38, 28, 32, 27 }

A turned off light might be adjacent to lights of different colors. For example, just before it turns on, the light at position (4, 3, 3) will be adjacent to lights of the last two colors. It will take the third color.

4)

{"4 7 6", "8 0 0", "3 2 3", "7 7 2", "7 5 1",
 "10 11 5", "4 9 7", "6 1 0", "10 1 1", "9 7 11",
 "11 3 11", "9 0 3", "10 2 0"}

Returns: {264, 18, 303, 236, 105, 124, 216, 44, 53, 146, 126, 80, 13 }

5)

{"29 13 9", "4 10 34", "11 26 16", "2 33 22", "27 31 14", "36 20 8"}

Returns: {14657, 12834, 12364, 5902, 12678, 5565 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EncodedSum

Math

Used in:

SRM 334

Used as:

Division I Level One

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7249

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10658&pm=7249

Problem Statement

You are given a String[] numbers, each element of which represents a positive integer written using the letters 'A' through 'J' instead of digits. You know that each letter represents exactly one digit, and each digit is represented by exactly one letter. You also know that none of the integers start with zero. Return the maximum possible sum of the given integers.

Definition

Class:	EncodedSum
Method:	maximumSum
Parameters:	String[]
Returns:	long
Method signature:	long maximumSum(String[] numbers)
(be sure your method is public)

Constraints

-

numbers will contain between 1 and 50 elements, inclusive.

-

Each element of numbers will contain between 1 and 12 characters, inclusive.

-

Each element of numbers will contain only uppercase letters between 'A' and 'J', inclusive.

-

There will be at least one letter between 'A' and 'J', inclusive, that never occurs as the first character of any element of numbers.

Examples

0)

{"ABC",
 "BCA"}

Returns: 1875

B = 9
A = 8
C = 7

1)

{"ABCDEFGHIJ"}

Returns: 9876543210

2)

{"ABCDEFGHIJ", 
 "J"}

Returns: 9876543202

We can not use J as 0. So,

J = 1
I = 0

3)

{"A", 
 "BB", 
 "CCC", 
 "DDDD", 
 "EEEEE", 
 "FFFFFF", 
 "GGGGGGG", 
 "HHHHHHHH", 
 "IIIIIIIII", 
 "AJJJJJJJJJ"}

Returns: 9973936905

4)

{"GHJIDDD",
 "AHHCCCA",
 "IIJCEJ",
 "F",
 "HDBIGFJAAJ"}

Returns: 9888114550

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NewMagicSquare

Math

Used in:

SRM 351

Used as:

Division I Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7247

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10675&pm=7247

Problem Statement

You are to populate a 5x5 square with each of the numbers between 1 and 25, inclusive. The numbers in each row must be in increasing order from left to right. Some of the cells are already filled in, but no more than one number per row. You must fill in the remaining cells.

You will be given a String[] square. Each row is given as a space-separated list of cells. Each cell is either a number written with two digits (numbers less than 10 have an additional leading zero) or two '?' characters which represent an empty cell. Your method should return a String[] in the same format, but with all the empty cells filled in. If there are no arrangements possible return an empty String[]. If there are several arrangements possible return the one with the smallest first number in the first row. If there are still several arrangements possible return the one with the smallest second number in the first row, and so on.

Definition

Class:	NewMagicSquare
Method:	completeTheSquare
Parameters:	String[]
Returns:	String[]
Method signature:	String[] completeTheSquare(String[] square)
(be sure your method is public)

Constraints

-

square will contain exactly 5 elements.

-

Each element of square will contain exactly 14 characters.

-

Each element of square will be a space-separated list of cells.

-

Each cell will be either a number written with two digits or two '?' characters.

-

Each element of square will contain at most one filled cell.

-

All numbers in square will be between 1 and 25, inclusive.

-

All numbers in square will be distinct.

Examples

0)

{"?? ?? ?? ?? ??", 
 "?? ?? ?? ?? ??", 
 "?? ?? ?? ?? ??", 
 "?? ?? ?? ?? ??", 
 "?? ?? ?? ?? ??"}

Returns: 
{"01 02 03 04 05",
"06 07 08 09 10",
"11 12 13 14 15",
"16 17 18 19 20",
"21 22 23 24 25" }

You are not limited by prefilled cells. The answer is the lexicographically smallest square.

1)

{"?? ?? 20 ?? ??", 
 "?? ?? ?? ?? ??", 
 "?? ?? ?? 05 ??", 
 "?? ?? ?? ?? ??", 
 "?? ?? ?? ?? ??"}

Returns: 
{"01 06 20 21 22",
"07 08 09 10 11",
"02 03 04 05 12",
"13 14 15 16 17",
"18 19 23 24 25" }

2)

{"?? ?? ?? ?? ??", 
 "?? ?? ?? ?? 24", 
 "?? ?? ?? ?? ??", 
 "?? ?? ?? ?? ??", 
 "21 ?? ?? ?? ??"}

Returns: { }

You should place four numbers greater than 21 into the 5th row. There are four such numbers - 22, 23, 24 and 25, but 24 is already used in the second row.

3)

{"?? ?? 15 ?? ??", 
 "02 ?? ?? ?? ??", 
 "?? ?? ?? 07 ??", 
 "?? ?? 16 ?? ??", 
 "?? ?? ?? ?? 21"}

Returns: 
{"01 03 15 17 18",
"02 08 09 10 22",
"04 05 06 07 23",
"11 12 16 24 25",
"13 14 19 20 21" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KnightTour

Simple Math, Simulation

Used in:

SRM 334

Used as:

Division II Level Two

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7245

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10658&pm=7245

Problem Statement

A knight is a chess piece that moves by simultaneously shifting one square along one axis and two squares along the other. A knight's tour of a chessboard is a sequence of moves made by a knight such that each square of the board is visited exactly once. If the final position in the tour is a knight's move away from the first position, the tour is called re-entrant. The picture below shows a re-entrant knight's tour for a 6x6 chessboard.

Josh is trying to find another re-entrant knight's tour on a 6x6 chessboard. He needs a program to make sure he doesn't make any mistakes.

You will be given a String[] cells containing the sequence of cells visited by the knight in order. Each element represents a single cell and is in the form "<letter><digit>" (quotes for clarity), where <letter> is a letter representing the column and <digit> is a digit representing the row. "A1" represents the bottom-left corner of the board, and "F6" represents the top-right corner (see the picture). Return the String "Valid" if cells contains a valid re-entrant knight's tour, and return "Invalid" otherwise (all quotes for clarity).

Definition

Class:	KnightTour
Method:	checkTour
Parameters:	String[]
Returns:	String
Method signature:	String checkTour(String[] cells)
(be sure your method is public)

Constraints

-

cells will contain exactly 36 elements.

-

Each element of cells will be in the form "<letter><digit>" (quotes for clarity), where <letter> is an uppercase letter between 'A' and 'F', inclusive, and <digit> is a digit between '1' and '6', inclusive.

Examples

0)

{"A1", "B3", "A5", "C6", "E5", "F3",
 "D2", "F1", "E3", "F5", "D4", "B5",
 "A3", "B1", "C3", "A2", "C1", "E2",
 "F4", "E6", "C5", "A6", "B4", "D5",
 "F6", "E4", "D6", "C4", "B6", "A4",
 "B2", "D1", "F2", "D3", "E1", "C2"}

Returns: "Valid"

The example from the statement.

1)

{"A1", "C2", "E3", "F5", "D4", "B3",
 "A1", "C2", "E3", "F5", "D4", "B3", 
 "A1", "C2", "E3", "F5", "D4", "B3", 
 "A1", "C2", "E3", "F5", "D4", "B3", 
 "A1", "C2", "E3", "F5", "D4", "B3", 
 "A1", "C2", "E3", "F5", "D4", "B3"}

Returns: "Invalid"

Some cells are not visited.

2)

{"D4", "F5", "D6", "B5", "A3", "B1", 
 "D2", "F1", "E3", "D1", "F2", "E4", 
 "F6", "D5", "B6", "A4", "B2", "C4", 
 "A5", "C6", "E5", "F3", "E1", "C2", 
 "A1", "B3", "C5", "E6", "F4", "E2", 
 "C3", "A2", "C1", "D3", "B4", "A6"}

Returns: "Invalid"

This tour is not re-entrant.

3)

{"D4", "F5", "D6", "B5", "A3", "B1", 
 "D2", "F1", "E3", "D1", "F2", "E4", 
 "F6", "D5", "B6", "A4", "B2", "C4", 
 "A5", "C6", "E5", "F3", "E1", "C2", 
 "A1", "B3", "C5", "A6", "B4", "A2", 
 "C3", "E2", "C1", "D3", "F4", "E6"}

Returns: "Valid"

4)

{"C5", "D3", "F2", "D1", "B2", "A4", 
 "B6", "D5", "C3", "E4", "F6", "B3", 
 "A1", "C2", "E1", "F3", "E5", "C6", 
 "A5", "C4", "A3", "B1", "D2", "F1", 
 "E3", "F5", "D6", "B5", "D4", "E6", 
 "F4", "E2", "C1", "A2", "B4", "A6"}

Returns: "Invalid"

"F6-B3" is not a valid knight move.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ExtendedHappyNumbers

Dynamic Programming, Math

Used in:

SRM 334

Used as:

Division I Level Two , Division II Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7244

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10658&pm=7244

Problem Statement

Given a positive integer N, raise each of its digits to the K-th power and sum those values to get S_K(N). For example, S₂(65) = 6² + 5² = 61. Now, consider a sequence N, S_K(N), S_K(S_K(N)) and so on. The happiness of N with respect to K is the smallest number in this sequence.

You will be given three ints A, B and K. Calculate the happiness of each integer between A and B, inclusive, with respect to K and return their sum.

Definition

Class:	ExtendedHappyNumbers
Method:	calcTheSum
Parameters:	int, int, int
Returns:	long
Method signature:	long calcTheSum(int A, int B, int K)
(be sure your method is public)

Constraints

-

A will be between 1 and 1,000,000, inclusive.

-

B will be between A and 1,000,000, inclusive.

-

K will be between 1 and 6, inclusive.

Examples

0)

Returns: 1

The sequence for 13 is 13, 10, 1, 1...

1)

Returns: 14

The sequences for numbers 1 to 5 are:

1: 1, 1, 1...

2: 2, 4, 16, 37, 58, 89, 145, 42, 20, 4...

3: 3, 9, 81, 65, 61, 37, 58, 89, 145, 42, 20, 4, 16, 37...

4: 4, 16, 37, 58, 89, 145, 42, 20, 4...

5: 5, 25, 29, 85, 89, 145, 42, 20, 4, 16, 37, 58, 89...

2)

Returns: 450

3)

Returns: 820

4)

Returns: 5169721292

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RailroadSeatNumeration

Simple Math, Simple Search, Iteration

Used in:

SRM 329

Used as:

Division I Level One , Division II Level Two

Writer:

dmytro

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7243

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10009&pm=7243

Problem Statement

In a certain European country, railroad cars consist of 9 compartments, each containing 4 seats. There are two possible numeration methods for the seats: the domestic numeration and the international numeration.

In the domestic numeration, the seats in the first compartment are numbered 1 through 4, the seats in the second compartment are numbered 5 through 8, and so on.
In the international numeration, every seat's number consists of two digits. The first digit is the number of the compartment and the second digit is the number of the seat within that compartment. Compartments are numbered 1 through 9, and the four seats within each compartment are numbered 1, 3, 4, 6 (in the same order as in the domestic numeration).

You are given a int[] tickets containing seat numbers in an unknown numeration. Assuming that every seat number in tickets is in the same numeration, convert them into the international numeration. Return the result as a String containing a single-space separated list of converted numbers in the same order that they are given in the input. If there are several possible return values, return "AMBIGUOUS" (quotes for clarity only). If the input cannot be interpreted as a valid list of seat numbers all in the same numeration, return "BAD DATA" (quotes for clarity only).

Definition

Class:	RailroadSeatNumeration
Method:	getInternational
Parameters:	int[]
Returns:	String
Method signature:	String getInternational(int[] tickets)
(be sure your method is public)

Constraints

- tickets will contain between 1 and 36 elements, inclusive.

- Each element of tickets will be between 1 and 100, inclusive.

- tickets will contain no duplicate elements.

Examples

0)

{1}

Returns: "11"

Seat number 1 exists only in the domestic numeration, and it corresponds to seat number 11 in the international numeration.

1)

{11}

Returns: "AMBIGUOUS"

Seat number 11 exists in both numerations, so we cannot figure out which numeration is used here.

2)

{45}

Returns: "BAD DATA"

No seat can be numbered 45 in any numeration.

3)

{5, 7, 6}

Returns: "21 24 23"

Remember to return tickets in the same order as in the input.

4)

{21, 24, 23}

Returns: "AMBIGUOUS"

5)

{8, 28}

Returns: "26 76"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StoneGame

Math, Sorting

Used in:

SRM 345

Used as:

Division I Level Two

Writer:

rusolis

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7238

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10669&pm=7238

Problem Statement

You and your friend are playing a game. There is a number of treasure chests hidden under piles of stones. That is, the i-th chest has stones[i] stones piled on top of it. You take turns taking exactly one stone from the top of one of the chests. Whoever takes the last stone from the top of a chest takes the chest and the treasure inside. The inside of the i-th chest is worth treasure[i]. The game objective is to gather as much treasure as possible.

Unfortunately, your friend is a cyborg and always makes the best possible move (maximizing his final win). Given stones and treasure, return the maximum total amount you can get from the chests given that you move first.

Definition

Class:	StoneGame
Method:	getScore
Parameters:	int[], int[]
Returns:	int
Method signature:	int getScore(int[] treasure, int[] stones)
(be sure your method is public)

Constraints

-

stones will contain between 1 and 50 elements, inclusive.

-

stones and treasure will contain the same number of elements.

-

Each element of stones will be between 1 and 10^6, inclusive.

-

Each element of treasure will be between 1 and 10^6, inclusive.

Examples

0)

{3,2}

{1,2}

Returns: 5

In your first move you take the stone from the 0-th chest and take its treasure. Then your friend must take a stone from the 1-st chest leaving you with one stone on the 1-st chest. You take the last stone in your second move and take the contents of the 1-st chest.

1)

{5,4,3,2,1}

{1,1,1,1,1}

Returns: 9

2)

{5,5}

{2,2}

Returns: 0

3)

{1}

{10}

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GroupSkills

Used in:

Used as:

Writer:

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6878

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10649&pm=6878

Problem Statement

A large committee of individuals is responsible for dealing with a wide variety of problems that come up. Any problem can be described in terms of various attributes about the problem. For instance, one problem may require a lot of planning, but not much technical skill. Another might require a moderate amount of planning, and very little technical skill.

Each member of this large committee has a certain ability level with respect to each of these attributes. A problem requies a certain level of proficiency with each different attribute in order to be solved. When a group of people works together, the proficiency of the group with respect to an attribute A is the maximum proficiency of a group member on A.

Because the committee is large, it has been suggested that it be divided into subgroups, so that the overall productivity of the committee can be improved. The productivity of a subgroup is described in terms of how large a range of problems it can solve, and the productivity of the committee as a whole is the sum of the productivity of the subgroups.

We can describe this system of attributes and abilities mathematically, by representing each person as a point in n-dimensional space. (Where n is the number of attributes we are examining.) The range of problems that can be solved by any group is then the volume of the minimal bounding hyper-box around the origin, and each of the points in the group. For example, the points (3, 5) and (6, 2), would have a bounding box that extends from (0,0) to (6,5), so the potential productivity of the group is 6 * 5 = 30.

Your method, getGroups, is given String[] members as input. Each element is a space-delimited list of integers, representing the ability levels of a single member, with respect to each attribute. Each element will contain the same number of ability values. Your method should return a int[], where each element of the return is an integer between 0 and n-1, inclusive, indicating a group that the member should belong to. (n is the number of members) For instance, if there are five members, returning {0,1,0,1,1} would create a group of 2 (containing the first and third individual) and a group of three containing the remainder.

Test cases are generated as follows: The number of members is selected at random, between 50 and 10000, inclusive. The number of attributes to be assigned to each member is selected randomly, between 3 and 20, inclusive. Then, each ability value is assigned, again at random, between 0 and 99, inclusive. All ranges are inclusive, and all random choices are uniform.

Your score for an individual test case will be the d^th root of volume/n*(1-time/100), where d is the number of dimensions and n is the number of members, and time is your execution time in seconds. Your overall score will simply be the sum of your scores on individual test cases.

Definition

Class:	GroupSkills
Method:	getGroups
Parameters:	String[]
Returns:	int[]
Method signature:	int[] getGroups(String[] members)
(be sure your method is public)

Notes

- The first few examples were generated with smaller sizes than the normal constraints, to help facilitate testing.

- The memory limit is 1024M.

- The time limit is 30 seconds per test case.

Constraints

- members will contain between 50 and 10000 elements, inclusive.

- Each element of members will be a space-delimited list of between 3 and 20 integers.

- Each element of members will contain the same number of integers.

- Each integer will be between 0 and 99, with no extra leading zeroes.

Examples

0)

"10"

Returns: "There are 5 members, and 2 abilities.

 3  5
 6  2
60 83
79 84
38 26
"

This committee contains the two individuals referred to in the problem statement. In this case, the best we can do is to put the first two users in one group, and then have three more groups of single individuals. This gives a volume of 12634.

1)

"11"

Returns: 
"There are 15 members, and 5 abilities.

38 26 23 94 99
76 32 18 60 72
 4 31 27 64 97
58 75  8 92 31
83 81 44 41 20
67 58 73 48 38
75 86 73 50 27
 3 86 71  8 69
 5 91 43 40 13
49 20 77 13 31
21 59 49 56 51
38 57 39 86 91
73 17 97 28 14
 7 36 22 57 67
66 41 42 74 19
"

The optimal volume here is over 1E10.

2)

"12"

Returns: 
"There are 50 members, and 10 abilities.

21 91 40 93 30 87 14 44 68 33
86 55 40 43 51 77 53  8 42  3
16 27  9 70 72 42 36 14 92  2
15 41 19 69 68 99 31 33 85 58
12 98 61 10 60 17 51  3 58 90
95 35 58 12 46 56 25 67 86  5
89 95 44 30 58  3 90 40 30 25
79 68 10 53  4 70  5 49 20 51
94 86 97 22 41 53 70 51 69 25
 1 69 23 61 46 69 15 58 56 62
32 41 84 59 19 45 84 25 21 22
14 81 71 36 88 90 61 18 70 59
93 86 36 87 98 68 82 89 14 39
65 89 74 36 56  4 75  0 96 32
98 55 63 84 42 69 75 51 29 24
 7 31 85 98 60  1 63 56  1 90
21 43 43 46 28 73 83 59 22 77
12 91  2 85 37 89 75 77 39 91
72 62 77 91 50 36 83 27 89 11
31 21 53  5 46 65 12  2 46 52
46 13 55 73 23 50 16  3 66 33
68 48 33 16  5 89 91 25 71 47
88 79 64  2 97 20 68 59 44  7
83 88 81 16 61 58 72 81 67 31
85 41 65 54 13 63 52 15 69 54
39 87 86 92 37 60 94 14 44 30
35 28 20 17 50 44 10 37 33 78
56 79 50 16 45 24  9 44 93 95
96 21 68  6 70 16 61 20 57 37
70 60  5 28 32 86 23 90 38 81
75 40 52  8  0  3 24 55 18 42
46 51 39 13  1 60 75 23 21 32
92 39  2 68  7 15 33 16 52 13
 6 51 25 16  5  0  2 35 54 73
47 39 12 80 92 47 86 45 72 39
 0 24 66 73 52 67 43 94 53 77
48 88 97 29  4 81 53 47 26 55
87 16 83 18 78 89  2 87 18 86
26 58 92 12 16 52 82  4  2 83
12 48 70 54 43 86 49 99  5 38
67 95 87 95 68 70 79 31 52 95
17 81 29  9 38 42 81 10 69 58
58 48 85 14 47 37 33 64  4 85
68 26 57  8 90 27 69 78 86 99
96 84 28 68 16 77 92 42 52 34
14 52 41 52 28 36 75  2 27 91
78 77 23 21  0 15 24  2 19 98
98 12 76 23 31 35 77 76 74 71
33 14 77 42 14 99 94 13  7  1
86 41 51 18 21 81  8 93 24 77
"

3)

"13"

Returns: "There are 200 members, and 20 abilities."

Download

4)

"14"

Returns: "There are 1000 members, and 3 abilities."

Download

5)

"15"

Returns: "There are 4958 members, and 3 abilities."

Download

6)

"16"

Returns: "There are 8681 members, and 4 abilities."

Download

7)

"17"

Returns: "There are 1626 members, and 13 abilities."

Download

8)

"18"

Returns: "There are 137 members, and 9 abilities."

Download

9)

"19"

Returns: "There are 10000 members, and 20 abilities."

This is the largest input size. Download

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ValidPlates

Dynamic Programming, Geometry, Math

Used in:

SRM 341

Used as:

Division I Level Three

Writer:

radeye

Testers:

PabloGilberto , brett1479 , Olexiy , Jan_Kuipers , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6876

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10665&pm=6876

Problem Statement

Inmates on planet Elba II are making license plates for the various departments of interplanetary vehicles of the Federation. All plates denote positive numbers using the digits '0'-'9'. No plate ever contains a leading 0.

Unfortunately, certain pairs of digits are considered obscene by different planets. Therefore, no plate can be created that contains those adjacent sequences of digits.

The plates are ordered by the value of the positive number on them. They are then numbered by their placement on that ordered list; this numbering is called the sequence number. Thus, the plate with sequence number 1 has "1" on it, the plate with sequence number 9 has "9" on it, and beyond that, the plates are determined by what digit pairs are legal. For instance, if only the digit sequence "10" was illegal, then the plate with sequence number 10 would be "11", and the plate with sequence digit 99 would be "111".

Your task as a lowly programmer peon on Elba II is to write a method to determine the plate number, given the set of digit pairs that are illegal and the sequence number of the plate. If there can be no plate with that sequence number, return the empty string.

If the plate has more than 50 digits, only return the first 47 digits followed by "..." (quotes for clarity).

The illegal digits will be given in the String[] profane. Each element of profane will contain a sequence of digit pairs, separated by spaces.

Definition

Class:	ValidPlates
Method:	getPlate
Parameters:	String[], int
Returns:	String
Method signature:	String getPlate(String[] profane, int seqno)
(be sure your method is public)

Constraints

-

seqno will be between 1 and 2,000,000,000, inclusive.

-

profane will contain between 0 and 50 elements, inclusive.

-

Each element of profane will contain between 2 and 50 characters, in the format described above.

-

Each element of profane will contain only spaces and digits ('0'-'9').

-

Each element of profane will consist of a sequence of digit pairs separated by single spaces, with no leading or trailing spaces.

Examples

0)

{}

Returns: "1000"

With no restrictions, the 1000th plate is simply "1000".

1)

{"10"}

Returns: "11"

If the digit sequence "10" is not allowed, the 10th plate must be 11.

2)

{"10"}

2000000000

Returns: "2277659869"

3)

{"00 01 02 03 04 05 06 07 08 09 11 12 13 14 15 16 17",
 "18 19 22 23 24 25 26 27 28 29 33 34 35 36 37 38 39",
 "44 45 46 47 48 49 55 56 57 58 59 66 67 68 69 77 78",
 "79 88 89 99 99 99 99 99"}

Returns: ""

Disallowing any digit pair where the digits do not decrease only permits a total of 1022 plates. Note that profane may contain duplicate elements.

4)

{"00 01 02 03 04 05 07 08 09",
 "10 11 12 13 14 15 17 18 19",
 "20 21 22 24 25 26 27 28 29",
 "30 31 32 33 34 36 37 38 39",
 "41 43 45 46 48",
 "52 53 54 55 56 58 59",
 "60 61 63 64 66 67 68 69",
 "70 72 73 74 75 76 77 78",
 "80 81 82 83 84 86 87 88 89",
 "90 91 92 94 95 96 97 98"}

2000000000

Returns: "79999999351623516571657999935799993"

5)

{"00 01 02 03 04 05 06 07 08 09",
 "10 11 12 13 14 16 17 19",
 "20 21 22 23 24 25 26 27 28 29",
 "30 31 32 33 34 35 36 38 39",
 "41 42 43 44 45 46 49",
 "50 52 53 54 55 57 58 59",
 "60 61 62 63 64 65 66 67 68 69",
 "70 72 73 74 75 76 77 78 79",
 "80 81 82 83 84 85 86 87 88 89",
 "90 91 92 93 94 95 98 99"}

2000000000

Returns: "37151515151515151515151515151515151515151515151..."

The final plate has 166,666,668 digits.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ChessTraining

Advanced Math, Dynamic Programming

Used in:

SRM 384

Used as:

Division I Level Three

Writer:

rasto6sk

Testers:

PabloGilberto , Olexiy , lovro , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6866

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10808&pm=6866

Problem Statement

Alice and Bob are hobby chess players. They would like to become the best in the world so they are training a lot. Today they are going to play the following game with queens on a 100 x 100 chessboard to improve their offensive skills.

In each turn a player must choose one queen and move with it. From position (x, y) a queen can be moved to (x - k, y) or (x, y - k) or (x - k, y - k), where k > 0. (Queens can move through squares containing other queens, and multiple queens can coexist on a single square). The two players alternate turns, and Alice goes first. The first player who moves any queen to the position (0,0) will become the winner. You are given the initial positions of the queens in the int[]s x and y, where (x[i], y[i]) is the position of the i-th queen. Suppose Alice and Bob are playing optimally. Return "Alice will win" if Alice can win or "Bob will win" otherwise (all quotes for clarity).

Definition

Class:	ChessTraining
Method:	game
Parameters:	int[], int[]
Returns:	String
Method signature:	String game(int[] x, int[] y)
(be sure your method is public)

Constraints

-

x will contain between 1 and 50 elements, inclusive.

-

y will contain the same number of elements as x.

-

Each element of x and y will be between 0 and 99, inclusive.

-

No queen will be at position (0,0) at the beginning.

Examples

0)

{3,4}

{3,5}

Returns: "Alice will win"

Alice can move a queen from (3,3) to (0,0) to win in her first move.

1)

{1}

{2}

Returns: "Bob will win"

No matter how Alice moves the queen, Bob can win in the next move.

2)

{5,7,3,5}

{8,3,7,8}

Returns: "Bob will win"

3)

{3,3,18,6,0,14,1}

{4,4,11,9,9,9,9}

Returns: "Alice will win"

4)

{1,2}

{3,3}

Returns: "Alice will win"

5)

{3,4,3}

{2,2,1}

Returns: "Bob will win"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LongLongNim

Math, Search

Used in:

SRM 330

Used as:

Division I Level Three

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Olexiy , misof

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6856

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10010&pm=6856

Problem Statement

LongLongNim is a game played by two players who alternate turns. n coins are arranged in a pack. A valid move consists of removing exactly X coins from the pack, where X is an element of the set moves. If a player cannot perform a valid move during his turn, he loses the game, and the other player, of course, wins.

You are given the set moves as a int[], and you are also given an int maxN. Return the number of different values of n between 1 and maxN, inclusive, that make the game possible to win for the second player (assuming both players play optimally).

Definition

Class:	LongLongNim
Method:	numberOfWins
Parameters:	int, int[]
Returns:	int
Method signature:	int numberOfWins(int maxN, int[] moves)
(be sure your method is public)

Constraints

-

maxN will be between 1 and 1000000000 (10⁹), inclusive.

-

moves will contain between 1 and 22 elements, inclusive.

-

Each element of moves will be between 1 and 22, inclusive.

-

moves will be sorted in strictly increasing order (i.e., no duplicates).

Examples

0)

{1,2,3}

Returns: 5

If n is a multiple of 4, the second player can win by simply removing 4-L coins each time, where L is the number of coins the first player removed on his last turn. If n is not a multiple of four, the first player can always choose to remove the remainder of dividing n by 4, thereby leaving a multiple of 4 and the second player in. After that, he just uses the strategy described at the beginning to win. Altogether, the second player only wins if n is a multiple of 4, and there are 5 multiples of 4 between 1 and 20.

1)

{1}

Returns: 499

The second player wins when n is even and loses when n is odd.

2)

1000000000

{1,2}

Returns: 333333333

Similarly to example 0, the second player only wins when n is a multiple of 3.

3)

{2,4,7,11,20}

Returns: 1637

Any player who is left with 0 or 1 coin loses because the least number of coins that can be removed is 2.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RPSChamps

Dynamic Programming, Math

Used in:

SRM 329

Used as:

Division I Level Three

Writer:

dmytro

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6845

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10009&pm=6845

Problem Statement

N people take part in a Rock-Paper-Scissors tournament. The purpose of the tournament is to assign every participant a distinct place from 1 to N.

The places are assigned by running a number of rounds of Rock-Paper-Scissors. In each round, each participant casts one of three figures - Rock, Paper, or Scissors - with equal probability. Rock beats Scissors, Paper beats Rock, and Scissors beats Paper. After all the participants have cast their figures, the round is replayed if one of the following occurred:

All participants cast the same figure.
Each of the three figures was cast at least once.

If the round is not replayed, then for every pair of participants who cast different figures, the one whose figure beat the other player's figure will take a higher place. Within each group of players who cast equal figures, an independent subtournament will be run using the same rules. Of course, if a group contains only one player, no rounds are needed to determine that player's placement within that group.

For example, consider a tournament between 5 players where the results of the first round are as follows:

Player 1 casts Rock
Player 2 casts Scissors
Player 3 casts Scissors
Player 4 casts Rock
Player 5 casts Scissors

The players will be divided into 2 groups: {P₁, P₄} and {P₂, P₃, P₅}. An independent subtournament will be run for each group. Since Rock beats Scissors, the players from the first group will take overall places in the range 1-2 depending on the results of their subtournament, and players assigned to the second group will take places in the range 3-5 depending on the results of their subtournament.

Given N, the number of participants in the tournament, return the expected number of rounds.

Definition

Class:	RPSChamps
Method:	numberOfMoves
Parameters:	int
Returns:	double
Method signature:	double numberOfMoves(int N)
(be sure your method is public)

Notes

-

The returned value must have absolute or relative error less than 1E-9.

-

If a round is replayed one or more times, every replay is counted towards the total number of rounds for that tournament.

Constraints

-

N will be between 1 and 500, inclusive.

Examples

0)

Returns: 0.0

Since there is only one participant, no rounds are needed to determine placement.

1)

Returns: 1.5

There is a 1/3 probability of each round being replayed. When a round is not replayed, all places are immediately determined.

2)

Returns: 3.0

3)

Returns: 35.59012622220019

4)

Returns: 5.509733035960696E34

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RepeatedAddition

Math

Used in:

TCCC06 Semi 3

Used as:

Division I Level Three

Writer:

lovro

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy , Jan_Kuipers

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6844

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10134&pm=6844

Problem Statement

Repeated addition is a tedious task in which an integer A is first written on a piece of paper with a plain pencil, and then the integer X is repeatedly added to the number on paper until that number becomes B.

Only one number is written on the paper at any given time. Addition is performed so that only digits that need changing are erased and replaced by new ones.

In order to estimate how many erasers will be needed, return the total number of digits erased if repeated addition is performed as above. The three integers will be given as three Strings.

Definition

Class:	RepeatedAddition
Method:	digitsErased
Parameters:	String, String, String
Returns:	long
Method signature:	long digitsErased(String A, String B, String X)
(be sure your method is public)

Notes

-

New digits may only be added to the left of the number already written (see example 5).

Constraints

-

A, B and X will represent integers between 1 and 10^16, inclusive.

-

A, B and X will not have leading zeroes.

-

A will be less than B.

-

(B-A) will be divisible by X.

Examples

0)

"2"

"6"

"1"

Returns: 4

We start with the number 2. Adding 1 repeatedly gives the numbers 3, 4, 5 and 6. Every time we add 1 we need to erase the digit that was previously written, amounting to 4 erasures.

1)

"88"

"107"

"19"

Returns: 2

Only one addition is performed. The two 8 digits must be erased and replaced by 0 and 7.

2)

"123"

"843"

"120"

Returns: 12

3)

"3"

"811"

"404"

Returns: 4

4)

"2043601634821768"

"4274721675435952"

"3653414"

Returns: 4522764117

5)

"12"

"123"

"111"

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Multifactorial

Simple Math, Simple Search, Iteration

Used in:

SRM 335

Used as:

Division I Level One , Division II Level Two

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6835

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10659&pm=6835

Problem Statement

A multifactorial of a number is a generalization of the factorial function. The k-multifactorial of n is denoted by fac_k(n). The k-multifactorial of n is the product of every positive number of the form n - X*k, where X is a non-negative integer. For example, the 3-multifactorial of 14 is 14*11*8*5*2 = 12320, and the 4-multifactorial of 5 is 5*1 = 5.

A formal definition of multifactorial is:

fac_k(n) = n if k >= n
fac_k(n) = n*fac_k(n-k) if k < n

You will be given n and k and have to return the value of fac_k(n) as a String with no leading zeroes (this value is always a positive integer). If fac_k(n) is strictly greater than 1000000000000000000 (10¹⁸), return "overflow" (quotes for clarity) instead.

Definition

Class:	Multifactorial
Method:	calcMultiFact
Parameters:	int, int
Returns:	String
Method signature:	String calcMultiFact(int n, int k)
(be sure your method is public)

Notes

-

1000000000000000000 (10¹⁸) fits in a long.

Constraints

-

n and k will each be between 1 and 2000000000 (2*10⁹), inclusive.

Examples

0)

Returns: "12320"

The first example in the problem statement.

1)

Returns: "5"

The second example in the problem statement.

2)

Returns: "overflow"

Way too big!

3)

2000000000

1900000000

Returns: "200000000000000000"

4)

Returns: "84232704000"

5)

2000000000

Returns: "overflow"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

QuadraticEquations

Math

Used in:

SRM 327

Used as:

Division I Level Two

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6832

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10007&pm=6832

Problem Statement

Young Andrew has just learned about quadratic equations. He was quite amazed by the fact that their solutions could look like (5+sqrt(3))/4, so he wants to dig into this issue. More specifically, given five numbers x, y, d, z and k, he wants to find the number of equations a*t²+b*t+c=0 such that (x+y*sqrt(d))/z is a solution of the equation (i.e., when substituting it for t the equation holds) and a, b and c are integers, -k <= a, b, c <= k. Notice that the equations he's looking for are not necessarily quadratic, i.e., a is allowed to be zero, as is b and/or c.

Definition

Class:	QuadraticEquations
Method:	howMany
Parameters:	int, int, int, int, int
Returns:	long
Method signature:	long howMany(int x, int y, int d, int z, int k)
(be sure your method is public)

Constraints

-

x, y and z will be between -1000 and 1000, inclusive.

-

z will not be equal to 0.

-

d will be between 1 and 1000, inclusive.

-

k will be between 0 and 1000000 (10⁶), inclusive.

Examples

0)

Returns: 3

The three possible equations are: 0*x²+0*x+0=0, 8*x²-20*x+11=0, -8*x²+20*x-11=0

1)

Returns: 1

The equation 0*x²+0*x+0=0 always holds.

2)

Returns: 7

The value described is simply 2. The equations are 0*x²+0*x+0=0, 0*x²+1*x-2=0, 0*x²-1*x+2=0, 1*x²-1*x-2=0, -1*x²+1*x+2=0, 1*x²-2*x+0=0, -1*x²+2*x+0=0.

3)

-1

-1

Returns: 7

It is still 2.

4)

-1

Returns: 153847

5)

Returns: 11

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FrogDerby

Math, Simple Search, Iteration

Used in:

TCHS SRM 18

Used as:

Division I Level Two

Writer:

rusolis

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6829

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10070&pm=6829

Problem Statement

You decided to put your pet frog in a frog derby. One of the objectives is to gather as many points as possible by repeatedly jumping in one constant direction, by a positive distance (which doesn't change from jump to jump). Your frog will receive points for occupying locations given in int[] x and int[] y, where x[i] and y[i] are the coordinates of the i-th location. If a single location occurs multiple times in x and y, then for each occurrence one point is awarded (see example 2).

The initial position of the frog is (0,0). Return the maximum amount of points that your frog can gather.

Definition

Class:	FrogDerby
Method:	getPoints
Parameters:	int[], int[]
Returns:	int
Method signature:	int getPoints(int[] x, int[] y)
(be sure your method is public)

Constraints

-

x and y will contain the same number of elements.

-

x and y will each contain between 2 and 50 elements, inclusive.

-

Each element of x and y will be between -10⁶ and 10⁶, inclusive.

Examples

0)

{1,0,0}

{0,1,0}

Returns: 2

The frog gets one point for occupying location (0,0). Then it has to choose between one of the two other points.

1)

{-1,1}

{0,0}

Returns: 1

2)

{1, 3, 4, 8, 4}

{0, 0, 1, 2, 1}

Returns: 3

If the frog will jump in the positive x direction, it will collect 2 points for locations (1, 0) and (3, 0). On the other hand, the frog can collect 3 points if jumping in the direction of location (4,1).

3)

{5, -4, 6, -9, -8, -6, -1, -4, 3, -924,
9, 8, 0, -129, 65, -313, 759, 8, -8, 5,
-9, -9, 2, -667, 798, -6, 231, 7, -209, -623,
0, 4, 0, -9, 159, -553, 787, 983, 356, -4, 3,
5, -98, -10, -3, -337, -874, -545, -5, -4}

{-504, 274, 5, -9, 572, -9, 90, -3, -10, 241,
113, -581, -755, -7, 240, -3, -54, 575, 5, 3,
3, 5, -7, -961, -3, -2, 9, 587, 4, -3,
214, -283, 115, 747, 2, -1, -52, 504, -8,
153, 494, 821, -760, 893, 1, 5, 338, -4, 974, 734}

Returns: 2

4)

{-14, -10, 15}

{7, 5, 0}

Returns: 2

5)

{-1,1,-2,-2,3,4,0,4,2,4,-2,-3}

{4,-3,-3,-2,3,4,-2,-3,2,4,-1,0}

Returns: 4

6)

{-1000000,-1000000}

{-1000000,-1000000}

Returns: 2

7)

{1,1,1,1,1,1,2,2,2,2,2,2,3,3,3,3,3,3,
 4,4,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,6,7,7,7,7,7,7}

{-2,-3,-4,-5,-6,-7,-1,-3,-4,-5,-6,-7,-1,-2,-4,-5,-6,-7,
 -1,-2,-3,-5,-6,-7,-1,-2,-3,-4,-6,-7,-1,-2,-3,-4,-5,-7,-1,-2,-3,-4,-5,-6}

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SalePitch

Math

Used in:

TCHS SRM 19

Used as:

Division I Level Two

Writer:

connect4

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6825

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10071&pm=6825

Problem Statement

Recently, your boss decided that all sales that your company makes should be in the form of "BUY X GET Y FREE", where X and Y are integers. For example, rather than advertising that your latest product is on sale for $4.00, when it normally sells for $6.00, he wants you to advertise it as a "BUY 2 GET 1 FREE" sale.

Given regular, the normal price of the item, and sale, the sale price of the item , return a String formatted as "BUY X GET Y FREE" (quotes for clarity only), where X and Y are positive integers with no leading zeroes. X and Y must be as small as possible (for example, return "BUY 2 GET 1 FREE" instead of "BUY 4 GET 2 FREE").

Definition

Class:	SalePitch
Method:	buyXGetY
Parameters:	String, String
Returns:	String
Method signature:	String buyXGetY(String regular, String sale)
(be sure your method is public)

Constraints

-

regular and sale will be formatted as "$X.YZ", where X represents an integer between 0 and 9999, inclusive, with no extra leading zeroes, and Y and Z are each between '0' and '9', inclusive.

-

The value represented by sale will be less than that represented by regular.

-

Neither regular nor sale will be "0.00".

Examples

0)

"$6.00"

"$4.00"

Returns: "BUY 2 GET 1 FREE"

The example from the problem statement.

1)

"$100.00"

"$0.50"

Returns: "BUY 1 GET 199 FREE"

2)

"$12.34"

"$5.67"

Returns: "BUY 567 GET 667 FREE"

3)

"$12.34"

"$8.64"

Returns: "BUY 432 GET 185 FREE"

4)

"$9069.96"

"$4972.81"

Returns: "BUY 497281 GET 409715 FREE"

5)

"$1000.00"

"$65.50"

Returns: "BUY 131 GET 1869 FREE"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SalaryCalculator

Simple Math

Used in:

SRM 325

Used as:

Division II Level One

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6822

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10005&pm=6822

Problem Statement

At a certain company, a worker is paid an hourly rate of P1 dollars for the first 200 hours he works each month. He is paid an hourly rate of P2 dollars for the remaining hours. Return the minimum number of hours he must work this month to earn salary dollars.

Definition

Class:	SalaryCalculator
Method:	calcHours
Parameters:	int, int, int
Returns:	double
Method signature:	double calcHours(int P1, int P2, int salary)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

P1 will be between 1 and 100, inclusive.

-

P2 will be between 1 and 100, inclusive.

-

salary will be between 1 and 1,000,000, inclusive.

Examples

0)

Returns: 100.0

The worker is paid 10 dollars per hour for the first 200 hours, and 15 dollars per hour for any hours beyond that. To earn 1000 dollars, he only needs to work 100 hours at 10 dollars per hour.

1)

Returns: 266.6666666666667

The worker is paid 10 dollars per hour for the first 200 hours for a total of 2000 dollars. To earn the extra 1000 dollars, he must work approximately 66.67 hours at 15 dollars per hour.

2)

Returns: 980200.0

The company does not like to pay for overtime work.

3)

Returns: 42380.260869565216

4)

Returns: 148.0487804878049

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PositiveID

Simple Math, String Parsing

Used in:

SRM 326

Used as:

Division I Level One , Division II Level Two

Writer:

jmzero

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6803

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10006&pm=6803

Problem Statement

You are investigating a robbery, and you are sure the robbery was committed by one of the suspects you have information on. Each element of suspects will contain a number of characteristics of that suspect in a comma separated list. For example, suppose we had the following list of suspects:

suspect 0: "blond,tall,skinny"
suspect 1: "short,skinny,blond,tattooed"
suspect 2: "scarred,bald"

You may assume that if a characteristic is not on the list for a suspect then that characteristic does not apply - so in this case we can be sure that suspect 0 is not "tattooed" or "bald" or anything else other than what's listed. Therefore, if we knew that the culprit was "tattooed", we would know for sure that suspect 1 is the guilty party. However, if we knew that the culprit was "skinny" and "blond" we would still be unsure whether suspect 0 or suspect 1 was the robber.

Return the maximum number of facts we could know such that the facts:

Are all consistent with at least one of the suspects.
Do not uniquely identify the culprit.

In the example above, the value is 2. We could know that the suspect is "skinny" and "blond" - but if we knew anything more than that about the culprit then we would be able to identify the culprit uniquely (or the facts would no longer be consistent with any of the suspects).

Definition

Class:	PositiveID
Method:	maximumFacts
Parameters:	String[]
Returns:	int
Method signature:	int maximumFacts(String[] suspects)
(be sure your method is public)

Constraints

-

suspects will contain between 1 and 50 elements, inclusive.

-

Each element of suspects will contain between 1 and 50 characters, inclusive.

-

Elements of suspects will contain only lowercase letters ('a'-'z') and commas (',').

-

Each element of suspects will not have a comma (',') as the first or last character.

-

Each element of suspects will not contain two adjacent commas.

-

Each element of suspects will not contain the same characteristic more than once.

Examples

0)

{"blond,tall,skinny",
"short,skinny,blond,tattooed",
"scarred,bald"}

Returns: 2

The example from the problem statement.

1)

{"gigantic,fluorescent,loud,male"}

Returns: 0

There's only one subject, and he should be easy to find. We cannot know any facts without being able to make a positive ID.

2)

{"medium,average,nondescript",
"medium,average,nondescript"}

Returns: 3

There's no way to tell these two apart - so we could know all 3 facts without being able to make an ID.

3)

{"big,tall,loud,happy,male,scarred,tattooed,dirty",
"short,male,beard,quiet,happy,tanned,handsome",
"female,pretty,blond,quiet",
"somnambulistic",
"happy,tiny,stout,male,tanned,beard,blond"}

Returns: 4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FixedPoint

Simple Math

Used in:

TCHS SRM 21

Used as:

Division I Level Two

Writer:

zhuzeyuan

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6795

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10073&pm=6795

Problem Statement

The country of Byteland can be represented as a plane of infinite size. If you place a map of Byteland on the ground anywhere within the country, there will be exactly one "fixed point". This is the point on the plane that is at the exact same location as its representation on the map.

The map of Byteland has been created and placed by performing the following three transforms, one by one in order, on the original plane.

1. Scale it to a smaller size using a positive double scaling factor scale. Each point (x, y) in the original plane is transformed to (scale*x, scale*y).
2. Translate it by a given vector translate. Each point (x, y) is transformed to (x+translate[0], y+translate[1]).
3. Rotate it by a given angle rotate (in radians). Each point (x,y) is transformed to (x*cos(rotate)-y*sin(rotate), y*cos(rotate)+x*sin(rotate)).

In conclusion, the fixed point (x, y) for this configuration must satisfy the following two equations:

(scale * cos(rotate) - 1) * x - scale * sin(rotate) * y = -translate[0] * cos(rotate) + translate[1] * sin(rotate)
scale * sin(rotate) * x + (scale * cos(rotate) - 1) * y = -translate[0] * sin(rotate) - translate[1] * cos(rotate)

Solve the above equation and return the fixed point as a double[] containing exactly 2 elements, where the first element is the x-coordinate and the second element is the y-coordinate. There will always be exactly one unique solution.

Definition

Class:	FixedPoint
Method:	find
Parameters:	double, double[], double
Returns:	double[]
Method signature:	double[] find(double scale, double[] translate, double rotate)
(be sure your method is public)

Notes

-

A return value with an absolute or relative error less than 1.0E-9 is considered correct.

Constraints

-

scale will be between 0.1 and 0.9, inclusive.

-

translate will contain exactly 2 elements.

-

Each element of translate will be between -1000 and 1000, inclusive.

-

rotate will be between -1000 and 1000, inclusive.

Examples

0)

0.5

{1, 0}

1.5707963267948966

Returns: {-0.39999999999999997, 0.8 }

After the scaling transform, (-0.4, 0.8) becomes (-0.2, 0.4). After the translation transform, (-0.2, 0.4) becomes (0.8, 0.4). Finally, after the rotation transform, (0.8, 0.4) becomes (-0.4, 0.8), which is the original point.

1)

0.5

{2, 0}

Returns: {4.0, 0.0 }

(4, 0) -> (2, 0) -> (4, 0) -> (4, 0)

The three "->"s represent scaling, translation, and rotation, respectively.

2)

0.1

{0, 0}

Returns: {0.0, -0.0 }

(0, 0) never moves whenever the translate vector is (0, 0).

3)

0.5

{1, 2}

0.785398163397

Returns: {-2.223469992542095, 2.065452845425795 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BisquareSums

Brute Force, Simple Math, Simple Search, Iteration

Used in:

TCHS SRM 17

Used as:

Division I Level One

Writer:

eleusive

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6791

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10069&pm=6791

Problem Statement

An integer b is a bisquare if two (possibly equal) integers x and y exist such that x² + y² = b. Given two ints, low and high, return the number of distinct bisquares between low and high, inclusive.

Definition

Class:	BisquareSums
Method:	getSums
Parameters:	int, int
Returns:	int
Method signature:	int getSums(int low, int high)
(be sure your method is public)

Constraints

-

low will be between 1 and 100, inclusive.

-

high will be between low and 100, inclusive.

Examples

0)

Returns: 4

0² + 1² = 1

0² + 2² = 4

1² + 1² = 2

1² + 2² = 5

1)

Returns: 0

7 is not a bisquare.

2)

Returns: 30

3)

Returns: 16

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DartThrow

Math

Used in:

TCHS SRM 19

Used as:

Division I Level One

Writer:

connect4

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6786

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10071&pm=6786

Problem Statement

Pistol Pete, the neighborhood game dealer, has offered to let you play his newest game. Pete's going to let you throw a dart at his wall containing several targets. Depending on what target you hit, you will win a fabulous prize!

You've been practicing a game like this lately, and you figure it's right up your alley. You will hit the target you aim at with prob percent probability. When you miss the target you aim at, you will hit either of the adjacent targets with equal probability. Since the targets are arranged in a circular fashion, if you miss target 0, then you will either hit target 1 or target n-1, where n is the total number of targets. See example 0 for clarification.

Pete has given you a int[] payout, in which the i-th element corresponds to the payout of hitting target i. You will also be given prob, the percent probability your dart will hit the target you aim for. The total number of targets is equal to the number of elements in payout. Given this information, return a double with the average payout that you will get from Pete if you play optimally.

Definition

Class:	DartThrow
Method:	bestScore
Parameters:	int[], int
Returns:	double
Method signature:	double bestScore(int[] payout, int prob)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1.0e-9 is considered correct.

Constraints

-

payout will contain between 3 and 50 elements, inclusive.

-

Each element of payout will be between 0 and 100, inclusive.

-

prob will be between 0 and 100, inclusive.

Examples

0)

{10,40,50}

Returns: 45.0

In this case, you have three options:

Aim at 10: Score = 10(0.8) + 50(0.1) + 40(0.1) = 17.0
Aim at 40: Score = 40(0.8) + 10(0.1) + 50(0.1) = 38.0
Aim at 50: Score = 50(0.8) + 40(0.1) + 10(0.1) = 45.0

Of the three options, the best score is 45, and so we return it.

1)

{10,40,50}

Returns: 40.25

This time, you don't throw as well. In this case, it is best to aim for the 50, scoring 50(0.61) + 40(0.195) + 10(0.195) = 40.25.

2)

{20,1,18,4,13,6,10,15,2,17,3,19,7,16,8,11,14,9,12,5}

Returns: 13.4

A standard dartboard.

3)

{20,1,18,4,13,6,10,15,2,17,3,19,7,16,8,11,14,9,12,5}

Returns: 15.4

Sometimes missing can be a good thing.

4)

{16,99,96,26,71,9,89,43,11,41,58,84,27,8,17,54,26,36,87}

Returns: 84.61

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RefactorableNumber

Brute Force, Math

Used in:

SRM 343

Used as:

Division I Level Three

Writer:

connect4

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6784

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10667&pm=6784

Problem Statement

A refactorable number is defined to be a number that is divisble by the number of distinct factors that it has. Examples of refactorable numbers include 1 (1 factor), 12 (6 factors), and 9 (3 factors), but not 7 (2 factors) or 16 (5 factors).

You will be given two ints, low and high. Return the number of refactorable numbers between low and high, inclusive.

Definition

Class:	RefactorableNumber
Method:	count
Parameters:	int, int
Returns:	int
Method signature:	int count(int low, int high)
(be sure your method is public)

Constraints

-

low will be between 1 and 2,000,000, inclusive.

-

high will be between low and 2,000,000, inclusive.

Examples

0)

Returns: 4

There are 4 refactorable numbers between 1 and 10, namely: 1, 2, 8, and 9.

1)

Returns: 12

2)

Returns: 0

3)

Returns: 315

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Survived

Geometry, Simple Math

Used in:

SRM 323

Used as:

Division I Level Two

Writer:

Pawa

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6782

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10003&pm=6782

Problem Statement

You have survived a shipwreck and need to swim to the land. You can swim at a speed of at most V meters per second. The ocean's stream moves you with a constant speed of U meters per second.

Imagine a Cartesian system of coordinates in which you are at point (0,0), and the ocean's stream moves in the positive direction of the x-axis. You are given four integers x, y, V and U. Return a double representing the minimum time in seconds in which you can reach point (x, y). If this point can't be reached, return -1.

Definition

Class:	Survived
Method:	minTime
Parameters:	int, int, int, int
Returns:	double
Method signature:	double minTime(int x, int y, int V, int U)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

x and y will be between -100 and 100, inclusive.

-

U and V will be between 0 and 100, inclusive.

Examples

0)

-1

Returns: 1.0

If you swim directly down (in the negative direction of the y-axis) for one second, you will have gone forward one meter. By that time, the ocean's stream will have taken you one meter in the positive direction of the x-axis, leaving you at point (1, -1).

1)

Returns: 1.4142135623730951

2)

Returns: -1.0

3)

Returns: 2.0593413823019864

4)

Returns: 0.0

5)

Returns: 1.3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ExtendedDominoes

Graph Theory, Math

Used in:

SRM 322

Used as:

Division I Level Two

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Olexiy , Mike Mirzayanov

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6779

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10002&pm=6779

Problem Statement

This problem statement contains superscripts that may not display correctly in some plugins. If that's the case, use the arena to see them.

You have recently bought a game of extended dominoes. Each domino is a rectangle partitioned into two squares, and each square contains a number between 0 and 9, inclusive. There are exactly 45 pieces - one for each pair of distinct numbers. Pieces may be reversed, so while there is only one piece containing the numbers 1 and 2, it can be used in either of the following ways:

   +---+---+     +---+---+
   | 1 | 2 |     | 2 | 1 |
   +---+---+     +---+---+

Unfortunately, some of the pieces have disappeared, but there is still a possible game left: How many ways are there to construct a cycle collection with all the remaining pieces?

A cycle collection is a set of 1 or more cycles that do not share pieces. A cycle is constructed by ordering and orienting the pieces in such a way that the left number of the piece in position i is equal to the right number of the piece in position i-1, and the left number of the piece in the first position is equal to the right number of the piece in the last position (positions are numbered from left to right).

   +---+---++---+---++---+---++---+---++---+---++---+---+
   | 1 | 2 || 2 | 5 || 5 | 4 || 4 | 2 || 2 | 8 || 8 | 1 |   
   +---+---++---+---++---+---++---+---++---+---++---+---+

   +---+---++---+---++---+---++---+---++---+---++---+---+
   | 1 | 2 || 2 | 4 || 4 | 5 || 5 | 2 || 2 | 8 || 8 | 1 |   
   +---+---++---+---++---+---++---+---++---+---++---+---+

   +---+---++---+---++---+---+  +---+---++---+---++---+---+
   | 1 | 2 || 2 | 8 || 8 | 1 |  | 4 | 5 || 5 | 2 || 2 | 4 |   
   +---+---++---+---++---+---+  +---+---++---+---++---+---+

The figure above shows three possible cycle collections that use the same set of pieces. We say that each piece is connected to the two pieces that surround it, and the first and last pieces are also connected. Two cycles are considered the same if each piece is connected to the same two other pieces in both cycles. Two cycle collections are the same if they contain the same set of cycles.

You will be given the existing pieces as a String[] pieces, where each element contains exactly two digits representing the two numbers on a single domino. Return the number of distinct cycle collections that can be formed with these pieces.

Definition

Class:	ExtendedDominoes
Method:	countCycles
Parameters:	String[]
Returns:	long
Method signature:	long countCycles(String[] pieces)
(be sure your method is public)

Notes

-

Remember that each cycle collection must use all the pieces, and no two cycles in a collection can share pieces.

Constraints

-

pieces will contain between 1 and 45 elements, inclusive.

-

Each element of pieces will contain exactly 2 characters.

-

Each character of each element of pieces will be a digit ('0'-'9').

-

In each element of pieces the value of its first character will be less than the value of its second character.

-

No two elements of pieces will be equal.

-

The number of cycles for pieces will be less than 2⁶³.

Examples

0)

{"12","25","45","24","28","18"}

Returns: 3

The example in the problem statement.

1)

{"01","12","23","34","45"}

Returns: 0

There is no way to form a cycle here.

2)

{"09","12","24","14","57","79","05"}

Returns: 1

The only possibility is:

   +---+---++---+---++---+---++---+---+  +---+---++---+---++---+---+
   | 0 | 9 || 9 | 7 || 7 | 5 || 5 | 0 |  | 1 | 2 || 2 | 4 || 4 | 1 |   
   +---+---++---+---++---+---++---+---+  +---+---++---+---++---+---+

3)

{"34","35","36","37","45","46","47","56","57","67"}

Returns: 243

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CauchyProduct

Brute Force, Math

Used in:

TCO07 Wildcard

Used as:

Division I Level One

Writer:

AdminBrett

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6778

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10842&pm=6778

Problem Statement

A power series takes the form:

  f(x) =  a₀ + a₁x + a₂x² + a₃x³ + ...

If we had another power series

  g(x) =  b₀ + b₁x + b₂x² + b₃x³ + ...

then we compute the product as follows:

  f(x)g(x) = a₀b₀ + (a₀b₁ + a₁b₀)x + (a₀b₂ + a₁b₁ + a₂b₀)x² + ...

More formally, we have

   c_k = sum (i = 0 to k) a_ib_k-i

where c_k is a coefficient of the power series for the product.

Given the series f(x) you must determine g(x) such that f(x)g(x) = 1 + 0x + 0x² + ... The first few a-values will be given in a int[] start. The remaining a-values will be an infinitely repeating sequence of the terms in repeat. For example, if start = { 1, 2 } and repeat = { 3, 4, 5 } then the resulting power series is

    1 + 2x + 3x² + 4x³ + 5x⁴ + 3x⁵ + 4x⁶ + 5x⁷ + ...

You will return the first n terms of g(x) as a String[] where the first element is b₀, the second is b₁ and so forth. Each b_i should be given in the form "p/q" where p and q are integers with no common factors (other than 1), and q is positive. If b_i equals 0, then use the string "0/1". Neither p nor q should have extra leading zeros, and if p is negative, it should have a single leading '-'.

Definition

Class:	CauchyProduct
Method:	findInverse
Parameters:	int[], int[], int
Returns:	String[]
Method signature:	String[] findInverse(int[] start, int[] repeat, int n)
(be sure your method is public)

Constraints

-

start will contain between 1 and 50 elements, inclusive.

-

repeat will contain between 1 and 50 elements, inclusive.

-

Each element of start will be between -20 and 20, inclusive.

-

Each element of repeat will be between -20 and 20, inclusive.

-

Element 0 of start will not be 0.

-

n will be between 1 and 1000, inclusive.

-

Each integer in each element of the return value will be between -100000 and 100000, inclusive.

Examples

0)

{1}

{1}

Returns: {"1/1", "-1/1", "0/1", "0/1", "0/1" }

1)

{1}

{2}

Returns: {"1/1", "-2/1", "2/1", "-2/1", "2/1" }

2)

{1,2}

{3,4,5}

Returns: 
{"1/1",
"-2/1",
"1/1",
"0/1",
"0/1",
"3/1",
"-9/1",
"9/1",
"0/1",
"-9/1",
"18/1",
"-36/1",
"45/1",
"-9/1",
"-63/1",
"126/1",
"-171/1",
"180/1",
"-36/1",
"-333/1" }

3)

{1,2}

{3,4,5}

Returns: 
{"1/1",
"-2/1",
"1/1",
"0/1",
"0/1",
"3/1",
"-9/1",
"9/1",
"0/1",
"-9/1",
"18/1",
"-36/1",
"45/1",
"-9/1",
"-63/1",
"126/1",
"-171/1",
"180/1",
"-36/1",
"-333/1",
"747/1",
"-927/1",
"720/1",
"99/1",
"-1818/1",
"3960/1",
"-4923/1",
"3123/1",
"2097/1",
"-10674/1",
"20457/1",
"-24552/1",
"13464/1",
"17379/1",
"-62865/1" }

4)

{2,3,4}

{5,6,7}

Returns: {"1/2", "-3/4", "1/8", "1/16", "1/32" }

5)

{-19,14,-8,-2,-19,12,-4}

{-6,-6,2,14,-5,-18,17,-8,8,
 -16,-2,-12,11,16,-12,-17,5,
  1,11,11,0,10,-14,8,1,4,
 -8,1,-16,16,19,-4,18,4,
 -11,-15,9,4,-8,10,-5,-9,9,-9,16,10}

Returns: {"-1/19", "-14/361", "-44/6859" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BComputation

Simple Math

Used in:

TCCC06 Round 2B

Used as:

Division I Level One

Writer:

AdminBrett

Testers:

PabloGilberto , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6777

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10112&pm=6777

Problem Statement

You will be given B₀, the first element of our sequence. The following equation must hold for all n > 0:

        0  =  B₀ + _n+1C₁B₁ + _n+1C₂B₂ + ... + _n+1C_nB_n

Here _aC_b is the standard binomial coefficient (see the notes). Return the value B_pos in the form "p/q" (quotes for clarity) where p and q are integers with no extra leading zeros and no common factors (other than 1). The denominator q must always be positive. If the returned value is 0 then return "0/1".

Definition

Class:	BComputation
Method:	getValue
Parameters:	int, int
Returns:	String
Method signature:	String getValue(int B0, int pos)
(be sure your method is public)

Notes

-

_aC_b has value a!/(b!(a-b)!) where a! = a*(a-1)*...*2*1.

Constraints

-

B0 will be between -100 and 100, inclusive.

-

pos will be between 0 and 15, inclusive.

Examples

0)

Returns: "1/1"

Here we simply return B0.

1)

Returns: "-1/2"

Using the given formula, we can compute B₁ = -B₀/₂C₁.

2)

Returns: "0/1"

3)

Returns: "-31786/1365"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ModularInequality

Geometry, Math

Used in:

SRM 325

Used as:

Division I Level Two , Division II Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6765

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10005&pm=6765

Problem Statement

You will be given a int[] A that contains N elements and an int P. Return the number of distinct integer values of X for which the following inequality is true:

|A₀ - X| + |A₁ - X| + ... + |A_N-1 - X| ≤ P

Definition

Class:	ModularInequality
Method:	countSolutions
Parameters:	int[], int
Returns:	int
Method signature:	int countSolutions(int[] A, int P)
(be sure your method is public)

Constraints

-

A will contain between 1 and 50 elements, inclusive.

-

Each element of A will be between -1,000,000,000 and 1,000,000,000 inclusive.

-

P will be between 0 and 1,000,000,000 inclusive.

Examples

0)

{1, 2, 3}

Returns: 5

The possible values for X are 0, 1, 2, 3 and 4.

1)

{10, 30, 15, -1, 17}

Returns: 7

2)

{0, 2, 3, -5, 10}

Returns: 0

3)

{-693}

Returns: 2531

4)

{965, -938, -396, -142, 926, 31, -720}

Returns: 1781

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RoomNumber

Simple Math, String Manipulation

Used in:

SRM 351

Used as:

Division II Level One

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6764

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10675&pm=6764

Problem Statement

You are going to stick the number of your room on the door. The shop near your house suggests wonderful sets of plastic digits. Each set contains exactly ten digits - one of each digit between 0 and 9, inclusive. Return the number of sets required to write your room number. Note that 6 can be used as 9 and vice versa.

Definition

Class:	RoomNumber
Method:	numberOfSets
Parameters:	int
Returns:	int
Method signature:	int numberOfSets(int roomNumber)
(be sure your method is public)

Constraints

-

roomNumber will be between 1 and 1,000,000, inclusive.

Examples

0)

Returns: 2

Two sets are required because each set contains only one '2' digit.

1)

Returns: 2

Each set contains one '6' digit and one '9' digit. '6' could be used as '9' and therefore two sets are enough.

2)

Returns: 1

3)

Returns: 6

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ConstitutiveNumbers

Math

Used in:

TCCC06 Round 2C

Used as:

Division I Level One

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6761

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10113&pm=6761

Problem Statement

Let's call a number constitutive if it can be expressed as a sum of three or more successive positive integers. For example, 14 is a constitutive number because 14 = 2+3+4+5, but 13 is not a constitutive number.

You will be given two ints A and B. Return the number of constitutive numbers between A and B, inclusive.

Definition

Class:	ConstitutiveNumbers
Method:	count
Parameters:	int, int
Returns:	int
Method signature:	int count(int A, int B)
(be sure your method is public)

Constraints

-

A will be between 1 and 1,000,000,000, inclusive.

-

B will be between A and A + 1000, inclusive.

Examples

0)

Returns: 6

The first 6 constitutive numbers are:

6 = 1 + 2 + 3
9 = 2 + 3 + 4
10 = 1 + 2 + 3 + 4
12 = 3 + 4 + 5
14 = 2 + 3 + 4 + 5
15 = 4 + 5 + 6

1)

Returns: 69

2)

Returns: 26

3)

Returns: 657

4)

1000000000

1000001000

Returns: 952

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Apportionment

Simple Math

Used in:

TCHS SRM 23

Used as:

Division I Level Two

Writer:

VitalyGoldstein

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6740

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10075&pm=6740

Problem Statement

A square is divided into N * M equal rectangles.

For example, here's a square divided into 2 * 3 rectangles:

+--+--+--+ |**|**|**| |**|**|**| |**|**|**| +--+--+--+ |**|**|**| |**|**|**| |**|**|**| +--+--+--+ Find the number of squares made up by these rectangles, i.e., all vertices of squares must coincide with one of the rectangles' vertices. You should count only squares with non-zero area. Two squares are equal if and only if they share the exact same set of vertices. Only count squares whose sides are parallel to the sides of the original square.

Definition

Class:	Apportionment
Method:	numberOfSquares
Parameters:	int, int
Returns:	long
Method signature:	long numberOfSquares(int N, int M)
(be sure your method is public)

Constraints

- N and M will each be between 1 and 100000, inclusive.

Examples

0)

Returns: 1

Here there is only square.

1)

Returns: 5

Here there are 4 smaller squares (each of the rectangles is a square), along with the one original square.

2)

Returns: 1

3)

Returns: 13

4)

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AdditionCycles

Simple Math

Used in:

SRM 326

Used as:

Division II Level One

Writer:

jmzero

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6736

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10006&pm=6736

Problem Statement

Start with any integer between 00 and 99, inclusive, written as two digits (use a leading zero if the number is less than 10). Add the two digits together. Now concatenate the rightmost digit of the first number with the rightmost digit of the sum to get a new number. If you repeat this process enough times, you'll end up back at the original number. For example:

			    Combine Second Digits of
Start With    Add Digits    the Original and the Sum
------------------------------------------------------
    26     :   2+6 = 08   :   "6" and "8" = 68 
    68     :   6+8 = 14   :   "8" and "4" = 84
    84     :   8+4 = 12   :   "4" and "2" = 42
    42     :   4+2 = 06   :   "2" and "6" = 26

In this case, it took us 4 steps to get back to where we started, so we would return 4. Starting with n, return the number of steps it takes to get back to n.

Definition

Class:	AdditionCycles
Method:	cycleLength
Parameters:	int
Returns:	int
Method signature:	int cycleLength(int n)
(be sure your method is public)

Constraints

-

n will be between 0 and 99, inclusive.

Examples

0)

Returns: 4

The example from the problem statement. It goes 26->68->84->42->26, so there's 4 steps for the cycle.

1)

Returns: 3

The cycle is 55->50->05->55. Remember to treat numbers under 10 as though there was a leading zero.

2)

Returns: 1

Zero comes back to zero at every step - so the length of the cycle is one (00->00)

3)

Returns: 12

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

UsingStats

Simple Math

Used in:

TCCC06 Qual 3

Used as:

Division I Level One

Writer:

AdminBrett

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6719

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10095&pm=6719

Problem Statement

You have been given a int[] vals that is missing one element. Luckily, you know the mean of the entire set (with the missing element present). Using this information, reconstruct the full data set and return the median.

Definition

Class:	UsingStats
Method:	getMedian
Parameters:	int[], int
Returns:	int
Method signature:	int getMedian(int[] vals, int mean)
(be sure your method is public)

Notes

-

The mean of a list of values is their average. The median of a list of values is determined by sorting the list, and then taking the middle element.

Constraints

-

vals will contain between 2 and 50 elements, inclusive.

-

vals will contain an even number of elements.

-

Each element of vals will be between -1000 and 1000, inclusive.

-

mean will be between -1000 and 1000, inclusive.

Examples

0)

{50,100}

Returns: 75

To have a 75 average, the missing value must be 75. This is also the median of the resulting set.

1)

{1,2,3,4}

Returns: 3

The missing value is 5. The resulting median is 3.

2)

{0,0,100,100}

Returns: 100

The missing value is 105, and the resulting median is 100.

3)

{889,820,404,-901}

Returns: 820

4)

{-211,-504,461,283,791,646,205,459,-186,516,-933,762,418,656,746,-368,888,270,-355,-207,-990,435,717,-338}

Returns: 418

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BusSeating

Brute Force, Geometry, Simple Math

Used in:

SRM 319

Used as:

Division I Level One , Division II Level Two

Writer:

NeverMore

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6715

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9999&pm=6715

Problem Statement

Three friends enter a bus. There are two rows of seats with 10 seats in each row along the left and right side of the bus. For this problem, consider the seats to be points. Each seat in the same row is separated from the one in front of it and the one behind it by exactly 1 meter, and from the one directly opposite it (i.e., in the other row) by exactly 2 meters. Some of the seats are occupied by passengers. The friends want to know which seats they should occupy so as to minimize the sum of the Euclidean distances between each pair of friends. Recall that the Euclidean distance is simply the length of the line segment joining two points.

Create a class BusSeating that contains a method getArrangement. The method takes two Strings as arguments, leftRow and rightRow. Each string is composed of the characters '-' and 'X' only, with '-' denoting an empty seat, and 'X' denoting an occupied seat. The seats are given in order from the front to the back of the bus in each row. The method should return a double corresponding to the sum of the Euclidean distances between friends in the optimal arrangment.

Definition

Class:	BusSeating
Method:	getArrangement
Parameters:	String, String
Returns:	double
Method signature:	double getArrangement(String leftRow, String rightRow)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

leftRow and rightRow will each contain exactly 10 characters.

-

leftRow and rightRow will contain only the characters '-' and uppercase 'X'.

-

There will be at least 3 empty seats among the 2 rows of seats.

Examples

0)

"----------"

"----------"

Returns: 4.0

The minimum sum of distances in this situation is achieved when the three friends sit behind each other in the same row of seats, giving a minimum distance of 4.0.

1)

"XXX-X-XX-X"

"-XXXX---XX"

Returns: 4.0

Once again, the friends can minimize the sum of distances by sitting behind each other in a row. This time, however, there is only one way to seat themselves in this manner.

2)

"XXXXXXXXXX"

"-XX-XX-X--"

Returns: 6.0

3)

"XXX-X-XX-X"

"XXX-X-XX-X"

Returns: 6.82842712474619

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ConstructBST

Advanced Math, Recursion

Used in:

SRM 319

Used as:

Division I Level Two

Writer:

NeverMore

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6714

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9999&pm=6714

Problem Statement

This statement contains images which must be viewed in the applet.

A Binary Search Tree (BST) is a tree data structure which obeys the following properties:

Each node has at most 2 children.
Each node except the root has exactly 1 parent.
There is exactly 1 root node. The root node does not have any parents.
If a node has a left child, all values in the left subtree are less than or equal to the value of the node itself.
If a node has a right child, all values in the right subtree are strictly greater than the value of the node itself.

A BST is constructed from a string of characters in the following way: The root node of the tree is assigned the value of the first character in the string. All subsequent characters are added as children of existing nodes subject to the above rules. Note that the tree is never altered in any other manner. In this problem, nodes are identified starting from the root node as 1, and following in order with nodes at the next level, etc. See the figure below for clarification.

You will be given the shape of a particular BST by specifying the identities of the nodes which constitute the tree, according to the above scheme. Note that you do not know the exact input string used to construct the given BST. You do know, however, that the first N uppercase letters were used to construct the given BST with N nodes. See the examples below for further clarification.

Create a class ConstructBST that contains a method numInputs. The method takes an int[] tree with a list of node numbers present in the tree and returns a long corresponding to the number of strings composed of the characters from 'A' to 'Z' that could have been used to produce the particular BST. Note that tree will always contain a root node numbered 1. Note also, that tree will represent a connected tree, that is, all nodes present in the tree will be reachable from the root node.

Definition

Class:	ConstructBST
Method:	numInputs
Parameters:	int[]
Returns:	long
Method signature:	long numInputs(int[] tree)
(be sure your method is public)

Constraints

- tree will contain between 1 and 26 elements, inclusive.

- Each element of tree will be between 1 and 2²⁶-1, inclusive.

- Each element of tree will be distinct.

- tree will represent a connected tree.

- tree will contain a root node numbered 1.

Examples

0)

{1, 2}

Returns: 1

This input represents a BST of the following shape:

Using the characters {'A','B'}, only the string "BA" can generate a tree with the given shape.

1)

{1, 3, 6}

Returns: 1

This input represents a BST of the following shape:

Using the characters {'A','B','C'}, only the string "ACB" can generate a tree with the given shape.

2)

{1, 2, 5, 3, 4}

Returns: 8

Using the characters {'A','B','C','D','E'} the following 8 strings generate a tree with the given shape: "DBACE", "DBAEC", "DBEAC", "DEBAC", "DBCAE", "DBCEA", "DBECA", "DEBCA".

3)

{1, 2, 4, 6, 3}

Returns: 6

4)

{2, 4, 3, 62, 7, 15, 1, 31, 5, 14, 28, 57, 56, 114}

Returns: 96096

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Dragon

Dynamic Programming, Simple Math

Used in:

TCHS SRM 12

Used as:

Division I Level Three

Writer:

Olexiy

Testers:

PabloGilberto , brett1479 , Cosmin.ro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6694

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10064&pm=6694

Problem Statement

An army of k knights is going to try to kill an evil dragon. The dragon has h heads, and the knights must cut off all his heads one by one to complete their mission. Their fight will go as follows:

First, the dragon will attack the knights as many times as he wants (as long he still has at least one head). Each time the dragon attacks, he will either kill one knight with a probability of probDragon or lose one of his heads otherwise. Of course, the dragon may choose not to attack any knights at all. After these attacks, the dragon will return to his cave, and the knights will attack him one by one. When a knight attacks, he will either cut off one of the dragon's heads with a probability of probKnight or get killed by the dragon otherwise. Each knight only gets one turn, so if he cuts off a head, he can NOT attack the dragon again.

If all the dragon's heads are cut off at any point in the fight, the knights' mission will be successful, and the surviving knights will return home with glory. Otherwise, the knights will all be dead and the dragon will still have at least one head on his wide shoulders. Assuming that the dragon acts optimally (tries to maximize the probability of staying alive), return the probability that the knights will complete their mission successfully.

Definition

Class:	Dragon
Method:	winFight
Parameters:	int, int, int, int
Returns:	double
Method signature:	double winFight(int h, int k, int probDragon, int probKnight)
(be sure your method is public)

Notes

-

The only thing that matters to the dragon is staying alive. The number of heads left (or the number of knights alive in case of his death) doesn't matter to him.

-

The returned value must be accurate to within a relative or absolute value of 1e-9.

Constraints

-

k will be between 1 and 100, inclusive.

-

h will be between 1 and 100, inclusive.

-

probDragon will be between 0 and 100, inclusive.

-

probKnight will be between 0 and 100, inclusive.

Examples

0)

Returns: 0.5

1)

Returns: 0.09561792499119559

The optimal strategy for the dragon is to attack until all the knights are killed (or until he is killed).

2)

Returns: 0.96875

Here, the dragon must follow the same strategy as above, but his chances are much lower.

3)

Returns: 0.0

The knights can not complete the mission here.

4)

Returns: 0.0625

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TransformArray

Simple Math

Used in:

TCHS SRM 43

Used as:

Division I Level One

Writer:

it4.kp

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6692

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10792&pm=6692

Problem Statement

We have an array of positive integers. We will transform this array by repeating the following operation until there are less than two elements left:

Choose the two elements that have the minimal absolute difference. If there are multiple such pairs, choose the one among them with the minimal sum. If there are still multiple pairs, choose any one of them.
Decrease both elements in the pair by 1.
Remove all zeros from the array.

It's easy to see that this process always ends in a finite number of steps.

For example, suppose we have an array of four integers {3, 2, 3, 2}. The transformation process goes like this:

Step 1: (3, 2, 3, 2) --> (3, 1, 3, 1) (decreasing values 2 and 2)

Step 2: (3, 1, 3, 1) --> (3, 3) (decreased elements became zeros, so we removed them)

Step 3: (3, 3) --> (2, 2)

Step 4: (2, 2) --> (1, 1)

Step 5: (1, 1) --> ()

Thus, we have an empty array at the end of the process.

You are given a int[] elements which represents the array to transform. Return the number of steps in the transformation process.

Definition

Class:	TransformArray
Method:	doTransform
Parameters:	int[]
Returns:	int
Method signature:	int doTransform(int[] elements)
(be sure your method is public)

Constraints

-

elements will contain between 1 and 50 elements, inclusive.

-

Each element of elements will be between 1 and 1000, inclusive.

Examples

0)

{3,2,3,2}

Returns: 5

The example from the problem statement.

1)

{3}

Returns: 0

There is already just one element in the array, so we do not have to perform the transformation at all.

2)

{1,2,3,4}

Returns: 4

The transformation process goes like this:

{1, 2, 3, 4} --> {1, 3, 4} --> {1, 2, 3} --> {1, 3} --> {2}

3)

{10,6,3,7,7,9,5,1,8,4}

Returns: 27

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Linez

Graph Theory, Math, Search

Used in:

MM 5

Used as:

Division I Level One

Writer:

wz

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6686

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10101&pm=6686

Problem Statement

Linez is a single-player board game played on a 9x9 grid. On each turn, the player must move one of the numbers on the board to an empty cell where a clear path (consisting of horizontally connected or vertically connected empty cells) exists between the new position and the old. If five or more same numbers are aligned in a row, column, or diagonal, they will be removed from the board. The player will gain 10+k*(k-5)/2 points (k being the number of removals) and can make another move. Otherwise, three more numbers will be placed onto the board at randomly chosen positions before the player can move again. The objective is to score as many points as possible before the whole board fills up. (An online version of the Linez game is available at http://linez.varten.net/.)

Your task is to write a class to play the Linez game. The method nextMove will be given the board configuration and the next three numbers. board will contain 9 Strings representing the rows of the board from top to bottom. Each element will contain 9 characters. Each character will be '1' to '7' representing the number on that cell, or '.' if that position is unoccupied. nextThree will contain 3 characters. Each element of nextThree will be '1' to '7' representing the number to be added to the board next turn. The return value of nextMove must contain 4 characters, the first two representing the original position of the number to be moved, the next two representing the target position. For example, to move the number "4" from "I8" to "F6" as shown below, return "I8F6".

You will have a total of 20 seconds for each test case. The memory limit is 64MB. Your final score will be the mean score on all the test cases.

Definition

Class:	Linez
Method:	nextMove
Parameters:	String[], String
Returns:	String
Method signature:	String nextMove(String[] board, String nextThree)
(be sure your method is public)

Notes

- Each number of nextThree will be chosen uniformly between 1 and 7, inclusive.

- Each empty cell has an equal probability to be chosen when the next number is added to the board.

- If your solution crashes, runs out of time, or tries to make an invalid move it will receive the points it has made so far for that test case.

Examples

0)

"149738788"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.....4...&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;......5..&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;......3..&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;545&quot;<br>"

1)

"1982697456"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.......5.&quot;,<br>&nbsp;&nbsp;&quot;3........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;....7....&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;773&quot;<br>"

2)

"2060431272"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;..6.....4&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;...1.....&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;154&quot;<br>"

3)

"1077274560"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;7........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;..6....2.&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;563&quot;<br>"

4)

"825809896"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;.6.......&quot;,<br>&nbsp;&nbsp;&quot;.....6...&quot;,<br>&nbsp;&nbsp;&quot;.4.......&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;745&quot;<br>"

5)

"1911009"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.6.4.....&quot;,<br>&nbsp;&nbsp;&quot;........6&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;151&quot;<br>"

6)

"149738789"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;......3..&quot;,<br>&nbsp;&nbsp;&quot;..3......&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;..2......&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;455&quot;<br>"

7)

"1109944003"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.....1...&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.6.......&quot;,<br>&nbsp;&nbsp;&quot;......5..&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;527&quot;<br>"

8)

"1732993602"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;.2.......&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;...6.....&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.......1.&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;564&quot;<br>"

9)

"1438702088"

Returns: 
"board:<br>{<br>&nbsp;&nbsp;&quot;........2&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.....2...&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;,<br>&nbsp;&nbsp;&quot;....5....&quot;,<br>&nbsp;&nbsp;&quot;.........&quot;<br>}<br>nextThree:<br>&nbsp;&nbsp;&quot;624&quot;<br>"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Divisibility

Math

Used in:

TCHS SRM 16

Used as:

Division I Level Three

Writer:

VitalyGoldstein

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6658

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10068&pm=6658

Problem Statement

Given a int[] a, return the number of integers between L and R, inclusive, that are divisible by at least one of the elements in a.

Definition

Class:	Divisibility
Method:	numDivisible
Parameters:	int, int, int[]
Returns:	int
Method signature:	int numDivisible(int L, int R, int[] a)
(be sure your method is public)

Constraints

-

L will be between 1 and 1000,000,000, inclusive.

-

R will be between L and 1000,000,000, inclusive.

-

a will contain between 1 and 18 elements, inclusive.

-

Each element of a will be between 1 and 1000,000,000, inclusive.

Examples

0)

{1}

Returns: 492

1)

{2}

Returns: 240

2)

{1,2}

Returns: 408655

3)

1000000000

{2,3}

Returns: 666666667

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MemorizingPi

Dynamic Programming, Simple Math

Used in:

TCO07 Qual 3

Used as:

Division I Level Two

Writer:

legakis

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6641

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10735&pm=6641

Problem Statement

You wish to impress your friends by memorizing several thousand digits of pi. You believe it is easiest to memorize groups of 3 or 4 digits at a time, and decide on the following rules for assigning a complexity value to any group of digits:


    all digits equal                   ("333" or "0000", but not "2233"): 1
    powers of 2, with no leading zeros ("512" or "4096", but not "0064"): 2
    consecutive ascending digits       ("012" or "5678", but not "1357"): 4
    consecutive descending digits      ("987" or "3210", but not "1098"): 5
    first and last digits equal        ("858" or "1761", but not "8882"): 7
    any two digits equal               ("655" or "0777", but not "9753"): 8
    all other groups                   ("832" or "2049"                ): 10

A group of digits should be assigned the lowest complexity value of the rules it matches. For example, the group "777" matches two rules (all digits equal and first and last digit equal), and it is assigned a complexity value of 1.

You are to write a method that takes a string of digits and breaks them up into groups of 3 or 4 such that the sum of the complexities for all the groups is minimized.

For example, the string of digits "2562222567" could be broken up into either "256 222 2567" with a complexity of 2+1+10=13, "256 2222 567" with a complexity of 2+1+4=7, or "2562 222 567" with a complexity of 7+1+4=12. The lowest of these three values is 7, so the correct answer is "256 2222 567".

The input will be provided as a String[] digits. Each element of digits will contain only digits ('0' - '9', inclusive). Use the concatenation of all elements as the input to your method. You are to return the same digits as a String[], with a single space inserted between adjacent groups in the same element. Each element can contain a maximum of 100 characters. When populating the String[], put as many groups as possible in the current element before starting a new one. A single group may not span multiple elements, and elements must not contain leading or trailing spaces.

There may be multiple ways to segment the string of digits that result in the same difficulty. Given two such segmentations, consider the first group at which they differ, and select the segmentation with the three-digit group over the one with the four-digit group. For example, the digits "2222225555555" could be segmented as "222 222 555 5555" or "222 222 5555 555", each with a difficulty of 4. The first difference is the third group, so we select the first choice because its third group has 3 digits.

Definition

Class:	MemorizingPi
Method:	segmentation
Parameters:	String[]
Returns:	String[]
Method signature:	String[] segmentation(String[] digits)
(be sure your method is public)

Constraints

-

digits must contain between 1 and 50 elements, inclusive.

-

Each element of digits must contain between 1 and 50 characters, inclusive.

-

Every character in digits must be a digit ('0'-'9').

-

There will be at least 6 characters total in digits.

Examples

0)

{ "2562222567" }

Returns: {"256 2222 567" }

This is the first example from the problem statement.

1)

{ "2222",
  "2",
  "25",
  "555",
  "555" }

Returns: {"222 222 555 5555" }

This is the second example from the problem statement.

2)

{ "31415926535897932384626433832795028841971693993751",
  "05820974944592307816406286208998628034825342117067",
  "98214808651328230664709384460955058223172535940812",
  "84811174502841027019385211055596446229489549303819",
  "64428810975665933446128475648233786783165271201909",
  "14564856692346034861045432664821339360726024914127",
  "37245870066063155881748815209209628292540917153643",
  "67892590360011330530548820466521384146951941511609" }

Returns: 
{"3141 5926 535 8979 3238 4626 433 832 7950 2884 1971 6939 9375 1058 2097 4944 5923 0781 6406 2862",
"0899 8628 0348 2534 2117 0679 8214 8086 5132 8230 6647 0938 4460 9550 5822 3172 5359 4081 2848 111",
"7450 2841 0270 1938 5211 0555 9644 6229 4895 4930 3819 6442 8810 9756 6593 3446 128 475 6482 3378",
"678 3165 2712 0190 914 5648 5669 234 6034 8610 454 3266 4821 3393 6072 6024 9141 2737 2458 7006 6063",
"1558 8174 8815 2092 0962 8292 5409 1715 3643 678 9259 0360 0113 3053 054 8820 4665 2138 4146 9519",
"4151 1609" }

The first 400 digits of pi.

3)

{ "111222333444555",
  "111222333444555",
  "111222333444555",
  "111222333444555",
  "1112223334445555",
  "111222333444555",
  "111222333444555",
  "111222333444555",
  "111222333444555",
  "11122233344445555" }

Returns: 
{"111 222 333 444 555 111 222 333 444 555 111 222 333 444 555 111 222 333 444 555 111 222 333 444 5555",
"111 222 333 444 555 111 222 333 444 555 111 222 333 444 555 111 222 333 444 555 111 222 333 4444",
"5555" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StandInLine

Greedy, Simple Math

Used in:

SRM 314

Used as:

Division I Level One , Division II Level Two

Writer:

zhuzeyuan

Testers:

PabloGilberto , brett1479 , Olexiy , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6631

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9994&pm=6631

Problem Statement

Soldiers at the Byterland South Border are ordered to stand in line each morning. They always choose their positions randomly to the displeasure of their general. One evening, the soldiers learn that their strict general has secretly recorded their standing positions from that morning, and that he will be checking their positions the next morning to make sure they are exactly the same.

Each soldier only remembers one thing from that morning: the number of people to his left that were taller than him. There are n soldiers, each with a different height between 1 and n, inclusive. Using this information, you must reconstruct the lineup from that morning.

You are given a int[] left, the ith element of which represents the number of taller soldiers to the left of the soldier with height i (where i is a 1-based index). Return a int[] containing the heights of the soldiers from left to right in the lineup. The input is guaranteed to produce a valid and unique output.

Definition

Class:	StandInLine
Method:	reconstruct
Parameters:	int[]
Returns:	int[]
Method signature:	int[] reconstruct(int[] left)
(be sure your method is public)

Constraints

-

left will contain between 1 and 10 elements, inclusive.

-

left[i] will be between 0 and n-i-1, inclusive (where n is the number of elements in left, and i is a 0-based index).

Examples

0)

{2, 1, 1, 0 }

Returns: {4, 2, 1, 3 }

The soldier of height 1 remembered there were 2 soldiers taller than him to his left.
The soldier of height 2 remembered there was 1 soldier taller than him to his left.
The soldier of height 3 remembered there was 1 soldier taller than him to his left.
The soldier of height 4 remembered there was no solder taller than him to his left.

The original order from left to right must have been 4, 2, 1, 3. This ordering satisfies all four conditions. For example, there are exactly two soldiers to the left of the soldier with height 1 that are taller than him (heights 4 and 2). A different ordering, like 4, 3, 1, 2, satisfies some, but not all of the four conditions. In this incorrect ordering, there are two soldiers to the left of the soldier with height 2 that are taller than him (heights 4 and 3), but the input states that there was only one.

1)

{0, 0, 0, 0, 0 }

Returns: {1, 2, 3, 4, 5 }

2)

{5, 4, 3, 2, 1, 0 }

Returns: {6, 5, 4, 3, 2, 1 }

3)

{6, 1, 1, 1, 2, 0, 0 }

Returns: {6, 2, 3, 4, 7, 5, 1 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BackyardTrees

Dynamic Programming, Recursion, Simple Math, Simple Search, Iteration

Used in:

SRM 328

Used as:

Division I Level Three

Writer:

_efer_

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6620

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10008&pm=6620

Problem Statement

This problem statement contains images that may not display properly if viewed outside of the applet.

Your backyard is a rectangular grid that measures width x height square meters. You would like to plant treeCount trees using the following rules:

- All trees must be planted at integer coordinates on the grid.

- All trees must lie on the same straight line.

- Each pair of trees must be at least distance meters away from each other.

For example, two (of many) ways in which four trees could be planted on a 10x10 grid if distance is 2 are depicted below:

Return the number of distinct ways in which the trees could be planted, modulo 1,000,000,000. Two layouts are considered distinct if there exists a point (x, y) such that one layout contains a tree at (x, y) and the other layout does not.

Definition

Class:	BackyardTrees
Method:	countWays
Parameters:	int, int, int, int
Returns:	int
Method signature:	int countWays(int treeCount, int width, int height, int distance)
(be sure your method is public)

Constraints

-

treeCount will be between 1 and 50, inclusive.

-

width will be between 1 and 500, inclusive.

-

height will be between 1 and 500, inclusive.

-

distance will be between 1 and 50, inclusive.

Examples

0)

Returns: 300

There are only two trees, and the distance between any two points with integer coordinates is always at least 1. Therefore, you can place the two trees at any two points with integer coordinates. There are 25 such points and this gives you 300 different ways to plant the trees.

1)

Returns: 2

The diagonal of the backyard has a length of 60, which is just enough to place 13 trees with a distance of 5 between each adjacent pair. Luckily, these 13 points are at integer coordinates, so you can place the trees along either of the two diagonals while satisfying all the rules.

2)

Returns: 88

3)

Returns: 102

You can place the trees along the rows or the columns of the grid, as well as on the two diagonals.

4)

Returns: 0

You can't plant 6 trees on the same line with the necessary distance between them on this grid.

5)

Returns: 490260662

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MarriageProblemRevised

Graph Theory, Math

Used in:

SRM 356

Used as:

Division I Level Two

Writer:

Pawa

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6608

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10765&pm=6608

Problem Statement

There are several unmarried men and women living in a society where marriage is defined as either one husband with one or more wives, or one wife with one or more husbands. You are given a String[] preferences. The j-th character of the i-th element of preferences is '1' (one) if the i-th man and the j-th woman are willing to be part of the same marriage, and '0' (zero) otherwise.

Your task is to group these people into the minimum possible number of marriages. Each person must be a member of exactly one marriage, and each marriage must contain only willing members. Return the number of marriages, or -1 if this is not possible.

Definition

Class:	MarriageProblemRevised
Method:	neededMarriages
Parameters:	String[]
Returns:	int
Method signature:	int neededMarriages(String[] preferences)
(be sure your method is public)

Constraints

-

preferences will contain between 1 and 12 elements, inclusive.

-

The length of each element of preferences will be betwen 1 and 12, inclusive.

-

All elements of preferences will be of the same length.

-

Each element of preferences will contain only '0' (zeroes) and '1' (ones).

Examples

0)

{"111"}

Returns: 1

Here, we have one man and three women, and everybody is willing to be in the same marriage. Therefore, we only need one marriage.

1)

{"100", "010", "001"}

Returns: 3

2)

{"00", "00"}

Returns: -1

Nobody is willing to be in the same marriage as anybody else, so there cannot be any marriages in this case.

3)

{"0001", "0001", "0001", "1111"}

Returns: 2

4)

{"11101011","00011110","11100100","01010000","01000010","10100011","01110110","10111111"}

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IQTest

Simple Math

Used in:

SRM 327

Used as:

Division II Level Two

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6600

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10007&pm=6600

Problem Statement

You've taken a lot of 'IQ'-style tests, and noticed a common pattern appearing among them. They ask you to continue a given sequence of numbers. Say you're given the numbers 1,2,3,4,5, and are asked: what's the next number? Of course, the answer is 6. A slightly more complicated sequence would be 3,6,12,24,48, where 96 is the answer. Or, if the test is really tough, it might be even 1,4,13,40, where 121 is an answer (the latter follows the rule "multiply by 3 and add 1").

You've decided to write an automatic solver for these problems. It will be based on the following proposition: the rule for generating the sequence is always "multiply by a and add b", where a and b are integer (not necessarily positive) numbers.

You are given a int[] previous containing the first several numbers of the sequence. If this sequence could not be constructed using the above rule, return "BUG". If it could, and you can uniquely determine the next number, return a string containing that number without spaces or extra leading zeroes. If there are several possible next numbers, return "AMBIGUITY" (quotes for clarity only).

Definition

Class:	IQTest
Method:	nextNumber
Parameters:	int[]
Returns:	String
Method signature:	String nextNumber(int[] previous)
(be sure your method is public)

Constraints

- previous will contain between 1 and 50 elements, inclusive.

- Each element of previous will be between -100 and 100, inclusive.

Examples

0)

{1, 2, 3, 4, 5}

Returns: "6"

1)

{3, 6, 12, 24, 48}

Returns: "96"

2)

{1, 4, 13, 40}

Returns: "121"

3)

{0}

Returns: "AMBIGUITY"

One cannot deduce anything from just one number.

4)

{-1, 2}

Returns: "AMBIGUITY"

There are many possibilities here: "multiply by -2 and add 0" with -4 as the next number, or "multiply by 1 and add 3" with 5, or "multiply by -1 and add 1" with -1, or "multiply by -5 and add -3" with -13, etc.

5)

{57, 57}

Returns: "57"

Sometimes just two numbers are enough to determine the next number. Although there are still many possibilities for a and b like "multiply by 1 and add 0" or "multiply by 2 and add -57", all of them yield 57 as the next number.

6)

{16, -8, 4, -2}

Returns: "BUG"

Here we're multiplying by -0.5, but non-integer multipliers are not allowed.

7)

{6, 5, 4, 3, 1}

Returns: "BUG"

There must have been some misprint.

8)

{-12, 12, -36, 60}

Returns: "-132"

It's "multiply by -2 and add -12".

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LuckyFives

Math

Used in:

TCHS SRM 25

Used as:

Division I Level Two

Writer:

Vedensky

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6586

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10077&pm=6586

Problem Statement

Some people think five is a lucky number. They roll several dice, and if they get five on strictly more than one fifth of the dice, they believe it will be a lucky day.

Given an int dice, the number of dice rolled, and an int sides, the number of sides on each die, return the probability of the day being lucky. For a die with N sides, the probability of rolling a five is 1/N.

Definition

Class:	LuckyFives
Method:	probability
Parameters:	int, int
Returns:	double
Method signature:	double probability(int dice, int sides)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

dice will be between 1 and 20, inclusive.

-

sides will be between 5 and 10, inclusive.

Examples

0)

Returns: 0.16666666666666666

If you roll one six-sided die, you will get five with a probability of 1/6.

1)

Returns: 0.19624485596707822

Here you roll five six-sided dice, and you need at least two fives.

2)

Returns: 0.3439

3)

Returns: 0.04317449528446337

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DessertMaker

Math

Used in:

TCHS SRM 13

Used as:

Division I Level Two

Writer:

jmzero

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6581

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10065&pm=6581

Problem Statement

You have a number of tasty ingredients and you want to know how many different banana split desserts you could make using those ingredients. In order for something to count as a banana split, it must have at least one "banana", at least one "ice cream", and at least one other ingredient (i.e., at least one ingredient that is not a "banana" or an "ice cream"). Ingredients with the same name are not distinguishable, and it doesn't matter what order the items are added to the dessert. For example, suppose you had the following 5 ingredients:

"ice cream","banana","chocolate","chocolate","peanuts"

You could make a total of 5 different banana splits, as shown below:

"ice cream","banana","chocolate","chocolate","peanuts"
"ice cream","banana","chocolate","peanuts"
"ice cream","banana","chocolate","chocolate"
"ice cream","banana","chocolate"
"ice cream","banana","peanuts"

Note that if you would have had 2 bananas, you would have had 10 possibilities - as adding a banana to each combination above makes a new dessert. Return the number of distinct banana splits you could create using the items given in ingredients.

Definition

Class:	DessertMaker
Method:	countBananaSplits
Parameters:	String[]
Returns:	int
Method signature:	int countBananaSplits(String[] ingredients)
(be sure your method is public)

Constraints

-

ingredients will contain between 1 and 30 elements, inclusive.

-

Each element of ingredients will contain between 1 and 50 characters, inclusive.

-

Each element of ingredients will contain only lowercase letters and spaces ('a'-'z',' ').

Examples

0)

{"ice cream","banana","chocolate","chocolate","peanuts"}

Returns: 5

The example from the problem statement.

1)

{"banana", "banana", "chocolate", "strawberries", 
"pineapple", "pineapple", "rice cream"}

Returns: 0

To make a banana split, you need "ice cream", "banana", and at least one other ingredient. We have a "banana" and plenty of other ingredients, but we don't have an "ice cream" so we have zero possibilities.

2)

{"ice cream", "ice cream", "banana", "banana", "chocolate",
 "chocolate"}

Returns: 8

To see the 8 possibilities, note that you can pick either one or two "ice cream"s, one or two "banana"s and one or two "chocolate"s (and 2*2*2=8). You cannot have no ice cream or no bananas - and we need to have at least one other ingredient so we need at least one chocolate. Note that {"ice cream","banana","chocolate"} counts as a different dessert than {"ice cream","ice cream","banana","banana","chocolate","chocolate"} because the ingredient list is not identical.

3)

{"foam", "apple", "whipped cream", "apple", "mushroom", 
"apple core", "ice cream", "ice cream", "banana", "giraffe", 
"mushroom", "spare tire", "ice cream", "banana", "foam", 
"wrench", "paper", "cherry", "alarm clock", "football" ,"apple", 
"apple"}

Returns: 138234

You don't know if it'll be good until you try it.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PyramidOfCubes

Simple Math, Simulation

Used in:

SRM 310

Used as:

Division I Level One

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6577

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9990&pm=6577

Problem Statement

Consider a N-level pyramid built of unit cubes. An example for N=3 can be seen in the image below.

Formally, a pyramid of size N has N levels, where the i-th level (counting from the top) contains an i by i grid of unit cubes.

You have K cubes. First, you select a suitable pyramid size as follows: If K is exactly the number of cubes necessary to build a pyramid of size N for some N, you pick that size. Otherwise, you pick the smallest pyramid size you can not build.

Now you start building the pyramid in a systematic bottom-up way. First you build the complete bottom level, then you build the level above that, etc. When building a level, also proceed in a systematic way, starting the next row only when the previous one is full.

For example, for 21 cubes you should get the following incomplete pyramid:

Given an int K specifying the number of cubes you have, return the surface area of the possibly incomplete pyramid you will build according to the instructions above.

Definition

Class:	PyramidOfCubes
Method:	surface
Parameters:	int
Returns:	double
Method signature:	double surface(int K)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

-

The bottom sides of the cubes on the bottommost level are a part of the surface.

Constraints

-

K will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 42.0

The first example from the problem statement.

1)

Returns: 58.0

The second example from the problem statement.

2)

Returns: 6.0

A single cube.

3)

Returns: 10.0

Two cubes next to each other.

4)

Returns: 47498.0

Quite a lot of cubes.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WordMath

Simple Math

Used in:

TCHS SRM 8

Used as:

Division I Level Two

Writer:

sql_lall

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6572

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10060&pm=6572

Problem Statement

A common task for math students is to solve 'word math' questions, where each distinct letter represents a distinct digit.

Given a list of word math numbers to add, your task is to calculate the greatest possible sum of those numbers.

For example, given the expression:

    TOP
+ CODER

the maximum sum possible by substituting numbers is:

    783
+ 98654
-------
  99437

with C = 9, D = 6, E = 5, O = 8, P = 3, R = 4 and T = 7.

Please note that, for this question, word math numbers are allowed to start with a zero.

Definition

Class:	WordMath
Method:	maximumSum
Parameters:	String[]
Returns:	int
Method signature:	int maximumSum(String[] summands)
(be sure your method is public)

Notes

-

Different letters must represent different digits, identical letters must represent identical digits.

-

Not all digits in the result must appear in the summands.

Constraints

-

summands will contain between 1 and 10 elements, inclusive.

-

Each element of summands will contain between 1 and 8 characters, inclusive.

-

Each element of summands will contain only uppercase letters ('A'-'Z').

-

summands will contain at most 10 distinct letters.

Examples

0)

{"TOP", "CODER"}

Returns: 99437

The example given in the problem statement.

1)

{"AAA", "AAA"}

Returns: 1998

With only one letter, the maximum sum is obtained by setting A = 9.

2)

{"A", "B", "C", "D", "E", "F", "G", "H", "I", "J"}

Returns: 45

Each letter is used once, and there are 10 different letters, so however the digits are distributed this must add up to 0 + 1 + ... + 8 + 9 = 45

3)

{"AB", "BA"}

Returns: 187

4)

{"READIEST","OPERATIC","TOPCODER","PREDICTS","RAPIDEST","ASTEROID","AIRSPEED"}

Returns: 563639653

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EscapeFromRectangle

Simple Math

Used in:

SRM 311

Used as:

Division II Level One

Writer:

gevak

Testers:

PabloGilberto , brett1479 , Olexiy , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6558

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9991&pm=6558

Problem Statement

You are currently at a point (x,y) inside a rectangle. The rectangle's bottom left corner is at (0,0) and its top right corner is at (w,h). Return the shortest distance you must travel in order to reach the rectangle's boundary.

Definition

Class:	EscapeFromRectangle
Method:	shortest
Parameters:	int, int, int, int
Returns:	int
Method signature:	int shortest(int x, int y, int w, int h)
(be sure your method is public)

Constraints

-

w and h will be between 2 and 1000, inclusive.

-

x will be between 1 and w - 1, inclusive.

-

y will be between 1 and h - 1, inclusive.

Examples

0)

Returns: 1

We can go either straight down or straight to the left.

1)

Returns: 1

Go straight to the upper boundary here.

2)

Returns: 347

Going straight to the right leads to success.

3)

Returns: 161

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ReverseSums

Simple Math, String Manipulation

Used in:

TCHS SRM 29

Used as:

Division I Level One

Writer:

jmzero

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6557

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10653&pm=6557

Problem Statement

To find the "reverse sum" of a number, we reverse the digits of the number and then add the original number to the reversed number. For example, to find the reverse sum of 1325, first reverse the digits to get 5231. Then, add the original number to get 5231+1325=6556.

Return the reverse sum of the given number N.

Definition

Class:	ReverseSums
Method:	getSum
Parameters:	int
Returns:	int
Method signature:	int getSum(int N)
(be sure your method is public)

Constraints

-

N will be between 1 and 99999, inclusive.

Examples

0)

Returns: 6556

The example from the problem statement. 1325 + 5231 = 6556.

1)

Returns: 101

100 + 001 = 101

2)

Returns: 162935

89437 + 73498 = 162935

3)

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BasketballStrategy

Geometry, Graph Theory, Math

Used in:

SRM 313

Used as:

Division I Level Three

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , legakis , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6546

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9993&pm=6546

Problem Statement

This problem statement contains images, subscripts and superscripts that may appear incorrectly or not appear at all in some plugins. In that case, use the standard view in the arena to see it correctly.

In a simplified version of basketball the goal is to score by getting the ball in a special scoring place. There are two teams, and each team contains the same number of players. When a player has possession of the ball, he has two choices: take a shot, or pass the ball to a teammate. When taking a shot, the player throws the ball in a straight line to the scoring place. When passing the ball, he throws the ball in a straight line to the target teammate. In both cases, at most one of the rival players will try to intercept the shot or pass.

The probability of a pass being successful is:

C_p * (1 - (ls / 150)²) * dr / (dr + 1)

And the probability of a shot being successful (score) is:

(C_s * dr / (dr + 1))^ln(ls)

Where C_p and C_s are constants defined for the problem instance, ls is the length of the shot or pass, dr is the distance between the intercepting rival and the ball trajectory and ln is the natural logarithm (logarithm in base e).

When trying to intercept a shot or a pass, only the best suitable player of the other team to do so (i.e., the one that produces the lowest dr) will try. If no player on the other team can do it, the factor dr/(dr+1) in the formula is considered to have a value of 1 (i.e., it is ignored). A player of the rival team is only allowed to try to intercept the ball if the line that passes through him and is perpendicular to the ball trajectory intersects the trajectory at some point between the two endpoints of the trajectory, inclusive.

For example, in this picture:

There are 3 players in each team, green players are your team and red players are rivals. Player 0 has the ball and has 3 options marked as blue lines, 2 passes and taking a shot. The shot, if taken, can be intercepted by any of the rivals, but only number 2 will try because he is clearly the nearest. The pass to player 1 is impossible to intercept for the rivals, because any player that can intercept that pass should be inside the gray area. The pass to player 2 can be intercepted by rivals 1 or 2. Rival player 0 is not on an intersecting perpendicular line, so he cannot try to intercept it. In this last case, rival 1 will try to intercept because he is nearer than rival 2.

You will be given two String[]s team and rivals with the same number of elements representing the members of each team. Each element of team and rivals will be in the format "X Y" where X and Y will be positive integers with no leading zeroes representing the x and y coordinates of that player in the field. You will also be given Cp and Cs, the constants for the probability calculations of each type of movement. When the game starts, the ball is in possession of the player on your team with index 0. The scoring place is at X=50, Y=0. Your team is only allowed to take one shot, and you are to determine and return the probability that your team will score if it follows the best strategy. A strategy consists of zero or more passes followed by a shot. If your team loses the ball at any point during the strategy, you will not score. See examples for further clarification.

Definition

Class:	BasketballStrategy
Method:	scoreProbability
Parameters:	String[], String[], double, double
Returns:	double
Method signature:	double scoreProbability(String[] team, String[] rivals, double Cp, double Cs)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

-

Pictures are just approximations. The players are considered to be perfect points with 0 surface and 0 length and trajectories and other lines are perfect lines with 0 surface.

-

The same rival may try to intercept many passes along the game (see example 3 for further clarification).

Constraints

-

team and rivals will each contain exactly N elements, where N is between 1 and 50, inclusive.

-

Each element of team and rivals will be two integers between 1 and 99, inclusive, with no leading zeroes, separated with exactly one space character, with no leading or trailing spaces.

-

All elements of team and rivals together will be distinct.

-

Cp and Cs will each be greater than 0 and less than or equal to 1.

Examples

0)

{"50 50","35 60","70 15"}

{"75 5","72 25","45 17"}

Returns: 0.6100612919616956

This is the example from the problem statement. The best strategy is to pass the ball to player 2 and make him shoot.

1)

{"50 4"}

{"50 5"}

0.99

0.5

Returns: 0.3825461314703953

There's no teammate to pass the ball to, so you must take the shot directly. Since the only rival player is not in a position to intercept, the probability of making the shot is 0.5^ln(4).

2)

{"50 4"}

{"50 3"}

0.5

0.5

Returns: 0.0

You can't pass the ball and your rival can perfectly block you; therefore it's impossible to score.

3)

{"50 50","40 50","40 40","40 30","50 20"}

{"50 41","44 29","48 27","45 41","48 64"}

0.999999

0.8

Returns: 0.25546407305110735

This picture illustrates the locations. The best strategy is marked in blue and the pink lines show possible interception lines from a nearest rival. Note that passes 2-3 and the shot taken by player 4 cannot be intercepted.

Here player 0 cannot take a shot because he will always be blocked. You should try to get the ball to player 4 so he can take the shot instead. Note that in this case it is better to make more passes and get to player 4 for the shot because the difficulty of longer passes and shots makes other strategies less likely to succeed.

4)

{"50 50","50 25"}

{"40 40","60 20"}

0.7

Returns: 0.20631213370921644

Note that getting closer can be better even if you are good at taking shots.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

InputBoxChecker

Greedy, Simple Math

Used in:

SRM 310

Used as:

Division II Level Two

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6542

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9990&pm=6542

Problem Statement

Imagine a simple input dialog box. The user is supposed to enter a positive integer from a given range into the box.

Recently you realized that sometimes you can tell that the user's input is invalid before he finishes entering the number. For example, if the valid range is 300 to 347, and the user wants to enter the number 372, as soon as he types "37" you can be sure that his input won't be valid.

More precisely, we call a number valid if it is a prefix of some number in the given range, and invalid otherwise.

You are given two ints smallest and largest (denoting the range of valid inputs), and a int[] numbers. The range of valid inputs contains all integers between smallest and largest, inclusive.

Write a method that will determine for each number in numbers whether it represents a valid input for the given range. Return a String[] that has the same number of elements as numbers. If the i-th element of numbers represents a valid input, the i-th element of the return value has to be "VALID", otherwise it has to be "INVALID" (quotes for clarity only).

Definition

Class:	InputBoxChecker
Method:	checkPrefix
Parameters:	int, int, int[]
Returns:	String[]
Method signature:	String[] checkPrefix(int smallest, int largest, int[] numbers)
(be sure your method is public)

Constraints

- smallest is between 1 and 2,000,000,000, inclusive.

- largest is between 1 and 2,000,000,000, inclusive.

- smallest is less than or equal to largest.

- numbers contains between 1 and 50 elements, inclusive.

- Each element in numbers is between 1 and 2,000,000,000, inclusive.

Examples

0)

{37}

Returns: {"INVALID" }

This is the example from the problem statement.

1)

{3, 31, 317, 3174, 310, 320}

Returns: {"VALID", "VALID", "VALID", "INVALID", "VALID", "VALID" }

Please note that smallest and largest represent an inclusive range.

2)

{7, 73, 734, 7349}

Returns: {"VALID", "VALID", "VALID", "INVALID" }

3)

{1,2,3,4,5,6,7,8,9}

Returns: 
{"INVALID",
"INVALID",
"INVALID",
"INVALID",
"INVALID",
"VALID",
"VALID",
"INVALID",
"INVALID" }

4)

1234567890

{123, 456, 789, 1234567, 7654321, 3245354, 325432532, 243212}

Returns: {"VALID", "VALID", "VALID", "VALID", "VALID", "VALID", "VALID", "VALID" }

Watch out for the time limit.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MedianOfNumbers

Simple Math

Used in:

SRM 308

Used as:

Division II Level One

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6528

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9988&pm=6528

Problem Statement

In a set of distinct numbers, the median is an element M such that the number of elements greater than M is equal to the number of elements smaller than M. For example, in a set {1, 4, 2, 5, 7} the median is 4 because two elements (5 and 7) are greater than 4 and 2 elements (1 and 2) smaller than 4. The set {1, 5, 8, 3} has no median because no element from it satisfies the definition above.

You are given a int[] numbers. Return the median of numbers or -1 if numbers has no median.

Definition

Class:	MedianOfNumbers
Method:	findMedian
Parameters:	int[]
Returns:	int
Method signature:	int findMedian(int[] numbers)
(be sure your method is public)

Constraints

-

numbers will contain between 1 and 50 elements, inclusive.

-

Each element of numbers will be between 1 and 100, inclusive.

-

All elements of numbers will be distinct.

Examples

0)

{1, 4, 2, 5, 7}

Returns: 4

The example from the statement.

1)

{1, 5, 8, 3}

Returns: -1

2)

{7}

Returns: 7

There are zero elements that are greater than 7 and zero elements that are smaller than 7.

3)

{7, 12}

Returns: -1

4)

{66, 53, 47, 86, 18, 21, 97, 92, 15}

Returns: 53

5)

{32, 54, 27, 4, 69, 96, 73, 1, 100, 15, 21}

Returns: 32

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FracSum

Math

Used in:

TCCC06 Round 2B

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6520

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10112&pm=6520

Problem Statement

We want to be able to express a fraction as a sum of two fractions that have small denominators. Specifically, given a fraction a/b, we want to find fractions c/d and e/f such that

a/b = c/d + e/f, where d and f are positive
max(d,f) is as small as possible

Create a class FracSum that contains a method decompose that is given a and b and that returns the smallest value for max(d,f).

Definition

Class:	FracSum
Method:	decompose
Parameters:	int, int
Returns:	int
Method signature:	int decompose(int a, int b)
(be sure your method is public)

Constraints

-

a and b will each be between 1 and 2,000,000,000, inclusive.

Examples

0)

Returns: 5

14/10 = 0/1 + 7/5 is one way to keep the denominators less than or equal to 5.

1)

Returns: 12

1/60 = -2/5 + 5/12

2)

Returns: 9

8/90 = -4/5 + 8/9

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IndictDates

Brute Force, Math

Used in:

TCHS SRM 12

Used as:

Division I Level One

Writer:

Pawa

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6515

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10064&pm=6515

Problem Statement

In some of the old historical chronicles the Indict system of chronology was used. Instead of a year, this system uses three integers, called indict, circle to the Sun, and circle to the Moon. Let's denote them as indict, circleSun, circleMoon.

Each of these three integers has a unique range. indict is between 1 and 15, circleSun is between 1 and 28, and circleMoon is between 1 and 19 (all ranges are inclusive). Initially, at year 1, all three of these numbers are equal to 1. Every year, all three numbers increase by 1, and whenever a number exceeds its upper bound (15, 28, and 19, respectively), it is reset to 1. For example, in year 16, indict = 1, circleSun = 16, and circleMoon = 16.

Given the ints indict, circleSun, and circleMoon, return the earliest year that the three numbers can represent. Time starts at year 1, so the return value will never be less than 1.

Definition

Class:	IndictDates
Method:	getYear
Parameters:	int, int, int
Returns:	int
Method signature:	int getYear(int indict, int circleSun, int circleMoon)
(be sure your method is public)

Constraints

-

indict will be between 1 and 15, inclusive.

-

circleSun will be between 1 and 28, inclusive.

-

circleMoon will be between 1 and 19, inclusive.

Examples

0)

Returns: 16

This is the example from the problem statement.

1)

Returns: 1

Initially we are at year 1.

2)

Returns: 5266

3)

Returns: 7980

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CommutePlan

Recursion, Simple Math

Used in:

TCHS SRM 29

Used as:

Division I Level Two

Writer:

jmzero

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6509

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10653&pm=6509

Problem Statement

Every morning, you drive distance kilometers down a curvy highway to work. Over time, you've noticed some possible shortcuts along the way. For each shortcut, you've recorded where along the highway it starts, where it rejoins the highway, and how long it is. The i-th elements of cutStart, cutEnd, and cutLength describe these three properties, respectively, for the i-th shortcut. The highway and all shortcuts are one way only. This means that you must not overshoot your destination, and you cannot go backwards to take advantage of a shortcut that begins earlier on the road. Figure out the shortest route you can take using any valid combination of shortcuts, and return its length.

Definition

Class:	CommutePlan
Method:	shortestRoute
Parameters:	int, int[], int[], int[]
Returns:	int
Method signature:	int shortestRoute(int distance, int[] cutStart, int[] cutEnd, int[] cutLength)
(be sure your method is public)

Constraints

-

distance will be between 1 and 1000, inclusive.

-

cutStart, cutEnd, and cutLength will each contain between 0 and 12 elements, inclusive.

-

cutStart, cutEnd, and cutLength will each contain the same number of elements.

-

Each element of cutStart, cutEnd, and cutLength will be between 0 and 1000, inclusive.

-

Each element of cutStart will be less than the corresponding element of cutEnd.

Examples

0)

{10,50}

{60,90}

{40,20}

Returns: 80

The first shortcut saves us 10 kilometers (as we get from 10 to 60, but only drive 40 kilometers). However, taking the first shortcut means we can't use the second one (which would save 20 kilometers). It's best to skip the first and use the second.

1)

{}

{}

{}

Returns: 1000

We're in for a long drive with no shortcuts.

2)

{0,0,50,100,110}

{50,50,100,151,140}

{10,20,10,10,90}

Returns: 70

Our best strategy is to use the shortcuts at indexes 0 and 2. This gets us to kilometer 100 in only 20 kilometers of driving. We can't use the shortcut at index 3 because it overshoots the destination. We don't want to use the shortcut at index 4 because it's actually longer than the regular path. Therefore we drive the last 50 kilometers down the regular road - 20+50=70.

3)

{0,20,80,50,160,140,420,450}

{10,60,190,70,180,160,901,900}

{9,45,100,15,14,14,5,0}

Returns: 432

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AntarcticaPolice

Graph Theory, Simple Math

Used in:

SRM 312

Used as:

Division I Level Two

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6501

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9992&pm=6501

Problem Statement

Year 2100. Humanity is starting to inhabit Antarctica. So far there are N towns, some of them connected with narrow one-way roads.

The president of Antarctica has decided to establish police in his country. The cost of building a police station in each town is given. However, there may not be a need to build a police station in every town. The only requirement is that every town must be reachable from some police station using roads.

As the next elections are approaching, the president doesn't want to expose large police expenses. Thus he wants the average cost of a built station to be as low as possible.

You are given a int[] costs, the i-th element of which represents the cost of building a police station in town i, and a String[] roads representing the layout of the one-way roads. The j-th character of the i-th element of roads is 'Y' if there is a road from town i to town j, or 'N' if there is not. Make the average cost of a built station to be as low as possible and return this cost.

Definition

Class:	AntarcticaPolice
Method:	minAverageCost
Parameters:	int[], String[]
Returns:	double
Method signature:	double minAverageCost(int[] costs, String[] roads)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute error of 1E-9.

Constraints

-

costs will contain between 1 and 50 elements, inclusive.

-

Each element of costs will be between 1 and 1000, inclusive.

-

roads will contain exactly N elements, where N is the number of elements in costs.

-

Each element of roads will contain exactly N characters.

-

Each character of each element of roads will be 'Y' or 'N'.

-

The ith character of the ith element of roads will be 'N'.

Examples

0)

{1,2,3,4}

{"NYNN","NNYN","NNNY","YNNN"}

Returns: 1.0

It is possible to get everywhere from anywhere (the towns form a big circle), so we need only the cheapest station.

1)

{1,2,3,4}

{"NYNN","NNYN","NNNY","NYNN"}

Returns: 1.0

Once again, the cheapest station is enough.

2)

{5,6,7,8}

{"NYNN","YNNN","NNNY", "NNYN"}

Returns: 6.0

We have two separate parts, so we build one cheapest station in each part : (5+7)/2=6.

3)

{10,5}

{"NY","NN"}

Returns: 7.5

We have three choices here: build a police station in town 0, in town 1, or in both towns. The second choice doesn't satisfy the requirements since it's impossible to get from town 1 to town 0. Of the two remaining choices, building both is better because it minimizes the average cost.

4)

{34,22,25,43,12}

{"NYNNY","YNNYN","NNNYY","NNNNN","NNNNN"}

Returns: 19.666666666666668

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ParallelepipedUnion

Geometry, Simple Math

Used in:

SRM 312

Used as:

Division I Level One , Division II Level Two

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6498

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9992&pm=6498

Problem Statement

You are given 2 rectangular parallelepipeds (rectangular solids) in space, edges parallel to coordinate axes. Compute the volume of their union.

For example, consider the two following parallelepipeds (they are divided into unit cubes for clarity):

and

When combined in the following manner, their union is a figure of volume 12 (it consists of 12 unit blocks: ten on the bottom level, and two on the top level):

You are given a String[] parallelepipeds containing exactly two elements. Each element represents a single parallelepiped, and is formatted as "x1 y1 z1 x2 y2 z2" (quotes for clarity only), where (x1, y1, z1) and (x2, y2, z2) are the coordinates of opposing corners of the parallelepiped.

Definition

Class:	ParallelepipedUnion
Method:	getVolume
Parameters:	String[]
Returns:	int
Method signature:	int getVolume(String[] parallelepipeds)
(be sure your method is public)

Constraints

-

parallelepipeds will contain exactly 2 elements.

-

Each element of parallelepipeds will be formatted as "x1 y1 z1 x2 y2 z2" (quotes for clarity only).

-

In each element of parallelepipeds, x1 < x2, y1 < y2, z1 < z2.

-

All coordinates will be integers between 1 and 100, inclusive, without extra leading zeroes.

Examples

0)

{"1 1 1 4 4 2", "3 2 1 5 3 3"}

Returns: 12

The example from the problem statement.

1)

{"1 1 1 2 2 2", "3 3 3 4 4 4"}

Returns: 2

Two unit cubes that do not intersect.

2)

{"1 10 20 5 15 23", "2 12 22 3 14 23"}

Returns: 60

One parallelepiped inside another.

3)

{"28 31 21 67 60 81","60 1 21 67 50 81"}

Returns: 80460

4)

{"34 3 50 37 6 53","36 1 51 38 4 55"}

Returns: 49

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PizzaDivision

Geometry, Simple Math, Simple Search, Iteration

Used in:

SRM 312

Used as:

Division II Level Three

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6493

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9992&pm=6493

Problem Statement

You want to divide a round pizza (represented by a circle) into two equal halves with one straight cut. The pizza contains several toppings, represented by points strictly inside the circle. The cut is called beautiful if the two halves of the pizza are mirror images of each other: for every topping in one half there is a topping in the other half in the symmetric point (we don't care about the toppings that are exactly on the cut).

For example, the cut represented by the red line in the following picture is the only beautiful cut for that pizza (black dots are toppings):

This pizza has four different beautiful cuts, all shown by red lines:

You are to count the number of different beautiful cuts for a given pizza. You are given a String[] toppings, each element representing a topping in the form "x y", where x and y are the coordinates of that topping. You may assume that the pizza is large enough to have all those toppings inside. The point of origin coincides with the center of the pizza (that is, the center of the pizza has the coordinates "0 0"). Return the number of different beautiful cuts, or -1 if there are infinitely many of them.

Definition

Class:	PizzaDivision
Method:	howMany
Parameters:	String[]
Returns:	int
Method signature:	int howMany(String[] toppings)
(be sure your method is public)

Notes

-

Two points A and B are symmetric with respect to line L, if and only if either A and B coincide and lie on L or L is perpendicular to AB and crosses it in its middle point.

Constraints

-

toppings will contain between 1 and 50 elements, inclusive.

-

Each element of toppings will be formatted as "x y" (quotes for clarity only), where x and y are integers between -500 and 500, inclusive, with no extra leading zeroes.

-

All elements of toppings will be different.

Examples

0)

{"0 110", "0 70", "-75 20", "75 20", "-25 -50", "25 -50"}

Returns: 1

The first example from the problem statement.

1)

{"0 70", "70 0", "0 -70", "-70 0"}

Returns: 4

The second example from the problem statement.

2)

{"0 0"}

Returns: -1

Any cut passing through the center suffices.

3)

{"3 -4"}

Returns: 1

4)

{"3 -4", "-3 4"}

Returns: 2

5)

{"1 2", "3 4"}

Returns: 0

6)

{"-300 100", "-200 100", "-100 100", "100 100", 
"200 100", "300 100", "-300 -100", "-200 -100", 
"-100 -100", "100 -100", "200 -100", "300 -100"}

Returns: 2

7)

{"-54 -83", "-46 54", "-5 -44", "-1 -31", "-14 47", 
"7 -5", "-45 -63", "-88 47", "-17 -9", "-26 -66", 
"40 56", "-67 69", "-49 -2", "2 62", "61 78", 
"-81 -32", "87 33", "-22 -53", "-43 -38", "57 28", 
"35 12", "-53 -15", "52 -16", "32 -44", "-73 68", 
"79 44", "3 56", "-66 26", "-87 41", "4 87", 
"22 53", "59 16", "-3 55", "3 19", "-26 8", 
"43 38", "54 46", "-16 22", "-3 -93", "45 63", 
"0 -37", "-7 5", "-40 -56", "40 19", "-8 -63", 
"-16 -89", "29 11", "-52 -21", "-58 -22", "4 -61"}

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TVSize

Simple Math

Used in:

TCHS SRM 5

Used as:

Division I Level One

Writer:

Uranium-235

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6486

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10057&pm=6486

Problem Statement

When shopping for TVs consumers may notice that a TV's size is given by its diagonal in inches. The aspect ratio of a screen is the ratio of its width to its height. Given the aspect ratio and the diagonal size in inches of a TV screen, you must compute its width and height in inches (see the notes and the first example for more information). If the width or the height is not an integer, round down to the nearest integer; for example, 1.7 would become 1.

You are tasked with writing a method which accepts 3 arguments: an int diagonal specifying the TV's diagonal in inches, an int height specifying the aspect ratio height, and an int width specifying the aspect ratio width. Your program should compute the actual height and width of the TV in inches and return them in a int[] where the first element is the TV's height and the second element is the TV's width.

Definition

Class:	TVSize
Method:	calcSize
Parameters:	int, int, int
Returns:	int[]
Method signature:	int[] calcSize(int diagonal, int height, int width)
(be sure your method is public)

Notes

-

Let W denote the width, H denote the height and D denote the diagonal of the screen. Then W*W + H*H = D*D and W * height = H * width.

Constraints

-

diagonal will be between 5 and 1000, inclusive.

-

height will be between 1 and 99, inclusive.

-

width will be between 2 and 100, inclusive.

-

width will be greater than height.

Examples

0)

Returns: {25, 45 }

     W = (width/height) * H

   D*D = W*W + H*H

  52^2 = (width/height)^2 * H^2 + H^2

  52^2 = (16/9)^2 * H^2 + H^2

     H = 25.49

     W = 45.32

1)

Returns: {3, 5 }

2)

Returns: {7, 10 }

3)

Returns: {3, 5 }

4)

Returns: {7, 8 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SpeedRadar

Simple Math, Simple Search, Iteration

Used in:

TCHS SRM 1

Used as:

Division I Level One

Writer:

ged

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6474

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10022&pm=6474

Problem Statement

A speed radar is installed in a highway zone where the maximum speed limit is maxLimit mph, and the minimum speed limit is minLimit mph. Any reading that is strictly above or below this interval is an infringement.

Periodically, the radar readings are analyzed to make sure that the sensors are working properly. It is assumed that most drivers obey speed limits, and therefore, the radar will be considered faulty if more than 10% of its readings are infringements.

Given the radar readings over a period of time, return the average speed of all cars that are driving within the speed limits. If the radar is faulty, return 0.0.

Definition

Class:	SpeedRadar
Method:	averageSpeed
Parameters:	int, int, int[]
Returns:	double
Method signature:	double averageSpeed(int minLimit, int maxLimit, int[] readings)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

maxLimit will be between 1 and 200, inclusive.

-

minLimit will be between 1 and maxLimit, inclusive.

-

readings will contain between 1 and 50 elements, inclusive.

-

Each element of readings will be between 1 and 200, inclusive.

Examples

0)

{45, 40, 50}

Returns: 45.0

With all drivers within the speed limits, the return value is just the average speed.

1)

{42,43,44,45,46,47,48,49,50,51}

Returns: 46.0

There is only one driver infringing the limit, and it represents 10% of the total readings. The average speed of the other readings is 46.0.

2)

{42,46,48,50,52}

Returns: 0.0

Only one reading is outside the given limits, but it represents 20% of the total number of readings. We therefore assume that the radar is not working and return 0.0.

3)

{25,45,45,43,24,9,51,55,60,34,61,23,40,40,47,49,33,23,47,54,54}

Returns: 41.68421052631579

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CrazyRunning

Math, Simulation

Used in:

SRM 313

Used as:

Division I Level Two

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , legakis , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6465

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9993&pm=6465

Problem Statement

John is locked in a mansion that is shaped like a star, with a number of corridors of distinct length that meet at a common point in the center. He is desperately looking for an exit, so he wants to check the end of every corridor to see if he can find one.

He is initially at the outer end of one of the corridors. In his desperation, he does not develop a good strategy, and instead, decides to do the following: He will run to the center, and when he gets there, he will randomly enter a different corridor than the one he came from. He will then run to the outer end of that corridor, turn back, and return to the center, where he will again randomly enter a different corridor than the one he just came from (but possibly a corridor he was in before that). He will repeat this process until he has visited the outer ends of all the corridors at least once. When he reaches the end of the final corridor, he will not run back to the center again.

You will be given a int[] corridors containing the lengths of all the corridors in meters. John starts in the corridor at index 0 and will run following the described strategy until he visits the ends of all the corridors at least once. Return the expected length of John's path.

Definition

Class:	CrazyRunning
Method:	expectedTime
Parameters:	int[]
Returns:	double
Method signature:	double expectedTime(int[] corridors)
(be sure your method is public)

Notes

-

John will not stop running until he has visited every corridor end.

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

corridors will contain between 2 and 50 elements, inclusive.

-

Each element of corridors will be between 1 and 1000000 (10⁶), inclusive.

Examples

0)

{10,20}

Returns: 30.0

He starts at the end of corridor 0 at time 0. At time 10 he is in the center, and his only option (since he never goes back to the same corridor he just came from) is to go to corridor 1. He reaches the end of corridor 1 at time 30.

1)

{150,150,150}

Returns: 900.0

He will start from corridor 0, get to the center at time 150, enter one of the other two corridors, run to the end and back to the center at time 450. From that moment on, he has 1/2 probability to finish in 150 seconds and 1/2 to do a useless run for 300 seconds and be in the same position again. So the answer is 450 + 1/2*150 + 1/2*1/2*450 + ... + ((1/2)ⁿ*((n-1)*300+150)) + ..., which is equal to 900.

2)

{100,150,200}

Returns: 875.0

3)

{1000,1000,900,1000,555,1000,2562}

Returns: 33550.32857142857

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MonthlyPayment

Greedy, Simple Math

Used in:

SRM 314

Used as:

Division I Level Three

Writer:

zhuzeyuan

Testers:

PabloGilberto , brett1479 , Olexiy , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6464

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9994&pm=6464

Problem Statement

Byterland Mobile, a mobile phone service provider, normally charges 10 cents per SMS (text message). In addition, it also offers monthly packs, which let you purchase a certain number of SMSs each month at a special price. You may purchase any number of these packs. If you exceed the number of SMSs covered by your monthly packs, the excess messages are charged at the normal rate.

You expect to send totalSMS SMSs each month, and you would like to minimize your monthly payment. There are two monthly packs available. The first pack costs pay1 cents and includes pack1 messages, and the second pack costs pay2 cents and includes pack2 messages. You may purchase any combination of these packs. Remember that it is sometimes cheaper to buy more SMSs than you actually need (see example #2). Return the minimal monthly payment in cents.

Definition

Class:	MonthlyPayment
Method:	minimalPayment
Parameters:	String, String, String, String, String
Returns:	long
Method signature:	long minimalPayment(String totalSMS, String pack1, String pay1, String pack2, String pay2)
(be sure your method is public)

Notes

-

For technical reasons, we cannot use long parameters, so we are using Strings instead.

Constraints

-

totalSMS will be an integer between 0 and 10¹², inclusive, with no extra leading zeroes.

-

pack1, and pack2 will each be an integer between 1 and 10¹², inclusive, with no extra leading zeroes.

-

pay1 and pay2 will each be an integer between 1 and 10¹³, inclusive, with no extra leading zeroes.

-

pay1 will be less than or equal to 20 * pack1.

-

pay2 will be less than or equal to 20 * pack2.

Examples

0)

"92"

"10"

"90"

"20"

"170"

Returns: 790

The first pack offers 10 messages for 90 cents, and the second pack offers 20 messages for 170 cents. You want to buy 92 messages, so you choose one of the first pack and four of the second pack. You will pay for the remaining 2 messages at the normal rate of 10 cents each. The total price is 90 + 170*4 + 10*2 = 790 cents.

1)

"90"

"10"

"90"

"20"

"170"

Returns: 770

2)

"99"

"10"

"90"

"20"

"170"

Returns: 850

We can buy five of the second pack. The total number of SMSs covered by the purchased packs exceeds 99, but this is the cheapest way.

3)

"10"

"1"

"11"

"20"

"300"

Returns: 100

Packs do not lead to a cheaper way in this case.

4)

"0"

"10"

"80"

"50"

"400"

Returns: 0

5)

"28"

"1"

"10"

"1"

"8"

Returns: 224

6)

"450702146848"

"63791"

"433956"

"115281"

"666125"

Returns: 2604279739220

7)

"45"

"6"

"12"

"7"

"14"

Returns: 90

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CalculatorDisplay

Simple Math

Used in:

TCHS07 Delta 2

Used as:

Division I Level Three

Writer:

ged

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6458

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10714&pm=6458

Problem Statement

You have a calculator with a screen that can display up to digits digits along with a single decimal point. If the result of an operation is a number that cannot fit on the screen, the calculator will show just "E" (quotes for clarity) rather than the actual result. Note that fractional numbers less than 1.0 are always shown without the leftmost 0 (for example, ".125"). Also note that integer numbers are never shown with a decimal point, so 4 would always be shown as "4", not "4." or "4.0"." Leading zeros are never displayed (at the left of integer part or the right in the fractional part).

Given a numerator n and denominator d, return the content of the calculator's screen after dividing n by d. For example, 10005 divided by 400 is 25.0125. A 6-digit display would show "25.0125" while a 5-digit display would show "E" (all quotes for clarity only).

Definition

Class:	CalculatorDisplay
Method:	numberDivision
Parameters:	int, int, int
Returns:	String
Method signature:	String numberDivision(int digits, int n, int d)
(be sure your method is public)

Constraints

-

digits will be between 1 and 20, inclusive.

-

n will be between 0 and 1,000,000,000, inclusive.

-

d will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: "25.0125"

The example from the problem statement.

1)

Returns: "E"

The same result would not fit in only five digits.

2)

Returns: ".125"

3)

Returns: "1234.5"

Note that the decimal point does not add a position, and the result occupies all of its five digits.

4)

Returns: "E"

To display the result would require an infinite number of fractional digits!

5)

987654321

Returns: "0"

The result is just zero. Note that the decimal point is not shown if the result is an integer.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TrainRobber

Greedy, Search, Simple Math

Used in:

SRM 307

Used as:

Division I Level Two

Writer:

Mike Mirzayanov

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6448

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9987&pm=6448

Problem Statement

This problem contains images best viewed from the applet.

A train is moving in the positive direction of the x-axis. The train consists of nCarriages carriages of equal length. Initially, at time 0, the coordinate of the rightmost end of the last carriage is length, the coordinate of the rightmost end of the second to last carriage is 2 * length, and so on. There is a robber located on the leftmost point of the roof of the last carriage.

Here is an example of a train with 4 carriages at time 0.

There are an infinite number of low bridges above the railway. Each bridge belongs to one bridge sequence. The k-th sequence consists of bridges located at the coordinates offset[k] + period[k] * j, for all non-negative integers j.

The blue bridges belong to sequence 0 and the red bridges belong to sequence 1. In this case, offset[0] = 3, period[0] = 4, offset[1] = 4, and period[1] = 2.

The train moves at a constant speed of trainSpeeed units per second, and the robber has a maximal speed of robberSpeed units per second. The robber cannot walk through the bridges when he is on the roof because they are too low. Therefore, whenever the robber is at the same coordinate as a bridge, he must either be between two carriages or at either end of the train. This allows him to duck and jump down into a safe area.

The robber's goal is to travel to the rightmost point of the first carriage as quickly as possible. He will stop walking and jump off the train when he reaches the rightmost point of the first carriage, or when nBridges have passed above him - whichever comes first. Return the position of the robber on the x-axis when he exits the train.

The offsets and periods of the bridge sequences are given in the String[]s offset and period. Each element of offset and period contains a space separated list of integers. The ith integers in offset and period are the offset and period of the ith bridge sequence. See example 0 for clarification.

Definition

Class:	TrainRobber
Method:	finalPosition
Parameters:	int, int, String[], String[], int, int, int
Returns:	double
Method signature:	double finalPosition(int length, int nCarriages, String[] offset, String[] period, int trainSpeed, int robberSpeed, int nBridges)
(be sure your method is public)

Notes

-

It is possible for multiple bridges to be located in the same position.

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

length will be between 1 and 1000000, inclusive.

-

nCarriages will be between 1 and 1000000, inclusive.

-

offset will contain between 1 and 50 elements, inclusive.

-

Each element of offset will contain between 1 and 50 characters, inclusive.

-

period will contain between 1 and 50 elements, inclusive.

-

Each element of period will contain between 1 and 50 characters, inclusive.

-

Each element of offset and period will contain one or more integers without leading zeroes separated by single spaces.

-

Each integer in offset and period will be between 1 and 1000000, inclusive.

-

offset and period will contain the same number of integers.

-

trainSpeed will be between 1 and 1000000, inclusive.

-

robberSpeed will be between 1 and 1000000, inclusive.

-

nBridges will be between 1 and 1000000, inclusive.

Examples

0)

{"3 4"}

{"4", "2"}

Returns: 14.0

The robber will walk to the rightmost end of the last carriage and then duck down between carriages to avoid the first two bridges (at coordinates 3 and 4). He will then walk to the rightmost end of the next carriage and duck down to avoid the next three bridges (at coordinates 6, 7, and 8). He will repeat this procedure once more to avoid the next three bridges (at coordinates 10, 11, and 12). He will finally reach the rightmost point of the first carriage when he is at coordinate 14.

1)

{"3 4"}

{"4 2"}

Returns: 3.0

The first bridge will pass when the robber is at coordinate 3.

2)

{"8 23"}

{"15 13"}

Returns: 75.0

3)

{"1 1"}

{"1 1"}

Returns: 50.0

4)

{"10", "15 63"}

{"23 42 11"}

Returns: 6355.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TroytownKeeper

Simple Math

Used in:

TCHS SRM 1

Used as:

Division I Level Three

Writer:

ged

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6441

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10022&pm=6441

Problem Statement

People enjoy mazes, but they also get them dirty. Arrows, graffiti, and chewing gum are just a few of the souvenirs people leave on the walls. You, the maze keeper, are assigned to whiten the maze walls. Each face of the wall requires one liter of paint, but you are only required to paint visible faces. You are given a map of the maze, and you must determine the amount of paint needed for the job.

The maze is described by a String[] maze, where each character can be either '#' (a wall) or '.' (an empty space). All '.' characters on the perimeter of the map are considered entrances to the maze. Upon entering the maze, one can only move horizontally and vertically through empty spaces, and areas that are not reachable by these movements are not considered visible. Each '#' represents a square block with four wall faces (each side of the square is a face). A face is visible if it is not directly adjacent to another wall (and is in a reachable area of the maze). For example, two adjacent blocks can have at most six visible faces since two of their faces are directly adjacent to each other. All exterior faces on the perimeter are considered visible.

For example, the following picture represents a trivial maze with just one (wide) entrance and only four empty reachable spaces:

To whiten this maze you must paint the faces highlighted in yellow above: 16 for its perimeter, plus 8 interior faces. Note that there are faces that are not visible and thus need not be painted.

Definition

Class:	TroytownKeeper
Method:	limeLiters
Parameters:	String[]
Returns:	int
Method signature:	int limeLiters(String[] maze)
(be sure your method is public)

Constraints

- maze will contain between 1 and 50 elements, inclusive.

- Each element of maze will contain between 1 and 50 characters, inclusive.

- All elements of maze will have the same number of characters.

- All characters in maze will be either '.' or '#'.

Examples

0)

{"##..#"
,"#.#.#"
,"#.#.#"
,"#####"}

Returns: 24

Example from the problem statement.

1)

{"##",
 "##"}

Returns: 8

Only the perimeter of the maze (which has no interior!) has to be painted.

2)

{"######"
,"#....."
,"#.####"
,"#.#..#"
,"#.##.#"
,"#....#"
,"######"}

Returns: 56

3)

{"######"
,"#....."
,"#..#.."
,"#....."
,"######"}

Returns: 36

4)

{"#.#.#.#"
,".#.#.#."
,"#.#.#.#"
,".#.#.#."}

Returns: 36

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CompositionTimeSignature

Simple Math, Simple Search, Iteration

Used in:

TCHS SRM 4

Used as:

Division I Level Two

Writer:

ivan_metelsky

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6423

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10023&pm=6423

Problem Statement

In music, each note has a relative duration. For example, a whole note lasts four times longer than a quarter note. Half notes, eighth notes, and sixteenth notes have one half, one eighth, and one sixteenth the duration of whole notes, respectively.

A musical composition is characterized by its time signature, which defines the number of beats per measure. Time signatures are written as fractions, where the numerator is the number of beats, and the denominator is the type of note represented by each beat. For example, a time signature of 2/4 indicates that each measure contains two beats, each of which are quarter notes. A time signature of 3/8 indicates that each measure contains three beats, each of which are eighth notes. For the purposes of this problem, we will only consider the following time signatures: 3/8, 2/4, 3/4 and 4/4.

It is difficult for an untrained musician to determine the time signature of a composition. It is even more difficult for a computer. You will be given a String duration containing the description of a composition. Each character of duration corresponds to a single note in the composition. 'W' denotes a whole note, 'H' a half note, 'Q' a quarter note, 'E' an eighth note, and 'S' a sixteenth note.

Determine the time signature of the composition using the following heuristic algorithm (which is not very good, but quite simple):

Consider all the available time signatures (3/8, 2/4, 3/4 and 4/4). Keep only the time signatures for which the composition would contain an integral number of measures, and discard the rest.
For each of the remaining time signatures, determine the number of notes in the composition that start and end in different measures. Keep only the time signatures for which this number is minimal.
Select the smallest of the remaining time signatures (where 3/8 < 2/4 < 3/4 < 4/4).

Return the time signature as a String ("3/8", "2/4", "3/4", or "4/4"), or return "?/?" (quotes for clarity only) if there are no time signatures left after step 1.

Definition

Class:	CompositionTimeSignature
Method:	getTimeSignature
Parameters:	String
Returns:	String
Method signature:	String getTimeSignature(String duration)
(be sure your method is public)

Constraints

- duration will have between 1 and 50 characters, inclusive.

- Each character in duration will be 'W', 'H', 'Q', 'E' or 'S'.

Examples

0)

"QQEEQEEEQEQ"

Returns: "4/4"

The total duration of the composition (in whole notes) is:

1/4+1/4+1/8+1/8+1/4+1/8+1/8+1/8+1/4+1/8+1/4 = 2.

The number of measures in the composition for different time signatures is:

for time signature 3/8: 2/(3/8) = 5 1/3 measures;
for time signature 2/4: 2/(2/4) = 4 measures;
for time signature 3/4: 2/(3/4) = 2 2/3 measures;
for time signature 4/4: 2/(4/4) = 2 measures.

So only time signatures 2/4 and 4/4 will be left after the first step of the algorithm. For time signature 2/4 the composition looks like this ('|' characters denote measure dividers, and 'Q' and 'E' characters show when each note starts):"

 Q   Q    E E Q    E E E Q    E Q   
|        |        |        |        |
|        |        |        |        |
|        |        |        |        |

For time signature 4/4 the composition looks like this:

 Q   Q   E E Q    E E E Q   E Q   
|                |                |
|                |                |
|                |                |

So the number of notes that start and end in different measures is 1 for time signature 2/4 and 0 for time signature 4/4. Therefore only time signature 4/4 is left after the second step of the algorithm.

1)

"S"

Returns: "?/?"

The composition is very short and will occupy less than one measure for any time signature.

2)

"EEEEEEEEEEEEEEEEEEEEEEEE"

Returns: "3/8"

The first two steps of the algorithm will not throw away any time signatures. So the smallest possible time signature 3/8 will be chosen on the third step.

3)

"QQQQQQQQQQQQ"

Returns: "2/4"

Here 3/8 and 3/4 will be thrown away after the second step of the algorithm and the smallest time signature among 2/4 and 4/4 will be chosen on the third step.

4)

"EQHQQWEEHSEEQWQEHHEEQSQEQHESQSWQESQEWWSSHQWQHQWSQW"

Returns: "3/4"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WinningTrick

Simple Math, Simple Search, Iteration

Used in:

TCHS SRM 4

Used as:

Division I Level One

Writer:

ivan_metelsky

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6421

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10023&pm=6421

Problem Statement

You will be running a race on a straight track, and you have devised the following trick to help you win. The weather forecast for the day of the race indicates that there will be a strong wind blowing directly from the finish line to the starting line. You ask the judges to allow you to run the race backward from the finish line to the starting line, and since they are unaware of your motives, they allow you to do so.

All participants, including you, will run at a constant speed for the duration of the race. Your competitors' speeds are given in the int[] speed, each element of which represents the speed of a competitor in meters per second. Your own speed in meters per second is given in the int yourSpeed.

The wind will blow at a constant speed of W meters per second. It will therefore increase your speed by W meters per second while decreasing the speed of each of your competitors by W meters per second. Return the minimum value of W that will allow you to win the race. Return 0.0 if you can win without the help of any wind. You will win the race even if you tie for first place.

Definition

Class:	WinningTrick
Method:	minimumSpeed
Parameters:	int[], int
Returns:	double
Method signature:	double minimumSpeed(int[] speed, int yourSpeed)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

speed will contain between 1 and 50 elements, inclusive.

-

Each element of speed will be between 1 and 10, inclusive.

-

yourSpeed will be between 1 and 10, inclusive.

Examples

0)

{4, 3, 2, 1}

Returns: 0.0

Here you are the fastest runner, so you don't need any wind to win the race.

1)

{3, 3}

Returns: 0.0

If there is no wind, then all the runners will tie for first place. As stated in the problem statement, you will win the race in this situation.

2)

{2, 3, 4, 5}

Returns: 2.0

If the wind's speed is 2.0 m/s, then your speed will be 3.0 m/s and speeds of your opponents will be 0.0 m/s, 1.0 m/s, 2.0 m/s, and 3.0 m/s. That is enough for you to tie for first place. Lower wind speeds will not allow you to win the race.

3)

{9}

Returns: 4.0

4)

{1, 1, 2, 2, 5, 2}

Returns: 1.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Conditional

Dynamic Programming, Math

Used in:

SRM 304

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , vorthys , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6412

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9825&pm=6412

Problem Statement

Conditional probability can be illustrated with dice problems. What is the probability that you rolled a 12 on a pair of normal 6-sided dice, given that at least one of the dice shows a 6? This is the same question as the following: roll a pair of dice until at least one of the dice shows 6 -- what is the probability that your final roll has 6 on BOTH dice. The surprising answer is 1/11 since of the 36 equally likely rolls, 11 have at least one 6 and 1 of these 11 has 6 on both dice.

Our goal is to solve a generalized version of this problem in which we roll nDice identical dice, each with sides labelled 1,2,...,maxSide. We want to know the probability that the sum of the dice is greater than or equal to theSum given that at least one of the dice shows the value v. Create a class Conditional that contains a method probability that is given nDice,maxSide, v, and theSum and that returns the desired conditional probability.

Definition

Class:	Conditional
Method:	probability
Parameters:	int, int, int, int
Returns:	double
Method signature:	double probability(int nDice, int maxSide, int v, int theSum)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

nDice and maxSide will be between 1 and 50, inclusive.

-

v will be between 1 and maxSide, inclusive.

-

theSum will be between 1 and maxSide*nDice, inclusive.

Examples

0)

Returns: 0.09090909090909091

This is the example above whose answer is 1/11. (Of course, the sum cannot be greater than 12.)

1)

Returns: 1.0

Given that at least one of the dice shows a 6 the sum of the 2 dice must be at least 7.

2)

Returns: 1.0

3)

Returns: 0.6

Two 3-sided (!) dice with at least one 2 showing: 12 22 32 21 23 are the 5 possible equally likely results, and 3 of the 5 have a sum greater than or equal to 4.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PowerCollector

Advanced Math, Recursion

Used in:

SRM 305

Used as:

Division I Level Three

Writer:

vorthys

Testers:

PabloGilberto , Olexiy , lovro , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6408

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9826&pm=6408

Problem Statement

Your friends collect butterflies and stamps, but you collect numbers. Your collection of prime numbers is the finest in three counties, and your collection of transcendental numbers has been featured on national talkshows. Lately you've decided to start collecting powers, that is, numbers that can be written in the form M^K, where M and K are positive integers with K > 1. However, you're wondering how big a box you'll need to hold them all. Given a number N, represented as a String, determine how many powers lie between 1 and N, inclusive. Return the number of powers as a String with no leading zeros.

Definition

Class:	PowerCollector
Method:	countPowers
Parameters:	String
Returns:	String
Method signature:	String countPowers(String N)
(be sure your method is public)

Constraints

-

N will contain between 1 and 19 characters, inclusive.

-

Each character in N will be a digit ('0'-'9').

-

The first character in N will not be zero ('0').

-

N will represent a number between 1 and 1000000000000000000 (10¹⁸), inclusive.

Examples

0)

"10"

Returns: "4"

The powers between 1 and 10 are 1, 4, 8, and 9.

1)

"36"

Returns: "9"

The powers between 1 and 36 are 1, 4, 8, 9, 16, 25, 27, 32, and 36.

2)

"1000000000000000000"

Returns: "1001003332"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LightSwitches

Greedy, Math

Used in:

SRM 306

Used as:

Division I Level Two

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Olexiy , lovro , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6407

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9986&pm=6407

Problem Statement

In a ballroom, there are some light bulbs and some switches that control those bulbs. However, the switches and the bulbs are not related in a logical way. Each switch is connected to a subset of the bulbs, and when a switch is flipped, all the bulbs connected to that switch change state (the ones that were off are turned on, and the ones that were on are turned off). Bulbs that are not connected to the flipped switch remain as they were.

The states of all the bulbs in the room can be described as a configuration of lights. If there are N bulbs, there are 2^N possible configurations. Two configurations are distinct if a bulb in one configuration has a different state than that same bulb in the other configuration.

You will be given the connections between the switches and bulbs as a String[] switches. The jth character of the ith element of switches is 'Y' if the ith switch is connected to the jth bulb, and 'N' otherwise. All the bulbs are initially off. Return the number of distinct configurations of lights that can be achieved using this setup.

Definition

Class:	LightSwitches
Method:	countPossibleConfigurations
Parameters:	String[]
Returns:	long
Method signature:	long countPossibleConfigurations(String[] switches)
(be sure your method is public)

Constraints

- switches will have between 1 and 50 elements, inclusive.

- Each element of switches will have exactly N characters, where N is between 1 and 50, inclusive.

- Each character of each element of switches will be 'Y' or 'N'.

Examples

0)

{"YYN",
 "NNY",
 "YYY",
 "NNN"}

Returns: 4

In this example, there are three bulbs and four switches. The first switch is connected to the first two lights, the second switch is connected to the third light, the third switch is connected to all three lights, and the fourth switch is connected to nothing.

The possible configurations are (- for OFF and + for ON):

- - - The initial configuration.

+ + - This can be achieved by flipping the first switch.

- - + This can be achieved by flipping the second switch.

+ + + This can be achieved by flipping the first switch and then the second switch.

1)

{"NNNNYYYNYYNYYYYYNYY"}

Returns: 2

There are only two possible configurations here - the initial configuration where all the bulbs are off, and the configuration that results from flipping the switch once.

2)

{"NYNYNYN",
 "YNYNYNY",
 "YYNNNYN",
 "NNNYNYN",
 "YYYYYNN",
 "YNNNNYN"}

Returns: 32

3)

{"YNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNNN",
 "NNNNNNNNNNNNNNNNNNNNNNNNNNNNNYNNNNNNNNNNNNNNNNNNNN"}

Returns: 1073741824

Each of the first 30 bulbs can be turned on and off individually while the remaining 20 bulbs are impossible to turn on. Any combination of states among the first 30 bulbs is possible, so the number of configurations is 2³⁰.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SeatingPlan

Dynamic Programming, Math

Used in:

SRM 320

Used as:

Division I Level Three

Writer:

lyc1977

Testers:

PabloGilberto , brett1479 , Olexiy , Mike Mirzayanov

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6400

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10000&pm=6400

Problem Statement

Right before the day of the final exam, a teacher is busy coming up with a seating assignment for the venue. The seats in the exam venue are arranged as m rows, each containing n seats, i.e., an m by n grid. The total number of students is exactly the same as the total number of seats, so all the seats will be occupied.

The teacher's task is complicated by the fact that there are k students who are suspected cheaters. In order to prevent cheating, the teacher will not allow any two suspected cheaters to sit in adjacent seats. Two seats are adjacent if and only if they are in adjacent columns of the same row, or adjacent rows of the same column.

The teacher's method for assigning the seats is simple. She finds a random seating assignment. Then, she checks if there are any suspected cheaters assigned to adjacent seats. If so, she repeats the process by finding another random assignment, and otherwise, she is done.

Your job is to determine the expected number of random seating assignments the teacher must generate before she finishes her task. Return this expected number as a String formatted "p/q" (quotes for clarity only), where p and q are relatively prime positive integers with no leading zeros. If there is no valid seating assignment, return "Impossible!" (quotes for clarity only).

Definition

Class:	SeatingPlan
Method:	expectedTrial
Parameters:	int, int, int
Returns:	String
Method signature:	String expectedTrial(int m, int n, int k)
(be sure your method is public)

Constraints

-

m will be between 1 and 80, inclusive.

-

n will be between 1 and 80, inclusive.

-

m*n will be less than or equal to 80.

-

k will be between 0 and 20, inclusive, and less than or equal to m*n.

Examples

0)

Returns: "Impossible!"

1)

Returns: "1/1"

Since there is no cheater, the teacher can finish the task with the first trial.

2)

Returns: "15/8"

Let S represent a suspected cheater, and N a non-cheater.

All possible acceptable seating plans:

SNS   SNN   SNN   NSN   NSN   NNS   NNS   NNN
NNN   NSN   NNS   SNN   NNS   SNN   NSN   SNS

And all possible unacceptable seating plans:

SSN   NSS   NNN   NNN   SNN   NSN   NNS
NNN   NNN   SSN   NSS   SNN   NSN   NNS

3)

Returns: "3/2"

4)

Returns: "70775996591300/172086661"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ExtraordinarilyLarge

Simple Math

Used in:

SRM 320

Used as:

Division I Level One , Division II Level Two

Writer:

lyc1977

Testers:

PabloGilberto , brett1479 , Olexiy , Mike Mirzayanov

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6398

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10000&pm=6398

Problem Statement

You need to handle two extraordinarily large integers. The good news is that you don't need to perform any arithmetic operation on them. You just need to compare them and see whether they are equal or one is greater than the other.

Given two Strings x and y, return either "x<y", "x>y" or "x=y" depending on the values represented by x and y. x and y each consist of a decimal integer followed zero or more '!' characters. Each '!' represents the factorial operation. For example, "3!!" represents 3!! = 6! = 720.

Definition

Class:	ExtraordinarilyLarge
Method:	compare
Parameters:	String, String
Returns:	String
Method signature:	String compare(String x, String y)
(be sure your method is public)

Notes

-

In case you don't know about factorials, here is a quick definition: 0! is defined as 1. For any positive integer n, n! is defined as n * [(n-1)!]. For example, 5! = 5 * 4 * 3 * 2 * 1 * 0! = 120.

Constraints

-

x and y will each contain between 1 and 50 characters, inclusive.

-

x and y will each consist of a non-negative integer less than 10⁹, with no extra leading zeros, followed by zero or more '!' characters.

Examples

0)

"0!"

"1"

Returns: "x=y"

1)

"9!"

"999999999"

Returns: "x<y"

2)

"9!!"

"999999999"

Returns: "x>y"

3)

"456!!!"

"123!!!!!!"

Returns: "x<y"

4)

"5!"

"120"

Returns: "x=y"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CityBuses

Brute Force, Simple Math, Simple Search, Iteration

Used in:

TCHS SRM 11

Used as:

Division I Level One

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6388

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10063&pm=6388

Problem Statement

You are given a String[] blocks representing the layout of a city. Each character of each element of blocks represents one city block. A 'B' character represents a bus stop, and a '-' represents all other spaces.

The fare for traveling on the bus is equal to the manhattan distance (difference in X-coordinates plus difference in Y-coordinates, see the first example for clarification) between the starting and ending bus stops. Return the largest possible fare for a trip from one bus stop to another.

Definition

Class:	CityBuses
Method:	maximumFare
Parameters:	String[]
Returns:	int
Method signature:	int maximumFare(String[] blocks)
(be sure your method is public)

Constraints

-

blocks will contain between 1 and 50 elements, inclusive.

-

Each element of blocks will contain between 1 and 50 characters, inclusive.

-

Each element of blocks will contain the same number of characters.

-

Each character of each element of blocks will be 'B' or '-'.

-

There will be at least two bus stops.

Examples

0)

{"B--",
 "B--",
 "--B"}

Returns: 4

Starting from the top-left, the coordinates of the bus stops are (0,0), (1,0), and (2,2). The distance is the difference in X-coordinates plus the difference in y-coordinates. So, the distance between each pair of bus stops is as follows:

(0,0) - (1,0) : 1 + 0 = 1
(1,0) - (2,2) : 1 + 2 = 3
(0,0) - (2,2) : 2 + 2 = 4

The largest distance (thus the highest fare) is 4.

1)

{"--B",
 "---",
 "-B-"}

Returns: 3

There's only one route we can take, and it has a distance of 3.

2)

{"--B-",
 "B---",
 "-B-B",
 "B---"}

Returns: 5

The largest distance here is from (0,2) to (3,0).

3)

{"BB"}

Returns: 1

A short, and unexciting bus ride.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TourCounting

Advanced Math, Dynamic Programming, Graph Theory, Recursion

Used in:

SRM 306

Used as:

Division I Level Three

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , Olexiy , lovro , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6386

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9986&pm=6386

Problem Statement

You are given a directed graph g, and you must determine the number of distinct cycles in g that have length less than k. Since this number can be really big, return the answer modulo m. A cycle is a non-empty sequence of nodes (not necessarily distinct) in which there is an edge from each node to the next node, and an edge from the last node in the sequence to the first node. Two cycles are distinct if their sequences are not identical. See example 0 for further clarification.

g will be given as a String[] where the jth character of the ith element indicates whether there is an edge from node i to node j ('Y' means there is one, and 'N' means there is not).

Definition

Class:	TourCounting
Method:	countTours
Parameters:	String[], int, int
Returns:	int
Method signature:	int countTours(String[] g, int k, int m)
(be sure your method is public)

Notes

-

The answer modulo m means that you must return the remainder of dividing the result by m.

Constraints

-

g will have between 1 and 35 elements, inclusive.

-

Each element of g will have exactly N characters, where N is the number of elements in g.

-

Each character of each element of g will be 'Y' or 'N'.

-

The ith character of the ith element of g will be 'N'.

-

k will be between 1 and 1000000 (10⁶), inclusive.

-

m will be between 1 and 1000000000 (10⁹), inclusive.

Examples

0)

{"NYNY",
 "NNYN",
 "YNNN",
 "YNNN"}

Returns: 12

The possible cycles with length less than 6 are:

(0,3) ; (3,0) ; (0,1,2) ; (1,2,0) ; (2,0,1)

(0,3,0,3) ; (3,0,3,0) ; (0,1,2,0,3) ; (0,3,0,1,2)

(1,2,0,3,0) ; (2,0,3,0,1) ; (3,0,1,2,0)

Note that (0,3), (3,0) and (0,3,0,3) are all considered different.

1)

{"NYNNNNN",
 "NNYNNNN",
 "NNNYNNN",
 "NNNNYNN",
 "NNNNNYN",
 "NNNNNNY",
 "YNNNNNN"}

Returns: 9

All cycles have lengths that are multiples of 7. For each starting node and each multiple of 7 there exists one cycle. There are 5 non-zero multiples of 7 that are less than 40 (7,14,21,28,35) and 7 possible starting nodes. Therefore, the total number of cycles is 5x7=35. 35 modulo 13 is 9.

2)

{"NYNY",
 "NNNN",
 "YYNY",
 "NYNN"}

1000000000

Returns: 0

The graph does not have cycles.

3)

{"NY",
 "YN"}

Returns: 0

Any number modulo 1 is zero.

4)

{"NYYNYYN",
 "YNYNYNY",
 "NYNYNYN",
 "YYYNYNY",
 "NNYYNNY",
 "NYYYNNY",
 "YYYYYYN"}

Returns: 72

5)

{"NYYY",
 "YNYY",
 "YYNY",
 "YNYN"}

Returns: 3564

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FountainOfLife

Math, Simulation

Used in:

TCHS SRM 2

Used as:

Division I Level One

Writer:

ivankovic

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6252

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10024&pm=6252

Problem Statement

A Fountain of Life is a special fountain that produces the elixir of life at a constant speed of elixir liters per second. A dark mage managed to cast a Curse of Death on the Fountain so in addition to the elixir it now produces a deadly poison at a constant speed of poison liters per second. Both the poison and elixir are collected in an infinitely large pool around the Fountain and form a mixture. The mixture will become deadly once the percentage of poison in the mixture is at least 50%. Your task is to calculate the time at which the mixture will become deadly. At the beginning (0-th second) the pool contains pool liters of 100% elixir.

Your program must return a double, the time in seconds at which the mixture becomes deadly. If the mixture never becomes deadly, return -1.0.

Definition

Class:	FountainOfLife
Method:	elixirOfDeath
Parameters:	int, int, int
Returns:	double
Method signature:	double elixirOfDeath(int elixir, int poison, int pool)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

elixir will be between 1 and 10000, inclusive.

-

poison will be between 1 and 10000, inclusive.

-

pool will be between 1 and 10000, inclusive.

Examples

0)

Returns: 2.0

At t = 0s there are 2 liters of 100% elixir.

At t = 1s there are 3 liters of elixir and 2 liters of poison for a total volume of 5 liters. 2 liters of poison is 40% of 5 liters so the mixture is still not deadly.

At t = 2s there are 4 liters of elixir and 4 liters of poison for a total volume of 8 liters. 4 liters of poison is exactly 50% of the mixture so it is now deadly.

1)

Returns: -1.0

With 200 liters of elixir per second and only 100 liters of poison per second, the mixture never becomes deadly.

2)

Returns: 10000.0

It might take a long time for the mixture to become deadly.

3)

Returns: 1.0001000100010001E-4

On the other hand, it might take a short time for the mixture to become deadly.

4)

Returns: 13.666666666666666

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ModelRailroad

Math

Used in:

TCO06 Semi 3

Used as:

Division I Level Two

Writer:

radeye

Testers:

PabloGilberto , lbackstrom , vorthys , Olexiy , Jan_Kuipers

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6244

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9982&pm=6244

Problem Statement

Your nephew was given a model railroad set as a gift. This railroad set contains pieces of track that can be combined to form a closed loop. There are two types of track: curved pieces, each of which is a 60 degree arc of a circle, and straight pieces. The radius of the arc is three feet, and each straight piece is two feet long.

You have six curved pieces, just enough to make a complete circle, and a given number of straight pieces. Your nephew wants to know how many different track layouts he can construct. Two layouts are considered equivalent if one can be rotated (but not flipped) to be equivalent to the other. Each layout must be a closed loop, with the pieces connected end-to-end. The pieces will only connect in a smooth curve; you cannot connect two pieces at an angle. All possible layouts for five or fewer straight pieces are shown in the figure below:

Definition

Class:	ModelRailroad
Method:	countTracks
Parameters:	int
Returns:	long
Method signature:	long countTracks(int straight)
(be sure your method is public)

Constraints

-

straight will be between 0 and 1000, inclusive.

Examples

0)

Returns: 1

The only possibility here is a perfect circle.

1)

Returns: 1

There is no way to use only one straight track and form a closed loop, so the extra piece is useless.

2)

Returns: 3

We can either use two straights on opposite sides to make a conventional oval track, or we can use three straights to make a rounded equilateral triangle, or we can make a perfect circle.

3)

Returns: 6

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StoneGameStrategist

Math

Used in:

SRM 309

Used as:

Division I Level Three

Writer:

_efer_

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6239

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9989&pm=6239

Problem Statement

You and a friend are playing a game in which you take turns removing stones from piles. Initially, every pile has at least as many stones as the pile to its left. This property must be maintained throughout the game. On each turn, you remove one or more stones from a single pile. You and your friend alternate turns until it is no longer possible to make a valid move. The last player to have made a move wins the game. Note that if you remove all the stones from a pile, it is still considered a pile.

You are said to have made a "winning move" if after making that move, you can eventually win no matter what your friend does. You are given a int[] piles representing the number of stones in each pile from left to right. It is your turn to move. Find a winning move and return it as a String formatted as "TAKE s STONES FROM PILE k" (quotes for clarity only), where s and k (a 0-based index) are each integers with no leading zeros. If there are multiple winning moves, choose the one that minimizes s. If there is still a tie, choose the one that minimizes k. If no winning move is possible, return the String "YOU LOSE" (quotes for clarity only).

Definition

Class:	StoneGameStrategist
Method:	play
Parameters:	int[]
Returns:	String
Method signature:	String play(int[] piles)
(be sure your method is public)

Constraints

-

piles will contain between 1 and 50 elements, inclusive.

-

Each element of piles will be between 1 and 1000, inclusive.

-

piles will be sorted in non-descending order.

Examples

0)

{6,6}

Returns: "YOU LOSE"

You can't win this game. Your friend will force you to take stones from the first pile at each turn, and then mirror your move by taking the same number of stones from the second pile.

1)

{6,12}

Returns: "TAKE 6 STONES FROM PILE 1"

If you take 6 stones from the second pile, you can follow the strategy outlined above.

2)

{3,6,6}

Returns: "TAKE 3 STONES FROM PILE 0"

3)

{3,5,9,11,16}

Returns: "TAKE 2 STONES FROM PILE 0"

4)

{32,136,251,369,403,593,624,657,729,731,769}

Returns: "YOU LOSE"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SingleElimination

Math

Used in:

TCCC06 Wildcard

Used as:

Division I Level Two

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479 , Yarin , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6238

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10135&pm=6238

Problem Statement

A single elimination tournament begins with teams numbered 1 through N, where N is a power of 2. In the first round, teams 1 and 2 compete against each other, teams 3 and 4 compete against each other, and so on up to teams N-1 and N. The N/2 losing teams are eliminated, and the N/2 winning teams advance to the second round.

In the second round, the winner of teams 1 and 2 compete against the winner of teams 3 and 4. The winner of teams 5 and 6 compete against the winner of teams 7 and 8. The winner of teams N-3 and N-2 compete against the winner of teams N-1 and N.

The tournament continues in this fashion, with half the remaining teams eliminated in each round, until there is only one team left. This team is the winner of the tournament. Obviously, the numeration of the teams is very important for determining the winner. You want your favorite team to win the tournament, so you want to find the order which gives your team the best chances to become the winner.

You will be given a String[] chances that contains exactly N elements, each containing exactly N space-separated probabilities. The j-th number in the i-th element of chances represents the probability (in percents) that team i will win a game against team j. The 1-based index of your favorite team in chances is team. You are to order the teams in such a way that your team will have the highest probability to win the tourney and return this probability as a double. See examples for further clarification.

Definition

Class:	SingleElimination
Method:	bestChance
Parameters:	String[], int
Returns:	double
Method signature:	double bestChance(String[] chances, int team)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

The number of elements in chances will be a power of 2 between 1 and 16, inclusive.

-

Each element of chances will be a single-space-separated list of integers, with no additional whitespace and no leading zeros.

-

Each element of chances will contain a number of integers equal to the number of elements in chances.

-

Each integer in chances will be between 0 and 100, inclusive.

-

The i-th integer in the j-th element of chances and the j-th integer in the i-th element of chances will sum to 100, if i != j.

-

The i-th integer if the i-th element of chances will be 0.

-

team will be between 1 and the number of elements in chances, inclusive.

Examples

0)

{"0 90 0 100", "10 0 50 100", "100 50 0 100", "0 0 0 0"}

Returns: 0.45

It's optimal for team 1 to play against team 4 in the first round. Team 1 always beats team 4, and to have any chances to win the tourney, needs team 2 to beat team 3 (with a 50%). Team 1 would then have a 90% chance of beating team 2 in the final game. Therefore, the correct answer is 0.5 * 0.9 = 0.45.

1)

{"0 90 0 100", "10 0 50 100", "100 50 0 100", "0 0 0 0"}

Returns: 0.9500000000000001

The third team has much better chances.

2)

{ "0" }

Returns: 1.0

3)

{ "0 50 50 50 50 50 50 50",
  "50 0 50 50 50 50 50 50",
  "50 50 0 50 50 50 50 50",
  "50 50 50 0 50 50 50 50",
  "50 50 50 50 0 50 50 50",
  "50 50 50 50 50 0 50 50",
  "50 50 50 50 50 50 0 50",
  "50 50 50 50 50 50 50 0" }

Returns: 0.125

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CyclicGame

Brute Force, Math

Used in:

SRM 318

Used as:

Division I Level Two

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6216

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9998&pm=6216

Problem Statement

You are playing a one-player game where several cells are arranged around a circle, and each cell contains a value. You have a bank that is initially empty, and you start on the 0-th cell. On each turn, you throw a typical six-sided die (each side has a distinct number between 1 and 6), and you move clockwise the number of cells indicated on the die. The value in the cell that you land on will be added to the bank. The goal is maximize the value of the bank.

Unfortunately, the sum of all the values on the cells is negative, so the expected value of the bank after a long game is also negative. Therefore, you should stop the game at the proper time.

You will be given a int[] cells that contains the values of the cells in clockwise order. The 0-th element of cells is the value of the 0-th cell. Return the expected value of the bank if you play optimally. See examples for further clarification.

Definition

Class:	CyclicGame
Method:	estimateBank
Parameters:	int[]
Returns:	double
Method signature:	double estimateBank(int[] cells)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

cells will contain between 2 and 15 elements, inclusive.

-

Each element of cells will be between -100 and 100, inclusive.

-

The sum of all elements in cells will be negative.

Examples

0)

{-10, 1, 1, 1, 1, 1, 1, 1, 1}

Returns: 1.3611111111111112

You are guaranteed get 1 point on the first turn. When you're on cell 1 or 2 (0-indexed), you can safely take another turn to get one more point, but if you're on cells 3 through 8, your best option is to stop the game.

The expected result for the bank value is 1 + 1/6*(1 + 1/6*1) + 1/6 = 1.36.

1)

{-10, 7, -5, 7}

Returns: 0.30434782608695654

You should stop the game if you're on cell 2 or 3.

2)

{-1, -2, 2}

Returns: 0.0

The expected result of any move is 1/3*(-1)+1/3*(-2)+1/3*2 = -1/3, so the best choice is not play at all.

3)

{-40, 9, 9, 9, 9, 9, -44, 9, 9, 9, 9, 9, -40, 15, 15}

Returns: 3.5653612433724144

You should stop the game if you're on cells 9 through 11 (where two cells with value -40 are reachable in one turn).

4)

{-36, 95, -77, -95, 49, -52, 42, -34, -1, 98, -20, 96, -96, 23, -52}

Returns: 12.395613307567126

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MislabeledWeights

Brute Force, Dynamic Programming, Greedy, Math, Simple Search, Iteration

Used in:

TC China 08 - 1A

Used as:

Division I Level Three

Writer:

dplass

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6208

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13673&pm=6208

Problem Statement

You are given a balance scale to weigh some items. Unfortunately the weights you use as counterbalances are not accurate. Some of them may be marked incorrectly - either 1 gram too heavy or one gram too light. (Some may be marked correctly.)

You are given a int[] weights representing the set of weights you have. The i-th of your weights is marked by weights[i] grams. The subset of your weights is called good if it's possible that all the real weights in it sum exactly to testWeight. Find the good subset with the minimum possible number of weights and return the number of weights in it. If there is no good subset of weights, your method should return -1.

Definition

Class:	MislabeledWeights
Method:	fewest
Parameters:	int[], int
Returns:	int
Method signature:	int fewest(int[] weights, int testWeight)
(be sure your method is public)

Notes

-

A weight labeled '1 gram' (represented as the integer 1 in the int[] of weights) can only be 1 or 2 grams. All other weights can be plus or minus 1 gram of their actual labeled weight.

-

There may be duplicates in the weights but you may only use each element at most once.

Constraints

-

weights will contain between 1 and 10 elements, inclusive.

-

Each element of weights will be between 1 and 1000, inclusive.

-

testWeight will be between 1 and 10000, inclusive.

Examples

0)

{1,1,1}

Returns: 3

The subset of all weights is the only good one. If all the real weights are 2 grams, then they sum up to 6 grams.

1)

{1,1,1}

Returns: -1

Even if each weight was actually 2 grams, there would still be no way for them to sum to 7 grams.

2)

{1,2,3,4,5}

Returns: 2

There are many good subsets. For example, {1, 5} (1 + 6 = 7 or 2 + 5 = 7), or {3, 4} (3 + 4 = 7 or 4 + 3 = 7), or {3, 5} (3 + 4 = 7 or 2 + 5 = 7), or other variants. In any case, the fewest number of weights in a good subset is 2.

3)

{1,2,3,4,5,6,7,8,9,10}

Returns: 6

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RugSizes

Brute Force, Simple Math

Used in:

SRM 304

Used as:

Division II Level One

Writer:

dgoodman

Testers:

PabloGilberto , vorthys , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6195

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9825&pm=6195

Problem Statement

Rugs come in various sizes. In fact, we can find a rug with any integer width and length, except that no rugs have a distinct width and length that are both even integers. For example, we can find a 4x4 rug, but not a 2x4 rug. We want to know how many different choices we have for a given area.

Create a class RugSizes the contains a method rugCount that is given the desired area and returns the number of different ways in which we can choose a rug size that will cover that exact area. Do not count the same size twice -- a 6 x 9 rug and a 9 x 6 rug should be counted as one choice.

Definition

Class:	RugSizes
Method:	rugCount
Parameters:	int
Returns:	int
Method signature:	int rugCount(int area)
(be sure your method is public)

Constraints

-

area will be between 1 and 100,000, inclusive.

Examples

0)

Returns: 2

The choices are 1 x 4 (or equivalently 4 x 1) and 2 x 2.

1)

Returns: 1

Only 1 x 8 is available. Note that 2 x 4 has the desired area, but is not available since its width and length differ and are both even numbers.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DivisorInc

Graph Theory, Math

Used in:

SRM 302

Used as:

Division I Level One , Division II Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , legakis , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6186

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9823&pm=6186

Problem Statement

There is an integer K. You are allowed to add to K any of its divisors not equal to 1 and K. The same operation can be applied to the resulting number and so on. Notice that starting from the number 4, we can reach any composite number by applying several such operations. For example, the number 24 can be reached starting from 4 using 5 operations: 4->6->8->12->18->24.

You will solve a more general problem. Given ints N and M, return the minimal number of the described operations necessary to transform N into M. Return -1 if M can't be obtained from N.

Definition

Class:	DivisorInc
Method:	countOperations
Parameters:	int, int
Returns:	int
Method signature:	int countOperations(int N, int M)
(be sure your method is public)

Constraints

-

N will be between 4 and 100000, inclusive.

-

M will be between N and 100000, inclusive.

Examples

0)

Returns: 5

The example from the problem statement.

1)

Returns: 14

The shortest order of operations is: 4->6->8->12->18->27->36->54->81->108->162->243->324->432->576.

2)

Returns: 10

The shortest order of operations is: 8748->13122->19683->26244->39366->59049->78732->83106->83448->83460->83462.

3)

Returns: 21

4)

Returns: -1

The number 99991 can't be obtained because it is prime.

5)

Returns: 0

We don't need any operations. N and M are already equal.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IntegerPalindrome

Math

Used in:

SRM 302

Used as:

Division I Level Two

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , legakis , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6184

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9823&pm=6184

Problem Statement

A positive integer is called a palindrome if it reads the same forward and backward. Integers containing leading zeros are not valid. For example, 12321 is a palindrome, but 123210 is not. You are given an int K. Return the K-th palindrome, where the 0th palindrome is 1, the 1st palindrome is 2, etc.

Definition

Class:	IntegerPalindrome
Method:	findByIndex
Parameters:	int
Returns:	long
Method signature:	long findByIndex(int K)
(be sure your method is public)

Constraints

-

K will be between 0 and 1000000000 (10⁹), inclusive

Examples

0)

Returns: 9

1)

Returns: 11

2)

Returns: 111

3)

Returns: 13731

4)

Returns: 137484731

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DynamiteBoxes

Dynamic Programming, Math

Used in:

SRM 297

Used as:

Division I Level Three

Writer:

igorsk

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6168

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9818&pm=6168

Problem Statement

Consider a 2 x 2 x height stack of cube-shaped boxes of identical size. The stack has height levels of boxes, each level containing 4 boxes arranged in a 2 x 2 pattern. Each box has a 50% probability of containing dynamite and a 50% probability of being empty. Two dynamite-filled boxes, A and B, are in the same dynamite cluster if:

a face of A touches a face of B
OR a face of A touches a face of some box C, and C is in the same dynamite cluster as B.

A stack is dangerous if it contains a dynamite cluster that contains at least dangerousClusterSize boxes. Given height and dangerousClusterSize, compute the probability that the stack is dangerous.

Definition

Class:	DynamiteBoxes
Method:	getProbability
Parameters:	int, int
Returns:	double
Method signature:	double getProbability(int height, int dangerousClusterSize)
(be sure your method is public)

Notes

-

Your answer must be within 1E-9 absolute or relative error.

Constraints

-

height will be between 1 and 30, inclusive.

-

dangerousClusterSize will be between 1 and 121, inclusive.

Examples

0)

Returns: 0.9375

Here, any stack that contains a dynamite-filled box is dangerous. There are 16 possible 2 x 2 x 1 stacks, each occurring with the same probability. Only one of the possible stacks is not dangerous - the stack with no dynamite-filled boxes. So, the answer is 15/16 = 0.9375.

1)

Returns: 0.5625

In this example, stacks that contain dynamite-filled boxes that don't touch any other dynamite-filled boxes are not dangerous. There are 7 such stacks: 1 with no dynamite-filled boxes, 4 with a single dynamite-filled box, and 2 with two dynamite-filled boxes each placed diagonally so that they don't touch each other. The answer then is 1 - 7/16 = 0.5625.

2)

Returns: 0.51171875

3)

Returns: 0.859130859375

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MixedUpPrimes

Dynamic Programming, Math, Recursion, String Parsing

Used in:

TCCC06 Qual 3

Used as:

Division I Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6163

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10095&pm=6163

Problem Statement

Using the operators '+', '-', '/', '*', and parentheses as many times as you wish, find expressions for the smallest and largest primes that use each element of values exactly once. A prime is an integer greater than 1 with no divisors except 1 and itself. Return a int[] with exactly two elements, where the first element is the smallest prime you can make, and the second is the largest. If no primes can be constructed, return an empty int[].

Definition

Class:	MixedUpPrimes
Method:	findPrimes
Parameters:	int[]
Returns:	int[]
Method signature:	int[] findPrimes(int[] values)
(be sure your method is public)

Notes

-

The division operator truncates its results. For example, 8/5 = 1.

-

The given numbers cannot be concatenated. For example, 8 and 5 cannot be combined to form 85.

Constraints

-

values will contain between 1 and 6 elements, inclusive.

-

Each element of values will be between 1 and 30, inclusive.

Examples

0)

{1,2}

Returns: {2, 3 }

We get 2 using 2*1. We get 3 using 2+1.

1)

{1,2,3}

Returns: {2, 7 }

Here we use 3-2+1=2 and 3*2+1 = 7.

2)

{1,2,3,4,5,6}

Returns: {2, 719 }

3)

{2,3,5,7,11,13}

Returns: {2, 15017 }

4)

{2,2,2,2,2,2}

Returns: {2, 17 }

5)

{8}

Returns: { }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FibonacciPositioning

Search, Simple Math, Sorting

Used in:

SRM 298

Used as:

Division I Level One , Division II Level Two

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6160

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9819&pm=6160

Problem Statement

The fibonacci sequence is a sequence of integers in which each number is equal to the sum of the two preceding numbers. The first two integers in the sequence are both 1. Formally:

F₁ = 1
F₂ = 1
F_i = F_i-1 + F_i-2 for each i > 2

The beginning of this sequence is 1,1,2,3,5,8,13,21.

We'll define the fibonacci position of an integer greater than or equal to 1 as follows:

The fibonacci position of 1 is 2 (since F₂ = 1)
The fibonacci position of any integer n > 1 such that F_i = n is i
The fibonacci position of any integer n > 1 such that it is strictly between F_i and F_i+1 is i+(n-F_i)/(F_i+1-F_i) (informally, this means it is linearly distributed between F_i and F_i+1)

As examples, if FP(n) is the fibonacci position of n,

FP(1)=2 (first rule)

FP(5)=5 (second rule F₅ = 5)

FP(4)=4.5 (third rule, is right in the middle of F₄ = 3 and F₅ = 5)

Given an integer n, return its fibonacci position as a double.

Definition

Class:	FibonacciPositioning
Method:	getFPosition
Parameters:	int
Returns:	double
Method signature:	double getFPosition(int n)
(be sure your method is public)

Notes

-

The returned value must be accurate to 1e-9 relative or absolute.

Constraints

-

n will be between 1 and 100000000 (10⁸), inclusive.

Examples

0)

Returns: 2.0

1)

Returns: 5.0

2)

Returns: 4.5

Examples from the problem statement.

3)

Returns: 11.2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OrderDoesMatter

Graph Theory, Greedy, Simple Search, Iteration

Used in:

SRM 298

Used as:

Division I Level Two

Writer:

soul-net

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6157

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9819&pm=6157

Problem Statement

Matrices are a common object in mathematics. A NxM matrix is basically a table with N rows of M values each. Given two matrices, one of size AxB and another of size CxD, the following multiplication rules apply:

You can only multiply them if B is equal to C.
The resultant matrix is of size AxD.

The number of elements in an AxB matrix is A multiplied by B. For example, a 3x7 matrix has 21 elements.

Given a list of matrices, determine if there's an ordering that allows you to multiply all of them. If multiple such orderings exist, choose the one where the result has the most elements. Return the number of elements in the result, or -1 if there is no valid ordering (see examples 0-3 for further clarification). The list of matrices is given as two int[]s, N and M, where the ith elements of N and M represent the number of rows and columns respectively of the ith matrix.

Definition

Class:	OrderDoesMatter
Method:	getOrder
Parameters:	int[], int[]
Returns:	int
Method signature:	int getOrder(int[] N, int[] M)
(be sure your method is public)

Notes

-

The association order is not important because we are only interested in the dimensions of the matrices.

Constraints

-

M will have between 1 and 50 elements, inclusive.

-

N and M will have the same number of elements.

-

Each element of N and M will be between 1 and 1000, inclusive.

Examples

0)

{7,3,3}

{3,7,3}

Returns: 49

Here we can legally multiply all the matrices in three different ways:

(3x3)*(3x7)*(7x3) = (3x3) (elements = 9)

(3x7)*(7x3)*(3x3) = (3x3) (elements = 9)

(7x3)*(3x3)*(3x7) = (7x7) (elements = 49)

The maximum number of elements is then 49.

1)

{3,5,5}

{5,1,5}

Returns: 3

There's only one legal way to multiply the matrices (3x5)*(5x5)*(5x1)=(3x1) so the answer is 3*1=3.

2)

{3,5,5}

{5,2,4}

Returns: -1

There is no legal way to multiply the matrices.

3)

{5,2,3}

{2,5,3}

Returns: -1

Again, no legal way to multiply them all.

4)

{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}

{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SkewSymmetric

Brute Force, Simple Math

Used in:

SRM 319

Used as:

Division II Level One

Writer:

NeverMore

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6151

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9999&pm=6151

Problem Statement

A skew symmetric matrix M satisfies M^T = -M, where M^T denotes the transpose of the matrix M and -M denotes the matrix obtained by multiplying each entry of M by -1. The transpose of a matrix M is obtained by replacing the element in the i'th row and j'th column of M with the element in the j'th row and i'th column of M. Note that this requires the diagonal elements of a skew-symmetric matrix to be equal to 0.

Create a class SkewSymmetric which contains a method minChanges. The method will take a String[] M, each element of which is a single space separated list of integers. The j'th number in the i'th element of M represents the value at row i and column j of the matrix. The method should return the minimum number of values in M that must be changed such that the resulting matrix is skew symmetric.

Definition

Class:	SkewSymmetric
Method:	minChanges
Parameters:	String[]
Returns:	int
Method signature:	int minChanges(String[] M)
(be sure your method is public)

Constraints

-

M will contain between 2 and 10 elements, inclusive.

-

Each element of M will be a single space separated list of exactly n integers, where n is the number of elements in M.

-

Each element of M will contain between 1 and 50 characters, inclusive.

-

Each integer in M will be between -99 and 99 inclusive, with no extra leading zeros.

-

The integer zero will be represented as '0' (quotes for clarity) only, and not '-0' (quotes for clarity) in M.

Examples

0)

{"1 2 8", "-2 1 0", "3 99 3"}

Returns: 5

One possible skew-symmetric matrix obtained by changing 5 elements in M is:

  0  2  -3
 -2  0 -99
  3 99   0

Note that the diagonal elements must be 0.

1)

{"0 1 1 1 1 1", "-1 0 1 1 1 1", "-1 -1 0 1 1 1", 
"-1 -1 -1 0 1 1", "-1 -1 -1 -1 0 1", "0 0 0 0 0 0"}

Returns: 5

2)

{"0 0 0 0", "0 0 0 0", "0 0 0 0", "0 0 0 0"}

Returns: 0

3)

{"1 0", "0 1"}

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Manhattan

Simple Math

Used in:

SRM 319

Used as:

Division I Level Three

Writer:

Jan_Kuipers

Testers:

PabloGilberto , lbackstrom , brett1479 , radeye , Olexiy , Andrew_Lazarev , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6149

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9999&pm=6149

Problem Statement

My whole family lives in Manhattan, and consists of n people numbered 0 through (n - 1). The roads in Manhattan are a bit peculiar: they all go from North to South or from West to East, and together they form a complete grid of roads. Therefore, the distance between two intersections (x,y) and (x',y') equals abs(x-x')+abs(y-y'). Knowing the intersections where my family members live, I'd like to find the two different persons with the furthest distance between them. You are to help me by returning a int[] containing the 0-based indices of the people who form the furthest pair. If there are several furthest pairs, return the one among them with the smallest first index. If there are still multiple pairs left, return the one among them with the smallest second index.

The intersection where the ith family member lives is defined by the following sequence:

x_i = (a * y_i-1 + b) % m, for i > 0.
y_i = (a * x_i + b) % m, for i >= 0.

with x₀=0.

Definition

Class:	Manhattan
Method:	furthestPair
Parameters:	int, int, int, int
Returns:	int[]
Method signature:	int[] furthestPair(int n, int a, int b, int m)
(be sure your method is public)

Constraints

-

n will be between 2 and 250,000, inclusive.

-

a, b and m will each be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: {2, 6 }

The intersections where my family members live are (0,13), (12,5), (2,4), (18,1), (20,15), (3,11), (21,22), (6,9), (7,16) and (10,14). The 2nd and 6th intersections (zero-indexed) are furthest apart. The distance is abs(2-21)+abs(4-22)=37.

1)

Returns: {0, 1 }

All of them live at (0,0), so all pairs have distance 0. The lexicographically first pair is {0, 1}. Please note that we are looking for two different persons, so pair {0, 0} is invalid.

2)

Returns: {0, 54 }

Intersections 0 (0,1023) and 54 (96346,97580) are furthest apart.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MonotoneSEMin

Math

Used in:

TCO06 Round 4

Used as:

Division I Level Two

Writer:

lars2520

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6142

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9925&pm=6142

Problem Statement

Given a sequence of bits (0's and 1's), we want to find an arbitrary monotonically increasing curve that best fits the bits. That is, the i^th bit is b(i), and we want to find some curve, f, such that for x<y, f(x) <= f(y), and the sum over i of (f(i)-b(i))² (the squared error) is minimized.

Given the sequence of bits as a String[] where you concatenate all the elements together, return the minimum possible squared error.

Definition

Class:	MonotoneSEMin
Method:	min
Parameters:	String[]
Returns:	double
Method signature:	double min(String[] bits)
(be sure your method is public)

Notes

-

Your return must have relative or absolute error less than 1e-9.

Constraints

-

bits will contain between 1 and 50 elements, inclusive.

-

Each element of bits will contain between 1 and 50 bits ('0' or '1'), inclusive.

Examples

0)

{"10001110"}

Returns: 1.5

The flat curve f(x) = 0.5 would give a squared error of 0.5²*8 = 2. Naturally, we can do better than this though, and it turns out that the best we can do is a squared error of 1.5.

1)

{"00"}

Returns: 0.0

2)

{"11"}

Returns: 0.0

3)

{"1010100101010101001010101001",
 "0101010100100010010001010101",
 "1110110101001011010111011011",
 "1010111101110110111000111100"}

Returns: 26.244842801985662

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheXGame

Brute Force, Math

Used in:

SRM 304

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

PabloGilberto , vorthys , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6137

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9825&pm=6137

Problem Statement

The X game is a two person game. The board is just a sequence of boxes, some of which are randomly marked with an X before the game begins. The two players alternate turns. On each turn the player whose turn it is marks 1 or more previously unmarked boxes. All her marks on the turn must be adjacent (with no wrap-around at the ends) to each other. The game continues until all the boxes are marked.

The number of points scored by a player on his turn is equal to the number of boxes he marked on that turn times a multiplier. The multiplier gets bigger and bigger as the game goes on:

first turn Player 1 multiplier=0
second turn Player 2 multiplier=1
third turn Player 1 multiplier=2
fourth turn Player 2 multiplier=4
fifth turn Player 1 multiplier=8
... etc.

A players wins the game if the sum of the points scored on all her turns is strictly greater than her opponent's sum. Create a class TheXGame that contains a method firstMove that is given a String board indicating how many boxes there are, and which ones are marked with X before the game begins. The method returns the smallest number of Xs that the first player can mark on her first turn (somewhere on the board) that will allow her to win the game if she plays optimally thereafter. If no first move puts the first player into a winning position, the method returns -1.

Definition

Class:	TheXGame
Method:	firstMove
Parameters:	String
Returns:	int
Method signature:	int firstMove(String board)
(be sure your method is public)

Constraints

-

board will contain between 1 and 50 characters, inclusive.

-

Each character in board will be 'X' or '-'.

-

board will contain at least one '-'.

Examples

0)

"X---X-X-"

Returns: 1

There are 8 boxes, 3 of them marked with X before the game begins. The first player can win by marking the third box. After that each player will only be able to mark one box one each turn, and the scoring will be: P1: 0*1; P2: 1*1; P1: 2*1; P2: 4*1; P1: 8*1 and player 1 wins with a score of 10 versus player 2's score of 5.

1)

"----"

Returns: 2

The first player can win by marking the middle two spaces. After that, each player will mark one on each turn so player 1 wins by a score of 2 to 1. If the first player just marked one of the middle spaces, then the second player would mark 2 and the first player would mark 1 leaving the game tied (2 to 2).

2)

"--XXX"

Returns: -1

The first player cannot win by marking both of them, since her first turn multiplier is 0!

3)

"--------X-----X----X"

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ApproximateDivision

Math

Used in:

SRM 389

Used as:

Division I Level One , Division II Level Two

Writer:

legakis

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6125

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=11123&pm=6125

Problem Statement

Division is an expensive operation for a computer to perform, compared to addition, subtraction, and even multiplication. The exception is when dividing by powers of 2, because this can be done either with a bit shift (for a fixed-point value) or by subtracting 1 from the exponent (for a floating-point value). In this problem, we will approximate the quotient of two numbers using only addition, multiplication, and division by powers of 2.

Consider the following identity:


     1      1      c^0     c^1     c^2
    --- = ----- = ----- + ----- + ----- + ...
     b     t-c     t^1     t^2     t^3

If t is a power of 2, then the denominator of each term will be a power of 2.

Given integers a, b, and terms, approximate a/b by computing the first terms terms of the identity above, and multiplying the result by a. Select t to be the smallest power of 2 greater than or equal to b.

Definition

Class:	ApproximateDivision
Method:	quotient
Parameters:	int, int, int
Returns:	double
Method signature:	double quotient(int a, int b, int terms)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

b will be between 1 and 10000, inclusive.

-

a will be between 0 and b, inclusive.

-

terms will be between 1 and 20, inclusive.

Examples

0)

Returns: 0.34375

In this case t is chosen to be 8, and therefore c is 3. The first two terms are 1/8 and 3/64.

1)

Returns: 0.875

If b is a power of two, the first term is equal to exactly 1/b, and all other terms are zero.

2)

Returns: 0.33333301544189453

3)

Returns: 8.481740951538086E-5

4)

Returns: 0.14285714285714285

5)

Returns: 0.0

6)

Returns: 0.78125

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Aquarium

Simple Math, Simple Search, Iteration

Used in:

SRM 293

Used as:

Division II Level One

Writer:

supernova

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6124

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9814&pm=6124

Problem Statement

You have a fish aquarium. You are given a int[] fishSizes, denoting the size of each fish in the aquarium. They've been getting along pretty well so far, but you would now like to add a new fish (called Bob). You know that fish sometimes eat each other. You estimate that a fish might eat another fish if and only if it is at least two times larger, but no more than ten times larger, than that other fish.

Considering this, you would like to choose Bob's size such that:

- Bob is not in danger of being eaten by any other fish (i.e., its size is not between 1/10 and 1/2, inclusive, the size of any other fish).

- Bob is not tempted to eat any other fish (i.e., no other fish in the aquarium has a size between 1/10 and 1/2, inclusive, of Bob's size).

Your task is to return the number of different integer sizes for Bob between minSize and maxSize, inclusive, that won't cause any eating "conflicts" with other fish.

Definition

Class:	Aquarium
Method:	peaceful
Parameters:	int, int, int[]
Returns:	int
Method signature:	int peaceful(int minSize, int maxSize, int[] fishSizes)
(be sure your method is public)

Notes

-

Mulitple fish may have the same size. Also, we know that the existing fish get along, so we do not need to worry about eating conflicts between existing fish, regardless of their relative sizes.

Constraints

-

minSize is between 1 and 1000, inclusive.

-

maxSize is between minSize and 1000, inclusive.

-

fishSizes has between 1 and 50 elements, inclusive.

-

Each element of fishSizes is between 1 and 1000, inclusive.

Examples

0)

{1}

Returns: 3

We want to check which sizes between 1 and 12 will satisfy our constraints. Since we have a fish of size 1 in the aquarium, a new fish with a size between 2 and 10 will put it in danger. The remaining available sizes for Bob are 1, 11 and 12. Thus, the answer is 3.

1)

{3}

Returns: 10

There are 10 valid sizes: 2, 3, 4, 5, 31, 32, 33, 34, 35 and 36. Note that Bob cannot have a size of 1 since it may be eaten by the size 3 fish in the aquarium.

2)

{10, 100, 500}

Returns: 4

3)

{1, 3, 9, 27, 243, 729}

Returns: 121

4)

{10, 11, 12, 13, 14, 16, 82, 83, 84, 85, 720, 730, 740, 750, 760, 770}

Returns: 147

5)

{941, 797, 120, 45, 7, 120}

Returns: 10

6)

{1, 4, 12, 25, 79, 556, 625, 800, 801, 950, 952, 954, 956, 958, 980, 1000}

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BuildBridge

Math, Simple Search, Iteration

Used in:

SRM 295

Used as:

Division I Level One , Division II Level Two

Writer:

ivankovic

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6122

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9816&pm=6122

Problem Statement

Suppose you have an infinite deck of cards all of length L and a table. What is the minimum number of cards required to build a "bridge" of length D over the edge of the table without the cards falling over?

For example if you have cards of length 10 centimeters and you want to create a 7.5 centimeter bridge you must use at least 2 cards. If you used a single card it would be 7.5 centimeters over the edge and 2.5 centimeters on the table and would consequently fall down. Using one 10 centimeter card you could maximally achieve a 5 centimeter bridge since that would be the equilibrium state (5 cm on the table and 5 cm over the table).

In more general terms, a stack of cards is in an equilibrium state if the center of mass of the entire stack is located above the surface of the table, and the center of mass of each contiguous substack is above the surface of the next card. Let us examine the following two cases:

As you can see we have 2 cards here. The center of their mass (C12) is halfway between their centers (C1 and C2) because the cards are identical. Since C12 is right above the edge of the table the stack is in equlibrium and as you can't push it further forward this is the maximal extension you can get (1/4 (first card) + 1/2 (second card))

Here we have 3 cards. First observe that the top two cards are simply the case presented above with only two cards. The center of their mass is located 1/4 of the card length from the right edge of the second card. Now we use this center and the center of the first card to locate the center of the entire stack. Note however that the mass contained in C23 is twice the mass contained in C1 and therefore the resulting center of mass (C123) is located 1/6 of the card length from the right edge of the bottom card. The total extension is therefore 1/6 + 1/4 + 1/2 = 11/12

Given an int D, the distance of the "bridge" and an int L, the length of the card, what is the minimal number of cards required for a stable bridge of length D?

Definition

Class:	BuildBridge
Method:	howManyCards
Parameters:	int, int
Returns:	int
Method signature:	int howManyCards(int D, int L)
(be sure your method is public)

Notes

-

Both D and L are given in centimeters.

Constraints

-

D will be between 1 and 9, inclusive.

-

L will be between 1 and 9, inclusive.

Examples

0)

Returns: 4

3 cards extend 11/12 cm over the table edge... this is close but not enough. 4 cards extend 25/24 cm over the table edge and this is just above 1 cm. Therefore you need at least 4 one centimeter cards to build a one centimeter bridge.

1)

Returns: 1

A single 6 cm card is more than enough for a 1 cm bridge.

2)

Returns: 1

If you place the card exactly half-way over the edge you get a stable 3 cm bridge.

3)

Returns: 2

You can't do more than 3 with a single card so at least 2 cards are needed.

4)

Returns: 36865412

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ScrabbleBet

Brute Force, Math

Used in:

SRM 293

Used as:

Division I Level One , Division II Level Two

Writer:

supernova

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6116

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9814&pm=6116

Problem Statement

One Saturday evening you are playing a game of online Scrabble. Your opponent is a very good player, but this time you managed to win. After a brief conversation, you are told: "I am clearly better than you, but one game is simply not enough to prove it." Your opponent then makess the following bet: "If we play 10 games, you will win less than 5 ... and this will happen every time, even if we try this 10 times in a row!".

You will solve a more general problem using the following parameters:

- an int trials denoting the number of meetings in which a set of games is played.

- an int games denoting the number of games that are to be played in each meeting.

- an int winsNeeded denoting the number of victories you need in one of the meetings to win the bet.

- an int winChance denoting the probability in percent of winning one particular game.

Return a double between 0 and 1, denoting the probability you have to win the bet.

Definition

Class:	ScrabbleBet
Method:	estimate
Parameters:	int, int, int, int
Returns:	double
Method signature:	double estimate(int trials, int games, int winsNeeded, int winChance)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

trials will be between 1 and 50, inclusive.

-

games will be between 1 and 20, inclusive.

-

winsNeeded will be between 1 and games, inclusive.

-

winChance will be between 0 and 100, inclusive.

Examples

0)

Returns: 0.9375

There are 4 possible ways a meeting could evolve:

- you lose both games.

- you lose game 1 and you win game 2.

- you win game 1 and you lose game 2.

- you win both games.

Your opponent has a 1/4 chance of not losing the bet after the first meeting. Since there are two meetings, your opponent's chances to win the bet are 1/4 * 1/4 = 1/16. Thus, you have a 15/16 chance to win the bet.

1)

Returns: 0.4375

This time your opponent has a 3/4 chance of not losing the bet after one meeting and a 9/16 chance of not losing the bet after the two meetings. Your chances are now 1 - 9/16 = 7/16.

2)

Returns: 0.5566860567603682

3)

Returns: 0.08448495352665641

4)

Returns: 0.0

5)

Returns: 1.0

6)

Returns: 0.9448701546682944

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SlowKeyboard

Simple Math, Simple Search, Iteration

Used in:

TCO06 Qual 7/9/14

Used as:

Division I Level One

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6105

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9903&pm=6105

Problem Statement

During a quest game, you need to open a door. The door has a keyboard and a small screen with 4 digit places. The door will open only if the digits shown on the screen are equal to the minutes and seconds of the correct time. Unfortunately, the keyboard is very slow, so it takes 1 second to press a key and 2 seconds to move to a different key. For example, pressing "0000" will take 4 seconds, and pressing "1212" will take 10 seconds (4 seconds for pressing keys and 3*2 = 6 seconds for moving to other keys).

You will be given the current time as "MM:SS". If the screen shows nothing when you start, return the minimum time needed to open the door.

Definition

Class:	SlowKeyboard
Method:	enterTime
Parameters:	String
Returns:	int
Method signature:	int enterTime(String time)
(be sure your method is public)

Notes

-

Seconds and minutes increase like a normal clock, so "00:00" will be the time one second after "59:59".

Constraints

-

time will be formatted as "MM:SS", where MM and SS are two-digit numbers between 00 and 59, inclusive.

Examples

0)

"59:56"

Returns: 4

The time will be "00:00" in 4 seconds, which is enough time to type "00:00".

1)

"59:59"

Returns: 6

Type "00:05" to open the door in 6 seconds.

2)

"33:12"

Returns: 8

3)

"16:35"

Returns: 9

The best choice is to type 1644 (takes 8 seconds) and wait 1 second.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Taxi

Math

Used in:

SRM 300

Used as:

Division II Level One

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6104

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9821&pm=6104

Problem Statement

The "taxicab distance" between two points in space is defined to be the distance that would need to be travelled to get from one to the other using segments that are parallel to the axes. This is generally longer than the (straight-line) distance between the two points.

We know the taxicab distance between two points. We want to know the maximum straight-line distance between them if they lie in the rectangular region { (x,y) | 0<=x<=maxX, 0<=y<=maxY }. Create a class Taxi that contains a method maxDis that is given maxX, maxY, and taxiDis and that returns the largest possible straight-line distance between the two points. If no two points within the given region have the given taxicab distance, return -1.0.

Definition

Class:	Taxi
Method:	maxDis
Parameters:	int, int, int
Returns:	double
Method signature:	double maxDis(int maxX, int maxY, int taxiDis)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

maxX and maxY are both between 1 and 1,000,000, inclusive.

-

taxiDis is between 0 and 1,000,000, inclusive.

Examples

0)

Returns: 3.0

The two points could lie in a straight line parallel to one of the axes. Then the straight-line distance would be the same as the taxicab distance.

1)

Returns: -1.0

No two points with 0<=x<=10, 0<=y<=3, have a taxicab distance between them that is as big as 24.

2)

Returns: 10.44030650891055

(5,0) and (2,10) are two points in this region whose taxicab distance is |2-5| + |10-0| = 13 and whose straight-line distance is sqrt(3*3 + 10*10) = sqrt(109).

3)

Returns: 5.0

4)

Returns: 976705.6560100387

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Regulars

Dynamic Programming, Math

Used in:

TCCC06 Wildcard

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , brett1479 , Yarin , vorthys , Olexiy , Jan_Kuipers

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6103

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10135&pm=6103

Problem Statement

Regular expressions are simple but powerful ways of describing patterns for strings of symbols. We will restrict our attention to describing binary strings using only the special symbol * which means "zero or more occurrences". So our simple regular expression will be a sequence of characters, all of which are '0', '1' or '*'. Furthermore, each '*' will be preceded by a '0' or a '1' and will apply to that single character.

For example, "01*00*" describes all strings that start with '0', then have zero or more '1's, then have a '0', and then have zero or more '0's. The shortest string that satisfies this description is "00".

Create a class Regulars that contains a method stringCt that is given a simple regular expression regex and an int maxLen and that returns the number of distinct strings that satisfy regex and contain between 0 and maxLen characters, inclusive.

Definition

Class:	Regulars
Method:	stringCt
Parameters:	String, int
Returns:	long
Method signature:	long stringCt(String regex, int maxLen)
(be sure your method is public)

Constraints

-

regex will contain between 1 and 50 characters, inclusive.

-

Each character in regex will be '0' (zero), '1' (one), or '*'.

-

Each '*' in regex will be immediately preceded by '0' or '1'.

-

maxLen will be between 1 and 50, inclusive.

Examples

0)

"0*"

Returns: 6

"","0","00","000","0000","00000" are the legal strings.

1)

"01*1*1*"

Returns: 3

"0","01","011" are the legal strings.

2)

"0*1*0*1*0*1*0*1*0*1*0*1*0*1*0*1*0*1*0*1*0*1*0*1*0*"

Returns: 1125899906842623

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TribbloTrouble

Math, Recursion, Simulation, String Parsing

Used in:

SRM 295

Used as:

Division I Level Three

Writer:

ivankovic

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6094

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9816&pm=6094

Problem Statement

We have decided to make a funnier programming language, and name it "Tribblo". The basic objects of the new programming language will be tiny two dimensional creatures called Tribbles. The way tribbles interact with their world will determine the flow of a program. For starters, only 5 objects that tribbles can interact with are defined.

'S' represents a spawning point. The program starts by summoning one tribble at this point. The tribble then begins moving in one of the four cardinal directions (up, down, left or right). The direction is chosen randomly and each direction has the same chance of being chosen (25%). If at any point during the program the tribble returns to the spawning point the tribble is destroyed causing the program to enter an infinite loop and never terminate.
A slash-router '/' (quotes for clarity) works like a mirror. When a tribble hits a slash-router, it will rotate 90 degrees and continue moving. If the tribble was originally moving left or right, it will rotate 90 degrees counterclockwise, and if it was originally moving up or down, it will rotate 90 degrees clockwise.
A backslash-router '\' (quotes for clarity) works similarly to the slash-router, but in the opposite direction. If the tribble was originally moving left or right, it will rotate 90 degrees clockwise, and if it was originally moving up or down, it will rotate 90 degrees counterclockwise.

For example if the code looks like this:
```
		...\..
		......
		S../..
```
a tribble that starts off going to the right moves like this:
```
		ttt\..
		...t..
		Stt/..
```
There is also a wherever machine 'W'. When a tribble hits this object, it will rotate 90 degrees either clockwise or counterclockwise (both possibilities are equally likely). For example, a tribble going left and hitting the machine has a 50% chance of going up and a 50% chance of going down. There will be at most 10 wherever machines.
The final object is the tribble-trouble object 'T'. If any tribble reaches a tribble-trouble object, the program terminates.

The tribblo world is a N*M matrix of characters, with empty squares represented as '.'. If a tribble exits the boundaries of the world, he falls off, causing the program to enter an infinite loop and never terminate. You will be given a String[] code containing a properly formatted Tribblo program. You need to determine the probability of the given Tribblo program terminating.

Definition

Class:	TribbloTrouble
Method:	terminates
Parameters:	String[]
Returns:	double
Method signature:	double terminates(String[] code)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

code will contain between 1 and 50 elements, inclusive.

-

Each element of code will contain between 1 and 50 characters, inclusive.

-

All elements of code will contain the same number of characters.

-

All elements of code will contain only 'S','T','/','\','W' or '.' characters.

-

There will be at most 10 'W' characters in code.

-

There will be exactly one 'S' character in code.

Examples

0)

{"..T..",
 "T.S.T",
 "..T.."}

Returns: 1.0

Whatever the initial direction of the tribble is, he is bound to enter a tribble-trouble. Therefore, the program will always terminate.

1)

{"./..T",
 ".\\..\\",
 "S.../"}

Returns: 0.25

A tribble that starts off moving to the right will rebound a bit around the routers and end up hitting the tribble-trouble. Any other starting direction will cause the tribble to fall off the board (please note that '\\' represents a single '\' character!)

2)

{"...W..T",
 ".......",
 "...S..."}

Returns: 0.125

The famous wherever object! The tribble has a 25% chance of initially going upwards. When it hits the wherever machine it has a 50% chance of going to the left and falling off and a 50% chance of going to the right and terminating the program. 25% * 50% = 12.5%

3)

{
 "T......",
 ".......",
 "....W.T",
 ".......",
 "\\S../.."
}

Returns: 0.375

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SpiralNumbers

Simple Math, Simple Search, Iteration

Used in:

SRM 303

Used as:

Division I Level One , Division II Level Two

Writer:

Snail

Testers:

PabloGilberto , brett1479 , Yarin , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6093

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9824&pm=6093

Problem Statement

Consider all positive integers written in the following manner (you can imagine an infinite spiral).

                 21  22  23  24  25  26
                 20   7   8   9  10 ...
                 19   6   1   2  11 ...
                 18   5   4   3  12 ...
                 17  16  15  14  13 ...

You task is to determine the position (row,column) of a given number N, assuming that the center (number 1) has position (0,0). Rows are numbered from top to bottom, columns are numbered from left to right (for example, number 3 is at (1,1)). Your method should return a string containing the position of N in form (R,C) where R is the row and C is the column. R and C must not contain any leading zeroes.

Definition

Class:	SpiralNumbers
Method:	getPosition
Parameters:	int
Returns:	String
Method signature:	String getPosition(int N)
(be sure your method is public)

Constraints

-

N will be between 1 and 2,147,483,647, inclusive.

Examples

0)

Returns: "(0,1)"

1)

Returns: "(1,1)"

2)

Returns: "(-1,-1)"

3)

Returns: "(2,-2)"

4)

Returns: "(-2,1)"

5)

Returns: "(-14,3)"

6)

Returns: "(-437,221)"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PreprimeNumbers

Search, Simple Math

Used in:

SRM 307

Used as:

Division II Level Three

Writer:

Mike Mirzayanov

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6083

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9987&pm=6083

Problem Statement

A number is preprime if it has exactly 4 positive integer divisors. For example, 6 is preprime because its divisors are 1, 2, 3, and 6. The integers 6, 8, 10, 14 form the beginning of an infinite sequence of preprime numbers. Find the n-th element of this sequence, where n is a 1-based index.

Definition

Class:	PreprimeNumbers
Method:	nthNumber
Parameters:	int
Returns:	int
Method signature:	int nthNumber(int n)
(be sure your method is public)

Constraints

-

n will be between 1 and 1000000, inclusive.

Examples

0)

Returns: 8

The beginning of an infinite sequence of preprime numbers is: 6, 8, 10, 14, ... The second number is 8.

1)

Returns: 14

The beginning of an infinite sequence of preprime numbers is: 6, 8, 10, 14, ... The fourth number is 14.

2)

Returns: 77

3)

Returns: 193539

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BigFibonacci

Math

Used in:

TCO06 Qual 5/6/12

Used as:

Division I Level Three

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6077

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9901&pm=6077

Problem Statement

Depicted below is the Fibonacci sequence:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

As you can see, each value from 2 on is the sum of the previous two values. Given the 0-based index of a Fibonacci number and an int M, return the index-th Fibonacci number modulo M.

Definition

Class:	BigFibonacci
Method:	fibNumber
Parameters:	String, int
Returns:	int
Method signature:	int fibNumber(String index, int M)
(be sure your method is public)

Constraints

-

index will be an integer between 0 and 10¹⁵, inclusive, with no extra leading zeroes.

-

M will be between 1 and 1000000 (10⁶).

Examples

0)

"7"

Returns: 3

1)

"5"

Returns: 0

2)

"0"

Returns: 0

3)

"17"

Returns: 1

4)

"54"

Returns: 177022

F₅₄ = 86267571272.

86267571272 % 341890 = 177022.

5)

"300"

Returns: 0

F₃₀₀ = 222232244629420445529739893461909967206666939096499764990979600.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FarFromPrimes

Brute Force, Math

Used in:

SRM 291

Used as:

Division II Level One

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6074

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9812&pm=6074

Problem Statement

A prime number is an integer greater than 1 that has no positive divisors other than 1 and itself. The first prime numbers are 2, 3, 5, 7, 11, 13, 17, ...

The number N is considered far from primes if there are no prime numbers between N-10 and N+10, inclusive, i.e., all numbers N-10, N-9, ..., N-1, N, N+1, ..., N+9, N+10 are not prime.

You are given an int A and an int B. Return the number of far from primes numbers between A and B, inclusive.

Definition

Class:	FarFromPrimes
Method:	count
Parameters:	int, int
Returns:	int
Method signature:	int count(int A, int B)
(be sure your method is public)

Constraints

-

A will be between 10 and 100000, inclusive.

-

B will be between A and 100000, inclusive.

-

(B - A) will be between 0 and 1000, inclusive.

Examples

0)

Returns: 4

The far from primes numbers are 3480, 3750, 3978 and 4038.

1)

Returns: 0

2)

Returns: 53

3)

Returns: 20

4)

Returns: 89

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LastMarble

Advanced Math, Dynamic Programming

Used in:

SRM 349

Used as:

Division I Level Three

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6067

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10673&pm=6067

Problem Statement

A bag is filled with a given quantity of red and blue marbles. In each turn, a player reaches into the bag and removes 1, 2, or 3 marbles. The player looks to see the color of the marbles, and announces how many of each color marble were removed. The last player to remove a red marble from the bag loses. You are given ints red and blue, the number of red and blue marbles initially in the bag. Before play begins, a friend removes several of the marbles from the bag, at random, without showing either of you, given in int removed.

Assuming you go first, and each player makes the optimal choice of number of marbles to remove, calculate the probability that you win the game.

Definition

Class:	LastMarble
Method:	winningChance
Parameters:	int, int, int
Returns:	double
Method signature:	double winningChance(int red, int blue, int removed)
(be sure your method is public)

Notes

-

Return value must be within 1e-9 absolute or relative error of the actual result.

Constraints

-

red will be between 1 and 100, inclusive.

-

blue will be between 1 and 100, inclusive.

-

removed will be between 0 and red - 1, inclusive.

Examples

0)

Returns: 0.5

Here, the best you can do is to select one marble. If you get the blue marble, then your opponent will get the red one, and you will win. You have a 50/50 chance.

1)

Returns: 0.3333333333333333

Taking three marbles would guarantee a loss. Taking two marbles gives you a 1/3 chance of winning. If you take one marble, you have a 2/3 chance of getting a blue marble. Your opponent then takes one marble, with a 1/2 chance of getting the red marble (and you winning). 2/3 * 1/2 = 1/3. The best you can do here is a 1/3 chance of winning.

2)

Returns: 0.6666666666666666

Once again, there's nothing to gain by taking all three marbles. Take two marbles, and you have a 2/3 chance of leaving the last red marble for your opponent. Take one marble, and you have a 2/3 chance of leaving your opponent with 1 red, 1 blue, and a 1/3 chance of leaving him with 2 red. Left with 1 and 1, your opponent takes 1 marble, and has a 50/50 shot of winning. Left with two reds, your opponent takes 1, and you definitely lose. Thus, you have only a 1/3 chance of winning by taking one marble initially. You take two marbles, and have a 2/3 chance of winning.

3)

Returns: 0.5

Here, one of the four marbles has been removed, so we have to consider what to do when we aren't sure how many red and blue marbles remain in the bag.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FirstToLast

Math

Used in:

TCO06 Round 1

Used as:

Division I Level Two

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6054

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9917&pm=6054

Problem Statement

We can rotate a positive integer by removing its leftmost digit and attaching it on the right end. Return the smallest positive value with no leading zeros such that rotating it is the same as multiplying it by p/q. If no such value exists less than 2000000000 (2 billion), return -1.

Definition

Class:	FirstToLast
Method:	getSmallest
Parameters:	int, int
Returns:	int
Method signature:	int getSmallest(int p, int q)
(be sure your method is public)

Notes

-

After rotating, the number may have leading zeros.

-

Rotating a value less than 10 does not change it.

Constraints

-

p and q will each be between 1 and 100 inclusive.

Examples

0)

Returns: 1

1)

Returns: 102564

2)

Returns: -1

3)

Returns: 100

4)

Returns: -1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumPermutationOrders

Math

Used in:

TCO06 Round 1

Used as:

Division I Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6052

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9917&pm=6052

Problem Statement

Let S = {1, 2,..., n} be a set of positive integers. A permutation on S is a function that takes each element of S to a distinct element of S (i.e., it is one-to-one). The identity permutation takes each element of S to itself. Given a permutation f on S, we can ask how many times f must be applied until we arrive at the identity permutation. The smallest such positive value is called the order of f (i.e., the smallest positive k such that f^k = identity). For example, suppose f behaves as follows (for n=3):

	1->2, 2->1, 3->3

Then applying f twice results in the identity permutation, since every element is taken to itself:

    1->2->1, 2->1->2, 3->3->3

Since applying f once is not the identity permutation, the order of f is 2. Considering all permutations on S, return how many possible orders there are.

Definition

Class:	NumPermutationOrders
Method:	howMany
Parameters:	int
Returns:	long
Method signature:	long howMany(int n)
(be sure your method is public)

Constraints

-

n will be between 1 and 1000, inclusive.

Examples

0)

Returns: 1

Here the only permutation is the identity.

1)

Returns: 2

Here there are two possible permutations: the identity (order 1), and the permutation that swaps 1 and 2 (order 2).

2)

Returns: 3

Here there are 3! = 6 possible permutations: the identity (order 1), 3 permutations that swap two elements (order 2), and 2 permutations that do not fix any element (order 3).

3)

Returns: 4

4)

Returns: 16

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

VectorCostSequence

Brute Force, Simple Math

Used in:

TCCC06 Round 1A

Used as:

Division I Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , vorthys , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6051

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10097&pm=6051

Problem Statement

Without consulting your data structures textbook, you have coded up a homemade Vector class. At any point in time the vector has a capacity, the maximum number of values it can hold, and a size, the number of values it currently holds. Typically, adding or removing an element costs 1. If you attempt to add a value to the vector when the size and capacity are equal, the capacity is doubled and then the element is added. This incurs a cost of c+1, where c is the capacity before the insertion. If removing an element makes the size exactly half (no rounding) of the capacity, then the cost is only 1, but the capacity is reduced to the size. Initially, the capacity is 1 and the size is 0. Return the smallest number of additions and removals that will produce the cost d.

Definition

Class:	VectorCostSequence
Method:	getSmallest
Parameters:	int
Returns:	int
Method signature:	int getSmallest(int d)
(be sure your method is public)

Constraints

-

d will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 1

Performing a single addition gives a cost of 1.

1)

Returns: 2

Adding an element and then removing it gives a cost of 2.

2)

Returns: 3

We can achieve a cost of 6 with 3 additions. The first costs 1, the second costs 2 and the last costs 3.

3)

Returns: 5

4)

Returns: 9

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

InverseCollatz

Math, Simulation

Used in:

TCO06 Round 2

Used as:

Division I Level Two

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6047

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9891&pm=6047

Problem Statement

Given a positive integer j greater than 1, the corresponding Collatz sequence is produced by repeatedly applying f to j (and continues even after we reach 1). The function f behaves as follows:

             { x/2    if x is even
   f(x)  =   {
             { 3x+1   if x is odd

Suppose someone began with the value y and has started (but not necessarily finished) generating the Collatz sequence. Each time they apply f they write down 'E' or 'O' to denote whether the argument was even or odd, respectively. Given the String s they have written down, you must return a String of the form (quotes for clarity) "ak+b". Here a and b are integers with no extra leading zeros. The returned string must make the following set the collection of all possible numbers that could have begun the sequence:

	P = { ak + b | k >= 0 and ak + b > 1}

If there are multiple possible return values, choose the one with b minimal.

Definition

Class:	InverseCollatz
Method:	getForm
Parameters:	String
Returns:	String
Method signature:	String getForm(String s)
(be sure your method is public)

Constraints

-

s will contain between 1 and 50 characters, inclusive.

-

Each character in s will be 'E' or 'O'.

-

An 'O' will never be immediately followed by another 'O' in s.

Examples

0)

"EEE"

Returns: "8k+0"

The argument was even 3 times in a row, so the original value was a positive multiple of 8.

1)

"OE"

Returns: "2k+1"

The initial number had to be odd. After multiplying by 3 and adding 1, the next value will definitely be even.

2)

"OEO"

Returns: "4k+3"

3)

"EEEEOEEEEOEEEEOEEEEOEEEEOEEEEOEEEEOEEEEOEEEEOEEEEO"

Returns: "2199023255552k+1014933810256"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Projections

Simple Math

Used in:

SRM 299

Used as:

Division I Level One , Division II Level Two

Writer:

Vovka

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6041

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9820&pm=6041

Problem Statement

This problem contains HTML superscripts and images which will not display correctly for plugin users

Consider a finite two-dimensional grid where each cell is either occupied or empty. You are given two Strings, front and right, the frontal and right projections of the grid, respectively. The i^th character of front indicates whether the i^th column of grid is completely empty or not ("." for empty, lowercase "x" if the column contains at least one occupied cell). The i^th character of right indicates whether the i^th row of grid is completely empty or not.

Return a int[] containing exactly two elements. The first element is the minimum possible number of occupied cells on the grid, and the second element is the maximum possible number of occupied cells.

Definition

Class:	Projections
Method:	count
Parameters:	String, String
Returns:	int[]
Method signature:	int[] count(String front, String right)
(be sure your method is public)

Constraints

-

front will contain between 1 and 50 elements, inclusive.

-

right will contain between 1 and 50 elements, inclusive.

-

Each character in front and right will be "." or "x".

-

Both front and right will contain at least one "x" character.

Examples

0)

"x"

"x"

Returns: {1, 1 }

There is only one cell on the grid and it is obviously occupied.

1)

"x."

".x"

Returns: {1, 1 }

There is only one possible 2x2 grid with such projections (dark squares represent occupied cells):

2)

"xxxx"

"x..x"

Returns: {4, 8 }

One possible assignment with the minimum possible number of cells occupied is the following:

The only possible assignment with the maximum possible number of cells occupied is the following:

3)

"x.x.x.x"

"x.x.x.x"

Returns: {4, 16 }

4)

"x...xx..x.xxx..x.xx."

".xx..xxx.xx."

Returns: {10, 70 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TemperatureScales

Simple Math

Used in:

SRM 299

Used as:

Division II Level One

Writer:

Vovka

Testers:

PabloGilberto , brett1479 , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6038

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9820&pm=6038

Problem Statement

Due to historical reasons people measure temperature in different scales, such as Fahrenheit and Celsius. Your task is to convert a temperature from one scale to another. It is known that both scales are linear with respect to each other (i.e., there are real numbers a and b such that temperature t presented in the first scale can be converted to the second by the law t'=a*t+b).

You are given 5 ints: f1, the freezing point of water in the first scale; b1, the boiling point of water in the first scale; f2, the freezing point of water in the second scale; b2, the boiling point of water in the second scale; and t, the temperature in the first scale. Return t converted into the second scale.

Definition

Class:	TemperatureScales
Method:	convert
Parameters:	int, int, int, int, int
Returns:	double
Method signature:	double convert(int f1, int b1, int f2, int b2, int t)
(be sure your method is public)

Notes

-

The return value must be within 1e-9 absolute or relative error of the actual result.

-

Because the boiling and the freezing points of water depend on the atmospheric pressure, you may assume that both the scales are under the same circumstances.

Constraints

-

f1,b1,f2,b2 and t will each be between -1000 and 1000, inclusive.

-

f1 will be less than b1.

-

f2 will be less than b2.

Examples

0)

Returns: 28.0

These are two identical scales, so temperatures in both of them coincide.

1)

Returns: 29.0

The second scale is shifted up 1 degree relative to the first scale.

2)

-1000

-999

-1000

Returns: 3999000.0

3)

-10

Returns: 3.7

4)

-123

Returns: -114.66666666666667

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AccountBalance

Simple Math, String Parsing

Used in:

SRM 288

Used as:

Division II Level One

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6036

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9809&pm=6036

Problem Statement

You are working for the financial institution TopBank, and you have been tasked with writing a module that will take an initial account balance, along with a list of that day's transactions, and return the ending balance for the day.

Each transaction will be either a credit, which adds funds to the account, or a debit, which removes funds from the account. If a debit exceeds the available funds at the time, then the account balance will go negative. You will be given an int startingBalance, the initial account balance. You will also be given a String[] transactions, the list of transactions for the day. Each element of transactions will be in the form "type amount" (quotes added for clarity). Each type will be 'C' or 'D', for credit or debit, respectively. Each amount will be an integer between 1 and 1000000, inclusive, with no leading zeros. You are to return an int representing the ending balance after processing all of the transactions.

Definition

Class:	AccountBalance
Method:	processTransactions
Parameters:	int, String[]
Returns:	int
Method signature:	int processTransactions(int startingBalance, String[] transactions)
(be sure your method is public)

Constraints

-

startingBalance will be between 0 and 1000000, inclusive.

-

transactions will have between 0 and 50 elements, inclusive.

-

Each element of transactions will be formatted as "type amount" (quotes added for clarity).

-

Each type will be 'C' or 'D'.

-

Each amount will represent an integer between 1 and 1000000, inclusive, with no leading zeros.

Examples

0)

{"C 1000", "D 500", "D 350"}

Returns: 250

This person had 100 dollars, got their paycheck, then went shopping at two different stores. 100 + 1000 - 500 - 350 = 250.

1)

{}

Returns: 100

With no transactions, the balance doesn't change by the end of the day.

2)

{"D 50", "D 20", "D 40"}

Returns: -10

Uh oh! This person's account is overdrawn.

3)

{"D 1234", "C 987", "D 2345", "C 654", "D 6789", "D 34567"}

Returns: 10580

Several transactions of both types.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CannonBalls

Dynamic Programming, Math

Used in:

SRM 288

Used as:

Division I Level Two

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6033

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9809&pm=6033

Problem Statement

Captain Brown Beard keeps his pirate ship stocked with a healthy supply of cannon balls. Because he is very tidy, he insists that all of the cannon balls be stacked into perfect tetrahedron shapes. Such a pyramid is constructed by arranging cannon balls into an equilateral triangle with side length n. Then, on top of that is stacked an equilateral triangle of side length n-1, and so on, until there is a single cannon ball placed on the top (this single cannon ball is a triangle of side length 1). For example, a stack of size 3 will have three layers that look like this (from top to bottom):

  X

  X
 X X

  X
 X X
X X X

So, each triangle will contain 1, 3, 6, 10, etc. cannon balls. Thus, any complete stack will have 1, 4, 10, 20, etc. cannon balls.

You are given an int n, the number of cannon balls loaded on the ship. You are to return an int indicating the least possible number of stacks into which the cannon balls can be piled.

Definition

Class:	CannonBalls
Method:	fewestPiles
Parameters:	int
Returns:	int
Method signature:	int fewestPiles(int n)
(be sure your method is public)

Constraints

-

n will be between 1 and 300000, inclusive.

Examples

0)

Returns: 1

This is the smallest single stack we can make.

1)

Returns: 2

A stack with 1 cannon ball, and a stack with 4 cannon balls.

2)

Returns: 3

9 = 4 + 4 + 1

3)

Returns: 3

4)

Returns: 2

91 = 56 + 35

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TurnOffLights

Brute Force, Math, Simple Search, Iteration

Used in:

SRM 288

Used as:

Division II Level Three

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6030

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9809&pm=6030

Problem Statement

You are given a 4x4 game board consisting of buttons which are either lit or unlit. The buttons are numbered 1-16, like so:

 1  2  3  4
 5  6  7  8
 9 10 11 12
13 14 15 16

Pressing a button changes the state of that button, along with the states of the buttons to the immediate left, right, top and bottom. Pressing and holding a button, which counts as two moves, changes only the state of that individual light.

The goal of the game is to turn off all of the lights. You are given a String[] board consisting of four elements, each containing four characters. Each character will be a '0' or '1', indicating whether each light is off or on, respectively. You are to return an int indicating the least number of moves necessary to turn off all of the lights.

Definition

Class:	TurnOffLights
Method:	fewestMoves
Parameters:	String[]
Returns:	int
Method signature:	int fewestMoves(String[] board)
(be sure your method is public)

Constraints

-

board will contain exactly 4 elements.

-

Each element of board will contain exactly 4 characters.

-

Each character of each element of board will be '0' (zero) or '1' (one).

Examples

0)

{"1100",
 "1000",
 "0000",
 "0000"}

Returns: 1

Press only the button in the upper left corner.

1)

{"0100",
 "1110",
 "0100",
 "0000"}

Returns: 1

Again, a single button press suffices.

2)

{"1000",
 "0000",
 "0000",
 "0000"}

Returns: 2

We need to press and hold the lit button, which costs us two moves.

3)

{"1100",
 "1000",
 "0000",
 "0001"}

Returns: 3

Press the upper left button (costs 1). Press and hold the lower right button (costs 2).

4)

{"1011",
 "1010",
 "0000",
 "0000"}

Returns: 2

Here, we push buttons 1 and 3. Notice that button 2 lights up after the first button push, but ends up unlit at the end.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DigitByDigit

Dynamic Programming, Simple Math

Used in:

SRM 294

Used as:

Division I Level Three

Writer:

legakis

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6022

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9815&pm=6022

Problem Statement

You have reached the final round of a game show, and it is time to determine the amount of your prize. The number of digits, n, in the amount has been determined based on your earlier performance during the game. You will be presented with a board containing n blank spaces and given n randomly-generated digits. You will be allowed to place each digit, one at a time, in any unoccupied space you want. You must decide where to place each digit before you see the next, and once you place a digit you cannot move it. After all n digits have been placed, the resulting n-digit number will be the value of your prize.

For example, assume you have earned a three-digit prize. If the first digit generated were a 2, you might choose to place that in the rightmost space, hoping that the next two digits will be larger. If the second digit were a 8, you might choose to place that in the leftmost space, because you would only regret that decision in the relatively unlikely event that the final digit is a 9. If the third digit were a 6, you would place that in the last remaining space (the middle), and your final prize would be 862.

You will be given the state of the number you are forming digit-by-digit as a String digits, possibly already in progress. This String will contain one character for each space on the board: '0' through '9', inclusive, indicate digits that have already been placed, and a '_' indicates a blank space on the board. Assuming you play optimally in order to maximize your expected winnings, return the expected value of the prize you will win.

At each step, each of the digits 0 through 9 will be presented to you with equal probability. Note that the digits already placed may not be the result of optimal play, but you should assume that you will play to maximize your expected winnings from this point forward.

Definition

Class:	DigitByDigit
Method:	expectedScore
Parameters:	String
Returns:	double
Method signature:	double expectedScore(String digits)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

digits will contain between 1 and 50 characters, inclusive.

-

digits will contain only the characters '_' and '0' through '9', inclusive.

Examples

0)

"_0"

Returns: 45.0

There is only one blank space, so you will only have one more digit to place. The final result will either be 0, 10, 20, 30, 40, 50, 60, 70, 80, or 90. The expected value, 45, is the average of these.

1)

"__"

Returns: 60.75

The highest expected value is achieved by putting the first digit in the left spot if it is 5, 6, 7, 8, or 9, and putting it in the right spot if it is 0, 1, 2, 3, or 4. The expected value can be computed as:

    5/10 * ((5+6+7+8+9)/5 * 10 + 4.5          ) +
    5/10 * (4.5           * 10 + (0+1+2+3+4)/5)

Any deviation from this strategy would result in a lower expected value.

2)

"_55_"

Returns: 6303.25

3)

"____0000000000000000"

Returns: 7.482735000000001E19

4)

"___6__3___"

Returns: 8.604871517066002E9

5)

"__________"

Returns: 8.882477600592714E9

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FixedSizeSums

Dynamic Programming, Math, Sorting

Used in:

SRM 287

Used as:

Division II Level Three

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6015

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9808&pm=6015

Problem Statement

You are given two positive integers, sum and count. Consider all possible ways to express sum as a sum of exactly count positive integers. Two ways are considered equal if we can obtain one from the other by changing the order of the summed numbers. For example, 8=3+2+1+1+1 is the same as 8=1+3+1+2+1, but not the same as 8=3+2+2+1. Thus we will only be interested in such summations where the summed integers are in non-increasing order.

For example, if sum=8 and count=3, the possible ways are:

8 = 6+1+1
8 = 3+3+2
8 = 4+2+2
8 = 4+3+1
8 = 5+2+1

We may now order these summations in the following way: Order them according to the first summand in decreasing order. In case of a tie, order them according to the second summand, etc. In general, to compare two summations, look at the first summand where they differ. The one where this summand is larger will be earlier in our order.

For our previous example, the correct order is:

8 = 6+1+1
8 = 5+2+1
8 = 4+3+1
8 = 4+2+2
8 = 3+3+2

You will be given three ints: sum, count and index, where index contains a zero-based index of a summation in the order defined above. Your method should return a String containing that summation in the form "SUM=SUMMAND(1)+...+SUMMAND(count)". If index is too large to specify a valid summation, return an empty string.

Definition

Class:	FixedSizeSums
Method:	kthElement
Parameters:	int, int, int
Returns:	String
Method signature:	String kthElement(int sum, int count, int index)
(be sure your method is public)

Notes

- You may assume that the total number of possible summations will never exceed 2,000,000,000.

Constraints

- sum is between 1 and 150, inclusive.

- count is between 1 and 150, inclusive.

- index is between 0 and 2,000,000,000, inclusive.

Examples

0)

Returns: "8=4+3+1"

This is the example from the problem statement. Look at the ordered list of possible summations and number them starting with zero.

1)

Returns: "13=13"

There is only one possibility here.

2)

Returns: "13=1+1+1+1+1+1+1+1+1+1+1+1+1"

Again, there is only one possible summation.

3)

Returns: ""

This is impossible. A sum of 10 positive integers is never equal to 7.

4)

Returns: "17=12+5"

The first five possible summations are: "17=16+1", "17=15+2", "17=14+3", "17=13+4", and "17=12+5".

5)

87654321

Returns: "140=40+31+15+15+9+7+4+4+2+2+2+2+2+2+1+1+1"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TwoEquations

Brute Force, Simple Math, String Parsing

Used in:

SRM 287

Used as:

Division I Level One , Division II Level Two

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6013

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9808&pm=6013

Problem Statement

You are given two Strings, first and second. Each of these strings contains a simple linear equation with variables x and y. Your task is to determine whether this pair of equations has a unique solution, and if so, to compute it.

Each of the equations is of the form "A*X + B*Y = C". The spaces must appear exactly as in this example, i.e., there is exactly one space both before and after the signs "+" and "=", and there are no other spaces. The coefficients A, B, and C are integers. If a coefficient is non-negative, the equation contains just the number, without the unary plus sign. If a coefficient is negative, it is always enclosed in parentheses, and it contains the unary minus sign. No coefficient will contain unnecessary leading zeroes.

If the pair of equations has a unique solution, return the solution formatted as a String of the form "X=A/B Y=C/D", where A, B, C, and D are integers such that both fractions A/B and C/D are reduced, and the numbers B and D are positive. The numbers should be encoded in the same way as the coefficients of the equations -- i.e., negative numbers must be enclosed in parentheses.

If the pair of equations has more than one solution, return the String "MULTIPLE SOLUTIONS". If the pair of equations has no solutions, return the String "NO SOLUTIONS".

Definition

Class:	TwoEquations
Method:	solve
Parameters:	String, String
Returns:	String
Method signature:	String solve(String first, String second)
(be sure your method is public)

Notes

- A fraction A/B is called reduced if and only if the greatest common divisor of A and B is 1. Note that each rational number corresponds to exactly one reduced fraction with B>0.

Constraints

- first and second will be formatted as described in the problem statement.

- All coefficients in both equations will be integers between -9 and 9, inclusive.

Examples

0)

"1*X + 2*Y = 6"

"1*X + (-4)*Y = (-3)"

Returns: "X=3/1 Y=3/2"

Multiply the first equation by two, then add the second equation to the first one. You will get a new equation: 3*X = 9. Thus X=3. If we substitute this into one of the original equations, we get Y=3/2.

1)

"(-3)*X + 0*Y = 7"

"0*X + 8*Y = 6"

Returns: "X=(-7)/3 Y=3/4"

This time we can compute each of the variables separately. Note that in the result, the numerator (not the denominator) of X is negative, and that it is enclosed in parentheses. Also, note that the value of Y is output as a reduced fraction.

2)

"1*X + 0*Y = 1"

"1*X + 0*Y = 1"

Returns: "MULTIPLE SOLUTIONS"

3)

"1*X + 3*Y = 1"

"2*X + 6*Y = (-1)"

Returns: "NO SOLUTIONS"

4)

"0*X + 0*Y = 0"

"(-3)*X + (-3)*Y = 0"

Returns: "MULTIPLE SOLUTIONS"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Truckloads

Recursion, Simple Math

Used in:

SRM 284

Used as:

Division II Level One

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6011

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8081&pm=6011

Problem Statement

We have a pile of crates at our warehouse that we want to load onto trucks. Our plan is to divide the pile in half forming two smaller piles, then continuing dividing each of the small piles in half until we get piles that will fit on a truck. (Of course, when we divide an odd number of crates in "half", one of the resulting piles will have one more crate than the other.) Our problem is to determine how many trucks we will need to ship the crates.

Create a class Truckloads that contains a method numTrucks that is given numCrates (the number of crates at the warehouse) and loadSize (the maximum number of crates that will fit in a truck) and that returns the number of trucks required.

Definition

Class:	Truckloads
Method:	numTrucks
Parameters:	int, int
Returns:	int
Method signature:	int numTrucks(int numCrates, int loadSize)
(be sure your method is public)

Constraints

-

numCrates will be between 2 and 10,000, inclusive.

-

loadSize loadSize will be be between 1 and (numCrates - 1), inclusive.

Examples

0)

Returns: 6

After the first division we have two piles each with 7 crates. Each of these piles must be divided giving us 2 piles of 3 and 2 piles of 4. The piles with 4 crates must be further divided giving us 2 piles of 3 and 4 piles of 2. Each of these piles fits into a truck, so we need 6 trucks.

1)

Returns: 15

We will eventually end up with 15 piles, each with just 1 crate.

2)

Returns: 256

1024 divides in half very nicely. We eventually end up with 256 piles, each containing 4 crates.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BasketsWithApples

Brute Force, Simple Math

Used in:

SRM 285

Used as:

Division II Level One

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6006

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8082&pm=6006

Problem Statement

We have some baskets containing apples, and we would like to perform the following procedure in a way that maximizes the number of remaining apples. First, we discard some (or none) of the baskets completely. Then, if the remaining baskets do not all contain the same number of apples, we remove excess apples from the baskets until they do.

You will be given a int[] apples where the i-th element of apples is the number of apples in the i-th basket. Return the number of apples remaining after the procedure described above is performed.

Definition

Class:	BasketsWithApples
Method:	removeExcess
Parameters:	int[]
Returns:	int
Method signature:	int removeExcess(int[] apples)
(be sure your method is public)

Constraints

-

apples will contain between 1 and 50 elements, inclusive.

-

Each element in apples will be between 0 and 1000, inclusive.

Examples

0)

{1, 2, 3}

Returns: 4

We should remove the first basket and leave two apples in each of the two remaining baskets.

1)

{5, 0, 30, 14}

Returns: 30

We should leave only the third basket.

2)

{51, 8, 38, 49}

Returns: 114

3)

{24, 92, 38, 0, 79, 45}

Returns: 158

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CoinGame

Math

Used in:

SRM 287

Used as:

Division I Level Three

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6005

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9808&pm=6005

Problem Statement

Two players play a simple game with a coin.

Given is a set S. Each element of S is a sequence of heads and tails, and all the sequences have the same length.

The first player starts the game by choosing a sequence from S. Then the second player chooses a different sequence from S. A fair coin is then thrown repeatedly until one of the chosen sequences appears as a set of consecutive throws. The player that has chosen this sequence wins.

You are given a String[] sequences containing the allowed sequences encoded as strings of 'H's and 'T's ('H' represents a head, 'T' represents a tail). Return the probability that the first player will win this game, given that both players play optimally.

Definition

Class:	CoinGame
Method:	bestProbability
Parameters:	String[]
Returns:	double
Method signature:	double bestProbability(String[] sequences)
(be sure your method is public)

Notes

-

The returned value must be accurate to 1e-9 relative or absolute.

Constraints

-

sequences contains between 2 and 50 elements, inclusive.

-

Each element of sequences contains only uppercase 'H' and uppercase 'T' characters.

-

Each element of sequences contains between 1 and 10 characters, inclusive.

-

Each element of sequences contains the same number of characters.

-

No two elements in sequences are equal.

Examples

0)

{"H", "T"}

Returns: 0.5

This game is as simple as it gets. The first player picks a head or a tail, then they flip a coin and look at the outcome. Each player has a 50% chance of winning this game.

1)

{"HHHHHHHHH", "TTTTTTTTT"}

Returns: 0.5000000000000011

Almost the same game, but quite a bit longer.

2)

{"HH", "HT"}

Returns: 0.5

This is another example of a fair game. Once a head occurs for the first time, the next throw decides which sequence will appear first.

3)

{"TTT", "HTT"}

Returns: 0.875

In this game, choice matters. The only way TTT can appear before HTT is if it appears in the first three throws. Otherwise the triplet we encounter immediately before seeing TTT for the first time is always HTT. Thus in all other cases HTT appears before TTT.

The first player knows this and he chooses HTT, which gives him a 7/8 chance of winning the game.

4)

{"HHH", "HHT", "HTH", "HTT", "THH", "THT", "TTH", "TTT"}

Returns: 0.33333333333333337

This game contains a wonderful paradox: being the first player is not always good.

5)

{"TTHTTHTTH", "HTTHTHHTT", "TTHHHHTHT", "TTTTTHTTT", "HHTTHTHHT"}

Returns: 0.5019379844961235

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BestDecomposition

Greedy, Math

Used in:

TCHS SRM 3

Used as:

Division I Level Three

Writer:

gevak

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5987

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10021&pm=5987

Problem Statement

A decomposition of a non-negative integer n is a list of non-negative integers that sum to exactly n. The product of a decomposition is the product of all its members. For example, if n = 4, the following decompositions are possible:

4 = 1+1+1+1, product is 1*1*1*1 = 1.

4 = 1+1+2, product is 1*1*2 = 2.

4 = 1+3, product is 1*3 = 3.

4 = 2+2, product is 2*2 = 4.

4 = 4, product is 4.

Given an int n, determine the decomposition of n with the maximal product, and return that product modulo 10007. In the example above, the maximal product is 4 (the product of the decomposition 2 + 2).

Definition

Class:	BestDecomposition
Method:	maxProduct
Parameters:	int
Returns:	int
Method signature:	int maxProduct(int n)
(be sure your method is public)

Constraints

-

n will be between 0 and 10000, inclusive.

Examples

0)

Returns: 0

1)

Returns: 1

2)

Returns: 6

5 = 2 + 3, 2 * 3 = 6

3)

Returns: 12

7 = 3 + 4, 3 * 4 = 12

4)

Returns: 4664

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IntegerGenerator

Simple Math, String Manipulation

Used in:

SRM 281

Used as:

Division I Level One , Division II Level Two

Writer:

lovro

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5984

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8078&pm=5984

Problem Statement

As part of a larger scale project, you need to write a component which generates consecutive positive integers. Only certain digits may appear in the input and in the integers generated, and leading zeros aren't allowed.

You are given a int[] allowed containing the list of allowed digits, and a String current representing the current integer. Return a String representing the first integer larger than current composed only of digits in allowed.

If current represents an invalid integer according to the first paragraph, return "INVALID INPUT" (quotes for clarity).

Definition

Class:	IntegerGenerator
Method:	nextInteger
Parameters:	int[], String
Returns:	String
Method signature:	String nextInteger(int[] allowed, String current)
(be sure your method is public)

Constraints

- allowed will contain between 0 and 10 elements, inclusive.

- Each element in allowed will be between 0 and 9, inclusive.

- allowed will contain no duplicates.

- current will contain between 1 and 10 digits ('0'-'9'), inclusive.

Examples

0)

{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }

"16"

Returns: "17"

With all digits available, the next number is 17.

1)

{ 0, 1, 2, 3, 4, 5, 6, 8, 9 }

"16"

Returns: "18"

The digit 7 is no longer allowed, so the next smallest valid integer is 18.

2)

{ 3, 5, 8 }

"548"

Returns: "INVALID INPUT"

The current number may not contain disallowed digits.

3)

{ 5, 3, 4 }

"033"

Returns: "INVALID INPUT"

Leading zeros aren't allowed either.

4)

{ 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 }

"999"

Returns: "1000"

5)

{ 0, 1, 2, 3, 4, 5 }

"0"

Returns: "INVALID INPUT"

The generator only works with positive integers.

6)

{ 1 }

"1"

Returns: "11"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MooresLaw

Math, Search

Used in:

SRM 287

Used as:

Division I Level Two

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5973

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9808&pm=5973

Problem Statement

Moore's law is a well-known prediction of the growth of computing power over time. This is the formulation we will use in this problem: The speed of new computers grows exponentially and doubles every 18 months. In this problem we will assume that reality precisely obeys this law.

Suppose that you have a hard computational task that would take 14 years to complete on a current computer. Surprisingly, starting its computation as soon as possible is not the best you can do. A better solution: Wait for 18 months and buy a better computer. It will be twice as fast, and therefore solve the task in 7 years. You would have the result 8.5 years from now. In the best possible solution you should wait for slightly over 4 years. The computer you'll be able to buy then will solve the task in approximately 2.2 years, giving a total of 6.2 years.

You have a computational task you want to solve as quickly as possible. You will be given an int years giving the number of years it would take on a computer bought today. Return a double giving the least number of years in which you will have the result of the task if you use the above approach.

Definition

Class:	MooresLaw
Method:	shortestComputationTime
Parameters:	int
Returns:	double
Method signature:	double shortestComputationTime(int years)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

-

The computation speed growth is a continuous exponential function satisfying the property from the problem statement.

Constraints

-

years will be between 1 and 1,000,000,000, inclusive.

Examples

0)

Returns: 6.2044816339207705

The example from the problem statement.

1)

Returns: 2.870893001916099

2)

Returns: 8.82533252835082

3)

Returns: 10.907221008843223

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SnailRace

Search, Simple Math

Used in:

SRM 290

Used as:

Division I Level Two

Writer:

hauser

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5968

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9811&pm=5968

Problem Statement

George wanted to arrange a race for his snail farm. He put all his snails on the starting line, shouted "GO!", and started watching the exciting race.

After an hour or two, he realized that snails are good tacticians. All of them were running at the same constant speed of snailSpeed meters per hour, probably saving strength for a rapid finish in the last meter. With distance meters remaining until the finish line, he decides to speed up the race and help his little friends by carrying each of them closer to the end. He needs to be careful, so he decides to carry only one snail at a time. George can walk georgeSpeed meters per hour. To keep the race fair, all the snails need to be moved by the same distance, and of course, all of them need to be transported before any of them reaches one meter from the finish line.

You are given four ints: snails, the number of snails, distance, the distance in meters remaining until the finish line, snailSpeed, the speed of each snail in meters per hour, and georgeSpeed, George's walking speed in meters per hour. Compute the shortest possible time (in hours) after which all the snails will be one meter from the finish line.

Definition

Class:	SnailRace
Method:	shortestTime
Parameters:	int, int, int, int
Returns:	double
Method signature:	double shortestTime(int snails, int distance, int snailSpeed, int georgeSpeed)
(be sure your method is public)

Notes

-

You can assume that lifting up and putting down a snail doesn't take any time.

-

George can start carrying the first snail immediately because he is currently standing exactly where his snails are.

-

After carrying each snail, George needs to go back to get the next one. He does so at the same speed (georgeSpeed meters per hour).

-

Returned value must be within 1.0e-9 absolute or relative error.

-

Constraints

-

snails will be between 1 and 50, inclusive.

-

distance will be between 2 and 1000, inclusive.

-

snailSpeed will be between 1 and 100, inclusive.

-

georgeSpeed will be between 1 and 10000, inclusive.

Examples

0)

Returns: 1.75

The snails have 10 meters to go before reaching the final meter. It takes George 0.75 hours to move the first snail 6 meters forward. At that time, the second snail will be at the 3rd meter. George immediately turns back and meets that snail at the 4th meter 0.25 hours later. Finally, it takes him 0.75 hours to carry the second snail to the 10th meter, where the first snail is, for a total of 1.75 hours.

1)

Returns: 0.502

In this case, we have 3 snails, and each will be carried 10.2 meters and run the remaining 0.8 meters on its own. The total time is 0.102 + 0.4 = 0.502 hours.

2)

Returns: 0.2

It is possible for a man to move slower than a snail! George can't help his snails, so he must wait 0.2 hours, letting the snails run on their own.

3)

Returns: 0.09323356231599604

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FactorialGCD

Math, Simple Search, Iteration

Used in:

SRM 283

Used as:

Division II Level Three

Writer:

gevak

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5963

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8080&pm=5963

Problem Statement

The greatest common divisor (GCD) of two positive integers a and b is the largest integer that evenly divides both a and b. In this problem, you will find the GCD of a positive integer and the factorial of a non-negative integer.

Create a class FactorialGCD with method factGCD which takes an int a and an int b as parameters and returns the GCD of a! (the factorial of a) and b.

Definition

Class:	FactorialGCD
Method:	factGCD
Parameters:	int, int
Returns:	int
Method signature:	int factGCD(int a, int b)
(be sure your method is public)

Notes

-

Assume 0! = 1.

Constraints

-

a will be between 0 and 2147483647, inclusive.

-

b will be between 1 and 2147483647, inclusive.

Examples

0)

Returns: 20

5! = 120, so GCD(120,20) = 20.

1)

Returns: 5040

7! = 5040, GCD(5040,5040) = 5040.

2)

Returns: 1

Note that 0! = 1.

3)

Returns: 1

4)

Returns: 8

4! = 24, so GCD(24,40) = 8.

5)

2097711064

2147483646

Returns: 2147483646

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BrokenClock

Simple Math, Simple Search, Iteration

Used in:

SRM 290

Used as:

Division I Level One , Division II Level Two

Writer:

hauser

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5962

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9811&pm=5962

Problem Statement

You have noticed that your digital clock does not show the correct current time. You know what the correct time is, so there should be no problem setting it. Your clock has two buttons - one is supposed to increment the hour by 1, and the other is supposed to increment the minute by 1. The hour is a two digit value between 00 and 23, inclusive, and the minute is a two digit value between 00 and 59, inclusive. The values wrap around, so pressing the hour button when the hour is 23 will change the hour to 00, and pressing the minute button when the minute is 59 will change the minute to 00. Pressing the hour button should never affect the minute value, and pressing the minute button should never affect the hour value (see note). However, the hour button on your clock is broken, and when pressed, increments both the hour and minute by 1. You want to find the minimal number of button presses needed to set the correct time on the clock.

For example, if the clock shows the time as 03:12 and you know the current time is 04:15, you should press the hour button once and the minute button twice for a total of three button presses. After pressing the hour button, the time changes to 04:13, and after pressing the minute button twice, the time changes to 04:15. You must perform the button presses immediately - you cannot wait until the time on the clock changes by itself.

You are given a String clockTime, the time shown on the clock, and a String currentTime, the correct current time, both formatted as "HH:MM" (quotes added for clarity), where HH is the hour value and MM is the minute value.

Definition

Class:	BrokenClock
Method:	fewestClicks
Parameters:	String, String
Returns:	int
Method signature:	int fewestClicks(String clockTime, String currentTime)
(be sure your method is public)

Notes

-

If the clock displays 23:59, pressing the hour button will change the time to 00:00, but pressing the minute button will change it to 23:00.

Constraints

-

clockTime and currentTime are each formatted as "HH:MM" (quotes added for clarity) where HH is a two digit integer between 00 and 23, inclusive, and MM is a two digit integer between 00 and 59, inclusive.

Examples

0)

"03:12"

"04:15"

Returns: 3

The example from the problem statement.

1)

"07:07"

"13:21"

Returns: 14

You have to press the hour button six times and the minute button eight times.

2)

"14:55"

"14:05"

Returns: 10

The minute button never changes the hour.

3)

"23:14"

"00:20"

Returns: 6

4)

"18:43"

"18:43"

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FactorialTower

Math, Simple Search, Iteration

Used in:

SRM 283

Used as:

Division I Level Two

Writer:

gevak

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5961

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8080&pm=5961

Problem Statement

Note: this problem statement contains an image that may not display properly if viewed outside the applet.

Given an int m and a int[] a containing n numbers, return the result of the following expression:

Definition

Class:	FactorialTower
Method:	exprValue
Parameters:	int[], int
Returns:	int
Method signature:	int exprValue(int[] a, int m)
(be sure your method is public)

Notes

-

The expression is calculated from top to bottom. See example 5.

-

"x mod y" means the remainder of x divided by y.

-

Assume 0! = 1.

Constraints

-

a will contain between 1 and 50 elements, inclusive.

-

Each element of a will be between 0 and 2147483647, inclusive.

-

m will be between 1 and 40000, inclusive.

Examples

0)

{2,2,2,2}

Returns: 6

Last digit of 65536.

1)

{3,8}

Returns: 76

(3!^8!) mod 100 = 76.

2)

{775,967,1,1,1}

Returns: 4832

3)

{0}

Returns: 1

Remember that 0! is 1.

4)

{5,4,123456789,987654321,687955994,1162330089,195458992,1687386387,
1092101949,1086091397,902287014,341660341,1600834655,131565486,1494304912,
384585199,1883009662,916903507,1895924341,397197724,1883021244,1616061080,
1437763283,621297237,1883141487,282508826,285957625,1249530903,1484124572,
1822993209,1668351723,174237628,1589170712,992959839,1281777023,1158939002,
1488964134,1806511164,1519656093,159671689,542573000,1571768398,1203500608,
1053387535,793607740,1535801392,1798307613,552983945,901802936,1023595016}

Returns: 0

5)

{2,3,2}

Returns: 4096

The expression is calculated from top to bottom.

(2! to the power of (3!^2!)) mod 36864 = 4096.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RobotTesting

Brute Force, Math

Used in:

SRM 285

Used as:

Division I Level Two

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5953

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8082&pm=5953

Problem Statement

A robot is placed randomly on a cell in a NxN square grid. The robot has a program consisting of several commands, where each command is either 'U' (move up), 'D' (move down), 'L' (move left), or 'R' (move right). The commands are executed in order, and the program is cyclical (i.e., after the last command is executed, it will start over from the first command). The robot stops moving only if it has left the grid or if it has executed 50,000 commands.

You will be given an int N and a String program. Return the expected number of commands that will be executed before the robot stops. You can assume that all the cells in the grid are equally likely to be the starting cell.

Definition

Class:	RobotTesting
Method:	estimateCommands
Parameters:	int, String
Returns:	double
Method signature:	double estimateCommands(int N, String program)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

N will be between 1 and 1000, inclusive.

-

program will contain between 1 and 50 characters, inclusive.

-

Each character in program will be either 'U', 'D', 'L' or 'R'.

Examples

0)

"L"

Returns: 1.5

If the robot starts in the left column, it will leave the grid after the first command. Otherwise, it will leave the grid after the second command. These two scenarios are equally likely, so the answer is 1.5.

1)

"LURD"

Returns: 12501.0

If the robot starts in the bottom right corner, it will execute 50,000 commands.

2)

"LDLDLDRRR"

Returns: 3.375

3)

"RRULDD"

Returns: 53.236623067776456

4)

"LLLLLDRRRRR"

Returns: 3806.5179340028694

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OperationsArrangement

Brute Force, Dynamic Programming, Math

Used in:

SRM 285

Used as:

Division II Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5952

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8082&pm=5952

Problem Statement

You are given a sequence of digits. You must insert either a '+' (addition) operator or a '*' (multiplication) operator between each pair of adjacent digits in such a way that minimizes the value of the resulting expression. The expression should be evaluated using the standard order of operations (multiplication has a higher precedence than addition).

You will be given a String sequence. Perform the procedure described above on the sequence and return the resulting expression. If there are several possible answers, return the one that comes first lexicographically. Note that '*' comes before '+' lexicographically.

Definition

Class:	OperationsArrangement
Method:	arrange
Parameters:	String
Returns:	String
Method signature:	String arrange(String sequence)
(be sure your method is public)

Constraints

-

sequence will contain between 2 and 50 characters, inclusive.

-

Each character in sequence will be a digit ('0'-'9').

Examples

0)

"222"

Returns: "2*2+2"

The minimal result can be obtained in three ways: "2*2+2", "2+2*2" and "2+2+2". The first one comes first lexicographically.

1)

"322"

Returns: "3+2*2"

2)

"307"

Returns: "3*0*7"

3)

"391118571"

Returns: "3+9*1*1*1+8+5+7*1"

4)

"111221911212"

Returns: "1*1*1*2*2*1+9*1*1+2*1*2"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Equidistance

Math

Used in:

SRM 281

Used as:

Division I Level Three

Writer:

lovro

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5949

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8078&pm=5949

Problem Statement

A number of items are arranged on a long shelf (infinitely long, in fact) in a retail store. Each item's position can be described with an integral offset from some fixed point on the shelf.

There seems to be no order in how the items are currently arranged on the shelf. The store management, however, wants the shelf to be as aesthetically pleasing as possible in order to attract more customers. The management chooses to rearrange the items on the shelf so that they become equidistant, meaning that the distance between each pair of adjacent items is the same. The positions of all items must remain integers after rearranging, and no two items may occupy the same position.

Moving an item requires effort, which is measured as the absolute value of the distance that an item is moved. The management wants the items to be rearranged using the minimum possible amount of total effort, where total effort is the sum of efforts required to move each item.

Given a int[] initial, the current positions of the items on the shelf, return the minimum total effort required to make the items equidistant.

Definition

Class:	Equidistance
Method:	minimumEffort
Parameters:	int[]
Returns:	long
Method signature:	long minimumEffort(int[] initial)
(be sure your method is public)

Constraints

-

initial will contain between 2 and 50 elements, inclusive.

-

Each element of initial will be between -2,000,000,000 and 2,000,000,000, inclusive.

Examples

0)

{ 1, 4, 7, 10 }

Returns: 0

The items are already equidistant (the distance between every two adjacent items is 3) so no work needs to be done.

1)

{ 4, 3, 1 }

Returns: 1

Moving the element at position 4 to position 5 makes the items equidistant with an effort of 1.

2)

{ 3, 3, 3 }

Returns: 2

The items are initially stacked one on top of another, but we don't allow this, so we move one of the items to one side and another one to the other side.

3)

{ -2000000000, 2000000000 }

Returns: 0

A pair of items at different positions is always equidistant.

4)

{ 2, 3, 4, 6, 8, 9, 10, 11, 12, 13, 14, 15, 16, 18 }

Returns: 8

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FindTriangle

Brute Force, Geometry, Math

Used in:

SRM 288

Used as:

Division I Level One , Division II Level Two

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5943

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9809&pm=5943

Problem Statement

You are given the coordinates of several vertices in space. Each vertex is colored 'R', 'G' or 'B'. You are to determine the maximum possible area of a triangle such that all three of its vertices are the same color, or all three of its vertices are different colors.

You are given a String[] points describing the vertices. Each element of points will be in the form "color x y z", where color is 'R', 'G', or 'B', and x, y, z are integers with no leading zeroes.

Definition

Class:	FindTriangle
Method:	largestArea
Parameters:	String[]
Returns:	double
Method signature:	double largestArea(String[] points)
(be sure your method is public)

Notes

-

A triangle with all three vertices colinear, or two vertices overlapping, has area 0.

-

Returned value must be within 1.0e-9 absolute or relative error.

Constraints

-

points will have between 5 and 50 elements, inclusive.

-

Each element of points will be formatted as "color x y z" (quotes added for clarity).

-

Each color will be 'R', 'G', or 'B'.

-

Each x, y and z will be an integer between 0 and 999, inclusive, with no leading zeros.

Examples

0)

{"R 0 0 0",
 "R 0 4 0",
 "R 0 0 3",
 "G 92 14 7",
 "G 12 16 8"}

Returns: 6.0

The coloring restrictions mean that we can only consider the first three points, which form a classic 3-4-5 triangle with an area of 6.

1)

{"R 0 0 0",
 "R 0 4 0",
 "R 0 0 3",
 "G 0 5 0",
 "B 0 0 12"}

Returns: 30.0

Our bet here is to take the red point at the origin, the green point, and the blue point. These actually form a 5-12-13 triangle. Area = 30.

2)

{"R 0 0 0",
 "R 0 4 0",
 "R 0 0 3",
 "R 90 0 3",
 "G 2 14 7",
 "G 2 18 7",
 "G 29 14 3",
 "B 12 16 8"}

Returns: 225.0

We have a lot more choices here.

3)

{"R 0 0 0",
 "R 1 1 0",
 "R 4 4 0",
 "G 10 10 10",
 "G 0 1 2"}

Returns: 0.0

All three red points are colinear.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ForceTest

Dynamic Programming, Math, Search, Simulation

Used in:

SRM 276

Used as:

Division I Level Three

Writer:

timmac

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5934

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8073&pm=5934

Problem Statement

Your company produces components used in construction. From time to time, it is necessary to run a series of tests on several of the components, to determine their breaking force. The goal of the testing is to determine the point at which the unit breaks, up to a given threshold. (Only integer forces are applied.)

You have a set of components to be used for testing. You are to find an optimal testing plan, minimizing the number of tests that will have to be performed (in the worst case). In the process of testing, you may destroy some or all of the test components, provided that in the end, the breaking force is known.

Unfortunately, no manufacturing process is perfect, so it is possible that one of your test components is defective. A defective component is defined as one that breaks under a lesser force than a typically produced component.

You are given int maxForce, the highest force at which you need to test the components. (They may have a higher breaking force than this, but you are not concerned with testing any higher force.) You are also given int testUnits, the number of units that are available for testing. You are to return the fewest number of tests necessary to conclusively determine the breaking force of a non-defective component.

Definition

Class:	ForceTest
Method:	fewestTests
Parameters:	int, int
Returns:	int
Method signature:	int fewestTests(int maxForce, int testUnits)
(be sure your method is public)

Notes

-

Assume that the (non-defective) component has a fixed breaking point. That is, if it breaks when tested at a given force, it will break whenever tested with a greater force. Likewise, if it passes testing for a given force, it will pass for any lower force.

-

The testing strategy may destroy all of the components that were made available for testing, as long as it finds the exact breaking force of the non-defective component.

-

All of the test components, except for possibly a single defective one, are identical, and will break under the same force.

-

It is not necessarily the case that one of the test components is defective, however, there will never be more than one defective component.

-

A defective component will always break under a lower force than a normal component.

Constraints

-

maxForce will be between 1 and 100, inclusive.

-

testUnits will be between 2 and 20, inclusive.

Examples

0)

Returns: 2

We have to do a maximum of two tests. If the first test should fail, we need to test the second unit to determine if the first was defective.

1)

Returns: 3

Here, we have to start by testing a force of 1. If the unit breaks, we have to retest with a force of 1 to determine if the first was a defect. Then, if the second test passes, we need a third test to determine if the good unit can withstand a force of 2.

Notice that if we had tested the first component with a force of 2, and it had failed, we would have only had a single unit left, and would not have been able to determine if a defective unit was present.

2)

Returns: 6

3)

Returns: 101

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TestCurve

Math

Used in:

SRM 276

Used as:

Division II Level One

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5927

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8073&pm=5927

Problem Statement

A teacher has graded a test, and you are given a int[] scores representing each student's raw score on the test. The teacher wants to convert the scores into grades such that a raw score of 0 receives a grade of 0, and the highest raw score achieved by any student receives a grade of 100. All other scores in between are calculated proportionally, always rounded down. You are to return a int[] (with the same number of elements as scores) containing the calculated grade for each student. Element i of the return should be the grade for scores[i].

Definition

Class:	TestCurve
Method:	determineGrades
Parameters:	int[]
Returns:	int[]
Method signature:	int[] determineGrades(int[] scores)
(be sure your method is public)

Constraints

-

scores will contain between 1 and 50 elements, inclusive.

-

Each element of scores will be between 0 and 10000, inclusive.

-

At least one element of scores will be greater than 0.

Examples

0)

{15, 27, 8, 33, 19, 50}

Returns: {30, 54, 16, 66, 38, 100 }

Since the highest score is a 50, which gets scaled to a grade of 100, everyone's grade is exactly twice their raw score.

1)

{0, 0, 0, 3}

Returns: {0, 0, 0, 100 }

All but one person did poorly on this test.

2)

{67, 89, 72, 100, 95, 88}

Returns: {67, 89, 72, 100, 95, 88 }

With a highest score of 100, the grade is exactly the raw score.

3)

{1234, 3483, 234, 5738, 3421, 5832, 4433}

Returns: {21, 59, 4, 98, 58, 100, 76 }

4)

{8765}

Returns: {100 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FallingBall

Simple Math

Used in:

SRM 289

Used as:

Division I Level One , Division II Level Two

Writer:

esteban

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5911

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9810&pm=5911

Problem Statement

In a popular game, a ball is dropped from the top of a triangle of cells containing n rows. The ball keeps falling down row by row until it reaches the bottom of the triangle. In each row, the ball can fall either left or right. The first row contains one cell, the second contains two, and so on. The game looks like the following picture (where a cell is the space between two consecutive points in a row):

The rows are numbered from top to bottom starting from zero, and the cells in each row are numbered from left to right starting from zero. Note that row i will have i+1 cells numbered 0 to i, and if the ball is on cell k of row i, it will either fall left to cell k of row i+1, or right to cell k+1 of row i+1.

Given a String[] cells, containing a list of cells, and an int n, the number of rows in the triangle, return the number of paths in which the ball passes through all of the given cells. Each element of cells will be formatted "<row> <cell>" (quotes for clarity), where <row> is the cell's row, and <cell> is the cell's position within that row.

Definition

Class:	FallingBall
Method:	howMany
Parameters:	String[], int
Returns:	int
Method signature:	int howMany(String[] cells, int n)
(be sure your method is public)

Constraints

-

cells will have between 1 and 50 elements, inclusive.

-

n will be between 1 and 30, inclusive.

-

Each element of cells will be formatted "<row> <cell>", where <row> and <cell> are each integers, with no extra leading zeros.

-

Each <row> in cells will be between 0 and n-1, inclusive.

-

In each element of cells, <cell> will be between 0 and <row>, inclusive.

Examples

0)

{"3 2","5 2"}

Returns: 6

This example is shown in the picture above. There are 3 ways to reach the cell (3,2), then only one way to reach the second cell (5,2), and two more ways of reaching the bottom. That gives a total of 6 ways of passing through the cells.

1)

{"0 0","0 0"}

Returns: 536870912

All the possible paths pass through the cell (0,0).

2)

{"0 0","29 0"}

Returns: 1

There is only one way to reach the bottom-right cell.

3)

{"10 0","10 1"}

Returns: 0

Two different cells in the same row can never be touched in the same path.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CuttingPoles

Simple Math, Simulation

Used in:

SRM 286

Used as:

Division II Level One

Writer:

ged

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5905

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8083&pm=5905

Problem Statement

A careless worker planted several poles in a row to build a fence. They all should be the same height, but they were cut at different sizes. The owner wants them not only all at the same height, but also as tall as possible.

Our solution will be to cut the tops of taller poles and "glue" those tops on top of the shorter ones. To do this, we will first sort the poles from tallest to shortest, and proceed as follows:

Cut the tip of the tallest pole, leaving its height equal to the average height of the poles (so we do not cut it anymore).
"glue" this piece on top of the shortest pole.
Re-sort the poles, and continue from the first step until all poles are the same height.

Write a class CuttingPoles with a method countCuts that takes a int[] of pole heights and returns the number of cuts needed to make them all the same height using the algorithm described.

Definition

Class:	CuttingPoles
Method:	countCuts
Parameters:	int[]
Returns:	int
Method signature:	int countCuts(int[] poles)
(be sure your method is public)

Constraints

-

poles will contain between 1 and 50 elements, inclusive.

-

Each element of poles must be between 1 and 1000, inclusive.

-

The average value of poles will be an integer.

Examples

0)

{1,3}

Returns: 1

Cropping the taller pole to a height of 2 and gluing its top piece onto the shorter pole leaves them both with the same height.

1)

{10,10,10}

Returns: 0

No cuts needed.

2)

{1,1,3,3}

Returns: 2

3)

{10,10,10,10,10,10,10,18}

Returns: 7

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SymbolFrequency

Simple Math, String Manipulation

Used in:

TCHS SRM 1

Used as:

Division I Level Two

Writer:

ged

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5902

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10022&pm=5902

Problem Statement

In written languages, some symbols may appear more often than others. Expected frequency tables have been defined for many languages. For each symbol in a language, a frequency table will contain its expected percentage in a typical passage written in that language. For example, if the symbol "a" has an expected percentage of 5, then 5% of the letters in a typical passage will be "a". If a passage contains 350 letters, then 'a' has an expected count of 17.5 for that passage (17.5 = 350 * 5%). Please note that the expected count can be a non-integer value.

The deviation of a text with respect to a language frequency table can be computed in the following manner. For each letter ('a'-'z') determine the difference between the expected count and the actual count in the text. The deviation is the sum of the squares of these differences. Blank spaces (' ') and line breaks (each element of text is a line) are ignored when calculating percentages.

Each frequency table will be described as a concatenation of up to 16 strings of the form "ANN", where A is a lowercase letter ('a'-'z') and NN its expected frequency as a two-digit percentage between "00" (meaning 0%) and "99" (meaning 99%), inclusive. Any letter not appearing in a table is not expected to appear in a typical passage (0%). You are given a String[] frequencies of frequency tables of different languages. Return the lowest deviation the given text has with respect to the frequency tables.

Definition

Class:	SymbolFrequency
Method:	language
Parameters:	String[], String[]
Returns:	double
Method signature:	double language(String[] frequencies, String[] text)
(be sure your method is public)

Notes

- The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

- frequencies will contain between 1 and 10 elements, inclusive.

- Each element of frequencies will be formatted as described in the statement.

- Each element of frequencies will contain between 6 and 48 characters, inclusive.

- No letter will appear twice in the same element of frequencies.

- The sum of the percentages in each element of frequencies will be equal to 100.

- text will contain between 1 and 10 elements, inclusive.

- Each element of text will contain between 1 and 50 characters, inclusive.

- Each element of text will contain only lowercase letters ('a'-'z') and spaces (' ').

- text will have at least one non-space character.

Examples

0)

{"a30b30c40","a20b40c40"}

{"aa bbbb cccc"}

Returns: 0.0

The first table indicates that 30% of the letters are expected to be 'a', 30% to be 'b', and 40% to be 'c'. The second table indicates that 20% are expected to be 'a', 40% to be 'b', and 40% to be 'c'. We consider the text to have length 10, as blank spaces are ignored.

With respect to the first table, there are 2 'a' where 3 were expected (a difference of 1), one more 'b' than expected (again a difference of 1) and as many 'c' as expected. The sum of the squares of those numbers gives a deviation of 2.0.

As for the second table, the text matches expected counts exactly, so its deviation with respect to that language is 0.0.

1)

{"a30b30c40","a20b40c40"}

{"aaa bbbb ccc"}

Returns: 2.0

Here we use the same tables as in the previous example, but with a different text. The counts for 'b' and 'c' each differ by 1 from the expected counts in the first table, and the counts for 'a' and 'c' each differ by 1 from the expected counts in the second table. The text has a deviation of 2.0 with respect to both tables.

2)

{"a10b10c10d10e10f50"}

{"abcde g"}

Returns: 10.8

Here, each of the letters 'a' through 'e' is expected to make up 10% of the letters (0.6 letters). Each of those letters actually appears once, so the difference is 0.4, which becomes 0.16 when squared. 50% of the letters (3 letters) are expected to be 'f', but 'f' does not appear at all. The square of this difference is 9.0. No 'g's are expected to appear, but there is one in the text. This adds 1.0 to the deviation. The final deviation for this table is: 0.16+0.16+0.16+0.16+0.16+9.0+1.0=10.8.

3)

{"a09b01c03d05e20g01h01i08l06n08o06r07s09t08u07x01"
,"a14b02c05d06e15g01h01i07l05n07o10r08s09t05u04x01"}

{"this text is in english" 
,"the letter counts should be close to"
,"that in the table"}

Returns: 130.6578

These two frequency tables correspond (roughly) to the frequencies found in the English and Spanish languages, respectively. The English passage, as expected, has a lower deviation in the first table than in the second one.

4)

{"a09b01c03d05e20g01h01i08l06n08o06r07s09t08u07x01"
,"a14b02c05d06e15g01h01i07l05n07o10r08s09t05u04x01"}

{"en esta es una oracion en castellano"
,"las ocurrencias de cada letra"
,"deberian ser cercanas a las dadas en la tabla"}

Returns: 114.9472

The same tables again, but with Spanish passage. This time the second table, which correspond to frequencies in Spanish, gives the lowest deviation.

5)

{"z99y01", "z99y01", "z99y01", "z99y01", "z99y01", 
 "z99y01", "z99y01", "z99y01", "z99y01", "z99y01"}

{"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
 "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
 "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
 "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
 "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
 "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
 "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
 "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
 "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa",
 "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"}

Returns: 495050.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ExtraBall

Simple Math

Used in:

SRM 286

Used as:

Division I Level One , Division II Level Two

Writer:

ged

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5891

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8083&pm=5891

Problem Statement

In a Bingo game, players have cards bearing a random selection of numbers ranging from 1 to 75. During the game, a blower containing exactly one ball for each of these numbers releases balls one at a time, without replacement, until a certain number of balls have been released. After each ball is released, the players will mark the cells on their cards that match the number on the ball. A player's objective in this game is to win prizes by matching the markings on his card with one or more predesignated patterns. Each pattern consists of the same number of cells as a card, and each cell in a pattern is either a 'X' or a '.'. A pattern is considered matched when all the cells on a card corresponding to its 'X's are marked. At the end of the game, each player wins all of the prizes corresponding to all the patterns matched by his card. For example, consider a card with four cells containing the numbers [1,10,2,3]. The winning patterns are given as "X...", "X..X", and "XXXX". If the balls released in a given game were 1, 2, 3, 4, and 5, you would mark the cells on the card containing the numbers 1, 2, and 3. The following two patterns would be matched by the card:

"X...", which represents a pattern that requires the first cell to be marked.
"X..X", a pattern that requires the cells at both ends of the card to be marked.

The card would not match the pattern "XXXX" because the second cell is not marked.

At the end of the game, one additional ball is released to give players a chance to win additional prizes. Determine the expected increase in your payout after this new ball is released. In other words, determine the expected payout of the patterns matched by the new ball, excluding all the patterns that were already matched before the new ball was released. In the example given above, there is a probability of 1/70 that the pattern "XXXX" will be matched after the additional ball is released (the additional ball would have to be 10). The expected increase in payout would therefore be 1/70 times the payout associated with that pattern.

You are given a int[] card containing the numbers on your card, and a int[] balls containing the sequence of balls that have already been released from the blower. You are also given a String[] patterns and a int[] prizes. The i-th element of prizes is the payout corresponding to the i-th element of patterns. As described above, one additional ball will be released from the blower. Return the expected increase in your payout after the new ball is released.

Definition

Class:	ExtraBall
Method:	expectedPayout
Parameters:	int[], int[], String[], int[]
Returns:	double
Method signature:	double expectedPayout(int[] card, int[] balls, String[] patterns, int[] prizes)
(be sure your method is public)

Notes

- All available balls have the same probability of being released.

- Your return value must have a relative or absolute error less than 1e-9.

Constraints

- card will contain between 1 and 25 elements, inclusive.

- balls will contain between 1 and 40 elements, inclusive.

- Each element of card and balls will be between 1 and 75, inclusive.

- No two elements of card will be equal.

- No two elements of balls will be equal.

- patterns will contain between 1 and 50 elements, inclusive.

- prizes and patterns will contain the same number of elements.

- The number of characters in each element of patterns will be equal to the number of elements in card.

- Each element of patterns will contain only uppercase 'X' and '.' characters.

- Each element of patterns will contain at least one 'X' character.

- Each element of prizes will be between 1 and 10000, inclusive.

Examples

0)

{1,2,3}

{1,2,4}

{"XXX"}

{10000}

Returns: 138.88888888888889

The full card pays a 10,000 jackpot. One of the 72 remaining balls will complete the pattern, thus (1/72)*10000 = 138.888888888 is the expected payout value.

1)

{1,2,3,4,5}

{6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26}

{"X.X.X"}

{10}

Returns: 0.0

Three balls (1, 3, and 5) are needed to get the prize, but since only one additional ball is released, the prize cannot be won.

2)

{29,16,2,35,75}

{75,4,16,3,21,44,2,38,11}

{"X....","X.X.X","XXX..","XXXXX"}

{10,100,300,1000}

Returns: 6.212121212121213

3)

{1,2,3,4,5,6,7,8,9,10}

{75}

{"X.........",".X........","..X.......","...X......","....X.....","XXXXXXXXXX"}

{50,40,30,20,10,1000}

Returns: 2.027027027027027

4)

{1,2,3,4}

{12,34,45,56,67,1,2,3,4}

{"X..X","XXXX"}

{10,100}

Returns: 0.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FewestFactors

Brute Force, Simple Math

Used in:

SRM 272

Used as:

Division I Level One , Division II Level Two

Writer:

gepa

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5886

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8069&pm=5886

Problem Statement

You will be given some decimal digits in a int[] digits. Build an integer with the minimum possible number of factors, using each of the digits exactly once (be sure to count all factors, not only the prime factors). If more than one number has the same (minimum) number of factors, return the smallest one among them.

Definition

Class:	FewestFactors
Method:	number
Parameters:	int[]
Returns:	int
Method signature:	int number(int[] digits)
(be sure your method is public)

Notes

-

A factor of an integer n is an integer k, such that n % k = 0 (% being the modulo operator).

-

The digit 0 can also be used as a leading zero, see example 1.

Constraints

-

digits will have between 1 and 5 elements, inclusive.

-

Each element of digits will be between 0 and 9, inclusive.

-

At least one element of digits will be non-zero.

Examples

0)

{1, 2}

Returns: 21

Using the digits 1 and 2 we can build the numbers 12 (which has 6 factors: 1, 2, 3, 4, 6 and 12) and 21 (which has 4 factors: 1, 3, 7 and 21). So we return 21, which is the number among them having the smallest number of factors.

1)

{6, 0}

Returns: 6

Note that we can use 0 as a leading zero, giving the number 6 that has 4 factors (1, 2, 3 and 6), less than the alternative 60 that has 12 factors.

2)

{4, 7, 4}

Returns: 447

Note that digits may contain duplicate digits. We have to use each digit as many times as it appears in the input.

3)

{1, 3, 7, 9}

Returns: 1973

4)

{7, 5, 4, 3, 6}

Returns: 36457

5)

{1,2,4}

Returns: 241

Both 241 and 421 are prime numbers, and thus have exactly 2 factors (241 has the factors 1 and 241, while 421 has the factors 1 and 421). All other numbers that we can build from these digits (124, 142, 214 and 412) have more than 2 factors. We have to use the tie-breaker here and return the smaller of (241, 421).

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RobotCollision

Simple Math, Simple Search, Iteration, Simulation

Used in:

SRM 273

Used as:

Division I Level Three

Writer:

supernova

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5878

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8070&pm=5878

Problem Statement

You work in the field of Robotics and you are doing some black-box testing. Two robots, Robbie and Speedy, are randomly placed in a rectangular room, which is divided into xSize * ySize cells. Each robot receives a few movement commands that are executed one by one, at the same time, by both the robots.

A move is represented by an uppercase letter, which is one of the following:

- 'U': the robot moves from the coordinates (x, y) to the coordinates (x - 1, y). This command is ignored when x = 0.

- 'D': the robot moves from the coordinates (x, y) to the coordinates (x + 1, y). This command is ignored when x = xSize - 1.

- 'L': the robot moves from the coordinates (x, y) to the coordinates (x, y - 1). This command is ignored when y = 0.

- 'R': the robot moves from the coordinates (x, y) to the coordinates (x, y + 1). This command is ignored when y = ySize - 1.

Two robots may collide if they start one of their turns from the same cell, end one of their turns in the same cell, or exchange positions at one of their turns. You will be given an int xSize and an int ySize denoting the dimensions of the rectangular room, a String commandsRobbie denoting the movement commands given to Robbie and a String commandsSpeedy denoting the movement commands given to Speedy. Your task is to return the probability that the two robots will collide, taking into acount every possible start position for both of the robots. The probability for each robot to start in any specific cell is the same for all cells.

Definition

Class:	RobotCollision
Method:	probability
Parameters:	int, int, String, String
Returns:	double
Method signature:	double probability(int xSize, int ySize, String commandsRobbie, String commandsSpeedy)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

xSize will be between 1 and 100, inclusive.

-

ySize will be between 1 and 100, inclusive.

-

commandsRobbie and commandsSpeedy will each contain between 0 and 10 characters, inclusive.

-

Each character in commandsRobbie and commandsSpeedy is either 'U', 'D', 'L' or 'R'.

-

commandsRobbie and commandsSpeedy have the same length.

Examples

0)

"L"

"R"

Returns: 0.27

In this example, Robbie goes one step left and Speedy goes one step right. Out of the 100 possible starting positions (10 for each robot), 27 of them will lead to collision. A collision happens in one of the following three ways:

- Robbie and Speedy start at the same cell. In this case we have an instant collision. There are 10 such starting positions.

- Robbie starts at Speedy's immediate right. In this case we have a frontal collision as the two robots approach each other. There are 9 such starting positions.

- Robbie starts two steps to the right from Speedy. In this case the robots end up in the same cell after they make their moves, so again, we have a collision. There are 8 such starting positions.

1)

"DRUL"

"DRUL"

Returns: 1.0

2)

"DRUL"

"RULD"

Returns: 0.4375

3)

"D"

"D"

Returns: 0.012

4)

""

""

Returns: 0.0010

5)

"U"

"D"

Returns: 2.97E-4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RogersPhenomenon

Simple Math

Used in:

SRM 277

Used as:

Division I Level One , Division II Level Two

Writer:

lovro

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5870

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8074&pm=5870

Problem Statement

The Will Rogers phenomenon is the apparent paradox which occurs when, upon moving an element from one set of numbers to another set, the means (averages) of both sets increase.

For example, the sets { 1, 2, 3 } and { 4, 5, 6 } have means 2 and 5, respectively. Moving the 4 to the first set would increase its mean to 2.5, while also increasing the mean of the second set to 5.5.

More precisely, we will consider the phenomenon to have occured if, upon moving a number between sets, the mean of both of the sets has strictly increased. An element may be moved from a set only if the set contains at least two elements.

You are to move exactly one number from one of the sets to the other. Given the initial configuration of the sets as two int[]s, set1 and set2, return the number of elements which trigger the phenomenon when chosen to be moved.

Definition

Class:	RogersPhenomenon
Method:	countTriggers
Parameters:	int[], int[]
Returns:	int
Method signature:	int countTriggers(int[] set1, int[] set2)
(be sure your method is public)

Notes

-

The sets may contain duplicate elements, all of which should be included when calculating averages.

Constraints

-

Both set1 and set2 will contain between 1 and 50 elements, inclusive.

-

Each element in set1 and set2 will be between -1000 and 1000, inclusive.

Examples

0)

{ 1, 2, 3 }

{ 4, 5, 6 }

Returns: 1

This is the example from the problem statement. The number 4 from the second set is the only one which triggers the Rogers phenomenon.

1)

{ 3, 100, 90 }

{ 5, 1, 18, 29 }

Returns: 0

2)

{ 1, 1, 1, 1, 1, 5 }

{ -10, -9, -8, -7, -6 }

Returns: 5

The sets may contain duplicate elements. Moving any of the 1's from the first set increases the means of both sets.

3)

{ 12, 94, 53, 43, 58, 85, 55, 83, 47, 57 }

{ 23, 100, 98, 27, 9, 70, 39, 39, 54 }

Returns: 4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AmountApproximation

Simple Math

Used in:

SRM 274

Used as:

Division II Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4845

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8071&pm=4845

Problem Statement

We must pay D dollars. Unfortunately, we only have bills of two denominations: p1 dollars and p2 dollars. So, we want to overpay as little as possible.

You will be given ints D, p1 and p2. Return the minimum number of dollars greater than or equal to D that can be paid with the given bills. Assume that we have an infinite supply of both p1 and p2 dollar bills.

Definition

Class:	AmountApproximation
Method:	approximate
Parameters:	int, int, int
Returns:	int
Method signature:	int approximate(int D, int p1, int p2)
(be sure your method is public)

Constraints

-

D will be between 1 and 1000000000 (10⁹), inclusive.

-

p1 will be between 1 and 1000000000 (10⁹), inclusive.

-

p2 will be between 1 and 1000000000 (10⁹), inclusive.

Examples

0)

Returns: 18

18 = 7 * 0 + 9 * 2

1)

Returns: 20

20 = 7 * 1 + 13 * 1

2)

Returns: 21

21 = 7 * 3 + 13 * 0

3)

Returns: 43

43 = 9 * 1 + 17 * 2

4)

Returns: 287398

287398 = 2345 * 104 + 7253 * 6

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RingImposition

Math, Recursion

Used in:

SRM 274

Used as:

Division I Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4839

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8071&pm=4839

Problem Statement

Numbers from the sequence seq are placed around a circle in order. During an imposition operation, each number becomes the sum of itself and the next number in order, modulo 100 (i.e., if the sum is greater than or equal to 100, 100 is subtracted from it). The last number in the sequence is summed with the first one, modulo 100.

You will be given a int[] seq and an int N. Return the seq after N imposition operations.

Definition

Class:	RingImposition
Method:	predict
Parameters:	int[], int
Returns:	int[]
Method signature:	int[] predict(int[] seq, int N)
(be sure your method is public)

Constraints

-

seq will have between 2 and 50 elements, inclusive.

-

Each element of seq will be between 0 and 99, inclusive.

-

N will be between 1 and 2000000000, inclusive.

Examples

0)

{1, 2, 3}

Returns: {8, 9, 7 }

After the first imposition operation the sequence become {1+2, 2+3, 3+1} or {3, 5, 4}. After the second imposition operation the sequence become {3+5, 5+4, 4+3} or {8, 9, 7}.

1)

{25, 0, 0, 0}

Returns: {0, 0, 0, 0 }

2)

{3, 15, 7, 1, 16}

Returns: {41, 50, 84, 97, 72 }

The sequence transformation is {3, 15, 7, 1, 16} -> {18, 22, 8, 17, 19} -> {40, 30, 25, 36, 37} -> {70, 55, 61, 73, 77} -> {25, 16, 34, 50, 47} -> {41, 50, 84, 97, 72}

3)

{3, 15, 7, 1, 16, 1, 72}

Returns: {88, 72, 62, 55, 11, 11, 21 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Superking

Math

Used in:

TCO05 Finals

Used as:

Division I Level One

Writer:

gepa

Testers:

PabloGilberto , lbackstrom , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4836

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8096&pm=4836

Problem Statement

We have an infinite chess board, and a new type of chess piece called a "superking". It can perform two types of moves:

Type-1: the normal king move - i.e., a move to a neighboring square in any of the eight directions horizontal, vertical or diagonal.
Type-2: a move two squares to the left, right, up or down.

The superking begins at some square in the infinite board and performs type1 Type-1 moves and type2 Type-2 moves. Return the number of possible squares that the superking can reach after performing these moves.

Definition

Class:	Superking
Method:	squares
Parameters:	int, int
Returns:	long
Method signature:	long squares(int type1, int type2)
(be sure your method is public)

Constraints

-

type1 and type2 will be between 0 and 100000000 (10⁸), inclusive.

Examples

0)

Returns: 1

No moves are made, superking remains at the starting square.

1)

Returns: 8

After one Type-1 move (normal king move), the superking can land in one of the 8 neighboring squares.

2)

Returns: 4

After one Type-2 move, the superking lands in one of the four squares at a distance of 2 from the starting square (to the left, right, up or down).

3)

Returns: 60

Let's assume that the superking starts at the red square at the center of the board shown below. After one Type-2 move, the superking can land in one of the blue squares. After the second Type-2 move, the superking can land in one of the red squares. After a final Type-1 move, the superking can land in any square neighboring a red square, i.e., one of the green squares. These are the possible final landing squares for the king after 1 Type-1 and 2 Type-2 moves, 60 in total (note that it is not important in which order we make the moves; here, we first did the two Type-2 moves and then the Type-1 move).

4)

Returns: 14713

5)

Returns: 35881

6)

100000000

100000000

Returns: 280000000400000001

The maximum return value.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RoundTable

Dynamic Programming, Math

Used in:

SRM 272

Used as:

Division I Level Two

Writer:

gepa

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4835

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8069&pm=4835

Problem Statement

There are countA representatives of a company A and countB representatives of a company B that are having a meeting at a round table. There are chairs chairs around the table and they want to sit down in such a way that no representative of company A is sitting closer than minDistance to a representative of company B (minDistance=1 means any seating is allowed, minDistance=2 means there must be at least one empty chair between representatives of different companies, etc.).

Return the number of ways that such a seating arrangement is possible. Two seating arrangements are different if at least one person is sitting in different chairs in the two arrangements (i.e., include in the count all possible rotations of each seating arrangement). Note also that two different representatives of the same company are to be treated as different persons, see example 5.

Definition

Class:	RoundTable
Method:	arrangements
Parameters:	int, int, int, int
Returns:	long
Method signature:	long arrangements(int countA, int countB, int chairs, int minDistance)
(be sure your method is public)

Notes

-

The return value will fit in a 64 bit signed int.

-

The input values are not guaranteed to allow a valid seating arrangement; if there is no seating arrangement that satisfies the input, return 0.

Constraints

-

countA and countB will each be between 1 and 5, inclusive.

-

chairs will be between 1 and 50, inclusive.

-

minDistance will be between 1 and 50, inclusive.

Examples

0)

Returns: 90

Each company sends one representative. The first one can sit in any of the 10 chairs, the second one in any of the remaining 9 chairs (since minDistance=1 he may sit arbitrarily close to the other one). So there are a total of 10 * 9 = 90 arrangements.

1)

Returns: 70

The same as example 0, but now the second one can not sit next to the first one, so only 7 chairs remain that he can choose from. This gives a total of 10 * 7 = 70 arrangements.

2)

Returns: 14

Company A sends one representative, who sits down in one of the 7 possible chairs. Since minDistance=3, two chairs next to him at each side must remain empty. This leaves only 2 chairs that the 2 representatives from company B have to share (2 possible combinations for which one takes which of the two chairs). This gives a total of 7 * 2 = 14 arrangements.

3)

Returns: 0

There are not enough chairs (5 + 3 = 8 representatives in total, but only 7 chairs).

4)

Returns: 0

Now there would be enough chairs, but since minDistance=3, we have to keep 2 chairs empty between the groups at each side, thus requiring at least 5 + 3 + 2 + 2 = 12 chairs.

5)

Returns: 6

Note that the two representatives of company A are treated as different persons, so there are a total of 3! = 6 possibilities to assign the three representatives to the three available chairs.

6)

Returns: 180000

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RandomChoice

Math

Used in:

TCO05 Semi 2

Used as:

Division I Level Three

Writer:

gepa

Testers:

PabloGilberto , lbackstrom , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4819

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8092&pm=4819

Problem Statement

We have to make a uniform random decision among k possible outcomes, but all we have available is an unfair coin.

The coin has a probability p_H of giving Heads and p_T = 1 - p_H of giving Tails in the first throw. Subsequent throws are dependent on the previous throw, and there is a probability p_HT of throwing Tails after a Heads throw and p_TH of throwing Heads after a Tails throw. Note that either Heads or Tails always comes out, so the probability of throwing Tails after a Tails throw is p_TT = 1 - p_TH and the probability of throwing Heads after a Heads throw is p_HH = 1 - p_HT.

In order to make a fair decision, we throw the coin n times. If there are k coin result sequences that are equally probable (independent of p_H, p_HT and p_TH), we can map each of these sequences to one of the k original decision outcomes. We repeat this with further coin result sequences, mapping as many of them as possible to the k original decision outcomes. At the end, some of the coin result sequences may remain unmapped. After we throw the coin n times, either one of the mapped sequences will come out, in which case we can directly make the fair decision by choosing the mapped outcome, or one of the unmapped sequences will come out, in which case we still cannot make a fair decision (we could then repeat making n further throws, until one of the mapped sequences comes out).

For example, let's say k = 3, and n = 6 (we have to choose among three outcomes, and throw the coin 6 times). In this case, the sequences "HTHHHH", "HHTHHH", "HHHTHH" and "HHHHTH" are equally probable (the given strings show the outcome of the 6 coin throws in order, with H representing Heads and T representing Tails; each of these sequences has a probability of p_H * p_HH * p_HH * p_HT * p_TH). So we can map three of these sequences to the three outcomes, and one sequence will remain unmapped. Similarly, we can map the sequences "HTTHHH", "HHTTHH" and "HHHTTH" to the three outcomes. We get similarly six further mappings if we exchange "H" and "T" in these sequences. It turns out that these are the only mappings that we can find in this case, meaning that we have mapped 12 of the 2⁶=64 possible sequences, with 52 sequences remaining unmapped. Note also that sequences that remain unmapped in one mapping step can still be used in further steps - i.e., if in the example above k was 2 instead of 3, and we mapped 2 of the first 4 mentioned sequences above to the 2 outcomes, the remaining 2 would also get mapped, since they still have the same probability. In general, if we have m equally probable outcomes, m % k of them will remain unmapped, while the other m - (m % k) outcomes will get mapped to some of the original decisions.

You will be given k, the number of outcomes in the decision you have to make, n, the number of coin throws you perform, and pH, pHT and pTH, the initial and subsequent conditional probabilities of the coin outcome (p_H, p_HT and p_TH from the above description, respectively). You are to return the probability that the n throws will be sufficient to make a decision - i.e., the probability that we will get one of the outcomes that we have mapped to one of the original decision outcomes.

Definition

Class:	RandomChoice
Method:	decisionProbability
Parameters:	int, int, double, double, double
Returns:	double
Method signature:	double decisionProbability(int k, int n, double pH, double pHT, double pTH)
(be sure your method is public)

Notes

-

When checking if two coin result sequences are equally probable, we don't take the given probabilities into account - i.e. the person performing the described procedure does not have any information about the probabilities. The probabilities are given in the method input since they are needed to compute the return value - i.e., after having decided which sequences are still unmapped, to compute the probability of one of these sequences coming up.

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

k will be between 2 and 1000, inclusive.

-

n will be between 1 and 1000, inclusive.

-

pH will be between 0.01 and 0.99, inclusive.

-

pHT will be between 0.01 and 0.99, inclusive.

-

pTH will be between 0.01 and 0.99, inclusive.

Examples

0)

0.5

0.5

0.5

Returns: 0.25

With n=4 we can get the following outcomes, each with the given probability:

HHHH  (pH * pHH * pHH * pHH)    THHH  (pT * pTH * pHH * pHH)
HHHT  (pH * pHH * pHH * pHT)    THHT  (pT * pTH * pHH * pHT)
HHTH  (pH * pHH * pHT * pTH)    THTH  (pT * pTH * pHT * pTH)
HHTT  (pH * pHH * pHT * pTT)    THTT  (pT * pTH * pHT * pTT)
HTHH  (pH * pHT * pTH * pHH)    TTHH  (pT * pTT * pTH * pHH)
HTHT  (pH * pHT * pTH * pHT)    TTHT  (pT * pTT * pTH * pHT)
HTTH  (pH * pHT * pTT * pTH)    TTTH  (pT * pTT * pTT * pTH)
HTTT  (pH * pHT * pTT * pTT)    TTTT  (pT * pTT * pTT * pTT)

The outcomes HHTH and HTHH are equally probable (independent of how the individual probabilities pH, pHT, pTH are chosen), so they can be mapped to the k=2 original outcomes. The same is true for the outcomes TTHT and THTT. The rest remains unmapped (there is no other pair with equal probabilities). To compute the return value, we now insert the given values for pH, pHT, pTH, and add the probabilities for the mapped outcomes (4 mapped outcomes, each with probability 0.5⁴, which gives the result 0.25).

1)

0.1

0.8

0.6

Returns: 0.3648

The same as the previous examples, but with different probabilities. The final result is now: 2 * p_H * p_HH * p_HT * p_TH + 2 * p_T * p_TT * p_TH * p_HT = 2 * 0.1 * (1.0 - 0.8) * 0.8 * 0.6 + 2 * (1.0 - 0.1) * (1.0 - 0.6) * 0.6 * 0.8 = 0.3648.

2)

0.5

0.5

0.5

Returns: 0.625

With n=6, we get the following equally probable outcome n-tuples:

 1: (HHHHTH, HHHTHH, HHTHHH, HTHHHH)
 2: (HHTHTT, HHTTHT, HTHHTT, HTTHHT)
 3: (TTTTHT, TTTHTT, TTHTTT, THTTTT)
 4: (TTHTHH, TTHHTH, THTTHH, THHTTH)
 5: (HHHTHT, HHTHHT, HTHHHT)
 6: (HHHTTH, HHTTHH, HTTHHH)
 7: (HHTHTH, HTHHTH, HTHTHH)
 8: (HTHTTT, HTTHTT, HTTTHT)
 9: (TTTHTH, TTHTTH, THTTTH)
10: (TTTHHT, TTHHTT, THHTTT)
11: (TTHTHT, THTTHT, THTHTT)
12: (THTHHH, THHTHH, THHHTH)
13: (HHTTTH, HTTTHH)
14: (HTHTTH, HTTHTH)
15: (TTHHHT, THHHTT)
16: (THTHHT, THHTHT)

Since here k=2, we can map all outcomes in all quadruples (1 - 4) and all pairs (13 - 16) and from each triple (5 - 12) we map a pair and leave one element unmapped. So in total we have mapped 40 outcomes. Since we have pH=pHT=pTH=0.5, the probability of each outcome is 0.5⁶, and the final result is 40 * 0.5⁶ = 0.625.

3)

0.5

0.5

0.5

Returns: 0.5625

The same example as the last one, but now with k=3. Now we can map all triples (5 - 12 from the previous example) to the k=3 outcomes and 3 elements from each quadruple (1 - 4), for a total of 36 mapped outcomes, giving 36 * 0.5⁶ = 0.5625.

4)

0.5

0.5

0.5

Returns: 0.0

With just one throw we can never be sure to make a fair decision.

5)

0.5

0.01

0.01

Returns: 0.9972747235292863

Be sure not to timeout.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DivisibilityRules

Math

Used in:

SRM 264

Used as:

Division I Level One , Division II Level Two

Writer:

Enogipe

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4816

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7998&pm=4816

Problem Statement

Many people know that a number is divisible by 3 if and only if the sum of its digits is divisible by 3, and similarly for divisibility by 9. Some know that a number is divisible by 6 if and only if the sum of the least significant digit (the ones place) and each of the other digits times four is divisible by 6, e.g., 792 is divisible by 6 and 4*7 + 4*9 + 1*2 = 66, which is divisible by 6. Of course, this is just in base 10. It turns out that for every number, in every base, there is a "divisibility rule".

Suppose you want to find a rule for dividing by some divisor in a certain numerationBase. Raising numerationBase to the i-th power and taking the result modulo divisor, you obtain a multiplier for the i-th digit of a number. For example, in base 10, dividing by 3, we get the multipliers:

10⁰ % 3 = 1 % 3 = 1
10¹ % 3 = 10 % 3 = 1
10² % 3 = 100 % 3 = 1
...

so if the result is divisible by 3 when each digit is multiplied by 1, the original must have been divisible by 3 as well.

When the same multiplier is used for digit j as for digit i, with j > i, a cycle has been detected and will repeat for the remainder of the rule.

Since both 3 and 9 have the same rule in base 10, namely, "multiply each digit by 1, sum them, and check to see if the result is divisible by 3 (or 9, respectively)", you wonder whether other digits have similar divisibility rules. Determine the number of digits in numerationBase which have the same divisibility rules as divisor. A number is considered a digit in a numerationBase if it is between 0 and numerationBase - 1, inclusive, but we will exclude 0 and 1 from consideration.

Definition

Class:	DivisibilityRules
Method:	similar
Parameters:	int, int
Returns:	int
Method signature:	int similar(int numerationBase, int divisor)
(be sure your method is public)

Notes

-

Here the 0-th digit in a number is the least significant digit, and so on.

-

The multipliers in the divisibility rule for a divisor must be less than divisor. For example, though the rule "multiply every digit by 4, sum the results, and check for divisibility by 3" would work for numerationBase 10, divisor 3, we do not consider it valid since 4 >= 3.

-

The result should always be at least 1: divisor has the same divisibility rules as divisor!

Constraints

-

numerationBase will be between 3 and 1000, inclusive.

-

divisor will be between 2 and numerationBase-1, inclusive.

Examples

0)

Returns: 2

Both 3 and 9 have the same divisibility rules in base 10: multiply each digit by 1, sum the results, and check for divisibility by 3 or 9 respectively.

1)

Returns: 2

2 and 5 have the same divisibility rules in base 10: add 1 times the 0-th digit and 0 times the other digits; see if the result is divisible by 2 or 5 respectively.

2)

Returns: 10

The identical rules are for digits 32, 40, 60, 80, 96, 120, 160, 240, and 480. Each has the following rule: Multiply the 0th, 2nd, 4th, 6th, etc. digits by 1, multiply the 1st, 3rd, 5th, etc. digits by 31, add the results, and check for divisibility by 32, 40, 60, 80, 96, 120, 160, 240, or 480.

3)

Returns: 1

4)

Returns: 7

5)

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TriCount

Math

Used in:

SRM 284

Used as:

Division I Level One

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4811

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8081&pm=4811

Problem Statement

We are interested in triangles that have integer length sides, all of which are between minLength and maxLength, inclusive. How many such triangles are there?

Two triangles differ if they have a different collection of side lengths, ignoring order. Triangles with side lengths {2,3,4} and {4,3,5} differ, but {2,3,4} and {4,2,3} do not. We are only interested in proper triangles; the sum of the two smallest sides of a proper triangle must be strictly greater than the length of the biggest side.

Create a class TriCount that contains a method count that is given ints minLength and maxLength and returns the number of different proper triangles whose sides all have lengths between minLength and maxLength, inclusive. If there are more than 1,000,000,000 return -1.

Definition

Class:	TriCount
Method:	count
Parameters:	int, int
Returns:	int
Method signature:	int count(int minLength, int maxLength)
(be sure your method is public)

Constraints

-

minLength is between 1 and 1,000,000, inclusive.

-

maxLength is between minLength and 1,000,000, inclusive.

Examples

0)

Returns: 3

The proper triangles with side lengths between 1 and 2 inclusive are {1,1,1} and {2,2,2} and {1,2,2}.

1)

Returns: 4

9,9,9 and 10,10,10 and 9,9,10 and 9,10,10

2)

Returns: -1

There are VERY many triangles with lengths in this range.

3)

Returns: 83540657

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BedroomFloor

Greedy, Math

Used in:

SRM 442

Used as:

Division I Level Two

Writer:

kalinov

Testers:

PabloGilberto , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4810

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13750&pm=4810

Problem Statement

You have decided to put new floor tiles on your bedroom floor. Consider an infinite pattern made of 1x5 wooden panels as in the picture below. The top-left corner of the picture has coordinates (0, 0). X coordinates increase from left to right, and y coordinates increase from top to bottom.

You have chosen a rectangular area within this infinite pattern that matches the exact size of your bedroom. The top-left corner of the rectangle is at (x1, y1) and the bottom-right corner is at (x2, y2). You want to reproduce this section on your bedroom floor.

The store that sells wooden floor panels only carries 1x5 panels. You can cut panels to get smaller panels, but you can't glue panels together to get larger ones. For example, you can cut a 1x5 panel to get one 1x3 panel and one 1x2 panel, or two 1x2 panel and one 1x1 panel, etc.

The picture above shows the rectangular area (8, 5, 20, 16). You need twenty-three 1x5 panels, six 1x2 panels and five 1x1 panels. You have to buy total of 27 panels to make these.

You are given ints x1, y1, x2 and y2. Return the minimum number of panels you must buy at the store to produce the pattern in the given rectangular area.

Definition

Class:	BedroomFloor
Method:	numberOfSticks
Parameters:	int, int, int, int
Returns:	long
Method signature:	long numberOfSticks(int x1, int y1, int x2, int y2)
(be sure your method is public)

Notes

-

You can throw away any part of a panel that you don't need.

Constraints

-

x1, y1, x2 and x2 will be between 0 and 1000000, inclusive.

-

x2 will be strictly greater than x1.

-

y2 will be strictly greater than y1.

Examples

0)

Returns: 5

This rectangular area contains five 1x5 panels.

1)

Returns: 5

This rectangular area contains two 1x5 panels and five 1x2 panels. We have to buy 5 panels to make these.

2)

Returns: 12

This rectangle contains twelve 1x3 panels. We can't glue panels together, so we have to buy 12 panels.

3)

Returns: 27

The example depicted in the problem statement.

4)

Returns: 200000000000

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ZCurve

Recursion, Simple Math

Used in:

SRM 266

Used as:

Division I Level Two , Division II Level Three

Writer:

supernova

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4808

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7999&pm=4808

Problem Statement

A Z-curve is a path that traces through all the points in a two-dimensional square grid in such a way that the four quadrants are visited in order: first the upper left, then the upper right, then the lower left, and finally the lower right. If those quadrants contain more than 1 cell, these cells are visited recursively, in the same manner. A Z-curve of order N is a path through a 2^N by 2^N grid. A Z-curve of order 1 is a simple Z-shape through a 2-by-2 grid, as shown below.

Here is a diagram of a Z-curve of order 2.

Notice the order each quadrant was visited:

- upper left quadrant: 0, 1, 2, 3

- upper right quadrant: 4, 5, 6, 7

- lower left quadrant: 8, 9, 10, 11

- lower right quadrant: 12, 13, 14, 15

You will be given a value N and coordinates r and c denoting the row and the column in a 2^N by 2^N grid. Coordinates range from 0 to (2^N)-1 inclusive, with the upper left corner at coordinates (0,0). Assuming you start from the upper left corner and the points are traversed in the order specified by a Z-curve of order N, determine how many steps it takes to reach the point at coordinates (r,c).

Definition

Class:	ZCurve
Method:	zValue
Parameters:	int, int, int
Returns:	int
Method signature:	int zValue(int N, int r, int c)
(be sure your method is public)

Constraints

-

N is between 1 and 15, inclusive.

-

r and c are between 0 and 2^N-1, inclusive.

Examples

0)

Returns: 11

1)

Returns: 0

2)

Returns: 63

(7,7) is in the lower right corner of the grid and, as shown in the following diagram, it is the last point visited.

3)

Returns: 63

The upper left quadrant of a Z-curve of order 4 is actually a Z-curve of order 3 and, because it is the first quadrant visited, the answer is the same as in the previous example.

4)

Returns: 262143

5)

Returns: 786432

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NearBirthdays

Dynamic Programming, Math

Used in:

TCO05 Finals

Used as:

Division I Level Two

Writer:

Yarin

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4786

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8096&pm=4786

Problem Statement

If more than 23 people are selected at random, the chance that two of them have birthdays on the same day is more than 50%. While this may sound counterintuitive, it is fairly easy to verify that this indeed is the case. Furthermore, only 14 people are needed for there to be more than a 50% chance that at least two of them have birthdays within one day of each other.

Create a class NearBirthdays containing the method probability which calculates the probability that at least two people among noPeople have birthdays within withinDays days (inclusive) of each other. The method should take as input an int noPeople, an int withinDays, and an int daysInAYear, the number of days in a year, and return the probability as a double. Assume that each day in a year is equally likely to be a birthday for someone.

Definition

Class:	NearBirthdays
Method:	probability
Parameters:	int, int, int
Returns:	double
Method signature:	double probability(int noPeople, int withinDays, int daysInAYear)
(be sure your method is public)

Notes

-

The last day of a year is within one day of the first day of a year.

-

A solution will be judged correct if the absolute error is less than 1e-9.

Constraints

-

noPeople will be between 2 and 100, inclusive.

-

withinDays will be between 0 and 100, inclusive.

-

daysInAYear will be between 100 and 1000, inclusive.

Examples

0)

Returns: 0.995

If the first person's birthday is on day 1 in the 200 day long year, the only time the second person's birthday isn't within 99 days is if he has a birthday on day 101. Hence the probability that both persons have birthdays within 99 days of each other is 199/200 = 0.995.

1)

Returns: 0.7063162427192686

This is a typical school class version: in a school class with 30 people, the likelihood that two of them are born on the same day is roughly 70%.

2)

Returns: 0.33373900738431983

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Springs

Advanced Math, Geometry

Used in:

TCO05 Round 3

Used as:

Division I Level Three

Writer:

lars2520

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4769

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8016&pm=4769

Problem Statement

Consider a group of metal springs supporting a rigid rod. The rod's weight is uniformly distributed along its length at a rate of 1 pound per inch. Each of the springs exerts an upwards force when it is compressed. This force is given by F_i = k_i*x_i+1/(max_i-x_i)² where F_i is the force, x_i is the amount the spring is compressed (x_i may be negative, in which case the spring is extended and the force may be downward), and max_i and k_i are inputs. Notice that as the compression approaches max, the force goes to infinity, so the spring will never be compressed by max or more. Given the positions, k's, and max's for the springs supporting the rod (corresponding elements of the inputs represent one spring), you are to determine how much each spring is compressed by the rod. You may assume that the leftmost spring supports the leftmost end of the rod, while the rightmost spring supports the rightmost end of the rod. Note that some of the springs may be negatively compressed (see examples).

There are three basic conditions that must be fulfilled by the compressions of the springs. First, the total force exerted upwards (the sum of the F's) must equal the weight of the rod. Second, since the rod is rigid, the compressions of the springs must be such that the tops of the springs are all in a line (with some constant slope). Third, the sum of the torques around every point where the rod touches a spring must be 0. The torques come from both the upward (or downward) forces exerted by the springs, and also from the weight of the rod. The torque around a point due to a spring is equal to the force exerted by the spring times the horizontal distance from the spring to the point. The torque around a point caused by the weight of the rod to the right of the point is equal to the weight of the portion of the rod to the right squared, and then divided by 2. The left side of the point is analogous. See examples for more information.

Definition

Class:	Springs
Method:	compression
Parameters:	int[], int[], int[]
Returns:	double[]
Method signature:	double[] compression(int[] positions, int[] ks, int[] maxs)
(be sure your method is public)

Notes

- In reality, the rotation of the rod would result in some more complicated effects which we will ignore for this problem.

- When none of the springs are compressed at all, their tops form a horizontal line.

Constraints

- positions, ks and maxs will each contain between 2 and 50 elements, inclusive.

- positions, ks and maxs will each contain the same number of elements.

- positions will be sorted in strictly ascending order.

- Each element of positions will be between 0 and 1000, inclusive.

- Each element of maxs and ks will be between 1 and 1000, inclusive.

Examples

0)

{0,1,3}

{1,1,1}

{1000,1000,1000}

Returns: {0.857141855426, 0.964284712354, 1.17857042621 }

The image above shows the approximate setup of the springs and rod. The values in maxs are large enough that we can ignore them in this discussion and our results won't be far off. The first spring is compressed by 6/7, the second by 27/28, and the third by 33/28. You will note that the sum of these three compressions is 3. Furthermore, the slope of the rod (3/28) matches the compression of the springs. Finally, we can calculate the torque at each location (negative values indicate counterclockwise torque):

                        Torque due to:
Position | Spring 0 | Spring 1 | Spring 2 | Weight of Left | Weight of Right
---------+----------+----------+----------+----------------+----------------
       0 |        0 | -27/28*1 | -33/28*3 |              0 | 3*3/2 = 9/2
       1 |  6/7 * 1 |        0 | -33/28*2 |    -1*1/2=-1/2 | 2*2/2 = 2
       3 |  6/7 * 3 |  27/28*2 |        0 |    -3*3/2=-9/2 | 0

You can easily verify that the sum of the torques at each of the three positions is 0.

When you solve the problem taking max into account, you find that each of the above values is approximately one millionth too high.

1)

{0,1,2,4}

{2,1,1,1}

{1,10,10,10}

Returns: {0.066863594314, 0.421263093855, 0.775662593396, 1.484461592477 }

2)

{1,99,101}

{1,100,100}

{1000,1000,1000}

Returns: {48.510296857713, 0.744851008845, -0.229954008478 }

3)

{0,1000}

{1,1000}

{1,1000}

Returns: {0.955235859695, 0.499999998999 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GridPointsOnCircle

Brute Force, Geometry, Simple Math

Used in:

SRM 260

Used as:

Division I Level One , Division II Level Two

Writer:

gepa

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4766

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7994&pm=4766

Problem Statement

You will be given rSquare, the square of the radius of a circle. You are to return the number of lattice points (points with integer coordinates) that lie on the circumference of a circle with this radius centered at the origin of the (cartesian) coordinate system.

Definition

Class:	GridPointsOnCircle
Method:	countPoints
Parameters:	int
Returns:	int
Method signature:	int countPoints(int rSquare)
(be sure your method is public)

Constraints

-

rSquare will be between 1 and 2,000,000,000, inclusive.

Examples

0)

Returns: 4

A circle with radius 1 centered at the origin goes through 4 lattice points: (1,0), (0,1), (-1,0) and (0,-1).

1)

Returns: 12

A circle with radius 5 goes through the points (+/-3, +/-4), (+/-4, +/-3), (0, +/-5) and (+/-5, 0) (12 points).

2)

Returns: 0

No lattice point is at distance sqrt(3) from the origin.

3)

Returns: 0

4)

Returns: 12

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FrogAndFly

Advanced Math, Geometry

Used in:

SRM 260

Used as:

Division I Level Three

Writer:

gepa

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4750

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7994&pm=4750

Problem Statement

There are two buildings opposite each other as in the figure below. On the left building, there is a rectangular window, with the lower and upper sides given by ylow and yhigh (the y-coordinate as shown in the image: starting with 0.0 at the bottom and increasing upwards). On the building on the opposite side there is also a window, but it is not necessarily rectangular. Its shape is a convex polygon, with the x- and y-coordinates (as shown in the image: x-coordinate increasing to the back, y-coordinate starting with 0.0 at the bottom and increasing upwards) of the corners given by the int[]s xwindow and ywindow (the i-th corner is at the x-coordinate xwindow[i] and at the y-coordinate ywindow[i]). Between the two buildings there is an opaque wall of height hwall, at a distance of dfrog from the left building and dfly from the right building (assume that the wall is infinitely thin).

A frog lies at some point on the window of the left building, and a fly lies at some point on the window of the right building. Assuming that the frog and fly are positioned randomly (uniformly) at some point on the windows, what is the probability that the frog can see the fly (i.e., the line of sight between them does not cross the wall)?

Definition

Class:	FrogAndFly
Method:	visibility
Parameters:	int, int, int, int, int, int[], int[]
Returns:	double
Method signature:	double visibility(int hwall, int dfrog, int dfly, int ylow, int yhigh, int[] xwindow, int[] ywindow)
(be sure your method is public)

Notes

-

The return value must be within 1e-9 absolute or relative error of the actual result.

Constraints

-

hwall will be between 0 and 100, inclusive.

-

dfrog will be between 1 and 100, inclusive.

-

dfly will be between 1 and 100, inclusive.

-

ylow will be between 0 and 100, inclusive.

-

yhigh will be between 0 and 100, inclusive.

-

ylow will be smaller than yhigh.

-

xwindow and ywindow will have between 3 and 50 elements, inclusive.

-

xwindow and ywindow will have the same number of elements.

-

Each element of xwindow will be between 0 and 100, inclusive.

-

Each element of ywindow will be between 0 and 100, inclusive.

-

The polygon defined by the coordinates represented by the elements of xwindow and ywindow will be a convex polygon with non-zero area. There will be no two identical points, and no three points will be collinear.

Examples

0)

{5, 5, 15, 15}

{5, 15, 15, 5}

Returns: 0.5

The windows on both sides are rectangular with the lower sides at height 5 and the upper sides at height 15. The wall is exactly in the middle between the buildings and has a height of 10. Due to the symmetric configuration, the probability of the fly being visible by the frog here is exactly 0.5 (50%).

1)

{5, 5, 15, 15}

{5, 15, 15, 5}

Returns: 0.02

The same situation as above, just the wall has now a height of 14. If both the fly and the frog are above a height of 13, we have a symmetric configuration again with probability 0.5 of the fly being visible by the frog. If the frog or the fly (or both) is below a height of 13, the fly will not be visible by the frog. The probability of both being above a height of 13 is 0.2 * 0.2 = 0.04, so the total probability is 0.04 * 0.5 = 0.02.

2)

{10, 20, 15}

{5, 5, 15}

Returns: 0.4166666666666665

A triangular window.

3)

{0, 10, 20, 30, 15}

{20, 10, 10, 20, 40}

Returns: 1.0

The wall has height 0, so even from the lowest point (ylow) the frog can always look at the fly.

4)

{10, 20, 30, 20}

{20, 10, 20, 30}

Returns: 0.0

The wall is now too high and hides the whole opposite window, so the frog can never look directly at the fly.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IsingModel

Simple Math

Used in:

SRM 260

Used as:

Division II Level One

Writer:

gepa

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4746

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7994&pm=4746

Problem Statement

The Ising model is a simple widespread model in statistical physics for simulating magnetic properties of matter. In this model, we consider a rectangular grid, and we associate each grid point with a value '+' or '-' (which physically represents the spin of the element positioned at that grid point).

When we have such a spin configuration, the total energy of this configuration is computed by adding the values contributed by each pair of neighboring cells (only horizontal and vertical direct neighbors are considered). If the pair consists of two cells with the same spin (both '+' or both '-'), this pair contributes a value of -1 to the total energy. Otherwise (one cell is '+' and its neighbor is '-'), the pair contributes a value of +1 to the total energy.

See example 0 for a detailed computation of the energy value.

You are given a String[] spins representing the spin configuration. You are to return the total energy of this configuration.

Definition

Class:	IsingModel
Method:	energy
Parameters:	String[]
Returns:	int
Method signature:	int energy(String[] spins)
(be sure your method is public)

Constraints

-

spins will have between 1 and 50 elements, inclusive.

-

Each element of spins will have between 1 and 50 characters, inclusive.

-

All elements of spins will have the same number of characters.

-

Each character of each element of spins will be either '+' or '-'.

Examples

0)

{"-++",
 "+-+"}

Returns: 3

There are a total of 7 neighboring pairs here: 4 horizontal (-+), (++), (+-) and (-+) and 3 vertical (-+), (+-) and (++). Pairs of type (+-) and (-+) contribute a value of +1 to the total energy, and pairs of type (--) and (++) contribute a value of -1. The total energy of this configuration is thus: E = 1 - 1 + 1 + 1 + 1 + 1 - 1 = 3.

1)

{"+"}

Returns: 0

With just one element, there is no neighboring pair, so the total energy is 0.

2)

{"++-+",
 "-++-",
 "+-+-",
 "++++"}

Returns: 4

3)

{"----",
 "---+",
 "-+++",
 "++++"}

Returns: -12

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TippingWaiters

Brute Force, Simple Math

Used in:

SRM 270

Used as:

Division II Level Two

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4745

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8067&pm=4745

Problem Statement

In a restaurant, if you were pleased by the waiter's service, you may leave him a tip -- you pay him more than the actual value of the bill, and the waiter keeps the excess money. In some countries, not leaving a tip for the waiter is even considered impolite. During my recent holiday I was having dinner in a foreign restaurant. The pamphlet from my travel agency informed me that the proper way of tipping the waiter is the following:

The sum I pay must be round, i.e., divisible by 5.
The tip must be between 5% and 10% of the final sum I pay, inclusive.

Clearly, sometimes there may be multiple "correct" ways of settling the bill. I'd like to know exactly how many choices I have in a given situation. I could program it easily, but I was having a holiday... and so it's you who has to solve this task. You will be given:

an int bill -- the amount I have to pay for the dinner
an int cash -- the amount of money I have in my pocket

Write a function that computes how many different final sums satisfy the conditions above.

Definition

Class:	TippingWaiters
Method:	possiblePayments
Parameters:	int, int
Returns:	int
Method signature:	int possiblePayments(int bill, int cash)
(be sure your method is public)

Notes

-

Assume that both bill and cash are in dollars.

-

All the money I have is in one-dollar banknotes.

Constraints

-

bill and cash are between 1 and 2,000,000,000, inclusive.

-

bill doesn't exceed cash.

Examples

0)

Returns: 0

4 isn't a round sum, and 5 is too much.

1)

Returns: 1

The only correct choice is to pay 25 dollars, thus leaving a tip of 2 dollars.

2)

Returns: 0

The same bill, but I don't have enough money to leave an appropriate tip.

3)

Returns: 1

This time, it is appropriate to pay either 235 or 240 dollars. Sadly, I don't have enough money for the second possibility.

4)

12345678

Returns: 14440

A large bill, but with that much money I don't care.

5)

1880000000

1980000000

Returns: 210527

6)

171000000

179999999

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HairCuts

Math, Simulation, String Parsing

Used in:

SRM 267

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4721

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8000&pm=4721

Problem Statement

Our barbershop opens at 9:00 am and closes at 5:00 pm, but (of course) the barber keeps working until all the customers who entered the shop before 5:00 have been served. Each customer enters the shop and if the barber is free, immediately starts getting his hair cut. Otherwise, the customer waits until everyone who entered before him has finished getting their hair cut.

We have the sequence of times when customers entered the shop and we know when the last customer left the shop. We also know that each haircut took at least 5 minutes. We want to get a bound on how long the longest haircut took.

Create a class HairCuts that contains a method maxCut that is given String[] enter and String lastExit and that returns the smallest possible time (in minutes) that the longest haircut took. If the inputs are inconsistent with the rule that each haircut takes at least 5 minutes, return -1.

The enter times and the lastExit are 5 character Strings in the format hh:mm with hh being a 12 hour time.

Definition

Class:	HairCuts
Method:	maxCut
Parameters:	String[], String
Returns:	double
Method signature:	double maxCut(String[] enter, String lastExit)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

lastExit and all elements of enter are formatted as described in the statement.

-

enter contains between 1 and 50 elements, inclusive.

-

Each hh in enter will equal "09","10","11","12","01","02","03", or "04.

-

The hh in lastExit will equal "09","10","11","12","01",...,"05", or "06".

-

Each time will have mm equal to "00","01",...,"58", or "59".

-

lastExit will be a time that is later than every enter time.

Examples

0)

{"04:22","09:00"}

"05:52"

Returns: 90.0

At 9:00 the first customer entered. The last (second) customer entered at 4:22 and was not done until 5:52. For the first customer to have delayed the second customer his cut would have to have taken more than 7 hours. So the smallest time for the longest haircut occurs when the first customer has a short cut, and the second customer is getting his hair cut all the time he is in the shop (from 4:22 to 5:52) which is 90 minutes.

1)

{"09:00","09:22","09:22"}

"10:11"

Returns: 23.666666666666863

If the first customer's cut takes 23 2/3 minute then the second and third customers are already waiting. They could both take the same amount of time. Since this keeps the barber busy all the time with 3 equal length haircuts, this must be the smallest time for the longest haircut.

2)

{"09:00","04:00","04:02"}

"04:09"

Returns: -1.0

This data would require two customers to get haircuts between 4:00 and 4:09 and that would violate the rule that each haircut takes at least 5 minutes.

3)

{  "04:40", "10:54", "12:30", "03:46", "04:48", "01:57", "04:47", "10:29", "10:39"}

"05:21"

Returns: 13.6666666666669

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

VariableSolve

Math

Used in:

TCO05 Round 1

Used as:

Division I Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , vorthys , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4715

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8019&pm=4715

Problem Statement

You will be given an equation of the form <side>=<side> where <side> is a list of <term>s separated by <op>s. Each <op> is either + or -, and each <term> is a positive length string of uppercase letters. Each letter denotes a variable taking on real values. No letter will occur in a <term> more than twice.

The <term>s are products of variables. As you would expect, the + and - operators take lower precedence than the multiplications within the <term>s. For example,

	ABC+ADF=PQ-PQ

is a properly formatted equation. Sometimes, by fixing a single variable at a particular value, we can force the entire equation to always be true. Return a String[] containing all such variables that satisfy this requirement. If a variable can be set to n distinct values all of which satisfy this requirement, then that variable should occur n times in the return. If a variable can be set to an infinite number of distinct values that satisfy this requirement, it should not be returned. The return should be sorted in alphabetical order.

Definition

Class:	VariableSolve
Method:	getSolutions
Parameters:	String
Returns:	String[]
Method signature:	String[] getSolutions(String equation)
(be sure your method is public)

Constraints

-

equation will contain between 3 and 50 characters inclusive.

-

equation will be formatted as described in the problem statement.

Examples

0)

"P=NP"

Returns: {"N", "P" }

Simpler than it looks: let N = 1 or P = 0.

1)

"RED+BLUE=PURPLE"

Returns: {"E" }

Only E = 0 guarantees the equation holds.

2)

"ABCD+ABCD-ABCD=ABCD"

Returns: { }

Each variable has an infinite number of values causing the equation to hold.

3)

"BAA+BA+B=P-P"

Returns: {"B" }

We cannot consider the complex solutions for A.

4)

"ABB-AB-AB+A=BCB-C"

Returns: {"B" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ClassScores

Simple Math, Simple Search, Iteration

Used in:

SRM 258

Used as:

Division II Level One

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4710

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7993&pm=4710

Problem Statement

A teacher has just finished grading the test papers for his class. To get an idea of how difficult the test was, he would now like to determine the most common score on the test. In statistics, this is called the "mode" of a set of data points. For instance, if the scores were {65, 70, 88, 70}, then the mode would be 70, since it appears twice while all others appear once.

Sometimes, in the case of a tie, the mode will be more than one number. For instance, if the scores were {88, 70, 65, 70, 88}, then the mode would be {70, 88}, since they both appear most frequently.

You are given a int[] scores. You are to return a int[] representing the mode of the set of scores. In the case of more than one number, they should be returned in increasing order.

Definition

Class:	ClassScores
Method:	findMode
Parameters:	int[]
Returns:	int[]
Method signature:	int[] findMode(int[] scores)
(be sure your method is public)

Constraints

-

scores will contain between 1 and 50 elements, inclusive.

-

Each element of scores will be between 0 and 100, inclusive.

Examples

0)

{65, 70, 88, 70}

Returns: {70 }

The first example from the problem statement.

1)

{88, 70, 65, 70, 88}

Returns: {70, 88 }

The second example from the problem statement.

2)

{92, 56, 14, 73, 22, 38, 93, 45, 55}

Returns: {14, 22, 38, 45, 55, 56, 73, 92, 93 }

With no duplicates, all of the elements are the most frequent (appearing once each).

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FloorTiling

Math

Used in:

TCO05 Round 2

Used as:

Division I Level One

Writer:

lars2520

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4709

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8017&pm=4709

Problem Statement

You are tiling a floor that is width by height units. You are using strips of tile that are size by 1 units. The long side of the tiles should run along the side of the floor that is width units long. See the diagram for more details on exactly how the tiles should be placed.

Note how each row is offset by offset units from the one below it. (When thinking of how to offset the rows, imagine infinite horizontal strips of tiles.) Also, notice that the bottom row is touching the side. As the diagram illustrates, you will not be able to tile the whole floor with pieces that are size by 1. You should return the area of the region that will not be covered when tiling according to the strategy shown in the image.

Definition

Class:	FloorTiling
Method:	tile
Parameters:	int, int, int, int
Returns:	int
Method signature:	int tile(int size, int offset, int width, int height)
(be sure your method is public)

Constraints

-

offset will be between 0 and size-1, inclusive.

-

size will be between 2 and floor(width/2), inclusive.

-

width and height will each be between 4 and 50, inclusive.

Examples

0)

Returns: 17

The example in the diagram above.

1)

Returns: 30

2)

Returns: 50

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Recipe

Simple Math, String Manipulation, String Parsing

Used in:

SRM 265

Used as:

Division I Level Two

Writer:

HardCoder

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4708

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8007&pm=4708

Problem Statement

While cooking your favorite recipe, you realize that you have put the wrong quantity of one or more of the ingredients into your mixing bowl. You must figure out the minimum amount of each ingredient that must be added to the bowl to fix your mistake. It is essential to end up with at least the quantities required in the recipe and to maintain the ingredient proportions.

For instance, if you used 2 cups of flour in a recipe that requires 3 cups, all you have to do is add 1 more cup. If, in another recipe, you used 2 teaspoons of salt where only 1 teaspoon was required, you must make sure that all of the recipe's ingredients are doubled to maintain the correct proportions.

You are able to measure quantities in teaspoons (tsp), tablespoons (Tbsp), and cups. A teaspoon is the smallest amount that can be added to the bowl. 3 teaspoons are equivalent to 1 tablespoon. 16 tablespoons are equivalent to 1 cup.

You will be given a String[] recipe that lists the required ingredients, and a String[] mixingBowl listing the ingredients that are in the bowl. Your program should return a String[] indicating the quantities of only the ingredients that must be added. The ingredients should be in the same order that they appear in recipe. If no ingredients need to be added, then the result should have 0 elements.

Each element of the result must indicate the maximum number of cups to be added, followed by the the maximum number of tablespoons, and finally the remaining teaspoons to be added. In general, each element should be formatted (quotes for clarity) as "QTY cups QTY Tbsp QTY tsp NAME", where each QTY is an integer with no leading zeros, and NAME is the name of the ingredient. If none of a certain unit needs to be added, then that unit should be excluded from the element.

Definition

Class:	Recipe
Method:	fix
Parameters:	String[], String[]
Returns:	String[]
Method signature:	String[] fix(String[] recipe, String[] mixingBowl)
(be sure your method is public)

Constraints

- recipe will contain between 1 and 50 elements, inclusive.

- mixingBowl will contain between 0 and 50 elements, inclusive.

-

Each element of recipe and mixingBowl will be in one of the following formats (quotes for clarity):

"QTY tsp NAME"
"QTY Tbsp NAME"
"QTY cups NAME"

- QTY will be an integer with no leading zeros between 1 and 99, inclusive.

- NAME will contain between 1 and 25, inclusive, uppercase letters ('A'-'Z').

- Each NAME in recipe will be distinct.

- Each NAME in mixingBowl will be distinct.

- Each NAME in mixingBowl will also appear in an element of recipe.

Examples

0)

{"4 cups FLOUR", "1 Tbsp SALT", "1 cups SUGAR", "1 tsp VANILLA"}

{"4 cups FLOUR", "1 Tbsp SALT", "1 Tbsp SUGAR", "1 Tbsp VANILLA"}

Returns: {"8 cups FLOUR", "2 Tbsp SALT", "2 cups 15 Tbsp SUGAR" }

This recipe requires 4 cups of FLOUR, 1 tablespoon of SALT, 1 cup of SUGAR and 1 teaspoon of VANILLA. There are two mistakes in mixingBowl:

1) Not enough SUGAR

2) Too much VANILLA

Since there is three times the required amount of VANILLA in mixingBowl, we must add enough to triple the other ingredients so that we end up with the same proportions. This is accomplished by adding 8 cups of FLOUR, 2 tablespoons of SALT and 2 cups plus 15 tablespoons of SUGAR.

1)

{"3 cups FLOUR", "1 tsp SALT"}

{"3 cups FLOUR", "2 tsp SALT"}

Returns: {"3 cups FLOUR" }

2)

{"1 cups FLOUR", "1 cups SUGAR", "1 cups MILK"}

{"2 cups FLOUR", "32 Tbsp SUGAR", "96 tsp MILK"}

Returns: { }

3)

{"2 cups FLOUR", "2 tsp SALT"}

{"1 cups FLOUR", "1 tsp SALT"}

Returns: {"1 cups FLOUR", "1 tsp SALT" }

4)

{"3 cups FLOUR"}

{"2 cups FLOUR"}

Returns: {"1 cups FLOUR" }

5)

{"71 tsp CINNAMON"}

{}

Returns: {"1 cups 7 Tbsp 2 tsp CINNAMON" }

6)

{"3 cups FLOUR","1 cups SUGAR","9 tsp SALT","9 Tbsp GINGER","2 cups MILK","21 tsp CINNAMON","5 Tbsp VANILLA"}

{"1 Tbsp SUGAR","8 tsp SALT","5 Tbsp CINNAMON","21 tsp VANILLA","44 tsp GINGER","3 cups FLOUR","3 cups MILK"}

Returns: 
{"2 cups FLOUR",
"1 cups 9 Tbsp 2 tsp SUGAR",
"2 Tbsp 1 tsp SALT",
"1 tsp GINGER",
"5 Tbsp 1 tsp MILK",
"6 Tbsp 2 tsp CINNAMON",
"1 Tbsp 1 tsp VANILLA" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StockQuotes

Simple Math

Used in:

SRM 257

Used as:

Division I Level Two

Writer:

lars2520

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4706

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8005&pm=4706

Problem Statement

A 'quote' is a message from a stock exchange that says at what price that exchange is currently willing to buy a given stock (the 'bid') and what price it is willing to sell the stock (the 'ask'). The 'spread' is defined as the difference between the ask and the bid. For our purposes, you can assume that the ask will always be greater than the bid and that the bid will be greater than zero. The 'inside quote' is defined as the highest bid from any exchange and the lowest ask from any exchange (they do not necessarily need to be the same exchange). The inside quote changes when any exchange improves upon the current inside quote or when the best exchange moves away from the inside exposing a lower bid or higher ask.

You will be given a String[] representing a number of quotes, in the order they are made. Each element of the input will represent a single quote and will be formatted as: "EXCHANGE BID ASK", where EXCHANGE is the index of the stock exchange making the quote and BID and ASK are as defined above. You are to issue a report based on the quotes. Each element of the report should be formatted as "EXCHANGE COUNT AVERAGE_SPREAD", where EXCHANGE is either the index of an EXCHANGE, as in the input, or 10, representing the inside quote. COUNT is the number of times that the quote (either bid or ask) for that exchange changed (or that the inside quote changed). AVERAGE_SPREAD is the average spread, averaged only over the quotes that caused the quote to change and with exactly 2 digits after the decimal point (rounded in the standard way to the nearest hundredth where .005 rounds up). The return should contain one entry for each exchange that issues one or more quotes in the input. It should be sorted by the index of the exchanges, with the entry for the inside spread coming last.

Definition

Class:	StockQuotes
Method:	report
Parameters:	String[]
Returns:	String[]
Method signature:	String[] report(String[] quotes)
(be sure your method is public)

Constraints

-

Each element of quotes will be formatted as "EXCHANGE BID ASK" where EXCHANGE is a digit between '0' and '9', inclusive, and BID and ASK are integers between 1 and 1000, inclusive, without leading zeros.

-

quotes will contain between 1 and 50 elements inclusive.

-

An exchange will never issue a quote that is the same is its existing quote (so the number of times that its quote changes will be identical to the number of quotes it issues).

-

ASK will be greater than BID in each element of quote.

-

The inside spread will always be greater than 0.

Examples

0)

{"0 10 14",
 "1 9 16",
 "2 11 15",
 "0 11 13",
 "1 10 15",
 "2 12 14",
 "0 9 15",
 "2 8 20"}

Returns: {"0 3 4.00", "1 2 6.00", "2 3 6.00", "10 6 2.83" }

The following table shows how the best bid and ask change as new bids come in:

              |     BEST
Exch|Bid |Ask | Bid|Ask | Changed
----+----+----+----+----+------
 0  | 10 | 14 | 10 | 14 | Yes
 1  |  9 | 16 | 10 | 14 | 
 2  | 11 | 15 | 11 | 14 | Yes
 0  | 11 | 13 | 11 | 13 | Yes
 1  | 10 | 15 | 11 | 13 |  
 2  | 12 | 14 | 12 | 13 | Yes
 0  |  9 | 15 | 12 | 14 | Yes
 2  |  8 | 20 | 10 | 15 | Yes

1)

{"8 931 944",
 "8 926 946",
 "8 926 951",
 "8 928 953",
 "8 929 954"}

Returns: {"8 5 21.60", "10 5 21.60" }

2)

{"2 711 730",
 "5 716 729",
 "7 711 734",
 "0 718 731",
 "5 713 731",
 "1 713 730"}

Returns: {"0 1 13.00", "1 1 17.00", "2 1 19.00", "5 2 15.50", "7 1 23.00", "10 4 13.75" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MissileTarget

Math, Search

Used in:

SRM 258

Used as:

Division II Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4705

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7993&pm=4705

Problem Statement

You are working for a defense agency that is testing the accuracy of a new missile guidance system. As part of this effort, several missiles have been fired off. Each missile fired was programmed with the same target coordinates, although the actual points of impact vary.

Your task is to determine the "best fit" point to describe the location where the missiles actually landed. To determine how well a point describes the location, calculate the cartesian distance from the point to each of the landing points. Then, total the sum of the squares of these distances. The best fit point is the point that minimizes this sum.

You are given int[]s x and y, both containing the same number of elements, where the i-th element of x and the i-th element of y describe the coordinates of the i-th missile landing point. You are to return a int[] with exactly two elements, describing the coordinates of the lattice point (point with integral coordinates) that is closest to the "best fit" point. The first element should be the x-coordinate, and the second element should be the y-coordinate.

Definition

Class:	MissileTarget
Method:	bestFit
Parameters:	int[], int[]
Returns:	int[]
Method signature:	int[] bestFit(int[] x, int[] y)
(be sure your method is public)

Notes

-

The cartesian distance between two points (x1, y1) and (x2, y2) is defined as Sqrt((x2-x1)^2 + (y2-y1)^2).

-

The return value must be within 1e-9 absolute or relative error of the actual result.

Constraints

-

x will contain between 1 and 50 elements, inclusive.

-

x and y will contain the same number of elements.

-

Each element of x will be between -1000000 and 1000000, inclusive.

-

Each element of y will be between -1000000 and 1000000, inclusive.

-

The actual (possibly non-lattice) best fit point will be at least 1e-2 closer to the correct return value than to any other lattice point.

Examples

0)

{750, -500, -250}

{-1000, 500, 500}

Returns: {0, 0 }

These three impacts are all pretty close to the origin, and sure enough, the origin is the best fit point.

1)

{765}

{834}

Returns: {765, 834 }

With only one point, it is its own best fit.

2)

{100, 200}

{200, 400}

Returns: {150, 300 }

With only two points, the best fit is the midpoint between the two.

3)

{123456, -987654, 97531, -86420}

{14703, 25814, 36924, -47036}

Returns: {-213272, 7601 }

4)

{0, 5, 5, 6, 8, 8}

{0, 0, 0, 0, 0, 0}

Returns: {5, 0 }

In this case, notice that the actual best fit point possible is (5.333, 0). If we look at lattice points only, then our best fit is (6, 0), however, we are interested in the lattice point that is closest to the actual best fit point, so we return (5, 0).

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ChutesAndLadders

Dynamic Programming, Math, Simple Search, Iteration, Simulation

Used in:

SRM 258

Used as:

Division I Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4701

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7993&pm=4701

Problem Statement

The board game Chutes and Ladders consists of 100 spaces, numbered 0 through 99. Initially, each player begins on the space 0. Each player takes turns rolling a pair of typical six-sided dice, and moves the number of spaces indicated on the dice. Each space of the board might be the start of a chute or a ladder, which immediately warps the player backward or forward to another space on the board. Once a player reaches or passes the last space on the board, that player wins the game.

Any space on the board, except for the first (0) or last (99) space, may be the start of a chute, a ladder, or neither. No space will have both a chute and a ladder, and no space will have more than one chute or ladder. A space that begins a chute or ladder will not be the end of another chute or ladder. Furthermore, no two adjacent spaces will both have a chute and/or ladder. A space may, however, be the landing space of more than one chute and/or ladder. There will be, at most, 20 chutes/ladders on the board

You are given int[]s startLadder and endLadder, whose corresponding elements define the starting and ending points of each of the chutes and ladders on the game board. For instance, startLadder[0] is the space that has a chute/ladder which ends at endLadder[0]. You are also given a int[] players indicating the current position of each player on the board. Player 0 will roll next, followed by player 1, etc.

You are to return a double[] indicating the probability of each player winning the game.

Definition

Class:	ChutesAndLadders
Method:	winningChance
Parameters:	int[], int[], int[]
Returns:	double[]
Method signature:	double[] winningChance(int[] startLadder, int[] endLadder, int[] players)
(be sure your method is public)

Notes

-

The return value must be within 1e-9 absolute or relative error of the actual result.

Constraints

-

startLadder will contain between 0 and 20 elements, inclusive.

-

endLadder will contain the same number of elements as startLadder.

-

Each element of startLadder will be between 1 and 98, inclusive.

-

Each element of endLadder will be between 0 and 98, inclusive.

-

No two elements of startLadder will be the same.

-

No two elements of startLadder will differ by 1.

-

No element of endLadder will equal an element of startLadder.

-

players will contain between 2 and 4 elements, inclusive.

-

Each element of players will be between 0 and 98, inclusive.

-

No element of player will equal an element of startLadder.

Examples

0)

{}

{}

{0, 0}

Returns: {0.6063557826968836, 0.3936442173031164 }

With no chutes or ladders to worry about, this is just a straight ahead race to the finish. As expected, the first player has an advantage.

1)

{ 7, 23, 42, 58, 87}

{35, 91, 11, 31, 22}

{0, 0, 0, 0}

Returns: 
{0.2850398049975441, 0.2591808222220256, 0.23726366951493458, 0.21851570326549555 }

Here, we've got a few chutes and ladders, and more players, which evens out the odds a bit.

2)

{}

{}

{0, 30}

Returns: {0.013280440302841312, 0.9867195596971587 }

With the second player starting a good way through the game, he has an advantage in spite of rolling second.

3)

{79, 70, 50, 27,  3,  8, 35, 20, 97, 94, 92, 86, 53, 63, 61, 46, 48, 15}

{98, 90, 66, 83, 13, 30, 43, 41, 77, 74, 72, 23, 52, 59, 18, 25, 10,  5}

{21, 32, 56, 41}

Returns: 
{0.17890364754713348, 0.13868643400691752, 0.5037066355391879, 0.17870328290676118 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MagicCube

Simple Math

Used in:

SRM 256

Used as:

Division I Level One , Division II Level Two

Writer:

lars2520

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4698

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7992&pm=4698

Problem Statement

We've all seen magic squares before. They are square grids full of numbers arranged so that the rows, columns and diagonals all have the same sum:

 8 1 6
 3 5 7
 4 9 2

In the above figure, each row, column and diagonal sums to 15.

We'd like to extend the magic square to the magic cube. In a magic cube, we'll ignore the diagonals, but would like the rows, columns and pillars (pillars are analogous to rows and columns, but in the third dimension) to all have the same sum. You will be given 27 numbers that form the 27 values in a 3x3x3 cube. The number at (i,j,k) in the cube will be represented by element i*9 + j*3 + k of the input.

We can define the 'magic score' of a cube as the difference between the largest sum and the smallest sum (where the sums come from rows, columns, and pillars). Your task is to try to make the cube slightly more magical by trying to decrease its magic score. You should try to find two numbers in the cube that can be swapped to lower the cube's magic score. You should return the minimum possible magic score of the cube after you perform one swap. If there is no swap that would lower the magic score, return the magic score without any swaps.

Definition

Class:	MagicCube
Method:	getScore
Parameters:	int[]
Returns:	int
Method signature:	int getScore(int[] nums)
(be sure your method is public)

Constraints

-

nums will contain exactly 27 elements, each between 1 and 100, inclusive.

Examples

0)

{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1}

Returns: 0

1)

{23,4,10,1,27,21,25,7,17,9,15,13,20,3,11,2,22,18,12,24,14,26,8,6,5,19,16}

Returns: 18

In the original cube, the magic score is 51-31=20. By swapping the numbers at (0,0,1) and (1,2,0), we can improve the magic score to 51-33=18

2)

{23,2,10,1,27,21,25,7,17,9,15,13,20,3,11,4,22,18,12,24,14,26,8,6,5,19,16}

Returns: 17

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GridGenerator

Simple Math

Used in:

SRM 256

Used as:

Division II Level One

Writer:

lars2520

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4688

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7992&pm=4688

Problem Statement

Consider the following grid of numbers:

 1 0  3  4   1
 4 5  8  15  20
 1 10 23 46  81
 0 11 44 113 240
 3 14 69 226 579

Aside from the top row and left column, each number is equal to the sum of the three numbers immediately left, above, and above-left of it. You will be given a int[], row, representing the first row of a similar grid, and a int[], col, representing the first column of the grid. Your task is to return the value of the lower rightmost location when the values are calculated in the same way. Hence, the above example would be represented by the input row = {1,0,3,4,1}, col = {1,4,1,0,3}.

Definition

Class:	GridGenerator
Method:	generate
Parameters:	int[], int[]
Returns:	int
Method signature:	int generate(int[] row, int[] col)
(be sure your method is public)

Constraints

-

row and col will contain the same number of elements.

-

row and col will contain between 2 and 10 elements, inclusive.

-

Each element of row and col will be between 0 and 9, inclusive.

-

The first element of row will be the same as the first element of col.

Examples

0)

{1,0,3,4,1}

{1,4,1,0,3}

Returns: 579

The example above.

1)

{9,9,9,9,9,9,9,9,9,9}

{9,9,9,9,9,9,9,9,9,9}

Returns: 13163067

The largest possible return.

2)

{0,0,0,0,0,0,0,0,0}

{0,0,0,0,0,0,0,0,0}

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

VideoEncode

Simple Math, String Parsing

Used in:

TCO05 Qual 1/3

Used as:

Division I Level One

Writer:

PabloGilberto

Testers:

lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4680

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8020&pm=4680

Problem Statement

You would like to compress a video file to fit within a specified file size. You are given the length of the video formatted as "HH:MM:SS" (quotes for clarity only), where HH, MM and SS are two-digit numbers specifying the number of hours, minutes and seconds, respectively. You are also given the desired file size in megabytes. Return the maximum bitrate in kbps (kilobits per second) at which you can encode the video without exceeding the desired size. Please refer to the notes for information on conversion between different units.

Definition

Class:	VideoEncode
Method:	bitrate
Parameters:	String, int
Returns:	double
Method signature:	double bitrate(String length, int desiredSize)
(be sure your method is public)

Notes

-

The return value must have absolute or relative accuracy within 1e-9.

-

One megabyte is equivalent to 1,048,576 bytes.

-

One byte is equivalent to 8 bits.

-

One kilobit is equivalent to 1,000 bits.

Constraints

-

length is formatted as "HH:MM:SS", where HH is a two-digit integer between 00 and 20, inclusive, MM is a two-digit integer between 00 and 59, inclusive, and SS is a two-digit integer between 00 and 59, inclusive.

-

desiredSize is between 50 and 8000, inclusive.

-

length will represent a time of at least 1 second.

Examples

0)

"00:00:01"

Returns: 419430.4

This video is 1 second long. To fit into a 50 megabyte file, it must be encoded at 419430.4 kbps. 50 megabytes is equivalent to 419430.4 kilobits.

1)

"20:59:59"

Returns: 887.695128242437

2)

"02:00:00"

Returns: 4660.337777777778

3)

"20:59:59"

Returns: 5.548094551515232

4)

"00:00:01"

Returns: 6.7108864E7

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ValetParking

Math

Used in:

SRM 267

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4679

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8000&pm=4679

Problem Statement

Valet parking is used to maximize the number of cars that we can park in our lot. The parking spaces are arranged in a 100 x 100 grid of squares. Each square can hold one car, and it is possible to drive a car onto any of the four orthogonally adjacent squares (provided that it is not already occupied by a car). A car may enter or leave the lot only on the corner square whose coordinates are (0,0).

The lot is full when all but one of the squares is occupied. Given the location of the one empty square and the location of the customer's car, we want to know how many times the valet will have to get into a car and drive it before he can maneuver the customer's car to the location (0,0). The valet is not allowed to drive any of the cars out of the lot.

Create a class ValetParking that contains a method minMoves that is given the coordinates (emptyRow and emptyCol) of the one empty square in the full lot, and the coordinates of the customer's car (cusRow and cusCol). The method returns the number of times the valet will have to move a car.

Definition

Class:	ValetParking
Method:	minMoves
Parameters:	int, int, int, int
Returns:	int
Method signature:	int minMoves(int emptyRow, int emptyCol, int cusRow, int cusCol)
(be sure your method is public)

Constraints

-

emptyRow, emptyCol, cusRow, and cusCol will be between 0 and 99, inclusive.

-

(emptyRow,emptyCol) is not the same position as (cusRow,cusCol).

Examples

0)

Returns: 0

The customer's car is already at the exit position.

1)

Returns: 1

The valet can immediately drive the customer's car to the empty exit position.

2)

Returns: 5

   One way to do this is:
     a) drive a car from 1,0 to 0,0
     b) drive the customer's car from 1,1 to 1,0
     c) drive a car from 0,1 to 1,1
     d) drive a car from 0,0 to 0,1
     e) drive the customer's car from 1,0 to 0,0

3)

Returns: 252

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ObjectPacking

Simple Math, Simple Search, Iteration

Used in:

SRM 253

Used as:

Division II Level One

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4675

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7227&pm=4675

Problem Statement

Given a rectangular object and several boxes (in this problem, we ignore the height of the box, so a box only has two dimensions) of different sizes, you want to find the box with the smallest area which is large enough to contain the object. When putting the object in the box, it's sides must be parallel with the sides of the box. Thus, you may only rotate the object 0, 90, 180 or 270 degrees (although for obvious reasons you only need to consider rotating with 0 and 90 degrees).

Create a class ObjectPacking which contains the method smallBox which takes an int objWidth, an int objLength (the width and length of the object), a int[] boxWidth, a int[] boxLength (the width and length of the boxes) and returns an int, the area of the smallest box that can fit the object. Element i in boxWidth and boxLength correspond to box i. If no box is big enough to contain the object, return -1.

Definition

Class:	ObjectPacking
Method:	smallBox
Parameters:	int, int, int[], int[]
Returns:	int
Method signature:	int smallBox(int objWidth, int objLength, int[] boxWidth, int[] boxLength)
(be sure your method is public)

Notes

-

There doesn't have to be any gap between the sides of an object and the sides of the box. Thus, an object with width 5 and length 7 will fit in a box with width 7 and length 5.

-

Return -1 if there is no box big enough to contain the object (see example 1).

Constraints

-

objWidth will be between 1 and 1000, inclusive.

-

objLength will be between 1 and 1000, inclusive.

-

boxWidth will contain between 1 and 50 elements, inclusive.

-

boxLength will contain between 1 and 50 elements, inclusive.

-

boxWidth will contain the same number of elements as boxLength.

-

Each element in boxWidth will be between 1 and 1000, inclusive.

-

Each element in boxLength will be between 1 and 1000, inclusive.

Examples

0)

{3}

{7}

Returns: 21

By rotating the object 90 degrees we can precisely fit it into the only box in the list, so the method should return 21 (7*3).

1)

{6,9,3}

{7,4,5}

Returns: -1

The object can't fit in any of the boxes, no matter if we rotate it or not. The method should thus return -1.

2)

{19,10,12,40}

{12,20,15,5}

Returns: 200

The object will fit in box 0, 1 and 3. The area of box 1 and 3 are 200 while the area of box 0 is 228, so the method should return 200.

3)

{36,42,18,37,33,5,30,10,29,9,11,16,48,50,34,44,33,12,31,41}

{42,45,46,24,23,21,21,8,26,25,48,12,10,45,18,6,12,22,42,45}

Returns: 1845

4)

{9,1,10}

{10,6,4}

Returns: 40

5)

{2,3,3,3,3}

{2,7,7,4,2}

Returns: -1

6)

{2,3,3,3,2}

{3,1,3,3,2}

Returns: 9

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CheatABit

Recursion, Simple Math

Used in:

TCO05 Qual 7/8

Used as:

Division I Level Three

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4673

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8026&pm=4673

Problem Statement

NOTE: This problem statement contains an image that may not display properly if viewed outside of the applet.

You have written several chess programs and want to have a tournament with them. All your programs have ratings, which entirely determine the result of each game (the player with a higher rating always wins).

Before the tournament all programs are placed in a list. You want to put yourself somewhere in this list (the total number of participants including you will be a power of 2). In every round, the first participant in the list plays the second, the third plays the fourth, and so on. Players who lose their games are eliminated and removed from the list, while the winners advance to the next round. In the next round the process is repeated with the list of winners. The tournament lasts until only one player (the winner of the tournament) is left.

For example, if players participating in the tournament have ratings {100, 300, 200, 150}, then Player 1 plays Player 2 and Player 3 plays Player 4. Players 2 and 3 win and meet in the final, where Player 2 wins.

You want to win the tournament at any price, so you enter a game winning cheat code whenever you lose. However, you want to cheat as rarely as possible. You need to find the place in the initial list which allows you to win the tournament with as few cheat codes as possible. You will be given the ratings of all the programs, in the order they are placed in the list. Given yourRating as well, return the minimal number of codes you must enter to win the tourney.

Definition

Class:	CheatABit
Method:	enterCodes
Parameters:	int[], int
Returns:	int
Method signature:	int enterCodes(int[] ratings, int yourRating)
(be sure your method is public)

Constraints

-

ratings will have 1, 3, 7, 15 or 31 elements.

-

Each element of ratings will be between 1 and 3000, inclusive.

-

ratings will not contain duplicate elements.

-

yourRating will be between 1 and 3000, inclusive.

-

yourRating will not be equal to any element of ratings.

Examples

0)

{1, 2, 3, 4, 6, 7, 8}

Returns: 1

One of the best strategies is to place yourself after player 2. In the first round you win over the player with rating 3, in the second round you will succeed against the player with rating 2, and only in the final will you need to cheat.

1)

{100, 200, 300}

Returns: 0

You win the tournament without any cheating.

2)

{100, 200, 300}

Returns: 2

You must cheat twice.

3)

{100, 1, 99, 2, 98, 3, 97, 4, 96, 5, 95, 6, 94, 7, 93}

Returns: 4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Pitches

Dynamic Programming, Math

Used in:

SRM 253

Used as:

Division I Level Three

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479 , radeye

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4667

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7227&pm=4667

Problem Statement

A struggling baseball pitcher is hoping to improve his results by analyzing the statistics of how various batters perform against each of his two types of pitches: his "fast ball" and his "curve ball". He has developed a model to help him decide which pitch to select in any given circumstance.

In the game of baseball (slightly simplified for this problem), each pitch thrown will result in one of three outcomes: a "strike", a "ball", or a "hit". If a batter ever gets a hit or accumulates 4 balls before accumulating 3 strikes, this is a victory for the batter. However, if he gets 3 strikes first, this is a victory for the pitcher. The running count of balls and strikes is collectively referred to as the "count".

For this analysis, both the pitcher and batter are modelled as having a table of probabilities computed before the game. For each of the 12 possible counts, the pitcher has a probability for selecting to throw a curve ball instead of a fast ball. Similarly, for each possible count, the batter has a probability for expecting the pitcher to throw a curve ball. Before each pitch, the pitcher randomly selects which pitch to throw and the batter randomly selects which pitch to expect strictly according to the probabilities in the table for the current count.

Computing the optimal values for the probabilities in this table depends on the statistics for how the batter performs for each of the 4 possible combinations of thrown and expected pitches. These statistics will be provided by an 8-element double[], stats, in the following form:


    pitcher throws   batter expects   ball      strike    hit
    --------------   --------------   --------  --------  -----------------------
    fast ball        fast ball        stats[0]  stats[1]  1 - (stats[0]+stats[1])
    fast ball        curve ball       stats[2]  stats[3]  1 - (stats[2]+stats[3])
    curve ball       fast ball        stats[4]  stats[5]  1 - (stats[4]+stats[5])
    curve ball       curve ball       stats[6]  stats[7]  1 - (stats[6]+stats[7])

The pitcher attempts to maximize his chance of getting 3 strikes, knowing that the batter will be attempting to maximize his chance of getting 4 balls or a hit. For a given count, the optimal probability for the pitcher to throw a curve ball is the probability that minimizes the batter's ability to succeed. Similarly, the optimal probability for the batter to expect a curve ball is the probability that minimizes the pitcher's ability to succeed. In other words, the optimal pair of probabilities for a given count are such that if either the pitcher's or the batter's probability were to change, the other would be able to improve their chances by changing their probability as well. The optimal pair of probabilities forms an equilibrium, where neither the batter nor the pitcher can improve their chances if the other does not change their probability.

For example, consider the following (unrealistic) statistics: { 0, 0, 0, 1, 0, 1, 0, 0 }, with a count of 3 balls and 2 strikes. In this case, if the batter expects the same pitch that the pitcher throws, he will get a hit, otherwise, it will be a strike. The optimal probabilities are for both the pitcher and batter to select a curve ball exactly 50% of the time. 50% is optimal for the pitcher because if he were to prefer one pitch or the other, the batter could improve his performance by preferring that same pitch. Similarly, 50% is optimal for the batter because if he preferred one pitch or the other, the pitcher would be able to take advantage of that fact by preferring the opposite pitch.

Given the statistics in the format described above as a double[] stats and the current number of balls and strikes, compute the probability that the pitcher will get a total of 3 strikes before the batter gets a hit or a total of 4 balls.

Definition

Class:	Pitches
Method:	strikeOut
Parameters:	double[], int, int
Returns:	double
Method signature:	double strikeOut(double[] stats, int balls, int strikes)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

stats will contain exactly 8 elements.

-

Each element of stats will be between 0.0 and 1.0, inclusive.

-

stats[0] + stats[1] will be less than or equal to 1.0.

-

stats[2] + stats[3] will be less than or equal to 1.0.

-

stats[4] + stats[5] will be less than or equal to 1.0.

-

stats[6] + stats[7] will be less than or equal to 1.0.

-

balls will be between 0 and 3, inclusive.

-

strikes will be between 0 and 2, inclusive.

Examples

0)

{ 0, 0,
  0, 1,
  0, 1,
  0, 0 }

Returns: 0.5

This is the example in the problem statement.

1)

{ 0.375, 0.25,
  0.375, 0.25,
  0.375, 0.25, 
  0.375, 0.25 }

Returns: 0.39208984375

2)

{ 0.33, 0,
  0, 1,
  0.44, 0,
  0, 1 }

Returns: 0.0

It doesn't matter which pitch the pitcher throws; if the batter expects a fast ball, he will always get a ball or a hit.

3)

{ 0, 1,
  0, 1,
  0, 0,
  0, 0 }

Returns: 1.0

It doesn't matter which pitch the batter expects; if the pitcher throws a fast ball, he will always get a strike.

4)

{ 0, 0.4,
  0.05, 0.75,
  0.2, 0.7,
  0.85, 0.1 }

Returns: 0.32194802205218886

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DigitFiller

Dynamic Programming, Simple Math

Used in:

TCO06 Qual 7/9/14

Used as:

Division I Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4662

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9903&pm=4662

Problem Statement

You have k objects divided evenly into num piles. Unfortunately, some of the digits of k may have been erased (replaced with 'X's in the input). Return the number of possible values that k could have been.

Definition

Class:	DigitFiller
Method:	howMany
Parameters:	String, int
Returns:	long
Method signature:	long howMany(String k, int num)
(be sure your method is public)

Constraints

-

k will contain between 2 and 18 characters inclusive.

-

Each character in k will be a digit ('0'-'9') or 'X'.

-

Character 0 of k will be a positive digit ('1'-'9').

-

num will be between 1 and 10000 inclusive.

-

The return value will be at least 1.

Examples

0)

"8X"

Returns: 1

Since the objects are divided evenly into 9 piles, 81 is the only possible solution.

1)

"1XX"

Returns: 10

Here there are 10 possible values k could have been.

2)

"14"

Returns: 1

None of the digits are missing.

3)

"9999999999999X"

Returns: 4

4)

"23X34XX24XX34X"

Returns: 58823

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PrimeStatistics

Simple Math, Simple Search, Iteration

Used in:

SRM 261

Used as:

Division I Level One , Division II Level Two

Writer:

misof

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4661

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7995&pm=4661

Problem Statement

It is a known fact that prime numbers are not evenly distributed. For example, almost all primes give the remainder 1 or 5 when divided by 6 (the only two exceptions are the primes 2 and 3). Your task is to write a program that will help explore this phenomenon.

You will be given three integers: lowerBound, upperBound and modulo. Return the remainder that occurs most often when we take all primes in the set { lowerBound, lowerBound+1, ... upperBound } and divide each of them by modulo. If there are multiple remainders that occur most often, return the smallest of them.

Definition

Class:	PrimeStatistics
Method:	mostCommonRemainder
Parameters:	int, int, int
Returns:	int
Method signature:	int mostCommonRemainder(int lowerBound, int upperBound, int modulo)
(be sure your method is public)

Notes

-

A prime number is a positive integer that has exactly two divisors. The first few primes are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...

Constraints

-

lowerBound and upperBound are between 1 and 200,000 inclusive.

-

lowerBound is less than or equal to upperBound.

-

modulo is between 2 and 1000 inclusive.

Examples

0)

Returns: 3

The primes in this interval are: 3, 5, 7, 11 and 13. Their remainders when divided by 5 are 3, 0, 2, 1 and 3, respectively. Thus the most common remainder is 3.

1)

Returns: 3

In this case each of the primes gives a different remainder. According to the tie-breaking rule the smallest of them is returned.

2)

Returns: 0

There are no primes in this interval. Each remainder occurs zero times, thus each of them is the most common remainder. Zero is the smallest possible remainder. Thus, according to the tie-breaking rule, zero is returned.

3)

Returns: 1

Almost all primes are odd; the only even prime is 2.

4)

Returns: 5

As mentioned in the introduction, almost all primes give the remainder 1 or 5 modulo 6. In this interval there are more primes of the second kind.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CountriesRanklist

Simple Math, Sorting

Used in:

SRM 270

Used as:

Division I Level One , Division II Level Three

Writer:

misof

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4658

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8067&pm=4658

Problem Statement

An unnamed international contest just finished. There were exactly four contestants from each of the participating countries. During the contest each of the contestants achieved a non-negative integer score (the higher, the better). The contestants were sorted according to their scores and the first part of the overall results (i.e., the best few contestants) was announced during the final ceremony. The organizers of the contest decided not to publish the remaining, lower part of the results.

In the Countries Ranklist the countries are ordered (in decreasing order) by the total score of their four contestants. If two or more countries have the same score, they are tied for the best place from the corresponding interval, and the places of the lower ranked countries remain unaffected. For example, if the total scores of countries A, B, C and D are 100, 90, 90 and 80, respectively, then B and C are tied for second place, and D is fourth. For further clarification, see examples 2 and 4.

A String[] knownResults will represent the published part of the results, with each of the elements describing one of the announced contestants. The elements have the form "COUNTRY CONTESTANT SCORE", where COUNTRY is the name of the country, CONTESTANT is the name of the contestant and SCORE is his score.

Your task will be to compute the best and the worst possible placement in the Countries Ranklist for each of the participating countries. You shall assume that from each country at least one contestant was announced and that all contestants not in the available part of the results scored strictly less than the worst contestant in the available part of rankings. (For example, if the worst announced contestant scored 47 points, then each of the not announced contestants from each of the participating countries could have scored at most 46 points.)

You are to return a String[] with one element for each country. The form of each element must be "COUNTRY BEST WORST", where COUNTRY is the name of the country, BEST and WORST are the best and the worst position this country could possibly have in the Countries Ranklist. Order this list so that the country names are given in alphabetical order. Note that country names are case sensitive, and that in alphabetical order all uppercase letters come before lowercase letters. The numbers BEST and WORST mustn't contain leading zeroes.

Definition

Class:	CountriesRanklist
Method:	findPlaces
Parameters:	String[]
Returns:	String[]
Method signature:	String[] findPlaces(String[] knownPoints)
(be sure your method is public)

Notes

- All scores (even the unknown ones) are non-negative integers.

Constraints

- knownResults contains between 1 and 50 elements, inclusive.

- Each of the elements in knownResults is of the form "COUNTRY CONTESTANT SCORE".

- Each COUNTRY and CONTESTANT in knownResults are strings containing between 1 and 10 letters ('a'-'z', 'A'-'Z').

- For each country knownResults contains at most 4 contestants.

- Each SCORE in knownResults is an integer between 1 and 600, inclusive, with no leading zeroes.

Examples

0)

{"Poland Krzysztof 101", "Ukraine Evgeni 30", "Ukraine Ivan 24"}

Returns: {"Poland 1 1", "Ukraine 2 2" }

The worst announced contestant is Ivan with 24 points. Each of the contestants that weren't announced had to score strictly less, i.e., at most 23 points. Thus the total score of Ukraine is at most 30+24+23+23 = 100 and Poland surely wins.

1)

{"Poland Krzysztof 100", "CzechRep Martin 30", "CzechRep Jirka 25"}

Returns: {"CzechRep 1 2", "Poland 1 2" }

This time, if the two missing Czech competitors scored 24 points each (and the remaining three from Poland scored 0), Czech Republic could still win. Note the order in which the countries are reported in the output.

2)

{"Slovakia Marian 270", "Hungary Istvan 24", "Poland Krzysztof 100", 
 "Hungary Gyula 30", "Germany Tobias 27", "Germany Juergen 27"}

Returns: {"Germany 2 4", "Hungary 2 4", "Poland 2 2", "Slovakia 1 1" }

This is an interesting case. Slovakia is sure to win, and Poland is sure to be second. But it is possible that Germany, Hungary and Poland have an equal total score of 100. In this case they are all tied for second place.

3)

{"usa Jack 14", "USA Jim 10", "USA Jim 10", "USA Jim 10", 
 "USA Jim 10", "usa Jack 14", "usa Jack 14", "Zimbabwe Jack 10"}

Returns: {"USA 2 2", "Zimbabwe 3 3", "usa 1 1" }

Case matters, "USA" and "usa" are two different countries. Contestant names don't matter, i.e., from "USA" there are four different contestants, all named "Jim".

4)

{"A a 9", "A b 9", "A c 9", "A d 9", 
 "B e 9", "B f 9", "B g 8", "B h 8",
 "C i 9", "C j 9", "C k 9", "C l 7",
 "D m 1", "D n 1", "D o 1", "D p 1"}

Returns: {"A 1 1", "B 2 2", "C 2 2", "D 4 4" }

All results have been announced, so everything is clear. A is first, B and C are tied for second, and D is fourth.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SpreadsheetColumn

Simple Math, String Manipulation

Used in:

SRM 261

Used as:

Division II Level One

Writer:

misof

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4651

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7995&pm=4651

Problem Statement

Many spreadsheet applications use positive integers to label rows of cells and strings to label columns of cells. Your task is to write a function that gets the number of the column and returns its label.

All 26 uppercase letters are used to label the columns. Column labels are ordered according to their length, and labels with the same length are ordered in alphabetical order. Thus, the first 26 columns have a one-letter label, the following 26*26 columns have a two-letter label. The sequence of the labels looks as follows:

A, B, C, ..., Z, AA, AB, ..., AZ, BA, BB, ..., ZY, ZZ

The columns are numbered from 1, i.e., column number 1 has the label A.

Definition

Class:	SpreadsheetColumn
Method:	getLabel
Parameters:	int
Returns:	String
Method signature:	String getLabel(int column)
(be sure your method is public)

Notes

- The constraints will guarantee that the column label is between "A" and "ZZ", inclusive

Constraints

- column will be between 1 and 702, inclusive.

Examples

0)

Returns: "A"

1)

Returns: "B"

2)

Returns: "AA"

3)

Returns: "DG"

4)

Returns: "ZZ"

Note that this is the largest possible input.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ModeProbability

Advanced Math

Used in:

TCO05 Semi 3

Used as:

Division I Level One

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4643

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8093&pm=4643

Problem Statement

You have a skewed random number generator that outputs the number i with percentage probs[i]. Given that you have generated n numbers, return the probability (between 0 and 1) that value has been generated more times than any of the other numbers.

Definition

Class:	ModeProbability
Method:	getProb
Parameters:	int[], int, int
Returns:	double
Method signature:	double getProb(int[] probs, int n, int value)
(be sure your method is public)

Notes

-

The returned value must be accurate to 1e-9 relative or absolute.

Constraints

-

probs will contain between 1 and 5 elements inclusive.

-

Each element of probs will be between 1 and 100 inclusive.

-

The elements of probs will sum to 100.

-

n will be between 1 and 15 inclusive.

-

value will be between 0 and N-1 inclusive, where N is the number of elements in probs.

Examples

0)

{50,50}

Returns: 0.25

Two equally occurring numbers. For 0 to occur more than 1 it needs to be generated twice in a row. Hence, the probability is 1/4.

1)

{50,50}

Returns: 0.5

Since we generate 9 numbers, one number will always occur more times than the other. By symmetry, 0 occurs more frequently with probability 1/2.

2)

{5,50,20,25}

Returns: 0.7947486656372071

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PartyGame

Dynamic Programming, Math

Used in:

TCO05 Round 2

Used as:

Division I Level Two

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4635

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8017&pm=4635

Problem Statement

You are playing a one-player game. The board for the game consists of several red and green cells ordered in a row. Initially you are located at the first cell. On each move, you roll an N-sided die with numbers from 1 to N on its sides and move the corresponding number of cells ahead. If you stop on a red cell, you jump back to the cell you started the move from. If you stop at green, you stay there. You win the game when you jump on the last cell or pass it by.

Given a String[] field, return the expected number of moves you will need to win the game (return -1 if you will never win). All characters in all elements of field will be either 'G' or 'R', for green and red cells respectively. The first character of the first element of field represents the cell where you are located at the start of the game. The last character of the last element of field represents the last cell. You should concatenate all Strings from field to get the complete game field.

Definition

Class:	PartyGame
Method:	numberOfMoves
Parameters:	String[], int
Returns:	double
Method signature:	double numberOfMoves(String[] field, int N)
(be sure your method is public)

Constraints

-

field will contain between 1 and 50 elements, inclusive.

-

Each element of field will contain between 1 and 50 characters, inclusive.

-

The total number of characters in the field must be at least 2.

-

Each element of field will contain only 'R' and 'G' characters.

-

The first character of the first element of field and the last character of the last element of field will both be 'G'.

-

N will be between 1 and 20, inclusive.

Examples

0)

{"GRG"}

Returns: 2.0

1)

{"GRRG"}

Returns: -1.0

2)

{"GGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG"}

Returns: 14.47619043642061

3)

{"GGRRRGRGRRGRRRGRRRRRRRRRRRGRRGRRRRRRRGRRRRRR",
 "RRRRRRRRRRRRRRRRRGRRRRRRRRRRRRGRRRRGRRRRRGRGR",
 "RRRGRRRRRRGGRRRRRRRRRRRRRRGRRRGRRRRRRGRRRRRRGR",
 "RRGRRRRGRRRRGRGRRRRRRRGRRGRRRRRRRRRRRRRRGRRRGGG",
 "RRRRRRRRRRRRRRRGRRGRRRRRRGRRRRRRRRGRRRRRRRRRRGRR",
 "GRRRRRGGGRRRRRGRRRRRRRRRRRGRRRRRRRGRRGRRRRRRRRRRR",
 "RRRRRRRRGGGGGGGGRRRRRRRRRRRRRRRRRRGRRRRRRRRGGGGGGG",
 "GGGGGGGGGRRRRRRRRRRRRRRRRRRGRRRRRRRRRRRRRRRRRRGRRR",
 "RRRRRGRGRRRRRRRRRRRRRRRGRRRRRRRRRRRGRRRRRRRRRRRRRG",
 "GRRRRRRRRRRRRRRRRRRGRRRRRRRRRRRRRRRGRRRGRRRRRRRRGR",
 "RRRRRRGRRGRRRRRRGRRRRRRRRRRRRRRRRGRGRGRRRRRRGRRRRG",
 "RGRRRRRRRRRGRRGRRRRRRGRRRRRRRGRRGRRGRGGGGGGGGRRRRR",
 "RRRRRRRRRRRRRGRRRRRRRRRGRRRRRRRRRRGRRRRRRGGGGGGGGG",
 "GGGGGGGGGGGGGGGGGGGGGGGGGGGGRRRRRRRRRRRRRRRRRRGGGG",
 "GRRRRRRRRRRRRRRRRRRGRRRGGGGGGGGGGRRRRRRRRRRRRRRRRR",
 "RGGGGGGGGGGGGGGGGGGGGGGGGGGRRRRRRRRRRRRRRRRRRGRRRR",
 "RRRGRRRRRRRRRGRRRRRRRRRRRGRRRRRRRRRRRRRRGRRRRRRRGG",
 "RRRRGGGGGGGGGGRRRRRRRRRRRRRRRRRRGGRRRGRGRRRRRRRRRR",
 "RRRRRGRRRRRRRRRGRGRRGRRGRRRRRRRRRRRRRRRRGGRRGRRRRR",
 "RRRRRRGRRRRRRRRRGGRRRRRGRRRRGRRRRRRRRGGRRRRRRRRRGR",
 "RRRGRRRRRRRRRRRRRRGGGRRRRRRRGRRRRRRRRRRRRRRRRGGGGG",
 "GGGGGGGRRRRRRRRRRRRRRRRRRGRRRGRRRRRRRRRRRRRGGRRRRG",
 "GRRRRRRRRRRRGRRRRRRRRRRRRRGGGGGGGGGGGGGGGGGGGGGGGG",
 "GGGGGGGGGGGGGGGRRRRRRRRRRRRRRRRRRGRRRRGGGGGGGGGGGR",
 "RRRRRRRRRRRRRRRRRGRRGRRGRRRRRGRRGRRRRRRRRRGRRRRRRR",
 "RRRRRRGGGGGGGGGGGGGGRRRRRRRRRRRRRRRRRRGRRRRRRRRRRG",
 "RRRRRRRRRGRRRRRRRRRRRRRRRRGRGRRRRRRRRRRGRRRRRRGRRR",
 "RRRRRRRRRGGRRRRRRRRRRRRRRRRRRGRRRRRGRRRRGRRRRRGRRR",
 "RRRGRRGRRRGRRRRRRRRRRGRRRRRRRRRRGGRRRRRRGGRRRRRRRR",
 "RRGRRRRRRRRRRRRGRGRRRGGRGRRGRRRGRRRRRRRRRRRGRRRRRR",
 "RGRRRRRRRRRRRRRGGRRRRRRRRRGRRRGRRRRRRRRRGRRRRGGRRR",
 "RRRRRRRRRRRRRRRGRRRRRRRRRGRGRRRRGGGGGGGGGRRRRRRRRR",
 "RRRRRRRRRGRRRRRRGRRRRRRRRRRGRRRRRRRGRRRRRRRRRRRRRR",
 "RRGRRRRRRRRRRRRRRRRRRGRRRRRRRRGRRRRGRGRRRRRRRRRRRG",
 "RGRRGRRRGRRRRRGRRRRRRRRRGRRRRRRRRRRGRRGRRRRRRRGRGG",
 "GRRRRRRRRRRRRRRRRRRGRRRRRRRRRRRRRRRRRGRRRRRRRGRRRR",
 "RRRRRGRRRRRRRGRGRRRRRRRRGGRRRRRRGRRRRRRRRRRRRGRRRR",
 "RRGRRRRRRRRRRRGRRGRRRRRRRRRRGRRRRRRRRRGRRRGRGRRGRR",
 "RRRRGRRRRRRRRRRGRRRRRRRRRRRRRRRGRRRRRRRGRRGGGGGGGG",
 "GGGGGGGGGGGGGGGGGGGGGGGGGGGGRRRRRRRRRRRRRRRRRRGRRR",
 "RGGRGGGGRRRRRRRRRRRRRRRRRRGRGRRRGGRRRRRRGGRRRRRRRG",
 "RRRRGRRRRRRRRRRRRGGGGGGRRRRRRRRRRRRRRRRRRGRRRRRRRR",
 "RRRRRRRGRRRRRRRRRRGRRGGGGGGGGGGGGGRRRRRRRRRRRRRRRR",
 "RRGRRRRRRRRRRRRRRRGGRRGRRRRGRRRRGRRRRRRRRRRRRGRGRG",
 "RGRRRRRRRGRRRRRRRGRRRGGRRRRRRRRGRRRRRRRRRGGGRRRRRR",
 "GGGGGGRRRRRRRRRRRRRRRRRRGRGRRRRRRRRRRRGRRRRRRGRRRR",
 "RRRRRRRGRRRRRRRRGRRRRRRRRRRRRRGGRRRRRRRRRRRRRRRRGR",
 "RRRRRRRRRRRRRGRRRRRRRRRRRRRRRRRGRRRRGRRRRRRRRRRGRR",
 "RRRRGRGRRRRRRRRGRRRRRGRRRRRRRRRRRRRRRGRRRRRRGRRRRR",
 "RRGRRGRRRRRRRGGRRGRRRRRRGRRRRRRRRRRRRRRRRRGRGRRRRG"}

Returns: -1.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TestingCar

Brute Force, Math

Used in:

SRM 276

Used as:

Division I Level Two

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479 , timmac

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4634

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8073&pm=4634

Problem Statement

A test driver in a car company tests a new prototype. For each test drive, he is given a list of restrictions, limiting his speed at certain moments in time. The test driver wants to reach as fast a speed as possible. You should write a program which will find the maximal speed he can reach without violating the restrictions.

You will be given a String[] restrictions, giving you the restrictions for the test-drive. Each element of restrictions will contain three integers S, T and D separated by single spaces. The restriction becomes active T seconds after the start of the test-drive and stays active for D seconds. While the restriction is active the car can not go faster than S meters per second. If two or more restrictions are applicable at the same time, the restriction with the minimal speed should be taken into account.

At the start of the test drive, the car is motionless. Given two ints, duration, the total duration of the test drive in seconds, and acceleration, the maximal possible acceleration of the car in meters per second squared, return the maximal speed allowed by the test-drive restrictions. Please note that acceleration applies both to increasing and decreasing speed (braking).

Definition

Class:	TestingCar
Method:	maximalSpeed
Parameters:	String[], int, int
Returns:	double
Method signature:	double maximalSpeed(String[] restrictions, int duration, int acceleration)
(be sure your method is public)

Notes

-

The car does not have to come to a complete stop at the final moment of the test drive. It can still be moving.

-

For the purposes of the problem you may assume the car has no speed limit at all.

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

restrictions will contain between 0 and 50 elements, inclusive.

-

Each element of restrictions will be formatted as "S T D".

-

In each element of restrictions, S, T and D will be separated by single spaces and contain no leading zeroes.

-

In each element of restrictions, S will be an integer between 0 and 100, inclusive.

-

In each element of restrictions, T will be an integer between 0 and duration, inclusive.

-

In each element of restrictions, D will be an integer between 0 and 1000, inclusive.

-

duration will be between 1 and 1000, inclusive.

-

acceleration will be between 1 and 25, inclusive.

Examples

0)

{"30 0 200"}

Returns: 30.0

The restriction doesn't allow us to go faster than 30 meters per second.

1)

{"30 0 200"}

Returns: 20.0

We only have enough time to reach 20 meters per second.

2)

{"50 0 40", "50 60 50"}

Returns: 150.0

The car can go above 50 meters per second only between the 40th and 60th second. Accelerating from the 40th to 50th second, and braking from the 50th to 60th allows you to reach 150 meters per second.

3)

{"50 30 10", "50 60 50"}

Returns: 175.0

4)

{"0 0 100", "0 200 100", "0 400 100", "0 600 100", "0 800 100"}

Returns: 2000.0

5)

{"0 0 100", "0 200 100", "0 400 100", "0 600 100", "0 800 100", "0 1000 100"}

Returns: 1000.0

6)

{"44 422 129", "45 1 29", "72 290 80", "2 1 331", "76 445 16", 
"76 204 429", "8 372 737", "21 159 538", "71 266 707", "99 73 933",
 "38 457 879", "42 24 299", "54 349 882", "6 352 909", "26 419 428",
 "51 327 311", "10 52 898", "75 10 702", "54 263 762", "75 404 223",
 "43 383 127", "86 433 521", "58 394 306", "33 379 514", "58 239 973",
 "89 301 765", "47 235 777", "75 355 190", "52 425 38", "59 140 347",
 "89 220 810", "47 72 724", "3 398 283", "0 224 266", "88 222 615",
 "25 149 85", "59 221 838", "14 87 86", "44 227 252", "73 330 936",
 "71 198 138", "54 186 141", "6 128 454", "5 123 719", "7 442 930",
 "59 174 505", "37 0 581", "9 198 168", "40 391 692", "49 320 419"}

Returns: 7.5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TheCoderMan

Brute Force, Simple Math, String Manipulation

Used in:

TCO05 Qual 5/10

Used as:

Division I Level Three

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4628

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8024&pm=4628

Problem Statement

You and your friends have viewed and rated several movies during past few weeks. "The CoderMan" is a new movie which is on this week and you want to know whether it's worth watching it.

You will be given a String yourEvaluations, containing your evaluations for all movies. The i^th character of yourEvaluations will correspond to the i^th movie and will be either a digit or 'X'. 'X' means you haven't watched the movie, and a digit between '0' and '9' represents your rating for it. Also you will be given a String[] friendsEvaluations, with each element representing movie ratings given by one of your friends. All elements of friendsEvaluations will be formatted the same as yourEvaluations. The last character of all elements of friendsEvaluations will represent "The CoderMan" - the movie you must rate (the last character of yourEvaluations will also represent "The CoderMan" and will always be 'X').

To rate "The CoderMan", you will need to calculate the deviation between you and each of your friends. It can be found as an average of absolute differences between you and your friend's ratings for all movies you both have watched (if there are no such movies, don't take the friend into account). For example, if you have rated 5 movies as "51X6X", and your friend's ratings are "2X97X", we count only the first and the fourth movies. This gives us the deviation equal to (|5 - 2| + |6 - 7|)/2 = (3 + 1)/2 = 2.

Throw away from your calculations all people whose deviation is greater than maximalDeviation and those who haven't rated "The CoderMan" yet. For all the people who are left, calculate and return the average of the ratings they've given to "The CoderMan". If none of your friends satisfies the criteria, return -1.

Definition

Class:	TheCoderMan
Method:	evaluateMovie
Parameters:	String, String[], int
Returns:	double
Method signature:	double evaluateMovie(String yourEvaluations, String[] friendsEvaluations, int maximalDeviation)
(be sure your method is public)

Notes

-

The return value must be within 1e-9 absolute or relative error of the actual result.

Constraints

-

yourEvaluations will contain between 2 and 50 characters, inclusive.

-

yourEvaluations will contain only digits ('0' - '9') and 'X' characters.

-

The last character in yourEvaluations will be 'X'.

-

friendsEvaluations will contain between 1 and 50 elements, inclusive.

-

yourEvaluations and each element of friendsEvaluations will be of the same length.

-

Each element of friendsEvaluations will contain only digits ('0' - '9') and 'X' characters.

-

maximalDeviation will be between 0 and 9, inclusive.

Examples

0)

"51X6X"

{"2X974", "2X976", "2X978"}

Returns: 6.0

The deviations between you and each of your friends are all equal to 2. All ratings given to "TheCoderMan" are taken into account.

1)

"51X6X"

{"2X971"}

Returns: -1.0

2)

"8XX"

{"1X7", "30X", "370", "917", "00X", "211"}

Returns: 7.0

3)

"X0123456789X"

{
"X01234567891",
"XX1234567892",
"XXX234567893",
"XXXX34567894",
"80123456789X",
"80123456788X",
"811234567891",
"80124456789X",
"801235567890",
"8XXXXX567899"
}

Returns: 3.8

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KthElement

Math, Search

Used in:

SRM 255

Used as:

Division II Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4622

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7228&pm=4622

Problem Statement

Let the function F(N) be a number of ones in the binary representation of the number N. For example F(279)=5 because 279 = (100010111)₂.

The sequence X is constructed using the following rules. The initial element X₀ is 0, and each successive elements X_i is A * F(X_i-1) + B.

You will be given integers A, B and K. Your method should return the X_K element. See examples for further explanation.

Definition

Class:	KthElement
Method:	find
Parameters:	int, int, int
Returns:	int
Method signature:	int find(int A, int B, int K)
(be sure your method is public)

Constraints

-

A will be between 0 and 1000000, inclusive.

-

B will be between 0 and 1000000, inclusive.

-

K will be between 1 and 1000000000, inclusive.

Examples

0)

Returns: 12

The sequence is 0, 12, 12, 12... and so on.

1)

Returns: 9

The sequence is 0, 7, 10, 9, 9, 9... and so on.

2)

500000001

Returns: 51

The sequence is 0, 21, 66, 51, 81, 66, 51, 81, 66... and so on. The sequence has a period of length 3 starting from X₂, so the 500000001th element will be the same as the element with index (500000001 - 2) mod 3 + 2.

3)

700000000

Returns: 478

The sequence is 0, 4, 83, 320, 162, 241, 399, 478, 557, 399, 478, 557, 399... and so on.

4)

900000000

Returns: 3993300

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BalancedGame

Simple Math, Simple Search, Iteration

Used in:

SRM 254

Used as:

Division II Level One

Writer:

Enogipe

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4617

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8006&pm=4617

Problem Statement

You will be given a String[], conflicts, where each element represents a single player in a multiplayer game. Element i represents player i, and character j of element i represents whether player i will win ('W'), tie ('T'), or lose ('L') against player j.

Your task is to ensure that each player wins against at least p% of the other players, and loses against at least q% of the other players. You should return the 0-based index of the first player in the input (lowest index) that does not meet these requirements, or -1 if all players meet them. Note that if there are N players total, then at least ceil((N-1)*p/100) of the characters in element i must be 'W' for player i to meet the requirements. The formula for losses is analogous.

Definition

Class:	BalancedGame
Method:	result
Parameters:	String[], int, int
Returns:	int
Method signature:	int result(String[] conflicts, int p, int q)
(be sure your method is public)

Notes

-

The i-th character of the i-th element of conflicts will always be 'T' and can be ignored.

-

The function 'ceil' in ceil((N-1)*p/100) returns the least integer greater than or equal to its argument. For example, ceil(1.5)=2 and ceil(4)=4.

Constraints

-

p and q will be between 0 and 100, inclusive.

-

conflicts will have between 2 and 50 elements, inclusive.

-

Each element of conflicts will have the same number of characters ('W', 'L' and 'T') as the number of elements in conflicts.

-

If the j-th character of the i-th element of conflicts is 'W', 'L', or 'T' then the i-th character of the j-th element will be 'L', 'W' or 'T' respectively.

-

The i-th character of the i-th element of conflicts will always by 'T'.

Examples

0)

{"TWWW",
 "LTWW",
 "LLTW",
 "LLLT"}

Returns: 0

Player 0 cannot lose and player 3 cannot win, so these players are not balanced. Return the lowest index of an unbalanced player.

1)

{"TWWW",
 "LTWW",
 "LLTW",
 "LLLT"}

Returns: -1

Now there are no balancing constraints, so even though player 0 cannot lose and player 3 cannot win, the characters are balanced.

2)

{"TTT",
 "TTT",
 "TTT"}

Returns: 0

Even with such lax balancing constraints, a perfectly matched set of characters is not balanced in the sense we are looking for.

3)

{"TLLLLLTWWWWTLLWWWT",
 "WTTWTTLLWLLWWLTLWW",
 "WTTWWTLWTWLWWWWLTW",
 "WLLTLTWWWTWLWLLWLT",
 "WTLWTLWWWWLLWLLWTW",
 "WTTTWTWLLWTLLWWWLW",
 "TWWLLLTLLWTWWWLLWW",
 "LWLLLWWTWLLWWLLLWT",
 "LLTLLWWLTTWLTWTLWT",
 "LWLTLLLWTTTLLLLWTW",
 "LWWLWTTWLTTTLLWWLL",
 "TLLWWWLLWWTTLWTTLL",
 "WLLLLWLLTWWWTWLLWW",
 "WWLWWLLWLWWLLTTWLL",
 "LTLWWLWWTWLTWTTTWT",
 "LWWLLLWWWLLTWLTTLW",
 "LLTWTWLLLTWWLWLWTW",
 "TLLTLLLTTLWWLWTLLT"}

Returns: 17

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TableSeating

Dynamic Programming, Math, Recursion

Used in:

SRM 249

Used as:

Division I Level One , Division II Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4616

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7224&pm=4616

Problem Statement

Your restaurant has numTables tables to seat customers. The tables are all arranged in a line. If a large party of customers comes in, a group of adjacent tables will be used. Which group of tables is entirely up to the customer. Since you cannot predict this, assume all possible choices occur with equal probability. What you can predict is the size of each group of customers that arrives. Element i of probs gives the probability, in percent, that an entering party will need i+1 tables. Assuming nobody leaves, return the expected number of tables you will use before a party must be turned away. This only occurs if there is no place to seat them.

Definition

Class:	TableSeating
Method:	getExpected
Parameters:	int, int[]
Returns:	double
Method signature:	double getExpected(int numTables, int[] probs)
(be sure your method is public)

Notes

-

Return values must be accurate to 1e-9, relative or absolute.

Constraints

-

numTables will be between 1 and 12 inclusive.

-

probs will contain between 1 and 12 elements inclusive.

-

Each element of probs will be between 0 and 100 inclusive.

-

The elements of probs will sum to 100.

Examples

0)

{100}

Returns: 4.0

Since every party needs only 1 table, you will always fill the restaurant before turning someone away.

1)

{0,100}

Returns: 3.3333333333333335

Now every party wants 2 tables. One third of the time, the first party will choose the middle 2 tables blocking anyone else from being seated. Two thirds of the time, the first party will choose 2 tables on the end allowing the restaurant to become full. Thus, the returned value is (1/3)*2 + (2/3)*4 = 10/3.

2)

{0,0,0,0,0,50,50}

Returns: 0.0

You have 5 tables, but every party needs 6 or 7 tables.

3)

{9,9,9,9,9,9,9,9,9,9,10}

Returns: 7.871087929710551

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TriangleType

Simple Math

Used in:

SRM 247

Used as:

Division II Level One

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4610

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7222&pm=4610

Problem Statement

In Euclidean Geometry, triangles can be categorized into one of three types based on their angle measures. A triangle is acute if all three angles are less than 90 degrees. A triangle is obtuse if one angle is greater than 90 degrees. Lastly, a triangle with one angle at exactly 90 degrees is a right triangle.

It could also be the case that three positive integers can not possibly form the side-lengths of a triangle. This happens when the length of one side is equal to or larger than the sum of the lengths of the other two sides, because it would not be possible to connect the end points of the three sides in such a way that a triangle was formed.

Write a method that takes as input three positive integer side-lengths of a triangle. Return "IMPOSSIBLE" if a triangle cannot be formed. Return "ACUTE" if the triangle is acute, "OBTUSE" if the triangle is obtuse, and "RIGHT" if the triangle is right.

Definition

Class:	TriangleType
Method:	type
Parameters:	int, int, int
Returns:	String
Method signature:	String type(int a, int b, int c)
(be sure your method is public)

Notes

-

For a triangle with side-lengths x, y, and z and x <= y <= z.

* The triangle is right if x*x + y*y = z*z.

* The triangle is obtuse if x*x + y*y < z*z.

* The triangle is acute if x*x + y*y > z*z.

* It is impossible to have x + y <= z.

Constraints

-

a, b, and c are between 1 and 10,000, inclusive.

Examples

0)

Returns: "RIGHT"

1)

Returns: "ACUTE"

2)

Returns: "OBTUSE"

3)

Returns: "IMPOSSIBLE"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GradingGridIns

Simple Math, Simple Search, Iteration, String Parsing

Used in:

SRM 264

Used as:

Division I Level Two

Writer:

Enogipe

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4608

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7998&pm=4608

Problem Statement

The Grid-In questions on the SAT require that the test-taker fill in a numerical answer from a small set of symbols. In particular, each answer is a String of four characters.

Each character is one of ' ' (a space), '.', '/', or a digit '0'-'9'.
Spaces are interpreted as unneeded characters. Whitespace must not be surrounded by non-space characters.
The '.' is a decimal point; only one may appear in any answer. The '/' is a division sign; only one may appear in any answer. No answer may contain both a '.' and a '/'.
All characters to the left of a '/' are interpreted as the numerator, and all characters to the right of a '/' are interpreted as the denominator. If there is a '/', both the numerator and the denominator must contain at least one digit '0'-'9', and the denominator must not be 0.
At least one digit '0'-'9' must appear in each answer.

A range will be given between a lower bound and upper bound, inclusive. Both bounds are specified as fractions with integer numerators and denominators. lower and upper are both int[]s containing two elements, the first the numerator and the second the denominator. An answer is correct if and only if either it lies between the bounds or there is no possible submission between the answer and one of the bounds. See example 1 for clarification.

An answer which satisfies the symbol constraints (the first item on the list) but does not satisfy other constraints (such as "1 23", "8//5", or "9.4." is considered malformed. Furthermore, any answer with a denominator of 0 is considered malformed.

You will be given a String[] answer whose elements each contain exactly 4 characters. You are to return a String[] with the same number of elements as the number of elements in answer. Each element of the return value should be one of three possible responses: "CORRECT" for a correct answer, "INCORRECT" if incorrect, or "MALFORMED" if the answer does not conform to the guidelines above. The i-th element of the return value should correspond to the i-th element of answer.

Definition

Class:	GradingGridIns
Method:	score
Parameters:	String[], int[], int[]
Returns:	String[]
Method signature:	String[] score(String[] answer, int[] lower, int[] upper)
(be sure your method is public)

Notes

-

Leading zeros are allowed.

-

An answer which has a denominator of 0 will be considered malformed.

Constraints

-

answer will contain between 1 and 50 elements, inclusive.

-

Each element of answer will contain exactly 4 characters.

-

Each character in an answer will be a ' ', '.', '/', or a digit '0'-'9'.

-

upper and lower will each contain exactly 2 elements between 0 and 9999, inclusive.

-

Neither lower[1] nor upper[1] will be 0.

-

lower[0] / lower[1] will be less than or equal to upper[0] / upper[1].

Examples

0)

{"4/7 "," 4/7","4/07","8/14",".571",".572"}

{4,7}

{4,7}

Returns: {"CORRECT", "CORRECT", "CORRECT", "CORRECT", "CORRECT", "CORRECT" }

Each of these is correct. Notice that neither .571 nor .572 are equal to 4 divided by 7.

1)

{" 4/7","1.01","1.02"," 000"}

{0,1}

{1,1}

Returns: {"CORRECT", "CORRECT", "INCORRECT", "CORRECT" }

Any answer within the allowed range is acceptable. Notice also that 1.01, which is greater than the upper bound, is acceptable because there are no possible submissions greater than 1 and less than 1.01.

2)

{"1.15","1 14","1.14"," 8/7"}

{1142,1000}

{1142,1000}

Returns: {"INCORRECT", "MALFORMED", "CORRECT", "CORRECT" }

3)

{"    ","...."," .  ","1 23","8//5","9.4.","85/ ","/123","123/"}

{1,1}

{1,1}

Returns: 
{"MALFORMED",
"MALFORMED",
"MALFORMED",
"MALFORMED",
"MALFORMED",
"MALFORMED",
"MALFORMED",
"MALFORMED",
"MALFORMED" }

4)

{"1/0 "}

{0,1}

{9999,1}

Returns: {"MALFORMED" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Grader

Simple Math

Used in:

SRM 244

Used as:

Division II Level One

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4588

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7219&pm=4588

Problem Statement

For the International Baccalaureate (IB) diploma, students are assigned integer grades between 1 and 7 inclusive, based on exams taken at the end of high school. Unfortunately, these results are never available in time to assist universities with admissions decisions. To counteract this problem, IB teachers are required to predict in advance how well each student will perform on the exams. As these predictions can have an enormous impact on a student's future, schools are naturally very interested in evaluating their accuracy.

Create a class Grader that contains a method grade, which is given a int[] predictedGrades and a int[] actualGrades. Corresponding elements in these arrays will represent the predicted and final grades, respectively, achieved by each student. The method should return a int[] with 7 elements, giving the percentage (rounded down) of predicted grades that differ from the actual grades by each value between 0 and 6 inclusive. Thus, element 0 of the return value should be the percentage of predictions that were correct, element 1 should be the percentage of predictions that differed by 1, etc.

Definition

Class:	Grader
Method:	grade
Parameters:	int[], int[]
Returns:	int[]
Method signature:	int[] grade(int[] predictedGrades, int[] actualGrades)
(be sure your method is public)

Constraints

-

predictedGrades and actualGrades will each contain between 1 and 50 elements inclusive.

-

predictedGrades and actualGrades will contain the same number of elements.

-

Each element of predictedGrades will be between 1 and 7 inclusive.

-

Each element of actualGrades will be between 1 and 7 inclusive.

Examples

0)

{1,5,7,3}

{3,5,4,5}

Returns: {25, 0, 50, 25, 0, 0, 0 }

The grade distribution is shown below.

Student | Predicted grade | Actual grade | Difference
--------+-----------------+--------------+-----------
   1    |        1        |       3      |     2
   2    |        5        |       5      |     0
   3    |        7        |       4      |     3
   4    |        3        |       5      |     2

Out of four predictions, one (25%) is off by 0 points, two (50%) are off by 2 points, and one (25%) is off by 3 points.

1)

{1,1,1}

{5,6,7}

Returns: {0, 0, 0, 0, 33, 33, 33 }

Note that percentages are rounded down.

2)

{3}

{3}

Returns: {100, 0, 0, 0, 0, 0, 0 }

3)

{1,5,3,5,6,4,2,5,7,6,5,2,3,4,1,4,6,5,4,7,6,6,1}

{5,1,3,2,6,4,1,7,5,2,7,4,2,6,5,7,3,1,4,6,3,1,7}

Returns: {17, 13, 21, 17, 21, 4, 4 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BoggleScore

Dynamic Programming, Math, Search

Used in:

SRM 349

Used as:

Division II Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479 , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4585

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10673&pm=4585

Problem Statement

In the word game Boggle, a player is presented with a 4x4 grid of letters and has the task of finding words hidden among the letters. A word may start at any location, and each succeeding letter of the word must be adjacent to the preceding letter horizontally, vertically, or diagonally.

In our version of the game, a player is restricted to finding words from a given list of acceptable words. The same letter may be used multiple times in the spelling of a word, and it is permitted to spell words that are part of longer words. For instance, in the following example, one could form the word SANDS, even though there is only a single S:

XXXX
XSAX
XDNX
XXXX

Notice that the above configuration would also yield other words, like SAND, AND, and SAD.

If a word can be formed in more than one way, it may be counted more than once; for instance, the word EYE may be counted multiple times here since it can be found in different directions (see examples):

XEYE
XXXX
XXXX
XXXX

Here, the word EYE could still be formed, but only once, since we are allowed to reuse letters:

XXEY
XXXX
XXXX
XXXX

Here, the word TREE may be formed two different ways (down-right-up or down-diagonal-down):

TEXX
REXX
XXXX
XXXX

The score for each word is the square of its length. Thus, three letter words are worth 9 points, four letter words are 16 points, etc.

You are given a String[] grid with exactly four elements, with each element containing 4 letters, describing the grid of letters you are to search. You are also given a String[] words, each element of which represents an acceptable word.

You are to return a long indicating the maximum score you can achieve after finding all possible paths to spell out acceptable words, summing together the scores from each individual word. Since the maximum score could potentially be quite large, return the result MOD 1E13 (10000000000000).

Definition

Class:	BoggleScore
Method:	bestScore
Parameters:	String[], String[]
Returns:	long
Method signature:	long bestScore(String[] grid, String[] words)
(be sure your method is public)

Constraints

-

grid will contain exactly four elements.

-

Each element of grid will contain exactly four characters.

-

Each character of each element of grid will be an uppercase ('A'-'Z') letter.

-

words will contain between 1 and 50 elements, inclusive.

-

Each element of words will contain between 1 and 50 characters, inclusive.

-

Each character of each element of words will be an uppercase ('A'-'Z') letter.

-

No two elements of words will be the same.

Examples

0)

{"XXEY",
 "XXXX",
 "XXXX",
 "XXXX"}

{"EYE"}

Returns: 9

From the problem statement. There's exactly one way to spell EYE, and it's worth 9 points.

1)

{"XEYE",
 "XXXX",
 "XXXX",
 "XXXX"}

{"EYE"}

Returns: 36

Also from the problem statement. Here, there are four ways to spell EYE. If we number the positions in the grid from 0-15 (top to bottom, left to right), then we can spell EYE by going: 123, 121, 321, 323.

2)

{"TEXX",
 "REXX",
 "XXXX",
 "XXXX"}

{"TREE"}

Returns: 32

Again, from the problem statement. There are two ways to spell TREE, a word worth 16 points.

3)

{"XXXX",
 "XSAX",
 "XDNX",
 "XXXX"}

{"SANDS", "SAND", "SAD", "AND"}

Returns: 59

Each word occurs once, so 25 + 16 + 9 + 9 = 59.

4)

{"TREX",
 "XXXX",
 "XXXX",
 "XXXX"}

{"TREE"}

Returns: 0

With only a single E on the board, we can't make the word TREE.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BrokenCalculator

Search, Simple Math

Used in:

SRM 241

Used as:

Division I Level Two

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4574

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7216&pm=4574

Problem Statement

You wish to enter a whole number onto your simple four-function calculator. Unfortunately for you, some of the keys are broken. Nonetheless, rather than buy a new calculator, you enjoy the challenge presented before you.

Your calculator is a very primitive one, and can only display positive numbers with up to three digits. Initially, your display does not show anything, until you press a number key. Any time an operation exceeds the number 999, it causes an error, and you cannot continue.

You are given int[] keys, indicating which numeric keys are still functional, and String operators indicating which of the four operators are available to you. Assume that the equals key is always available. Finally, you are given int target, indicating the number you wish to display.

When you perform a division, your calculator performs an integer division, dropping any remainder. Thus, pressing "23/7=" yields 3, and "3/8" yields 0. Pressing the equals key completes any calculation, and any subsequent key presses after pressing equals discards the current display, and starts a new calculation.

You are to return an int indicating the minimum number of key presses necessary to display the target number. If it is not possible to ever get your display to show the target number, return -1.

Definition

Class:	BrokenCalculator
Method:	fewestKeys
Parameters:	int[], String, int
Returns:	int
Method signature:	int fewestKeys(int[] keys, String operators, int target)
(be sure your method is public)

Notes

-

Like most simple four function calculators, pressing any operator has the effect of performing an "equals" on anything entered so far, and operations are performed in exactly the order entered. Thus, 2 + 2 * 3 = evaluates to 12 (instead of 8, as with typical order of operations).

Constraints

-

keys will contain between 1 and 10 elements, inclusive.

-

Each element of keys will be between 0 and 9, inclusive.

-

No two elements of keys will be the same.

-

operators will contain between 1 and 4 characters, inclusive.

-

Each character of operators will be '+', '-', '*', or '/'.

-

No two characters of operators will be the same.

-

target will be between 1 and 999, inclusive.

Examples

0)

{0, 1, 2, 3}

"+"

Returns: 4

Here, if we type "2 + 3 =", our calculator will display "5", thus, we need four key presses.

1)

{0}

"+-*/"

Returns: -1

With only a "0" to press, no operations will get us to the number 5.

2)

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

"/-+*"

Returns: 3

With all of the keys available to us, we need only type in the number we want. Notice that the order in which we define the operators doesn't matter.

3)

{1, 2, 4, 8}

"+-*/"

Returns: 8

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ColorCode

Simple Math

Used in:

SRM 250

Used as:

Division II Level One

Writer:

Softwalker

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4566

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7225&pm=4566

Problem Statement

An electronics manufacturer has called you in to make a program to decode resistor color codes. You are given a String[] code containing three elements corresponding to the first three color bands on a resistor. Return the # of Ohms the resistor represents.

The first two bands of resistors represent the value, while the third is a multiplier, as shown in the following chart:

Color:      Value:       Multiplier:

black         0                   1
brown         1                  10
red           2                 100
orange        3               1,000
yellow        4              10,000
green         5             100,000
blue          6           1,000,000
violet        7          10,000,000
grey          8         100,000,000
white         9       1,000,000,000

For example if you are given { "yellow", "violet", "red" }, you would return 4700.

Definition

Class:	ColorCode
Method:	getOhms
Parameters:	String[]
Returns:	long
Method signature:	long getOhms(String[] code)
(be sure your method is public)

Notes

-

Actual resistors can have a 4th and even a 5th band representing the tolerance, and the amount the value might change in 1,000 hours of use, respectively, but for our purposes we will only deal with the first three bands.

Constraints

-

code consists of 3 elements each containing one of the color words above, all in lower case.

Examples

0)

{ "yellow", "violet", "red" }

Returns: 4700

The example from the problem statement.

1)

{ "orange", "red", "blue" }

Returns: 32000000

2)

{ "white", "white", "white" }

Returns: 99000000000

The maximum possible.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Conglutination

Brute Force, Simple Math, String Manipulation

Used in:

SRM 246

Used as:

Division II Level Two

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4562

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7221&pm=4562

Problem Statement

You are developing a new software calculator. Some people use the calculator to check the sums of several numbers, but they sometimes get unexpected results because they forget to press the 'plus' button. You have almost solved this problem, but a small method is still required.

You will be given a String conglutination and an int expectation. Your method should split conglutination into two numbers A and B so that A + B = expectation. Return the result as a String in the form "A+B" (quotes for clarity only). A and B must contain at least one digit each. Leading zeros are allowed and they must be preserved in the result. If there are several possible splits, choose the one with the smallest value of A. Return an empty String if there are no possible splits.

Definition

Class:	Conglutination
Method:	split
Parameters:	String, int
Returns:	String
Method signature:	String split(String conglutination, int expectation)
(be sure your method is public)

Constraints

-

conglutination will contain between 2 and 20 characters, inclusive.

-

conglutination will contain only digits ('0'-'9').

-

The first character of conglutination will not be zero.

-

expectation will be between 1 and 1000000000, inclusive.

Examples

0)

"22"

Returns: "2+2"

1)

"536"

Returns: "5+36"

2)

"123456000789"

Returns: "1234560+00789"

Be careful with leading zeros.

3)

"123456789"

Returns: ""

4)

"112"

Returns: "1+12"

The value of A should be as small as possible.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Straights

Simple Math

Used in:

SRM 245

Used as:

Division II Level One

Writer:

Enogipe

Testers:

PabloGilberto , lbackstrom , brett1479 , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4561

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7220&pm=4561

Problem Statement

You are playing a game of cards in which the number of straights, i.e., sets of consecutive-valued cards, determines the strength of your hand. You will be given a int[] hand, where the i-th element of hand is the number of cards of value i in your hand. You should return the number of straights of length k. For example, suppose you have the hand:

2 of spades
2 of diamonds
2 of clubs
3 of clubs
4 of hearts
4 of clubs

You would be given hand = { 0, 3, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0 }. The number of two-card straights is 5:

2 of spades, 3 of clubs
2 of diamonds, 3 of clubs
2 of clubs, 3 of clubs
3 of clubs, 4 of hearts
3 of clubs, 4 of clubs

Definition

Class:	Straights
Method:	howMany
Parameters:	int[], int
Returns:	int
Method signature:	int howMany(int[] hand, int k)
(be sure your method is public)

Notes

-

Straights do not wrap around: if hand is {1,0,0,0,0,0,0,0,0,0,0,0,1}, you have no straights of length 2.

Constraints

-

hand will contain exactly 13 elements.

-

Each element of hand will be between 0 and 4 inclusive.

-

k will be between 1 and 13 inclusive.

Examples

0)

{0,3,1,2,0,0,0,0,0,0,0,0,0}

Returns: 5

The example given.

1)

{1,1,1,1,1,1,1,1,1,1,1,1,1}

Returns: 9

Say hand[0] references Aces. There are 9 ways to make a straight of length 5: Ace-Five up to Nine-King.

2)

{4,4,4,4,4,4,4,4,4,4,4,4,4}

Returns: 67108864

3)

{4,0,4,0,4,0,4,0,4,0,4,0,4}

Returns: 0

Straights do not wrap around; we have no straights here.

4)

{1,2,3,4,1,2,3,4,1,2,3,4,1}

Returns: 31

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DivToZero

Simple Math

Used in:

SRM 262

Used as:

Division II Level One

Writer:

Softwalker

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4556

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7996&pm=4556

Problem Statement

You are given an integer num from which you should replace the last two digits such that the resulting number is divisible by factor and is also the smallest possible number. Return the two replacement digits as a String.

For instance:

if num = 275, and factor = 5, you would return "00" because 200 is divisible by 5.

if num = 1021, and factor = 11, you would return "01" because 1001 is divisible by 11.

if num = 70000, and factor = 17, you would return "06" because 70006 is divisible by 17.

Definition

Class:	DivToZero
Method:	lastTwo
Parameters:	int, int
Returns:	String
Method signature:	String lastTwo(int num, int factor)
(be sure your method is public)

Constraints

-

factor must be between 1 and 100, inclusive.

-

num must be between 100 and 2,000,000,000, inclusive.

Examples

0)

2000000000

Returns: "00"

1)

Returns: "02"

2)

Returns: "00"

3)

Returns: "15"

4)

Returns: "72"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OddDigitable

Graph Theory, Math

Used in:

SRM 255

Used as:

Division I Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4527

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7228&pm=4527

Problem Statement

An odd-digitable number is a positive integer which consists of only odd digits. For example, 1, 7, 15, 91 and 73353 are odd-digitable numbers, but 2, 70, 94 and 72653 are not odd-digitable.

You will be given integers N and M. Your method should return the smallest odd-digitable number that equals M modulo N. Your method should return "-1"(quotes for clarity only) if there are no such odd-digitable numbers.

Definition

Class:	OddDigitable
Method:	findMultiple
Parameters:	int, int
Returns:	String
Method signature:	String findMultiple(int N, int M)
(be sure your method is public)

Constraints

-

N will be between 2 and 100000, inclusive.

-

M will be between 0 and N-1, inclusive.

Examples

0)

Returns: "7"

1)

Returns: "-1"

2)

Returns: "319"

3)

Returns: "791957"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PrisonCells

Search, Simple Math

Used in:

SRM 273

Used as:

Division II Level Three

Writer:

supernova

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4526

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8070&pm=4526

Problem Statement

You are the most popular programmer in town and the mayor needs your help. This time he wishes to reorganize the town's detention system. All the inmates are held in an underground rectangular-shaped prison, with cells situated on m rows and n columns. When opened, the cells communicate with each other vertically and horizontally. Thus, the distance between two cells is defined as the Manhattan distance:

(absolute value of difference in x-coordinates) + (absolute value of difference in y-coordinates)

The mayor's plan is to reduce the conflicts by placing the prisoners as far from each other as possible. There are nr prisoners to place and each cell can hold at most one prisoner. The goal is to put the prisoners in cells such that the minimum of all the distances between two occupied cells is as high as possible.

Given an int m, an int n and an int nr representing the number of rows, the number of columns and the number of prisoners, respectively, return an int denoting the highest possible minimum distance between two occupied cells.

Definition

Class:	PrisonCells
Method:	scatter
Parameters:	int, int, int
Returns:	int
Method signature:	int scatter(int m, int n, int nr)
(be sure your method is public)

Constraints

-

m is between 1 and 4, inclusive.

-

n is between 1 and 4, inclusive.

-

nr is between 2 and n*m, inclusive.

Examples

0)

Returns: 5

The best way is to put the two prisoners in two opposing corners, like in the diagram below:

* - - -
- - - -
- - - *

1)

Returns: 4

In this case there are 3 distances to consider: between prisoner 1 and prisoner 2, between prisoner 1 and prisoner 3 and between prisoner 2 and prisoner 3. A possible solution, with none of the three distances less than 4, is given below:

* - - -
- - - *
- - - -
- * - -

2)

Returns: 3

Everyone in the corner:

* - - *
- - - -
- - - -
* - - *

Out of the 6 possible distances, 2 have a length of 6 and 4 have a length of 3. So, the answer should be 3.

3)

Returns: 1

Every cell is occupied, so the smallest distance between two prisoners is clearly 1.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FracCount

Brute Force, Simple Math

Used in:

SRM 247

Used as:

Division II Level Two

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4522

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7222&pm=4522

Problem Statement

It is possible to assign a unique integer value to each irreducible fraction between 0 and 1. (This shows that there are a countable infinity of fractions.) The usual way to number them is shown below


1/2  1/3  2/3  1/4  3/4  1/5  2/5  3/5  4/5  1/6  5/6  1/7  ...

Notice that 2/4, for example, does not get listed because it reduces to 1/2. Given an irreducible fraction we want to find where it appears in the above counting order, where 1/2 is counted as 1, 1/3 as 2, etc.

Create a class FracCount that contains a method position that is given the numerator and denominator of an irreducible fraction between 0 and 1 and that returns its position in the counting order.

Definition

Class:	FracCount
Method:	position
Parameters:	int, int
Returns:	int
Method signature:	int position(int numerator, int denominator)
(be sure your method is public)

Constraints

-

numerator will be between 1 and denominator - 1 inclusive.

-

denominator will be between 2 and 1,000 inclusive.

-

The greatest common divisor of numerator and denominator will be 1.

Examples

0)

Returns: 1

1/2 is at position 1 in the counting order

1)

Returns: 11

5/6 is at position 11 in the counting order

2)

Returns: 304191

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TimeCard

Simple Math, String Manipulation

Used in:

SRM 257

Used as:

Division II Level Three

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4520

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8005&pm=4520

Problem Statement

When I start my shift at work I punch in my starting time, and when I leave I punch out. The times are printed on a card using exactly 8 characters in the format

           hh:mm,xx

where hh is the 2 digit representation of the hour, mm is the 2 digit representation of the minute, and xx is either am or pm. The ':' and ',' are literal. "12:00,am" denotes midnight, while "12:00,pm" denotes noon.

The difference between that time I punch in and the time I punch out is the amount of time I have worked so, for example, if I punch in at 03:33pm and punch out at 03:34pm I have worked 1 minute.

No shift is allowed to be more than 20 hours long. This is my last shift of the week and I am supposed to work 40 hours during the week. Create a class TimeCard that contains a method leave that is given a String[] time of all the times on this week's timecard and that returns a String (using the same format) that tells when I can leave and have exactly 40 hours for the week. Return "BELOW 40" or "ABOVE 40" if it is not possible to get exactly 40 hours. In all cases, the return should contain exactly 8 characters.

The elements of time alternate: punch in time, punch out time, punch in time, ... with the final element being the time I just punched in on my final shift.

Definition

Class:	TimeCard
Method:	leave
Parameters:	String[]
Returns:	String
Method signature:	String leave(String[] time)
(be sure your method is public)

Constraints

-

time will contain an odd number of elements between 1 and 49 inclusive.

-

Each element of time will be formatted as above.

-

In each element of time hh will be between 01 and 12 inclusive.

-

In each element of time mm will be between 00 and 59 inclusive.

-

time will contain no shift that exceeds 20 hours in duration.

Examples

0)

{"03:00,pm"}

Returns: "BELOW 40"

This is my one and only shift, and I am only allowed to work 20 hours on a shift.

1)

{"09:00,am","05:00,pm","09:00,am","05:00,pm",
    "09:00,am","05:00,pm","09:00,am","05:00,pm","09:00,am"}

Returns: "05:00,pm"

I have worked 4 previous shifts of 8 hours, so I need 8 hours on this shift to make 40.

2)

{"12:00,am","08:00,pm","12:00,am","08:00,pm","12:00,am"}

Returns: "12:00,am"

I have already worked 2 shifts of 20 hours so I already have exactly 40 hours. I should go home immediately.

3)

{"12:00,pm","08:00,pm","12:00,am","08:00,pm","12:00,am"}

Returns: "12:00,pm"

4)

{"09:00,am","04:31,pm","09:00,am","04:31,pm",
     "09:00,am","05:00,pm","09:00,am","05:00,pm","03:53,am"}

Returns: "12:51,pm"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CalcRoot

Brute Force, Math

Used in:

SRM 246

Used as:

Division I Level Three

Writer:

Andrew_Lazarev

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4519

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7221&pm=4519

Problem Statement

You are developing a new calculator with a square root function. To make things simple for your clients, you have decided to approximate square roots as simple fractions, rather than displaying a long sequence of digits.

You will be given N and D and should return the fraction closest to sqrt(N) for which the denominator is not greater than D. The fraction should be returned in the form "A/B" where A and B are positive integers with no common factors greater than one.

Definition

Class:	CalcRoot
Method:	approximate
Parameters:	int, int
Returns:	String
Method signature:	String approximate(int N, int D)
(be sure your method is public)

Constraints

-

N will be between 1 and 1000000, inclusive.

-

D will be between 1 and 1000, inclusive.

Examples

0)

Returns: "2/1"

1)

Returns: "7/3"

sqrt(5) = 2.236

2)

Returns: "31/9"

sqrt(12) = 3.464

3)

Returns: "98462/639"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PowerDigit

Math

Used in:

TCO06 Round 2

Used as:

Division I Level One

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4515

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9891&pm=4515

Problem Statement

We need to know the k-th digit in x to the power y. A value of 0 for k means that the digit of interest is the rightmost digit, a value of 1 means the digit next to the rightmost digit, etc.

Create a class PowerDigit that contains a method digitK that is given x, y, and k and that returns the k-th digit (an integer in the range 0 to 9 inclusive) in x to the power y. If there is no k-th digit in x to the power y return -1.

Definition

Class:	PowerDigit
Method:	digitK
Parameters:	int, int, int
Returns:	int
Method signature:	int digitK(int x, int y, int k)
(be sure your method is public)

Constraints

-

x is between 0 and 10,000, inclusive.

-

y is between 1 and 10,000, inclusive.

-

k is between 0 and 4, inclusive.

Examples

0)

Returns: 2

2^10 = 1024 so the digit 1 is 2.

1)

Returns: -1

1024 does not have a digit 4 (the 1 in 1024 is digit 3)

2)

Returns: 6

2^1000 is a very large number. But digit 0 is predictable since with succeeding powers it follows the sequence 2, 4, 8, 6, 2, 4, 8, 6, 2, ....

3)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Abacus

Simple Math, String Manipulation

Used in:

SRM 292

Used as:

Division I Level One , Division II Level Two

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4512

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9813&pm=4512

Problem Statement

An abacus can be used to do arithmetic. The version that we have has 6 horizontal threads, each with nine beads on it. The beads on each thread are always arranged with just one gap, possibly at one of the ends. However many beads are adjacent and at the right end of the thread is the digit value of the thread. The value on the abacus is read by taking the digits in order from top thread to bottom thread and arranging them from left to right (so the top thread is the one that contains the most significant digit).

Create a class Abacus that contains a method add that is given a String[] original and a number val and that returns a String[] showing the abacus after val has been added to the original abacus.

Both in original and in the return, the String[] will contain exactly 6 elements representing the 6 threads in order from top thread to bottom thread. Each element will contain a lowercase 'o' to represent each bead and three consecutive hyphens '-' to indicate the empty part of the thread. Each element will thus contain exactly 12 characters.

Definition

Class:	Abacus
Method:	add
Parameters:	String[], int
Returns:	String[]
Method signature:	String[] add(String[] original, int val)
(be sure your method is public)

Constraints

-

original will contain exactly 6 elements.

-

Each element of original will contain exactly 12 characters, 9 lowercase 'o's and 3 consecutive '-'s.

-

val will be between 0 and 999,999 inclusive.

-

val added to the original abacus will result in a value that can be shown on the abacus.

Examples

0)

{"ooo---oooooo",
 "---ooooooooo",
 "---ooooooooo",
 "---ooooooooo",
 "oo---ooooooo",
 "---ooooooooo"}

Returns: 
{"ooo---oooooo",
"---ooooooooo",
"---ooooooooo",
"---ooooooooo",
"o---oooooooo",
"ooooo---oooo" }

When we add 5 to the original, it is necessary to "carry" 1 to the next thread up. This shows the arithmetic 699979 + 5 = 699984

1)

{"ooo---oooooo",
 "---ooooooooo",
 "---ooooooooo",
 "---ooooooooo",
 "oo---ooooooo",
 "---ooooooooo"}

Returns: 
{"oo---ooooooo",
"ooooooooo---",
"ooooooooo---",
"ooooooooo---",
"ooooooooo---",
"ooooooooo---" }

This shows 699979 + 21 = 700000

2)

{"ooooooooo---",
 "---ooooooooo",
 "ooooooooo---",
 "---ooooooooo",
 "oo---ooooooo",
 "---ooooooooo"}

Returns: 
{"oooooooo---o",
"---ooooooooo",
"ooooooooo---",
"---ooooooooo",
"oo---ooooooo",
"---ooooooooo" }

3)

{"o---oooooooo",
 "---ooooooooo",
 "---ooooooooo",
 "---ooooooooo",
 "---ooooooooo",
 "---ooooooooo"
}

Returns: 
{"---ooooooooo",
"ooooooooo---",
"ooooooooo---",
"ooooooooo---",
"ooooooooo---",
"ooooooooo---" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TaxTable

Math

Used in:

SRM 267

Used as:

Division II Level One

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4511

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8000&pm=4511

Problem Statement

For those who file jointly and have a taxable income of at least $100,000 the tax for 2004 is calculated from the following table. To calculate your tax, you find the appropriate bracket for your taxable income, multiply your taxable income by the multiplier, and then subtract the subtraction value.



    At_least   Less_than    Multiplier       Subtraction
    100,000     117,250        25%             6,525.00

    117,250     178,650        28%            10,042.50

    178,650     319,100        33%            18,975.00

    319,100        -           35%            25,357.00

When I find out how much tax someone had to pay, I want to be able to figure out what their taxable income was. Create a class TaxTable that contains a method income that is given the taxAmount and calculates the taxable income whose tax is closest to taxAmount. This result is returned, rounded to the nearest dollar (.5 rounds up). If the taxAmount is too low to have come from the table, return -1.

Definition

Class:	TaxTable
Method:	income
Parameters:	int
Returns:	int
Method signature:	int income(int taxAmount)
(be sure your method is public)

Constraints

- taxAmount will be between 0 and 1,000,000, inclusive.

- All values within 1e-6 of the taxable income corresponding to taxAmount will round to the same integer.

Examples

0)

Returns: 200000

The tax on $200,000 is 33% * 200,000 - 18975 which is 47025.

1)

Returns: -1

Anybody who has taxable income of at least $100,000 has a tax that is greater than $1000

2)

Returns: 200003

The tax on $200,000 is exactly $47,025. For each dollar above that we must pay 33 cents additional tax. So the income that results in a tax of exactly $47,026 is $200,003.0303030303.... which rounds to $200,003. Note that a return of 200002 would be incorrect, even though the tax on that amount would be 47025.66 which is close to 47026.

3)

Returns: 319027

4)

Returns: 117266

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ComputationalComplexity

Simple Math, Simple Search, Iteration

Used in:

SRM 243

Used as:

Division II Level One

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4510

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7218&pm=4510

Problem Statement

You are testing several algorithms and you want to find the fastest one for your task. Computational complexities of these algorithms will be given to you in three int[]s - constant, power and logPower. The i^th algorithm needs on average constant[i]*N^power[i]*ln^logPower[i](N) operations to solve your task.

Given an int N, the size of your task, return the 0-based index of the fastest algorithm. In case of a tie, return the smallest index.

Definition

Class:	ComputationalComplexity
Method:	fastestAlgo
Parameters:	int[], int[], int[], int
Returns:	int
Method signature:	int fastestAlgo(int[] constant, int[] power, int[] logPower, int N)
(be sure your method is public)

Notes

-

ln(x) in the formula means natural logarithm of x. It can be computed as:

- Math.log(x) in java

- log(x) in C++

- Math.Log(x) in C# and VB.

Constraints

-

constant, power and logPower will have the same number of elements.

-

constant, power and logPower will each have between 1 and 50 elements, inclusive.

-

N will be between 1 and 1000, inclusive.

-

All elements of power and logPower will be between 0 and 5, inclusive.

-

All elements of constant will be between 1 and 100, inclusive.

Examples

0)

{5, 50, 45}

{2, 1, 1}

{0, 1, 1}

Returns: 2

The first algorithm needs 5*400*400 = 800000 operations. The second one needs about 50*400*ln(400) (approximately 170000) and the third is even a bit faster.

1)

{5, 50, 45}

{2, 1, 1}

{0, 1, 1}

Returns: 0

For the small N the first algorithm works faster.

2)

{100}

{5}

{5}

Returns: 0

3)

{32, 33, 58, 93, 8, 27, 43, 69, 95, 77,
 57, 73, 87, 87, 50, 92, 67, 20, 2, 46,
 73, 48, 25, 90, 48, 18, 28, 26, 20, 33,
 59, 48, 69, 4, 19, 13, 10, 78, 55, 90}

{5, 0, 1, 4, 0, 3, 5, 4, 3, 3,
 0, 5, 0, 5, 5, 3, 0, 4, 1, 1,
 4, 0, 2, 4, 0, 0, 3, 2, 0, 0,
 4, 3, 5, 0, 2, 4, 3, 4, 3, 0}

{2, 2, 2, 0, 4, 5, 2, 3, 4, 5,
 0, 0, 1, 4, 2, 5, 2, 4, 5, 0,
 5, 4, 3, 0, 4, 1, 1, 3, 3, 0,
 1, 5, 2, 1, 1, 4, 0, 0, 2, 3}

Returns: 33

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RedundantStrings

Recursion, Simple Math

Used in:

SRM 238

Used as:

Division II Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4505

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6537&pm=4505

Problem Statement

A string composed of a's and b's is either redundant or non-redundant. A string is redundant if and only if it can be expressed as a shorter string replicated multiple times. For example, the string "ababab" is redundant since it is 3 copies of "ab" concatenated together. The string "ab" is called a root of "ababab". The string "aaaa" has 2 roots: "aa" and "a". A nice result in formal languages states that every redundant string has exactly 1 non-redundant root (it may have many redundant roots).

Only considering strings composed of a's and b's, return the number of redundant strings that have the given length.

Definition

Class:	RedundantStrings
Method:	howMany
Parameters:	int
Returns:	int
Method signature:	int howMany(int length)
(be sure your method is public)

Constraints

-

length will be between 1 and 60 inclusive.

Examples

0)

Returns: 0

There are no redundant strings of length 1.

1)

Returns: 2

Both "aa" and "bb" are redundant.

2)

Returns: 4

Here the redundant strings are "aaaa", "bbbb", "abab", and "baba".

3)

Returns: 34

4)

Returns: 33814

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AirTravel

Advanced Math, Geometry, Graph Theory, Search

Used in:

SRM 241

Used as:

Division II Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4501

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7216&pm=4501

Problem Statement

You are working for a shipping company, TopShipper, that specializes in shipping products by air. Your cargo jets transport items between a set of airports. From each airport, you can travel directly to some subset of the other airports. (Some airports may be too far, or may not have a safe passageway.) The ability to travel from one airport to another does not guarantee the ability to travel directly in the opposite direction.

You are about to send out a cargo plane on a trip to pick up a large shipment of a certain product. Unfortunately, only one other airport has this product for pickup, and you aren't guaranteed that there is a safe, direct route to the other airport. You may have to travel through one or more other airports to get to your final destination. Nonetheless, you wish to ultimately end up at the airport that has your desired product, and which you can get to by travelling the shortest possible distance.

You are to return a double indicating the number of miles travelled by the cargo plane along the optimal route from the origin to the destination. If no such route exists, return -1.

Given two coordinates, (lat1, lon1) and (lat2, lon2), the shortest distance between them is across an arc known as a great circle. The arclength along a great circle, between two points on the earth can be calculated as:

radius * acos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon1 - lon2))

For purposes of this problem, the radius of the earth is 4000 miles.

You are given the latitude and longitude coordinates of each airport in latitude and longitude. The i-th element of latitude corresponds to the i-th element of longitude. You are also given String[] canTravel. The i-th element of canTravel is a space-delimited list of the 0-based indices of the airports that can be reached from airport i. Finally, you are given origin and destination, the indices of the airports at which you start and end your trip.

Definition

Class:	AirTravel
Method:	shortestTrip
Parameters:	int[], int[], String[], int, int
Returns:	double
Method signature:	double shortestTrip(int[] latitude, int[] longitude, String[] canTravel, int origin, int destination)
(be sure your method is public)

Constraints

-

latitude, longitude, and canTravel will contain between 1 and 20 elements, inclusive.

-

latitude, longitude, and canTravel will each contain the same number of elements.

-

Each element of latitude will be between -89 and 89, inclusive.

-

Each element of longitude will be between -179 and 179, inclusive.

-

Each element of canTravel will be a space-delimited list of integers, with no leading zeroes.

-

Each integer represented in each element of canTravel will be between 0 and n - 1, where n is the number of elements in latitude.

-

origin and destination will be between 0 and n - 1, inclusive, where n is the number of elements in latitude.

-

No two airports will reside at the same latitude and longitude.

Examples

0)

{0, 0, 70}

{90, 0, 45}

{"2", "0 2", "0 1"}

Returns: 10612.237799994255

Here, we are looking to travel from airport 0 to airport 1.

Using the given formula, we calculate that the distance from 0 to 1 is 6283, from 0 to 2 is 5306, and from 1 to 2 is 5306.

A direct route from airport 0 to 1 would be fastest, if such a route were allowed. Since it is not, we have to travel through airport 2.

1)

{0, 0, 70}

{90, 0, 45}

{"1 2", "0 2", "0 1"}

Returns: 6283.185307179586

Here, we have the same three airports, and there is a safe route between any two. Thus, we take the direct route, which is quickest.

2)

{0, 30, 60}

{25, -130, 78}

{"1 2", "0 2", "1 2"}

Returns: 0.0

We are free to travel as we wish, but since our destination is the same as our point of origin, we don't have much travel to do.

3)

{0, 20, 55}

{-20, 85, 42}

{"1", "0", "0"}

Returns: -1.0

Notice here that we could go from airport 2 to airport 0, but not from 0 to 2. Given the available routes, there is no way we can get from airport 0 to airport 2.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BlackjackWinner

Math

Used in:

SRM 241

Used as:

Division II Level One

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4500

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7216&pm=4500

Problem Statement

In the game of blackjack, if the player scores higher than the dealer or the dealer goes over 21, and the player does not go over 21, then he wins his bet (in addition to keeping his original wager). If he scores 21 or less, and the same as the dealer, the hand is a push, and he keeps his bet. Otherwise, if he scores lower than the dealer, or goes over 21 (regardless of whether or not the dealer also does so), then he loses his bet.

A "blackjack" is a special kind of 21 point hand that beats all other hands. In such a case, the player wins 1.5 times his original bet. If both dealer and player have a blackjack, then the hand is a push. Note that if the dealer has a blackjack, and the player has a 21 (but does not have blackjack), then the dealer wins, and the player loses his wager.

You are given an int bet indicating the players wager, an int dealer indicating the dealer's score, and an int player indicating the player's score. Finally, you are given an int blackjack, which will be equal to 1 if the player has a blackjack, or 0 otherwise. Likewise, you are given the int dealerBlackjack.

You are to return the amount of money the player wins or loses on the hand. A win should return a positive number, either the player's bet, or 1.5 times his bet. A loss should be returned as a negative number. A push should return 0.

Definition

Class:	BlackjackWinner
Method:	winnings
Parameters:	int, int, int, int, int
Returns:	int
Method signature:	int winnings(int bet, int dealer, int dealerBlackjack, int player, int blackjack)
(be sure your method is public)

Constraints

-

bet will be between 2 and 100, inclusive, and will be even.

-

dealer will be between 17 and 26, inclusive.

-

dealerBlackjack will be 0 or 1.

-

dealerBlackjack may only be 1 if dealer is 21.

-

player will be between 4 and 30, inclusive.

-

blackjack will be 0 or 1.

-

blackjack may only be 1 if player is 21.

Examples

0)

Returns: 10

Here, the player beats the dealer (without blackjack), and wins his bet.

1)

Returns: -26

Here, the player loses... even though both dealer and player have 21, the dealer has a blackjack.

2)

Returns: 150

Here, the dealer went over, so as long as the player didn't go over, he's a winner. In fact, since he has a blackjack, he wins 1.5 times his original bet.

3)

Returns: -78

Even though the dealer went over, so did the player, so the player loses.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Musical

Math

Used in:

SRM 247

Used as:

Division I Level One

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4495

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7222&pm=4495

Problem Statement

n children walk around a circle with n-1 evenly-spaced chairs. When the music stops, each one tries to get to the nearest chair. One of them is bound to fail thus providing a lesson about life. We want to identify the loser.

The children start evenly spaced around the circle, with the first child, A, located right next to a chair. The child who follows A as they walk around the circle is B, the one who follows B is C, etc. The children all start walking when the music starts at a speed that will get them all the way around the circle in 10 seconds. When the music stops, they each try to get to the nearest chair.

Create a class Musical that contains a method loser that is given n (the number of children) and time (the number of seconds the music plays). The method should return the name of the loser as a String containing just one uppercase letter.

It may be helpful to note that the child who is farther from any chair than each other child is always the loser.

Definition

Class:	Musical
Method:	loser
Parameters:	int, double
Returns:	String
Method signature:	String loser(int n, double time)
(be sure your method is public)

Constraints

-

n will be between 2 and 26 inclusive.

-

time will be between 1.0 and 100.0 inclusive.

-

For all values within 1.0 E-9 of time the same child would be the loser.

Examples

0)

1.2

Returns: "B"

Starting from their original positions they walk for 1.2 seconds. When the music stops the closest chair to A is the first chair, the one he started at. Meanwhile B has moved to the point where now that chair is also the closest chair for him. But A is closer than B so B is the loser. (C is closest to the second chair and has no competition for that one.)

1)

12.0

Returns: "A"

The children walk all the way around the circle and a little farther before the music stops. The situation is almost the same now as in the previous case, with A and B racing for the first chair, but this time A is farther away than B.

2)

100.0

Returns: "N"

3)

15.0

Returns: "A"

The 2 children start out with A next to the chair and B on the other side of the circle. After 15 seconds, they have gone around the circle one and a half times, so B is next to the chair and A is the loser.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PolyominoCut

Graph Theory, Recursion, Simple Math

Used in:

SRM 242

Used as:

Division I Level Three

Writer:

gepa

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4489

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7217&pm=4489

Problem Statement

You are given a rectangular board consisting of width times height small squares. Return the number of different ways there are to cut a k-polyomino out of this board, so that the remaining part remains connected.

A k-polyomino is a connected set of k squares. The figure below shows as an example all possible pentominoes (5-polyominoes) ignoring any translations, rotations or reflections.

Connected means side-connected here (both in the polyomino definition and in the requirement for the remaining part of the board) - i.e., you must be able to go from any square to any other by only going through squares and square-sides but not square-corners.

For two ways of cutting a polyomino out of the grid to be different and be counted separately it suffices if at least one grid square is included in the first polyomino but not in the other.

The example below shows some polyomino cuts for k=7. The two on the left (red) are not counted, since they leave the remaining grid disconnected, while the one on the right (green) is counted.

Definition

Class:	PolyominoCut
Method:	count
Parameters:	int, int, int
Returns:	int
Method signature:	int count(int k, int width, int height)
(be sure your method is public)

Constraints

-

k will be between 1 and 8, inclusive.

-

width and height will be between k+1 and 800, inclusive.

Examples

0)

Returns: 200

There is only one 1-polyomino (called monomino), and this can be cut out anywhere on the grid.

1)

Returns: 480

There are in total 484 ways to cut a triomino (3-polyomino) out of a 10x10 square, but 4 of them leave a square in the corner not connected (see figure below), so only 480 satisfy the problem requirements.

2)

Returns: 1704053350

The worst case fits in an int.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Flush

Brute Force, Math

Used in:

SRM 245

Used as:

Division I Level One , Division II Level Two

Writer:

Enogipe

Testers:

PabloGilberto , lbackstrom , brett1479 , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4487

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7220&pm=4487

Problem Statement

You are playing a card game in which large flushes, or sets of cards of the same suit, are beneficial. Your next move is to draw number cards: the larger the flush you get, the better. You wish to know the expected size of the largest flush in the cards you draw. The deck will consist of some number of cards of four suits, given as suits. The ith element of suits is the number of cards of that suit in the deck. Return a double, the expected size of the largest flush your hand will make.

The expected size of the largest flush is calculated as follows: For each possible hand, multiply the size of the largest flush in that hand by the probability of getting that hand. Then add all of these values together to get the expected size of the largest flush. For example, if half of the possible hands give you a flush of size 3, and the rest give you one of size 2, the expected value is (0.5 * 3) + (0.5 * 2) = 2.5. Also, recall that there are n Choose k = n!/k!/(n-k)! ways to select k cards of one suit out of a total of n cards in that suit, where ! denotes the factorial operation. Thus, if suits = {3,3,3,3}, then there are (3 Choose 3) * (3 Choose 2) * (3 Choose 1) * (3 Choose 0) = 1 * 3 * 3 * 1 = 9 ways to get 3 cards of the first suit, 2 of the second, 1 of the third, and none of the fourth.

Definition

Class:	Flush
Method:	size
Parameters:	int[], int
Returns:	double
Method signature:	double size(int[] suits, int number)
(be sure your method is public)

Notes

- Look out for overflow! A 32-bit datatype may not be large enough.

- Your return value must have an absolute or relative error less than 1e-9.

Constraints

- suits will contain exactly four elements.

- Each element of suits is between 0 and 13, inclusive.

- number is between 0 and the sum of the elements of suits, inclusive.

Examples

0)

{2,2,2,2}

Returns: 1.1428571428571428

Draw the first card; you have a 1 out of 7 chance to draw the matching suit for your second card. The expected size is thus (1/7 * 2) + (6/7 * 1) = 8/7 = 1.1428571428571428.

1)

{1,4,7,10}

Returns: 10.0

You are drawing all of the cards, so your largest flush will be of size 10.

2)

{13, 13, 13, 13}

Returns: 13.0

If you get 12 cards of each suit, you must have drawn 48 cards, so drawing 49, 50, 51, or 52 cards must give you a flush of size 13.

3)

{13, 13, 13, 13}

Returns: 8.351195960938014

4)

{13,13,13,13}

Returns: 0.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DivisibilityCriteria

Math, Simulation

Used in:

SRM 239

Used as:

Division II Level Three

Writer:

supernova

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4481

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6538&pm=4481

Problem Statement

It is well known that a number is divisible by 2 if and only if its rightmost digit is divisible by 2. A number is divisible by 3 if and only if the sum of its digits is divisible by 3. Assessing divisibility by 7 is a bit more complicated: starting from the rightmost digit, we multiply the first digit by 1, the second by 3, the third by 2, the fourth by 6, the fifth by 4, the sixth by 5, the seventh by 1, the eighth by 3 and so on ... Then, we sum up these results. The number thus obtained is divisible by 7 if and only if the initial number was divisible by 7.

In this problem, you will be given an int N representing the number of digits the number has, and a prime number P. Your task is to find a divisibility criterion for a number with N digits with a prime P. More specifically, you should assign a factor for each digit, such that their sum is divisible by P if and only if the N-digit number is divisible by P.

In order to ensure the uniqueness of the solution, we add the following restrictions:

- all the factors must be between 0 and P-1 inclusive.

- the factor for the rightmost digit should be 1.

- if the N-digit number has leading zeros, the returned factors should still work.

Return a int[] representing the factors assigned to each digit, starting with the leftmost digit.

Definition

Class:	DivisibilityCriteria
Method:	multipliers
Parameters:	int, int
Returns:	int[]
Method signature:	int[] multipliers(int N, int P)
(be sure your method is public)

Constraints

-

P is a prime number less than 100.

-

N is between 1 and 18, inclusive.

Examples

0)

Returns: {5, 4, 6, 2, 3, 1 }

We know that the rightmost digit should be multiplied by a factor of 1. Now we want to find the factor for the next digit. Let's consider the number 35, which is divisible by 7. The factor for digit '3' can now be found from the following formula: 3 * x + 5 * 1 mod 7 = 0, where x is between 0 and 6 (see the problem statement). This leads us to the unique solution, x=3. To find the next factor, we take a three digit number which is divisible by 7, let's say 532. If we denote by y the factor of '5', we should have: 5 * y + 3 * 3 + 2 * 1 mod 7 = 0. This leads us to the unique solution, y=2. Proceeding analogously for the next digits of the number, we obtain successively the factors 6, 4 and 5.

1)

Returns: {1, 10, 1, 10, 1, 10, 1 }

2)

Returns: {3, 12, 9, 10, 1 }

3)

Returns: {0, 1 }

Note that only the rightmost digit counts when assessing the divisibility with 2, so if the number has more than one digit, all the other factors are 0.

4)

Returns: {45, 53, 15, 50, 5, 49, 34, 81, 76, 27, 90, 9, 30, 3, 10, 1 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BoxUnion

Geometry, Simple Math

Used in:

SRM 237

Used as:

Division I Level One , Division II Level Two

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4463

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6536&pm=4463

Problem Statement

NOTE: This problem statement contains an image that may not display properly if viewed outside of the applet.

Given a list of two-dimensional rectangles, compute the area of their union. For example, the union of the three rectangles shown in the figure below:

cover an area of 35 units.

The list of rectangles will be given as a String[], where each element describes one rectangle. Each String will be formatted as 4 space-separated integers with no leading zeros, giving the coordinates of the left, bottom, right, and top of the rectangle (in that order). The three rectangles shown above would be given as:

    { "1 3 5 6",
      "3 1 7 5",
      "4 4 9 7" }

Definition

Class:	BoxUnion
Method:	area
Parameters:	String[]
Returns:	int
Method signature:	int area(String[] rectangles)
(be sure your method is public)

Constraints

-

rectangles will contain between 1 and 3 elements, inclusive.

-

Each element of rectangles will be formatted as described in the problem statement.

-

For each rectangle, the left coordinate will be less than the right coordinate and the bottom coordinate will be less than the top coordinate.

-

All coordinates will be between 0 and 20000, inclusive.

Examples

0)

{ "200 300 203 304" }

Returns: 12

A single rectangle with area 12.

1)

{ "0 0 10 10",
  "20 20 30 30" }

Returns: 200

Two disjoint rectangles, each of area 100.

2)

{ "0 500 20000 501",
  "500 0 501 20000" }

Returns: 39999

These two rectangles intersect at a single point.

3)

{ "4 6 18 24",
  "7 2 12 19",
  "0 0 100 100" }

Returns: 10000

The third rectangle completely overlaps the first two.

4)

{ "1 3 5 6",
  "3 1 7 5",
  "4 4 9 7" }

Returns: 35

This is the example from the problem statement.

5)

{ "0 0 20000 20000",
  "0 0 20000 20000",
  "0 0 20000 20000" }

Returns: 400000000

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MirrorPath

Geometry, Simple Math, Simple Search, Iteration

Used in:

SRM 237

Used as:

Division II Level Three

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4462

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6536&pm=4462

Problem Statement

NOTE: This problem statement contains an image that may not display properly if viewed outside of the applet.

You will be given the map of a maze containing mirrors. There will be exactly two openings on the boundary of the maze. A laser shined through one opening will reflect off the mirrors and exit through the other opening. You are to write a method that outputs the map of the maze with the laser's path drawn in it.

Mirrors are always at a 45-degree angle to the axis of the maze, and deflect the laser at a right angle. The maze will consist of walls ('#'), open spaces ('.'), and mirrors ('/' and '`') arranged on a regular grid. Your method should replace some or all of the '.' characters in the map with '|', '-', and '+' characters, indicating the open spaces where the laser travels vertically, travels horizontally, and crosses its own path, respectively.

For example, given the following three mazes:


    #######    #######    #######
    ##....#    ##/..`#    ##/..`#
    ##.##.#    ##.##.#    ##.##.#
    ##.##.#    ##.##.#    ##.##.#
    ..`...#    ...../#    ../../#
    ##.####    ##.####    ##.####
    ##.####    ##.####    ##.####

the laser would be reflected as shown in the following figure:

and the solutions for each of these three examples are as follows:


    #######    #######    #######
    ##....#    ##/--`#    ##/--`#
    ##.##.#    ##|##|#    ##|##|#
    ##.##.#    ##|##|#    ##|##|#
    --`...#    --+--/#    --/--/#
    ##|####    ##|####    ##|####
    ##|####    ##|####    ##|####

Note that the laser can bounce of both sides of the same mirror.

Definition

Class:	MirrorPath
Method:	path
Parameters:	String[]
Returns:	String[]
Method signature:	String[] path(String[] map)
(be sure your method is public)

Notes

-

Since '\' is a special character, we will use the '/' (forward slash) and '`' (back quote) characters to indicate mirrors in the input.

Constraints

-

map will contain between 3 and 50 elements, inclusive.

-

The length of each element of map will be the same, and be between 3 and 50, inclusive.

-

map will contain only the characters '#', '.', '/', and '`'.

-

Exactly 2 characters on the boundary of map will be '.'. All other characters on the boundary will be '#'.

-

The characters in the four corners of map will be '#'.

-

The map will be such that if a laser is shined through one opening on the boundary, it will exit through the other opening.

Examples

0)

{ "#.#",
  "#.#",
  "#.#" }

Returns: {"#|#", "#|#", "#|#" }

1)

{ "############",
  "#######/....",
  "######//####",
  "#####//#####",
  "####//######",
  "..../#######",
  "############" }

Returns: 
{"############",
"#######/----",
"######//####",
"#####//#####",
"####//######",
"----/#######",
"############" }

2)

{ "#######",
  "##/..`#",
  "##.##.#",
  "##.##.#",
  "...../#",
  "##.####",
  "##.####" }

Returns: {"#######", "##/--`#", "##|##|#", "##|##|#", "--+--/#", "##|####", "##|####" }

This is the second example in the problem statement.

3)

{ "###########.#",
  "#/........./.",
  "#.#########.#",
  "#`........./#",
  "#############" }

Returns: 
{"###########|#",
"#/---------/-",
"#|#########|#",
"#`---------/#",
"#############" }

This is similar to the third example in the problem statement.

4)

{ "########.##",
  "#./......`#",
  "#../.`....#",
  "#.`...../.#",
  "#....`.../#",
  "###.#######" }

Returns: 
{"########|##",
"#./-----+`#",
"#.|/-`..||#",
"#.`+-+--/|#",
"#..|.`---/#",
"###|#######" }

5)

{ "##.########",
  "#.........#",
  "..`.`.....#",
  "#..`......#",
  "#.`.`.`...#",
  "#....`....#",
  "#...`.`.`.#",
  "#.........#",
  "#.....`./.#",
  "#.........#",
  "###########" }

Returns: 
{"##|########",
"#.|.......#",
"--`-`.....#",
"#.|`|.....#",
"#.`-`-`...#",
"#...|`|...#",
"#...`-`-`.#",
"#.....|.|.#",
"#.....`-/.#",
"#.........#",
"###########" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ComputerExpert

Simple Math, String Parsing

Used in:

SRM 236

Used as:

Division II Level Three

Writer:

dimkadimon

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4460

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6535&pm=4460

Problem Statement

A human expert uses his prior knowledge to analyze a set of observations that are presented to him. These days, companies are starting to explore the benefits of computerized expert systems. Expert systems attempt to model the way human experts think and arrive at conclusions. Knowledge obtained in this way is more reliable, cheaper and reproducible.

facts contains all the observations presented to the expert. rules is a set of rules that the expert can use to arrive at new conclusions. rules will be formatted as (<FACT>/.../<FACT>),...,(<FACT>/.../<FACT>) -> <FACT>. In the input, '/' represents the OR operator and ',' represents the AND operator. Hence, the above input represents a boolean expression like (<FACT> OR ... OR <FACT>) AND ... AND (<FACT> OR ... OR <FACT>) -> <FACT>. Each <FACT> represents a sequence of uppercase characters and the character '_'. Note: brackets and parentheses are only used for clarity and are not part of the input.

A rule composed solely of AND will fire only if all the facts listed in the rule are known. Similarly, a rule composed solely of OR will fire if any of the facts listed in the rule are known. Once a rule has fired, its outcome fact can be added to the knowledge of the expert (if not already known).

Given a String[] of facts and a String[] of rules return a String[] of all outcome facts, sorted in ascending alphabetical order. If there are no outcome facts then return an empty String[].

Definition

Class:	ComputerExpert
Method:	operate
Parameters:	String[], String[]
Returns:	String[]
Method signature:	String[] operate(String[] facts, String[] rules)
(be sure your method is public)

Constraints

-

facts will contain between 1 and 50 elements inclusive.

-

Each element of facts will contain between 1 and 50 characters inclusive.

-

Elements of facts will only contain characters 'A'-'Z' and the character '_'.

-

rules will contain between 1 and 50 elements inclusive.

-

Each element of rules will contain between 6 and 50 characters inclusive.

-

Each element in rules will be formatted as (<FACT>/.../<FACT>),...,(<FACT>/.../<FACT>) -> <FACT>. In the input, '/' represents the OR operator and ',' represents the AND operator. Each <FACT> must be a sequence of uppercase characters 'A'-'Z' and the character '_'. Note: brackets and parentheses are only used for clarity and are not part of the input.

Examples

0)

{"SKY_IS_CLOUDY","HAVE_MONEY"}

{"HAVE_MONEY,BAD_WEATHER -> WATCH_MOVIE","SKY_IS_CLOUDY -> BAD_WEATHER",
"GOOD_WEATHER -> PLAY_SOCCER"}

Returns: {"BAD_WEATHER", "WATCH_MOVIE" }

In this simplistic example we want to decide whether to watch a movie or play soccer. We observe that SKY_IS_CLOUDY and that we HAVE_MONEY. The second rule tells us that if SKY_IS_CLOUDY then we have BAD_WEATHER. So we conclude that the weather is bad. Knowing this fact, we can now use the first rule that tells us that if we HAVE_MONEY and BAD_WEATHER then we WATCH_MOVIE. So we choose to watch a movie. The third rule never gets fired.

1)

{"NEEDLE_LEAF","KEEPS_LEAVES"}

{"KEEPS_LEAVES -> EVERGREEN","NEEDLE_LEAF -> GYMNOSPERM",
"EVERGREEN,GYMNOSPERM -> PINE_TREE"}

Returns: {"EVERGREEN", "GYMNOSPERM", "PINE_TREE" }

In this example we try to classify a plant. Since it has a NEEDLE_LEAF we know its a GYMNOSPERM. Since it KEEPS_LEAVES we know its an EVERGREEN. An EVERGREEN and a GYMNOSPERM must be a PINE_TREE.

2)

{"I"}

{"I -> I","P -> CONSONANT", "Z -> CONSONANT", "A/E/I/O/U -> VOWEL"}

Returns: {"VOWEL" }

I is a VOWEL. Note that there is no point firing the first rule, because we already know the outcome fact I.

3)

{"Y","W","L","T","H","J","G","T","F","P","T","P","P","N"}

{"C/V,J,F/T,N,W,L -> M","N/L,F,B/N/E,Y -> C",
"M,G,G,S/F/Q,G,S/G,H/Z,W,F,C,Q/F,M -> E"}

Returns: {"C", "E", "M" }

4)

{"G","H"}

{"A/B/C/D/E/F,G/Z -> Y", "H,H,H,H,H,H,H,H -> Z"}

Returns: {"Z" }

5)

{"A","B","_X", "X_"}

{"A/B,C -> D","A,B,C -> D","X -> Y","_X_ -> Y"}

Returns: { }

Here there are no rules fired. Note that "_X" and "X_" are not the same as "X" or "_X_".

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HammingNumbers

Advanced Math, Search

Used in:

SRM 236

Used as:

Division I Level Two

Writer:

dimkadimon

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4459

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6535&pm=4459

Problem Statement

Hamming numbers were first introduced as an exercise by Richard W. Hamming, the creator of Hamming codes. By definition, a Hamming number is a positive number that can be factored as the product of some arbitrarily chosen factors. For example, if the chosen factors = {2,3,5} then 90 = 2*3*3*5 is a Hamming number, but 70 = 2*5*7 is not because it is also divisible by 7. Note that 1 is always a Hamming number no matter what the chosen factors are.

Given a int[] of the chosen factors and an int n, return the n-th smallest Hamming number that can be obtained with these factors. n is 1-based, so the first number occurs when n = 1. If the result is above 2147483647 (32 bit signed integer maximum) then return -1.

Definition

Class:	HammingNumbers
Method:	getNumber
Parameters:	int[], int
Returns:	int
Method signature:	int getNumber(int[] factors, int n)
(be sure your method is public)

Constraints

-

factors will contain between 1 and 50 elements inclusive.

-

Each element in factors will be between 2 and 300 inclusive.

-

n will be between 1 and 100000 inclusive.

Examples

0)

{2,3,5}

Returns: 24

The first 15 Hamming numbers generated by factors 2, 3 and 5 are: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24.

1)

{2,2,2,4,4,4,8,8,8}

Returns: 1024

These numbers are all powers of 2. Thus the 11th Hamming number must be 2^10 = 1024.

2)

{7,9,14,6}

Returns: 4802

3)

{4,11,15,21,29,28}

Returns: 2146636800

Watch out for overflow. This is the last number before we have to return -1.

4)

{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,
97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,
181,191,193,197,199,211,223,227,229}

Returns: 532287

Factors contain the first 50 primes.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TopFive

Advanced Math, Brute Force, Simulation

Used in:

SRM 243

Used as:

Division I Level Two

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4453

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7218&pm=4453

Problem Statement

You regularly participate in problem solving contests. During a contest all contestants must solve 3 problems, submitting their solutions to the judges for some points. After the competition, the judges will check the correctness of the problems, and award 0 points for incorrect problems.

You want to know your result as soon as possible and you hate waiting for the judges to finish their work. You are ambitious and you are only interested in knowing if you will finish among the top 5 people. Thus you decide to write your own program to determine your probability of getting a top 5 spot. Notice that if someone gets the same score as you, they will go above you on the top scorers list.

You will be given two String[]s - results, giving you the points all people have scored for their problems (prior to being judged), and accuracies, the submission accuracies for all people (the i^th element of results corresponds to the i^th element of accuracies). Each element of results and accuracies will contain three space-delimited integers without extra leading zeroes. For the i^th contestant the corresponding element of results contains the points this contestant received for his three solutions, and the corresponding element of accuracies represents the probabilities in percents of these solutions to be correct.

Given the points you have (you think all your solutions are correct), return the probability you will make the top 5.

Definition

Class:	TopFive
Method:	findProbability
Parameters:	String[], String[], int
Returns:	double
Method signature:	double findProbability(String[] results, String[] accuracies, int points)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

results and accuracies will have the same number of elements.

-

results will have between 1 and 50 elements, inclusive.

-

Each element of results and accuracies will contain between 5 and 50 characters, inclusive.

-

Each element of results will be formatted as "A B C", where A, B and C are integers between 0 and 1000, inclusive.

-

Each element of accuracies will be formatted as "A B C", where A, B and C are integers between 0 and 100, inclusive.

-

All integers in both results and accuracies will NOT contain any leading zeroes.

-

points will be between 0 and 2000, inclusive.

Examples

0)

{"200 200 200",
"200 200 200",
"200 200 200",
"200 200 200",
"200 200 200"}

{"100 100 100",
"100 100 100",
"100 100 100",
"100 100 100",
"0 0 50"
}

Returns: 0.5

The first four people always solve their problems correctly (getting 600 points each) and finish higher than you. Your success depends on the fifth person, who has a 50-50 chance of solving the 3rd problem, and beating you.

1)

{"200 200 200",
"200 200 200",
"200 200 200",
"200 200 200",
"200 200 200"}

{"100 100 100",
"100 100 100",
"100 100 100",
"100 100 100",
"100 100 100"}

Returns: 0.0

Your performance isn't good enough for you to have any chance of making the top 5.

2)

{"928 209 594", "547 408 596", "190 865 494", "353 392 962", "6 252 267",
 "817 671 562", "631 78 290", "593 292 312", "59 51 286", "553 541 487",
 "466 318 271", "605 892 562", "596 261 63", "865 895 625", "893 479 586",
 "759 596 476", "157 407 819", "509 695 861", "696 730 430", "271 221 0",
 "922 296 640", "999 456 654", "320 550 805", "835 808 711", "9 161 670",
 "82 737 480", "939 12 363"}

{"84 87 72", "39 60 84", "56 78 48", "0 80 59", "11 69 94",
 "100 53 77", "87 77 55", "0 67 7", "89 63 3", "4 69 99", 
"58 9 49", "81 8 84", "81 85 55", "84 68 28", "7 1 46", 
"30 50 51", "16 82 8", "60 17 88", "44 30 67", "20 65 65", 
"40 75 73", "38 97 20", "82 38 88", "90 78 58", "58 30 66",
 "3 95 50", "76 60 57"}

Returns: 0.8657569451352308

3)

{"200 200 200",
"200 200 200",
"200 200 200",
"200 200 200",
"600 600 600"}

{"100 100 100",
"100 100 100",
"100 100 100",
"100 100 100",
"75 75 75"
}

Returns: 0.015625

The fifth contestant must fail all his problems.

4)

{"200 200 200",
"200 200 200",
"200 200 200",
"200 200 200",
"33 33 33",
"33 200 200"}

{"100 0 0",
"0 0 100",
"0 100 0",
"100 100 100",
"100 100 100",
"33 80 50"
}

Returns: 0.10000000000000009

The last contestant must fail both the second and third problems to grant you a top 5 spot. The correctness of his first problem does not affect the result.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DiscCover

Dynamic Programming, Geometry, Math

Used in:

TCO05 Semi 3

Used as:

Division I Level Three

Writer:

gepa

Testers:

PabloGilberto , lbackstrom , Yarin , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4452

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8093&pm=4452

Problem Statement

We are given a disc of radius discRadius and want to cover it using numDiscs small discs - i.e., place the small discs flat above the original disc in such a way that no point of the original disc is visible (assuming the small discs are opaque). All smaller discs we use for the covering have the same radius.

We perform the covering using the following procedure:

In the first step, we split the disc into several rings using concentric circles (with the same center as the original disc). Note that the innermost "ring" will have an inner radius 0, and thus will actually be a disc. We are free to split the disc into as many rings and at whatever positions we want (i.e., use circles of arbitrary radii). The example below shows a disc split into three rings (blue, green and red).
In the second step, we regard each of the rings independently, and try to cover each of them using some number of the small discs. We can either use one small disc, which has to be centered at the center of the original disc, or use three or more discs, whose centers must be the vertices of a regular polygon centered at the center of the original disc. The example below shows one such case: The innermost ring (red, actually a disc) is covered by one small disc (which has the same radius as the red disc), the green ring is covered by 6 small discs centered at the vertices of a regular hexagon around the center, and the outermost blue ring is covered by 12 small discs centered at the vertices of a regular 12-gon. Please note that we try to cover each ring totally independently of the others, i.e., ignore that parts in one ring may have been covered already by the discs used to cover another ring (in the example below, the discs used to cover the green ring would also cover parts of the blue and red rings, but we ignore this fact).

In summary, we have the freedom to choose the number and size of the rings that the original disc is split into, how many of the numDiscs discs are used for covering each of the rings, and the distance from the center at which the small discs for each ring are placed. We will have to choose these parameters such that a covering using this procedure is possible using the smallest possible discs.

Given discRadius, the radius of the original disc, and numDiscs, the total number of small discs to use, return the minimum radius that the small discs must have so that a covering using the above procedure is possible.

The example shown above is only one possibility to cover the original disc using 19 small discs (which turns out to be the optimal one for the used procedure). The figure below shows as an example another (non-optimal) possibility: here, the original disc is split only into two rings, and 5 of the small discs are used to cover the inner (green) ring, the other 14 small discs are used to cover the outer (blue) ring. It is clear here that too much space is wasted in the outer ring (that ring was chosen too narrow), so this can not be an optimal solution.

Definition

Class:	DiscCover
Method:	minRadius
Parameters:	double, int
Returns:	double
Method signature:	double minRadius(double discRadius, int numDiscs)
(be sure your method is public)

Notes

-

When covering one ring with small discs, we ignore that there are parts of this ring covered already by the discs used for other rings.

-

The innermost "ring" will be a disc (i.e. the inner radius will be 0).

-

There may be just one "ring" in total (i.e. all smaller discs build a single regular polygon around the center).

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

discRadius is between 1.0 and 1000.0, inclusive.

-

numDiscs is between 1 and 2000, inclusive.

Examples

0)

1000.0

Returns: 1000.0

Here we can use only one disc to cover the given one. This must be at least as large as the original one.

1)

500.0

Returns: 500.0

Using a second disc doesn't help much.

2)

100.0

Returns: 86.60254037844385

Three discs of radius r placed in a triangle configuration around the center can cover a disc of maximum radius 2 * r / sqrt(3) (the centers of the small discs must be placed in a distance of 2 * r / 3 from the centers to achieve this maximum). So, to cover a disc of radius discRadius, we need three discs of radius discRadius * sqrt(3) / 2. This optimum is shown in the figure below:

3)

100.0

Returns: 70.71067811865474

This is the traditional game that can be found in some amusement parks, where you have to cover a disc using four smaller ones. The small discs must be at least 0.707 ( = sqrt(2)/2 ) times smaller than the disc to cover. The optimal configuration is shown below:

4)

200.0

Returns: 59.085199376486976

The example from the problem statement. The first configuration given in the problem statement is the optimal one for 19 discs.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumberSplit

Dynamic Programming, Graph Theory, Simple Math

Used in:

SRM 242

Used as:

Division II Level Three

Writer:

gepa

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4451

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7217&pm=4451

Problem Statement

We start with an integer and create a sequence of successors using the following procedure: First split the decimal representation of the given number into several (at least two) parts, and multiply the parts to get a possible successor. With the selected successor, we repeat this procedure to get a third number, and so on, until we reach a single-digit number.

For example, let's say we start with the number 234. The possible successors are:

23 * 4 = 92,
2 * 34 = 68 and
2 * 3 * 4 = 24.

If we select 68 as the successor, we then generate 6 * 8 = 48 (the only possibility), from this we generate 4 * 8 = 32 and finally 3 * 2 = 6. With this selection, we have generated a sequence of 5 integers (234, 68, 48, 32, 6).

Given the starting number, start, return the length of the longest sequence that can be generated with this procedure. In the example, the given sequence would be the longest one since the other selections in the first step would give the sequences: (234, 92, 18, 8) and (234, 24, 8), which are both shorter than (234, 68, 48, 32, 6).

Definition

Class:	NumberSplit
Method:	longestSequence
Parameters:	int
Returns:	int
Method signature:	int longestSequence(int start)
(be sure your method is public)

Notes

-

There can not exist an infinite sequence.

-

Although we use no leading zeros in the decimal representation of the number we start with, the parts we get by splitting the number may have leading zeros (e.g. from 3021 we can get 3 * 021 = 63).

Constraints

-

start is between 1 and 100000, inclusive.

Examples

0)

Returns: 1

A single-digit number is already the last number.

1)

Returns: 4

For two-digit numbers, there is always only one possible sequence. Here: 97 -> 63 -> 18 -> 8 (4 numbers).

2)

Returns: 5

The example from the problem statement.

3)

Returns: 7

Here, it is optimal to make a three way split in the first step - i.e. use 8*7*6=336 as the first successor. Although a two way split would lead to a larger number (87*6=522 or 8*76=608), both these choices would lead in the end to a shorter sequence. The optimal sequence is: 876, 8*7*6=336, 33*6=198, 19*8=152, 1*52=52, 5*2=10, 1*0=0.

4)

Returns: 29

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DiceThrows

Dynamic Programming, Math

Used in:

SRM 242

Used as:

Division I Level Two

Writer:

gepa

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4450

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7217&pm=4450

Problem Statement

The players A and B are playing a game with dice. Player A throws numDiceA of his dice, while player B throws numDiceB of his dice. Each of them adds the pips on his dice, and the player with the higher sum wins the game (if both get the same sum, it is a draw). The variables sidesA and sidesB have 6 elements each, and describe how many pips are on each side of the dice of player A and player B respectively. Each die has exactly 1/6 probability for each possible outcome.

Given the number of dice numDiceA and numDiceB each player throws, and their configurations sidesA and sidesB, compute the probability that player A wins the game.

Definition

Class:	DiceThrows
Method:	winProbability
Parameters:	int, int[], int, int[]
Returns:	double
Method signature:	double winProbability(int numDiceA, int[] sidesA, int numDiceB, int[] sidesB)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

numDiceA and numDiceB are between 1 and 200, inclusive.

-

sidesA and sidesB each contain exactly 6 elements.

-

Each element of sidesA and sidesB is between 1 and 100, inclusive.

Examples

0)

{1,2,3,4,5,6}

{1,2,3,4,5,6}

Returns: 0.41666666666666663

This is the simple case, where each player throws a normal die once. Of the 36 possible outcomes, 6 are a tie (both players throw the same number), 15 a win for A and 15 a win for B. So player A wins 15/36 of the games.

1)

{1,3,8,18,45,100}

{1,4,10,21,53,100}

Returns: 0.25240407058279035

2)

{1,1,1,2,2,2}

{1,1,1,1,1,1}

Returns: 0.25

Note that dice can have several equal sides. Here, player B gets a sum of 3. Player A can beat that only if he gets a 2 on both his throws, giving him a 1/4 chance of winning.

3)

{6,5,4,3,2,1}

{3,4,6,5,1,2}

Returns: 0.49416239842107595

Note that sidesA and sidesB need not be sorted.

4)

{1,1,1,1,1,2}

{1,1,1,1,1,1}

Returns: 1.5306467074865068E-78

There is a 6^-100 probability of player A winning (all his throws are 2).

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MassiveNumbers

Simple Math, String Parsing

Used in:

SRM 236

Used as:

Division II Level One

Writer:

dimkadimon

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4448

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6535&pm=4448

Problem Statement

Massive numbers can be represented using the exponent notation. For example, 3^100 is 3 raised to the power of 100. 3 is the base and 100 is the exponent.

Suppose we want to compare two massive numbers. Instead of computing the exact value of each number we can rely on a useful mathematical trick. Suppose m = a^b and n = c^d are two massive numbers. Let R be a relationship operator: less, equal or greater. Then we have the following:

If b*Log(a) R d*Log(c) then it is also the case that m R n,
where a, b, c, d, m and n are defined above.

So which is greater: 3^100 or 2^150? Let's do the math. 100*Log(3) = 47.7..., 150*Log(2) = 45.2.... Since 47.7 > 45.2, our rule tells us that 3^100 > 2^150.

Given two numbers numberA and numberB return the larger number formatted exactly the same as the input. numberA and numberB will be formatted as <base>^<exponent>. Constraints will ensure that numberA and numberB are not equal.

Definition

Class:	MassiveNumbers
Method:	getLargest
Parameters:	String, String
Returns:	String
Method signature:	String getLargest(String numberA, String numberB)
(be sure your method is public)

Notes

-

In Java, the log of a number can be found with Math.log().

-

In C++, the log of a number can be found with log().

-

In C# and VB, the log of a number can be found with Math.Log().

Constraints

-

numberA and numberB will contain between 3 and 9 characters inclusive.

-

numberA and numberB will be formatted as <base>^<exponent>, where <base> and <exponent> are integers between 1 and 1000 inclusive. <base> and <exponent> cannot have leading zeroes.

-

The relative difference between b*Log(a) and d*Log(c) (where a, b, c and d are defined in the problem statement) will be at least 1e-6.

Examples

0)

"3^100"

"2^150"

Returns: "3^100"

Above example.

1)

"1^1000"

"2^1"

Returns: "2^1"

numberA is equal to 1, while numberB is equal to 2.

2)

"893^605"

"396^906"

Returns: "396^906"

3)

"999^1000"

"1000^999"

Returns: "999^1000"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Synchro

Math

Used in:

TCO06 Qual 4/11/15

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4446

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9900&pm=4446

Problem Statement

Synchronize your watches to 12:00 ....... now!

We have a collection of watches whose hands move continuously. Create a class Synchro that contains a method resynch that is given a int[] watch telling how many minutes the hand of each watch advances in an hour and that returns the position of the minute hands (in minutes past the hour) at the first time when the minute hands all exactly agree again.

Each element of watch describes a different watch. The returned value should be a non-negative double less than 60. Ignore (or rip off!) the hour hands.

Definition

Class:	Synchro
Method:	resynch
Parameters:	int[]
Returns:	double
Method signature:	double resynch(int[] watch)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

watch will contain between 2 and 10 elements, inclusive.

-

Each element of watch will be between 1 and 200, inclusive.

Examples

0)

{59,59,59}

Returns: 0.0

These watches are a little slow but they stay synchronized. So the first time that the minute hands are resynchronized is arbitrarily close to 0.

1)

{60,53}

Returns: 34.28571428571427

After 8 hours the first watch has its minute hand at 0 and the other watch has circled 7 times and has its minute hand at 4 minutes. The faster watch then catches up in 4/7 of an additional hour, and at that point both minute hands are at 34.285.

2)

{120,40}

Returns: 30.0

The faster watch catches the slower one in 3/4 of an hour at which point they are both at the half hour position.

3)

{1, 2, 4, 8, 16, 32, 64, 128}

Returns: 0.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PerforatedSheet

Geometry, Math

Used in:

SRM 235

Used as:

Division I Level Two

Writer:

the_one_smiley

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4436

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6534&pm=4436

Problem Statement

The blueprints for a large building call for a rectangular metal sheet of uniform thickness and density that has rectangular holes punched out at various positions. You are responsible for analyzing the stability of the building. To accomplish this, you need to determine the position of the perforated sheet's center of mass. The center of mass of a set of pointlike objects is defined as (Sum over all objects of object mass * object position)/(Total mass of all objects). In other words, it is the weighted average position of all the points. This definition also applies to continuous sets containing an infinite number of points, with the sum replaced by an integral and the masses replaced by a density function. For example, the center of mass of a uniformly dense rectangular sheet is just the center of the rectangle.

Write a class PerforatedSheet with a method getCenterOfMass that takes two ints sheetWidth and sheetHeight, four int[]s x, y, width, and height, and returns a double[] containing the coordinates of the perforated sheet's center of mass. If the holes consume the entire sheet (the center of mass is undefined in this case), return an empty double[]. Otherwise, return a double[] with exactly two elements, with the first equal to the x-coordinate and the second equal to the y-coordinate. The sheet is positioned with one corner at (0,0) and the opposite corner at (sheetWidth,sheetHeight). Hole i has one corner at (x[i],y[i]) and its opposite corner at (x[i]+width[i],y[i]+height[i]).

Definition

Class:	PerforatedSheet
Method:	getCenterOfMass
Parameters:	int, int, int[], int[], int[], int[]
Returns:	double[]
Method signature:	double[] getCenterOfMass(int sheetWidth, int sheetHeight, int[] x, int[] y, int[] width, int[] height)
(be sure your method is public)

Notes

-

It is possible for the holes to separate the sheet into two or more disconnected pieces. The definition of center of mass still applies.

-

Return values with either an absolute or relative error of less than 1e-9 are considered correct.

Constraints

-

sheetWidth and sheetHeight will be between 1 and 2,000,000, inclusive.

-

x, y, width and height will each contain between 0 and 50 elements, inclusive.

-

x, y, width and height will contain the same number of elements.

-

Each element of width and height will be a positive number.

-

Each of the holes represented by the inputs will be within the sheet (though they may touch the edges), and none of them will overlap.

Examples

0)

{}

{}

{}

{}

Returns: {2.5, 5.0 }

The center of mass of a uniform rectangle is just its center.

1)

{0, 1}

{0, 0}

{1, 9}

{5, 1}

Returns: {5.5, 3.0 }

The holes here just trim the edges of the sheet, leaving a smaller rectangle.

2)

{1}

{1}

{1}

{1}

Returns: {2.5416666666666665, 2.5416666666666665 }

Cutting out a small hole shifts the center of mass slightly.

3)

{335076, 665632, 210102, 714135, 229942, 149776, 675634, 502085, 393066, 115215,
80993, 272343, 434287, 593760, 589713, 485801, 395389, 755380, 417327, 477023}

{104509, 23182, 103471, 62180, 5040, 10186, 45286, 107985, 36936, 87885,
63846, 58794, 89480, 85195, 64703, 96341, 89224, 7727, 71438, 39128}

{24578, 20552, 3332, 254, 21489, 21158, 35061, 37453, 21881, 216,
32930, 31555, 5121, 36687, 6949, 3512, 8049, 30019, 37252, 8001}

{2240, 3152, 4625, 3508, 4206, 5262, 1750, 627, 3983, 3192,
3609, 3361, 1135, 2580, 4158, 1356, 583, 5408, 5521, 2742}

Returns: {411084.49564976187, 55331.97175632337 }

4)

{0}

{0}

{1234567}

{314159}

Returns: { }

The hole consumes the entire sheet.

5)

{1, 0}

{0, 1}

{1999999, 1}

{2000000, 1999999}

Returns: {0.5, 0.5 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StepperMotor

Simple Math, Simple Search, Iteration

Used in:

SRM 235

Used as:

Division I Level One , Division II Level Two

Writer:

the_one_smiley

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4427

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6534&pm=4427

Problem Statement

A stepper motor consists of a metal rotor surrounded by several identical electromagnets. When a pulse of current is sent through the appropriate electromagnet, the rotor rotates by a fixed angular increment known as one "step". A simple computer known as the motion controller regulates the electromagnets and keeps track of the current position of the rotor as an integer. A clockwise step adds 1 and a counterclockwise step subtracts 1 from this position, which is relative to an arbitrary zero point and can be negative. Since stepper motors provide precise control over the motion of the rotor, they have applications ranging from floppy drives to medical imaging devices to industrial fabrication machinery.

You are writing software that communicates with the motion controller for a stepper motor with n steps in one complete revolution. The apparatus driven by your motor is purely rotational, so rotor position p is identical to position p+i*n, where i is any integer. You have the rotor's current position and a list of target positions, and you wish to move the rotor to the nearest position that is identical to one of the target positions. Write a class StepperMotor with a method rotateToNearest that takes an int n, an int current, and a int[] target, and returns an int that is the minimum number of steps (signed positive for clockwise or negative for counterclockwise) necessary to reach one of the targets from position current. If there is a tie between a positive number and negative number for the smallest value, return the positive number.

Definition

Class:	StepperMotor
Method:	rotateToNearest
Parameters:	int, int, int[]
Returns:	int
Method signature:	int rotateToNearest(int n, int current, int[] target)
(be sure your method is public)

Notes

-

The answer will always be between -floor((n-1)/2) and floor(n/2), inclusive.

-

Beware of overflow.

Constraints

-

n will be between 1 and 2147483647, inclusive.

-

current will be between -2147483648 and 2147483647, inclusive.

-

target will contain between 1 and 50 elements, inclusive.

-

Each element of target will be between -2147483648 and 2147483647, inclusive.

Examples

0)

{-2, -3, 4, 5, 6, 9999999}

Returns: -1

From position 0, rotating one step counterclockwise puts the rotor in position -1, which is equivalent to 9999999.

1)

{10, 8, 6, 4, 2}

Returns: 1

With only two different positions, one step either clockwise or counterclockwise will move the rotor from an odd position to an even position. The tiebreaker favors +1 over -1.

2)

-2147483648

{-2147483648, -2147483648, 2147483647, 2147483647}

Returns: 0

A step here just causes the rotor to spin in a full circle, so all positions are identical.

3)

{64077, -567273, 105845, -279980, 35557,
-286190, -652879, -431665, -634870, -454044}

Returns: -11

4)

1000000000

1403466951

{1233321992, 11423750, 1356595134, 1130863021, 1183514764,
1943494859, 1714480374, 1529875954, 1738756510, 1190153525}

Returns: -46871817

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RemoteRover

Geometry, Math, Search

Used in:

SRM 235

Used as:

Division I Level Three

Writer:

the_one_smiley

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4022

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6534&pm=4022

Problem Statement

This problem statement contains an image.

You are responsible for planning the operation of a remote control rover that is exploring a distant planet. Your team of scientists has identified a target of interest, and they want the rover to reach it as soon as possible. The rover can change directions in a negligible amount of time, but its maximum speed is dependent on the terrain it is traversing. Consider a rectangle with the rover's initial position and the target at opposite corners (the target is close enough that the curvature of the planet's surface can be neglected), as displayed in the example below. The rectangle is divided into parallel strips of terrain with different widths, and each strip has its own limit on the maximum speed of the rover. Your goal is to find the route that will minimize the travel time to the target.

Example 0: The rover starts in the lower left corner and the target is in the upper right. Covering more horizontal distance in the thin strip where the maximum speed is high yields a shorter total travel time compared to the shortest-path time.

Write a class RemoteRover with a method optimalTravel that takes a int[] width containing the widths of each strip, a int[] speed containing the maximum speeds of the rover in each strip, and an int offset that is the distance parallel to the strips the target is offset from the rover's initial position, and returns the minimum amount of time it will take for the rover to reach the target.

Definition

Class:	RemoteRover
Method:	optimalTravel
Parameters:	int[], int[], int
Returns:	double
Method signature:	double optimalTravel(int[] width, int[] speed, int offset)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1e-9 is considered correct.

Constraints

-

width will contain between 1 and 50 elements, inclusive.

-

speed will contain between 1 and 50 elements, inclusive.

-

width and speed will contain the same number of elements.

-

Each element of width will be between 1 and 10000, inclusive.

-

Each element of speed will be between 1 and 1000, inclusive.

-

offset will be between 0 and 10000, inclusive.

Examples

0)

{100, 300, 200}

{100, 50, 75}

Returns: 17.042083785318038

The example from the problem statement.

1)

{1155, 6184, 2783, 7540, 8156}

{570, 810, 875, 172, 642}

Returns: 69.38271426584203

An offset of 0 means the target is directly across the strips from the initial position, so there is no reason to deviate from a straight path.

2)

{5000}

{50}

Returns: 223.60679774997894

The shortest and quickest path here is a straight line to the target.

3)

{9033, 8232, 8842, 6518, 2358, 1115, 941, 928, 220, 8460}

{50, 50, 50, 50, 50, 50, 50, 50, 50, 50}

Returns: 954.1368054948935

The speed limits in each of the strips are identical, so they might as well be a single wide strip.

4)

{9236, 7065, 2283, 506, 6432, 9812, 3133, 1397, 7052, 3729,
2556, 9954, 1367, 6440, 5141, 3091, 2879, 1346, 7080, 1036,
7503, 7775, 433, 7579, 6520, 2287, 1971, 3879, 1725, 8200,
1830, 2774, 3850, 7509, 8531, 7493, 1511, 9399, 9679, 2124,
791, 3432}

{956, 799, 481, 194, 993, 444, 571, 986, 815, 910,
98, 847, 650, 487, 419, 434, 410, 812, 374, 751,
307, 134, 134, 955, 758, 73, 932, 360, 135, 588,
218, 936, 674, 494, 157, 556, 881, 292, 851, 890,
886, 912}

Returns: 501.6129192127166

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NoisySensor

Simple Math

Used in:

SRM 235

Used as:

Division II Level One

Writer:

the_one_smiley

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4019

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6534&pm=4019

Problem Statement

You are processing data obtained from a temperature sensor in a physics experiment. The data consists of an array of integers that represents the measured temperature as a function of time. Unfortunately, the sensor is of poor quality and has introduced some random noise into the data. You have decided to apply a median filter to the temperature data in order to reduce the effect of this noise.

In the context of this problem, median filtering is an operation on an array that replaces each element i except the first and last with the median value of itself and its two immediate neighbors (the three elements i, i-1, and i+1). The first and last elements are missing a neighbor, so median filtering does not affect them.

Write a class NoisySensor with a method medianFilter that takes a int[] data with the noisy sensor values at each time point and returns a int[] with the median-filtered version of data.

Definition

Class:	NoisySensor
Method:	medianFilter
Parameters:	int[]
Returns:	int[]
Method signature:	int[] medianFilter(int[] data)
(be sure your method is public)

Notes

-

The median of 3 numbers is the "middle number". To find the median, sort the 3 numbers, and then look at the second element.

Constraints

-

data will contain between 1 and 50 elements, inclusive.

-

Each element of data will be between -2147483648 and 2147483647, inclusive.

Examples

0)

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Returns: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

Here the median filter produces no change.

1)

{10, 1, 9, 2, 8}

Returns: {10, 9, 2, 8, 8 }

Here are the medians computed:

Median of 10, 1, 9 : 9
Median of 1, 9, 2  : 2
Median of 9, 2, 8  : 8

2)

{500, 500, 500, 500, 500}

Returns: {500, 500, 500, 500, 500 }

3)

{-2147483648, 2147483647}

Returns: {-2147483648, 2147483647 }

4)

{432296535, 1983848899, -434724194, 135703525, -1146336142,
-680568092, -1183352724, 1337550909, -1597342716, -1901441857,
1726722019, -558651015, 649930787, 1889036519, 1752815826,
930647381, -852547667, 2028345278, -1835531493, -1040566300,
-1566043783, -1282411107, -1123988603, 2132078516, -1169614369,
-523503536, 1466102514, -2003903121, -779001645, 1919742042,
1210980485, -9273881, 1033032137, -1474003783, 296280591,
920184999, -1235054743, -1329769514, -1727085135}

Returns: 
{432296535, 432296535, 135703525, -434724194, -680568092, -1146336142, -680568092, -1183352724, -1597342716, -1597342716, -558651015, 649930787, 649930787, 1752815826, 1752815826, 930647381, 930647381, -852547667, -1040566300, -1566043783, -1282411107, -1282411107, -1123988603, -1123988603, -523503536, -523503536, -523503536, -779001645, -779001645, 1210980485, 1210980485, 1033032137, -9273881, 296280591, 296280591, 296280591, -1235054743, -1329769514, -1727085135 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OptimalTax

Math

Used in:

TCO05 Round 3

Used as:

Division I Level Two

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4013

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8016&pm=4013

Problem Statement

A city has several different tax schemes. In each scheme, the taxpayer pays a percentage of his income plus a fixed base amount every year. Each citizen is free to choose an optimal tax scheme for his income after the end of each year.

You will be given two int[]s, fixedBase and percent (elements with equal indices describe the same tax scheme). Given an index of a tax scheme, return the minimal non-negative income this scheme is optimal for (choosing any other tax scheme results in a tax which is strictly greater). If this scheme is not optimal for any income, return -1.

Definition

Class:	OptimalTax
Method:	optimalIncome
Parameters:	int[], int[], int
Returns:	double
Method signature:	double optimalIncome(int[] fixedBase, int[] percent, int index)
(be sure your method is public)

Notes

-

The return value must be within 1e-9 absolute or relative error of the actual result

Constraints

-

fixedBase and percent will contain between 2 and 50 elements, inclusive.

-

fixedBase and percent will contain the same number of elements.

-

Each element of fixedBase will be between 0 and 10000, inclusive.

-

Each element of percent will be between 0 and 100, inclusive.

-

index will be between 0 and number of elements in fixedBase - 1, inclusive.

Examples

0)

{10, 5, 3}

{0, 10, 20}

Returns: 50.0

The first scheme forces a taxpayer to pay 10 units of tax regardless of income. The second scheme leads to the same tax for an income of 50. The first scheme is optimal for any income greater than that.

1)

{6000, 435, 3325, 2345, 0}

{ 0, 45, 33, 13, 100}

Returns: 5968.75

2)

{1, 0, 0, 0}

{9, 6, 7, 8}

Returns: -1.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FastSpider

Brute Force, Math

Used in:

SRM 243

Used as:

Division II Level Three

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=4004

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7218&pm=4004

Problem Statement

Imagine an ideally elastic band of length 1 foot, one end of which is connected to a wall. A spider sits at the connected end, while the other end is carried by a man. At time 0, the man starts walking away from the wall, passing manSpeed feet per second. At the same moment, the spider (represented by a single point) starts crawling along the band, covering spiderSpeed feet per second.

Your program should return an int, representing the time in seconds, rounded to the nearest integer, when the spider will overtake the man. If this will never happen, return -1.

Definition

Class:	FastSpider
Method:	findTime
Parameters:	double, double
Returns:	int
Method signature:	int findTime(double spiderSpeed, double manSpeed)
(be sure your method is public)

Notes

-

Don't forget that while the man is walking he is stretching the band, which moves the spider with it.

-

All movement is continuous.

Constraints

-

spiderSpeed will be between 0.2 and 0.5, inclusive.

-

manSpeed will be between 1 and 5, inclusive.

-

The answer, prior to rounding, will not be within 0.01 of x.5 for any integer x.

-

If the spider will ever overtake the man, it will take 1 hour (3600 seconds) or less.

Examples

0)

0.25

Returns: 54

1)

0.5

Returns: 6

2)

0.5

4.8877377

Returns: 3600

3)

0.2

Returns: 147

4)

0.47

2.78

Returns: 133

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PipeCuts

Simple Math, Simulation

Used in:

SRM 233

Used as:

Division I Level One , Division II Level Two

Writer:

ValD

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3994

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6532&pm=3994

Problem Statement

A 100 meter long pipe must be cut in two places. It can only be cut at certain places, where it was originally welded from smaller pipes. If the two cut locations are chosen at random (each potential location has equal probability of being chosen), find the probability of a resulting pipe being longer than L meters.

Create a method named probability that accepts a int[] weldLocations and int L as parameters. It should calculate the probability of one or more resulting pipes being strictly longer than L if the two cut locations are chosen at random from weldLocations. Each element in weldLocations represents the number of meters from the left end of the pipe.

Definition

Class:	PipeCuts
Method:	probability
Parameters:	int[], int
Returns:	double
Method signature:	double probability(int[] weldLocations, int L)
(be sure your method is public)

Notes

-

Your return value must have a relative or absolute error less than 1e-9.

Constraints

-

weldLocations will have between 2 and 50 elements, inclusive.

-

Each element in weldLocations will be between 1 and 99, inclusive.

-

weldLocations will not contain duplicate elements.

-

L will be between 1 and 100, inclusive.

Examples

0)

{25, 50, 75}

Returns: 1.0

Any random set of cuts results in a pipe being longer than 25 meters.

1)

{25, 50, 75}

Returns: 0.0

This time, it is impossible to cut the pipe such that some resulting pipe is longer than 50 meters.

2)

{25, 50, 75}

Returns: 1.0

3)

{99, 88, 77, 66, 55, 44, 33, 22, 11}

Returns: 0.7222222222222222

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CheckerPolygon

Geometry, Math

Used in:

TCCC05 Semi 3

Used as:

Division I Level Two

Writer:

Yarin

Testers:

PabloGilberto , lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3992

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6552&pm=3992

Problem Statement

A convex polygon is placed on a large checkerboard with the polygon vertices lying on the grid intersections. Calculate the number of light and dark squares lying entirely inside the polygon. Assume that the polygon edges are infinitely thin. In the picture below, 28 light squares and 26 dark squares are enclosed by the polygon. The upper left corner (coordinates 0,0) will always be a dark square.

Create a class CheckerPolygon containing the method countSquares which takes two int[], X and Y, describing the convex polygon. Element i in X and Y is the coordinate for the ith vertex in the polygon. The method should return a int[] containing exactly two elements: the first element is the number of light squares entirely enclosed by the polygon, and the second element the number of dark squares entirely enclosed by the polygon.

Definition

Class:	CheckerPolygon
Method:	countSquares
Parameters:	int[], int[]
Returns:	int[]
Method signature:	int[] countSquares(int[] X, int[] Y)
(be sure your method is public)

Notes

-

The vertices in the polygon may be ordered clockwise or counter-clockwise.

Constraints

-

X and Y will contain between 3 and 50 elements, inclusive.

-

X will contain the same number of elements as Y.

-

Each element in X and Y will be between 0 and 10000, inclusive.

-

The polygon described by X and Y will be convex.

-

There will not be three points lying on the same line.

Examples

0)

{1,2,5,8,11,10,6,4,2}

{7,5,2,1,2,8,11,11,9}

Returns: {26, 28}

This is the example in the problem statement.

1)

{1,5000,5001,10000,10000,5001,5000,1}

{4999,0,0,4999,5000,9999,9999,5000}

Returns: {25000000, 24990001}

2)

{1,3,6}

{3,6,1}

Returns: {1, 1}

3)

{537,127,987,2390}

{173,98,12,107}

Returns: {90908, 90911}

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StockHistory

Greedy, Math, Simulation

Used in:

SRM 232

Used as:

Division II Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3971

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6521&pm=3971

Problem Statement

You have recently been given a one-time bonus at work, along with a pay raise. In the interest of putting your new found money to good use, you have decided to invest in the stock market. To learn about recent market history, you have acquired historical data on several stocks you might be interested in purchasing.

For experiment's sake, you want to evaluate the potential performance of your selected stocks. What you are wondering is how much money you could have made if, at the beginning, you had an initial investment of int initialInvestment dollars, and each month thereafter you had an additional int monthlyContribution dollars. Assume that you may buy any number of shares of stocks at the beginning of each month (including fractional numbers of shares), and that at the end of the timeframe (at the beginning of the last month) represented in the data, you sell all of your holdings. You may not sell stocks in the intermediate period. (See examples for clarification.)

You are given a String[], stockPrices, in which each element lists the prices of each stock at the beginning of a month. Each element of stockPrices is in the form "stock0 stock1 ..." (quotes added for clarity), where each stocki is a positive integer with no leading zeroes. The first element of stockPrices gives the initial prices, the second element gives the prices at the beginning of the first month after you start investing, and so on.

You are to return an int indicating the maximum earnings (profit) you could make by the end of the timeframe. You should round your result to the nearest integer.

Definition

Class:	StockHistory
Method:	maximumEarnings
Parameters:	int, int, String[]
Returns:	int
Method signature:	int maximumEarnings(int initialInvestment, int monthlyContribution, String[] stockPrices)
(be sure your method is public)

Constraints

-

initialInvestment will be between 0 and 10000, inclusive.

-

monthlyContributon will be between 0 and 1000, inclusive.

-

stockPrices will contain between 2 and 50 elements, inclusive.

-

Each element of stockPrices will contain between 1 and 50 characters, inclusive.

-

Each element of stockPrices will be formatted as a space delimited list of positive integers.

-

Each integer represented in an element of stockPrices will be between 1 and 999, inclusive.

-

Each element of stockPrices will represent the same number of integers.

-

The result prior to rounding will not be within 0.01 of x.5, where x is an integer.

Examples

0)

{"10 20 30", "15 24 32"}

Returns: 500

Clearly the first stock is a bigger gain than either of the others. We go all in on it.

1)

{"10", "9"}

Returns: 0

We're best off not buying any shares, rather than buying and losing money.

2)

{"40 50 60",
 "37 48 55",
 "100 48 50",
 "105 48 47",
 "110 50 52",
 "110 50 52",
 "110 51 54",
 "109 49 53"}

Returns: 239

Remember that we can't sell any shares until the beginning of the last month. So, let's work backwards, and figure out what the best way to invest our money is. During the second to last month (month 6), the stock prices are 110, 51 and 54, all higher than the prices that we would sell at, so we don't buy anything during that month.

At the beginning of month 5, the price of the third stock is a little lower than its final price, so we invest our 20 in that, and make a meager 20*((53/52)-1). The prices are the same at the beginning of month 4, so we do the same thing.

At the beginning of month 3, the prices have changed, but it is still best to invest in the third stock. Note that the profit we make investing in the third stock during month 3 is larger than it is if we save our money and invest later. Hence, we make a profit of 20*((53/47)-1) on our 20 from month 3.

At the beginning of month 2, it is best to save all of our money, and then invest in the third stock during the next month when the price is lower. At the beginning of month 1, you should clearly invest in the first stock. You should save all of your money from the initial investment until the price of the first stock goes down a little. So, to summarize:

month | action
------+-------
    0 | save
    1 | buy stock 0 (120/37 shares)
    2 | save
    3 | buy stock 2 (40/47 shares)
    4 | buy stock 2 (20/52 shares)
    5 | buy stock 2 (20/52 shares)
    6 | save
    7 | sell (3.243 shares of stock 0, 1.620 shares of stock 2)
Total sales price : 439.389
Total investment  : 200
Profit            : 239.389

Notice that you always either invest all of your money at the beginning of a month, or else save all of it. When you know the future prices, there is no reason to invest only some of your money.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AutoLoan

Advanced Math, Search

Used in:

SRM 258

Used as:

Division I Level One , Division II Level Two

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3970

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7993&pm=3970

Problem Statement

Auto dealerships frequently advertise tempting loan offers in order to make it easier for people to afford the "car of their dreams". A typical sales tactic is to show you various cars, and then talk in terms of what your monthly payment would be, to say nothing of how much you are actually paying for the car, how much interest you pay, or how long you have to make payments.

A typical auto loan is calculated using a fixed interest rate, and is set up so that you make the same monthly payment for a set period of time in order to fully pay off the balance. The balance of your loan starts out as the sticker price of the car. Each month, the monthly interest is added to your balance, and the amount of your payment is subtracted from your balance. (The payment is subtracted after the interest is added.) The monthly interest rate is 1/12 of the yearly interest rate. Thus, if your annual percentage rate is 12%, then 1% of the remaining balance would be charged as interest each month.

You have been checking out some of the cars at your local dealership, TopAuto. An excited salesman has just approached you, shouting about how you can have the car you are looking at for a payment of only monthlyPayment for only loanTerm months! You are to return a double indicating the annual percentage rate of the loan, assuming that the initial balance of the loan is price.

Definition

Class:	AutoLoan
Method:	interestRate
Parameters:	double, double, int
Returns:	double
Method signature:	double interestRate(double price, double monthlyPayment, int loanTerm)
(be sure your method is public)

Notes

-

Because of the way interest is compounded monthly, the actual interest accrued over the course of a year is not necessarily the same as (balance * yearly interest rate). In fact, it's usually more.

-

In a real situation, information like this would typically need to be disclosed, but since you aren't at a point of signing any paperwork, the salesman has no legal obligation to tell you anything.

-

The return value must be within 1e-9 absolute or relative error of the actual result.

Constraints

-

price will be between 1 and 1000000, inclusive.

-

monthlyPayment will be between 0 and price / 2, inclusive.

-

loanTerm will be between 1 and 600, inclusive.

-

The resulting interest rate will be between 0 and 100, inclusive.

Examples

0)

Returns: 1.3322616182218813E-13

Noting that 68 payments of 100 equals the total price of 6800, so there is no interest.

1)

Returns: 9.56205462458368

Here, we do pay a little interest. At 9.562% annual interest, that means each month we pay 0.7968% of the balance in interest. Our payment schedule looks like this:

Month | + Interest | - Payment | = Balance
------------------------------------------
      |            |           |  2000.00
   1  |     15.94  |   510.00  |  1505.94
   2  |     12.00  |   510.00  |  1007.94
   3  |      8.03  |   510.00  |   505.97
   4  |      4.03  |   510.00  |     0.00

2)

Returns: 7.687856394581649

This is similar to what purchasing a new car with no money down might look like, if you make payments for 4 years.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Stitch

Simple Math, String Manipulation

Used in:

SRM 231

Used as:

Division I Level One , Division II Level Two

Writer:

lars2520

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3946

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6520&pm=3946

Problem Statement

Many image editing programs have the ability to stitch two images together to form one larger image. In this problem, you will be given two images, represented by String[]'s. Each String[] represents a bitmap, where the ASCII value of character j of element i represents the color of the pixel in row i, column j of the image. Your task is to stitch the two images together. Specifically, image A goes to the left of image B and overlap pixels from the right of A and the left of B overlap. To prevent any obvious artifacts from the stitching, you want to gradually blend the stitched region from image A to image B. The i^th pixel (indexed from 1) from the left in the overlapping region should have a value of

((overlap+1-i)*a+(i*b))/(overlap+1)

where a and b are the values of the pixels from A and B, respectively. Hence, the leftmost pixels in the overlapping region should have values of

(overlap*a+b)/(overlap+1).

In all cases, you should round the pixel values to the nearest integer, rounding 0.5 up.

Definition

Class:	Stitch
Method:	stitch
Parameters:	String[], String[], int
Returns:	String[]
Method signature:	String[] stitch(String[] A, String[] B, int overlap)
(be sure your method is public)

Constraints

- A will contain between 1 and 50 elements, inclusive.

- B will contain the same number of elements as A.

- Each element of A will contain the same number of characters.

- Each element of B will contain the same number of characters.

- Each element of A and B will contain between overlap+1 and 50 characters, inclusive.

- overlap will be between 0 and 49, inclusive.

- Each character in A and B will have ASCII value between 32 and 126, inclusive.

Examples

0)

{"AAAAAA"}

{"JJJJJ"}

Returns: { "AACEFHJ" }

First, line up the two images:

 AAAAAA
   JJJJJ

Then, blend the overlapping region:

 AACEFHJ

1)

{"14ABCD",
 "25EFGH",
 "36IJKL"}

{"ABCD14",
 "EFGH25",
 "IJKL36"}

Returns: { "14ABCD14",  "25EFGH25",  "36IJKL36" }

2)

{" 32ygfd",
 "3uh53G:",
 ")O83gh3"}

{"hsd$*(PH",
 "3G:$)(*P",
 "gh86$PBB"}

Returns: { " 32ygmd$*(PH",  "3uh53G:$)(*P",  ")O83gh76$PBB" }

3)

{"A"}

{"A"}

Returns: { "AA" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CakeDivision

Dynamic Programming, Simple Math

Used in:

SRM 237

Used as:

Division I Level Two

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3944

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6536&pm=3944

Problem Statement

You have a rectangular cake of a given length and width, and want to divide it into a certain number of equal-area rectangular pieces. Each cut you make must be parallel to the sides of the cake, and must completely cut one of the existing pieces into two parts. (Therefore, cutting the cake into N pieces will require exactly N-1 cuts.)

You prefer square pieces to those with a larger aspect ratio. (Here, we define the "aspect ratio" of a piece to be the length of its longer side divided by the length of its shorter side.) You should cut the cake in such a way as to minimize the maximum aspect ratio of all the resulting pieces.

For example, if the cake is 2x3, and you want to cut it into six pieces, you can cut it into six 1x1 pieces. Each piece has an aspect ratio of 1.0, which is the smallest possible aspect ratio. Therefore, this solution is optimal.

One way to cut a 5x5 cake into 5 pieces is to first cut it into two pieces of sizes 2x5 and 3x5. Cut the smaller of these two in half (each of size 2 x 5/2) and the larger in thirds (each of size 3 x 5/3). The largest aspect ratio of these five pieces is 3/(5/3) = 1.8. There is no way to cut this cake into 5 equal-area pieces that all have an aspect ratio of less than 1.8

Definition

Class:	CakeDivision
Method:	ratio
Parameters:	int, int, int
Returns:	double
Method signature:	double ratio(int length, int width, int pieces)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

length and width will be between 1 and 1000, inclusive.

-

pieces will be between 1 and 10, inclusive.

Examples

0)

Returns: 1.0

This is the first example in the problem statement.

1)

Returns: 1.8

This is the second example in the problem statement.

2)

Returns: 1.0

The cake can be cut into 9 squares.

3)

Returns: 50.0

The optimal solution is to cut the cake into 10 50x1 pieces.

4)

Returns: 1.2573099415204678

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LargeSignTest

Advanced Math

Used in:

SRM 231

Used as:

Division I Level Two

Writer:

lars2520

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3943

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6520&pm=3943

Problem Statement

A sign test is a test that is performed to determine if the results of an experiment are statistically significant. In particular, it looks at a number of similar trials, where each trial's outcome is either positive or negative. It calculates the probability that the results of your experiments would be at least as unbalanced as they actually turned out to be if the outcomes of each trial were totally random - a 50% chance of being positive and a 50% chance of being negative. For example, the probability of the five trials being split 4-1 or 5-0 is 12/32: 2 out of 32 times the results will be 5 negatives or 5 positives and 10 out of 32 times the results will have 4 negatives or 4 positives. Hence, the p-value of an outcome with 4 positives and 1 negative is 12/32 = 0.375. To make this more concrete, the p-value of N trials, K of which are negative can be calculated as

where the numerator of the fraction is the binomial coefficient: N!/(i!(N-i)!). There is one exception to this though: when K*2 is equal to N, the p-value is simply 1 (the above equation gives the wrong result).

This is all quite simple, when N and K are small, but what if they are rather large? Your task is to compute the p-value, given N and K, where 0<=K<=N<=1,000,000 and 0<N. You should return this value as a percentage with exactly one digit after the decimal point (don't forget the percent sign). You should use standard rounding when formatting your return. You need not worry about borderline cases as the constraints ensure that the percentage will not be within 1e-3 of XX.X5, where each X represents a digit.

Definition

Class:	LargeSignTest
Method:	pvalue
Parameters:	int, int
Returns:	String
Method signature:	String pvalue(int N, int K)
(be sure your method is public)

Constraints

-

N will be between 1 and 1,000,000, inclusive.

-

K will be between 0 and N, inclusive.

-

The percentage will not be within 1e-3 of XX.X5, where each X represents a digit.

Examples

0)

Returns: "37.5%"

The p-value in this case is (choose(5,0)+choose(5,1))/2^N-1 = (1+5)/16 = 6/16 = 3/8 = 37.5%

1)

Returns: "100.0%"

2)

Returns: "0.0%"

3)

Returns: "4.1%"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Mixture

Advanced Math, Brute Force

Used in:

SRM 231

Used as:

Division I Level Three

Writer:

lars2520

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3942

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6520&pm=3942

Problem Statement

You are trying to create a very precise mixture of a number of different chemicals. The exact amounts of the chemicals are given as a int[], desiredMixture, where desiredMixture[i] indicates how much of chemical i is required. You will be given a String[], availableMixtures, each element of which represents a mixture of chemicals that may be purchased (the chemical components for the mixture might not be available in pure form). Each element of availableMixtures will be formatted as a single-space separated list of integers, where the i^th integer in availableMixtures[j] indicates how much chemical i is present in mixture j. Additionally, there will be one extra, final integer in each element of availableMixtures indicating the price of that mixture. You need not purchase the available mixtures in integral amounts. Hence if an element of availableMixtures were "3 5 9", you could purchase a mixture with 3 units of chemical 0 and 5 units of chemical 1 for a price of 9, and you could also purchase a mixture with 1.5 units of chemical 0 and 2.5 units of chemical 1 for a price of 4.5.

Your task is to determine the lowest price that the desired mixture can be achieved for. If it is impossible to achieve the desired mixture, return -1.

Definition

Class:	Mixture
Method:	mix
Parameters:	int[], String[]
Returns:	double
Method signature:	double mix(int[] mixture, String[] availableMixtures)
(be sure your method is public)

Constraints

-

mixture will contain between 1 and 10 elements, inclusive.

-

Each element of mixture will be between 1 and 10, inclusive.

-

availableMixtures will contain between 1 and 10 elements, inclusive.

-

Each element of availableMixtures will be formatted as N+1 single-space separated integers, where N is the number of elements in mixtures.

-

Each integer in availableMixtures will be between 0 and 10, inclusive, with no extra leading zeros.

Examples

0)

{1,2,3}

{"1 0 0 1","0 1 0 2","0 0 1 3"}

Returns: 14.0

Here, there are three chemicals, and each one is available in only its pure form. Given the prices of the three chemicals and the desired quantities, the total cost is 1*1+2*2+3*3=14.

1)

{1,2,3}

{"1 0 0 1","0 1 0 2","0 0 1 3","2 2 2 4"}

Returns: 10.0

Here, it is cheaper if we buy some of the mixture of all three chemicals.

2)

{1,1,1,1,1,1,1,1,1,1}

{"10 9 9 9 9 9 9 9 9 10 0",
 "0 10 9 9 9 9 9 9 9 0 0",
 "0 0 10 9 9 9 9 9 9 0 0",
 "0 0 0 10 9 9 9 9 9 0 0",
 "0 0 0 0 10 9 9 9 9 0 0",
 "0 0 0 0 0 10 9 9 9 0 0",
 "0 0 0 0 0 0 10 9 9 0 0",
 "0 0 0 0 0 0 0 10 9 0 0",
 "0 0 0 0 0 0 0 0 10 1 0",
 "0 0 0 0 0 0 0 0 0 10 1"}

Returns: -1.0

This mixture is impossible. It can almost be achieved, but the closest you can get is to have the right amount of the first 9 chemicals, but just a little bit too much of the last one.

3)

{7,7,8,10}

{"9 0 4 8 4",
 "8 8 9 0 1",
 "0 10 3 10 7",
 "10 2 2 0 1",
 "8 9 10 2 6",
 "1 2 5 8 8",
 "4 7 8 9 6",
 "2 10 6 8 10",
 "6 3 9 7 1",
 "3 6 9 9 1"}

Returns: 3.5855425945563804

The following table shows which mixtures to purchase to achieve the desired mixture as cheaply as possible:

 i | amount
---+--------
 0 | 202  / 943
 2 | 239  / 943
 3 | 595  / 1886
 9 | 1808 / 2829

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DiskCut

Dynamic Programming, Simple Math

Used in:

SRM 233

Used as:

Division I Level Three

Writer:

ValD

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3936

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6532&pm=3936

Problem Statement

The process of producing silicon chips is long and complex. Special care must be taken when cutting a delicate silicon disk. A contractor has hired you to work just in this area. As it turns out, his cutting machine can make only one type of cut: one that starts in the center of the disc, ends at the perimeter and has a length equal to the radius. Such a cut can easily ruin the entire piece being cut. Because of this, the area of the piece being cut is also the price of the cut. Consider an example where you must cut a disk whose area is 100 into 3 pieces whose areas are 33%, 33% and 34% of the disk. The best way to cut them is by first making two cuts around the 34% piece, which costs 100 units per cut. Then make a single cut on the remaining piece of size 66 to get two 33% pieces, which costs 66 units. Thus, the minimum cost would be 266 units of money.

Write a method named minCost that takes an int area and an int[] percent, and returns the minimum cost of cutting a disk of size area into different pieces with sizes from percent. Note that the order of the elements of percent is unimportant, as you only need to achieve the required percentages.

Definition

Class:	DiskCut
Method:	minCost
Parameters:	int, int[]
Returns:	double
Method signature:	double minCost(int area, int[] percent)
(be sure your method is public)

Notes

-

Your return value must have a relative or absolute error less than 1e-9.

Constraints

-

area will be between 1 and 1000, inclusive.

-

percent will have between 2 and 50 elements, inclusive.

-

Each element in percent will be between 1 and 100, inclusive.

-

The elements in percent will sum up to 100.

Examples

0)

{25,25,25,25}

Returns: 12.0

The best way to cut these pieces is by first making two cuts, resulting in two 50% pieces. Then, cut each piece in half. All this costs just 12.0 units.

1)

{20,20,20,20,20}

Returns: 17.0

2)

{10, 40, 30, 20}

Returns: 2.9

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Buoyancy

Geometry, Math

Used in:

TCCC05 Semi 1

Used as:

Division I Level One

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3932

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6550&pm=3932

Problem Statement

An object can float only if it is less dense than water. A floating object displaces an amount of water equal to its weight. We are given an object (that may or may not float) and a container of water and we want to calculate the water level that will result when we place the object in the container. All weights are given in grams, all lengths are given in centimeters, and a cubic centimeter of water weighs one gram.

The container is a tall rectangular box (with no top) with horizontal dimensions wid x len. It is originally filled with water to a height of waterHt. The object is a rectangular solid that is 1 x 1 x objHt. The weight of the object is objWt. When placed in the water, the object remains upright whether it floats or rests on the bottom.

Create a class Buoyancy that contains a method waterLevel that is given wid, len, waterHt, objWt, and objHt and that returns the height of the water after the object has been placed in the container.

Definition

Class:	Buoyancy
Method:	waterLevel
Parameters:	double, double, double, double, double
Returns:	double
Method signature:	double waterLevel(double wid, double len, double waterHt, double objWt, double objHt)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9

Constraints

-

wid and len will be between 1.2 and 10.0 inclusive.

-

waterHt, objWt, and objHt will be between 0.1 and 500.0 inclusive.

Examples

0)

Returns: 120.0

The object ends up on the bottom of the container, completely submerged. The final height of the water must be 120 since the total volume of the water and submerged object is 2*2*100 + 80 and that is equal to the new water level times the container's cross-section, 120*2*2.

1)

Returns: 133.33333333333334

This object also sinks, but does not get completely submerged. In the final situation, the total volume of the water and the part of the object that is submerged is 2*2*100 + 1*1*133.33 and that is equal to 2*2*133.3.

2)

Returns: 102.5

This object is very buoyant. It floats, with 10 units of its length submerged, displacing 10 grams of water. The total volume of the water and the submerged part of the object is then 2*2*100 + 10 and that is equal to 2*2*102.5.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SalesPromotion

Dynamic Programming, Math, Simulation

Used in:

SRM 232

Used as:

Division I Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3923

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6521&pm=3923

Problem Statement

Your friend has recently been looking through a catalog, and has selected several items she wishes to buy. Because of a sales promotion, she has earned credit towards free or discounted products. Each item has a cost, and a point value. For her referrals, your friend has earned a certain number of points which may be redeemed for items, and a certain number of "half price" items. Additionally, she receives a fixed percentage discount on all other items (this is not cumulative with half-price items). All prices are rounded up after applying discounts.

Your friend's order is subject to the following restrictions:

Each item must be purchased with points, purchased at half price, or purchased at the fixed discount rate.
Purchasing an item with points is all or nothing; you cannot, for instance, pay for an item partially with points and pay the remainder in cash.
All points must be used.
All half-price items must be used.
All items on the wishlist must be purchased.

Your friend is very excited to place her order, but is very frustrated with what she has found to be a confusing incentive system. Being frugal-minded, she wants to get everything on her wishlist at the least possible out-of-pocket expense. Knowing your enjoyment of these type of problems, she has come to you for assistance.

You are given an int, points, indicating the number of points your friend must spend; an int, halfPrice, indicating the number of items which are to be purchased at half price; and an int, discount, indicating the fixed discount percentage on all remaining items. Finally, you are given a String[], items, indicating the list of items on your friend's wishlist. Each element of items will be in the form "pointValue price" (quotes added for clarity), where pointValue and price are both positive integers with no leading zeros. pointValue and will be between 1 and 9999, inclusive. price will be between 1 and 99999, inclusive. You are to return an int indicating the minimum out of pocket expense your friend must pay to get the items on her wishlist.

Definition

Class:	SalesPromotion
Method:	bestPrice
Parameters:	int, int, int, String[]
Returns:	int
Method signature:	int bestPrice(int points, int halfPrice, int discount, String[] items)
(be sure your method is public)

Notes

-

The cost of an individual item purchased at half price or the fixed discount rate should always round up when necessary.

Constraints

-

points will be between 0 and 15000, inclusive.

-

halfPrice will be between 0 and n, inclusive, where n is the number of elements of items.

-

discount will be between 0 and 49, inclusive.

-

items will contain between 1 and 50 elements, inclusive.

-

Each element of items will be in the form described in the problem statement.

-

There will be at least one way to place the order that uses all of the points and half price items.

Examples

0)

{"150 500", "350 1000", "500 600", "450 800"}

Returns: 940

Here, we're better to use our 500 points on the first two items, rather than the third item. Then, we use our half price discount on the item priced 800 (since it's more expensive than the item priced 600), which costs 400. Finally the item priced 600 we buy for 540 (10% discount), totalling 940.

1)

{"150 450", "350 700", "500 1200", "450 800"}

Returns: 1320

The best solution is to buy items 0 and 1 with points, item 2 at half price, and pay full price (less the discount) for item 3.

2)

{"200 500", "300 700", "400 900", "500 1100", "600 1300"}

Returns: 2200

There's more than one way to use our points, so we have to find the most cost effective.

3)

{"100 100", "100 200", "100 150", "150 300"}

Returns: 750

With no points or discounts of any kind, we just need to add up the total cost.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LocalMax

Advanced Math, Search

Used in:

TCCC05 Finals

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3565

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6554&pm=3565

Problem Statement

We want to find the location of a local maximum in an unknown function. y = f(x) is a continuous real-valued function defined on the real numbers. We already have a number of data pairs, (xi, yi), and we need to find a small interval on the x axis that is guaranteed to contain at least one local (or global) maximum. But taking a sample from this function is quite expensive so we are only allowed to take N samples. Our problem is to choose them in such a way as to minimize the size of the interval that we determine.

The sampling will be done sequentially: we choose a value of x and find the corresponding y value, f(x). We repeat this process N times, choosing the x value based on all the data collected so far. We are willing to assume that no two y values will be exactly equal to each other.

Create a class LocalMax that contains a method length that is given N, the number of samples we can take, and double[]s xData and yData (the existing data pairs). It will return the worst case length for our interval around a local maximum using optimal sampling. If it is not possible to make such a guarantee, it returns -1.0.

Definition

Class:	LocalMax
Method:	length
Parameters:	int, double[], double[]
Returns:	double
Method signature:	double length(int N, double[] xData, double[] yData)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9

Constraints

-

N will be between 0 and 25 inclusive.

-

xData will contain between 1 and 50 elements inclulsive.

-

yData will contain the same number of elements as xData.

-

The elements of yData will be distinct.

-

The elements of xData will be distinct.

-

Each element of xData and yData will be greater than 0.0 and less than 10000.0.

Examples

0)

{3,4,5}

{3,4,5}

Returns: -1.0

From the data we already have we cannot guarantee that this function even has a local maximum -- it might be monotonically increasing.

1)

{3,4,5}

{3,5,4}

Returns: 2.0

We know that there is a local maximum between x=3 and x=5.

2)

{3,5,8}

{35,923.2,17}

Returns: 2.0

Here is one way (there are others) get an interval of length 2 or less with just two additional samples. Take the first sample at x=6.5. The worst case is that the corresponding y value is less than 923.2. In that case we know that the interval (3,6.5) contains a local maximum, and that the y value at x=5 is greater than either endpoint y value. Take the second sample at x=4.7. In the worst case the corresponding value of y will be bigger than 923.2, in which case we could conclude that there is a local max somewhere in the interval (3,5).

3)

{3,4,6,5}

{32,53,68,47}

Returns: 1.0

If we take a sample at x=4.0+epsilon, for some tiny epsilon, then the worst case would be that the corresponding y value would be smaller than 53. In that case the interval between 3.0 and 4.0+epsilon would contain a local maximum. So by choosing epsilon arbitrarily small, we get an interval whose length is (arbitrarily close to) 1.0.

4)

{1,4.3,7.2,95.4,534.0}

{72, 83, 19, 25.3, 624.0}

Returns: 1.4500000000000002

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PascalCount

Math

Used in:

SRM 230

Used as:

Division I Level Two

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3564

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6519&pm=3564

Problem Statement

The top few rows of Pascal's triangle are drawn below:

                 1
               1   1
             1   2   1
           1   3   3   1
         1   4   6   4   1

The leftmost and rightmost values of a particular row are always 1. An inner value v can be found by adding together the 2 numbers found immediately above v, on its right and left sides. For example, the 6 in the above figure is the sum of the two 3s above it. Return the number of values in row i of Pascal's triangle that are evenly divisible by d. The rows are 0-based, so row 3 contains 1,3,3,1.

Definition

Class:	PascalCount
Method:	howMany
Parameters:	int, int
Returns:	int
Method signature:	int howMany(int i, int d)
(be sure your method is public)

Notes

-

The jth element (0-based) of row i can be computed by the formula:

   	  i!

    ---------------

      j! * (i-j)!

where k! = 1*2*...*k and 0! = 1.

Constraints

-

i will be between 0 and 5000000 inclusive.

-

d will be between 2 and 6 inclusive.

Examples

0)

Returns: 2

Row 3 is 1,3,3,1 so there are 2 elements divisible by 3.

1)

Returns: 0

Row 3 has no elements that are divisible by 4.

2)

Returns: 3

1,4,6,4,1 has 3 elements divisible by 2.

3)

Returns: 1

Row 4 has a single element divisible by 6.

4)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Disaster

Advanced Math, Dynamic Programming

Used in:

TCCC05 Semi 1

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3563

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6550&pm=3563

Problem Statement

We need to get corn to the starving victims of a disaster. We will load up a truck and choose a route to the disaster site. But the roads are bad, and the more we put on the truck, the greater is the probability that we will get stuck somewhere on our route and be unable to deliver the corn.

The probability of successfully completing any segment of our route is the product of the goodness of the road segment (a value between 0.0 and 1.0 inclusive) and the lightness of our load, defined to be 1.0 - b*load where b is a specified constant and load is the amount of corn we carry. Loads that would yield a negative lightness value are not possible.

The road segments go between villages. They are described by a String[] roads. The k-th element of roads lists the goodness of the road segments from village k to each of the villages in order. The goodness from village k to village j may be different from the goodness from village j to village k. (The goodness from village k to village k is always 1.) A goodness of 0 indicates that there is no useable road segment. Village 0 is where the truck and corn are located, while village 1 is the site of the disaster.

Create a class Disaster that contains a method expected. The method is given b (the coefficient in the lightness calculation) and roads. It returns the expected amount of corn that can be delivered if we choose the best load and route.

Definition

Class:	Disaster
Method:	expected
Parameters:	double, String[]
Returns:	double
Method signature:	double expected(double b, String[] roads)
(be sure your method is public)

Constraints

-

b will be between .01 and 1.0 inclusive.

-

roads will contain n elements, where n will be between 2 and 25 inclusive.

-

Each element of roads will contain between 3 and 50 characters inclusive.

-

Each element of roads will contain n values and n-1 spaces separating the values.

-

Each value will be a real value between 0.0 and 1.0 inclusive.

-

Each value will be expressed as "0", "1", or as a decimal point followed by digits ('0'-'9')

-

Each value will contain between 1 and 4 digits inclusive.

-

The k-th value in the k-th element of roads will be "1".

Examples

0)

1.0

{"1 0 1","0 1 0","1 .9 1"}

Returns: 0.13333333333333336

There is only one reasonable route, namely from village 0 to village 2 to village 1. If x is the load we put on the truck, then the probability of getting to village 2 is (1-x)*1.0 and the probability of getting from village 2 to village 1 is (1-x)*.9 so the probability of getting our load to the disaster site is the product of those two. The expected amount of corn delivered is x times that probability giving x*(1.0*(1-x))*(.9*(1-x)). This is maximized when we make the load be 1/3 and gives us an expected amount of (1/3)*(2/3)*(.6)

1)

0.5

{"1 0 1 0","0 1 0 0","0 0 1 0","1 .9 1 1"}

Returns: 0.0

There is no route between village 0 and village 1.

2)

.8

 {"1 .8 .6","1 1 1","1 1 1"}

Returns: 0.25

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SortEstimate

Math, Search

Used in:

SRM 230

Used as:

Division I Level One , Division II Level Two

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3561

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6519&pm=3561

Problem Statement

You have implemented a sorting algorithm that requires exactly c*n*lg(n) nanoseconds to sort n integers. Here lg denotes the base-2 logarithm. Given time nanoseconds, return the largest double n such that c*n*lg(n) <= time.

Definition

Class:	SortEstimate
Method:	howMany
Parameters:	int, int
Returns:	double
Method signature:	double howMany(int c, int time)
(be sure your method is public)

Notes

-

lg(n) = ln(n)/ln(2) where ln denotes the natural log.

-

Your return value must have a relative or absolute error less than 1e-9.

Constraints

-

c will be between 1 and 100 inclusive.

-

time will be between 1 and 2000000000 inclusive.

Examples

0)

Returns: 4.0

Given 8 nanoseconds we can sort 4 integers since

	1*4*lg(4) = 4*2 = 8

1)

Returns: 4.0

Now that c = 2 we need twice as many nanoseconds to sort 4 integers.

2)

12392342

Returns: 23104.999312341137

We can almost sort 23105 integers, but not quite.

3)

2000000000

Returns: 7.637495090348122E7

Largest possible return.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

InequalityChecker

Brute Force

Used in:

SRM 230

Used as:

Division II Level One

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3560

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6519&pm=3560

Problem Statement

Using mathematical induction it is possible to prove the following inequality when n>1:

	s = 1³ + 2³ + ... + (n-1)³ < n⁴/4 < 1³ + 2³ + ... + n³ = S

Given n return (S+s)/2 - n⁴/4 as a int[] with 2 elements. Elements 0 and 1 denote the numerator and denominator of the return value, respectively, when written in least terms (reduced).

Definition

Class:	InequalityChecker
Method:	getDifferences
Parameters:	int
Returns:	int[]
Method signature:	int[] getDifferences(int n)
(be sure your method is public)

Constraints

-

n will be between 2 and 100 inclusive.

Examples

0)

Returns: { 1,  1 }

We have

s = 1^3 = 1
S = 1^3 + 2^3 = 9
(S+s)/2 = (1+9)/2 = 5
n^4/4 = 16/4 = 4

Since 5-4 = 1, we return the fraction 1/1.

1)

Returns: { 9,  4 }

We have

s = 1^3 + 2^3 = 9
S = 1^3 + 2^3 + 3^3 = 36
(S+s)/2 = 45/2
n^4/4 = 81/4

We return the fraction 9/4.

2)

Returns: { 2500,  1 }

Largest case.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ATaleOfThreeCities

Brute Force, Simple Math

Used in:

SRM 239

Used as:

Division I Level One , Division II Level Two

Writer:

supernova

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3543

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6538&pm=3543

Problem Statement

As a result of ever increasing traffic jams, subway transportation in big cities has become a must. A train can actually take you from your home to your office faster than a car can. But what happens if you have your office in another city? In this problem we consider three different cities: A, B and C. Each of these cities has its own subway transportation system and you can go from a station to any other in the same city without having to leave the underground. A big project is now underway, and the goal is to merge the subway lines such that transportation between these cities becomes available soon. In order to achieve this, it was decided that two tunnels would be constructed, each of them connecting two subway stations in two different cities. This has to be done at a minimal cost, so it is important which subway stations are chosen. Also consider that the only factor in determining the cost is the distance between the two subway stations connected by a tunnel.

You will be given a int[] ax, a int[] ay, a int[] bx, a int[] by, a int[] cx and a int[] cy with the following signification:

ax and ay represent the coordinates of the subway stations in city A i.e (ax[i],ay[i]) is the point denoting the place of the i-th station

bx and by represent the coordinates of the subway stations in city B i.e (bx[i],by[i]) is the point denoting the place of the i-th station

cx and cy represent the coordinates of the subway stations in city C i.e (cx[i],cy[i]) is the point denoting the place of the i-th station

Return the minimal added distance of the two tunnels such that all three cities become connected.

Definition

Class:	ATaleOfThreeCities
Method:	connect
Parameters:	int[], int[], int[], int[], int[], int[]
Returns:	double
Method signature:	double connect(int[] ax, int[] ay, int[] bx, int[] by, int[] cx, int[] cy)
(be sure your method is public)

Notes

-

Your return value must have an absolute or relative error less than 1e-9.

Constraints

-

ax, ay, bx, by, cx, and cy will each contain between 2 and 50 elements, inclusive.

-

Each element of ax, ay, bx, by, cx, and cy is between -100 and 100, inclusive.

-

The number of elements in ax is equal to the number of elements in ay.

-

The number of elements in bx is equal to the number of elements in by.

-

The number of elements in cx is equal to the number of elements in cy.

-

There are no subway stations with identical coordinates.

Examples

0)

{0,0,0}

{0,1,2}

{2,3}

{1,1}

{1,5}

{3,28}

Returns: 3.414213562373095

The tunnel connecting the subway station in city A at (0,2) with the subway station in city C at (1,3) has a length of about 1.41 and the tunnel connecting the subway station in city A at (0,1) with the subway station in city B at (2,1) has a length of 2.

1)

{-2,-1,0,1,2}

{0,0,0,0,0}

{-2,-1,0,1,2}

{1,1,1,1,1}

{-2,-1,0,1,2}

{2,2,2,2,2}

Returns: 2.0

2)

{4,5,11,21,8,10,3,9,5,6}

{12,8,9,12,2,3,5,7,10,13}

{34,35,36,41,32,39,41,37,39,50}

{51,33,41,45,48,22,33,51,41,40}

{86,75,78,81,89,77,83,88,99,77}

{10,20,30,40,50,60,70,80,90,100}

Returns: 50.323397776611024

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HingedDoor

Simple Math, Simulation

Used in:

SRM 275

Used as:

Division II Level One

Writer:

NeverMore

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3531

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8072&pm=3531

Problem Statement

We've all seen hinged doors before, perhaps in the entrance to a kitchen. Have a look at the figure below to make things clear. This particular hinged door works as follows: From "rest position" (the solid line below), the door is pushed at one end, and it swings out through an angle (in the image, this corresponds to "1st swing"). Then, when the door is released, it swings to the other side (this is shown in the image as "2nd swing"), but this time, the angle through which it swings is reduced to a known fraction of the previous angle. Then, the direction is reversed again and once more, the angle reduced by the same fraction. Once the angle drops to 5.0 degrees or below, the door doesn't swing any more, but rather, it returns to "rest position".

Create a class HingedDoor which contains a method numSwings. The method takes an int initialAngle and an int reduction as input and returns an int corresponding to the number of times the door will swing before coming to rest when initially displaced by initialAngle. Remember that each time the door will swing through an angle reduction times less than the angle it swung through the previous time.

Definition

Class:	HingedDoor
Method:	numSwings
Parameters:	int, int
Returns:	int
Method signature:	int numSwings(int initialAngle, int reduction)
(be sure your method is public)

Constraints

-

initialAngle will be between 0 and 90, inclusive.

-

reduction will be between 2 and 10, inclusive.

Examples

0)

Returns: 4

In this example, the door begins with an initial angle of 50 degrees. Then, the door will swing through a reduced angle of (1/2)*(50) = 25 degrees on the first swing. At this point, the door will reverse direction, and swing through an angle of (1/2)*(25) = 12.5 degrees. Continuing in this way, the door will swing once more through (1/2)*(12.5) = 6.25 degrees, and then through (1/2)*(6.25) = 3.125 degrees. At this point, the door will come to rest. Therefore, the correct return value is 4, since the door took 4 swings before coming to rest.

1)

Returns: 2

2)

Returns: 2

3)

Returns: 0

Careful! The initial angle is already below 5 degrees, so the door won't swing at all, but rather, return to rest position immediately.

4)

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MultiRead

Simple Math

Used in:

SRM 305

Used as:

Division II Level One

Writer:

vorthys

Testers:

PabloGilberto , Olexiy , lovro , Andrew_Lazarev

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3526

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9826&pm=3526

Problem Statement

In many computer systems, multiple processes can read from the same resource during the same clock cycle, but only a single process can write to the resource during a clock cycle. Reads and writes cannot be mixed during the same clock cycle. Given a history of the reads and writes that occurred during a particular computation as a String trace, and an int procs representing the number of processes used by the computation, calculate the minimum duration of the computation in clock cycles. The trace represents each read as an 'R' and each write as a 'W'.

For example, if trace is "RWWRRR" and procs is 3, then the minimum number of clock cycles is 4: one for the first read, one each for the two writes, and one for the last group of reads.

Definition

Class:	MultiRead
Method:	minCycles
Parameters:	String, int
Returns:	int
Method signature:	int minCycles(String trace, int procs)
(be sure your method is public)

Constraints

- trace will contain between 1 and 50 characters, inclusive.

- Each character in trace will be 'R' or 'W'.

- procs will be between 1 and 10, inclusive.

Examples

0)

"RWWRRR"

Returns: 4

The example above.

1)

"RWWRRRR"

Returns: 5

Now the final group of 'R's takes two cycles.

2)

"WWWWW"

Returns: 5

3)

"RRRRRRRRRR"

Returns: 3

4)

"RWRRWWRWRWRRRWWRRRRWRRWRRWRRRRRRRRRWRWRWRRRRWRRRRR"

Returns: 30

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TreeSpreading

Dynamic Programming, Simple Math, Simple Search, Iteration

Used in:

SRM 227

Used as:

Division I Level Two

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3518

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6516&pm=3518

Problem Statement

A farmer is planting a line of trees across the front of his house. He has four different kinds of trees he would like to plant. However, for aesthetic reasons, he does not want two of the same type of tree next to each other. Beyond that, any arrangement of trees is considered acceptable.

You are given ints a, b, c, and d, indicating how many of each type of tree the farmer is going to plant. You are to return a long indicating the number of acceptable ways in which the trees can be ordered.

Definition

Class:	TreeSpreading
Method:	countArrangements
Parameters:	int, int, int, int
Returns:	long
Method signature:	long countArrangements(int a, int b, int c, int d)
(be sure your method is public)

Notes

-

Each tree of a given type is identical to others of the same type, thus swapping the positions of two of the same type of tree does not consitute a new arrangement.

Constraints

-

a, b, c, and d will be between 0 and 10, inclusive.

Examples

0)

Returns: 2

There are only two trees to place, and they can go in either order.

1)

Returns: 2

There are two possible arrangements: ABAB or BABA. Any others have two identical trees adjacent to one another.

2)

Returns: 24

Since all four trees are different, they can be arranged in any order, so the answer is 4!.

3)

Returns: 96

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TreePlanting

Dynamic Programming, Recursion, Simple Math

Used in:

SRM 227

Used as:

Division II Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3515

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6516&pm=3515

Problem Statement

A farmer wants to plant a row of trees along the front of his house. He has two different kinds of trees, some which are plain looking, and other, more expensive, fancy trees. He wishes to plant the trees in such a way that not all of the fancy trees are grouped together, so he insists that no two fancy trees be adjacent to one another.

You are given an int total indicating the total number of trees to be planted, and an int fancy which is the number of fancy trees. You are to return a long indicating the number of possible tree arrangements that meet the farmer's criteria of having no two fancy trees adjacent to one another.

Definition

Class:	TreePlanting
Method:	countArrangements
Parameters:	int, int
Returns:	long
Method signature:	long countArrangements(int total, int fancy)
(be sure your method is public)

Notes

-

You may assume that each fancy tree is identical to one other, and likewise for the plain trees.

-

If no valid arrangements are possible, the return value should be 0.

Constraints

-

total will be between 1 and 60, inclusive.

-

fancy will be between 1 and 60, inclusive.

-

fancy will be less than or equal to total.

Examples

0)

Returns: 3

Here, we have two plain trees, and two fancy trees. There are only three acceptable arrangements: PFPF, FPPF or FPFP. Any other arrangement would have two fancy trees next to each other.

1)

Returns: 3

There is only one fancy tree, and it can go in any of three locations.

2)

Returns: 0

There is no way to place all three fancy trees without two of them being next to each other.

3)

Returns: 35

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

QuadrilateralSearch

Advanced Math, Geometry, Search, Simple Search, Iteration

Used in:

SRM 227

Used as:

Division I Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3514

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6516&pm=3514

Problem Statement

You are given a circle of diameter d, with n points equally spaced around the circumference. The points are numbered in order around the circle 0, 1, 2, ... , n-1. Of those n points, c of them are colored red. The points that are colored red are given by the generator function (g * k) % n, for k = 0, 1, 2, ..., c-1.

You are given ints d, n, c, and g. You are to return a double indicating the largest area of a quadrilateral formed from four of the colored points.

Definition

Class:	QuadrilateralSearch
Method:	findLargest
Parameters:	int, int, int, int
Returns:	double
Method signature:	double findLargest(int d, int n, int c, int g)
(be sure your method is public)

Notes

-

The % operator is the modulus (remainder) operator.

-

Notice that it makes no difference which point is point 0, and in which direction around the circle the points are numbered.

Constraints

-

d will be between 1 and 1000, inclusive.

-

n will be between 4 and 1000000000, inclusive.

-

c will be between 4 and 500, inclusive.

-

c will be less than or equal to n.

-

g will be between 1 and n-1, inclusive, and will be relatively prime to n.

Examples

0)

Returns: 48.9142858122447

Here, we have only four points that are colored red: 0, 3, 6, and 9. It's just a simple matter of calculating the area of the quadrilateral.

1)

Returns: 179.10027343916573

Here, we have six points, so there are 15 possible quadrilaterals. We choose the largest of these.

2)

Returns: 0.028489712517284715

Here, with 50 points, there are a lot of possible quadrilaterals, but they are all long and flat, so even with such a large circle, they have a very small area.

3)

Returns: 4965.195939678256

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NestedRandomness

Dynamic Programming, Math

Used in:

TCCC05 Qual 5

Used as:

Division I Level Three

Writer:

lars2520

Testers:

PabloGilberto , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3510

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6527&pm=3510

Problem Statement

Consider a function randomInt(integer N) that takes an integer N and returns an integer uniformly at random in the range 0 to N-1. If that function is nested, as in randomInt(randomInt(N)), the probability distribution changes, and some numbers are more likely than others. Given an int nestings defining the number of times the function is nested (1 indicates randomInt(N), 2 indicates randomInt(randomInt(N)), and so on), an int N and an int target, return the probability that the result of nestings nested calls to randomInt with the parameter N will result in target.

Definition

Class:	NestedRandomness
Method:	probability
Parameters:	int, int, int
Returns:	double
Method signature:	double probability(int N, int nestings, int target)
(be sure your method is public)

Notes

-

Calling randomInt(0) causes an error to occur, and hence can never cause an outcome of target.

-

Your return must have a relative or absolute error less than 1E-9.

Constraints

-

N will be between 1 and 1000, inclusive.

-

nestings will be between 1 and 10, inclusive.

-

target will be between 0 and N-nestings, inclusive.

Examples

0)

Returns: 0.21666666666666667

There are 3 ways of ending up with a 1 after calling randomInt(randomInt(5)). The inner call can result in a 4, 3, or a 2. Each of these possibilities occurs with a probability of 1/5. The probabilities of achieving a 1 with each of those results are 1/4, 1/3, and 1/2, respectively. This gives us a final probability of (1/5)*(1/4+1/3+1/2) = 13/60.

1)

Returns: 0.19942680776014104

2)

Returns: 1.0461776397050886E-30

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TimeOfPossession

Simple Math, String Parsing

Used in:

TCCC05 Qual 5

Used as:

Division I Level One

Writer:

lars2520

Testers:

PabloGilberto , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3507

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6527&pm=3507

Problem Statement

In many sports, the time of possession is a much talked about statistic. This indicates the amount of time during a game that a particular team possesses the ball. In this problem, you will calculate the time of possession given the relevant events of the game. You will be given a String[], each element of which is formatted as "EVENT TIME", where EVENT is either "A", "B", "SWITCH", or "END". An "A" indicates that team A gains possession of the ball, while a "B" indicates that team B gains possession of the ball. "SWITCH" indicates that the ball changes possession from one team to the other (there are only two teams). "END" indicates the end of the game. Each TIME will be formatted as "minutes:seconds" where seconds contains exactly two digits, and minutes contains no extra leading zeros. Your task is to return a String formatted as "minutes:seconds" in the same format as the input, indicating the total time of possession for team A. The input will be sorted in non-descending order by time, and the first element will be either "A 0:00" or "B 0:00", while the last element, and only the last element, will have EVENT = "END".

Definition

Class:	TimeOfPossession
Method:	getTime
Parameters:	String[]
Returns:	String
Method signature:	String getTime(String[] times)
(be sure your method is public)

Notes

-

If multiple events occur at the same time, assume that the one that appears earlier in the input actually occurs earlier (see example 2).

Constraints

-

times will contain between 2 and 50 elements, inclusive.

-

Each element of times will be formatted as "EVENT TIME"

-

Each EVENT will be "A", "B", "END", or "SWITCH".

-

The first EVENT will be "A" or "B", and the first TIME will be "0:00".

-

The last EVENT will be "END".

-

Each TIME will be between "0:00" and "999:59", inclusive, and the minutes will not have any extra leading zeros, while the seconds will contain exactly 2 digits.

-

The TIMEs will be sorted in non-descending order.

Examples

0)

{"A 0:00","SWITCH 1:23","END 3:00"}

Returns: "1:23"

A possesses the ball for the first 1:23, but never gets it again.

1)

{"A 0:00","SWITCH 1:23","SWITCH 4:50","END 15:00"}

Returns: "11:33"

2)

{"A 0:00","SWITCH 0:00","END 15:00"}

Returns: "0:00"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TimeAnalysis

Simple Math, String Parsing

Used in:

TCCC05 Qual 3

Used as:

Division I Level Three

Writer:

lars2520

Testers:

PabloGilberto , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3502

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6525&pm=3502

Problem Statement

An important part of any algorithm is its runtime. This is usually specified as an equation with a number of variables. For example, the runtime of many popular sorting algorithms is N*lg(N), meaning that the amount of time it takes to run the algorithm is proportional to N times the base 2 logarithm of N.

Your task is to write a method that approximates how long an algorithm will run, given its runtime and the values of the parameters involved. For this approximation, you should assume that a computer can execute 1 billion (1E9) operations per second. You will be given a String[], variables, each element of which is of the form "VAR VALUE", where VAR is an uppercase letter, and VALUE is an integer greater than 0. You will also be given a String, equation, conforming to the following grammar:

  equation ::= TERM '*' equation | TERM '+' equation | TERM
  TERM ::= VAR | 'lg(' VAR ')' | VAR^INT | INT^VAR
  VAR ::= a VAR from variables
  INT ::= an integer between 2 and 9, inclusive, with no leading zeros.

You should calculate the time it takes to run the algorithm by evaluating equation with the given variables to obtain the total number of operations. You should return a String in the form "DURATION UNITS", where UNITS is either "nanoseconds", "microseconds", "milliseconds", "seconds", "minutes", "hours", "days", or "years". You should use the largest unit for which DURATION is greater than or equal to 1. You should truncate any fractional part of DURATION.

Definition

Class:	TimeAnalysis
Method:	time
Parameters:	String[], String
Returns:	String
Method signature:	String time(String[] variables, String equation)
(be sure your method is public)

Notes

-

The base 2 logarithm of a number N, can be calculated as log(N)/log(2), where log computes a logarithm in some other base.

-

'^' denotes exponentiation.

-

Use the standard order of operations.

-

Assume that every year has exactly 365 days.

-

equation will contain no spaces.

Constraints

-

variables will contain between 1 and 26 elements, inclusive.

-

Each element of variables will be formatted as "VAR VALUE", where VAR is an uppercase letter, and VALUE is an integer.

-

Each element of variables will have a unique VAR.

-

Each VALUE will be between 2 and 1000000000 (1E9), inclusive, with no leading zeros.

-

equation will be contain between 1 and 50 characters, inclusive.

-

equation will be formatted as specified in the statement.

-

Each variable used in equation will be present in variables.

-

The return value will be less than 1000 years.

-

When the correct units are chosen, the duration will not be within 1e-3 of an integer.

Examples

0)

{"N 1000"}

"N*lg(N)"

Returns: "9 microseconds"

With N=1000, N*lg(N) = 1000 * 9.966 operations. This takes a little under 10 microseconds, so you should return "9 microseconds".

1)

{"N 1000000000","M 10"}

"M*N*lg(N)"

Returns: "4 minutes"

2)

{"N 1000","M 205"}

"N^2*M+M^3"

Returns: "213 milliseconds"

3)

{"N 30"}

"2^N*N^2"

Returns: "16 minutes"

4)

{"N 29"}

"3^N*N^2"

Returns: "1 years"

Despite the bad grammar, you should return "1 years", not "1 year".

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Driving

Math, Search

Used in:

TCCC05 Round 2

Used as:

Division I Level Three

Writer:

lars2520

Testers:

PabloGilberto , lbackstrom , Yarin , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3501

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6529&pm=3501

Problem Statement

With gasoline prices as they are, driving can be expensive. By always driving at the optimal speed, however, you can minimize the cost. To do this, you must take 3 factors into account.

1) The cost of your time. The faster you get where you are going, the more time you have to do other things.

2) The cost of speeding tickets. If you drive too fast, there is a risk that you will get a speeding ticket.

3) The cost of operating the vehicle (gasoline plus wear and tear).

You have collected some data pertaining to these three factors, and would now like to calculate the optimal speed to drive at. You will be given an int, costOfTime, representing the price at which you value an hour of your time. You will be given a String[], tickets, indicating the cost and likelihood of getting a ticket at various speeds. Finally, you will be given a String[], costPerMile, indicating the cost of operating your vehicle at different speeds.

Each element of tickets will be formatted as "SPEED PROBABILITY COST", indicating the probability per mile of receiving a ticket when travelling at the given speed. If you are travelling at a speed that does not correspond to any element of tickets, you should use linear interpolation to determine the probability of receiving a ticket (see examples). However, the cost of the ticket will be the cost of the ticket for the highest speed less than or equal to the travel speed. Note that if you are travelling at a speed less than the minimum SPEED in tickets, you cannot receive a ticket. Also, you should assume that each mile of road is independent and if you receive a ticket during one mile, that does not affect the probability of receiving a ticket during the next mile. Furthermore, you should assume that you will not receive more than one ticket in a single mile.

Each element of costPerMile will be formatted as "SPEED COST" indicating the cost per mile of travelling at a given speed. You should again interpolate to find the cost of speeds not in costPerMile. Your car cannot travel faster than the highest SPEED in costPerMile, and the smallest SPEED in costPerMile will always be 0.

You should find the speed that gives the lowest expected cost per mile and return that cost.

Definition

Class:	Driving
Method:	lowestCost
Parameters:	int, String[], String[]
Returns:	double
Method signature:	double lowestCost(int costOfTime, String[] tickets, String[] costPerMile)
(be sure your method is public)

Notes

-

You need not worry about the time that it takes to receive and deal with a ticket as this is already factored into the costs given to you.

-

Your return must have a relative or absolute error less than 1E-9.

Constraints

-

costOfTime will be between 1 and 1000, inclusive.

-

tickets will contain between 1 and 50 elements, inclusive.

-

costPerMile will contain between 2 and 50 elements, inclusive.

-

Each element of tickets and costPerMile will contain at most 50 characters.

-

Each element of tickets will be formatted as "SPEED PROBABILITY COST".

-

Each element of costPerMile will be formatted as "SPEED COST".

-

Each SPEED in both inputs will be between 0 and 200, inclusive.

-

Each PROBABILITY will be between 0 and 0.1, inclusive.

-

Each COST in tickets will be between 1 and 1000000, inclusive.

-

Each COST in costPerMile will be between 0 and 5, exclusive.

-

All numbers in the inputs will be formatted as sequences of 1 or more digits, with an optional decimal point. They may contain extra leading or trailing zeros.

-

The smallest SPEED in costPerMile will be 0.

-

The largest SPEED in tickets will be greater than or equal to the largest SPEED in costPerMile.

-

Both String[] inputs will be sorted in ascending order by SPEED.

-

tickets will be sorted in non-descending order by COST and PROBABILITY.

-

No two SPEEDS in costPerMile will be within 1 of each other.

-

No two SPEEDS in tickets will be within 1 of each other.

Examples

0)

{"80 0.001 100"}

{"0 0.01","30 0.40","55 0.37","65 0.42","75 0.53"}

Returns: 1.1882396974191325

At 67.42 miles per hour, the cost of operating the vehicle is found by linear interpolation. That is, imagine drawing a straight line from (65,0.42) to (75,0.53). Then, find the y-value of the point on this line corresponding to x = 67.42. That is the cost per mile of operating the vehicle (0.44662 here). In this case, there are no tickets, so we need not worry about that. The cost of the time is 0.74162 per mile, for a total of 0.44662+0.74162 = 1.18824.

1)

{"60 0.00001 50","65 0.00003 70","70 0.0001 110","75 0.001 180"}

{"0 0.01","30 0.40","55 0.37","65 0.42","75 0.53"}

Returns: 1.1907307692308355

In this case, there is some risk of getting a ticket. The cheapest speed is just a hair under 65 so that you only have to pay 50 if you get a ticket.

2)

{"60 0.00001 50","65 0.00003 70","70 0.0001 110","75 0.001 180"}

{"0 0.01","30 0.40","55 0.37","65 0.42","75 0.53"}

Returns: 1.9105714285715127

Same as example 1, but with a higher value on time.

3)

{"60.50 0.00002 50.53","65 0.00007 70",
 "070 0.0002 150","75 0.002 200",
 "080.001 0.004 300","85. 0.004 1000000",
 "150 0.004 1000000"}

{"0 0.50","30 0.40","55.5 0.37","65 0.42","75 0.63","80 0.87","95 1.30"}

Returns: 13.978039215687371

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Symbolic

Advanced Math, Simple Search, Iteration

Used in:

TCCC05 Semi 1

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3499

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6550&pm=3499

Problem Statement

Let I_Zero denote the real interval from 0 to 1/3, including 0 but not including 1/3. Let I_One denote the real interval from 1/3 to 1 including both endpoints.

We have a dynamic system, in which real values are generated by the following rule: x_t+1 = f(x_t) where f is the function

               f(x) =  3x        (for x in I_Zero) 
                      (3-3x)/2   (for x in I_One)

The trajectory of a value c is the sequence of real values that would be generated by the system starting with c. These would be c, f(c), f(f(c)), etc. The "itinerary" of c is defined to be the sequence of 0's and 1's indicating whether the corresponding trajectory values are in I_Zero or I_One.

For example, the trajectory of 1/2 is 1/2,3/4,3/8,15/16,3/32,9/32, ... so its itinerary is 1,1,1,1,0,0,...

Given a value and the itinerary of an unknown value c, we would like to determine whether the given value is less than or greater than c. Since an itinerary is an infinite sequence, we will be given only the first part of an itinerary, so it may be impossible to determine whether the given value is smaller or larger than c.

Create a class Symbolic that contains a method compare that is given value as a decimal String and a int[] itin (the first elements in the itinerary of the unknown c). The method returns -1, 0, or 1 depending on whether value is less than c, indeterminate, or greater than c.

Definition

Class:	Symbolic
Method:	compare
Parameters:	String, int[]
Returns:	int
Method signature:	int compare(String value, int[] itin)
(be sure your method is public)

Constraints

- value will contain between 2 and 20 characters inclusive.

- value will consist of a decimal point followed by digits '0'-'9'.

- itin will contain between 1 and 50 elements inclusive.

- Each element of itin will be 0 or 1.

Examples

0)

".5"

{1,1,1,1,0}

Returns: 0

The first elements of the itinerary of 0.5 match the values in itin, so we cannot determine whether 0.5 is less than, equal to, or greater than c.

1)

".300000"

{1,1,1,1,0}

Returns: -1

0.3 is less than 1/3 so it is in I_Zero. c is between 1/3 and 1.0 since its itinerary starts in I_One. So 0.3 is less than c.

2)

".6"

{1,1,0,1,0,0}

Returns: 1

The trajectory of .6 is .6,.6,.6,.6,... If c were greater than or equal to .6, then f(c) would be less than or equal to (3 - 3*.6)/2 = .6 and f( f(c) ) would be greater than or equal to .6 which contradicts the fact that the third element of itin is 0. Therefore, .6 must be greater than c.

3)

".00"

{0,0,0,0,0}

Returns: 0

Indeterminate: value may either be less than or equal to c. (It cannot be greater than c since a number less than .0 has no itinerary.)

4)

".1111111111111111111"

{0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1}

Returns: 0

Be careful about the precision of your calculations.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ManhattanMovement

Geometry, Simple Math

Used in:

SRM 226

Used as:

Division I Level One , Division II Level Three

Writer:

the_one_smiley

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3498

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6515&pm=3498

Problem Statement

You are in a big flat city, and wish to travel to a road. The road is an infinite straight line that may have any orientation, but you are restricted to only moving in the four cardinal directions. If the city is represented by the xy-plane, your starting location is the point (x0, y0) and the road is the line a*x + b*y = 1. You can change directions at any point and travel as far as you want in each direction, but you can only travel parallel to the x or y-axis. Write a class ManhattanMovement with a method getDistance that takes four ints a, b, x0, and y0 and returns the shortest distance you must travel in order to reach the road.

Definition

Class:	ManhattanMovement
Method:	getDistance
Parameters:	int, int, int, int
Returns:	double
Method signature:	double getDistance(int a, int b, int x0, int y0)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1e-9 is considered correct.

Constraints

-

a, b, x0, and y0 will all be between -2147483648 and 2147483647, inclusive.

-

a and b will not both equal zero.

Examples

0)

-2

Returns: 1.5

Moving straight south (in the negative y-direction) yields the shortest distance.

1)

Returns: 60.97297297297297

Moving either straight south or straight west yields the same minimum distance.

2)

-100

-999999

Returns: 999998.99

3)

-2147483648

Returns: 100000.00000000047

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MovingAvg

Simple Math, Simple Search, Iteration

Used in:

SRM 304

Used as:

Division II Level Two

Writer:

dgoodman

Testers:

PabloGilberto , vorthys , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3495

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9825&pm=3495

Problem Statement

When data is collected at regular intervals, trends in the data are sometimes easier to see by looking at a moving average. The moving average of length k at a particular time is the average of the k most recently collected data values. So at time t it is the average of the data reported at times t,t-1,...,t-(k-1). The moving average is not defined at time t unless we have data for the preceding k-1 times.

We have a sequence of data values and want to look at the moving averages of length k of those values. Specifically, we want to know how much the largest moving average exceeds the smallest moving average.

Create a class MovingAvg that contains a method difference that is given k and double[] data. It returns the difference between the largest and smallest moving average of length k in data.

Definition

Class:	MovingAvg
Method:	difference
Parameters:	int, double[]
Returns:	double
Method signature:	double difference(int k, double[] data)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

k will be between 1 and 10, inclusive.

-

data will contain between k and 50 elements, inclusive.

-

Each element of data will be between 0.0 and 1000.0 inclusive.

Examples

0)

{3,8,9,15}

Returns: 6.5

The moving averages are (3+8)/2, (8+9)/2, and (9+15)/2 which are 5.5, 8.5, and 12.0. So the difference between the largest and smallest is 12.0 - 5.5 = 6.5

1)

{17,6.2,19,3.4}

Returns: 4.533333333333335

The moving averages are (17+6.2+19)/3 and (6.2+19+3.4)/3 which are 14.0666666... and 9.533333...

2)

{6,2.5,3.5}

Returns: 0.0

There is only 1 moving average of length 3, so the smallest and biggest moving average are the same.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BridgePts

Simple Math, Simple Search, Iteration

Used in:

SRM 257

Used as:

Division II Level Two

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3494

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8005&pm=3494

Problem Statement

A deck of cards contains 52 cards. Each card has a suit (Clubs,Diamonds,Hearts,Spades) and a value (Ace,2,3,...,9,10,Jack,Queen,King). In the game of bridge a hand consists of 13 cards from the deck.

A player needs to evaluate his hand, giving it a point value. The standard method is as follows: count 4 points for each Ace, 3 points for each King, 2 points for each Queen, and 1 point for each Jack. For each suit, count 1 point if the hand contains exactly two cards of that suit, 2 points if exactly one card, and 3 points if the hand contains no cards of that suit. The point value of the hand is the sum of all these points.

Create a class BridgePts that contains a method pointValue that is given a int[] hand and that returns the point value of the hand.

Each element of hand indicates a card. The clubs are numbered 1 to 13, the diamonds are 14 to 26, the hearts are numbered 27 to 39, and the spades are numbered 40 to 52. Within each suit, the cards are numbered in the order Ace, 2, 3, ..., 9, 10, Jack, Queen, King. So, for example, the King of Hearts is numbered 39 and the Ace of Spades is numbered 40.

Definition

Class:	BridgePts
Method:	pointValue
Parameters:	int[]
Returns:	int
Method signature:	int pointValue(int[] hand)
(be sure your method is public)

Constraints

-

hand will contain exactly 13 elements, all distinct.

-

Each element of hand will have a value between 1 and 52 inclusive.

Examples

0)

{25,14,15,16,17,18,19,20,21,22,23,24,26}

Returns: 19

This hand contains all diamonds, so it has one Ace, one King, one Queeen, and one Jack, and it contains no cards in three suits. So its point value is 4 + 3 + 2 + 1 + 3 + 3 + 3 = 19.

1)

{2,3,4,15,18,28,29,30,41,42,43,16,17}

Returns: 0

This hand contains only 2's, 3's, 4's and one 5. It has 3 or 4 cards in each suit.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ExperimentalAnalyzer

Simple Math, String Parsing

Used in:

SRM 226

Used as:

Division II Level Two

Writer:

the_one_smiley

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3493

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6515&pm=3493

Problem Statement

You have collected data from a research study. Each experiment in this study has its own set of values for the relevant variables and an outcome of either 0 or 1. You wish to analyze the data to determine which variables can independently predict the outcome using a simple threshold. In this problem, a variable v is an independent predictor if there exists a threshold t such that every experiment with v less than or equal to t has the same outcome, every experiment with v greater than t has the other outcome, and both outcomes are each attained by at least one experiment (otherwise, the research study should probably be redesigned).

Write a class ExperimentalAnalyzer with a method getPredictors that takes a String[] data containing the outcome and variable values for each experiment and returns a int[] containing the one-based indices of all the independent predictors, sorted in increasing order. Each element of data corresponds to one experiment and will contain its outcome (either 0 or 1) followed by its list of variable values (which are non-negative integers). The value list for each experiment will be arranged in the same order, with the value for the first variable immediately following the outcome.

Definition

Class:	ExperimentalAnalyzer
Method:	getPredictors
Parameters:	String[]
Returns:	int[]
Method signature:	int[] getPredictors(String[] data)
(be sure your method is public)

Notes

-

If all the experiments have identical outcomes, there can be no independent predictors.

Constraints

-

data will contain between 2 and 50 elements, inclusive.

-

Each element of data will contain between 3 and 50 characters, inclusive.

-

Each element of data will contain an outcome (0 or 1) followed by one or more variable values (integers between 0 and 2147483647 inclusive, with no extra leading zeroes), all separated by single spaces.

-

Each element of data will contain the same number of variable values.

Examples

0)

{
"0 10 20 20 0",
"1 20 30 17 98765",
"0 10 30 29 1234567",
"1 20 40 10 42"}

Returns: { 1,  3 }

There are two experiments with outcome 0 and two with outcome 1. Variable 1 (the first column after the outcome) is an independent predictor because the experiments with outcome 0 have values of 10 or less, while experiments with outcome 1 have values greater than 10. Variable 2 is not an independent predictor because two experiments with the same value have different outcomes. Variable 3 is an independent predictor, but unlike Variable 1, the experiments with outcome 1 have the smaller values. Variable 4 is not an independent predictor since there is no threshold that can separate the values for the different outcomes.

1)

{
"1 220 212 247 764 928 956 946 66 640 983 125 994",
"0 816 835 98 81 783 267 946 584 309 757 876 670"}

Returns: { 1,  2,  3,  4,  5,  6,  8,  9,  10,  11,  12 }

With only two experiments with distinct outcomes, a variable will be an independent predictor unless it has the same value in both experiments.

2)

{
"0 1944914038 1696137778 1525367830",
"0 1547932733 1185820653 1500052399",
"0 230149443 1358715189 501418065",
"0 1676118083 1499656529 2103271593",
"0 1441540020 1189300515 1544659186"}

Returns: { }

All the experiments have outcome 0, so there are no independent predictors.

3)

{
"0 163869663 388719849 383049741",
"1 1982032201 1346175990 1500891700",
"0 436834674 559375803 994453722",
"0 652316051 372955428 361692727",
"1 1946362869 1204080206 2066121600",
"0 840867095 22073435 1166658385",
"1 1864235269 2041251772 1847305529",
"0 852306016 447986701 407997336",
"1 1183214776 728141214 1985649244",
"0 70064437 7110416 107908753",
"1 1383409284 1328770197 1942831571",
"1 1023334064 1596272317 1226876467",
"1 2068895243 1481323649 1955807390",
"0 758836687 541737411 312747384",
"1 1432983907 1475284843 1512945413",
"1 1512506825 1933755150 2041997368",
"1 2041700103 1859742986 1995865005",
"0 323696628 328891715 893352493",
"1 1623710967 1193592990 1871502957",
"0 9241593 127579695 36337622",
"1 1935123182 1332735215 1400991717",
"1 2130762600 1874898210 1234793873",
"0 411777048 142083649 61450530",
"1 1042383468 1979605937 1276643901",
"0 219279208 371281702 65383690",
"0 948808405 243728462 984221323",
"0 999393888 131231007 1186873391",
"1 1294115986 1618148416 1324126407",
"1 1710811842 2024808989 1696767048",
"1 1399327255 1317859960 1427366434",
"0 145887863 452552798 165691442",
"0 685701683 334764463 1001631935",
"1 1596433536 1911594193 1533322508",
"0 128647261 372955025 1051296077",
"0 946946329 548039713 83591687",
"1 1490995704 1541151932 2052868342",
"0 805037508 405134691 593191395",
"1 2048614262 1171142414 1309623012",
"1 1024870244 1791074791 1778846631",
"1 1403452711 2033486235 1555085078",
"0 900806815 269954427 806033528",
"1 1598931622 938905156 1474311731",
"1 1468418323 749319445 2060324871",
"0 407246582 393808982 163347811",
"0 52629967 643176802 619367349"}

Returns: { 1,  2,  3 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WordNumber

Math

Used in:

SRM 267

Used as:

Division II Level Three

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3488

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8000&pm=3488

Problem Statement

It is possible to number all the words that could be formed from a specified alphabet. One way to do it is to put the words in order based on length, with words of common length ordered alphabetically. Using this scheme, if we use the alphabet consisting of just the 3 letters 'a', 'b', and 'c' then the words are numbered:

   1:a 2:b 3:c 4:aa 5:ab 6:ac 7:ba 8:bb   etc.

There are an infinite number of possible words, but each has its own positive number.

We want to be able to find the word that corresponds to any given number. Create a class WordNumber that contains a method theWord that is given alpha, the number of letters in the alphabet, and n, the number of a word. It returns the String that is the word corresponding to n.

The alphabet to be used is the first alpha letters of the normal lowercase alphabet, with their usual alphabetical ordering.

Definition

Class:	WordNumber
Method:	theWord
Parameters:	int, int
Returns:	String
Method signature:	String theWord(int alpha, int n)
(be sure your method is public)

Constraints

-

alpha will be between 2 and 26, inclusive.

-

n will be between 1 and 2,000,000,000, inclusive.

Examples

0)

Returns: "ab"

See the table above.

1)

Returns: "aaa"

Extending the table above, we find that word 12 is "cc" so the next word, word 13, must be the first 3 letter word.

2)

2000000000

Returns: "flhomvx"

3)

Returns: "qn"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TestScores

Advanced Math, Dynamic Programming

Used in:

SRM 226

Used as:

Division I Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3486

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6515&pm=3486

Problem Statement

Many types of standardized testing award each test taker a score that is based on how an individual performs when compared to the rest of the population. This is done, in part, to correct for inherent differences in the level of difficulty of different tests, and to make the score values more meaningful. For instance, saying that someone has an IQ of 130 (where the score is based upon 100 being "average") is more useful that simply saying that someone correctly answered 25 out of 40 questions on "Joe's Intelligence Test".

Standardized scoring typically utilizes two common statistical tools: mean and standard deviation. "Mean" is commonly called the average. Mean is calculated by summing all scores, and dividing by the total number of scores.

Standard deviation is calculated in a multi-step process.

First, let m = the mean.
Then, for each score, x, calculate the square of its deviation from the mean, (x - m) ^ 2.
Sum the individual squares, and divide by the total number of scores.
Finally, take the square root of that result.

Once these figures are calculated, a raw score can be converted to a standardized score by determining how many standard deviations above or below the mean raw score is. A point value is then assigned to the mean and standard deviation. For instance, some intelligence tests have a mean score of 100 points, and a standard deviation of 15 points.

You have been assigned the task of writing a program that will calculate the standardized score for an individual, given their raw score (number of questions correct). Specifically, it has been explained to you that 1000 points is the average score, and each standard deviation is 300 points. Thus, if an individual's raw score is 1.5 standard deviations above average, their standardized score would be 1450 points.

The test in question has already been administered to a sufficiently large set of testers. Unfortunately, the raw scores of each test individual have been lost. However, a summary of the results, namely the percentage of individuals who correctly answered each question, is still available, and you have been told that this will suffice to determine the mean and standard deviation of the original data set. Since the set of testers was very large, you can assume that the percentage of people who got a question correct represents the probability of any given person correctly answering that question.

You are given a double[] questions, where each element of questions indicates the percentage of individuals who correctly answered that question. You are also given an int testScore indicating the number of questions correctly answered by a new test subject. Using the scoring methodology explained above, you are to return a double indicating the standardized score that should be awarded to this individual.

Definition

Class:	TestScores
Method:	weightedScore
Parameters:	double[], int
Returns:	double
Method signature:	double weightedScore(double[] questions, int testScore)
(be sure your method is public)

Notes

-

The return value must be within 1e-09 absolute or relative error of the correct answer.

-

You may assume that percentages of correct responses for each question are based upon an indefinitely large set of test data.

-

For those familiar with typical statistical terminology, note here that we are using a "population standard deviation", since it is assumed that we are dealing with a sufficiently large set of test data.

Constraints

-

questions will contain between 1 and 50 elements, inclusive.

-

Each element of questions will be between 0.001 and 0.999, inclusive.

-

testScore will be between 0 and n, inclusive, where n is the number of questions.

Examples

0)

{0.5, 0.5}

Returns: 1000.0

This is a simple case, since the average score is 1, a raw score of 1 is a standardized score of 1000.

1)

{0.5, 0.5, 0.5}

Returns: 1519.6152422706632

Out of 8 test takers, 1 will get no questions correct, 3 will get 1 question correct, 3 will get 2 questions, and 1 will get all 3. We calculate a mean of 1.5, and a standard deviation of Sqrt(3)/2 = 0.866025.

A score of 3 is 1.5 above the mean, which is 1.73205 * SD. We can then calculate the standardized score.

2)

{0.2, 0.3, 0.4}

Returns: 1806.6323435772447

With harder questions, scores will tend to be lower (mean score is now 0.9), and a perfect score is weighted higher.

3)

{0.2, 0.3, 0.4}

Returns: 654.3004241811809

Same questions as above, but notice here that because of the expected low scores, even getting no questions correct doesn't get too low of a standardized score.

4)

{0.9, 0.9, 0.9, 0.9}

Returns: -800.0

On a fairly easy test, notice that it's possible to score below zero.

5)

{ 0.956062, 0.592855, 0.405804,
  0.484474, 0.633413, 0.219248,
  0.801282, 0.724066, 0.886559,
  0.794041, 0.324220 }

Returns: 1037.5680868214772

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AutoAdjust

Brute Force, Simple Math

Used in:

TCCC05 Round 3

Used as:

Division I Level One

Writer:

lars2520

Testers:

PabloGilberto , lbackstrom , Yarin , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3483

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6530&pm=3483

Problem Statement

Most image editing programs have the ability to adjust an image's brightness and contrast. When adjusting the brightness of an image, an integer value is either added or subtracted from the color value of each pixel. When adjusting the contrast of an image, the color value of grey is first subtracted from the color value of each pixel, then the color value is multiplied by an integer and divided by 100, and finally the value of grey is added back to the color value. When adjusting both brightness and contrast, the brightness is adjusted first, and then the contrast is adjusted. If, after applying either adjustment, the color value of a pixel is below the minimum color value or above the maximum color value, then the color value for that pixel is set at the minimum or maximum, respectively (32 and 95 in this problem).

In this problem, we will consider a greyscale image, where each pixel is represented by an ASCII character between 32 and 95, inclusive. Grey is indicated by 63.5 (hence no pixel is exactly grey). Your task is to adjust the brightness and contrast of an image so that the darkest pixels in the image are black (32), and the brightest pixels in the image are white (95). To do this, you may adjust the brightness by any integer value between -100 and 100, inclusive, and you may adjust the contrast by any integer value between 100 and 20,000, inclusive. When a pixel's value is not an integer after the adjustment, round its value to the nearest integer (0.5 rounds up). To prevent loss of detail, you should adjust the brightness and contrast in such a way that the contrast is adjusted as little as possible. If there are multiple ways to do this with the minimum contrast adjustment, you should pick the one with the smallest absolute brightness adjustment. You should return a String[] representing the adjusted image.

Definition

Class:	AutoAdjust
Method:	adjust
Parameters:	String[]
Returns:	String[]
Method signature:	String[] adjust(String[] image)
(be sure your method is public)

Notes

- There will always be a way to perform the adjustment.

Constraints

- image will contain between 1 and 50 elements, inclusive.

- Each element of image will contain between 1 and 50 characters, inclusive.

- Each element of image will contain the same number of characters.

- There will be at least two different color values in image.

- Each character in image will have ASCII value between 32 and 95, inclusive.

Examples

0)

{"------------",
 "--TTT--CCC--",
 "---T---C----",
 "---T---CCC--",
 "------------"}

Returns: 
{ "            ",
 "  ___  CCC  ",
 "   _   C    ",
 "   _   CCC  ",
 "            " }

'-', 'C', and 'T' have ASCII values of 45, 67, and 84, respectively. By decreasing the brightness by 1, and then adjusting the contrast by 159, these three values are transformed as follows:

(45 - 1 - 63.5) * 159 / 100 + 63.5 = 32.495
(67 - 1 - 63.5) * 159 / 100 + 63.5 = 67.475
(84 - 1 - 63.5) * 159 / 100 + 63.5 = 94.505

Rounding these values, we get 32, 67 and 95.

1)

{"            ",
 "  ___  CCC  ",
 "   _   C    ",
 "   _   CCC  ",
 "            "}

Returns: 
{ "            ",
 "  ___  CCC  ",
 "   _   C    ",
 "   _   CCC  ",
 "            " }

The minimum and maximum values are already 32 and 95, so nothing needs to be done (brightness = 0, contrast = 100).

2)

{"AB"}

Returns: { " _" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Fairness

Simple Math, Sorting

Used in:

TCCC05 Qual 1

Used as:

Division I Level One

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3477

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6523&pm=3477

Problem Statement

Why should the alphabetic ordering of names put so much emphasis on the first letter in each name? In the spirit of fairness to all the letters in a name, let's compute the average alphabetical position of the letters in each name, and order the names accordingly.

We can define the "value" of a name to be the average position of the letters in that name, counting an 'A' as 1, 'B' as 2, and so on up to 'Z' as 26. So, for example, the value of "BOB" would be (2+15+2)/3 = 6.3333. When given a list of names, we will order them by putting them in order of increasing value. When 2 or more names have exactly the same value, we will break the tie by placing the names that were earlier on the original list earlier on the ordered list.

Create a class Fairness that contains a method fairSort that is given a String[] names and that returns a String[] containing the same names sorted according to the above method. The elements in the return should, of course, not contain any leading or trailing spaces.

Definition

Class:	Fairness
Method:	fairSort
Parameters:	String[]
Returns:	String[]
Method signature:	String[] fairSort(String[] names)
(be sure your method is public)

Constraints

-

names will contain between 1 and 50 elements inclusive.

-

Each element of names will contain between 1 and 20 characters inclusive.

-

Each character in each element of names will be an uppercase letter, 'A'-'Z'.

Examples

0)

{"BOB","AAAAAAA","TOM"}

Returns: { "AAAAAAA",  "BOB",  "TOM" }

BOB = 6.333, AAAAAAA = 1.0, TOM = 16

1)

{"ABE","ABLE","ABE"}

Returns: { "ABE",  "ABE",  "ABLE" }

2)

{"PANE","TOM","BONE","AAAA"}

Returns: { "AAAA",  "PANE",  "BONE",  "TOM" }

PANE and BONE are tied, and since PANE comes before BONE in the given list, it must come before BONE in the sorted list.

3)

{"BONE","TOM","PANE","AAAA"}

Returns: { "AAAA",  "BONE",  "PANE",  "TOM" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PrimeAnagrams

Brute Force, Simple Math

Used in:

SRM 223

Used as:

Division I Level Two , Division II Level Three

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3458

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5869&pm=3458

Problem Statement

You will be given a string of digits that supposedly come from three prime numbers. The digits will be given in a random order. Your task is to find the three prime numbers, if they exist. If there are three such primes, return them sorted least to greatest. If there is more than one possible set of three primes, return the set with the smallest product. If there is no such set, return { }.

For example, the five digits of the primes 5, 13, and 19 could be given to you as "39151". There are several other sets of prime numbers that could also be rearranged to give this input, for example { 5, 31, 19 } and { 3, 11, 59 }. The set with the smallest product is { 5, 13, 19 }, so those are the three primes your method should return.

Each digit of each prime will be present in the input. For example, if the input contains exactly two occurrences of the digit "1" (as in the example above), you must use the digit "1" exactly twice.

Any zeros in the input may not be used as leading zeros in any of the three primes.

Definition

Class:	PrimeAnagrams
Method:	primes
Parameters:	String
Returns:	int[]
Method signature:	int[] primes(String anagram)
(be sure your method is public)

Notes

-

If you find two sets of primes with the same product, you have made a startling discovery!

Constraints

-

anagram will contain between 3 and 8 characters, inclusive.

-

Each character of anagram will be a digit.

Examples

0)

"39151"

Returns: { 5,  13,  19 }

This is the example from the problem statement.

1)

"921179"

Returns: { 2,  17,  199 }

2)

"01123"

Returns: { 2,  3,  101 }

The input may have a leading zero, but the primes may not. {2, 3, 011} is not a valid answer.

3)

"0707070"

Returns: { }

4)

"222"

Returns: { 2,  2,  2 }

5)

"123"

Returns: { }

1 is not prime.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ArithSeq

Math

Used in:

SRM 224

Used as:

Division I Level Three

Writer:

vorthys

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3455

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5870&pm=3455

Problem Statement

An arithmetic sequence of length n is a sequence of n numbers in which the difference between each pair of adjacent numbers is some constant delta. For example, the sequence 1,6,11,16 is an arithmetic sequence of length 4 with delta=5. Now, consider the infinite set

    { 1, 3, 4, 7, 8, 9, ... }

This set is of particular interest to mathematicians because it contains arbitrarily long arithmetic sequences for any delta, yet it contains no infinitely long arithmetic sequences. The set is contructed by keeping or dropping successive groups of positive integers according to the following pattern: keep one (1), drop one (2), keep two (3,4), drop two (5,6), keep three (7,8,9), drop three (10,11,12), and so on.

Given n and delta, your task is to find the earliest arithmetic sequence contained in the set that has the given length and delta. In other words, you should find the smallest number A such that all integers of the form A+i*delta are in the set, for all i between 0 and n-1, inclusive. You should return A.

Definition

Class:	ArithSeq
Method:	minStart
Parameters:	int, int
Returns:	long
Method signature:	long minStart(int n, int delta)
(be sure your method is public)

Constraints

-

n is between 2 and 30, inclusive.

-

delta is between 1 and 100000000, inclusive.

Examples

0)

Returns: 1

The sequence is 1, 4, 7.

1)

Returns: 9

2)

Returns: 3661

3)

Returns: 1001001

4)

100000000

Returns: 670380219057

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OneArmedBandit

Math, Simulation

Used in:

SRM 226

Used as:

Division I Level Two

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3443

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6515&pm=3443

Problem Statement

You are at the local casino, and notice that the slot machines are set up with a progressive jackpot that continues to grow until someone wins it. Being mathematically-minded, you decide that you will only play the slot machine when the progressive jackpot is high enough that the overall odds are in your favor. In other words, when the expected payout rate is greater than the cost of playing.

Being meticulous, you have taken note of the payoff table for non-jackpot payouts, and have likewise noted the symbols that must line up in order to win the jackpot. Additionally, you have observed many players, and through careful record keeping, have determined the order of the symbols appearing on each on the wheels on the slot machine. It has also been your observation that each wheel appears to operate independently, and has an equal chance of stopping at any given location.

You are given a String[], wheels, where each element of wheels represents the symbols that appear on a wheel of the slot machine. Each character of each element of wheels indicates a single symbol on that wheel. Each symbol is denoted by a capital letter. You are also given a String, jackpotLine, indicating the required symbols to win the jackpot. Finally, you are given a String[], payoffTable, indicating the various ways to win a payout. Each element of payoffTable will be in the form "[payoutLine] [payoutAmount]", where [payoutLine] is the required symbols, and [payoutAmount] is an integer with no leading zeros. A '-' character in any of the payout lines or the jackpotLine indicates that any symbol can appear in that position.

You are to return a double indicating the minimum amount of the progressive jackpot that pushes the overall expected payout rate high enough to make the odds favorable. If the jackpot can never be high enough to make the odds favorable, return -1.

Definition

Class:	OneArmedBandit
Method:	progressiveJackpot
Parameters:	String[], String, String[]
Returns:	double
Method signature:	double progressiveJackpot(String[] wheels, String jackpotLine, String[] payoffTable)
(be sure your method is public)

Notes

-

In this example, the slot machine has only a single payout line, and you play only a single coin at a time.

-

The slot machine is set up so that all wheels are equally likely to land on any location.

-

If the symbols line up in such a way that more than one payout line applies, then all applicable payouts are awarded.

Constraints

-

wheels will contain between 1 and 10 elements, inclusive.

-

Each element of wheels will contain between 1 and 50 'A'-'Z' characters, inclusive.

-

Each element of wheels must have the same number of characters.

-

The character length of jackpotLine will be equal to the number of elements in wheels.

-

Each character of jackpotLine will be 'A'-'Z', or a dash ('-').

-

payoffTable will contain between 0 and 50 elements, inclusive.

-

Each element of payoffTable will be of the form "[payoutLine] [payoutAmount]".

-

The character length of [payoutLine] will be equal to the number of elements in wheels.

-

Each character of [payoutLine] will be 'A'-'Z', or a dash ('-').

-

Each value of [payoutAmount] will represent an integer between 1 and 999999, inclusive, with no leading zeros.

-

The expected payout from payoffTable will not be within 1e-6 of 1.

Examples

0)

{"ABC", "ABC", "ABC"}

"AAA"

{"BBB 5", "CCC 2"}

Returns: 20.0

This is a very simple slot machine with three distinct symbols on each of three wheels.

The chances of any particular symbol appearing on a specific wheel are 1/3, and hence the chances of any particular line appearing are 1/27.

So, the expected payout for the two non-jackpot lines are 5/27 and 2/27, totally 7/27. Our jackpot line needs an expected payout of 20/27 for our total expected payout to let us break even.

Using the equation for expected outcome gives us:

expected = probability * payout
=> payout = expected / probability

Solving, we need a payout of at least 20 to break even.

1)

{"ABC", "ABC", "ABC"}

"AAA"

{"AAB 4", "AA- 3", "AB- 2"}

Returns: 8.0

We're on the same slot machine, but with a different payout configuration that utilizes the wildcard slot. Here, the probabilities for each of the payout lines are 1/27, 1/9, and 1/9. So, the expected gains are 4/27, 3/9, and 2/9, totalling 19/27. Thus, the jackpot line must have an expected payoff of 8/27. Solving, like above, we need the jackpot to be at least 8.

2)

{"ABC", "ABC", "ABC"}

"AAA"

{"AA- 5", "A-- 2"}

Returns: 0.0

Here we have an interesting scenario, where the machine actually pays out, on average, more than what is put into it, without even considering the big jackpot. So, we don't care what the progressive jackpot is up to.

3)

{"ABC", "ABC", "BBC"}

"AAA"

{"AAB 4", "AA- 3", "AB- 2"}

Returns: -1.0

The casino that is running this machine looks a little shady, since it's not even possible to win the jackpot at all. Therefore, it's never statistically a good idea to play this machine.

4)

{"DABCDBCDCD", "BCDBDACDCD", "DCDADBCDBC", "DBDCABCDCD"}

"AAAA"

{}

Returns: 10000.0

This particular machine is all or nothing. With 10 symbols on each of 4 wheels, you have a 1 in 10,000 chance of hitting the big jackpot.

5)

{"DABCDBCDCD", "BCDBDACDCD", "DCDADBCDBC", "DBDCABCDCD"}

"AAAA"

{"AAAE 20"}

Returns: 10000.0

Here, the only non-jackpot payout is impossible (this is a shady casino!), so this is, in effect, the same as the above example.

6)

{"KACACEIBGCVDAKMACAAW",
 "CECMBDBJCLHFNDCBDDNB",
 "BYAGBJFDAGBHEGEFVXDR",
 "UDWFABFAHDXACICQHAEH",
 "EBHOCHABAHBDAUBZHHAB"}

"KJ--Z"

{"Z-U-U 23",
 "YUBSA 142",
 "Q-AN- 92",
 "ZA-CX 133",
 "-BE-Z 125"}

Returns: 3500.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

KingOfTheCourt

Advanced Math, Simulation, Sorting

Used in:

SRM 222

Used as:

Division I Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3440

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5868&pm=3440

Problem Statement

You and several friends are playing a tennis game called king of the court. The idea behind the game is that one person is the "king of the court", and each of the other players, in turn, tries to win two points before the king wins one point. An opponent who successfully scores two points without allowing the king to score becomes the new king of the court; otherwise, he returns to the back of the line to wait to play again. When the king is defeated, the winner becomes the new king, and the king returns to the back of the line. A player is declared the winner when he or she has been the king and consecutively defeated each of the other opponents.

You are given a int[] ability, where each element of ability is the relative skill level of each given player. The first element of ability refers to the player who is king initially. The remaining players are lined up to play, in the same order that they appear in ability.

On any given turn, the probability that a player A will win the point against player B is based upon their relative skill level. Thus, if two players have skill levels A and B, the probability that the first player will win the point (regardless of who is king) is A/(A+B).

You are to return a double indicating the probability that the player who is king initially will go on to win the game.

Definition

Class:	KingOfTheCourt
Method:	chancesOfWinning
Parameters:	int[]
Returns:	double
Method signature:	double chancesOfWinning(int[] ability)
(be sure your method is public)

Notes

-

At the start of the game, the king has not yet defeated any opponents.

-

Your return must have an absolute or relative error less than 1e-9.

Constraints

-

ability will contain between 2 and 7 elements, inclusive.

-

Each element of ability will be between 1 and 99, inclusive.

Examples

0)

{ 1, 1 }

Returns: 0.8

Here, it is just you and a friend of the same ability. So, on any given point either of you has a 50% chance of winning. Thus, on each round, whoever is king has 75% odds, and the non-king has 25% odds.

Thus, there is a 75% chance you win the game on the first round, or a 25% chance that you go to another round, at which point there's a 25% chance of you once again becoming king. This suggests the following equation, where p is the probability that you win the game:

p = .75p + .25 * .25p

Solving, we get p = 80%

1)

{ 2, 1 }

Returns: 0.9350649350649349

Here, you are twice as good as your friend, so the chances of you winning a round as king are 8/9. Your chances of winning while not king are 4/9. In an equation similar to above:

p = (8/9) * p + (1/9) * (4/9) * p

Solving, we get p = 72 / 77

2)

{ 1, 2 }

Returns: 0.5844155844155844

Here, your friend is better than you. But, starting as king gives you some advantage.

p = (5/9) * p + (4/9) * (1/9) * p

Solving, we get p = 45 / 77

3)

{ 1, 1, 1, 1 }

Returns: 0.5065812082824602

Now it's you with three other friends. Note that even though you're all of equal ability, starting as king provides a serious advantage.

4)

{ 47, 82, 65, 99, 2, 14, 9 }

Returns: 0.22734781036506918

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

YahtzeeRoll

Advanced Math, Brute Force, Simulation

Used in:

SRM 222

Used as:

Division II Level Three

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3439

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5868&pm=3439

Problem Statement

The game of Yahtzee is a popular dice game in which players roll 5 dice, and may (optionally) re-roll some or all of the dice on two further rolls. After all three rolls, the best "hand" that can created from the values showing on all of the dice is scored, and the player is awarded points. There are several different types of hands, and a player may only get points for each type of hand once per game.

You are playing Yahtzee, and have taken two of your three rolls. The values showing on the five dice are given in the int[] dice. Based upon the empty slots still available on your score card, and the values showing on the dice, you want to know which dice to re-roll in order to obtain the highest possible expected point outcome. Remember that, statistically speaking, your expected outcome is the probability of an event taking place multiplied by the payoff (in this case, points earned) by that event.

Looking over your scorecard, you realize that the only four remaining items are full house (three of a kind and two of a kind), worth 25 points, small straight (4 consecutive values, no wrapping), worth 30 points, large straight (all five dice are consecutive values), worth 40 points, and Yahtzee (all five dice show the same value), worth 50 points.

You are to return a double indicating the expected score outcome when the player optimally chooses which dice to re-roll.

Definition

Class:	YahtzeeRoll
Method:	bestChoice
Parameters:	int[]
Returns:	double
Method signature:	double bestChoice(int[] dice)
(be sure your method is public)

Notes

-

The game of Yahtzee uses standard, six-sided dice, with values 1 through 6.

-

Although Yahtzee includes many different ways to score points, it is assumed for this problem that the four hands described in the problem are the only ones available.

-

If the dice form a large straight, 40 points are scored. Even though the hand technically also could be used as a small straight, no additional points are scored for the small straight.

-

For both small and large straights, the values do not wrap; so, 5,6,1,2 is not a small straight.

-

Your return must have an absolute or relative error less than 1e-9.

Constraints

-

dice will contain exactly five elements.

-

Each element of dice will be between 1 and 6, inclusive.

Examples

0)

{ 1, 1, 1, 1, 2 }

Returns: 8.333333333333334

Here, keeping all of your 1's and re-rolling the 2 gives you a 1/6 chance of scoring 50 points. Alternately, keeping the 2 and re-rolling one of your 1's gives you a 1/6 chance in scoring 25 points for the full house. Thus, the best option is to go for the Yahtzee. The probability of 1/6 multiplied by 50 points gives the expected 8.333 points.

1)

{ 1, 1, 1, 2, 2 }

Returns: 25.0

Here, you already have a full house. Re-rolling anything is risky when keeping what you have is a guaranteed 25 points.

2)

{ 2, 3, 4, 5, 5 }

Returns: 33.333333333333336

Here, we already have ourselves a small straight, but by re-rolling one of the 5's, we have a chance at a large straight if we roll either a 1 or a 6. So, we have a 1/3 chance of scoring 40 points, or a 2/3 chance of keeping our 30 points. (1/3) * 40 + (2/3) * 30 = 33.333.

3)

{ 2, 2, 3, 4, 4 }

Returns: 17.77777777777778

At first glance, it might seem like re-rolling our 3 and going for a full house is the safest best. This is a 1/3 chance of scoring 25 points = 8.333 expected points. But, if we keep (2, 3, 4) and re-roll the other two, we actually have a 1/9 chance of making a large straight, and a 4/9 chance of making a small straight. (1/9) * 40 + (4/9) * 30 = 160/9 = 17.778 expected points, which is a much better choice.

4)

{ 6, 1, 3, 5, 5 }

Returns: 9.722222222222221

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NthFraction

Advanced Math, Sorting

Used in:

TCCC05 Round 2

Used as:

Division I Level Two

Writer:

lars2520

Testers:

PabloGilberto , Yarin , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3436

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6529&pm=3436

Problem Statement

Given an int, bound, consider the infinite set of all reduced fractions whose numerator is a positive integer and whose denominator is a positive integer less than or equal to bound. Now, find the N^th smallest (indexed from 1) fraction and return it as a String in the form "a/b", with no leading zeros in either integer. See example 0 for further clarifications.

Definition

Class:	NthFraction
Method:	getFraction
Parameters:	int, int
Returns:	String
Method signature:	String getFraction(int N, int bound)
(be sure your method is public)

Notes

- A reduced fraction is one of the form a/b for which there is no integer g > 1 such that both a and b are divisible by g.

Constraints

- N will be between 1 and 2,000,000,000, inclusive.

- bound will be between 1 and 1000, inclusive.

Examples

0)

Returns: "4/3"

The ordered set of fractions is

{1/3, 1/2, 2/3, 1/1, 4/3, 3/2, 5/3, ...}

1)

Returns: "18/55"

2)

Returns: "1/1000"

3)

Returns: "1000000/1"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WaiterTipping

Simple Math, String Parsing

Used in:

SRM 219

Used as:

Division II Level One

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3111

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5865&pm=3111

Problem Statement

You have just finished eating your Chinese food, and the waiter has brought you the bill. You note the untaxed total on the bill, given as an int in total. Additionally, you know the tax rate in your locale, given as an int in taxPercent. Lastly, you have counted how much money you have, given as an int in money.

Since you feel the service was excellent, you want to give as large a tip as you can afford. You are to return the largest integral value of tip such that:

total + floor(total*taxPercent/100) + floor(total*tip/100) <= money

If there is no non-negative value of tip that satisfies the above inequality, return -1 (you don't have enough money to pay the bill and tax).

Definition

Class:	WaiterTipping
Method:	maxPercent
Parameters:	int, int, int
Returns:	int
Method signature:	int maxPercent(int total, int taxPercent, int money)
(be sure your method is public)

Notes

-

total and money are given in cents

-

Although certainly unusual, it is perfectly permissible to leave a tip that is larger than the original bill.

Constraints

-

total and money will be between between 100 and 100000, inclusive.

-

taxPercent will be between 0 and 100, inclusive.

Examples

0)

Returns: 10

Here, you pay 500 for the bill and 50 for tax, leaving you 50 for the tip, which is 10% of the original bill total.

1)

Returns: 10

Similar to above, but here you have 54 cents for tip, but this will still only get you 10%.

2)

Returns: -1

Uh-oh, looks like you don't have enough money!

3)

Returns: 111

226 + floor(226*48/100) + floor(226*111/100) =

226 + floor(10848/100) + floor(25086/100) =

226 + 108 + 250 =

584

4)

Returns: 415

123 + floor(123*52/100) + floor(123*415/100) =

123 + floor(6396/100) + floor(51045/100) =

123 + 63 + 510 =

696

5)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FolderSize

Simple Math, Simple Search, Iteration

Used in:

SRM 218

Used as:

Division I Level One , Division II Level Two

Writer:

timmac

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3102

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5864&pm=3102

Problem Statement

When files are stored on disk, typically they are stored in "clusters". Each cluster has a fixed size, and the amount of space consumed by a file is always a multiple of the cluster size. Thus, if the cluster size is 100 bytes, a 165 byte file will actually use 200 bytes of storage, resulting in 35 bytes of wasted space.

We want to determine which areas of our disk storage are wasting the most space. You will be given a String[] files, each element of which contains a folder number followed by a space, followed by a file size. You will also be given an int folderCount indicating the total number of folders on our disk. The folders are numbered 0 through folderCount - 1. Finally, you will be given an int clusterSize, indicating how large each disk cluster is.

You are to return a int[], containing exactly folderCount elements, each element of which is the total amount of wasted space for that folder. Each element of the return value corresponds to the folder with the same index.

Definition

Class:	FolderSize
Method:	calculateWaste
Parameters:	String[], int, int
Returns:	int[]
Method signature:	int[] calculateWaste(String[] files, int folderCount, int clusterSize)
(be sure your method is public)

Notes

-

While many systems use a cluster size that is a power of two, no such restriction exists here.

-

There may be folders that have no files in them. (Wasted space for such a folder is 0.)

Constraints

-

clusterSize will be between 1 and 1000000, inclusive

-

folderCount will be between 1 and 50, inclusive

-

files will contain between 0 and 50 elements, inclusive

-

Each element of files will contain between 3 and 50 characters, inclusive

-

Each element of files will be in the form "<folder> <size>" (quotes added for clarity)

-

Each value of <folder> will be between 0 and folderCount - 1, inclusive

-

Each value of <size> will be between 0 and 1000000, inclusive

-

<folder> and <size> may contain leading zeros

Examples

0)

{"0 55", "0 47", "1 86"}

Returns: { 48,  14,  0 }

Here, in folder 0, we have two files. The first requires 2 clusters, and wastes 45 bytes, the second uses 1 cluster and only wastes 3 bytes. The waste for folder 0 is 48 bytes. Folder 1 only has a single file, which wastes 14 bytes. Folder 2 has no files in it, and thus wastes 0 bytes.

1)

{"0 123", "2 456", "4 789", "6 012", "8 345"}

Returns: { 73,  0,  34,  0,  93,  0,  86,  0,  47,  0 }

Note here that we can use a leading zero in the file size, and that only every other folder even has a file in it.

2)

{}

Returns: { 0,  0,  0,  0,  0 }

The cluster size really doesn't matter since our disk is empty.

3)

{"0 93842", "1 493784", "2 43212", "3 99327", "4 456209",
"5 947243", "6 59348", "7 58237", "8 5834", "9 492384",
"0 58342", "3 538432", "6 1432", "9 453983", "2 4321",
"4 583729", "6 6974", "8 9864", "4 43211", "8 38437"}

Returns: { 27696,  886,  19922,  14306,  18616,  19612,  44671,  9218,  35805,  20488 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ImageSteganography

Encryption/Compression, Simple Math, String Manipulation

Used in:

SRM 225

Used as:

Division II Level Three

Writer:

Kawigi

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3094

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5871&pm=3094

Problem Statement

Steganography is a method of cryptography where a message or entire document can be hidden inside of another file or image which shows no evidence that there is data hidden in it. Typically, the message or document to be sent is first encrypted and compressed, and then combined with an existing file in the bits that are less significant.

For example, the encrypted, compressed file could be combined with a bitmap image, and each byte of the file could be encrypted into the lowest two bits of 4 pixel values. The result would be that there is a 1/4 chance that a given pixel is completely unchanged, and a 3/4 chance that it is changed, but by such a small amount that it is essentially undetectable.

While it is not as secure or efficient, you could quite easily encrypt a message into a bitmap image with no encryption or compression, and your message would be protected by the fact that the image has no distinguishable traits that suggest that a message is hidden in it. You will be given an "image" and you will encode a given message into it and return the new image. The returned image should be in the same format as the original image.

The image will be in the format of a String[] where each three digits represent a number from 0 to 255, inclusive (leading zeros will be added as necessary), which is a pixel value in the image. You will also be given a String, message which contains the message you would like to encode into the image. You will first encode the message into numbers representing the characters in the message - spaces will be 0, 'A'-'Z' will be 1-26, 'a'-'z' will be 27-52, '0'-'9' will be 53-62, and 63 will be used for any space after the message. All these numbers can be represented in binary with 6 digits. You will put each pair of bits (representing a number between 0 and 3) into the lowest two bits of the values in the image. For each character, you will put in the lowest two bits, then the middle two, then the highest two, and then continue to the next character. You will put them in the lowest two bits of the first pixel on the first row, then the second pixel on the first row, and so on until you get to the end of the first row, then the first pixel on the second row, and so on. Once you are out of characters, continue substituting the lowest two bits of each pixel value as if the current character were represented by number 63.

Definition

Class:	ImageSteganography
Method:	encode
Parameters:	String[], String
Returns:	String[]
Method signature:	String[] encode(String[] image, String message)
(be sure your method is public)

Notes

-

The number of pixels in image may not be a multiple of 3, but you should continue inserting the message as if there was room to finish the last character.

Constraints

-

image will have between 1 and 50 elements, inclusive.

-

The number of characters in each element of image will be a multiple of 3 between 3 and 48, inclusive.

-

message will have between 1 and 50 characters, inclusive.

-

There will be enough room in image to encode message.

-

Each element of image will be made up of 3-digit numbers between 0 and 255, inclusive, padded with zeros if necessary.

-

The characters in message will be spaces, numbers, and upper- and lower-case letters.

Examples

0)

{"255123212001201222"}

"hi"

Returns: { "254120214003200222" }

This single-pixel-thick image is still big enough to encode this message.

1)

{"255123212","001201222"}

"hi"

Returns: { "254120214",  "003200222" }

Same message, but with the second letter on a different row.

2)

{"123234213001023213123145",
 "222111121101213198009",
 "121122123124125",
 "132212093039",
 "213110"}

 "Hello 1"

Returns: 
{ "120234212003023213122145",
 "222110121102213198010",
 "120120120126125",
 "135215095039",
 "215111" }

Notice that the image doesn't strictly need to be rectangular, letters from the message might need to wrap to multiple lines, and the whole image may not have a multiple of 3 "pixels".

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CubeSum

Math

Used in:

TCO04 Wildcard

Used as:

Division I Level One

Writer:

lars2520

Testers:

PabloGilberto , Yarin , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3083

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5885&pm=3083

Problem Statement

Given an int, N, return the number of ways to represent N as the sum of 4 non-negative perfect cubes. Do not count different permutations of the same 4 cubes more than once. For example, (0,0,0,1) is the same as (1,0,0,0).

Definition

Class:	CubeSum
Method:	count
Parameters:	int
Returns:	int
Method signature:	int count(int N)
(be sure your method is public)

Constraints

-

N will be between 1 and 100,000,000, inclusive.

Examples

0)

Returns: 1

Keep in mind that 0 is a perfect cube so 1 can be represented as 0+0+0+1

1)

Returns: 1

1+1+1+1 = 4

2)

Returns: 4

0     + 1     + 7*7*7*   + 12*12*12 = 0  + 1   + 343  + 1728 = 2072
0     + 7*7*7 + 9*9*9    + 10*10*10 = 0  + 343 + 729  + 1000 = 2072
2*2*2 + 4*4*4 + 10*10*10 + 10*10*10 = 8  + 64  + 1000 + 1000 = 2072
4*4*4 + 4*4*4 + 6*6*6    + 12*12*12 = 64 + 64  + 216  + 1728 = 2072

3)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RearrangeFurniture

Greedy, Math

Used in:

SRM 220

Used as:

Division I Level Three

Writer:

Kawigi

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3076

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5866&pm=3076

Problem Statement

Kawigi's furniture is all in the wrong places in his new apartment. He needs to move all of it into the appropriate spots. The problem is that he has so much furniture and very limited room to move it in. Because of this, the only action he can take to rearrange his furniture is to swap two pieces of furniture.

He would like to exert as little physical effort as possible in doing this task, where the effort of swapping two pieces of furniture is defined as the sum of the weights of the two objects to be swapped. You need to figure out what the minimum effort required to put all of the furniture in the correct places.

You will be given two int[]s, the first is the weights of each piece of furniture (element 0 of the int[] will be the weight of furniture 0, element 1 will be the weight of furniture 1, etc). The second int[] is the location where each piece of furniture is supposed to end up (furniture 0 starts out in location 0, furniture 1 starts out in location 1, etc). You are to find and return the minimum cost required to put the furniture in their rightful locations.

Definition

Class:	RearrangeFurniture
Method:	lowestEffort
Parameters:	int[], int[]
Returns:	int
Method signature:	int lowestEffort(int[] weights, int[] finalPositions)
(be sure your method is public)

Constraints

-

weights and finalPositions will each have between 1 and 50 elements.

-

weights and finalPositions will have the same number of elements.

-

finalPositions will have the numbers 0 through n-1 inclusive, exactly once, where n is the number of elements in the array.

-

The elements in weights will be between 1 and 10000.

Examples

0)

{5, 4, 7, 3, 10}

{1, 2, 0, 4, 3}

Returns: 33

One way to do this with the minimum effort is like so:

step 0: {0, 1, 2, 3, 4}

step 1: {0, 2, 1, 3, 4} (cost: 11)

step 2: {1, 2, 0, 3, 4} (cost: 9)

step 3: {1, 2, 0, 4, 3} (cost: 13)

1)

{3, 6, 2, 4, 10, 3}

{0, 1, 2, 3, 4, 5}

Returns: 0

Look at that - no work to be done!

2)

{10, 3, 123, 498, 12, 13, 14, 45, 32, 67,
 111, 234, 543, 2, 12, 1, 56, 67, 78, 89,
 12, 90, 23, 77, 345, 543, 242, 560, 121, 232,
 980, 10000, 12, 1, 6, 98, 67, 44, 21, 456,
 3231, 456, 23, 14, 678, 65, 45, 23, 99, 23}

{49, 48, 47, 46, 45, 44, 43, 42, 41, 40,
 39, 38, 37, 36, 35, 34, 33, 32, 31, 30,
 29, 28, 27, 26, 25, 24, 23, 22, 21, 20,
 19, 18, 17, 16, 15, 14, 13, 12, 11, 10,
 9, 8, 7, 6, 5, 4, 3, 2, 1, 0}

Returns: 20597

On this one, you just have to swap two elements into place 25 times.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TaglishTranslator

String Manipulation, String Parsing

Used in:

SRM 220

Used as:

Division II Level Three

Writer:

Kawigi

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3070

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5866&pm=3070

Problem Statement

Tagalog is one of the major languages spoken in the Philippines. Since the USA occupied the Philippines from 1899 to 1946, it has been the custom of Tagalog-speakers to use English words and conjugate them as if they were Tagalog words, creating a language they call "Taglish".

You are to write an English-Taglish translator that will convert a simple English sentence into a Taglish sentence by conjugating the verb and adjusting the syntax according to Tagalog grammar rules.

The English sentence will come in the format:

	<subject> <verb> (<object>)

The <subject> will be either a single-word name or the word "The" followed by a single-word thing. The <verb> will be a single word, or a word preceded by the word "will". It is in the future tense if it is preceded by the word "will", past tense if the verb ends in the letters "ed", or present tense otherwise. If there is an object, it will be in the format of the subject ("name" or "the thing"), but it also may be preceded by the word "to". Note that "the", "will" or "to", or the suffix "ed" may be in any case or mixed case. If the verb is preceded with the word "will" and ends with "ed", it should be considered future tense.

The returned String will be in the format:

	<re-conjugated verb> <subject> (<object>)

The verb conjugation works as follows:

Past Tense - Put "nag" at the beginning of the word, and remove the "ed" from the end of it.
Present Tense - Double the first syllable and put "nag" at the beginning of the word.
Future Tense - Double the first syllable and put "mag" at the beginning of the word, and remove the word "will" from before the verb.

In the present and future tense, the "first syllable" is defined as any consonants at the beginning of the word followed by exactly one vowel (where a vowel is a upper- or lower-case a, e, i, o, or u and a consonant is any other letter).

If the <subject> in the English sentence is a thing, omit the word "the" in the Taglish sentance and prepend the Tagalog article, "ang" to the subject to form the Taglish subject. If the <subject> is a name, prepend the Tagalog article "si" to the English name.

If there was an object in the English sentence, the <object> in the Taglish sentence is the object from the English sentence preceded by a Tagalog article which depends on the nature of the object:

If the object is a thing and wasn't preceded by the word "to" in the English sentence, it is preceded by the word "ng" in the Taglish sentence (and the word "the" is dropped).
If the object is a name and wasn't preceded by the word "to", it is preceded by the word "ni".
If the object is a thing and was preceded by the word "to", it is preceded by the word "sa" (and the words "to" and "the" are dropped).
If the object is a name and was preceded by the word "to", it is preceded by the word "kay" (and the word "to" is dropped).

Case should be preserved in both the words that are carried over and in any doubling of syllables, but new words or letters added to words should be added in lower-case.

Definition

Class:	TaglishTranslator
Method:	translate
Parameters:	String
Returns:	String
Method signature:	String translate(String sentence)
(be sure your method is public)

Notes

- 'y' is never a vowel in Tagalog.

- The only distinction between a name and a thing is the presence of the word "the".

- Remember that the object may be preceded by two words - "to" and "the". If both are present, the "to" will precede the "the" (as in English).

- Do not change the case of letters in any words. When doubling syllables, use the same case as they were in the existing syllable. When adding other letters or words into the translation, use lower-case letters.

- "To", "the" and "will" will always be "control" words if they appear in the place where they could be used as a "control" word.

Constraints

- sentence will have a valid subject and verb, and will either end with the verb or have a valid object.

- Each word in sentence will have at least one vowel (a, e, i, o, or u).

- sentence will be between 3 and 50 characters in length, inclusive.

- sentence will have between 2 and 7 words, inclusive, delimited by single spaces.

- sentence will contain only upper- and lower-case letters and spaces.

- sentence will not have any leading or trailing spaces.

- sentence will not have any consecutive spaces (words in sentence will be delimited by single spaces).

- The verb in the sentence will not be "ed".

Examples

0)

"The fox jumps to the dog"

Returns: "nagjujumps ang fox sa dog"

These sentences don't allow that many descriptive words.

1)

"tomek codes"

Returns: "nagcocodes si tomek"

Almost as simple of a sentence as we can take.

2)

"tHe mAn plAyEd ThE pIAnO"

Returns: "nagplAy ang mAn ng pIAnO"

Don't forget, control words should be noticed insensitive to case, but case still matters!

3)

"Bob will Filed the taxes"

Returns: "magFiFiled si Bob ng taxes"

"Will" takes preference over "ed".

4)

"Matthew walked to Mathew"

Returns: "nagwalk si Matthew kay Mathew"

5)

"StrongBad kicked TheCheat"

Returns: "nagkick si StrongBad ni TheCheat"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WinningProbability

Advanced Math

Used in:

SRM 218

Used as:

Division I Level Three

Writer:

lars2520

Testers:

PabloGilberto , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3069

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5864&pm=3069

Problem Statement

You favorite sports team is heading into a big playoff series against its big rival. They've gone head to head a number of times previously, and the inputs, prevWins and prevLosses, summarize the results. Now, there are gamesLeft games left in the series, and your team must win at least mustWin of them in order to win the series. You want to know what the probability is that they will accomplish this.

To that end, you've come up with the following strategy. First, you will assume that there is some probability, p, that your team will win each game, and you will assume that each game is independent. For a given value of p, you can thus calculate the probability that your team won and lost as it did in the past. Now, let's say that for a given value of p, p₁, the probability of the previous games turning out as they did is q₁, and similarly for p₂, the probability is q₂. From this, you've decided that the true probability of your team winning a game is (q₁/q₂) times more likely to be p₁ than it is to be p₂. Considering all possible values of p, and taking into account the relative probabilities of each, determine the probability that your team will win the series.

Definition

Class:	WinningProbability
Method:	probability
Parameters:	int, int, int, int
Returns:	double
Method signature:	double probability(int prevWins, int prevLosses, int gamesLeft, int mustWin)
(be sure your method is public)

Notes

-

Your return must have an error of less than 1e-9.

Constraints

-

prevWins and prevLosses will each be between 0 and 100, inclusive.

-

gamesLeft will be between 1 and 15, inclusive.

-

mustWin will be between 1 and gamesLeft, inclusive.

Examples

0)

Returns: 0.75

Consider a few illustrative values of p:

    | prob of  | prob of 
 p  | previous | winning series
----+----------+---------------
0.0 | 0.0      | 0.0
0.1 | 0.01     | 0.1
0.2 | 0.04     | 0.2
0.3 | 0.09     | 0.3
0.4 | 0.16     | 0.4
0.5 | 0.25     | 0.5
0.6 | 0.36     | 0.6
0.7 | 0.49     | 0.7
0.8 | 0.64     | 0.8
0.9 | 0.81     | 0.9
1.0 | 1.0      | 1.0

So, p is 4 times more likely to be 1.0 than it is to be 0.5, and is definitely not 0. Considering only these values of p, and taking a weighted average, we find that the probability of winning the series is 0.786. Clearly, considering only 11 values of p does not yield the required accuracy, but if you consider all possible values, you find that your team has a probability of 0.75 of winning the series.

1)

Returns: 0.0142857142857

After losing the first 3 games of the ALCS, the Red Sox had a probability of less than 2% of winning the series, according to this model.

2)

Returns: 0.9995284409077

Your team only needs to win 1 out of 5 games, and in the past it has won 20/23, so your odds are high.

3)

Returns: 0.0454545454545

Your team has never won in the past, so its unlikely they will this time.

4)

Returns: 0.5

With no previous games, all values of p are equally likely, and as you would expect, there is a 50% chance that your team will win.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Hangman42

Math, Recursion, Simulation

Used in:

SRM 229

Used as:

Division I Level Three

Writer:

AdrianKuegel

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3068

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6518&pm=3068

Problem Statement

"Hangman for two" is a game based on the popular Hangman game. In this version of the game, the computer randomly selects a word from its word database and displays a line of dashes, each of which represents one character of the selected word. Then two players alternately try to find out the selected word.

Each turn, the current player may guess one character. If the character occurs in the word, all occurrences of this character are displayed and the current player may continue guessing, otherwise the other player continues. Whenever the current player thinks he knows the word, he can also guess the word directly instead of guessing a character (but only during his turn). If he is right, the game stops and he has won, otherwise the other player continues with guessing either a character or a word.

Now, two players want to try out this game. As they know the word database the computer uses, they try to use this information to find a strategy for maximizing the probability of winning. They ask you if you can tell them the probability that the starting player wins, if both players use a strategy for maximizing their probability of winning the game.

Definition

Class:	Hangman42
Method:	probability
Parameters:	String[]
Returns:	double
Method signature:	double probability(String[] words)
(be sure your method is public)

Notes

-

You can assume the probability that the computer selects a certain word is 1 / number of words.

-

The probability for winning is the same as the number of words for which the strategy used guarantees a win, divided by the total number of words.

Constraints

-

words contains between 1 and 10 elements, inclusive.

-

Each element of words consists of between 1 and 50 lowercase letters, inclusive.

-

Each element of words contains the same number of characters.

-

All elements of words are distinct.

Examples

0)

{"top","web","cam","buy","now"}

Returns: 0.6

The optimal guess for player 1 is 'w'. If this guess is correct, either "w--" or "--w" is displayed and player 1 can guess again. In both cases it is obvious which word the computer selected, so player 1's guess will guarantee him a win for both possibilities. If the guess is not correct, player 2 can for example guess that the word is "top". If this guess is not right, player 1 can guess one of the two remaining words (for example "cam"). So, player 1's strategy leads to a win if the word was either "web", "cam" or "now". That means his probability of winning is 3/5 = 0.6 .

1)

{"a"}

Returns: 1.0

The smallest word database.

2)

{"ozeexsuaihtuucqghqsjzqzugmaebvdrddyztehr",
"lvjvwhqyeqpapbjusjtxfbcgfbsudrbhpydzryyp",
"cigacdzesqanrlflmsxvhvtvtnzelbzlopcchdob",
"edqogzausmjxzoagpsssxwnmfranrrswjsdgqcqv",
"ptvbnhdcecegnnsofcxaqtizrkwvazfngvzgcsqb",
"guiqkikpwwbzgpvtikaaxxjitqkqfughdlmjtdax",
"gbubcxhxscszrcuzbggjmnzlzihftpmpmaamtxcp",
"tuijqvgvbiwbyjhjmkmmqlmhayvdqhlkpptqqide",
"yidryvjmpbjkdzhmhtoynhbwlbsehcbymltrddsj"}

Returns: 0.8888888888888888

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FractionSplit

Simple Math, Simulation

Used in:

SRM 234

Used as:

Division I Level One , Division II Level Two

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3055

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6533&pm=3055

Problem Statement

Unit fractions are defined by having 1 in the numerator position. Any positive fraction of the form n/d can be rewritten as a finite sum of distinct unit fractions. When n<d, such a sum can be found by repeatedly subtracting the largest possible unit fraction until you reach 0.

For example, if you begin with 4/5 then the largest unit fraction you can subtract is 1/2. You are then left with 3/10. The largest unit fraction you can subtract from 3/10 is 1/4. You are then left with 1/20. The largest unit fraction you can subtract is 1/20 leaving you with 0. You should return a String[] giving the sequence of fractions you subtract, in the order you subtract them. Each should be given in the form "1/q" where q is a positive integer with no leading zeros. In the example just given, you would return

 {"1/2","1/4","1/20"}

Definition

Class:	FractionSplit
Method:	getSum
Parameters:	int, int
Returns:	String[]
Method signature:	String[] getSum(int n, int d)
(be sure your method is public)

Constraints

-

d will be between 2 and 16 inclusive.

-

n will be between 1 and d-1 inclusive.

Examples

0)

Returns: {"1/2", "1/4", "1/20" }

The example above.

1)

Returns: {"1/2", "1/6" }

1/2 is the largest unit fraction that can be subtracted from 2/3. The unit fraction 1/6 remains after the subtraction.

2)

Returns: {"1/2" }

1/2 is the largest unit fraction you can subtract.

3)

Returns: {"1/2", "1/3", "1/10", "1/240" }

4)

Returns: {"1/2", "1/3", "1/10" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SquareLanguage

Math, String Manipulation

Used in:

SRM 238

Used as:

Division I Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3050

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6537&pm=3050

Problem Statement

The problem statement contains superscripts that are viewable in the applet.

Let S be a set of distinct strings. We form the new set S² by collecting all distinct strings of the form xy, where the prefix x is in S, and the suffix y is in S as well. Suppose S is defined as follows:

   S = {aⁱ b^j c^k d^m | la <= i <= ua, lb <= j <= ub, lc <= k <= uc, ld <= m <= ud }

Here aⁱ denotes the letter 'a' repeated i times. For example,

	a³ b² c⁰ d¹ = aaabbd

You will be given l_ and u_ as the first and second elements of _bounds respectively (here _ denotes a, b, c, or d). Return the number of strings in S².

Definition

Class:	SquareLanguage
Method:	howMany
Parameters:	int[], int[], int[], int[]
Returns:	long
Method signature:	long howMany(int[] abounds, int[] bbounds, int[] cbounds, int[] dbounds)
(be sure your method is public)

Notes

-

The set notation T = { x | prop } means that T contains all elements x such that prop is true.

Constraints

-

abounds, bbounds, cbounds and dbounds will each contain exactly 2 elements.

-

In abounds, bbounds, cbounds and dbounds element 0 will not be greater than element 1.

-

In abounds, bbounds, cbounds and dbounds element 0 will be between 0 and 100 inclusive.

-

In abounds, bbounds, cbounds and dbounds element 1 will be between 0 and 100 inclusive.

Examples

0)

{0,100}

{0,0}

{0,0}

{0,0}

Returns: 201

Here there are 201 possible strings. Each one is distinguished by the number of a's it contains.

1)

{0,1}

{0,1}

{0,0}

{0,0}

Returns: 12

The 12 strings in S² are "", "a", "b", "aa", "ab", "ba", "bb", "bab", "aab", "abb", "aba", and "abab".

2)

{1,100}

{10,90}

{20,80}

{30,70}

Returns: 410390615610000

Here there is no danger of duplicates.

3)

{0,20}

{0,30}

{0,40}

{0,47}

Returns: 1641220888605

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FractionCounting

Simple Math

Used in:

TCO06 Qual 4/11/15

Used as:

Division I Level One

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3049

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9900&pm=3049

Problem Statement

Consider the following set (see notes for clarification):

  S = {  p/q  |   w <= p <= x,  y <= q <= z  }

Given w, x, y, and z return the number of distinct elements in S.

Definition

Class:	FractionCounting
Method:	howMany
Parameters:	int, int, int, int
Returns:	int
Method signature:	int howMany(int w, int x, int y, int z)
(be sure your method is public)

Notes

-

S is the set of all rational numbers whose numerators are between w and x inclusive, and whose denominators are between y and z inclusive.

Constraints

-

x and z will be between 1 and 100, inclusive.

-

w will be between 1 and x, inclusive.

-

y will be between 1 and z, inclusive.

Examples

0)

Returns: 1

Only the value 1/1 is being considered.

1)

Returns: 10

Here S contains the values 1,...,10.

2)

Returns: 3

Here the values are 1/1, 1/2, 2/1, and 2/2. Since 2/2 = 1/1 the answer is 3.

3)

Returns: 7

4)

Returns: 6087

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MultiReplacer

Math

Used in:

SRM 230

Used as:

Division I Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3046

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6519&pm=3046

Problem Statement

Let f be a function that takes a string composed of a's, b's, and c's, and replaces every occurrence of 'a' with arep, 'b' with brep, and 'c' with crep. Your code will compute the length of (quotes for clarity):

	f( f( f( ... f(a) ... ) ) ) : f applied iter times to the string "a"

Since the lengths can grow very large with only a few iterations, you will return the length mod m. For example, if

	arep = abc
	brep = c
	crep = ba
	iter = 3
	m = 7

then you will find the length of

	f(f(f(a))) = f(f(abc)) = f(abccba) = abccbabacabc ,

which is 12. Then you will compute 12 mod 7 = 5, and return 5.

Definition

Class:	MultiReplacer
Method:	length
Parameters:	String, String, String, int, int
Returns:	long
Method signature:	long length(String arep, String brep, String crep, int iter, int m)
(be sure your method is public)

Constraints

-

arep, brep, and crep will contain between 1 and 50 characters inclusive.

-

Each character in arep, brep, and crep will be 'a', 'b', or 'c'.

-

iter will be between 1 and 2000000000 inclusive.

-

m will be between 2 and 2^31-1 inclusive.

Examples

0)

"abc"

"c"

"ba"

Returns: 5

Same as above.

1)

"b"

"c"

"a"

2000000000

Returns: 1

2)

"b"

"c"

"aa"

Returns: 1024

3)

"acabbcabbabac"

"cababcababcabcabacbacbabcacb"

"acbacbabcababcabababbabcbcab"

2000000000

2000000000

Returns: 1876480521

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Generators

Brute Force, Simple Math

Used in:

SRM 243

Used as:

Division I Level One , Division II Level Two

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3043

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=7218&pm=3043

Problem Statement

Let p be a prime number. Z_p is a set of numbers from 1 to (p - 1), inclusive. An element a of Z_p is a generator of Z_p if the set {1, a%p, (a*a)%p, (a*a*a)%p, ..., (a^(p-2))%p} is equal to Z_p (here '%' represents the modulus operator).

You will be given a prime p. Write a method that returns a int[], containing all generators of Z_p that are less than p in ascending order.

Definition

Class:	Generators
Method:	find
Parameters:	int
Returns:	int[]
Method signature:	int[] find(int p)
(be sure your method is public)

Notes

-

For all a and b, (a * b) % p is equal to ((a % p) * (b % p)) % p.

Constraints

-

p is a prime between 3 and 1000, inclusive.

Examples

0)

Returns: {2 }

For p = 3 set {1, a % 3} must be equal to {1, 2} - so the only generator is 2.

1)

Returns: {2, 3 }

Let's check all numbers between 2 and (p - 1), inclusive, for being a generator.

a = 2. a² % 5 = 4. a³ % 5 = 8 % 5 = 3. The set {1, a, a², a³} is equal to {1, 2, 4, 3} and contains all non-zero numbers from Z₅. Thus 2 is a generator.

a = 3. a² % 5 = 4. a³ % 5 = 2. The set {1, a, a², a³} is equal to {1, 3, 4, 2} and contains all non-zero numbers from Z₅. Thus 3 is a generator.

a = 4. a² % 5 = 1. a³ % 5 = 4. The set {1, a, a², a³} is equal to {1, 4, 1, 4} and does NOT contain all non-zero numbers from Z₅. Thus 4 is NOT a generator.

2)

Returns: {2, 6, 7, 11 }

3)

Returns: {2, 3, 10, 13, 14, 15 }

4)

Returns: 
{10, 15, 19, 20, 22, 23, 29, 31, 33, 34, 44, 45, 46, 51, 53, 60, 61, 67, 68, 70, 71, 73, 80, 83, 87, 89, 90, 93, 99, 101, 106, 109, 114, 116, 118, 120, 124, 130, 132, 134, 139, 143, 151, 152, 154, 160, 161, 166, 171, 176, 177, 183, 185, 186, 194, 198, 203, 205, 207, 213, 217, 219, 221, 223, 228, 231, 236, 238, 244, 247, 248, 250, 254, 257, 264, 266, 267, 269, 270, 276, 277, 284, 286, 291, 292, 293, 303, 304, 306, 308, 314, 315, 317, 318, 322, 327 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Crossroads

Geometry, Greedy, Simple Math

Used in:

SRM 217

Used as:

Division II Level Three

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3042

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5863&pm=3042

Problem Statement

You are watching a car race. Each car starts a different point on the x-axis, travels at the same speed, and starts at the same time. However, each car is travelling along a different road (which extends to infinity in one direction, and is stopped by the x-axis in the other direction), and each road has its own direction specified by an angle between 1 and 179, inclusive. An angle of 90 indicates that the road heads directly in the positive y direction, while an angle of 1 indicates that the road heads just a little bit north of the positive x direction. Note that cars never head in the negative y direction.

Sometimes, two or more roads intersect at some point. When this happens, the car that reaches the intersection first is able to block the intersection so that no other cars can pass through it. If two cars reach an intersection at the same time, the one with the lower index passes, while the other one is blocked.

In this picture, the cars following the red paths make it through all of the intersections, while the cars on the gray paths are blocked.

You will be given a int[] angles, where the i^th element of angles is the angle between the x-axis and the road that the i^th car drives on, in degrees. The order of the elements of angles corresponds to the order of the cars along the x-axis (no two cars start at the exact same location), with the first element of angles corresponding to the car with the leftmost starting position on the x-axis.

Your method should return a int[] containing the 0-based indices of all the cars that will pass all of the intersections along their roads. Your return should be sorted in ascending order.

Note that the exact locations of the cars along the x-axis do not matter. All that matters is their order, and the directions in which they head.

Definition

Class:	Crossroads
Method:	getOut
Parameters:	int[]
Returns:	int[]
Method signature:	int[] getOut(int[] angles)
(be sure your method is public)

Constraints

-

angles will contain between 1 and 50 elements, inclusive.

-

Each elemtent of angles will be between 1 and 179, inclusive.

Examples

0)

{105, 75, 25, 120, 35, 75}

Returns: { 0,  1,  5 }

The example from the problem statement.

1)

{1, 1, 1, 1, 1, 1}

Returns: { 0,  1,  2,  3,  4,  5 }

No two cars' paths will ever intersect, so they all pass all intersections.

2)

{13}

Returns: { 0 }

Only one car.

3)

{90, 123, 1, 23, 132, 11, 28, 179, 179, 77, 113, 91}

Returns: { 0 }

The first car passes all intersections. The last car will be stopped by the first car. All other cars are between those two, and will be stopped by one of them.

4)

{179, 89, 90, 91, 1}

Returns: { 0,  2,  4 }

Neither the first nor the last car will intersect with any other car. Car 1 and car 3 will both be stopped by car 2.

5)

{89, 91}

Returns: { 0 }

Both cars reach the intersection at the same time, and hence only the first one passes.

6)

{140, 118, 54, 166, 151, 44, 90, 5, 14, 6,
 64, 129, 74, 33, 134, 25, 11, 95, 65, 145,
 29, 162, 24, 147, 45, 103, 63, 97, 120, 156,
 167, 170, 19, 28, 100, 144, 161, 13, 157, 148}

Returns: { 0,  1,  6 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ParenReduction

String Manipulation, String Parsing

Used in:

SRM 224

Used as:

Division II Level Three

Writer:

vorthys

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3035

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5870&pm=3035

Problem Statement

In mathematics, we don't bother to parenthesize every expression. For example, we write "a*b+c*d" instead of "((a*b)+(c*d))". To make sense of unparenthesized expressions, we depend on two ideas: precedence and associativity. For this problem, we will only consider the operations of exponentiation ('^'), multiplication ('*'), division ('/'), addition ('+'), and subtraction ('-').

There are three levels of precedence. Exponentiation has the highest precedence, multiplication and division have the middle level of precedence, and addition and subtraction have the lowest level of precedence. Unless overridden by parentheses, an operator with a higher level of precedence is executed before an operator with a lower level of precedence. For example, "a+b*c" means "a+(b*c)", and "d^e/f" means "(d^e)/f".

The order of execution among unparenthesized operators at the same level of precedence is determined by associativity. Exponentiation is right associative, meaning that, when there are several exponentiation operators, the rightmost is executed first. For example, "a^b^c" means "a^(b^c)". Division and subtraction are left associative, meaning that, when there are several divisions or several subtractions, the leftmost is executed first. For example, "a-b-c" means "(a-b)-c". Multiplication and addition are associative, meaning that, when there are several multiplication operators or several addition operators, it doesn't matter which one is executed first. For example, "a*b*c" can mean either "(a*b)*c" or "a*(b*c)" because the two parenthesizations are equivalent.

When mixing different unparenthesized operators at the same level of precedence, either multiplication and division or addition and subtraction, the interplay between associativity and left associativity is complicated. The operators can be executed in any order as long as each division or subtraction is executed before the operator to its immediate right. For example, "a*b/c*d" can mean "((a*b)/c)*d" or "(a*(b/c))*d" or "a*((b/c)*d)" but not "(a*b)/(c*d)" or "a*(b/(c*d))". Similarly, "a-b+c-d" can mean "((a-b)+c)-d" or "(a-b)+(c-d)" but not "a-((b+c)-d)" or "a-(b+(c-d))" or "(a-(b+c))-d".

You will be given a fully parenthesized expression as a String expr satisfying the following grammar:

   <expr> = <lowercase letter>
          | "(" <expr> <op> <expr> ")"
   <op>   = "^" | "*" | "/" | "+" | "-"

No letter will be used more than once in the same expression. Your task is to remove all unnecessary parentheses and return the resulting expression, also as a String. The expression cannot be changed in any way other than removing parentheses. For example, "(a-(b+c))" cannot be changed to "a-b-c". Similarly, you should make no use of algebraic laws other than those described above. For example, "(a-(b-(c-d)))" cannot be changed to "a-(b-c)-d".

Definition

Class:	ParenReduction
Method:	pretty
Parameters:	String
Returns:	String
Method signature:	String pretty(String expr)
(be sure your method is public)

Constraints

- expr contains between 1 and 49 characters, inclusive.

- Each character of expr is a lowercase letter ('a'-'z'), a parenthesis ('(',')'), or a binary operator ('^','*','/','+','-').

- No letter appears more than once in expr.

- expr satisfies the grammar given in the problem statement.

Examples

0)

"(a-(b/(c^d)))"

Returns: "a-b/c^d"

Exponentiation has higher precedence than division and division has higher precedence than subtraction.

1)

"(e*((f+(g+h))*i))"

Returns: "e*(f+g+h)*i"

Multiplication has higher precedence than addition. Both are associative.

2)

"(((a-(b-c))-d)^((e/f)/(g/h)))"

Returns: "(a-(b-c)-d)^(e/f/(g/h))"

Subtraction and division are both left associative.

3)

"x"

Returns: "x"

4)

"((a+((l-g)+o))^((r/i)*((t/h)*m)))"

Returns: "(a+l-g+o)^(r/i*t/h*m)"

5)

"(((((t-(k/(o*m)))*(c*f))*((n/j)+(v-z)))^l)/(x-h))"

Returns: "((t-k/(o*m))*c*f*(n/j+v-z))^l/(x-h)"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StringOfPowers

Dynamic Programming, Simple Math

Used in:

TCO04 Finals

Used as:

Division I Level Three

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , Yarin , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3006

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5886&pm=3006

Problem Statement

A friend of mine once told me that his phone number, 642-5616, is easy to remember because it is made up of only powers of 2: "64" + "256" + "16". This made me wonder how many numbers of various lengths had this property.

Given ints b and digits, write a method to compute how many integers of the given number of digits can be formed by concatenating various powers of the given base. Use only non-negative powers of the base (including b⁰, which equals 1).

For example, given b = 12, and digits = 4, there are 8 such numbers:

    1111: "1" + "1" + "1" + "1"
    1112: "1" + "1" + "12"
    1121: "1" + "12" + "1"
    1144: "1" + "144"
    1211: "12" + "1" + "1"
    1212: "12" + "12"
    1441: "144" + "1"
    1728: "1728"

Definition

Class:	StringOfPowers
Method:	count
Parameters:	int, int
Returns:	long
Method signature:	long count(int b, int digits)
(be sure your method is public)

Constraints

-

b will be between 2 and 999999999, inclusive.

-

digits will be between 1 and 18, inclusive.

Examples

0)

Returns: 8

This is the example in the problem statement.

1)

Returns: 64

The first digit must be a 1, and the remaining 6 digits can each be zero or one. Therefore, there are 2⁶ = 64 possibilities.

2)

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LargestCircle

Brute Force, Geometry, Simple Math

Used in:

SRM 212

Used as:

Division II Level Three

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3005

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5858&pm=3005

Problem Statement

NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.

Given a regular square grid, with some number of squares marked, find the largest circle you can draw on the grid that does not pass through any of the marked squares. The circle must be centered on a grid point (the corner of a square) and the radius must be an integer. Return the radius of the circle.

The grid will be given as a String[], with each character representing a square. A '.' represents an empty square, and a '#' represents a marked square.

The circle may intersect the corner of a marked square, but may not pass through the interior. For example, given the grid:


  { "############",
    "###......###",
    "##.######.##",
    "#.########.#",
    "#.##..####.#",
    "#.##..####.#",
    "#.########.#",
    "#.########.#",
    "#.########.#",
    "##.######.##",
    "###......###",
    "############" }

two circles can be drawn with radii 1 and 5, as shown below:

Therefore, your method should return 5.

Circles may not extend outside of the grid, and must have a radius of at least 1. If no such circle exists, return 0.

Definition

Class:	LargestCircle
Method:	radius
Parameters:	String[]
Returns:	int
Method signature:	int radius(String[] grid)
(be sure your method is public)

Constraints

-

grid will contain between 1 and 50 elements, inclusive.

-

Each element of grid will contain between 1 and 50 characters, inclusive.

-

Each element of grid will contain the same number of characters.

-

Each element of grid will contain only the characters '.' and '#'.

Examples

0)

{ "####",
  "#..#",
  "#..#",
  "####" }

Returns: 1

Only one circle fits in this grid -- a circle of radius 1, in the center of the grid.

1)

{ "############",
  "###......###",
  "##.######.##",
  "#.########.#",
  "#.##..####.#",
  "#.##..####.#",
  "#.########.#",
  "#.########.#",
  "#.########.#",
  "##.######.##",
  "###......###",
  "############" }

Returns: 5

This is the example from the problem statement.

2)

{ ".........." }

Returns: 0

The grid must be at least two squares wide and tall in order for any circles to fit.

3)

{ "#######",
  "#######",
  "#######",
  "#######",
  "#######" }

Returns: 0

4)

{ "#####.......",
  "#####.......",
  "#####.......",
  "............",
  "............",
  "............",
  "............",
  "............",
  "............",
  "............" }

Returns: 4

A circle of radius 4 fits in this grid, as shown here:

5)

{ "#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.",
  "...#...#...#...#...#...#...#...#...#...#...#...#..",
  "#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.",
  ".#...#...#...#...#...#...#...#...#...#...#...#...#",
  "#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.",
  "...#...#...#...#...#...#...#...#...#...#...#...#..",
  "#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.",
  ".#...#...#...#...#...#...#...#...#...#...#...#...#",
  "#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.",
  "...#...#...#...#...#...#...#...#...#...#...#...#.#",
  "#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#.#." }

Returns: 0

6)

{ ".........................#........................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  "..................................................",
  ".................................................." }

Returns: 24

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WinningRecord

Brute Force, Simple Math

Used in:

SRM 212

Used as:

Division I Level One , Division II Level Two

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3003

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5858&pm=3003

Problem Statement

If a baseball team loses 15 games in a row, and then wins its next 5, there are a number of ways this could be reported. A fan of the team could brag that they have won all 5 of their last 5 games. However, it could also be truthfully said that they have won 5 out of their last 10 games, or only 25% of their last 20 games.

Given a String results with the results of the last several games a team has played, determine how many of their most recent games to consider to find the team's worst and best percentages of winning. Return a int[] with 2 elements. The first element should be how many of the team's most recent games to consider to give their best winning record (5, in the above example). The second element should be how many of the team's most recent games to consider to give their worst winning record (20, in the above example).

The String results will contain only the characters 'W' and 'L', where 'W' indicates a win, and 'L' indicates a loss. The left-most character represents the most recent game, and the right-most character represents the least recent game. The string for the example above would be "WWWWWLLLLLLLLLLLLLLL".

Never consider fewer than 3 games. When considering 7 games (for example), they must be the 7 most recent games, not any 7 from the list. If different numbers of games give the same winning record, choose the larger number of games.

Definition

Class:	WinningRecord
Method:	getBestAndWorst
Parameters:	String
Returns:	int[]
Method signature:	int[] getBestAndWorst(String games)
(be sure your method is public)

Constraints

-

results will contain between 3 and 50 characters, inclusive.

-

Each character of results will be either 'W' or 'L'.

Examples

0)

"WWWWWLLLLLLLLLLLLLLL"

Returns: { 5,  20 }

This is the example from the problem statement.

1)

"WWWWWW"

Returns: { 6,  6 }

No matter how many games you consider, the team's winning record is 100% and the losing record is 0%.

2)

"LWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLW"

Returns: { 50,  3 }

3)

"WLWLWLLWWLWLWWWWWWWLWLLLLLLLLLLLLWWLWLLWWWLLLWLWLW"

Returns: { 19,  33 }

4)

"LWWLWWLWWLLLW"

Returns: { 9,  12 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PlayGame

Brute Force, Greedy, Simple Math

Used in:

SRM 217

Used as:

Division I Level One , Division II Level Two

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3002

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5863&pm=3002

Problem Statement

You are playing a computer game and a big fight is planned between two armies. You and your computer opponent will line up your respective units in two rows, with each of your units facing exactly one of your opponent's units and vice versa. Then, each pair of units, who face each other will fight and the stronger one will be victorious, while the weaker one will be captured. If two opposing units are equally strong, your unit will lose and be captured. You know how the computer will arrange its units, and must decide how to line up yours. You want to maximize the sum of the strengths of your units that are not captured during the battle.

You will be given a int[] you and a int[] computer that specify the strengths of the units that you and the computer have, respectively. The return value should be an int, the maximum total strength of your units that are not captured.

Definition

Class:	PlayGame
Method:	saveCreatures
Parameters:	int[], int[]
Returns:	int
Method signature:	int saveCreatures(int[] you, int[] computer)
(be sure your method is public)

Constraints

-

you and computer will have the same number of elements.

-

you and computer will contain between 1 and 50 elements, inclusive.

-

Each element of you and computer will be between 1 and 1000, inclusive.

Examples

0)

{5, 15, 100, 1, 5}

{5, 15, 100, 1, 5}

Returns: 120

Your units with strengths of 100 and 15, along with one of your strength 5 units, can avoid capture.

1)

{1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 
 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000,
 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000,
 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000,
 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000}

{1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 
 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000,
 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000,
 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000,
 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000}

Returns: 0

All units are equally strong, so all your units are captured.

2)

{1, 3, 5, 7, 9, 11, 13, 15, 17, 19}

{2, 4, 6, 8, 10, 12, 14, 16, 18, 20}

Returns: 99

You assign your weakest unit to the computer's strongest unit. Then you assign all your other units in such a way that each of your units has a strength one higher than the opposing unit. So all your units except the weakest one avoid capture.

3)

{2, 3, 4, 5, 6, 7, 8, 9, 10, 11}

{10, 9, 8, 7, 6, 5, 4, 3, 2, 1}

Returns: 65

All your units can win.

4)

{651, 321, 106, 503, 227, 290, 915, 549, 660, 115,
 491, 378, 495, 789, 507, 381, 685, 530, 603, 394,
 7, 704, 101, 620, 859, 490, 744, 495, 379, 781,
 550, 356, 950, 628, 177, 373, 132, 740, 946, 609,
 29, 329, 57, 636, 132, 843, 860, 594, 718, 849}

{16, 127, 704, 614, 218, 67, 169, 621, 340, 319,
 366, 658, 798, 803, 524, 608, 794, 896, 145, 627,
 401, 253, 137, 851, 67, 426, 571, 302, 546, 225,
 311, 111, 804, 135, 284, 784, 890, 786, 740, 612,
 360, 852, 228, 859, 229, 249, 540, 979, 55, 82}

Returns: 25084

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SureThing

Dynamic Programming, Math

Used in:

TCO04 Semifinal 3

Used as:

Division I Level Three

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=3001

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5884&pm=3001

Problem Statement

Various numbers of different-colored (but otherwise identical) marbles are placed in a bag. Marbles are randomly removed from the bag one at a time. You are given the opportunity to guess the color of each marble immediately before it is removed, and with each guess you place a wager. If the color of the marble matches your guess you win the amount of your wager, otherwise you lose that amount.

Each wager can be anywhere from 0 to the total amount of money you have at the time of your wager, inclusive. Your goal is to carefully choose your wagers in order to guarantee yourself the highest possible winnings in the end. Given the total number of marbles of each color initially in the bag and $1.00, determine the greatest amount of money you can guarantee yourself to end up with.

For example, if the bag starts with 1 blue, 1 red, and 1 yellow marble, your best strategy is to wager zero on the first two marbles and then wager everything on the third marble, guaranteeing yourself $2.00 at the end. If you wager anything on either of the first two marbles, there is a chance that you will guess wrong and lose money. Even after doubling your money on the last marble you could end up with less than $2.00. So in this case, the answer is 2.

You can always end up with $2.00 by waiting until there is only one marble left. But often you can do better than that. If the bag begins with 1 blue and 2 red marbles, your best strategy is to bet 1/3 of your money on red. If you are correct (the first marble is red), you will end up with 4/3, bet nothing on the second marble, and then double your money betting on the last marble to 8/3. If you are incorrect (and the first marble is blue) you will have 2/3 left, but you will be able to double your money twice (because you know the last two marbles are both red), thus ending up with 8/3. Notice that you don't care if your first guess is right or wrong -- either outcome leads to ending up with 8/3.

Definition

Class:	SureThing
Method:	maximum
Parameters:	int[]
Returns:	double
Method signature:	double maximum(int[] marbles)
(be sure your method is public)

Notes

-

Don't worry about betting an integral number of coins. Assume your money is infinitely divisible. Wagers such as 1/3 and sqrt(2) are perfectly legal.

-

Your return must have an absolute or relative error less than 1e-9.

Constraints

-

marbles will contain between 1 and 6 elements, inclusive.

-

Each element of marbles will be between 1 and 100, inclusive.

Examples

0)

{ 1, 1, 1 }

Returns: 2.0

This is the first example in the problem statement.

1)

{1, 2}

Returns: 2.666666666666667

This is the second example in the problem statement.

2)

{10}

Returns: 1024.0

With 10 marbles all the same color, you can "guess" correctly 10 times, doubling your money each time.

3)

{26, 26}

Returns: 9.081329549427792

This is the version of the game that you can play with a deck of cards, guessing if each one will be black or red.

4)

{1, 2, 3, 4, 5, 100 }

Returns: 1.6979400579163614E16

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

grafixClick

Simple Math

Used in:

SRM 211

Used as:

Division II Level One

Writer:

Eeyore

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2996

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5857&pm=2996

Problem Statement

Note: This problem statement includes an image that may not appear if you are using a plugin. For best results, use the Arena editor.

You have been hired to work on a graphics application called grafix. The interface includes several buttons that the user can click on during a session. One of these is the Save button, which appears in the application window as a rectangle composed of pixels. The location of each pixel is given by a pair of integers that specify the pixel's row number and column number, in that order. Such an integer pair is called the window coordinates of a pixel. Rows are numbered from top to bottom, and columns are numbered from left to right.

The top left corner of the Save button has window coordinates (20, 50), meaning that it is a pixel occupying the 20th row from the top and the 50th column from the left. The bottom right corner of the Save button has window coordinates (39, 99). If the user clicks her mouse on any pixel within or on the border of the rectangle defined by these points, she is considered to have activated the Save button. Below is a magnified image of the Save button, showing the numbers of its rows and columns.

Given a sequence of mouse clicks, your job is to determine which ones have activated the Save button. For each mouse click, the int[] mouseRows contains the row number of its window coordinates, while the int[] mouseCols contains its column number. The values in each int[] are in corresponding order, so the nth element of mouseRows and the nth element of mouseCols make up the window coordinates of the nth mouse click. You are to return a int[] containing, in ascending order, the zero-based index of each mouse click that activates the Save button.

Definition

Class:	grafixClick
Method:	checkSaveButton
Parameters:	int[], int[]
Returns:	int[]
Method signature:	int[] checkSaveButton(int[] mouseRows, int[] mouseCols)
(be sure your method is public)

Notes

-

Window coordinates are not the same as Cartesian coordinates. Follow the definition given in the first paragraph of the problem statement.

Constraints

-

mouseRows contains between 1 and 50 elements, inclusive

-

mouseRows and mouseCols each contain the same number of elements

-

each element in mouseRows is between 0 and 399, inclusive

-

each element in mouseCols is between 0 and 599, inclusive

Examples

0)

{20, 39, 100}

{99, 50, 200}

Returns: { 0,  1 }

The first click, with window coordinates (20, 99), falls on the top right corner of the Save button. The second click is on the bottom left corner at (39, 50). The third click has window coordinates (100, 200) and falls outside the button.

1)

{0, 100, 399}

{0, 200, 599}

Returns: { }

None of these clicks activate the Save button.

2)

{30}

{75}

Returns: { 0 }

Bull's-eye!

3)

{10, 20, 30, 30, 30, 30, 34, 35, 345}

{10, 20, 30, 50, 60, 80, 34, 35, 345}

Returns: { 3,  4,  5 }

4)

{57, 28, 18, 25, 36, 12, 33, 44, 13, 32,
 32, 51, 11, 27, 8, 51, 17, 34, 10, 16,
 47, 57, 20, 57, 32, 14, 13, 37, 10, 16,
 49, 37, 52, 8, 18, 44, 50, 43, 11, 1,
 21, 22, 17, 35, 28, 53, 56, 16, 11, 44}

{146, 22, 41, 88, 123, 99, 43, 110, 25, 64,
 141, 110, 70, 34, 99, 103, 60, 64, 142, 109,
 133, 144, 72, 68, 25, 32, 21, 140, 30, 105,
 32, 72, 114, 97, 35, 131, 103, 110, 133, 81,
 125, 36, 76, 78, 77, 47, 50, 94, 22, 20}

Returns: { 3,  9,  17,  22,  31,  43,  44 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Rank

Simple Math

Used in:

TCO04 Qual 3

Used as:

Division I Level One

Writer:

lars2520

Testers:

PabloGilberto , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2990

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5875&pm=2990

Problem Statement

At a recent competition, each competitor received an integer score between 0 and 100, inclusive. Now, you need to rank the competitors from first to last. First place (the highest score) is ranked 1, second is ranked 2, and so on. In the event of a tie, all of the tied competitors should receive the average of the ranks they would have received if there were put in some order (it doesn't matter what order, the average is always the same). For example, if there is a tie between two people for first place, then ordering them would give one competitor rank 1, and the other rank 2. The average of these is 1.5, so both competitors receive a rank of 1.5.

You should return a double[] containing the ranks of the competitors, each of whose elements corresponds to the element of score with the same index.

Definition

Class:	Rank
Method:	rank
Parameters:	int[]
Returns:	double[]
Method signature:	double[] rank(int[] scores)
(be sure your method is public)

Constraints

-

scores will contain between 1 and 50 elements, inclusive.

-

Each element of scores will be between 0 and 100, inclusive.

Examples

0)

{49,48,49}

Returns: { 1.5,  3.0,  1.5 }

There is a tie for first place between competitors 0 and 2. Hence they each get ranked 1.5, while competitor 1 gets ranked 3.

1)

{10}

Returns: { 1.0 }

2)

{3,4,2,0,9,8,6,7,1,2,3,5,4,1}

Returns: 
{ 8.5,  6.5,  10.5,  14.0,  1.0,  2.0,  4.0,  3.0,  12.5,  10.5,  8.5,  5.0,  6.5,  12.5 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

QuizShow

Brute Force, Simple Math

Used in:

SRM 223

Used as:

Division I Level One

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2989

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5869&pm=2989

Problem Statement

You are a contestant on a TV quiz show. Throughout the game, you and your 2 opponents have accumulated points by answering trivia questions. At the end of the game, the three of you are given one final question. Before you hear the question, each contestant must decide how many points he or she wishes to wager. Each contestant who answers the question correctly will gain a number of points equal to his or her wager, while the others will lose a number of points equal to their respective wagers. The contestant who ends up with the highest score after the final question wins the game.

It has come to the point in the game where you must select your wager. You can bet any amount between zero and your current score, inclusive. Given your current score, the scores of your two opponents, and how much you believe each of your opponents will wager, compute how much you should wager in order to have the highest probability of winning the game. Assume that you and your opponents each independently have a 50% chance of answering the final question correctly.

You will be given the three scores as a int[], scores. The first element is your score, the next element is your first opponent's score, and the last element is your second opponent's score. You will also be given wager1 and wager2, the amount of your first and second opponents' wagers, respectively.

Your goal is to maximize your chance of winning uncontested. As far as you're concerned, ending in a tie is as bad as losing. If there are multiple wagers that give you the same highest probability of winning, return the smallest such wager. If you have no chance of winning, return zero.

Definition

Class:	QuizShow
Method:	wager
Parameters:	int[], int, int
Returns:	int
Method signature:	int wager(int[] scores, int wager1, int wager2)
(be sure your method is public)

Constraints

-

scores will contain exactly 3 elements.

-

Each element of scores will be between 0 and 10000, inclusive.

-

wager1 will be between 0 and scores[1], inclusive.

-

wager2 will be between 0 and scores[2], inclusive.

Examples

0)

{ 100, 100, 100 }

Returns: 76

If you bet 76, you have a 50% chance of winning. In this case, it doesn't matter if your opponents are right or wrong. If you are right, you win. Otherwise, you lose. If you wager less than 76, your chance of winning drops below 50%, and if you wager more, your chance of winning will not increase. Therefore, the correct answer is 76.

1)

{ 10, 50, 60 }

Returns: 0

Even if your opponents are both wrong, they will end up with 20 and 19 points. Since you cannot win (even if you wager 10), the correct answer is 0.

2)

{ 10, 50, 60 }

Returns: 10

This is the same as the previous example, except in this case your opponents will each end up with 19 points if they are both wrong. Now, you have a 12.5% chance of winning if you wager 10.

3)

{ 2, 2, 12 }

Returns: 1

4)

{ 10000, 10000, 10000 }

Returns: 9999

5)

{ 5824, 4952, 6230 }

Returns: 694

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Roxor

Advanced Math, Dynamic Programming

Used in:

SRM 216

Used as:

Division I Level Three

Writer:

dgarthur

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2987

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5862&pm=2987

Problem Statement

Roxor is a 2-player game that is played with several piles of stones, numbered 0, 1, ..., n-1. To make a move, a player chooses three piles with numbers i, j, and k such that i < j, j <= k, and pile i has at least one stone in it. The player then removes one stone from pile i, and adds one stone to piles j and k. Note that j may equal k, and that two stones are added for each stone removed. Players make moves alternately until it is no longer possible to make a valid move. This will always happen eventually, and the last player to have moved is then declared the winner. See example 0 below for a description of an entire game.

You are said to have made a "winning move" in Roxor, if after making that move, you can eventually win no matter what the opponent does. Note that a winning move does not necessarily end the game immediately, but if you make only winning moves, you will win eventually.

For this task, you will be given a int[] piles, representing the number of stones in each pile within a game of Roxor. You must find i, j, k with i < j and j <= k such that removing one stone from pile i and adding one stone to piles j and k is a winning move. If there are multiple winning moves, you should choose one that minimizes i. If there is more than one of these, you should choose one that minimizes j. If there is still a tie, choose the one that minimizes k.

If there is at least one winning move, you should return {i, j, k} as described above. Otherwise, return {}.

Definition

Class:	Roxor
Method:	play
Parameters:	int[]
Returns:	int[]
Method signature:	int[] play(int[] piles)
(be sure your method is public)

Constraints

-

piles will contain between 2 and 15 elements inclusive.

-

Each element of piles will be between 0 and 1000 inclusive.

-

At least one element of piles other than the last element will be larger than 0.

Examples

0)

{0, 0, 1, 0, 1, 100}

Returns: { 2,  4,  5 }

You have 7 legal moves in this position:

{2, 3, 3}, {2, 3, 4}, {2, 3, 5}, {2, 4, 4}, {2, 4, 5}, {2, 5, 5}, and {4, 5, 5}.

If you make the move, {2, 4, 5}, the piles become {0, 0, 0, 0, 2, 101}.

Your opponent then has to make the move, {4, 5, 5}, which makes the piles become {0, 0, 0, 0, 1, 103}.

Finally, you can make the move, {4, 5, 5}, so the piles become {0, 0, 0, 0, 0, 105}.

Your opponent now has no legal moves, so you have won. Thus, {2, 4, 5} is a winning move.

1)

{1000, 1000, 1000, 1000, 1000}

Returns: { }

Your opponent can always beat you from this position by simply copying your moves. This will ensure that there is always an even number of stones in each pile at the beginning of your turn. As such, you will never take the last stone from any pile, and therefore, you cannot win.

2)

{2, 1, 1, 1, 5}

Returns: { 0,  1,  1 }

3)

{14, 301, 391, 410, 511, 681, 58, 259, 981, 81, 5, 42, 251, 401, 120}

Returns: { 2,  5,  14 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Refactoring

Brute Force, Simple Math

Used in:

SRM 216

Used as:

Division I Level Two

Writer:

dgarthur

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2986

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5862&pm=2986

Problem Statement

You have been hired to do some refactoring. You are not really sure what that is, but you think it has something to do with factoring a number multiple times.

Recall that a factorization of a positive integer n is a collection of at least two positive integers, each larger than one, whose product is n. Note that the order of the numbers in a factorization is ignored, so 2*12 and 12*2 represent the same factorization of 24. In fact, 24 has precisely 6 valid factorizations: 2*2*2*3, 2*2*6, 2*3*4, 2*12, 3*8, and 4*6.

To prepare for your job, write a program that, given an int n, returns the number of unique factorizations of n.

Definition

Class:	Refactoring
Method:	refactor
Parameters:	int
Returns:	int
Method signature:	int refactor(int n)
(be sure your method is public)

Constraints

-

n will be between 2 and 2,000,000,000 inclusive.

Examples

0)

Returns: 6

This is the example from the problem statement.

1)

Returns: 0

9973 is a prime number, so there are no valid factorizations of 9973.

2)

Returns: 295

3)

1916006400

Returns: 7389115

The number of factorizations will never be larger than this.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FuelConsumption

Brute Force, Simple Math

Used in:

SRM 217

Used as:

Division II Level One

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2980

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5863&pm=2980

Problem Statement

You are taking your car on a long trip and have only a limited amount of fuel. You know how many liters of fuel your car uses per hour for certain speeds and you'd like to know how far a certain amount of fuel will take you when travelling at the optimal speed.

You will be given a int[] velocities and a int[] consumptions. velocities specifies a number of velocities in kilometers per hour. The i^th element of consumptions is the amount of fuel (in milliliters) the car will consume in 1 hour, if your speed is equal to the i^th element of velocities. In addition, you will be given an int fuel specifying the total amount of fuel in milliliters. Your method should return a double, equal to the maximum distance that the car can travel (in kilometers) with the given amount of fuel, and travelling at a constant velocity equal to one of the elements of velocities.

Definition

Class:	FuelConsumption
Method:	maximalDistance
Parameters:	int[], int[], int
Returns:	double
Method signature:	double maximalDistance(int[] velocities, int[] consumptions, int fuel)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

velocities and consumptions will contain the same number of elements.

-

velocities and consumptions will each contain between 1 and 50 elements, inclusive.

-

Each element of velocities will be between 5 and 250, inclusive.

-

Each element of consumptions will be between 1000 and 20000, inclusive.

-

fuel will be between 100 and 50000, inclusive.

-

velocities will not contain duplicate elements.

Examples

0)

{100}

{10000}

Returns: 100.0

At 100 km/hour, you consume 10 liters of fuel per hour. You have 10 liters, so you can cover 100 kilometers.

1)

{70, 80, 90, 100, 60, 110}

{4000, 4000, 4000, 4000, 4000, 4000}

Returns: 1100.0

Here, your car consumes the same amount of fuel at different velocities. In such cases the faster you drive the further you go.

2)

{250, 240, 230, 220, 210, 211}

{5000, 4500, 4000, 3500, 3000, 3000}

Returns: 3516.6666666666665

3)

{5, 10, 20, 40, 80}

{1000, 2500, 6250, 9000, 18000}

Returns: 239.16

4)

{5, 10, 20, 40, 80, 160}

{1000, 2500, 6250, 8000, 9500, 20000}

Returns: 402.79578947368424

5)

{240, 195, 130, 133, 15, 160, 111, 206, 72, 149,
 146, 115, 235, 183, 102, 96, 163, 61, 196, 52,
 87, 139, 33, 7, 90, 67, 118, 227, 197, 114}

{14837, 2981, 17292, 18591, 4832, 7461, 17991, 18369, 18291, 9400,
 15179, 3317, 2595, 2441, 6936, 8028, 14973, 18981, 12503, 7816,
 2883, 6385, 6230, 18157, 16567, 9310, 2866, 4687, 14171, 4477}

Returns: 2871.6184971098264

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GeneticCrossover

Advanced Math

Used in:

TCO04 Qual 3

Used as:

Division I Level Three

Writer:

lars2520

Testers:

PabloGilberto , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2974

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5875&pm=2974

Problem Statement

In genetics, most large animals have two copies of every gene - one from each parent. In the simplest genetic model, each of the genes takes on one of two forms, dominant or recessive, usually represented by an uppercase and lowercase letter of the same value, respectively ('A' and 'a', for example). The pair of genes typically contributes to the external qualities of the animal in one of two ways. If one or two genes are uppercase, the dominant gene is said to be expressed. If both genes are lowercase, then the recessive gene is said to be expressed.

Additionally, there may be some gene dependencies. If one pair of genes is dependent on another pair of genes, then the first gene may only be expressed dominantly if the gene it depends on is also expressed dominantly. These dependencies are indicated by a int[], dependencies. If element i of dependencies is j, it means that gene i can only be expressed dominantly if gene j also is (both i and j are indexed from 0). If gene j is expressed recessively, then gene i must be also, regardless of the actual genes at position i. If an element of dependencies is -1, it means that the gene is not dependent on any other gene, and is expressed as described in the first paragraph. Chains may exist within dependencies where i depends on j, which in turn depends on k. However, a gene may not depend on itself, and there will be no looping dependencies.

In this problem you are to predict a certain quality about an animal, given N pairs of genes from each of its parents, and some information about those N genes. The first parent's two copies of the genes are given by p1a and p1b, while the second parent's are given by p2a and p2b. For each of the N genes, each parent contributes one of its two genes to its children (characters with the same indices in p1a, p1b, p2a, and p2b correspond to the same gene). For example, if p1a = "ABC" and p1b = "abc", the first parent would contribute an 'A' or an 'a' to its child's first pair of genes, a 'B' or a 'b' to its child's second pair and so on. Similarly, the second parent would also contribute a single gene to its child's first pair of genes, one to its second pair and so on.

Thus, the offspring end up with N genes from each parent. Each pair of corresponding genes contributes in some way to a certain quality we are interested in. If the i^th pair of genes is expressed dominantly, we add dom[i] to a running sum (which is initialized to 0), otherwise we add rec[i]. Given that each parent contributes one of its two genes entirely at random (with a 50% chance of either), you are to determine the expected value the offspring will have for the quality we are interested in (the running sum), and return that value.

Definition

Class:	GeneticCrossover
Method:	cross
Parameters:	String, String, String, String, int[], int[], int[]
Returns:	double
Method signature:	double cross(String p1a, String p1b, String p2a, String p2b, int[] dom, int[] rec, int[] dependencies)
(be sure your method is public)

Notes

-

Your return must have a relative or absolute error less than 1e-9.

Constraints

-

Let N be the number of genes, where N is between 1 and 50, inclusive.

-

p1a, p1b, p2a and p2b will each contain exactly N characters.

-

dom, rec, and dependencies will each contain exactly N elements.

-

Corresponding characters of p1a, p1b, p2a and p2b will have the same value (but may be uppercase or lowercase).

-

Each element of dependencies will be between -1 and N-1, inclusive.

-

dependencies will not contain any cycles.

-

Each element of dom and rec will be between -100 and 100, inclusive.

Examples

0)

"AaaAA"

"AaaAA"

"AaaAA"

"AaaAA"

{1,2,3,4,5}

{-1,-2,-3,-4,-5}

{-1,-1,-1,-1,1}

Returns: -5.0

Since every copy is the same, the animal is guaranteed to have two pairs of "AaaAA". This means that the first and fourth genes will be dominantly expressed, while the others will be recessively expressed. Note that the last gene is dependent on gene 1, which is recessively expressed.

1)

"AbegG"

"ABEgG"

"aBEgg"

"abegG"

{5,5,5,5,5}

{1,1,1,1,1}

{-1,0,1,2,3}

Returns: 14.25

Here, we have a chain of dependencies, where gene 1 depends on gene 0, 2 depends on 1, and so on. For the first gene, the animal is guaranteed to get an 'A' from its first parent, and an 'a' from its second parent. This means that gene 0 will be expressed dominantly, contributing 5 to the sum. The next gene has a 75% chance of being expressed dominantly (it will only be expressed recessively if a 'b' comes from each parent). The third gene also has a 75% chance of being expressed dominantly, assuming that the second gene was expressed dominantly. The fourth gene is guaranteed to be expressed recessively, and hence so is the final gene.

This gives us 3 possible scenarios, denoted below, where a 'D' indicates a gene is expressed dominantly, and an 'R' means recessively:

Genes | Sum | Prob
------+-----+-------
DDDRR | 17  | 0.5625
DDRRR | 13  | 0.1875
DRRRR | 9   | 0.25

The expected value is thus 17*0.5625+13*0.1875+9*.25 = 14.25

2)

"XyMpdnVsbinDvqBpcWGDLfsmQtZpeirvTmoRmBASfqqrFS"

"xYmpdnVsBINdvQBPCwgDlFSmQTzpEIrVtmoRmbaSfqQRfS"

"XYMpdnvsBINdVQbpCWgDlfSMqTzPeIrVTMOrmbaSfQqrFs"

"XYMpDnVSBIndvQBPCWGDlFsMqtzpEiRVTMORMBASFqQrfS"

{-82,-35,-51,52,87,25,8,27,-12,-10,-63,-36,-95,-35,-98,95,-76,7,36,-35,92,23,-94,
 -31,-30,36,51,-49,-19,-3,19,32,58,82,-36,-87,-54,-17,-40,32,-91,-56,0,-16,70,42}

{-36,77,90,50,83,66,-94,-66,-22,-83,-86,-89,-55,-3,-51,18,-41,-91,91,32,-25,-60,
 5,79,100,85,60,98,55,95,-67,-46,-26,48,-64,16,-36,-95,-54,19,96,79,78,-91,-12,35}

{-1,-1,1,-1,3,-1,-1,1,3,5,4,0,-1,-1,2,8,5,4,-1,10,11,14,3,-1,
15,-1,7,-1,8,-1,-1,15,-1,-1,30,-1,26,26,-1,-1,-1,-1,-1,31,0,3}

Returns: -356.875

3)

"fOai"

"Foai"

"fOAI"

"FOAi"

{96,21,-34,-81}

{77,-2,20,25}

{-1,0,-1,-1}

Returns: 44.5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Diving

Brute Force, Simple Math, String Parsing

Used in:

SRM 215

Used as:

Division I Level One

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2960

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5861&pm=2960

Problem Statement

In diving competitions each dive is assigned a numeric rating by 5 different judges. Each dive also has a "degree of difficulty." The score for the dive is obtained by throwing out a highest and a lowest rating, and then multiplying the degree of difficulty times the sum of the remaining three ratings.

Each rating must be a decimal number between 0.0 and 10.0 inclusive, having exactly one digit to the right of its decimal point. Furthermore, the digit to the right of the decimal point must be a 0 or a 5. The degree of difficulty must be between 1.0 and 4.0 inclusive and have exactly one digit (possibly 0) to the right of its decimal point. Exactly 3 characters are used to express the degree of difficulty and each rating, with the exception that a rating of 10.0 uses 4 characters.

We know the score that our diver needs on her final dive to win a medal. We know the degree of difficulty of her final dive. But when the ratings appear on the scoreboard, one of the ratings appears as "?.?" due to an electronic malfunction. What is the smallest legal rating from that judge that will result in a medal?

Create a class Diving that contains a method needed that is given a String difficulty, the degree of difficulty, a String need that is the score needed for a medal expressed with exactly 2 digits to the right of its decimal point, and a String ratings containing the 5 ratings given to our diver except that one of them appears as "?.?". ratings will have no leading or trailing spaces and will have exactly one space between its 5 parts.

The method returns the smallest legal rating that would result in a medal for our diver, expressed as a String as described above. If no legal rating would give her a medal, return "-1.0".

Definition

Class:	Diving
Method:	needed
Parameters:	String, String, String
Returns:	String
Method signature:	String needed(String difficulty, String need, String ratings)
(be sure your method is public)

Constraints

-

difficulty will be a legally expressed degree of difficulty.

-

need will be a value between 0 and 120 inclusive and will contain a decimal point followed by exactly two digits.

-

need will contain no more than 6 characters (but may have leading zeroes).

-

ratings will consist of 4 legally expressed ratings and "?.?", separated by 4 single spaces (' ').

Examples

0)

"3.2"

"50.32"

"5.5 7.5 10.0 ?.? 4.5"

Returns: "0.0"

Even if the unknown rating is thrown out as the low rating, the resulting score is 3.2*(5.5+7.5+4.5) which exceeds the needed score of 50.32.

1)

"3.2"

"50.32"

"5.5 5.5 10.0 ?.? 4.5"

Returns: "5.0"

If the unknown rating is no help, then our score would be 3.2*(5.5 + 5.5 + 4.5) = 49.60 which is too low. If the unknown rating is 5.0, then it will replace the 4.5 yielding a score of 3.2*(5.5+5.5+5.0) = 51.2 which is enough for a medal.

2)

"4.0"

"120.00"

"9.5 10.0 ?.? 10.0 10.0"

Returns: "10.0"

We need to be able to count 3 ratings of 10.0 to achieve 120.00. One of the existing 10.0's will be thrown out as the high rating, so we need a perfect 10.0 to get a medal.

3)

"4.0"

"120.00"

"9.5 10.0 ?.? 9.5 10.0"

Returns: "-1.0"

Even a 10.0 will leave us short of the needed score of 120.

4)

"2.3"

".01"

"0.0 0.0 ?.? 0.0 0.5"

Returns: "0.5"

5)

"3.3"

"47.85"

"0.5 5.5 3.5 7.0 ?.?"

Returns: "5.5"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Volleyball

Math, Recursion

Used in:

TCO04 Round 3

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2959

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5880&pm=2959

Problem Statement

In the current "rally scoring" used in volleyball, each serve results in one point, either for the serving team or for the receiving team. Whoever wins the point is the server on the next point. The winning team is the first team to win at least 15 points and be at least 2 points ahead of the other team.

Suppose that two teams are playing a game, and that they are evenly matched. On each point, whichever team serves has a fixed probability, probWinServe, that they will win the point. (Of course, the receiving team will win the point with probability 1.0 - probWinServe.)

Create a class Volleyball that contains a method win that is given sScore (the current score of the serving team), rScore (the current score of the receiving team), and probWinServe. It returns the probability that the serving team will win the game.

Definition

Class:	Volleyball
Method:	win
Parameters:	int, int, double
Returns:	double
Method signature:	double win(int sScore, int rScore, double probWinServe)
(be sure your method is public)

Notes

-

The returned value must be accurate to within a relative or absolute value of 1E-9.

Constraints

-

sScore and rScore will be between 0 and 100 inclusive.

-

probWinServe will be greater than or equal to 0.01

-

probWinServe will be less than or equal to .99

-

If either sScore or rScore is greater than 14, then sScore=rScore or else sScore=rScore+1.

-

If sScore equals 0, then rScore will also be 0.

Examples

0)

.5

Returns: 0.5

The teams are tied, and it doesn't matter who is serving since probWinServe is 0.5. So the chance of either team winning is the same.

1)

0.01

Returns: 3.355704697986578E-27

In order for the serving team to win this game it would have to win its next 13 serves and then do well after that. So its probability of winning is less than .01 to the 13th power.

2)

0.4

Returns: 0.046377890909090946

3)

0.01

Returns: 0.6662085066547871

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BikeRace

Simple Math, Simple Search, Iteration, Simulation, Sorting

Used in:

SRM 228

Used as:

Division I Level One , Division II Level Two

Writer:

dgoodman

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2958

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=6517&pm=2958

Problem Statement

A pursuit race is run on a circular track. The participants each start at the same start line, but each at a different time based upon their performance in earlier races. Whenever a rider is passed by another rider, he is eliminated from the race. If a previous rider circled the track and reached the start line at or before the time when a contestant is scheduled to start, then that contestant is eliminated at the time the rider reached the start line.

Suppose that the racers each go at a constant speed. Create a class BikeRace that contains a method eliminated that is given track, the length of the track, String[] name, the names of the contestants, a int[] start, the start times of the contestants, and a int[] speed, the speeds of the contestants. It returns a String[] giving the names of the eliminated contestants in the order in which they were eliminated. In case of simultaneous eliminations, list the simultaneously eliminated riders in alphabetical order.

track is in feet, speed is in feet per second, and start is in seconds. Element i of speed, start, and name applies to contestant i.

Definition

Class:	BikeRace
Method:	eliminated
Parameters:	int, String[], int[], int[]
Returns:	String[]
Method signature:	String[] eliminated(int track, String[] name, int[] start, int[] speed)
(be sure your method is public)

Constraints

-

track will be between 1000 and 5000 inclusive.

-

name will contain between 2 and 50 elements inclusive.

-

name, start, and speed will all contain the same number of elements.

-

Each element of name will contain between 1 and 50 characters inclusive.

-

Each character in each element of name will be an uppercase letter 'A'-'Z'.

-

The elements of name will be distinct.

-

Each element of start will be between 0 and 1000 inclusive.

-

The elements of start will be distinct.

-

Each element of speed will be between 1 and 50 inclusive.

Examples

0)

{"A","B","C"}

{ 0, 100,180}

{30, 30, 30}

Returns: { "C" }

Rider A starts at time 0 and goes 3000 feet before B starts at time 100. A passes the start line at time 160, before C can start, thereby eliminating C. But B and A can never catch each other since they are going the same speed so they are never eliminated.

1)

{"BO","JO", "AL"}

{ 10,  0,    15 }

{ 12,  2,    10 }

Returns: { "JO",  "AL" }

JO goes 20 feet (10 seconds at 2 feet/sec) before BO starts at time 10. JO is eliminated at time 12 since both JO and BO have gone 24 feet. AL starts at time 15 but is eventually caught by BO since BO is going at a higher speed.

2)

{"BOBO","JOHNNY","ANNA"}

{67,0,15}

{50,45,3}

Returns: { "BOBO",  "ANNA" }

3)

{"B","J","A"}

{66,0,15}

{50,45,3}

Returns: { "A",  "J" }

4)

{"TOM","TOMMY","BILL","SPEEDY","JIMMY"}

{100,120,110,0,1000}

{50,50,50,50,50}

Returns: { "BILL",  "JIMMY",  "TOM",  "TOMMY" }

SPEEDY just manages to circle the track before any of the others can start. So the other four are all eliminated at the same time, and are listed in alphabetical order.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NegativePhotoresist

Graph Theory, Math, Search, String Parsing

Used in:

SRM 210

Used as:

Division I Level Three

Writer:

the_one_smiley

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2946

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5856&pm=2946

Problem Statement

You are responsible for fabricating a circuit board for an engineering firm. The circuit consists of pinholes (where pins of various components will be inserted) connected by metal traces. For this problem, assume that pinholes can be treated as points in a plane and metal traces can be treated as straight line segments connecting two pinholes.

A highly simplified description of the fabrication process follows. The circuit pattern is cut out of a sheet of opaque material, forming a mask. A sheet of metal is covered with a thin film of material, called negative photoresist, that hardens when exposed to ultraviolet light. The mask is placed over the photoresist and illuminated with ultraviolet light, hardening the photoresist where the light passes through the mask. Finally, the metal sheet is bathed in an etching solution, which destroys the metal except where it is protected by hardened photoresist. The remaining metal forms the circuit.

After a long period of carefully laying out the circuit board, you have the mask prepared. Just before you illuminate the photoresist with ultraviolet light, your boss rushes in and gives you some last minute requirements: the sum of the lengths of the shortest metal trace paths between each pair of pinholes must be under a certain limit, and the board has to be ready by tomorrow. In other words, if you find the shorest path between every pair of connected pins, the sum of the lengths of all these shortest paths must be under the limit. There is no way you can redesign everything in one day, so you decide to improvise. By tilting the mask around its x-axis before you illuminate the photoresist, the circuit will be shrunk along the y-direction; only the projection of the mask on the plane of the photoresist is important since you are shining light through it (assume the light rays are parallel to the z-axis and ignore diffraction effects). Since this also moves the locations of the pins, you want to tilt the mask as little as possible.

Write a class NegativePhotoresist with a method minimumTilt that takes a String[] pinConnections specifying for each pinhole its mask-plane coordinates and its connections to other pinholes and an int limit, and returns as a double the minimum non-negative angle (in radians) the mask must be rotated around the x-axis such that the sum of the lengths of the shortest paths between each pair of pinholes is less than limit. If there is no path between a pair of pinholes, omit that pair from the sum.

Each element of pinConnections corresponds to one pinhole. Element i will begin with a pair of integers specifying the x and y coordinates of pinhole i separated by a single comma. Following this is a space-separated list of zero or more integers specifying the zero-based indices of the pinholes that i connects to. All integers are non-negative and may have leading zeroes. For this problem, pinholes are directly connected if and only if they are specified to connect in pinConnections. In other words, overlapping or coinciding metal traces do not create a connection.

Definition

Class:	NegativePhotoresist
Method:	minimumTilt
Parameters:	String[], int
Returns:	double
Method signature:	double minimumTilt(String[] pinConnections, int limit)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1e-9 radians is considered correct.

-

There can only be up to one connection between a pair of pinholes. If an index j appears multiple times in element i of pinConnections, there is still only one metal trace between pinholes i and j.

-

The sum over all pairs of the shortest path lengths will be minimized when the mask is rotated by Pi / 2 radians.

-

Pairs are unordered. The pair (pinhole i, pinhole j) is the same as (pinhole j, pinhole i).

Constraints

-

The correct answer will be between 0.01 and 1.55, inclusive.

-

pinConnections will contain between 2 and 50 elements, inclusive.

-

Elements of pinConnections will contain at most 50 characters.

-

Elements of pinConnections will be formatted "X,Y P₁ P₂ P₃ ..." (quotes are for clarity) where X and Y are between 0 and 100000 inclusive, and each of the indices P_j will be separated by a single space and will be between 0 inclusive and the number of elements in pinConnections exclusive.

-

If pinhole i connects to pinhole j, pinhole j will also connect to pinhole i.

-

A pinhole will not connect to itself.

-

limit will be between 1 and 1,000,000,000, inclusive.

Examples

0)

{"3,0 2 3",
"13,0 2 3",
"0,2 0 1",
"8,50 0 1",
"3,100000 5",
"100000,3 4",
"8432,221"}

Returns: 1.4454078077996135

Pinholes 0, 2, 1, and 3 form a cycle (in that order). When the mask is laid flat, the shortest path between pinholes 0 and 1 goes through pinhole 2. However, if the mask is tilted by more than 1.4454039026103331 radians, the shortest path between pinholes 0 and 1 switches to go through pinhole 3. The shortest path between pinholes 2 and 3 always goes through pinhole 0, regardless of the angle. Pinholes 4 and 5 form a separate component that contains only one connection. Pinhole 6 is not connected to anything, and therefore does not influence the total path length.

1)

{"3,0 2 3",
"13,0 2 3",
"0,2 0 1",
"8,50 0 1",
"3,100000 5",
"100000,3 4",
"8432,221"}

Returns: 0.010604469396671205

This is the same mask as in Example 0. It only has to be tilted slightly to achieve a total shortest path length of 141601.

2)

{"3,0 2 3",
"13,0 2 3",
"0,2 0 1",
"8,50 0 1",
"3,100000 5",
"100000,3 4",
"8432,221"}

Returns: 1.5491503047781332

This is the same mask as in Example 0. It has to be tilted until it is almost standing on its edge to achieve a total shortest path length of 100065.

3)

{"76492,66181 1",
"74004,26736 0 14",
"22967,14922",
"5781,62226",
"82836,93961 23",
"87218,72769 19",
"93356,54263 21 23",
"31487,92953",
"4108,40237 25",
"90459,36018 18",
"86769,8014",
"6311,25772 13",
"9507,63470 20",
"30653,48087 11 15",
"84214,63941 1",
"87079,8036 13",
"10892,10164 25 23",
"31650,57394",
"12181,22580 9",
"8820,66849 5",
"63222,10057 12",
"85163,78521 6",
"73264,56781",
"45982,63119 4 6 16",
"96653,33496",
"4728,75705 8 16",
"93821,30582",
"9948,22812"}

Returns: 1.078664288678656

4)

{"26749,31005 7 12 37 22 3 31 18 14 22 43 18 47 27",
"89443,23479 37 20 18 45 4 28 45 48 45 48 42 43",
"26624,91482 8 10 9 47 38 7 26 38 7 15 24 33 13 19",
"74780,3281 5 35 24 0 32 6 7 40 16 44 27 29 27 42",
"64491,34646 12 42 9 10 25 1 14 22 32 28 16 24 49",
"57611,97350 3 6 16 38 37 26 7 46 47 9 34 17 36 33",
"54900,19650 5 41 17 21 3 41 45 9 45 24 7 29 49 33",
"37779,84466 30 37 0 43 36 2 5 45 31 2 3 13 17 6 27",
"68486,19205 2 14 42 44 17 34 25 41 38 43 10 49 11",
"86915,28119 21 31 2 40 31 12 49 41 4 22 5 34 6 46",
"81402,18667 40 2 17 17 18 8 4 12 38 12 15 26 42 12",
"76982,50425 29 29 13 8 36 49 16 27 26 28 27 34 46",
"43766,59005 15 27 0 9 4 22 10 10 49 44 37 10 34 24",
"71619,57051 36 47 48 39 11 45 32 42 30 7 29 2 34",
"95436,51350 8 18 23 22 17 23 22 16 0 48 19 4 24 19",
"18419,71778 29 12 31 23 24 30 36 26 10 18 45 36 2",
"58370,12207 48 33 5 14 19 47 11 28 44 3 18 32 4 46",
"93954,84580 33 21 10 8 47 35 32 6 10 14 43 22 5 7",
"37005,46508 14 29 22 1 10 0 23 37 15 0 31 16 31 41",
"25700,33156 20 25 35 40 38 16 14 22 14 23 27 25 2",
"87882,64415 19 35 35 33 1 24 26 24 34 41 34 31 29",
"80610,20042 9 27 35 28 46 17 37 28 36 37 6 41 34",
"55546,68119 39 18 34 14 12 0 14 9 0 17 39 4 19 27",
"12701,80882 30 32 15 14 37 42 14 47 18 33 47 19 46",
"14048,1355 15 20 20 3 28 42 14 12 2 49 45 25 6 4",
"27482,63293 49 38 45 19 8 39 4 38 47 38 46 19 24",
"48215,66574 35 41 32 30 20 41 5 2 15 35 10 11 49",
"53613,76037 21 12 40 11 42 46 0 3 49 11 19 3 22 7",
"90922,15011 21 30 40 40 40 21 44 24 1 16 4 11 49",
"67445,91022 15 11 35 47 18 11 38 20 13 38 3 32 6",
"93451,40067 41 23 7 28 26 47 42 15 44 49 31 13 31",
"25947,11589 9 15 9 40 39 0 30 7 18 20 30 35 43 18",
"98403,23751 47 37 44 26 23 17 3 13 48 4 16 42 29",
"32918,74706 17 16 39 47 41 20 23 36 5 35 2 6 43 43",
"9851,96894 8 22 44 36 20 21 5 20 12 9 43 13 46 11",
"86305,55072 37 21 26 29 20 3 20 17 19 46 26 33 31",
"66150,16273 45 13 39 7 21 34 15 11 45 39 15 33 5",
"95275,37494 1 35 32 43 7 0 21 23 5 39 44 21 18 12",
"16184,79884 40 25 39 5 8 2 19 10 47 2 25 29 25 29",
"77000,48925 33 22 36 38 25 37 13 31 40 46 40 36 22",
"19246,92639 10 38 9 28 19 28 28 48 31 27 39 39 3",
"37419,96699 30 26 33 6 9 8 45 26 21 6 20 46 18 43",
"65611,72059 8 30 23 4 44 24 10 13 27 3 32 1 48 48",
"78307,80168 37 7 8 17 0 31 34 41 48 33 33 48 1 48",
"35276,57349 8 32 45 34 30 37 28 42 12 46 16 49 3",
"10106,992 36 25 44 41 1 7 36 13 15 6 6 1 24 49 1",
"43647,68652 21 5 35 44 39 27 41 9 25 16 34 23 11",
"7588,43383 32 33 29 2 17 13 30 38 23 16 25 5 23 0",
"39549,20275 16 13 40 14 32 43 1 1 42 43 42 43",
"49470,43071 25 9 8 12 30 11 44 26 28 27 24 45 4 6"}

45315043

Returns: 1.4635199471353126

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Unblur

Greedy, Simple Math

Used in:

TCO04 Semifinal 3

Used as:

Division I Level One

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2945

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5884&pm=2945

Problem Statement

A simple way to blur an image is to replace each pixel with the average of it and its neighboring pixels. The value of each pixel in the blurred image is computed by adding the values of the 3x3 region centered at the corresponding pixel of the original image, and dividing by 9.

When computing the value of pixels on the border, the 3x3 region will fall partially outside of the original image. Assume that pixels outside of the original image are black.

For example, given the following original image:

the algorithm described above results in the following blurred image:

Write a method that will, given a blurred image, return the original image. The original image will contain only black and white pixels. All pixels on the top and bottom rows and left and right columns of the original image will be black. All values of the blurred image will therefore be: 0 (black), 1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9, or 9/9 (white).

The blurred image will be given as a String[]. Each character in the blurred image will be a character between '0' and '9', inclusive, giving the value of that pixel multiplied by nine. For example, the blurred image above would be given as:


{ "1233321000000000123332100000000000000000000",
  "1244422233222332334343323322232112332223321",
  "1255523344343443545343434434343233432334432",
  "0033303455465775633011445546454355753457753",
  "0033303333364543533011433336333364521346542",
  "0033303455464532445343545546454355753446542",
  "0022202344342200234343434434343233432323221",
  "0011101233221100123332223322232112332211111" }

Return the original image as a String[]. For each pixel in the original image, return a '.' if it is black and '#' if it is white. For example, the original image for the example above would be returned as:

{ "...........................................",
  ".#####...........#####.....................",
  "...#...####.####.#...#.####.###..####.####.",
  "...#...#..#.#..#.#.....#..#.#..#.#....#..#.",
  "...#...#..#.####.#.....#..#.#..#.###..####.",
  "...#...#..#.#....#...#.#..#.#..#.#....#.#..",
  "...#...####.#....#####.####.###..####.#..#.",
  "..........................................." }

Definition

Class:	Unblur
Method:	original
Parameters:	String[]
Returns:	String[]
Method signature:	String[] original(String[] blurred)
(be sure your method is public)

Constraints

-

blurred will contain between 1 and 50 elements, inclusive.

-

Each element of blurred will have a length between 1 and 50, inclusive, and contain only characters between '0' and '9', inclusive.

-

Each element of blurred will have the same length.

-

blurred will be the result of blurring a black and white image.

Examples

0)

{ "1221",
  "1221",
  "1221" }

Returns: { "....",  ".##.",  "...." }

All pixels in the center two columns are adjacent to two white pixels in the source image. The remaining pixels are adjacent to only one.

1)

{ "00000",
  "00000",
  "00000",
  "00000" }

Returns: { ".....",  ".....",  ".....",  "....." }

A solid black image blurs to all zeros.

2)

{ "0011212121100",
  "0123333333210",
  "0123333333210",
  "1233333333321",
  "1233333333321",
  "1233333333321",
  "0112121212110" }

Returns: 
{ ".............",
 "...#.#.#.#...",
 "..#.#.#.#.#..",
 ".............",
 ".#.#.#.#.#.#.",
 "..#.#.#.#.#..",
 "............." }

original:

blurred:

3)

{ "1233321000000000123332100000000000000000000",
  "1244422233222332334343323322232112332223321",
  "1255523344343443545343434434343233432334432",
  "0033303455465775633011445546454355753457753",
  "0033303333364543533011433336333364521346542",
  "0033303455464532445343545546454355753446542",
  "0022202344342200234343434434343233432323221",
  "0011101233221100123332223322232112332211111" }

Returns: 
{ "...........................................",
 ".#####...........#####.....................",
 "...#...####.####.#...#.####.###..####.####.",
 "...#...#..#.#..#.#.....#..#.#..#.#....#..#.",
 "...#...#..#.####.#.....#..#.#..#.###..####.",
 "...#...#..#.#....#...#.#..#.#..#.#....#.#..",
 "...#...####.#....#####.####.###..####.#..#.",
 "..........................................." }

This is the example from the problem statement.

4)

{ "0000123210000",
  "0012456542100",
  "0135789875310",
  "0258988898520",
  "1479865689741",
  "2589742479852",
  "2589742479852",
  "1479865689741",
  "0258988898520",
  "0135789875310",
  "0012456542100",
  "0000123210000" }

Returns: 
{ ".............",
 ".....###.....",
 "...#######...",
 "..#########..",
 "..####.####..",
 ".####...####.",
 ".####...####.",
 "..####.####..",
 "..#########..",
 "...#######...",
 ".....###.....",
 "............." }

original:

blurred:

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Arcs

Geometry, Search, Simple Math

Used in:

SRM 212

Used as:

Division I Level Three

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2944

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5858&pm=2944

Problem Statement

NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.

Given a regular grid of size W x H with various squares blocked out, find a path from point (0,0) to point (W,H) that does not pass through any of the blocked-out squares. The path must consist only of 90-degree arcs (quarters of circles). The radius of each arc must be an integer, and therefore begin and end on an integer grid point. The tangents at each end of every arc must be parallel to the x or y axis.

Arcs may intersect the corner of a blocked-out square and even pass between two that share a corner (as shown in the examples below), but may not pass through the interior of any blocked-out square.

The grid will be given as a String[], with a '.' representing an empty square and a '#' representing a blocked-out square. For example, given the following 12 x 8 grid:


  { "....########",
    "###..###...#",
    "..##..#.##.#",
    "...##..#...#",
    "....#..#...#",
    "....#..###..",
    "....####.##.",
    "..........#." }

there is a path from (0,0) to (12,8) consisting of 4 arcs, as shown in the following figure:

Find the path that contains the fewest number of arcs, and return the number of arcs in that path. If there is no path, return -1.

Definition

Class:	Arcs
Method:	numArcs
Parameters:	String[]
Returns:	int
Method signature:	int numArcs(String[] grid)
(be sure your method is public)

Constraints

-

grid will contain between 1 and 50 elements, inclusive.

-

Each element of grid will have a length between 1 and 50, inclusive, and will contain only the characters '.' and '#'.

-

All elements of grid will have the same length.

Examples

0)

{ "..",
  ".." }

Returns: 1

A single arc of radius 2, centered at (0,2) or (2,0), forms a path from (0,0) to (2,2).

1)

{ "...",
  "..." }

Returns: -1

There can only be a path between opposite corners if the dimensions of the grid are both even or both odd. In this case, the dimensions are 3 x 2, so no path exists.

2)

{ "....",
  ".##.",
  ".##.",
  ".##.",
  ".##.",
  "...." }

Returns: 7

Seven arcs of radius 1 are required in this example.

3)

  { "....########",
    "###..###...#",
    "..##..#.##.#",
    "...##..#...#",
    "....#..#...#",
    "....#..###..",
    "....####.##.",
    "..........#." }

Returns: 4

This is the example in the problem statement.

4)

{ ".....#................",
  "....#.................",
  "....#.................",
  "....#.....#...........",
  "....#.................",
  "....#....#.#..........",
  "....#.......#####.....",
  "....#.....#.....#.....",
  "....#.....#.....#.....",
  "....#....#.#....#.....",
  "....#....#.#.....#....",
  "....#....#.#......#...",
  "....#....#.#.##.#..###",
  "....#....#....#......." }

Returns: 5

There is a path consisting of 5 arcs, as shown in the following figure. Notice that the path may cross itself:

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SumOfSquareRoots

Math, Simple Search, Iteration

Used in:

SRM 212

Used as:

Division I Level Two

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2943

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5858&pm=2943

Problem Statement

The expression "sqrt(12) + sqrt(48)" can be simplified as follows:

    sqrt(12) + sqrt(48) = sqrt(4*3) + sqrt(16*3)
                        = 2*sqrt(3) + 4*sqrt(3)
                        = 6*sqrt(3)
                        = sqrt(36*3)
                        = sqrt(108)

Given a list of integers, A, return a second list of integers, B, such that the sum of the square roots of the elements in B equals the sum of the square roots of the elements in A. B should contain as few elements as possible. The list with the fewest elements is guaranteed to be unique. The elements in your returned list B should be sorted from smallest to largest.

A will be given as a int[]. Return B as a int[] also.

For example, given the integers { 9, 16, 25 }, the sum of the square roots is 3 + 4 + 5, which is 12. The sum of the square roots of the list { 121, 1 } is also 12, but there is an even shorter list: { 144 }, which is the correct answer.

Definition

Class:	SumOfSquareRoots
Method:	shortestList
Parameters:	int[]
Returns:	int[]
Method signature:	int[] shortestList(int[] A)
(be sure your method is public)

Constraints

-

A will contain between 1 and 50 elements, inclusive.

-

Each element of A will be between 1 and 1000, inclusive.

Examples

0)

{12, 48}

Returns: { 108 }

This is the first example in the problem statement.

1)

{9, 16, 25}

Returns: { 144 }

This is the second example in the problem statement.

2)

{4, 3}

Returns: { 3,  4 }

The square root of 4 plus the square root of 3 is ~3.7320508. There is no way to express this as the square root of a single integer, so the correct answer is { 3, 4 }.

3)

{1, 1, 1}

Returns: { 9 }

4)

{5, 3, 5}

Returns: { 3,  20 }

5)

{1, 3, 5, 12, 20}

Returns: { 1,  27,  45 }

6)

{1, 2, 4, 8, 16, 32, 64, 128, 256, 512 }

Returns: { 961,  1922 }

7)

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
  11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
  21, 22, 23, 24, 25, 26, 27, 28, 29, 30,
  31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
  41, 42, 43, 44, 45, 46, 47, 48, 49, 50 }

Returns: 
{ 13,  14,  15,  17,  19,  21,  22,  23,  26,  29,  30,  31,  33,  34,  35,  37,  38,  39,  41,  42,  43,  46,  47,  54,  63,  90,  99,  180,  300,  450,  784 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PseudoPrimeTest

Math, Simple Search, Iteration

Used in:

SRM 208

Used as:

Division II Level Two

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2939

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5854&pm=2939

Problem Statement

A famous probabilistic primality test makes use of Fermat's Little Theorem from number theory. The theorem states

         p-1
	b     %   p  =  1

for all primes p, with b satisfying 1 < b < p, and % denoting modulus or remainder. To refresh your memory, a prime is an integer greater than 1 whose only factors are 1 and itself. In order to test some potential prime q we do the following:

Choose some b-value and compute b^(q-1) % q.
If this value is not 1 then you know q is not prime.
If this value is 1, then you are more sure q is prime than before.

Given q you will try each b-value beginning with 2 until you reach q-1. If at least one of the b-values fails the test stated above (do not produce 1) then return the lowest failing b-value. If all pass return q.

When computing b^(q-1) % q the numbers can get enormous unless certain measures are taken. For one thing, after each multiplication you can apply the modulus. For example,

	190^11 % 300  =  ((190^5 % 300) * (190^6 % 300)) % 300  .

In addition, repeated squaring can speed up the exponentiation process. For example,

	a^9 = a*a*a*a*a*a*a*a*a      requires 8 multiplications but
        a^9 = a*((a^2)^2)^2          requires 4 multiplications.

We can combine the two methods above as illustrated in the following example where we compute a^11 % 12:

	a^11 % 12 = (a * (a^10 % 12)) % 12 
        a^10 % 12 = (a^5 % 12)^2 % 12 
        a^5  % 12 = (a * (a^4 % 12)) % 12 
        a^4  % 12 = (a^2 % 12)^2 % 12 
	a^2  % 12 = (a*a) % 12

Definition

Class:	PseudoPrimeTest
Method:	firstFail
Parameters:	int
Returns:	int
Method signature:	int firstFail(int q)
(be sure your method is public)

Constraints

-

q will be between 3 and 32000 inclusive.

Examples

0)

Returns: 3

Since 2^2 % 3 = 4 % 3 = 1 simply return 3.

1)

Returns: 7

Here we have

   2^1728 % 1729 = 1
   3^1728 % 1729 = 1
   4^1728 % 1729 = 1
   5^1728 % 1729 = 1
   6^1728 % 1729 = 1
   7^1728 % 1729 = 742

so 7 is returned.

2)

Returns: 3

3)

Returns: 7

4)

Returns: 3

5)

Returns: 31859

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CampLunches

Simple Math, Simple Search, Iteration

Used in:

TC China 08 - 1A

Used as:

Division I Level One

Writer:

dplass

Testers:

PabloGilberto , lbackstrom , brett1479 , Olexiy , ivan_metelsky

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2931

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13673&pm=2931

Problem Statement

My two kids go to different summer camps, and each day we go over their lunch menus. I noticed that both camps have a different set of lunches that repeat on a regular basis.

You will be given the repeating menu of lunches for each camp. Each schedule will start at the first element on the first day, which is designated as day zero (0). Return the first day that both camps serve the same lunch, or -1 if they will never serve the same lunch on the same day.

Definition

Class:	CampLunches
Method:	firstMatching
Parameters:	String[], String[]
Returns:	int
Method signature:	int firstMatching(String[] menu1, String[] menu2)
(be sure your method is public)

Notes

- The days start at zero (i.e., the first day of camp is day zero).

- There may be repeats within each individual menu. See Example 2.

Constraints

- menu1 and menu2 will each contain between 1 and 50 elements, inclusive.

- Each element of each menu will contain only lower case letters ('a' - 'z') and spaces (' ').

- Each element of each menu will contain between 2 and 50 characters, inclusive.

Examples

0)

{"pbj", "pizza"}

{"pbj", "pizza"}

Returns: 0

They are the same on the very first day. Even though they are also the same on the second day, we are looking for the first time they are the same.

1)

{"pbj", "pizza"}

{"pizza", "pbj"}

Returns: -1

They will never be the same on the same day.

2)

{"pbj", "pizza"}

{"pizza", "pbj", "pizza"}

Returns: 3

The sequence of lunches is pbj/pizza, pizza/pbj, pbj/pizza, pizza/pizza, so on the third day (starting from zero) they are the same.

3)

{"pbj"}

{"pizza", "tuna", "pbj"}

Returns: 2

4)

{"pizza", "pbj", "meatballs", "peanut butter and jelly", "pizza hero"}

{"pbj", "meatballs", "peanut butter and jelly", "pizza hero"}

Returns: 16

Note, "pizza" is not the same lunch as "pizza hero".

5)

{"pizza"}

{"pizza ", "pizza"}

Returns: 1

Watch out for trailing spaces.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Crossings

Geometry, Math, Simulation

Used in:

SRM 217

Used as:

Division I Level Two

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2929

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5863&pm=2929

Problem Statement

You are watching a car race. Each car starts at a different point on the x-axis, travels at the same speed, and starts at the same time. However, each car is travelling along a different road (which extends to infinity in one direction, and is stopped by the x-axis in the other direction), and each road has its own direction specified by an angle between 1 and 179, inclusive. An angle of 90 indicates that the road heads directly in the positive y direction, while an angle of 1 indicates that the road heads just a little bit north of the positive x direction.

Sometimes, two or more roads intersect at some point. When this happens, the car that reaches the intersection first is able to block the intersection so that no other cars can pass through it. If two cars arrive at an intersection at the same time, the car that appears earlier in the input (lower index) will be the only car to pass through.

In this picture, the cars following the red paths at 0, 10 and 50 pass all intersections, while the cars following the gray paths are stopped (see example 0).

You will be given two int[]s, positions, and angles, where the i^th car corresponds to the i^th element of positions and the i^th element of angles. The i^th element of positions is the x coordinate of the i^th car. The i^th element of angles is the angle in degrees between the x-axis and the road that the i^th car travels on. Your method should return a int[] containing the 0-based indices of all the cars that will pass all the intersections along their roads. Your return should be sorted in ascending order.

Definition

Class:	Crossings
Method:	getOut
Parameters:	int[], int[]
Returns:	int[]
Method signature:	int[] getOut(int[] positions, int[] angles)
(be sure your method is public)

Constraints

-

positions and angles will contain the same number of elements.

-

Each element of positions will be between 0 and 1000000, inclusive.

-

Each element of angles will be between 1 and 179, inclusive.

-

Each element of positions will be unique.

Examples

0)

{0, 40, 20, 10, 30, 50}

{105, 40, 30, 75, 135, 75}

Returns: { 0,  3,  5 }

The example from the problem statement.

1)

{0, 40, 20}

{40, 40, 140}

Returns: { 0,  1 }

2)

{10, 20}

{89, 91}

Returns: { 0 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TransportCounting

Brute Force, Simple Math

Used in:

SRM 207

Used as:

Division II Level One

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2928

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5853&pm=2928

Problem Statement

You are studying public transportation, and you want to know how many buses are going down a particular one-way street every minute. You are driving along the street by car, and counting the buses you meet or overtake. After some time, you stop counting and report the result. In this problem, you may assume that the street is a straight line, and that your car and all of the buses can only go along this line in the same direction.

You will be given an int, speed, giving your speed in meters per minute. You will also be given a int[] positions, specifying how far ahead of you each of the buses is in meters at time 0, and a int[] velocities, specifying the velocities of the buses in meters per minute. The i^th element of velocities and the i^th element of positions specify the velocity and position of the i^th bus, respectively. Finally, an int, time, tells you how many minutes you should count the buses you pass for.

You should return the number of buses you will overtake or meet during time minutes. If you meet one or several buses at the first or at the final moment, count them also.

Definition

Class:	TransportCounting
Method:	countBuses
Parameters:	int, int[], int[], int
Returns:	int
Method signature:	int countBuses(int speed, int[] positions, int[] velocities, int time)
(be sure your method is public)

Constraints

-

positions and velocities will contain the same number of elements.

-

positions will contain between 0 and 50 elements, inclusive.

-

speed and time will both be between 0 and 1000 inclusive.

-

All elements of positions and velocities will be between 0 and 1000, inclusive.

Examples

0)

{0}

{0}

Returns: 1

Though the duration of your counting is 0, you still can count the first bus.

1)

{10, 10}

{0, 1}

Returns: 1

There are four buses.

The first bus starts 10 meters from you and does not move - so you will reach it in the final moment of your measurement.

The second bus starts from the same point as the first one, but goes away from you, covering 1 meter per minute. Thus you won't catch it.

2)

{10, 10}

{0, 1}

Returns: 2

The same example as before, except time is equal to 3 minutes. This extra minute allows you to meet three buses.

3)

{10,20,30,40,50,60,70,80,90,100,
110,120,130,140,150,160,170,180,190,200,
210,220,230,240,250,260,270,280,290,300,
310,320,330,340,350,360,370,380,390,400,
410,420,430,440,450,460,470,480,490,500}

{10,20,30,40,50,60,70,80,90,100,
110,120,130,140,150,160,170,180,190,200,
210,220,230,240,250,260,270,280,290,300,
310,320,330,340,350,360,370,380,390,400,
410,420,430,440,450,460,470,480,490,500}

Returns: 50

4)

{0,0,0}

{4,5,6}

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GetThemAll

Brute Force, Math

Used in:

SRM 207

Used as:

Division I Level Three

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2926

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5853&pm=2926

Problem Statement

You have an infinite chessboard with several black pieces placed on it. You have a white knight on the same chessboard, which starts from the (0, 0) point, and you want to know how fast it can capture all the black pieces.

You will be given a String[] pieces, containing information about black pieces. Each element of pieces will be formatted as "X Y", where X and Y are integer numbers between -1000000 and 1000000, inclusive. Your method should return the minimum number of moves needed to capture all the black pieces, assuming none of them move.

Definition

Class:	GetThemAll
Method:	quickKnight
Parameters:	String[]
Returns:	int
Method signature:	int quickKnight(String[] pieces)
(be sure your method is public)

Notes

-

A knight's jump moves him 2 cells along one of the axes, and 1 cell along the other one. In other words, if a knight is at (0,0), it may move to (-2, -1), (-2, 1), (2, -1), (2, 1), (-1, -2), (1, -2), (-1, 2) or (1, 2).

-

The knight starts at (0, 0).

Constraints

-

pieces will contain between 0 and 9 elements, inclusive.

-

Each element of pieces will be formatted as "X Y", where X and Y are integer numbers without extra leading zeroes.

-

X and Y will be between -1000000 and 1000000, inclusive, in each element of pieces.

-

All elements of pieces will be different.

-

There are no pieces at (0, 0).

Examples

0)

{"1 2"}

Returns: 1

Just one move.

1)

{"2 -1", "2 1", "-2 1", "-2 -1"}

Returns: 7

The knight should return to the starting position several times.

2)

{"0 1"}

Returns: 3

The knight needs 3 jumps to move to any adjacent cell.

3)

{"0 7", "7 7", "7 0"}

Returns: 15

4)

{"-1000000 -1000000", "1000000 1000000", "1000000 -1000000", "-1000000 1000000"}

Returns: 3666668

One really big square, containing the maximal possible distance between two pieces.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MovingAverages

Simple Math

Used in:

SRM 209

Used as:

Division II Level One

Writer:

Wernie

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2924

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5855&pm=2924

Problem Statement

Moving averages are well known in stock charts analysis. They are used to emphasize the direction of a trend and to smooth out fluctuations. Athletes may use moving averages to analyze their training results.

Given a String[] times containing the times from successive training sessions (e.g. the time to cycle a certain leg) and an int n, return a int[] containing the n-moving averages in seconds for these times, with each average rounded down.

Each element of times is in the format "hh:mm:ss" (quotes for clarity), where hh, mm and ss are two digit numbers (with a leading zero if necessary) indicating the number of hours, minutes and seconds, respectively.

A n-moving average is the average (i.e. the arithmetic mean) of n consecutive times. So for t times given, t-n+1 n-moving averages are to be calculated. The first average is composed from the times 1 to n, the second average from the times 2 to n+1 and so on, the last average is composed from the times t-n+1 to t.

Definition

Class:	MovingAverages
Method:	calculate
Parameters:	String[], int
Returns:	int[]
Method signature:	int[] calculate(String[] times, int n)
(be sure your method is public)

Constraints

- times contains between 1 and 50 elements, inclusive.

- Each element of times is in the format "hh:mm:ss" (quotes for clarity), where

hh is a two digit number (with a leading zero if necessary) between 0 and 23, inclusive,

mm is a two digit number (with a leading zero if necessary) between 0 and 59, inclusive,

ss is a two digit number (with a leading zero if necessary) between 0 and 59, inclusive.

- n is between 1 and the number of elements in times, inclusive.

Examples

0)

{"01:19:10", "01:17:40", "01:19:44", "01:17:23", "01:17:07"}

Returns: { 4731,  4695,  4684 }

4731 (01:18:51) is the average of of the first three times, namely 01:19:10, 01:17:40, and 01:19:44.

4695 (01:18:15) is the average of the middle three times (01:17:40, 01:19:44, 01:17:23).

Finally, 4684 (01:18:04) is the average of the last three times (01:19:44, 01:17:23, 01:17:07).

1)

{"01:19:10", "01:17:40", "01:19:44", "01:17:23", "01:17:07"}

Returns: { 4750,  4660,  4784,  4643,  4627 }

The 1-moving averages are just the times given.

2)

{"01:19:10", "01:17:40", "01:19:44", "01:17:23", "01:17:07"}

Returns: { 4692 }

The 5-moving averages of five times is just one value, the average of all the five values.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HexagonalSums

Search, Simple Math

Used in:

SRM 205

Used as:

Division I Level Two , Division II Level Three

Writer:

Rustyoldman

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2921

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5851&pm=2921

Problem Statement

Note to plugin users: this problem contains images which may not display properly with some plugins

Figurate numbers are numbers which form a scalable pattern of nested geometric figures. The hexagonal numbers (1,6,15,28,45,66,91,120,153...) form the following figures with points arranged in a plane as nested hexagons.

In the year 1830, the great mathematician, Legendre, proved that every integer larger than 1719 can be formed as the sum of exactly four hexagonal numbers (although many larger integers can also be formed as the sum of fewer than four hexagonal numbers). This was pretty much the last word on the subject until much later, in the year 1990, when this result was improved to three hexagonal numbers for all "sufficiently large" integers.

In this problem we ask the slightly different question: "what is the minimum number of hexagonal numbers that is required to form a particular sum?" Let's call this MLHS(n), for Minimum Length Hexagonal number Sum totaling to n. Here are the first few terms of MLHS(n):

n  MLHS(n)  a minimum length sum
1    1      1
2    2      1+1
3    3      1+1+1
4    4      1+1+1+1
5    5      1+1+1+1+1
6    1      6
7    2      1+6
8    3      1+1+6
9    4      1+1+1+6
10   5      1+1+1+1+6
11   6      1+1+1+1+1+6
12   2      6+6

For n greater than 1719, we know MLHS(n) <= 4 due to Legendre's result. But since our problem is different we can actually establish much tigher bounds. Six is the highest possible answer which only occurs for MLHS(11) and MLHS(26).

The largest n that has MLHS(n) = 6 is 26,

The largest n that has MLHS(n) = 5 is 130,

The largest n that has MLHS(n) = 4 is 146858.

Given a number, N, return MLHS(n), the minimum number of terms required to form a sum of N, when each term is a hexagonal number.

Definition

Class:	HexagonalSums
Method:	minLength
Parameters:	int
Returns:	int
Method signature:	int minLength(int N)
(be sure your method is public)

Constraints

- N will be between 1 and 1000000 inclusive.

Examples

0)

Returns: 6

1+1+1+1+6+15

1)

Returns: 5

1+28+28+28+45

2)

Returns: 4

1+1+1326+145530

3)

Returns: 3

6+258840+741153

4)

Returns: 2

285390+714610

5)

Returns: 1

145530 is the 269th hexagonal number

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Untypeset

Recursion, Simple Math, String Manipulation

Used in:

SRM 206

Used as:

Division II Level Three

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2919

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5852&pm=2919

Problem Statement

There are several software packages that typeset mathematical expressions. For example, the expression "(31+24/12)/(5+6) + 16" might be typeset like this:


    "       24       "
    " 31 + ----      "
    "       12   + 16"
    "-----------     "
    "   5 + 6        "

Write a method that takes such a typeset mathematical expression and evaluates it, returning the numerical value of the expression. If given the expression above, your method should return 19.

The input expression will be a two-dimensional array of characters, given as a String[]. Expressions will be built out of other expressions, rectangular portions of the given array. Every expression will be in one of three forms:

integer constant: The expression will be exactly one character high, will consist solely of digits, and will not contain any leading zeros.
addition: The expression will be constructed out of left and right subexpressions. Zero or more rows of spaces will be added above and below each subexpression and will give them the same height. Three columns of that height will be placed between them, containing all spaces, except for a single '+' character anywhere in the middle column.
division: The expression will be constructed out of top and bottom subexpressions. One or more columns of spaces will be added to the left and right of each subexpression to give them the same width. One row consisting entirely of '-' characters will be placed between them.

Example:

The expression above has one column (column 12) with all spaces except for a single '+' character. Therefore, this expression is built by adding two subexpressions together. If we take the regions to the left and right of column 12, and remove all rows and columns on the edges containing only spaces, we get the following two subexpressions:


    "       24  "
    " 31 + ---- "
    "       12  "  and  "16"
    "-----------"
    "   5 + 6   "

The right subexpression contains only digits, so it evaluates to the value 16. The left subexpression has one row (row 3) with all '-' characters. Therefore, this expression is built by dividing two subexpressions. If we take the regions above and below row 3, and remove all rows and columns on the edges containing only spaces, we get the following two subexpressions:


    "      24 "
    "31 + ----"  and  "5 + 6"
    "      12 "

Here, both subexpressions are addition. The right subexpression adds "5" and "6", resulting in the value 11. The left subexpression is built by adding two more subexpressions:


               " 24 "
    "31"  and  "----"
               " 12 "

The left side evaluates to the value 31, and the right side evaluates to the division of the subexpressions "24" and "12". Working back up, 24 divided by 12 is 2, added to 31 is 33, divided by 11 is 3, plus 16 is 19.

Definition

Class:	Untypeset
Method:	evaluate
Parameters:	String[]
Returns:	int
Method signature:	int evaluate(String[] expression)
(be sure your method is public)

Notes

-

All division is guaranteed to have an integer result with no remainder.

-

Note that division by zero is not possible.

Constraints

-

expression will contain between 1 and 50 elements, inclusive.

-

Each element of expression will contain between 1 and 50 characters, inclusive.

-

Each element of expression will be the same size.

-

Each element of expression will consist entirely of characters in the String "0123456789-+ ".

-

expression will be formatted according to the rules specified in the problem statement.

-

The result, all integer constants, and all intermediate computed values will be between 1 and 1000000, inclusive.

Examples

0)

{ "2801" }

Returns: 2801

1)

{ "  625       ",
  "------------",
  "        5   " }

Returns: 125

Any number of spaces could be added to the left or right of the numerator and denominator of fractions. But the row of '-' characters will always span the entire row.

2)

{ "       ",
  "500    ",
  "       ",
  "    +  ",
  "       ",
  "       ",
  "      1",
  "       ",
  "       " }

Returns: 501

Any number of blank rows could be added above and below the subexpressions before addition.

3)

{ "   120   ",
  "  -----  ",
  "    10   ",
  "---------",
  "    6    ",
  "   ---   ",
  "    2    " }

Returns: 4

Nested fractions are never ambiguous. There can never be two rows of '-' characters that fill an entire row.

4)

{ "       24       ",
  " 31 + ----      ",
  "       12   + 16",
  "-----------     ",
  "   5 + 6        " }

Returns: 19

This is the example from the problem statement.

5)

{"3 + 4 + 6"}

Returns: 13

6)

{ " 1     4     9 ",
  "--- + --- + ---",
  " 1     2     3 " }

Returns: 6

Three or more terms may be added together. This may be (1/1 + 4/2) + 9/3, or 1/1 + (4/2 + 9/3). Both will give the same result.

7)

{ "34      ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "   +    ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "        ",
  "     924" }

Returns: 958

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TinSoldiers

Advanced Math

Used in:

SRM 203

Used as:

Division I Level Two

Writer:

Eeyore

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2910

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5849&pm=2910

Problem Statement

Little Gretchen is making tin soldiers stand at attention in a single line. She is an egalitarian general, freely mixing soldiers of different ranks. For example, if she had two lieutenants, two sergeants, and one private, she could line them up in the following 16 ways.


    llpss
    llsps
    llssp
    lplss
    lpsls
    lslps
    lslsp
    lspls
    lspsl
    lsslp
    lsspl
    pllss
    sllps
    sllsp
    slpls
    slslp

Before you object that the list is incomplete, you should know that Gretchen considers mirror images to be equivalent. For example, since "sspll" is the same as "llpss" from back to front, she counts them as one.

You are given a int[] containing the number of soldiers of each rank. Return an int stating the number of ways they can be lined up, ignoring reflections.

Definition

Class:	TinSoldiers
Method:	lineUps
Parameters:	int[]
Returns:	int
Method signature:	int lineUps(int[] rankCounts)
(be sure your method is public)

Constraints

-

rankCounts contains between 1 and 5 elements, inclusive

-

each element of rankCounts is between 1 and 5, inclusive

-

there are fewer than 2^31 ways for Gretchen to line up the soldiers

Examples

0)

{2, 2, 1}

Returns: 16

This case is illustrated above.

1)

{2, 2, 2}

Returns: 48

One more private makes for many more line-ups.

2)

{5}

Returns: 1

There is only one way to line up five soldiers of the same rank.

3)

{5, 1}

Returns: 3

Look out for reflections!

4)

{4, 5}

Returns: 66

Here we have four soldiers of one rank, and five soldiers of another.

5)

{4, 2, 2, 5, 4}

Returns: 643245120

In this case, Gretchen can spend months and years lining up her soldiers.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SensorGrid

Recursion, Simple Math

Used in:

SRM 206

Used as:

Division I Level Two

Writer:

legakis

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2906

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5852&pm=2906

Problem Statement

You are working for a company that manufactures high-resolution grids of sensors, such as those used in digital cameras. While the probability of any one sensor being defective is low, it is likely that a very large grid of sensors will have a few defects. For consumer products, this is just accepted, and sometimes the artifacts caused by non-functioning sensors can be hidden with filtering in software.

For high-end products, however, your company wishes to provide defect-free sensor grids. They plan to do this by making extremely high-resolution grids, locating the defective sensors, and then finding a (hopefully) large rectangular region within that grid that does not contain any defects.

Given the width and height of the sensor grid, and the locations of all defects, find the rectangular region in the grid with the largest area (width times height) that does not contain any defective sensors. The locations of the defects are given as zero-indexed coordiantes, where (0,0) is the upper-left corner of the sensor grid. Return a int[] with 4 elements, in this order: the x coordinate of the upper-left corner of the rectangle, the y coordinate of the upper-left corner of the rectangle, the width of the rectangle, and the height of the rectangle. If there are more than one rectangle with the same largest area, return the one with smallest y coordinate. If there are more than one with the same largest area and smallest y coordinate, return the one with the smallest x coordinate. If there are more than one with the same largest area and upper-left corner, return the one with the greatest width.

Definition

Class:	SensorGrid
Method:	largestRectangle
Parameters:	int, int, int[], int[]
Returns:	int[]
Method signature:	int[] largestRectangle(int width, int height, int[] x, int[] y)
(be sure your method is public)

Notes

-

"upper-left" refers to the corner closest to (0,0).

-

The width is measured parallel to the x axis, and the height is measured parallel to the y axis.

-

The ith point (starting at point 0) is given by (x[i], y[i]).

Constraints

-

width will be between 1 and 40000, inclusive.

-

height will be between 1 and 40000, inclusive.

-

x will contain between 1 and 50 elements, inclusive.

-

y will contain the same number of elements as x.

-

Each element of x will be between 0 and width-1, inclusive.

-

Each element of y will be between 0 and height-1, inclusive.

-

There will be no duplicate points.

-

There will be at least one functional sensor.

Examples

0)

{ 1, 5, 1, 5, 3, 7, 3, 7 }

{ 0, 0, 2, 2, 4, 4, 6, 6 }

Returns: { 2,  0,  3,  4 }

Four 3x4 rectangles fit between the defects, as show in the following figure:

Of these, two have the smallest y coordiante (zero), and of those two, the rectangle at position (2,0) has the smallest x coordinate.

1)

{ 5, 4 }

{ 2, 4 }

Returns: { 0,  0,  5,  4 }

Two rectangles with the same area fit between the defects, as show in the following figure:

They both have the same upper-left position, so we return the one with the larger width.

2)

{ 1, 3, 5, 7, 11, 13, 15,
  1, 3, 5, 7, 11, 13, 15,
  1, 3, 5, 7, 11, 13, 15,
  1, 3, 5, 7, 11, 13, 15,
  1, 3, 5, 7, 11, 13, 15,
  1, 3, 5, 7, 11, 13, 15,
  1, 3, 5, 7, 11, 13, 15 }

{ 1, 1, 1, 1, 1, 1, 1,
  3, 3, 3, 3, 3, 3, 3,
  5, 5, 5, 5, 5, 5, 5,
  7, 7, 7, 7, 7, 7, 7,
  10, 10, 10, 10, 10, 10, 10,
  12, 12, 12, 12, 12, 12, 12,
  14, 14, 14, 14, 14, 14, 14 }

Returns: { 8,  0,  3,  16 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Uptime

Math, String Parsing

Used in:

SRM 213

Used as:

Division I Level Two , Division II Level Three

Writer:

dplass

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2893

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5859&pm=2893

Problem Statement

When sending automated emails, it is useful if the system sends the time the server was started, and how long it has been up.

Write a method, calcUptime which is given two Strings which describe the time the server was started and the current time, and calculates the amount time the system has been "up". The time the system was started and the current time (now) will be given in the following format:

	day month year at hh:mm:ss AM/PM

The day of the month will be between 1 and 31, inclusive, (or 30, 29, or 28, depending on the month and year). Month will be a 3-letter abbreviation (Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec.) hh, mm, and ss will always be two digits, with leading zeros if less than 10. Year will be between 1900 and 2199, inclusive. The word 'at' will always be in lower case, and either AM or PM (always upper case) will always be present. (Note that 12:00 PM is considered noon and 12:00 AM is considered midnight of the day that is just starting.)

For example:

	7 Jun 2004 at 04:41:32 PM

Your method should return a String in the following format:

	#d #h #m #s

where each number is immediately adjacent to the units that it represents. Numbers should not have a leading zero. If any of the numbers are zero, omit that section. The maximum number of seconds returned is 59, the maximum number of minutes returned is 59, the maximum number of hours returned is 23, and there is no maximum number of days.

For example, an uptime period of zero days, 16 hours 36 minutes and zero seconds would be represented as:

	16h 36m

Definition

Class:	Uptime
Method:	calcUptime
Parameters:	String, String
Returns:	String
Method signature:	String calcUptime(String started, String now)
(be sure your method is public)

Notes

-

Note that 12:00 PM is considered noon and 12:00 AM is considered midnight of the day that is just starting.

-

You must take leap years into account. Leap years are divisible by 4, except for years divisible by 100, unless they are also divisible by 400. Therefore, 1996 and 2000 were leap years, but 1900 was not, and the year 2100 will not be.

-

The 3-letter month abbreviations are Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec. The number of days in each of the corresponding months in a non-leap year is: 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31. In a leap year the number of days in each month is: 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31.

-

Do NOT consider "Daylight savings" when calculating uptime.

Constraints

-

started and now will be between "1 Jan 1900 at 12:00:00 AM" and "31 Dec 2199 at 11:59:59 PM", inclusive.

-

started and now will both be in the format described in the problem statement.

-

now will never be before started

Examples

0)

"7 Jun 2004 at 04:41:32 PM"

"8 Jun 2004 at 07:16:28 PM"

Returns: "1d 2h 34m 56s"

1)

"7 Jun 2004 at 04:41:32 PM"

"7 Jun 2004 at 04:41:32 PM"

Returns: ""

Zero days, zero hours, zero minutes, zero seconds should return "".

2)

"28 Feb 2004 at 01:23:45 PM"

"1 Mar 2004 at 12:34:56 AM"

Returns: "1d 11h 11m 11s"

Remember leap years.

3)

"28 Feb 2005 at 01:23:45 PM"

"1 Jan 2015 at 12:34:56 AM"

Returns: "3593d 11h 11m 11s"

Don't show years.

4)

"25 Jan 1922 at 05:58:52 AM"

"26 Feb 2190 at 11:53:14 AM"

Returns: "97918d 5h 54m 22s"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TriangleCount

Math

Used in:

SRM 199

Used as:

Division I Level One , Division II Level Two

Writer:

legakis

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2889

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5074&pm=2889

Problem Statement

Given an equilateral triangle with side length N divided into a triangular grid of triangles with side length 1, count the total number of triangles present in the grid. For example, if N is 4:


         /\
        /__\
       /\  /\
      /__\/__\
     /\  /\  /\
    /__\/__\/__\
   /\  /\  /\  /\
  /__\/__\/__\/__\

Here there are ten right-side-up and six up-side-down triangles with a side length of 1, six right-side-up and one up-side-down triangles with a side length of 2, three right-side-up triangles with a side length of 3, and one right-side-up triangle with a side length of 4. The total number of triangles is 27.

Definition

Class:	TriangleCount
Method:	count
Parameters:	int
Returns:	int
Method signature:	int count(int N)
(be sure your method is public)

Constraints

-

N will be between 1 and 500, inclusive.

Examples

0)

Returns: 5

There are four small triangles and one big triangle.

1)

Returns: 27

This is the example from the problem statement.

2)

Returns: 256275

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DogWoods

Geometry

Used in:

SRM 201

Used as:

Division I Level Three

Writer:

zoidal

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2887

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5872&pm=2887

Problem Statement

This problem uses subscripts and superscripts which may not display properly for plugin users.

We've all heard the riddle "How far can a dog run into the woods?", where the expected answer is "halfway". However, this is only correct if worded as "How far can a dog run directly into the woods?". We're here today to solve the actual problem, where "running into" is defined as moving in a way such that for any two times t₁>0 and t₂>0, t₁<t₂ if and only if distance(position(t₁))>distance(position(t₂)), where distance(p) is the distance (in a straight line) from the center of the woods to a position, and position(t) is the dog's position at time t. Complicating (and making more realistic) our problem are the trees in the woods. Each tree is defined by x and y coordinates, and a diameter. As any dog owner can attest, it is in a dog's nature to run in circles. Our dog is slightly demented, so his nature is to run in clockwise circles centered at the center of the woods until he hits a tree. If he hits a tree, he runs counterclock-wise around the tree until he is able to travel clockwise tangent to the center of the woods.

You are to create a class DogWoods, with a method howFar, which takes int[]s containing the x and y coordinates, and the diameters of each tree. The method will also take parameters startx and starty, which are the starting x and y coordinates for the dog. The ith element of x corresponds to the ith element of y, which corresponds to the ith element of diameter. The dog is determined to have reached the center of the woods when the dog's distance to the center is <= 10 units. Your method must return the distance that would be travelled by the dog, while obeying his nature, before he reaches the center of the woods. Your return value must be within 1e-9 relative or absolute error of the correct value.

The location (0,0) is the center of the woods, with the positive x axis extending to the right, and the positive y axis extending up (a standard Cartesian plane).

If the dog would run an infinitely long distance while obeying his nature, then your method should return -1.

Given two circles with the following equations,

(x - x₀)² + (y - y₀)² = r₀² (A circle centered at (x₀,y₀) with radius r₀)

x² + y² = r₁² (A circle centered at (0,0) with radius r₁)

their points of intersection are given by:

x = x₀ / 2 - x₀(r₀² - r₁²) / 2d + y₀p / 2d

y = y₀ / 2 - y₀(r₀² - r₁²) / 2d - x₀p / 2d

and

x = x₀ / 2 - x₀(r₀² - r₁²) / 2d - y₀p / 2d

y = y₀ / 2 - y₀(r₀² - r₁²) / 2d + x₀p / 2d

where

d = x₀² + y₀²

p = sqrt(((r₀ + r₁)² - d)(d - (r₁ - r₀)²))

Definition

Class:	DogWoods
Method:	howFar
Parameters:	int[], int[], int[], int, int
Returns:	double
Method signature:	double howFar(int[] x, int[] y, int[] diameter, int startx, int starty)
(be sure your method is public)

Notes

-

The dog will always obey his nature as described.

-

The dog may not run through any part of a tree.

-

Trees are to be considered exactly round.

-

The dog should be treated as a mathematical point. I.e., it has no diameter.

-

The distance around a circle is pi * diameter.

-

pi ~ 3.14159265358979.

Constraints

-

x, y, and diameter will all have the same number of elements.

-

x will have between 1 and 50 elements, inclusive.

-

Every element of x and y will be between -1000 and 1000, inclusive.

-

Every element of diameter will be between 1 and 100, inclusive.

-

startx and starty and will be between -1000 and 1000, inclusive.

-

The closest that the perimeter of any two trees will be to each other is 1e-6.

-

For any two trees a and b, the distance of the closest point to the center of a will not be within 1e-6 of the distance of the furthest point to the center of b.

-

No tree will completely cover the circle of diameter 20 at the center of the woods.

-

For every tree, the circle of diameter 20 will either not intersect that tree, or it will intersect by at least 1e-6 units at the greatest width of intersection.

-

The dog will not start in the midst of a tree.

Examples

0)

{0}

{10}

{10}

-14

Returns: 23.64281561414452

The dog travels until it meets the tree, covering 18.431923291703267 units, and then travels around the tree until it is within 10 units of the center, for another 5.2108923224412536 units.

In the image, the red lines represents the dog's path, the black circle the tree, and the blue circle the center of the forest.

1)

{40,15,-5}

{7,25,11}

{26,12,23}

-49

Returns: 531.3835950099849

In this image, the red lines represents the dog's path, the black circles the trees, and the blue circle the center of the forest.

2)

{3}

{3}

{3}

Returns: -1.0

The dog can continue spiraling around the center never meeting a tree.

3)

{15}

{15}

{1}

Returns: 0.0

The dog started within 10 units of the center, and therefore cannot travel any further.

4)

{-220,-204,-187,-11,16,211,-180,87,272,-118,-1,16,187,113,71,217,-12,78}

{232,-162,60,-125,-22,-266,-120,-242,87,-148,50,-218,161,-232,249,215,11,-79}

{53,8,77,74,4,42,36,31,73,84,67,59,33,18,94,87,13,59}

-255

Returns: 3564.170613418495

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NoOrderOfOperations

String Parsing

Used in:

SRM 200

Used as:

Division II Level One

Writer:

antimatter

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2868

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5075&pm=2868

Problem Statement

When evaluating a mathematical expression, there is the possibility of ambiguity. If you wanted to know the result of "3 + 5 * 7", you might first evaluate the (3+5) and get 56, or first evaluate the (5*7) and get 38. This ambiguity can be resolved by using the order of operations: first do multiplication and division (from left to right), and then after all those are done, do addition and subtraction (again from left to right). Here, the correct result would be the 38.

While this is unambiguous, it certainly is somewhat annoying. You think it would be easier if people did all math from left to right, all the time, and want to make a simple expression evaluator to do so.

The expression will be given to you as a String expr. It will consist of one digit numbers (0 through 9) alternating with operators (+, -, or *), with no spaces between them. Thus, expr would follow the format Digit Operator Digit Operator .... Digit. For example, the expression given above would be given as "3+5*7".

Your method should return an int representing the value of the expression when evaluated from left to right.

Definition

Class:	NoOrderOfOperations
Method:	evaluate
Parameters:	String
Returns:	int
Method signature:	int evaluate(String expr)
(be sure your method is public)

Constraints

-

expr will be between 1 and 17 characters in length, inclusive.

-

expr will contain an odd number of characters.

-

expr will follow the format Digit Operator Digit Operator ... Digit, where each Digit is a single character from '0' to '9', and each Operator is either +, -, or *.

Examples

0)

"3+5*7"

Returns: 56

First we add 3 + 5 to get 8. Then, we multiply 8 by 7 to get 56.

1)

"4-8*9*1"

Returns: -36

Results can be negative.

2)

"0"

Returns: 0

3)

"1*2*3*4*5*6*7*8*9"

Returns: 362880

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RegularSeason

Brute Force, Simple Math, Sorting

Used in:

SRM 207

Used as:

Division I Level One , Division II Level Two

Writer:

Olexiy

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2866

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5853&pm=2866

Problem Statement

A new basketball season will start this autumn, and you want to predict its results. You have been watching the tournaments for ages and following the teams closely, so you can exactly determine the probability that a particular team will win a match vs some other team. Now you want to know, given these probabilities, how many games each of the teams is expected to win in the upcoming tournament.

You will be given a String[], teams. Each element of teams will be formatted as "NAME P₁ P₂ ... P_N", where NAME is the name of the team, and P₁, P₂, ..., P_N are the probabilities that this team will win home games against the 1^st, 2^nd, ..., N^th teams, respectively (the i^th probability for the i^th team will always be equal to 0). Ties are not possible due to the rules, so if the i^th team has a probability p of beating the j^th team in a home game, then the j^th team has a probability of (100-p) of beating the i^th team when the i^th team is at home. Finally, you will be given an int rounds, which gives you the number of rounds in the championship. This means that team A will play 2*rounds games against each other team B (rounds as the visitors and rounds as the home team). You should predict the expected number of games each team will win in the tournament. You should round your prediction to the nearest integer (.5 rounds up).

The return value should be a String[], with each element formatted as "NAME NUMBER", where NAME is the name of the team, and NUMBER is the predicted number of wins. NUMBER should have no extra leading zeroes. The return value should be sorted by NUMBER in decreasing order (so the first element of the result will represent the most probable champion). If several teams have the same rounded number of wins, sort them using predicted number of wins before rounding (again in decreasing order); if a tie still remains, sort the tied teams by NAME in ascending alphabetical order.

Definition

Class:	RegularSeason
Method:	finalStandings
Parameters:	String[], int
Returns:	String[]
Method signature:	String[] finalStandings(String[] teams, int rounds)
(be sure your method is public)

Notes

- If a team has a probability of p that it will win a particular game, then that game contributes p/100 to the expected number of games the team will win. However, it is advisable that you wait to divide by 100 until you have completed the summation of the expected number of wins (in order to avoid problems with floating point precision).

Constraints

- teams will contain between 2 and 20 elements, inclusive.

- No element of teams will contain more than 50 characters.

- Each element of teams will be formatted as "NAME P₁ P₂ ... P_n".

- Each NAME will contain only uppercase letters ('A'-'Z').

- P₁, P₂, ..., P_n will each be an integer between 0 and 100, inclusive, with no extra leading zeros.

- The i^th probability of the i^th element of teams will be 0.

- rounds will be between 1 and 10, inclusive.

- No two elements of teams will have the same NAME.

Examples

0)

{"A 0 10 50",
"B 100 0 100",
"C 50 10 0"}

Returns: { "B 19",  "A 6",  "C 6" }

Teams A and C are each expected to win half of their games against the other. A and C will both lose all their road games against team B. They are both expected to win 0.5 home games against B (0.1 * 5). Summarizing and rounding 0.5 up will give us the result:

B - 19 wins.
A - 6 wins.
C - 6 wins.

Be aware of rounding AFTER calculating the summary for each team. Also, the sum of predictions for all teams may be NOT equal to the sum of games played (there were 30 games played, but teams are predicted to have 31 wins after the rounding).

1)

{"SPURS 0 33 67 100",
"LAKERS 67 0 33 100",
"WOLVES 33 67 0 100",
"KINGS 0 75 75 0"}

Returns: { "SPURS 8",  "LAKERS 7",  "WOLVES 7",  "KINGS 3" }

2)

{"A 0 10 20 30 40 50 60 70 80 90",
"AA 90 0 10 20 30 40 50 60 70 80",
"AAA 80 90 0 10 20 30 40 50 60 70",
"AAAA 70 80 90 0 10 20 30 40 50 60",
"AAAAA 60 70 80 90 0 10 20 30 40 50",
"AAAAAA 50 60 70 80 90 0 10 20 30 40",
"AAAAAAA 40 50 60 70 80 90 0 10 20 30",
"AAAAAAAA 30 40 50 60 70 80 90 0 10 20",
"AAAAAAAAA 20 30 40 50 60 70 80 90 0 10",
"AAAAAAAAAA 10 20 30 40 50 60 70 80 90 0"}

Returns: 
{ "A 90",
 "AA 90",
 "AAA 90",
 "AAAA 90",
 "AAAAA 90",
 "AAAAAA 90",
 "AAAAAAA 90",
 "AAAAAAAA 90",
 "AAAAAAAAA 90",
 "AAAAAAAAAA 90" }

Don't forget about alphabetical order.

3)

{"WF 0 0 71 10 62 87 49 75 50","OZ 38 0 79 55 36 96 63 17 37",
"C 13 75 0 96 61 2 33 5 64","LCG 13 85 87 0 60 72 86 1 12",
"GDDYC 71 62 21 6 0 17 63 34 32","B 37 66 81 81 53 0 61 80 90",
"XK 14 63 40 25 13 86 0 6 43","YVN 57 30 55 22 31 11 81 0 13",
"SKGAN 28 79 90 79 75 62 36 86 0"}

Returns: 
{ "SKGAN 99",
 "WF 93",
 "B 92",
 "LCG 84",
 "YVN 80",
 "OZ 76",
 "GDDYC 72",
 "C 63",
 "XK 62" }

4)

{
"ZSN 0 61 70 44 69 40 84 59 20",
"SJKB 95 0 88 39 99 18 90 58 44",
"EBIUF 63 71 0 5 28 26 41 90 71",
"MA 73 90 39 0 40 91 31 39 57",
"NPT 35 74 75 74 0 74 14 20 27",
"JVY 68 92 37 52 11 0 91 20 52",
"ZBOW 66 44 69 9 8 7 0 2 35",
"HH 31 70 14 39 6 68 73 0 20",
"P 70 62 66 54 9 55 5 98 0"}

Returns: 
{ "MA 94",
 "NPT 92",
 "P 89",
 "JVY 84",
 "SJKB 77",
 "ZSN 75",
 "EBIUF 74",
 "HH 74",
 "ZBOW 61" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ShoelaceLength

Geometry, Math

Used in:

SRM 213

Used as:

Division II Level Two

Writer:

dplass

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2848

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5859&pm=2848

Problem Statement

My shoelace broke the other day. I was too lazy to take it out and figure out how long it was, so I decided to calculate the length based on the number of eyelets and their separation.

The "horizontal" distance between the eyelets can increase or decrease from the bottom to the top of the shoe. The startWidth is how far apart they are at the bottom (near the toes) and the endWidth is how far apart they are at the top (near the tongue of the shoe). This distance increases (or decreases) linearly from bottom to top. Furthermore, the "vertical" distance, spread, between eyelets is constant.

Write a method, calculate, which calculates the length of the entire shoelace, given the initial distance between the eyelets (startWidth), the final distance between the eyelets (endWidth), distance between each pair of vertically adjacent eyelets (spread) and the number of pairs of eyelets (numPairs).

You should assume all laces follow this general pattern:

  |----| <- startWidth  

  O----O    -
   \  /     |
    \/      | <- spread
    /\      |
   /  \     |
  O    O    -
   \  /
    \/
    /\
   /  \
  O    O

  |----| <- endWidth

In this illustration, startWidth and endWidth are identical, and numPairs is 3.

Definition

Class:	ShoelaceLength
Method:	calculate
Parameters:	int, int, int, int
Returns:	double
Method signature:	double calculate(int startWidth, int endWidth, int spread, int numPairs)
(be sure your method is public)

Notes

-

startWidth may be greater than, equal to, or less than endWidth.

-

Your return value must have a relative or absolute error less than 1e-9.

-

The units of measurement are irrelevant.

-

The length of lace that it takes to go around or through each eyelet should be ignored.

-

The length of lace needed to actually tie a knot is not included.

Constraints

-

numPairs is the number of PAIRS of eyelets, and will be between 2 and 50, inclusive.

-

startWidth, endWidth, and spread will each be between 1 and 99, inclusive.

Examples

0)

Returns: 6.47213595499958

These are my topsiders. Remember to add the start width across the bottom pair of eyelets.

1)

Returns: 111.1786186482248

2)

Returns: 102.17861864822481

Nearly the same configuration as the previous case, except the width goes from 1 to 10 instead of 10 to 1.

3)

Returns: 3.8284271247461903

4)

Returns: 107.97663296253066

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ChangeOptimizer

Advanced Math

Used in:

SRM 195

Used as:

Division I Level Three

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2827

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5070&pm=2827

Problem Statement

Johnny Indecision has a change purse with some change in it. However, he is deathly afraid of having to figure out what might happen if he has to spend some of it. This fear arises because there may be more than one way to give out a certain amount of change. For example, if he has 1 dime (worth 10 cents) and 2 nickels (worth 5 cents apiece), there are two ways to make 10 cents. He also does not want to incur any more change, so he wants to be sure that he has exact change for any amount up to the amount of money he has.

So he would like to exchange his current change with some more predictable coins at the bank. As the bank clerk, you must solve Johnny's dilemma by giving him enough change to allow him to be able to spend any amount of money up to the amount he currently has, but the coins you give him must provide exactly one way to make each of those amounts. In addition, he would like to have as few coins as possible, even if it means having more smaller denomination coins. For example, if Johnny brings 49 cents to the bank, and the only coins available are 1, 10, and 25 cent pieces, there are three valid options:

one 25-cent piece and 24 1-cent pieces
four 10-cent pieces and nine 1-cent pieces
49 1-cent pieces

Each of these combinations results in only one way to make 1 to 49 cents, but the second way is preferable because it has the least number of coins of the three options. If multiple ways exist which have the fewest coins possible, return the way which has the most coins of the highest denomination. If multiple ways have an equal number of coins with the highest denomination, then return the way with the most coins of the second highest denomination, and so on. For example, with a monetary system that includes 1, 3, 6, and 2-cent pieces, and a balance of 11 cents, there are two answers with four coins:

two 1-cent pieces, a one 3-cent piece, and a 6-cent piece
one 1-cent piece, two 2-cent pieces, and a 6-cent piece

The first way is preferable because of its higher valued 3-cent piece.

You will be given a int[] coinTypes, which will be a list containing the value of each type of coin in the monetary system (which will always include a coin valued at 1). You will also be given an int value specifying the amount of money Johnny has. The return value should be a int[] indicating how many coins of each type you should give Johnny back. Element i of the return value should be how many coins valued at coinTypes[i] should be given to Johnny.

Definition

Class:	ChangeOptimizer
Method:	fewestCoins
Parameters:	int[], int
Returns:	int[]
Method signature:	int[] fewestCoins(int[] coinTypes, int value)
(be sure your method is public)

Constraints

-

coinTypes has between 1 and 50 elements, inclusive.

-

Each element of coinTypes is between 1 and 100,000,000, inclusive.

-

There will be no repeated values in coinTypes.

-

There will be exactly one element in coinTypes equal to 1.

-

value is between 1 and 1,000,000,000, inclusive.

Examples

0)

{1,10,25}

Returns: { 9,  4,  0 }

From the problem statement

1)

{1,3,6,2}

Returns: { 2,  1,  1,  0 }

From the problem statement

2)

{1,2,3,4,5,6,7,8,9,10}

Returns: { 1,  1,  0,  1,  0,  0,  0,  154320,  0,  0 }

3)

{91001,3567,222123,4456,1,732234,123793,982312,14781}

65864135

Returns: { 0,  0,  0,  0,  14780,  0,  0,  0,  4455 }

4)

{1,10,100,1000,10000}

Returns: { 1000000,  0,  0,  0,  0 }

5)

{147323, 544149, 649, 26, 3473340, 267243, 6946680, 587,
 13893360, 17103552, 27786720, 60400539, 83360160, 68414208,
 72482916, 1, 687, 4758}

333440639

Returns: { 0,  0,  0,  182,  1,  0,  1,  0,  1,  0,  2,  0,  3,  0,  0,  25,  0,  729 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Education

Math

Used in:

SRM 196

Used as:

Division II Level One

Writer:

dgoodman

Testers:

zoidal , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2826

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5071&pm=2826

Problem Statement

Even students who hate math find one calculation very useful -- what is the lowest score I can get on the last test and pull out a certain grade? Let's write a program to help them minimize their education.

We will assume that an average score of 90 or higher is rewarded with an A grade, 80 or higher (but less than 90) is a B, 70 or higher (but less than 80) is a C, 60 or higher (but less than 70) is a D. All test scores are integers between 0 and 100 inclusive and the average is NOT rounded -- for example an average of 89.99 does NOT get you an A.

Create a class Education that contains a method minimize that is given a String desire indicating the desired grade and a int[] tests containing the scores on all but the final test. The method returns the lowest possible test score for the final test that will earn at least the desired grade. If even a perfect score won't get the desired grade, return -1.

The desired grade will be given as a String of length 1, either "A", "B", "C", or "D".

Definition

Class:	Education
Method:	minimize
Parameters:	String, int[]
Returns:	int
Method signature:	int minimize(String desire, int[] tests)
(be sure your method is public)

Constraints

-

desire will be "A", "B", "C", or "D"

-

tests will contain between 0 and 20 elements inclusive.

-

Each element of tests will be between 0 and 100 inclusive.

Examples

0)

"A"

{0,70}

Returns: -1

Even a perfect 100 on the last test will only produce an average score of 56.66 so it is not possible to earn an A.

1)

"D"

{100,100,100,100,100,100}

Returns: 0

Nice scores! Even the worst possible score of 0 will give an average of 85.7 earning a B which satisfies your meager desire.

2)

"B"

{80,80,80,73}

Returns: 87

An 87 added to these scores will just exactly improve your average from 78.25 to 80.

3)

"B"

{80,80,80,73,79}

Returns: 88

4)

"A"

{80}

Returns: 100

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Soma

Brute Force, Geometry

Used in:

SRM 198

Used as:

Division I Level Three

Writer:

Rustyoldman

Testers:

lbackstrom , brett1479 , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2824

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5073&pm=2824

Problem Statement

Soma is a three dimensional puzzle invented by Piet Hein. You have seven pieces which are formed by joining cubes at their faces. (They are all of the non-convex shapes that can be so formed with four or fewer cubes). Six of the pieces are formed from four cubes and one is formed by three cubes. There are 27 cubes total. The pieces can be described by the following arrays which show how high cubes are stacked in each grid cell, and are also shown in the picture below.

1 1 1   1 1 1   0 1 1
1 0 0   0 1 0   1 1 0

1 1   0 2   2 0   1 2
1 0   1 1   1 1   0 1

The pieces can be translated and rotated into any orientation, to build larger shapes, but can not be reflected (as in a mirror) or disassembled. Pieces may touch, but not intersect. Each piece is used exactly once in a solution.

Given pattern (a shape composed of 27 cubes, not necessarily connected), try to arrange the seven soma pieces into the same shape as pattern. In other words, you are constructing pattern using the seven pieces. Return the number of distinct solutions for pattern.

What is meant by "distinct":

In a valid solution each cube in pattern will be occupied by a cube from exactly one of the seven pieces. You could assign a number between 1 and 7 inclusive to each pattern cube to indicate which piece occupies that pattern cube. Two solutions are distinct if this assignment is different at one or more pattern cubes. Thus removing a piece which has rotational symmetry, rotating it, and putting it back "in the same place" does not produce a new distinct solution. But a rearrangement of some or all of the pieces which is equivalent to rotating or reflecting the entire pattern (assuming pattern has such symmetry) is considered distinct by this definition. For example the pattern, "21112", can be constructed in exactly two distinct ways using the pieces "211" and "12". The distinct ways are "211"-"12" and "21"-"112".

The pattern will be specified in a String[] similar to the arrays showing the individual pieces above. Each character indicates how many cubes are stacked at that location, starting from a common plane at a height of zero.

For example:

{"333",
 "333",
 "333"}

specifies a 3x3x3 cube which is possible to construct with the seven soma pieces in 11520 distinct (as defined above) ways, so return 11520.

Definition

Class:	Soma
Method:	letMeCountTheWays
Parameters:	String[]
Returns:	int
Method signature:	int letMeCountTheWays(String[] pattern)
(be sure your method is public)

Notes

-

If no rotational symmetries are involved, there are 24 possible orthogonal orientations resulting from rotations in three dimensions. Visualize the 3x2 "L" shaped piece (which has no rotational symmetry). The top (long end) of the "L" can point in six directions x,y,z,-x,-y,-z. For each of those, the short leg of the "L" can point in one of four directions. 6 x 4 = 24

-

Each of the other six pieces does have some rotational symmetry, and thus fewer possible distinct orientations.

-

The rotation of a point about a line passing through the origin can be calculated using a single, vector by matrix, multiplication: [x y z]*M=[rx ry rz] where M is a 3 by 3 matrix, [x y z] is the original point and [rx ry rz] is the rotated point.

-

Vector by matrix multiplication is defined as: for(i) { r[i]=0 ; for(j) { r[i]+=p[j]*M[j][i] } } where p is the original point and r is the rotated point.

-

The matrix for 90 degree rotation about the x axis is: {{1,0,0},{0,0,1},{0,-1,0}}

-

The matrix for 90 degree rotation about the y axis is: {{0,0,-1},{0,1,0},{1,0,0}}

-

The matrix for 90 degree rotation about the z axis is: {{0,1,0},{-1,0,0},{0,0,1}}

-

The easiest way to generate all possible orthogonal orientations is to rotate about the x axis (0,90,180 or 270 degrees), then about the y axis (0,90,180 or 270 degrees) then about the z axis (0,90,180,270 degrees). That is 64 combinations of rotations (4x4x4). Try all 64 and throw away those that produce duplicate results.

-

Sequences of rotations in three dimensions are non-commutative. The order in which you apply the rotations matters.

-

There are 240 fundamental patterns to form the cube, proven by the great mathematician, Prof. John H. Conway. 240 x 24 rotations x 2 (for mirror reflection) = 11520. There are 96 ways to rotate individual pieces in each of the 11520 "distinct" ways. 11520 x 96 = 1105920 which is the "over a million ways to build a cube" number the manufacturer uses.

Constraints

-

pattern will contain between 2 and 27 elements, inclusive.

-

Each element of pattern will consist of between 2 and 27 characters, inclusive.

-

Each element of pattern will have the same number of characters.

-

Each character in each element of pattern will be a digit between '0' and '9' inclusive.

-

The sum of all the digits in pattern will be exactly equal to 27.

Examples

0)

{"333",
 "333",
 "333"}

Returns: 11520

The cube.

1)

{"345",
 "234",
 "123"}

Returns: 2800

The crystal.

2)

{"3330000",
 "0033300",
 "0000333"}

Returns: 28

The wall.

3)

{"21111111",
 "21111111",
 "21111111"}

Returns: 0

The chase lounge, impossible.

4)

{"67",
 "77"}

Returns: 1520

The tower.

5)

{"010000000000000000000000000",
 "110000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000000",
 "000000000000000000000000022",
 "000000000000000000000000022",
 "000000000000000000000002222",
 "000000000000000000000002222"}

Returns: 76

Replication.

6)

{"11100110001",
 "01001100111",
 "00000000000",
 "20002012011",
 "11011001001"}

Returns: 1

Disjoint.

7)

{"121",
 "222",
 "121",
 "121",
 "333"}

Returns: 78

The monument.

8)

{"020",
 "010",
 "010",
 "020",
 "343",
 "353"}

Returns: 42

The gallows.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BigCube

Math

Used in:

SRM 192

Used as:

Division II Level Two

Writer:

Rustyoldman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2823

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4780&pm=2823

Problem Statement

This problem contains HTML superscripts which may not display properly for plugin users. Please use the applet to view the problem statement and examples

You are given a list of integer intervals, ranges, where each interval is specified by a String of the form "<low>-<high>" (quotes for clarity). Here "<low>" and "<high>" represent non-negative integers (sequences of characters between '0' and '9' inclusive with no leading zeros) which are separated by a single hyphen '-'.

Your task is to find the largest integer that is in at least one of the intervals and is a perfect cube. Return this integer in a String with no extra leading zeros and only the digits '0'-'9'. In other words, find the largest integer in the intervals that is equal to n³ for some integer n. If there is no perfect cube in the intervals, return the empty string, "" (quotes for clarity).

For example {"1-1000000000001"} would return "1000000000000" which is 10000³.

Definition

Class:	BigCube
Method:	largestCube
Parameters:	String[]
Returns:	String
Method signature:	String largestCube(String[] range)
(be sure your method is public)

Notes

-

C++ users: the 64 bit integer type is long long.

Constraints

-

range will have between 1 and 50 elements inclusive.

-

Each element of range will contain between 3 and 31 characters inclusive.

-

Each element of range will be of the form "<low>-<high>" where <low> and <high> are separated by exactly one hyphen, '-'.

-

Each character of <low> and <high> will be a digit between '0' and '9' inclusive.

-

<low> and <high> will contain no leading zeros.

-

<low> and <high> will be between 0 and 1000000000000000000 (1e15) inclusive.

-

<low> will be less than or equal to <high>

Examples

0)

{"1-1000000000001"}

Returns: "1000000000000"

The example from above: 10000³

1)

{"10-999999999999990","11-999999999999991","12-999999999999992",
 "13-999999999999993","14-999999999999994","15-999999999999995",
 "16-999999999999996","17-999999999999993","18-999999999999994",
 "19-999999999999999"}

Returns: "999970000299999"

99999³

2)

{"0-3","10-20","30-60","80-120"}

Returns: "1"

3)

{"999700030000-999999999999","999400119993-999700029998",
 "999100269974-999400119991","998800479937-999100269972"}

Returns: ""

4)

{"0-0","2-2","3-3","4-4","5-5","6-6","7-7","9-9","10-10","12-12",
 "14-14","16-16","18-18","20-20","22-22","24-24","26-26","28-28",
 "30-30","32-32","34-34","36-36","38-38","40-40","42-42","44-44",
 "46-46","48-48","50-50","52-52","54-54","56-56","58-58","60-60",
 "62-62","65-65","67-67","69-69","71-71","73-73","75-75","77-77",
 "79-79","81-81","83-83","85-85","87-87","89-89","99-99",
  "999970000300000-999999999999999" }

Returns: "0"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DigitMultiples

Brute Force, Simple Math

Used in:

SRM 192

Used as:

Division I Level One

Writer:

Rustyoldman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2450

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4780&pm=2450

Problem Statement

You are given two strings of digits, single and multiple. Your job is to find the length of the longest substring (which may be the whole string) of digits in single such that there is a corresponding substring (of the same length) in multiple which satisfies the following constraint. Each digit in the substring of multiple is the same exact integer multiple of the corresponding digit in the substring of single. So "48" is a multiple (4) of "12", but "72" is not a multiple of "36". Multiplication factors from 0 to 9 are possible. Leading zeros are *allowed* in single and multiple and all substrings.

For example: in "3211113321571" and "5555266420", here are a few (but not all) of the multiples:

"3211113321571"        "5555266420"
"-----------7-"  x 0 = "---------0"
"--------2----"  x 1 = "----2-----"
"--11---------"  x 6 = "-----66---"
"321----------"  x 2 = "------642-"
"--1111-------"  x 5 = "5555------"
"-----13321---"  x 2 = "----26642-"

The answer is 5, the length of the longest string with a multiple, "13321".

Definition

Class:	DigitMultiples
Method:	getLongest
Parameters:	String, String
Returns:	int
Method signature:	int getLongest(String single, String multiple)
(be sure your method is public)

Notes

-

Each digit multiple must be exactly a single digit. For example: '3' x 4 never matches.

Constraints

-

single will have between 1 and 50 characters inclusive.

-

multiple will have between 1 and 50 characters inclusive.

-

each character of single will be between '0' and '9' inclusive.

-

each character of multiple will be between '0' and '9' inclusive.

Examples

0)

"3211113321571"

"5555266420"

Returns: 5

The example from above. Longest multiple = "13321" x 2 = "26642"

1)

"100200300"

"100400600"

Returns: 8

"00200300" x 2 = "00400600"

2)

"111111111100000000000000000000000000000000000"

"122333444455555666666777777788888888999999999"

Returns: 9

3)

"000000000000"

"000000000000"

Returns: 12

Any integer multiple works here.

4)

"11111111111"

"11111111111"

Returns: 11

The factor is one.

5)

"89248987092734709478099"

"00000000000000000000000"

Returns: 23

The factor is zero.

6)

"11111111111111111111111111111111111111111111111111"

"00000000000000000000000001111111111111111111111111"

Returns: 25

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ChangePurse

Advanced Math

Used in:

SRM 195

Used as:

Division II Level Three

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2442

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5070&pm=2442

Problem Statement

Johnny Indecision has a change purse with some change in it. However, he is deathly afraid of having to figure out what might happen if he has to spend some of it. This fear arises because there may be more than one way to give out a certain amount of change. For example, if he has 1 dime (worth 10 cents) and 2 nickels (worth 5 cents apiece), there are two ways to make 10 cents. He also does not want to incur any more change, so he wants to be sure that he has exact change for any amount up to the amount of money he has.

So he would like to exchange his current change with some more predictable coins at the bank. As the bank clerk, you must solve Johnny's dilemma by giving him enough change to allow him to be able to spend any amount of money up to the amount he currently has, but the coins you give him must provide exactly one way to make each of those amounts. If multiple ways exist to give Johnny change, return the one with the most coins of the highest denomination. If multiple ways exist which have the most coins of the highest denomination, return the one with the most coins of the second-highest denomination, and so on. For example, if Johnny brings 49 cents to the bank, and the only coins available are 1, 10, and 25 cent pieces, there are three valid options:

one 25-cent piece and 24 1-cent pieces
four 10-cent pieces and nine 1-cent pieces
49 1-cent pieces

Each of these combinations results in only one way to make 1 to 49 cents, and even though it does not produce the fewest coins, the first way is preferable because it contains a high-valued 25 cent piece.

You will be given a int[] coinTypes, which will be a list containing the value of each type of coin in the given monetary system (which will always include a coin valued at 1). You will also be given an int value specifying the amount of money Johnny has. The return value should be a int[] indicating how many coins of each type you should give Johnny back. Element i of the return value should be how many coins valued at coinTypes[i] should be given to Johnny.

Definition

Class:	ChangePurse
Method:	optimalCoins
Parameters:	int[], int
Returns:	int[]
Method signature:	int[] optimalCoins(int[] coinTypes, int value)
(be sure your method is public)

Constraints

-

coinTypes has between 1 and 50 elements, inclusive.

-

Each element of coinTypes is between 1 and 1000000, inclusive.

-

There will be no repeated values in coinTypes.

-

There will be exactly one element in coinTypes equal to 1.

-

value is between 1 and 1000000000, inclusive.

Examples

0)

{1,25,10}

Returns: { 24,  1,  0 }

The example from the problem statement.

1)

{1,7}

Returns: { 49,  0 }

Note that {7,6} is an invalid return because even though it equals 49 cents, and it allows all values between 1 and 49, it would allow multiple ways to make 7 cents. This is the thing that Johnny fears the most.

2)

{11,5,10,1}

Returns: { 9,  0,  0,  10 }

3)

{29210, 58420, 350520, 708072, 720035, 230, 42355,
 1, 59006, 985, 236024, 163, 701040}

929579039

Returns: { 1,  5,  1,  0,  0,  126,  0,  229,  0,  0,  0,  0,  1325 }

4)

{795, 5536, 26, 915, 18590, 60840, 49140, 2,
 119700, 162235, 369000, 383936, 478800, 505995,
 949, 95984, 455, 8, 420, 239400, 276800, 191968,
 619305, 654810, 706420, 393120, 738000, 767872,
 425880, 786240, 830400, 676, 4500, 851760, 957600,
 648940, 1, 112, 180, 457}

687245439

Returns: 
{ 0,  0,  0,  0,  0,  0,  0,  3,  0,  0,  0,  1,  0,  0,  0,  1,  0,  13,  0,  0,  0,  1,  0,  0,  0,  0,  0,  894,  0,  0,  0,  0,  0,  0,  0,  0,  1,  856,  0,  0 }

5)

{494208, 722376, 731798, 809064, 920448, 1, 988416, 9152, 158,
 991014, 282720, 40132, 608, 143, 289755, 734, 579510, 828400,
 330338, 816, 460224, 27456, 675783, 331, 436, 82368, 729, 306,
 202266, 247104, 414200, 705}

419088383

Returns: 
{ 1,  0,  0,  0,  0,  142,  423,  2,  0,  0,  0,  0,  0,  63,  0,  0,  0,  0,  0,  0,  0,  2,  0,  0,  0,  2,  0,  0,  0,  1,  0,  0 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ComplexIntegers

Advanced Math

Used in:

SRM 198

Used as:

Division II Level Three

Writer:

Rustyoldman

Testers:

brett1479 , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2439

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5073&pm=2439

Problem Statement

Warning: This problem statement makes extensive use of html superscripts and subscripts and will not be displayed properly with plugins. Use the applet window to read this problem statement.

A complex number can be represented by a+bi where a and b are real numbers and i is the square root of negative one (ie. i*i = -1), a so-called "imaginary" number. "a" is called the "real part" of the complex number, and "bi" is called the "imaginary part." Complex numbers where the real part and the imaginary part (ignoring the i) are both integers are called complex integers, or Gaussian integers. Two complex integers a+bi and c+di can be multiplied yielding a complex integer (ac-bd)+(ad+bc)i. Once we have complex integers and complex integer multiplication defined, one wonders if there are complex primes similar to the primes of the positive integers. Yes there are, but they are a little different.

Let us pause to define a few terms here.

A "prime number" is a positive integer greater than one that has no positive integer factors other than one and itself.
A "composite number" is a positive integer that has at least one positive integer factor other than one and itself.
The "norm" of the complex number z, where z=a+bi, is written |z|² and is defined as a²+b² (this is actually the L₂ norm).
F and G are "complex integer factors" of z if F and G are complex integers and F * G = z (F may equal G).

Complex Integers can be divided into four categories.

Complex Zeros, 0, satisfy the equation z * 0 = 0 for all complex numbers z. There is one complex zero, (0+0i)
Complex Units, I, satisfy the equation |z * I|² = |z|² for all complex numbers z. There are four complex integers which are complex units (0+1i), (0-1i), (1+0i) and (-1+0i)
Complex Primes, P, have |P|² > 1 and have no complex integer factor, F, such that |P|² > |F|² > 1
Complex Composites, C, have at least one complex integer factor, F, such that |C|² > |F|² > 1

After a bit of not particularly obvious algebraic manipulation we find the following somewhat easy-to-test rules:

For complex integers, z = a+bi
if |z|² = 0, then z is a complex zero.
if |z|² = 1, then z is a complex unit.
if |z|² > 1 , and p is any prime number that also satisfies p % 4 = 3
- if a (or b) is zero and b (or a) is equal to some p or -p, then z is a complex prime.
- if a (or b) is zero and b (or a) is not equal to any p or -p, then z is a complex composite.
- if a and b are both non-zero and |z|² is a prime number then z is a complex prime.
- if a and b are both non-zero and |z|² is a composite number then z is a complex composite .

Given two int[]s, realPart and imaginaryPart, return a String[] where the k'th element of the answer is "zero", "unit", "prime", or "composite" corresponding to the complex integer (realPart[k]+imaginaryPart[k]i)

For example:

{ 0,     1,       0,     1,       -1,      2,           0,       0,          -3}
{ 0,     0,      -1,     1,        1,      0,          -3,       5,          -2}
returns
{"zero", "unit", "unit", "prime", "prime", "composite", "prime", "composite", "prime"}

Some factorizations of the composites are:

(2+0i) = (1+1i)*(1-1i)
(0+5i) = (1+2i)*(2+1i)

Definition

Class:	ComplexIntegers
Method:	classify
Parameters:	int[], int[]
Returns:	String[]
Method signature:	String[] classify(int[] realPart, int[] imaginaryPart)
(be sure your method is public)

Constraints

-

realPart will contain between 1 and 50 elements inclusive.

-

imaginaryPart will contain the same number of elements as realPart

-

each element of realPart will be between -10000 and 10000 inclusive.

-

each element of imaginaryPart will be between -10000 and 10000 inclusive.

Examples

0)

{ 0,     1,       0,     1,       -1,      2,           0,       0,          -3}

{ 0,     0,      -1,     1,        1,      0,          -3,       5,          -2}

Returns: 
{ "zero",
 "unit",
 "unit",
 "prime",
 "prime",
 "composite",
 "prime",
 "composite",
 "prime" }

The example from above.

1)

{2,3,4,5,2,3,4,5,2,3,4,5,2,3,4,5}

{2,2,2,2,3,3,3,3,4,4,4,4,5,5,5,5}

Returns: 
{ "composite",
 "prime",
 "composite",
 "prime",
 "prime",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "prime",
 "prime",
 "composite",
 "prime",
 "composite" }

2)

{0,0,0,0,0,0,0,0,0,-19,23,29,31,37,-41}

{15,2,-3,5,-7,11,-13,17,0,0,0,0,0,0,0}

Returns: 
{ "composite",
 "composite",
 "prime",
 "composite",
 "prime",
 "prime",
 "composite",
 "composite",
 "zero",
 "prime",
 "prime",
 "composite",
 "prime",
 "composite",
 "composite" }

3)

{99,-39,0,0,97,1003,9998,1119}

{0,0,35,-129,-2,-232,9997,1120}

Returns: 
{ "composite",
 "composite",
 "composite",
 "composite",
 "prime",
 "prime",
 "prime",
 "prime" }

4)

{0,  0,0,1,-1,   1,1,-1,-1,   2,-2,0,0,  1,1,2,2,-1,-1,-2,-2, 
     3,-3,0,0,   1,1,3,3,-1,-1,-3,-3,    2,2,-2,-2,  0,0,4,-4,
                 1,1,4,4,-1,-1,-4,-4 }

{0,  1,-1,0,0,   1,-1,1,-1,   0,0,2,-2,  2,-2,1,-1,2,-2,1,-1,  
     0,0,-3,3,   3,-3,1,-1,3,-3,1,-1,     2,-2,2,-2,  4,-4,0,0,
                 4,-4,1,-1,4,-4,1,-1 }

Returns: 
{ "zero",
 "unit",
 "unit",
 "unit",
 "unit",
 "prime",
 "prime",
 "prime",
 "prime",
 "composite",
 "composite",
 "composite",
 "composite",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "composite",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime",
 "prime" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ChipRace

Advanced Math

Used in:

SRM 199

Used as:

Division I Level Two

Writer:

legakis

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2436

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5074&pm=2436

Problem Statement

Poker tournaments are usually played with chips of various denominations. For the purpose of this problem, assume that $5 and $25 chips are in play. At a predetermined time in the tournament, the $5 chips are removed from play and traded up for the equivalent value of $25 chips. For example, if a player has ten $5 chips, these would be replaced by two $25 chips. This is fine, as long as the number of $5 chips held by each player is a multiple of 5. However, it is likely that players will have a few chips left over after trading in their $5 chips in multiples of 5. These remaining chips are called "odd chips", and there are several way to deal with these. One method is to hold a "chip race".

To begin the chip race, the dealer determines the total number of $25 chips that will be awarded, by counting all the odd chips and dividing by 5 (rounding to the nearest integer). Then, the deck of cards is shuffled, and each player receives one card face up for each of his odd chips. The player with the highest card on the table is awarded one $25 chip, and then his cards are collected and removed. Then, the player with the highest card remaining is awarded the next $25 chip (if there are more than one), and his cards are collected and removed. This is repeated until all of the $25 chips have been awarded. Note that each player can win at most one $25 chip.

A standard deck consists of 52 cards, with 13 values and 4 suits. This is not important for this problem. Assume that the deck of cards consists of 52 unique cards, numbered 1 through 52.

For example, if there are five players, with 2, 3, 1, 0, and 2 odd chips, and if they are dealt the following cards:


    player  odd chips  cards
    ------  ---------  -------
    1       2          49, 35
    2       3          2, 24, 4
    3       1          27
    4       0
    5       2          3, 15

The total number of odd chips is 8, so two $25 chips would be awarded. Player 1 has the highest card (a 49), and would receive the first $25 chip. After his cards are removed, player 3 has the highest remaining card (a 27), and would receive the second $25 chip. Notice that even though player 1 initially had the first and second highest card, he still is only awarded a single chip. Players 2, 4, and 5 receive nothing.

Curious players may question the fairness of this technique. You are to answer such questions by writing a method to compute each player's probability of winning a chip in the chip race. You will be given a int[] chips, which contains the number of odd chips held by each player, and are to return a double[] with each player's probability of winning a chip. The returned double[] should have the same number of elements as chips, and element i of the returned double[] should correspond to element i of chips.

Definition

Class:	ChipRace
Method:	chances
Parameters:	int[]
Returns:	double[]
Method signature:	double[] chances(int[] chips)
(be sure your method is public)

Notes

-

The number of $25 chips awarded is equal to the total number of odd chips divided by 5 (rounded to the nearest integer).

-

No player can win more than one $25 chip.

-

Each element of the returned double[] must have an absolute or relative error of no more than 1e-9.

Constraints

-

chips will contain between 1 and 10 elements, inclusive.

-

Each element in chips will be between 0 and 4, inclusive.

Examples

0)

{ 1, 1 }

Returns: { 0.0,  0.0 }

There are only two $5 chips, and 2/5 rounds down to zero. So no $25 chips are awarded.

1)

{ 1, 2 }

Returns: { 0.3333333333333333,  0.6666666666666666 }

There are three $5 chips, and 3/5 rounds up to 1, so one $25 chip is awarded. Three cards are dealt, and player 1 has a 1/3 chance of getting the highest card and player 2 has a 2/3 chance of getting the highest card.

2)

{ 3, 2, 3 }

Returns: { 0.725,  0.55,  0.725 }

Two $25 chips are awarded. Player 2 has a 1/4 chance of winning the first chip. If either one of the other players wins the first chip, he will then have a 2/5 chance of winning the second chip. (1/4) + (3/4)*(2/5) = 0.55. Since there are a total of two chips awarded, the players' probabilities must sum to 2. Since each of the other players have the same chance of winning a chip, their probabilities are each 1/2 of (2 - 0.55), which is 0.725.

3)

{ 0, 1, 2, 3, 4 }

Returns: 
{ 0.0,  0.23452380952380952,  0.4412698412698413,  0.6083333333333334,  0.7158730158730159 }

4)

 { 0, 1, 1, 0, 0, 0, 0, 1, 1, 0 }

Returns: { 0.0,  0.25,  0.25,  0.0,  0.0,  0.0,  0.0,  0.25,  0.25,  0.0 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TablePartitions

Advanced Math

Used in:

TCCC '04 Semifinals 2

Used as:

Division I Level Two

Writer:

Yarin

Testers:

zoidal , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2434

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5077&pm=2434

Problem Statement

A table in a database consists of rows and columns. Rows correspond to elements in the table, and columns correspond to fields in the elements. In this problem we will only deal with elements that have integer fields in the range 0 to 100, inclusive. The columns will be named sequentially with lower case letters, starting with 'a', then 'b' and so on. So an element in a table with 4 columns may be described like this: "a=3, b=10, c=15, d=0". Note that all fields in an element must contain an integer value in the valid range, i.e. no field may be omitted.

A large table in a database can be a performance hog. One way to avoid this is to logically partition the table into several smaller tables. This is done by giving each partition a set of constraints on the columns, specifying which rows in the large table should go to which partition.

Given the constraints for the partitions of a table, write a class that determines whether the partitions are well formed (see below). The constraints will be given as a String[] where each element corresponds to one partition. Each element contains a space separated list of constraints, where each constraint is in the form "<column><operator><value>" (quotes for clarity only) where <column> is a table column, <operator> is one of the relational operators '=', '<', '>', '<=', '>=', and <value> is an integer between 0 and 100, inclusive (without leading zeros). The constraints for each partition represents a conjunction, i.e. all constraints must hold (see example 1).

For instance, if we have 3 partitions and a table with 2 columns, the constraints might look like this: {"a>3", "a<=3 b>5", "b<6 a<=3"}. Element "a=4, b=3" would then go to the first partition, element "a=3, b=9" would go to the second partition and element "a=0, b=5" would go to the third partition.

The partitioning is badly constructed if one or more of the criteria below holds:

Empty partition: A partition is empty if the constraints are constructed so that no valid element can fulfill them (see example 1). If one or more partitions are empty, return the String "EMPTY".
Overlapping partitions: If there exists a valid element that satisfies the constraints for two or more partitions (see example 2), return the String "OVERLAP".
Incomplete partitioning: If there exists a valid element that satisfies none of the constraints (see example 4), return the String "INCOMPLETE".

If several of the criteria above holds for the partitions, return the first that holds (i.e. "EMPTY" has highest priority, followed by "OVERLAP" and finally "INCOMPLETE").

Otherwise the partitioning is well formed; that is, an arbitrary valid element can go into exactly one partition and no partition is empty. In this case you should return the String "OK".

Create a class TablePartitions containing the method validate which takes an int n, the number of columns in the table, and a String[] partitions containing the constraints for each partition in the format above. The method should "EMPTY", "OVERLAP", "INCOMPLETE" or "OK" (the meanings of these Strings are explained above).

Definition

Class:	TablePartitions
Method:	validate
Parameters:	int, String[]
Returns:	String
Method signature:	String validate(int n, String[] partitions)
(be sure your method is public)

Notes

- A partition might have no constraints, meaning that all elements can go into this partition (see example 6).

- Remember that the integer fields in a valid element is always between 0 and 100, inclusive.

- There can be multiple constraints on the same column in one partition, see example 0.

- All quotes around the return Strings above are for clarity only.

Constraints

- n will be between 1 and 8, inclusive.

- partitions will contain between 1 and 50 elements, inclusive.

- Each element in partitions will contain between 0 and 50 characters, inclusive.

- Each element in partitions with more than 0 characters will contain a space separated list of constraints in the format specified above.

- There will be no leading or trailing spaces in the elements in partitions.

- Each constraint in the elements in partitions will be separated with exactly one space.

Examples

0)

{"a>3 a>2",
 "a<=3 b>5",
 "b<6 a<=3"}

Returns: "OK"

This is the example in the problem statement with the addition of a redundant constraint in the first partition. This doesn't affect the partitioning though, so the method returns "OK" since all elements with a>3 go into the first partition, while the other two partitions require that a is no more than 3 and that b is 6 or greater (second partition) or 5 or less (third partition).

1)

{"a=0 a=1",
 "a>=2"}

Returns: "EMPTY"

The first partition requires that a is both 0 and 1 which obviously is a contradiction. Thus no element can go into this partition and therefore it's an empty partition. The method returns "EMPTY".

2)

{"a>=5",
 "b<=6"}

Returns: "OVERLAP"

The element "a=10, b=0" satisfies the constraints in both partitions, so there clearly is an overlap.

3)

{"d<17 b<40",
 "d>=17 d<65 b<39",
 "d>=65 b<39",
 "d>=17 d<22 b=39",
 "d>=22 d<47 b=39",
 "d>=47 b>=39 b<61",
 "d<9 b>=40 b<61 a<51",
 "d<9 b>=61 b<89 a<51",
 "d<28 d>=9 b>=40 b<75 a<=50",
 "d<28 d>=9 b>=75 b<89 a<=50",
 "d>=28 d<47 b>=40 b<97",
 "d<28 b>=89",
 "d>=28 d<65 b>=97",
 "d>=47 d<65 b>=61 b<97",
 "d>=65 d<=100 b>=61",
 "d>=0 d<28 b>=40 b<89 a>50"}

Returns: "OK"

4)

{"d<17 b<40",
 "d>=17 d<65 b<39",
 "d>=65 b<39",
 "d>=17 d<22 b=39",
 "d>=22 d<47 b=39",
 "d>=47 b>=39 b<61",
 "d<9 b>=40 b<61 a<51",
 "d<9 b>=61 b<88 a<51",
 "d<28 d>=9 b>=40 b<75 a<=50",
 "d<28 d>=9 b>=75 b<89 a<=50",
 "d>=28 d<47 b>=40 b<97",
 "d<28 b>=89",
 "d>=28 d<65 b>=97",
 "d>=47 d<65 b>=61 b<97",
 "d>=65 d<=100 b>=61",
 "d>=0 d<28 b>=40 b<89 a>50"}

Returns: "INCOMPLETE"

Element "a=0, b=88, c=0, d=0" doesn't satisfy any constraint, and there are no overlaps nor empty partitions, so the method returns "INCOMPLETE".

5)

{""}

Returns: "OK"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MnemonicMemory

Brute Force, Simple Search, Iteration, String Parsing

Used in:

SRM 357

Used as:

Division II Level One

Writer:

ValD

Testers:

PabloGilberto , brett1479 , Olexiy , lovro

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2432

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10766&pm=2432

Problem Statement

It is often helpful to have a mnemonic phrase handy for a math test. For example, the number 25735 can be remembered as "is there anybody out there". If we count the number of characters in every word, we would get the sequence 2, 5, 7, 3, 5, which represents the original number!

Unfortunately for you, your professor likes to make the students memorize random numbers and then test them. To beat the system, your plan is to come up with mnemonic phrases that will represent the numbers you must memorize.

You are given a String number and a String[] dictionary. Return a single space delimited list of words, where each word is an element of dictionary, and no element of dictionary is used more than once. The phrase must contain exactly n words, where n is the number of digits in the number, and the length of the i-th word must be equal to the i-th digit of the number for all i. If more than one phrase is possible, return the one that comes first alphabetically (in other words, if you have several words of the same length, you should use them in alphabetical order).

Definition

Class:	MnemonicMemory
Method:	getPhrase
Parameters:	String, String[]
Returns:	String
Method signature:	String getPhrase(String number, String[] dictionary)
(be sure your method is public)

Constraints

-

dictionary will contain between 1 and 50 elements, inclusive.

-

Each element of dictionary will contain between 1 and 9 characters, inclusive.

-

Each element of dictionary will contain only lowercase letters ('a'-'z').

-

number will contain between 1 and 50 characters, inclusive.

-

number will contain only digits between '1' and '9', inclusive.

-

There will always be a possible solution with the given dictionary.

Examples

0)

"25735"

{"is", "there", "anybody", "out", "there"}

Returns: "is there anybody out there"

The example from the problem statement.

1)

"31415926"

{"may", "i", "have", "a", "large", "container", "of", "coffee"}

Returns: "may a have i large container of coffee"

Make sure you use words of the same length in alphabetical order.

2)

"1212"

{"a", "aa", "a", "aa"}

Returns: "a aa a aa"

3)

"11111111122"

{"a", "b", "d", "c", "a", "e", "f", "z", "zz", "za", "az", "e"}

Returns: "a a b c d e e f z az za"

4)

"2222"

{"ab", "cd", "ef", "a", "b", "ab"}

Returns: "ab ab cd ef"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Mortgage

Math, Search

Used in:

SRM 189

Used as:

Division II Level Three

Writer:

lars2520

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2427

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4765&pm=2427

Problem Statement

When purchasing a new home, the purchasers often take out a loan to pay for it. In this problem, we will be considering loans with the following terms:

At the beginning of each month, the purchasers pay a fixed amount towards settling the loan, which decreases the amount they owe.
At the end of the month, the amount the purchasers owe increases due to interest. Each month, 1/12 of the annual interest rate is added to the amount owed. Hence, if the annual interest rate is 12%, then the debt increases by 1% each month. You may assume that the amount owed after adding interest is always rounded up to the nearest dollar greater than or equal to the actual value.

Your task is, given the annual interest rate in tenths of a percent, the original amount of the loan, and the period over which the loan is to be repaid, calculate the minimum integral monthly payment so that the loan is repaid in term years or less. All monetary units are in dollars.

For example, if loan = 1000, interest = 50, and term = 1, then the loan is for $1000, to be paid back in one year, at an annual interest rate of 5%, or (5/12)% per month. If the purchasers pay back $86 every month, then the total amount owed will be as follows after each month:

month | after making payment | after interest accrues
------+----------------------+------------------------------------
 1    | 1000 - 86 = 914      | ceiling(914 * (1 + 5/12/100)) = 918
 2    | 918 - 86  = 832      | ceiling(832 * (1 + 5/12/100)) = 836
 3    | 836 - 86  = 750      | 754
 4    | 754 - 86  = 668      | 671
 5    | 671 - 86  = 585      | 588
 6    | 588 - 86  = 502      | 505
 7    | 505 - 86  = 419      | 421
 8    | 421 - 86  = 335      | 337
 9    | 337 - 86  = 251      | 253
 10   | 253 - 86  = 167      | 168
 11   | 168 - 86  = 82       | 83
 12   | 86 is more than enough to pay off the rest

Clearly, 85 a month wouldn't be enough, since we just barely paid off the loan at 86.

Definition

Class:	Mortgage
Method:	monthlyPayment
Parameters:	int, int, int
Returns:	int
Method signature:	int monthlyPayment(int loan, int interest, int term)
(be sure your method is public)

Constraints

-

loan will be between 100 and 2,000,000,000, inclusive.

-

interest will be between 1 and 1,000,000, inclusive.

-

term will be between 1 and 1000, inclusive.

Examples

0)

Returns: 86

From the problem statement.

1)

2000000000

Returns: 671844808

interest = 6000 means that the monthly interest is a whopping 50%!

2)

Returns: 988143

The interest is so high that even if we had 1000 years to pay back the loan, we'd still have to pay almost a million dollars a month.

3)

Returns: 10868

4)

1999999999

Returns: 1976284585

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EigenVector

Brute Force, Math

Used in:

SRM 192

Used as:

Division I Level Two , Division II Level Three

Writer:

Rustyoldman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2423

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4780&pm=2423

Problem Statement

A matrix is a rectangular (two-dimensional) array of numbers. A vector is a linear sequence of numbers, a one dimensional array. There are row vectors and column vectors. We use only column vectors in this problem. How to multiply a matrix by a column vector (vector on the right) to yield another column vector is described in the notes section.

A right eigenvector, X, of a square matrix, A, is a (nonzero) column vector that satisfies AX=kX, where k is a nonzero scalar constant called an eigenvalue (usually represented by lambda). In other words, multiplying the matrix by the eigenvector yields a vector which is proportional to the eigenvector. For the vectors to be proportional by the factor k, each element of the resulting vector is k times the corresponding element of X, k*X[i].

Given a matrix, find the smallest right eigenvector of that matrix where each element of the eigenvector is an integer. Smallest is defined by the L₀ norm, which is the sum of the absolute values of the elements of the vector. The first nonzero element of the eigenvector should be positive (if it is not positive, multiply all the elements by -1). If there are equally small integer eigenvectors, return the lexicographically first eigenvector. A vector v₁ comes before v₂ lexicographically if v₁ has a smaller element in the first position for which the two vectors differ.

To simplify this problem, the input matrix, A, will be at most 5 by 5 and will always have an integer eigenvector with L₀ norm between 1 and 9 inclusive.

Some valid vectors (L₀ = 5, in lexicographic order):

{0,0,0,5}

{0,0,2,-3}

{1,0,-2,2}

{1,0,1,3}

Some invalid vectors:

{0,0,0} vector must be nonzero

{0,0,-1} first nonzero element must be positive

{0,-1,3} first nonzero element must be positive

{-1,2,3} first nonzero element must be positive

For example:

{"1 0 0 0 0",
 "0 1 0 0 0",
 "0 0 1 0 0",
 "0 0 0 1 0",
 "0 0 0 0 1"}

The identity matrix, I, is unusual in terms of eigenvalues and eigenvectors. All the eigenvalues are 1, and every nonzero vector is an eigenvector. The first one in our ordering is {0,0,0,0,1}.

Definition

Class:	EigenVector
Method:	findEigenVector
Parameters:	String[]
Returns:	int[]
Method signature:	int[] findEigenVector(String[] A)
(be sure your method is public)

Notes

-

To calculate matrix-column vector multiplication, AX = Y, where A is an n by n matrix, and X and Y are length n column vectors, use something like: for(i) { Y[i] = 0 ; for(j) { Y[i] = Y[i] + A[i,j] * X[j] ; } }

Constraints

-

A will be the string representation of an n by n integer matrix where n is between 2 and 5 inclusive. Each element of A represents a row of the matrix with n integer elements in each row.

-

A will contain exactly n elements (rows).

-

Each element of A will contain exactly n integers (characters between '0' and '9' inclusive, optionally preceded by a minus sign '-'), each separated by a single space.

-

There will be no leading or trailing spaces in each element of A. For example: "10 2 0 -4" (quotes for clarity)

-

Each of the integers in A will be between -1000 and 1000 inclusive, with no leading zeros.

-

The matrix A will have at least one integer right eigenvector having an L₀ norm between 1 and 9 inclusive.

Examples

0)

{"1 0 0 0 0",
 "0 1 0 0 0",
 "0 0 1 0 0",
 "0 0 0 1 0",
 "0 0 0 0 1"}

Returns: { 0,  0,  0,  0,  1 }

The example from above, the identity matrix.

1)

{"100 0 0 0",
 "0 200 0 0",
 "0 0 333 0",
 "0 0 0 42"}

Returns: { 0,  0,  0,  1 }

All diagonal matrices (including the identity matrix) will have the same answer: n-1 zeros followed by a one.

2)

{"10 -10 -10 10",
 "20 40 -10 -10",
 "10 -10 10 20",
 "10 10 20 5"}

Returns: { 1,  -5,  2,  0 }

3)

{"30 20","87 2"}

Returns: { 2,  3 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WorldPeace

Advanced Math, Math, Sorting

Used in:

SRM 204

Used as:

Division I Level Three

Writer:

vorthys

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2420

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5850&pm=2420

Problem Statement

You have decided to organize a grassroots campaign for world peace. Your plan is to assign ordinary citizens into groups of k penpals such that each group contains citizens from k different countries. People in each group will exchange letters in an effort to increase their understanding of each other's cultures. Given k and the populations of the participating countries as a int[] countries, you must determine the maximum number of groups that can be formed.

Note that no individual may be assigned to more than one group, and that some individuals may be left without a group.

Definition

Class:	WorldPeace
Method:	numGroups
Parameters:	int, int[]
Returns:	long
Method signature:	long numGroups(int k, int[] countries)
(be sure your method is public)

Constraints

-

k is between 2 and 20, inclusive.

-

countries contains between k and 50 elements, inclusive.

-

Each element of countries is between 1 and 1000000000 (one billion), inclusive.

Examples

0)

{ 4,4,4,4,4 }

Returns: 5

Suppose the countries are Canada, China, Poland, Sweden, and the USA. Then you can make 5 groups as follows:

     Canada, China,  Poland, Sweden
     Canada, China,  Poland, USA
     Canada, China,  Sweden, USA
     Canada, Poland, Sweden, USA
     China,  Poland, Sweden, USA

1)

{ 1,2,3,4,5,6 }

Returns: 3

Suppose the countries are designated 1 through 6, according to population. Then three groups are possible:

   2,3,4,5,6
   2,3,4,5,6
   1,3,4,5,6

There are six people left unassigned, but they come from only three different countries, so they cannot be made into another group.

2)

{ 1000000000, 1000000000, 1000000000, 1000000000, 1000000000, 1000000000 }

Returns: 3000000000

3)

{ 96, 17, 32, 138, 112, 50, 7, 19, 412, 23, 14, 50, 47, 343, 427, 22, 39 }

Returns: 166

4)

{ 638074479, 717901019, 910893151, 924124222, 991874870, 919392444, 729973192, 607898881, 
  838529741, 907090878, 632877562, 678638852, 749258866, 949661738, 784641190, 815740520, 
  689809286, 711327114, 658017649, 636727234, 871088534, 964608547, 867960437, 964911023, 
  642411618, 868318236, 793328473, 849540177, 960039699, 998262224, 775720601, 634685437, 
  743766982, 826321850, 846671921, 712570181, 676890302, 814283264, 958273130, 899003369, 
  909973864, 921987721, 978601888, 633027021, 896400011, 725078407, 662183572, 629843174, 
  617774786, 695823011 }

Returns: 3983180234

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PolynomialMultiplier

Math, String Parsing

Used in:

SRM 188

Used as:

Division II Level Three

Writer:

legakis

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2418

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4760&pm=2418

Problem Statement

Two polynomials are multiplied together by multiplying each term in the first polynomial with each term in the second polynomial, and adding all of these individual products together. For example:


      (4*x^4 + 1) * (3*x^5 + 7*x)
    = (4*x^4 * 3*x^5) + (4*x^4 * 7*x) + (1 * 3*x^5) + (1 * 7*x)
    = 12*x^9 + 28*x^5 + 3*x^5 + 7*x

This can be simplified by combining the two x^5 terms:


    = 12*x^9 + 31*x^5 + 7*x

Write a program which multiplies two polynomials, and simplifies the product by combining terms with the same exponent. Each polynomial will be a function of x, and will consist of one or more terms separated by " + " (a space, '+', and another space). Each term will be in one of the following forms:


    1
    #
    x
    x^#
    #*x
    #*x^#
    (Each '#' character represents a single digit between '2' and '9', inclusive.)

Your program should return the product as a sum of terms, each in one of the formats above, except that the coefficients and exponents in your return value may be larger than a single digit. (Note that coefficients and exponents of 1 are omitted.) In between each term, insert the String " + " (a space, '+', and another space). You should output the terms in order from largest exponent of x to smallest exponent of x. If two or more terms have the same exponent, add their coefficients together to combine them into a single term.

Definition

Class:	PolynomialMultiplier
Method:	product
Parameters:	String, String
Returns:	String
Method signature:	String product(String f1, String f2)
(be sure your method is public)

Notes

-

The terms in the input functions will not necessarily be sorted by exponent of x.

-

There may be multiple terms in the input function with the same exponent of x.

Constraints

-

f1 and f2 will each contain between 1 and 50 characters, inclusive.

-

f1 and f2 will conform to the formatting rules in the problem statement.

Examples

0)

"1 + x"

"1 + x"

Returns: "x^2 + 2*x + 1"

      (1 + x) * (1 + x)
    = 1 + x + x + x*x
    = x^2 + 2*x + 1

Remember to combine terms with equal exponents, and sort from greatest to smallest exponent.

1)

"4*x^4 + 1"

"3*x^5 + 7*x"

Returns: "12*x^9 + 31*x^5 + 7*x"

This is the example from the problem statement.

2)

"1 + x + 1 + x"

"5 + 5"

Returns: "20*x + 20"

3)

"8*x^5"

"9*x^7"

Returns: "72*x^12"

4)

"5*x^3 + x^4 + 8 + 2*x^6"

"3*x^5 + 4*x + 7*x^9"

Returns: 
"14*x^15 + 7*x^13 + 35*x^12 + 6*x^11 + 59*x^9 + 15*x^8 + 8*x^7 + 28*x^5 + 20*x^4 + 32*x"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GravityBomb

Simulation, String Manipulation

Used in:

SRM 200

Used as:

Division II Level Two

Writer:

antimatter

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2417

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5075&pm=2417

Problem Statement

Tetris is one of those games that is everywhere; there aren't too many people who haven't seen it in some form or another since its conception in 1985. The concept is fairly simple. You have a vertically-oriented rectangular grid. Pieces, which are made up of some number of 1x1 blocks, fall downwards. Whenever an entire row of the grid is full of blocks, all of the blocks in that row disappear and all the pieces above are shifted downwards by a row.

TopCoder member antimatter is not very good at Tetris. The pieces drop too fast, he says. He's been toying with the idea of coding his own version, with one twist: the addition of the Gravity Bomb, which does not appear on the board. When the Gravity Bomb is activated, if any block is immediately above an empty space, it falls into that space. This process is repeated until there are no more blocks immediately above empty spaces. Then, any completed row of blocks will be removed and the blocks above them shifted downwards, until there are no more complete rows.

The board has a fixed width and height, and the initial state of the board will be represented as a String[] board. The first element of board is the top row, the second element is the row immediately below it, and so on. The character 'X' will represent the presence of a block, and the character '.' will represent an empty space. Your method should return the state of the board after the Gravity Bomb is used, in the same format. Your return value should have the same number of rows and columns as the input.

Definition

Class:	GravityBomb
Method:	aftermath
Parameters:	String[]
Returns:	String[]
Method signature:	String[] aftermath(String[] board)
(be sure your method is public)

Constraints

- board will contain between 1 and 50 elements, inclusive

- each element of board will contain between 1 and 50 characters, inclusive

- each element of board will be the same length

- each character in board will be either 'X' or '.'

Examples

0)

{"..X",
 "X.X",
 ".X."}

Returns: { "...",  "...",  "..X" }

After the Gravity Bomb is used, the board looks like this:

... ..X XXX Then we remove the completed line at the bottom and move all blocks above downwards.

1)

{"...",
 "X..",
 ".X."}

Returns: { "...",  "...",  "XX." }

Here there are no complete lines.

2)

{"XXXXXX",
 "......",
 "......"}

Returns: { "......",  "......",  "......" }

3)

{"XX.XX....XX"}

Returns: { "XX.XX....XX" }

4)

{"X",".",".",".",".",".",".",".",".",".",".",".",".",
 ".",".",".",".",".",".",".",".",".",".",".",".",".",
 ".",".",".",".",".",".",".",".",".",".",".",".",".",
 ".",".",".",".",".",".",".",".",".",".","."}

Returns: 
{ ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 ".",
 "." }

5)

{"XXX", "XXX"}

Returns: { "...",  "..." }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NCMultiplication

Advanced Math, Search

Used in:

SRM 200

Used as:

Division I Level Two

Writer:

antimatter

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2416

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5075&pm=2416

Problem Statement

The usual longhand scheme for multiplying two numbers A and B is to multiply the last digit of B by A, shift left by one digit, multiply the second-to-last digit of B by A, and so on. This process is illustrated below:

   36
x  15
-----
  180
+ 36
-----
  540

But let's say we didn't multiply in the usual way. Let us define a new method of multiplication called "NC-Multiplication", where the "NC" stands for "No Carry". It is called this because we do not carry when numbers exceed 9, no matter what. To multiply 36 by 15 in this manner, we would do:

     3  6
x    1  5
---------
    15 30
+ 3  6
---------
  3 21 30

and so the result would be {3, 21, 30}.

You will be given a int[] digits, that represents the result of NC-multiplying two numbers together. You wish to factor this result by finding the two numbers that multiplied together to form the result. There may be multiple pairs of numbers that work. If we call the larger number A and the smaller B, then we want the pair such that A - B is minimized. Of this pair, your method should return a long that is equal to A. If no such A and B exist that NC-multiply to digits, your method should return -1.

Definition

Class:	NCMultiplication
Method:	findFactors
Parameters:	int[]
Returns:	long
Method signature:	long findFactors(int[] digits)
(be sure your method is public)

Constraints

-

digits will contain between 1 and 15 elements, inclusive.

-

All elements of digits will be between 0 and 2000, inclusive.

-

At least one element in digits will be nonzero.

-

The number represented by digits will be less than 10¹⁴ = 100000000000000.

-

There will be no leading or trailing zeros in digits.

Examples

0)

{3,21,30}

Returns: 36

36 and 15 NC-Multiply together to make {3,21,30}, as seen above.

1)

{15,3,6}

Returns: 512

2)

{4,20,25}

Returns: 25

25 NC-Multiplied by 25.

3)

{6,61,124,129,90,27}

Returns: 6773

4)

{8,14,22,95,125,120,73,9,9}

Returns: -1

5)

{6, 5, 32, 68, 113, 143, 143, 124, 100, 75, 48, 23, 7, 1}

Returns: 65864431

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MusicalChairs

Simple Math

Used in:

TC China 08 - 1B

Used as:

Division I Level Two

Writer:

Eeyore

Testers:

PabloGilberto , brett1479 , Olexiy , marian , ivan_metelsky , ged

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2407

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13674&pm=2407

Problem Statement

In the game of Musical Chairs, n players walk around a circle of n-1 chairs while music plays on the stereo. When the music stops, everyone hurries to claim a chair. The player who is left standing gets knocked out of the game.

You are given a String[] playerNames containing the names of the players, ordered according to their position at the start of the game, such as the following.

  {"Emma Sue", "Billy Bob Thornton", "Joe", "Cassius Clay"}

You are also given a String chairs describing the arrangement of chairs with an 'h' (lowercase letter H) for each chair and exactly one '.' (period) indicating a gap. The i-th character of chairs corresponds to the i-th element of playerNames. For instance, the chairs might be arranged as follows.

  "hh.h"

The player by the gap is the one who gets knocked out. For example, if the four players above are in their starting order when the music stops, then Joe gets knocked out.

For each second of music, the players advance one position. From the original order shown above, for example, the players' order changes to the following after one second.

  {"Cassius Clay", "Emma Sue", "Billy Bob Thornton", "Joe"}

Given an int seconds specifying the number of seconds that the music is played, return the name of the player who gets knocked out.

Definition

Class:	MusicalChairs
Method:	knockedOut
Parameters:	String[], String, int
Returns:	String
Method signature:	String knockedOut(String[] playerNames, String chairs, int seconds)
(be sure your method is public)

Constraints

-

playerNames will contain between 2 and 50 elements, inclusive.

-

Each element of playerNames will contain between 1 and 50 characters, inclusive.

-

playerNames will contain only letters ('A'-'Z', 'a'-'z') and spaces (' ').

-

chairs will contain the same number of characters as the number of elements in playerNames.

-

Exactly one character in chairs will be '.', and all the other characters will be 'h'.

-

seconds will be between 0 and 600, inclusive.

Examples

0)

{"Emma Sue", "Billy Bob Thornton", "Joe", "Cassius Clay"}

"hh.h"

Returns: "Billy Bob Thornton"

The example from the problem statement.

1)

{"Emma Sue", "Billy Bob Thornton", "Joe", "Cassius Clay"}

"hh.h"

Returns: "Joe"

After 4 seconds, the players are exactly at the same positions as in the beginning.

2)

{"Jack Dempsey", "Joe Louis", "Rocky Marciano",
 "Cassius Clay", "George Foreman", "Mike Tyson"}

"h.hhhh"

Returns: "Mike Tyson"

3)

{"  itchy   ", "SCRATCHY"}

".h"

Returns: "  itchy   "

4)

{"Moe", "Larry", "Curly", "Moe"}

"hh.h"

Returns: "Moe"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GolfScore

Simple Math, String Manipulation

Used in:

SRM 186

Used as:

Division II Level One

Writer:

Eeyore

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2405

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4750&pm=2405

Problem Statement

A full-sized golf course consists of 18 lawns known as holes. The player's objective is to strike a ball with his club in such a way that it travels from a specified point at one end of the lawn to a specified point at the other, and to do so with as few strokes as he can. Associated with each hole is a positive number, the par, which is the number of strokes it is expected to take a competent golfer to complete the hole.

A player's performance on an individual hole is described by a phrase that depends on the number of strokes he took relative to par. To make a "bogey", for example, means that the player has completed a hole in one stroke more than the par value, and a "double bogey" is two strokes over par. Two strokes under par, on the other hand, is an "eagle", while the "albatross", a rare bird indeed, is three strokes under par. The following is a complete dictionary of scoring phrases.

    
    "triple bogey"  three strokes over par
    "double bogey"  two strokes over par
    "bogey"         one stroke over par
    "par"           exactly par 
    "birdie"        one stroke under par
    "eagle"         two strokes under par
    "albatross"     three strokes under par
    "hole in one"   exactly one stroke

The managers of Gravel Mountain Golf Course have contracted you to implement a score-management system that will translate a single player's scores from the above jargon to a numerical total. You are given a int[] specifying the par value of each of the course's 18 holes in playing order. You are also given a String[] such that the nth String describes the player's score on the nth hole. The reported scores will be valid and complete. Compute the player's total score and return it as an int.

Definition

Class:	GolfScore
Method:	tally
Parameters:	int[], String[]
Returns:	int
Method signature:	int tally(int[] parValues, String[] scoreSheet)
(be sure your method is public)

Constraints

-

parValues and scoreSheet each contain exactly 18 elements

-

each element of parValues is between 1 and 5, inclusive

-

each element of scoreSheet is one of the eight phrases listed above

-

no element of scoreSheet describes an impossible score

Examples

0)

{1, 1, 1, 1, 1, 1,
 1, 1, 1, 5, 5, 5,
 5, 5, 5, 5, 5, 5}

{"bogey", "bogey", "bogey", "bogey", "bogey", "bogey",
 "bogey", "bogey", "bogey", "eagle", "eagle", "eagle",
 "eagle", "eagle", "eagle", "eagle", "eagle", "eagle"}

Returns: 45

The player took 9*2 = 18 strokes on the front nine and 9*3 = 27 on the back nine for a total score of 18+27 = 45.

1)

{3, 2, 4, 2, 2, 1,
 1, 1, 3, 2, 4, 4,
 4, 2, 3, 1, 3, 2}

{"bogey", "double bogey", "par", "double bogey", "double bogey", "triple bogey",
 "triple bogey", "triple bogey", "bogey", "double bogey", "par", "par",
 "par", "double bogey", "bogey", "triple bogey", "bogey", "double bogey"}

Returns: 72

This player takes four strokes on every hole.

2)

{3, 2, 4, 2, 2, 1,
 1, 1, 3, 2, 4, 4,
 4, 2, 3, 1, 3, 2}

{"eagle", "birdie", "albatross", "birdie", "birdie", "par",
 "hole in one", "par", "eagle", "birdie", "albatross", "albatross",
 "albatross", "birdie", "eagle", "hole in one", "eagle", "birdie"}

Returns: 18

This can only be Tiger Woods.

3)

{4, 1, 3, 3, 4, 4,
 1, 4, 2, 3, 3, 5,
 4, 1, 4, 4, 2, 1}

{"triple bogey", "triple bogey", "bogey", "par", "triple bogey", "double bogey",
 "triple bogey", "triple bogey", "par", "eagle", "bogey", "bogey",
 "birdie", "par", "triple bogey", "eagle", "triple bogey", "triple bogey"}

Returns: 77

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CutoffRounder

Math

Used in:

SRM 189

Used as:

Division II Level One

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2404

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4765&pm=2404

Problem Statement

Often, when we round a real valued number to an integer, we round up if the fractional part is 0.5 or greater, and down if the fractional part is less than 0.5. In this problem, you are to write a method round, which takes a real valued number as a String, num, and a cutoff as a String, cutoff. cutoff will be formatted exactly as "0.####", where each '#' represents a digit ('0'-'9'). At least one of the digits to the right of the decimal point in cutoff will be non-zero. Your task is to round num up if its fractional part is greater than cutoff, and down otherwise, and return the result as an int. To avoid issues with double imprecision, the fractional part of num will not be exactly equal to cutoff

Hence, the traditional rounding method described in the opening sentence would be represented by cutoff = "0.5000"

Definition

Class:	CutoffRounder
Method:	round
Parameters:	String, String
Returns:	int
Method signature:	int round(String num, String cutoff)
(be sure your method is public)

Constraints

- cutoff will be formatted exactly as "0.####", where each '#' represents a digit ('0'-'9').

- num will be a sequence of one or more digits ('0'-'9'), with an optional decimal point ('.').

- num will contain between 1 and 10 characters, inclusive.

- The fractional part of num will not be exactly equal to cutoff.

Examples

0)

"003.656930"

"0.5000"

Returns: 4

0.65693 is greater than 0.5000, so we round up.

1)

".001"

"0.0001"

Returns: 1

A very low cutoff.

2)

"1.99999999"

"0.9999"

Returns: 2

3)

"135"

"0.6531"

Returns: 135

4)

"135."

"0.6531"

Returns: 135

5)

"1356.13671"

"0.1367"

Returns: 1357

6)

"0.00010001"

"0.0001"

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BoxLoader

Simple Math

Used in:

SRM 192

Used as:

Division II Level One

Writer:

Rustyoldman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2403

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4780&pm=2403

Problem Statement

Your company has a new box loading robot. It is your job to program it to pack items into the shipping boxes. The robot does not have a very large program memory so you are restricted to placing all the items into the boxes in the same orientation. Each item is a rectangular solid with dimensions itemX by itemY by itemZ. The box is also rectangular with the dimensions boxX by boxY by boxZ. The items can be placed in the box in any orthogonal orientation (ie. the sides of the items must be parallel to the sides of the box), but only whole items can be placed in the box. Your task here is to determine the greatest number of items that can be packed into the box (with all the items in the same orientation).

For example, if the box is 100x98x81 units and the items are 3x5x7 units, then orienting the items so they are 5x7x3, allows them to fit in the box in a 20x14x27 grid, filling the entire box, which is optimal: 7560 items.

Definition

Class:	BoxLoader
Method:	mostItems
Parameters:	int, int, int, int, int, int
Returns:	int
Method signature:	int mostItems(int boxX, int boxY, int boxZ, int itemX, int itemY, int itemZ)
(be sure your method is public)

Notes

-

There are six possible orientations for an item.

Constraints

-

boxX, boxY and boxZ will be between 1 and 1000 inclusive.

-

itemX, itemY and itemZ will be between 1 and 1000 inclusive.

Examples

0)

Returns: 7560

The example from above.

1)

Returns: 0

That's not going to fit!

2)

Returns: 100

There is going to be some empty space in this box, as none of the box dimensions is an exact multiple of an item dimension. Orienting the items so that the 30 unit dimension goes in the box's 301 unit direction wastes the least space. 10 items can fit leaving only one unit of waste in that dimension.

3)

Returns: 833

A less obvious example of minimizing the wasted space.

4)

Returns: 20

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OfficeParking

Simulation

Used in:

SRM 187

Used as:

Division II Level One

Writer:

Rustyoldman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2400

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4755&pm=2400

Problem Statement

The TopCoder office building is filled with very efficient people. Each of these people always parks their car in the closest (to the building) available parking space. The parking spaces are arranged linearly, with space number one being the closest to the building, space number two being the second closest to the building, etc.

Given a sequence of employee arrivals and departures, determine the number of parking spaces used that day. The parking lot is empty at the beginning of the day. Names are case sensitive.

For example in the sequence of events below:

{"Alice arrives",
 "bob arrives",
 "Alice departs",
 "Charles arrives",
 "bob departs",
 "Charles departs"}

Alice parks in space 1
bob parks in space 2
Alice vacates space 1
Charles parks in space 1
bob vacates space 2
Charles vacates space 1

The total number of parking spaces used is 2.

Definition

Class:	OfficeParking
Method:	spacesUsed
Parameters:	String[]
Returns:	int
Method signature:	int spacesUsed(String[] events)
(be sure your method is public)

Notes

-

HINT: If the maximum number of people at the office building at once is N, then there is never a reason for anyone to park in the (N+1)^st spot, as one of the first N spots must have been available when they arrived.

Constraints

-

events will have between 0 and 50 elements inclusive.

-

Each element of events must contain between 9 and 50 characters, inclusive.

-

Each element of events is formatted as "<name> <action>" (quotes for clarity).

-

Each <name> contains between 1 and 42 characters, inclusive.

-

Each <name> contains only letters ('a'-'z', 'A'-'Z').

-

Each <name> and <action> are separated by exactly one space character.

-

Each <action> is either "arrives" or "departs".

-

Departures will always have a matching arrival (with the exact same case sensitive name) in a previous element of events.

-

There will not be two arrivals of the exact same case sensitive name without an intervening departure of the exact same name.

Examples

0)

{"Alice arrives","bob arrives","Alice departs",
 "Charles arrives","bob departs","Charles departs"}

Returns: 2

The example above.

1)

{"AdminBrett arrives","lbackstrom arrives","AdminBrett departs","mike arrives",
 "TheFaxman arrives","AdminBrett arrives","lbackstrom departs","dok arrives",
 "AdminBrett departs","gt arrives","AdminBrett arrives","lbackstrom arrives",
 "AdminBrett departs","jhughes arrives","jhughes departs","TheFaxman departs",
 "MaryJoe arrives","AdminBrett arrives","AdminBrett departs","AdminBrett arrives"}

Returns: 6

2)

{"SnapDragon arrives","tomek arrives","JohnDethridge arrives","ZorbaTHut arrives",
 "snewman arrives","reid arrives","NGBronson arrives","Yarin arrives",
 "bstanescu arrives","mathijs arrives","radeye arrives","bladerunner arrives",
 "dgarthur arrives","venco arrives","dmwright arrives","WishingBone arrives",
 "Eryx arrives","antimatter arrives","ChristopherH arrives","lars arrives",
 "biggnate arrives","JanKuipers arrives","dary arrives","haha arrives","grotmol arrives",
 "XuChuan arrives","Ryan arrives","LunaticFrindge arrives","Wasteland arrives",
 "RunningWild arrives","hampster arrives","RalphFurmaniak arrives",
 "kyky arrives","qubits arrives","Rustyoldman arrives","turuthok arrives",
 "Vulpecular arrives","Eeyore arrives","wackes arrives","Ishan arrives",
 "dimkadimon arrives","dplass arrives","Olorin arrives","TangentZ arrives",
 "NeverMore arrives","Pops arrives","srowan arrives","tjq arrives",
 "vorthys arrives","schveiguy arrives"}

Returns: 50

3)

{"AdminBrett arrives","AdminBrett departs","AdminBrett arrives","AdminBrett departs",
 "AdminBrett arrives","AdminBrett departs","AdminBrett arrives","AdminBrett departs",
 "AdminBrett arrives","AdminBrett departs","AdminBrett arrives","AdminBrett departs",
 "AdminBrett arrives","AdminBrett departs","AdminBrett arrives","AdminBrett departs"}

Returns: 1

4)

{"snapdragon arrives","SnapDragon arrives",
 "AdminBrett arrives","AdminBrett departs",
 "SnapDragon departs","snapdragon departs"}

Returns: 3

5)

{"departs arrives","arrives arrives","arrives departs","departs departs"}

Returns: 2

Note that the first words are the names, and the second words are the actions.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

OddsAndEvens

Math

Used in:

SRM 194

Used as:

Division I Level Two

Writer:

dimkadimon

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2394

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5069&pm=2394

Problem Statement

Any integer is either odd or even. An even number is a number which divides by 2 without leaving any remainder. All other numbers are odd. We can create an arithmetic that deals with addition and multiplication of odd and even numbers. For example, the sum of two even numbers will also be an even number, but the sum of an odd and an even number must be an odd number. Here is the list of all possible sums and products in this arithmetic:

EVEN + EVEN = EVEN
EVEN + ODD = ODD
ODD + ODD = EVEN

EVEN * EVEN = EVEN
EVEN * ODD = EVEN
ODD * ODD = ODD

A list of integers is chosen. For each unique pair of numbers in the list we record their sum and product. Given the final contents of String[] sums and String[] products, where each element is either "ODD" or "EVEN", return the number of odd and even numbers in the original list. The corresponding elements in sums and products are NOT necessarily calculated from the same pair of numbers. Your return must be formatted as "EVEN <x> ODD <y>" where <x> is the number of evens and <y> is the number of odds. If the original list cannot be constructed then return "IMPOSSIBLE".

Definition

Class:	OddsAndEvens
Method:	find
Parameters:	String[], String[]
Returns:	String
Method signature:	String find(String[] sums, String[] products)
(be sure your method is public)

Constraints

-

sums will contain N(N-1)/2 elements where N is an integer between 2 and 10 inclusive.

-

products will contain the same number of elements as sums.

-

each element in sums will be either "ODD" or "EVEN".

-

each element in products will be either "ODD" or "EVEN".

Examples

0)

{"EVEN"}

{"ODD"}

Returns: "EVEN 0 ODD 2"

The only sum is even. Thus the two numbers are either both even or both odd. If the two numbers are both even then their product will also be even. This contradicts what we have in products. If the two numbers are both odd then their product will also be odd. This agrees with products. Thus there are two odd numbers.

1)

{"ODD"}

{"ODD"}

Returns: "IMPOSSIBLE"

If the sum is odd then one number is odd and the other is even. The product of an odd and even number is even. This contradicts products. Thus this is IMPOSSIBLE.

2)

{"EVEN","EVEN","EVEN"}

{"EVEN","EVEN","EVEN"}

Returns: "EVEN 3 ODD 0"

The sum and product of any two even numbers are always even. Here there are 3 even numbers.

3)

{"EVEN","ODD","ODD"}

{"ODD","EVEN","EVEN"}

Returns: "EVEN 1 ODD 2"

Two numbers are odd and one number is even. The two odd numbers give us one even sum and one odd product. The even number combined with the other two odd numbers gives two odd sums and two even products.

4)

{"ODD","EVEN","ODD","EVEN","ODD","EVEN"}

{"ODD","EVEN","EVEN","EVEN","ODD","ODD"}

Returns: "EVEN 1 ODD 3"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Percents

Brute Force, Math

Used in:

SRM 188

Used as:

Division I Level One , Division II Level Two

Writer:

legakis

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2386

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4760&pm=2386

Problem Statement

Statistics can be misleading, even if they are technically correct. For example, if you were told that 71.43% of people polled answered "yes" to a question, the two digits after the decimal place imply high precision, and that many people must have been polled in order to arrive at that level of accuracy. However, in this example, if only 7 people were polled and 5 answered "yes", (5/7)*100 = 71.43 (rounded to the nearest hundredth of a percent). Given a percentage rounded to two decimal places, we want to determine the minimum number of people who could have been polled.

Create a class Percents with a method minSamples. This method will take a String percent that gives the percentage of people who responded "yes" to a poll, rounded to the nearest hundredth of a percent. The String percent will be of the form "xx.xx%", where each 'x' represents a digit between '0' and '9', inclusive. The method should return an int, the minimum possible number of people who could have been polled to result in that percentage.

Definition

Class:	Percents
Method:	minSamples
Parameters:	String
Returns:	int
Method signature:	int minSamples(String percent)
(be sure your method is public)

Notes

-

All percentages are rounded to the nearest hundredth of a percent. In case the difference is exactly 0.005, round up.

-

The answer will be between 1 and 10000, inclusive, as any percentage to two decimal places can be achieved with 10000 people.

-

Note that, if there were d people, then the number of people who responded "yes" must be either floor(d*percent/100) or ceil(d*percent/100).

Constraints

-

percent will contain exactly 6 characters (with leading and/or trailing zeros if necessary), and will be between "00.00%" and "99.99%", inclusive.

Examples

0)

"25.00%"

Returns: 4

1 out of 4 is 25.00%.

1)

"66.67%"

Returns: 3

2 out of 3 is 66.67%, rounded to 2 decimal places.

2)

"66.66%"

Returns: 2858

1905 is 66.6550034895032% of 2858. 1905/2858 is the fraction with the smallest denominator that equals 66.66 when rounded to two decimal places.

3)

"71.43%"

Returns: 7

This is the example from the problem statement.

4)

"00.00%"

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumericalIntegral

Advanced Math, String Manipulation

Used in:

SRM 187

Used as:

Division I Level Two

Writer:

Rustyoldman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2375

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4755&pm=2375

Problem Statement

This problem contains HTML superscripts and images which will not display correctly for plugin users

Given two real numbers x1 and x2, calculate an approximation to the integral of e^{-x^2} evaluated between the limits from x1 to x2, which is accurate to the nearest 0.00001. Return the answer in a String, as a fixed point number with exactly five digits to the right of the decimal point and exactly one digit to the left of the decimal point.

For example: x1 = -0.5 and x2 = 0.5 returns "0.92256"

Definition

Class:	NumericalIntegral
Method:	integrate
Parameters:	double, double
Returns:	String
Method signature:	String integrate(double x1, double x2)
(be sure your method is public)

Notes

-

e^{-x^2} can be calculated in C++ with exp(-x*x) in math.h.
e^{-x^2} can be calculated in C# with Math.Exp(-x*x). The Math class is in the System namespace.
e^{-x^2} can be calculated in Java with Math.exp(-x*x).
e^{-x^2} can be calculated in Visual Basic with Exp(-x*x) in the System.Math namespace.

-

- The integral of a function is the area inside the closed figure formed by (on the top) the function between the limits of x=x1 and x=x2, (on the sides) vertical line segments at x=x1 and x=x2, and (on the bottom) the portion of the x axis between x=x1 and x=x2. This is shown by the shaded area above (the graph shows the function we are integrating, e^{-x^2}).

- The integral of e^{-x^2} is known to have no closed form, so don't waste time looking in a table of integrals for an exact formula.

- Because of the 2e-6 constraint, about 40% of randomly chosen x1 and x2 values will be too close to a possible rounding error and will be rejected. This is not an error. It gives you more room for numerical errors.

Constraints

- x1 will be less than x2.

- x2-x1 will be between 0.00001 and 1.00000 inclusive.

- x1 will be between -10.0 and 10.0 inclusive.

- x2 will be between -10.0 and 10.0 inclusive.

- To avoid rounding errors the inputs x1 and x2 must be chosen so that the answer is not within 2e-6 of 0.000005 + a multiple of 0.00001

Examples

0)

-0.5

0.5

Returns: "0.92256"

The example from above. This is the largest possible answer given the constraints of this problem.

1)

0.0

0.1

Returns: "0.09967"

2)

-9.0001

-9.0

Returns: "0.00000"

Values are very small out here.

3)

2.71828183

3.14159265

Returns: "0.00010"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MagicSquare

Simple Math

Used in:

SRM 188

Used as:

Division II Level One

Writer:

legakis

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2366

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4760&pm=2366

Problem Statement

A magic square is a 3x3 array of numbers, such that the sum of each row, column, and diagonal are all the same. For example:


    8 1 6
    3 5 7
    4 9 2

In this example, all rows, columns, and diagonals sum to 15.

You will be given a int[] representing the nine numbers of a magic square, listed left-to-right, top-to-bottom. However, one of these numbers will be replaced by a -1. Write a method to determine which number was removed. For example, if the 7 was removed from the magic square above, you would be given { 8, 1, 6, 3, 5, -1, 4, 9, 2 }, and your program should return 7.

The completed magic square will consist of exactly 9 distinct positive integers.

Definition

Class:	MagicSquare
Method:	missing
Parameters:	int[]
Returns:	int
Method signature:	int missing(int[] square)
(be sure your method is public)

Constraints

-

square will contain exactly 9 elements.

-

Each element of square will either be -1 or be between 1 and 100, inclusive.

-

Exactly one element of square will be -1.

-

The eight elements of square that are not -1 will be distinct.

-

The input will be such that a number between 1 and 100, inclusive, can be found to complete the magic square, and it will not be equal to any of the other 8 numbers in the square.

Examples

0)

{ 8, 1, 6, 3, 5, -1, 4, 9, 2 }

Returns: 7

This is the example from the problem statement.

1)

{ -1, 1, 6, 3, 5, 7, 4, 9, 2 }

Returns: 8

The same square, but this time with the number 8 removed.

2)

{ 5, 15, 13, 19, 11, 3, 9, 7, -1 }

Returns: 17

The missing number is 17.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CantorSet

Advanced Math

Used in:

SRM 284

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2355

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8081&pm=2355

Problem Statement

The Cantor Set is an important mathematical construction devised by the 19th century mathematician Georg Cantor. It is defined as follows:

Start with the set of real numbers from 0.0 to 1.0 inclusive, which is denoted by [0.0, 1.0]. Then

At step 1, remove the open middle third of [0.0, 1.0] ("open" means not including its endpoints).
At step 2, remove the open middle thirds of the 2 remaining intervals.
...
At step k, remove the open middle thirds of the 2^(k-1) remaining intervals.
...

The Cantor Set is the part of [0.0, 1.0] that is not removed by this process.

We want software to help determine if a given number is in the Cantor Set. Create a class CantorSet that contains a method removed that is given a String value that represents a real number in [0.0, 1.0] and returns the step at which value is removed in the above construction. If it is not removed before step 1,000,000 return 0 indicating that it is highly likely that it is in the Cantor Set.

Definition

Class:	CantorSet
Method:	removed
Parameters:	String
Returns:	int
Method signature:	int removed(String value)
(be sure your method is public)

Constraints

-

value will contain between 2 and 50 characters, inclusive.

-

The first character in value will be '.'.

-

All characters in value after the first will be digits '0'-'9'.

Examples

0)

".200"

Returns: 2

.2 is in the middle third of the lower third of [0.0, 1.0] so it is removed in step 2.

1)

".74928"

Returns: 14

2)

".975"

Returns: 0

This number is in the Cantor Set.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RaceApproximator

Simple Math

Used in:

SRM 184

Used as:

Division II Level One

Writer:

Running Wild

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2353

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4740&pm=2353

Problem Statement

If a runner races a distance D in time T, and later races a distance 2D, that runner will likely take more than 2T time to finish it. An examination of how times change with distances for a given runner can lead to the following approximation for the time it will take that runner to finish a given distance. Given two races with distances D₁ and D₂ which a runner ran in times T₁ and T₂, respectively, the approximate time it will take a runner to run a distance D is given by: T₁*e^(ln(T₂/T₁)*ln(D₁/D)/ln(D₁/D₂)).

When you race it is nice to have a time in mind that you'd like to be able to finish your race in. You are somewhat new to running and have only run two races of different distances. You are running a third race soon, and you want to use this equation to give you an estimate of how fast you should run. Since your upcoming race is a distance that falls between your first and second races' distances, you know this approximation will probably be fairly accurate. Create a class RaceApproximator with a method timeToBeat that takes ints d1, t1, d2, t2, and raceDistance, and returns a String that is the time you should be able to run in your upcoming race. d1, t1, d2 and t2 represent your shorter race's distance, your time in that race, your longer race's distance, and your time in that race, respectively. raceDistance is the distance of your upcoming race. All distances are in meters and all times are in seconds. Your return value should be truncated to an integer value, and formatted as "h:mm:ss" (all quotes are for clarity only) with"h" being the number of hours, "mm" being the number of minutes, and "ss" being the number of seconds.

Definition

Class:	RaceApproximator
Method:	timeToBeat
Parameters:	int, int, int, int, int
Returns:	String
Method signature:	String timeToBeat(int d1, int t1, int d2, int t2, int raceDistance)
(be sure your method is public)

Notes

-

In C++ e^x can be done with exp(x), and the natural log, ln(x), can be done with log(x), both functions are in math.h.

-

In C# e^x can be done with Math.Exp(x), and the natural log, ln(x), can be done with Math.Log(x). The Math class is in the System namespace.

-

In Java e^x can be done with Math.exp(x), and the natural log, ln(x), can be done with Math.log(x).

-

In Visual Basic e^x can be done with Exp(x), and the natural log, ln(x), can be done with Log(x), both functions are in the System.Math namespace.

Constraints

-

d1, t1, d2, t2, and raceDistance will all be between 1 and 10000, inclusive.

-

d1 will be less than d2

-

t1 will be less than t2

-

raceDistance will be greater than d1 and less than d2

-

To make the approximation reliable, all speeds (distance/time) will be between 1 meter/second and 10 meters/second, inclusive.

-

To avoid rounding errors, the return will never be within 1e-9 of an integer value.

Examples

0)

Returns: "0:03:57"

Suzy Favor Hamilton's times for 800 meters and 5000 meters indicate that she should run 1500 meters in 3:57, which, in fact, is her time for 1500 meters.

1)

Returns: "0:02:30"

You can run 400 meters in 65 seconds, and 1600 meters in 5 minutes and 50 seconds, so you can probably run 800 meters in about 2 minutes and 30 seconds.

2)

Returns: "0:18:00"

3)

Returns: "1:06:00"

4)

Returns: "0:21:06"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BagOfHolding

Brute Force, Math

Used in:

SRM 184

Used as:

Division II Level Two

Writer:

Running Wild

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2348

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4740&pm=2348

Problem Statement

You are in possesion of a special Bag of Holding. You can put any items in this bag that you want and it never becomes bulkier or heavier. Whenever you want to take something out of the bag you just reach in and pull it out, if it isn't obscured by other items. Whenever you put an item in the bag, it will obscure all items already in the bag that are as small or smaller than it, preventing you from pulling those items out of the bag.

You have quite a few items that you want to keep in the bag, and you are wondering if you put all the items in the bag randomly, what are the odds that you'll be able to reach a certain item. Clearly you will only be able to reach that item if no items as big or bigger than it were put into the bag after it, and the ordering of items smaller than the item in question doesn't matter. Create a class BagOfHolding with a method oddsReachable that takes a int[] sizes, which contains the sizes of each item, and an int item, which is the index of the item in sizes that you are concerned with (the first item in the sizes is item 0), and returns a double that is the percent chance that you will be able to reach that item if you put all the items into the bag at random.

Definition

Class:	BagOfHolding
Method:	oddsReachable
Parameters:	int[], int
Returns:	double
Method signature:	double oddsReachable(int[] sizes, int item)
(be sure your method is public)

Constraints

-

sizes will contain between 1 and 10 elements, inclusive.

-

Every element of sizes will be between 1 and 10000, inclusive.

-

item will be between 0 and the number of elements in sizes-1, inclusive.

Examples

0)

{1,2,3}

Returns: 0.5

There are six orders in which these items could be put in the bag: {1,2,3}, {1,3,2}, {2,1,3}, {2,3,1}, {3,1,2}, {3,2,1}. We want to be able to reach the item with a size of 2, and we will be able to in 3 of the 6 orderings, so we return .5.

1)

{1,2,3}

Returns: 1.0

Same items, but this time we want to be able to reach the item with a size of 3. Since it is larger than all of the other items we will always be able to reach it, so we return 1.

2)

{1,1,2,3}

Returns: 0.5

Like example 0, but now there is another item of size 1. Remember that {1,1,2,3} can be two different orderings, since there are two distinct items of size 1.

3)

{1,2,3,4,5,6,7,8,9,10}

Returns: 0.16666666666666666

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SquareFree

Advanced Math

Used in:

SRM 190

Used as:

Division I Level Three

Writer:

dgarthur

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2342

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4770&pm=2342

Problem Statement

A positive integer is said to be squarefree if it is divisible by no perfect square larger than 1. For example, the first few squarefree numbers are {1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, ...}. Create a class SquareFree that contains a method getNumber, which is given an int n. The method should return the n^th smallest squarefree number. Note this is 1-indexed, so if n = 1, the method should return the smallest squarefree number.

Definition

Class:	SquareFree
Method:	getNumber
Parameters:	int
Returns:	int
Method signature:	int getNumber(int n)
(be sure your method is public)

Constraints

-

n will be between 1 and 1,000,000,000 inclusive.

Examples

0)

Returns: 1

One is the smallest squarefree number.

1)

Returns: 19

See the list of squarefree numbers given in the problem statement.

2)

Returns: 163

3)

Returns: 2030745

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ScoringEfficiency

Simple Math, Simulation

Used in:

SRM 190

Used as:

Division II Level One

Writer:

dgarthur

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2341

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4770&pm=2341

Problem Statement

In basketball, players can attempt either two point or three point field goals, and if they are fouled, they can also attempt one point free throws. Since missing a free throw or a field goal often results in losing possession of the ball, it is important to make the most of each shot attempt. Traditionally, this efficiency has been measured by shooting percentage, which is defined as:

                            Field goals made
   Shooting percentage = ---------------------
                         Field goals attempted

Unfortunately, this formula is problematic since it does not account for either free throws or the different types of field goals. Therefore, a new formula, called points per shot, is gaining prominence. This is given by:

                                         Total points
   Points per shot = -----------------------------------------------------
                     (Field goals attempted) + 0.5*(Free throws attempted)

Consider, for example, a player that makes 4 of 5 two point field goals, 3 of 7 three point field goals, and 7 of 9 free throws. The player has earned 4*2 + 3*3 + 7*1 = 24 points with 5+7=12 field goal attempts and 9 free throw attempts. Thus, the player has earned 24/16.5 = 1.45454545... points per shot.

Create a class ScoringEfficiency that contains a method getPointsPerShot, which is given a String[] gameLog. This will give the history of one player's shot attempts, with each element being equal to one of the following strings (quotes for clarity):

- "Made 2 point field goal"
- "Missed 2 point field goal"
- "Made 3 point field goal"
- "Missed 3 point field goal"
- "Made free throw"
- "Missed free throw"

Given this history, the method should return the player's points per shot, as computed above.

Definition

Class:	ScoringEfficiency
Method:	getPointsPerShot
Parameters:	String[]
Returns:	double
Method signature:	double getPointsPerShot(String[] gameLog)
(be sure your method is public)

Notes

-

Return values with either a relative or absolute error less than 1.0E-9 will be accepted.

Constraints

-

gameLog will contain between 1 and 50 elements inclusive.

-

Each element of gameLog will be one of the six strings listed above.

Examples

0)

{"Made 3 point field goal",
 "Missed 2 point field goal"}

Returns: 1.5

This player has 3 total points, 2 field goals attempted, and 0 free throws attempted, so he has earned 3/2 = 1.5 points per shot.

1)

{"Made free throw",
 "Missed free throw",
 "Missed free throw",
 "Missed free throw",
 "Made free throw"}

Returns: 0.8

This player has 2 total points, 0 field goals attempted, and 5 free throws attempted, so he has earned 2/2.5 = 0.8 points per shot.

2)

{"Made 2 point field goal", "Made 2 point field goal", "Made 2 point field goal", 
 "Made 2 point field goal", "Missed 2 point field goal",
 "Made 3 point field goal", "Made 3 point field goal", "Made 3 point field goal",
 "Missed 3 point field goal", "Missed 3 point field goal", 
 "Missed 3 point field goal", "Missed 3 point field goal",
 "Made free throw", "Made free throw", "Made free throw", 
 "Made free throw", "Made free throw", "Made free throw", 
 "Made free throw", "Missed free throw", "Missed free throw"}

Returns: 1.4545454545454546

This is the example from the problem statement.

3)

{"Made 2 point field goal", "Missed free throw",
 "Made free throw", "Missed free throw", "Made free throw", 
 "Made 2 point field goal", "Made 2 point field goal",
 "Missed 2 point field goal", "Missed 2 point field goal",
 "Made 3 point field goal", "Missed 2 point field goal",
 "Made 2 point field goal", "Missed 2 point field goal",
 "Made 3 point field goal", "Missed 2 point field goal",
 "Missed 2 point field goal", "Missed 3 point field goal",
 "Made free throw", "Made free throw", 
 "Missed 3 point field goal", "Missed 2 point field goal",
 "Missed 2 point field goal", "Made 2 point field goal",
 "Missed 2 point field goal", "Made 2 point field goal",
 "Missed 3 point field goal"}

Returns: 0.9565217391304348

This log is from a game by NBA superstar Vince Carter. He had 22 points, 20 field goals attempted, and 6 free throws attempted, so he earned 22/23 = 0.956521739... points per shot.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CountGame

Simple Math, Simulation

Used in:

SRM 183

Used as:

Division II Level One

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2337

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4735&pm=2337

Problem Statement

The Counting Game is a game played between two players. The first player starts counting at 1, and can say no more than maxAdd numbers. The second player continues counting from where the first player left off. The two players alternate, each one contributing at least one but no more than maxAdd numbers. The player who says the goal number is the winner.

For example, if maxAdd is 3 and the goal is 20, then a game (between bad players A and B) might go like this:

A: 1,2,3 ... B: 4,5 ... A: 6 ... B: 7,8,9 ... A: 10,11,12 ... B: 13 ... A: 14 ... B: 15,16 ... A: 17,18 ... B: 19,20

Since player B said the goal number, she was the winner.

There is a perfect strategy for this game. When maxAdd is 3, if you end your turn by saying 16, then no matter whether your opponent contributes 1, 2, or 3 numbers you will be able to count to 20 on your next turn. Similarly, if you end your turn by saying 12, then no matter what your opponent does you can end your next turn by saying 16, and thus win on your following turn.

Create a class CountGame to help you play this game. It should contain a method howMany that is given maxAdd, the most numbers you may say on each turn, goal, the goal number, and next, the number that you must start counting on. The method should return how many numbers you should say. If there is no way for you to force a win, then the method should return -1.

Definition

Class:	CountGame
Method:	howMany
Parameters:	int, int, int
Returns:	int
Method signature:	int howMany(int maxAdd, int goal, int next)
(be sure your method is public)

Notes

-

If there is a play that forces a win, it is unique.

Constraints

-

maxAdd will be between 2 and 8 inclusive.

-

goal will be between 1 and 1000 inclusive.

-

next will be between 1 and goal inclusive.

Examples

0)

Returns: 3

This is the game where each player can contribute 1, 2 or 3 numbers and the goal is 20. It is your turn and you must start at 10 (presumably because your opponent ended his previous turn at 9). You should count 10,11,12 since, as shown above, when maxAdd is 3 you can force a win if you end your turn by saying 12.

1)

Returns: 5

Count 10,11,12,13,14. Then whatever your opponent does, you will be able to win by counting to 20 on your next turn. Even if he says just 15, you can reach 20 since maxAdd is 5.

2)

Returns: -1

Whatever you do, your opponent will be able to end his next turn by saying 14. Then you won't be able to count up to 20, but even if you say just one number, your opponent will be able to win on his turn.

3)

Returns: 1

Here the next number is the goal, so we just add that one number to the sequence and win.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PresentationComp

Encryption/Compression, Math, String Manipulation

Used in:

SRM 221

Used as:

Division I Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2332

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5867&pm=2332

Problem Statement

In algebra, a presentation is a convenient way to describe a set. The presentation includes what the atomic elements of the set are, and what relations are used to simplify strings of atoms. These atoms are usually called generators. In this problem we will be looking at a set whose generators are x and y. You will be given a String expression consisting of x's and y's. The simplifying rules are:

1) Any occurrence of yyyyyy can be deleted from the string.
2) Any occurrence of xxxxxxxx can be deleted from the string.
3) Any occurrence of xy can be replaced by yyyyyx.

Two strings A and B are equivalent if there is a string C such that A can be simplified into C and B can be simplified into C by applying the rules above 0 or more times. Return the shortest string equivalent to expression. If there are multiple possible solutions, return the one that comes first alphabetically.

Definition

Class:	PresentationComp
Method:	simplify
Parameters:	String
Returns:	String
Method signature:	String simplify(String expression)
(be sure your method is public)

Constraints

-

expression will contain between 1 and 50 characters inclusive.

-

Each character in expression will be x or y.

Examples

0)

"xxxxxxxxyyyyyy"

Returns: ""

Simplifies greatly.

1)

"xy"

Returns: "xy"

Doesn't get much simpler.

2)

"yyxx"

Returns: "xxyy"

Use the one that comes first alphabetically.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CuboidJoin

Geometry, Math

Used in:

SRM 191

Used as:

Division II Level Three

Writer:

Ishan

Testers:

lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2329

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4775&pm=2329

Problem Statement

A cuboid is a rectangular solid. Given a few cuboids, which may or may not overlap, you have to find out the total volume enclosed by them. A volume is considered enclosed if it falls completely within at least one of the specified cuboids. A volume that is in between several cuboids, but not inside any of them, is not considered enclosed.

The input is given as a int[], cuboids. The first 6 elements of cuboids describe the first cuboid, the next 6 the second cuboid and so on. The 6 elements specify the left-bottom-front vertex and then the right-top-back vertex. Each vertex is specified by 3 elements which refer to its x, y and z coordinates respectively.

For instance, if cuboids = {0,0,0,1,1,1}, it would mean there is one cuboid whose left-bottom-front vertex is (0,0,0) and whose right-top-back vertex is (1,1,1). In this case the volume enclosed would be 1. However, if cuboids = {0,0,0,1,1,1,1,1,1,2,2,2}, it would mean there are two cuboids, one whose left-bottom-front vertex is (0,0,0) and right-top-back vertex is (1,1,1), and another whose left-bottom-front vertex is (1,1,1) and right-top-back vertex is (2,2,2). In this case, the enclosed volume would be 2.

Definition

Class:	CuboidJoin
Method:	totalVolume
Parameters:	int[]
Returns:	long
Method signature:	long totalVolume(int[] cuboids)
(be sure your method is public)

Notes

-

The cuboids are always aligned with the grid. In other words, the cuboids are never tilted or twisted with respect to the axes.

-

The x coordinate increases from left to right, the y coordinate from bottom to top, and the z coordinate from front to back.

Constraints

-

cuboids will contain between 0 and 30 elements, inclusive.

-

The number of elements in cuboids will be a multiple of 6.

-

Each element of cuboids will be between -5000 and 5000, inclusive.

-

As is explained in the problem statement, each cuboid is specified as a block of six elements x1,y1,z1,x2,y2,z2. In each such block, x1 is less than or equal to x2, y1 is less than or equal to y2 and z1 is less than or equal to z2.

Examples

0)

{0,0,0,1,1,1}

Returns: 1

There is just one cuboid which is a 1-by-1-by-1 cube. Hence, the volume enclosed is 1*1*1 = 1.

1)

{0,0,0,1,1,1,1,1,1,2,2,2}

Returns: 2

There are two cuboids, both of which are 1-by-1-by-1 cubes. Hence, the volume enclosed is 1*1*1 + 1*1*1 = 2.

2)

{0,0,0,4,4,4,0,0,0,1,1,1}

Returns: 64

There are two cuboids. One is a 1-by-1-by-1 cube and another is a 4-by-4-by-4 cube. The volume enclosed is 4*4*4 = 64 as the 1-by-1-by-1 cube is completely enclosed within the 4-by-4-by-4 cube.

3)

{-5000,-5000,-5000,5000,5000,5000}

Returns: 1000000000000

4)

{0,0,0,1,2,3,5,5,5,6,6,6}

Returns: 7

5)

{}

Returns: 0

6)

{0,0,0,1,1,0}

Returns: 0

The answer is 0 because "flat" solids enclose no volume.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TurretDefense

Simple Math, Simulation

Used in:

TCCC '04 Qual. 4

Used as:

Division I Level One

Writer:

brett1479

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2323

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5003&pm=2323

Problem Statement

*** You may only submit a given problem once - no resubmissions will be accepted. ***

"Incoming! Fire the defense turrets at these coordinates! Go go go!"

You have been given a list of incoming targets that must be shot down in the order they are given. Assuming your turret is aimed at some location, it will take time to move the turret and fire at a different location. If you are currently aimed at point (a,b), and you must move to aim at point (c,d), the time required is the absolute difference in first coordinates plus the absolute difference in second coordinates. For example, starting at (3,7) it will take 4 seconds to aim at point (5,5). Along with the coordinates of each incoming target, you are also given their arrival times. The turret must be fired precisely at the arrival time in the direction of the target. Immediately after firing, the turret can be moved to aim at the next location (no time is lost firing). Your method will return the index of the earliest target that cannot be shot down. For example, let's assume

    xs    = {3,5,6}
    ys    = {7,5,6}
    times = {11,15,16}.

Your turret always begins aimed at (0,0) at time 0. Since the first target is arriving at location (3,7) at time 11 you have 11 seconds to move there and fire. This is 1 second more than is needed. At time 11 you fire the turret, and immediately start moving to aim at (5,5). Since the second target arrives at time 15, you have 4 seconds to aim. This is exactly enough time. At time 15, you fire at the second target. Unfortunately, the third target will arrive before you can shoot it down. You would return 2 since target 2 (third target) is the earliest one you couldn't shoot down. If you could shoot them all down, return -1. As shown above, xs[i],ys[i] are the coordinates, and times[i] is the arrival time of target i.

Definition

Class:	TurretDefense
Method:	firstMiss
Parameters:	int[], int[], int[]
Returns:	int
Method signature:	int firstMiss(int[] xs, int[] ys, int[] times)
(be sure your method is public)

Notes

-

xs will contain between 2 and 50 elements inclusive.

-

ys and times will contain the same number of elements as xs.

-

Each element of xs will be between 0 and 1000 inclusive.

-

Each element of ys will be between 0 and 1000 inclusive.

-

Each element of times will be between 1 and 1000000 inclusive.

-

The elements of times will be in strictly increasing order.

Examples

0)

{3,5,6}

{7,5,6}

{11,15,16}

Returns: 2

From above.

1)

{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}

{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}

{2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32}

Returns: -1

A target arrives every 2 seconds. Luckily it only takes 2 seconds to switch from target to target.

2)

{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}

{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}

{2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,31}

Returns: 15

Same as before, but now you only have 1 second to switch to the final target.

3)

{1000,0,1000,0,1000,0,1000,0,1000,0,
 1000,0,1000,0,1000,0,1000,0,1000,0,
 1000,0,1000,0,1000,0,1000,0,1000,0,
 1000,0,1000,0,1000,0,1000,0,1000,0,
 1000,0,1000,0,1000,0,1000,0,1000,0}

{1000,0,1000,0,1000,0,1000,0,1000,0,
 1000,0,1000,0,1000,0,1000,0,1000,0,
 1000,0,1000,0,1000,0,1000,0,1000,0,
 1000,0,1000,0,1000,0,1000,0,1000,0,
 1000,0,1000,0,1000,0,1000,0,1000,0}

{2000,4000,6000,8000,10000,12000,14000,16000,18000,20000,
 22000,24000,26000,28000,30000,32000,34000,36000,38000,40000,
 42000,44000,46000,48000,50000,52000,54000,56000,58000,60000,
 62000,64000,66000,68000,70000,72000,74000,76000,78000,80000,
 82000,84000,86000,88000,90000,92000,94000,96000,98000,100000}

Returns: -1

Takes a while, but you hit them all.

4)

{4,5}

{4,5}

{7,8}

Returns: 0

5)

{1,2,3,4,15}

{1,2,3,4,15}

{100,200,300,400,405}

Returns: 4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BorelSets

Math, Search

Used in:

TCCC '04 Qual. 4

Used as:

Division I Level Two

Writer:

brett1479

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2322

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5003&pm=2322

Problem Statement

*** You may only submit a given problem once - no resubmissions will be accepted. ***

Suppose there is a universal set called U containing the integers between 1 and size inclusive. You will be given some subsets of U. A subset of U is a set of numbers that are in U. The set can contain no numbers (empty set), every number in U, or anything in between. Each subset will be given as a String containing a single space-delimited list of the numbers in the set. The Borel Field B (also called sigma-algebra) generated by subsets is the smallest collection of sets satisfying the following statements:

1) All of the sets in subsets are in B,
2) if X and Y are sets in B then X union Y is in B,
3) if X is a set in B then the complement of X is in B.

Given two sets of numbers, the union is the set of all numbers that are in either or both. The complement of a set X contains all numbers that are in U but not in X (if U=X the complement of X is empty). Given subsets you will return how many distinct sets are in the Borel Field it generates. When comparing sets to see if they are distinct, note that duplicate elements within a set are ignored. In other words, a set does not have any duplicates, but a description of the set may. For example, the sets "1 1 2", "1 2", and "2 2 1" are indistinguishable as sets, but "1 2 3" is distinct from the previous three.

Definition

Class:	BorelSets
Method:	howMany
Parameters:	int, String[]
Returns:	int
Method signature:	int howMany(int size, String[] subsets)
(be sure your method is public)

Constraints

-

size will be between 1 and 10 inclusive.

-

subsets will contain between 1 and 50 elements inclusive.

-

Each element of subsets will contain between 0 and 50 characters inclusive.

-

Each element of subsets will either be an empty string, or a single space-delimited list of integers. Each integer in the list will be between 1 and size inclusive, and will have no leading zeros.

-

Each element of subsets will not have any leading or trailing spaces.

Examples

0)

{"1 2",""}

Returns: 4

We have that

   U = "1 2 3 4".

We know "1 2", and "" are in the resultant Borel Field. By taking the complement of "1 2" we get "3 4". By taking the complement of "" we get "1 2 3 4". There are no other sets in the Borel Field.

1)

{"","1","2","3","4","5","6","7","8","9","10"}

Returns: 1024

2)

{"","1 1 2","1 1 2 2 1 1","","2 1 1"}

Returns: 4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

QuickTableau

Brute Force, Math, Sorting

Used in:

TCCC06 Qual 2

Used as:

Division I Level Three

Writer:

AdminBrett

Testers:

PabloGilberto , Cosmin.ro , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2321

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10094&pm=2321

Problem Statement

A Young tableau is a two-dimensional array of integers such that each row and column is sorted in ascending order (rows left-to-right, columns top-to-bottom). Given a int[] table with exactly 16 elements, all of which are distinct, you will return the fewest number of swaps required to turn table into a Young tableau. table should be interpreted as a 4 x 4 array of integers. More visually,

  table = { A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P }

corresponds to the following 4 x 4 array

  A  B  C  D
  E  F  G  H
  I  J  K  L
  M  N  O  P ,

where A through P are integers.

Definition

Class:	QuickTableau
Method:	numSwaps
Parameters:	int[]
Returns:	int
Method signature:	int numSwaps(int[] table)
(be sure your method is public)

Constraints

-

table will contain exactly 16 elements.

-

table will contain no repeated elements.

-

Each element of table will be between 1 and 16, inclusive.

Examples

0)

{
 1,  2,  3,  4,
 5,  6,  7,  8,
 9, 10, 11, 12,
13, 14, 15, 16
}

Returns: 0

We already have a Young tableau.

1)

{
16, 15, 14, 13,
12, 11, 10,  9,
 8,  7,  6,  5,
 4,  3,  2,  1
}

Returns: 6

2)

{
 2,  1,  3,  4,
 5,  6,  7,  8,
 9, 10, 11, 12,
13, 14, 15, 16
}

Returns: 1

Here we only need to swap the first 2 values.

3)

{
 4,  3,  2,  1,
 5,  6,  7,  8,
 9, 10, 11, 12,
13, 14, 15, 16
}

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Apothecary

Greedy, Math

Used in:

SRM 204

Used as:

Division I Level One , Division II Level Three

Writer:

vorthys

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2312

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5850&pm=2312

Problem Statement

An accurate scale is one of the most important tools of the apothecary (an old-time pharmacist). To measure the weight of an object, the apothecary places the object on one pan of the scale, along with some weights of known size, and adds more weights of known size to the other pan until the scales balance. For example, if an object weighs 17 grains, the apothecary could balance the scales by placing a 1-grain weight and a 9-grain weight in the pan with the object, and a 27-grain weight in the other pan.

The apothecary owns weights in a range of sizes starting at 1 grain. In particular, he owns one weight for each power of 3: 1 grain, 3 grains, 9 grains, 27 grains, etc. Determine, for an object weighing W grains, how to distribute the weights among the pans to balance the object. This distribution will be unique. Return a int[] of the weights used. The sign of each weight should be negative if the weight goes in the same pan as the object, and positive if it goes in the other pan. The int[] should be arranged in increasing order.

Definition

Class:	Apothecary
Method:	balance
Parameters:	int
Returns:	int[]
Method signature:	int[] balance(int W)
(be sure your method is public)

Constraints

-

W is between 1 and 1000000, inclusive.

Examples

0)

Returns: { -9,  -1,  27 }

The example above.

1)

Returns: { 1 }

A 1-grain weight is placed in the pan opposite the object being measured.

2)

Returns: { -243,  -9,  81,  2187 }

A 9-grain weight and a 243-grain weight are placed in the pan with the object, and an 81-grain weight and a 2187-grain weight are placed in the opposite pan.

3)

Returns: { -531441,  -59049,  -6561,  -243,  -27,  1,  81,  729,  2187,  1594323 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SlayingDeer

Math, Simulation

Used in:

SRM 182

Used as:

Division I Level One , Division II Level Two

Writer:

dgarthur

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2308

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4730&pm=2308

Problem Statement

Although TopCoder member Running Wild is a vegetarian, he has recently decided that he would eat venison if he could catch a deer himself. Before committing too much time and effort to this endeavor, Running Wild would like to estimate his chances at success. To do this, he assumes that he will run at a constant speed of A meters per minute without ever getting tired. Similarly, a deer will run at a constant speed of B meters per minute, but after every 30 minutes of running, it must stop and rest for 15 minutes. Finally, Running Wild also assumes that he will begin at a given distance of C meters behind the deer, and that they will always be running in the same fixed direction.

Create a class SlayingDeer that contains a method getTime, which is given an int A, an int B, and an int C, representing the quantities described above. The method should return the number of minutes (rounded up) it will take for Running Wild to catch the deer. If Running Wild will never catch the deer, the method should return -1.

Definition

Class:	SlayingDeer
Method:	getTime
Parameters:	int, int, int
Returns:	int
Method signature:	int getTime(int A, int B, int C)
(be sure your method is public)

Notes

-

If Running Wild and the deer are at precisely the same position, then Running Wild is considered to have caught the deer.

Constraints

-

A and B will be between 1 and 1000 inclusive.

-

C will be between 1 and 100000 inclusive.

Examples

0)

Returns: 20

Running Wild gains one meter per minute over the first 20 minutes before catching the deer.

1)

Returns: 34

As in the previous example, Running Wild will gain 1 meter per minute for the first 30 minutes. Then, however, the deer stops and rests. Running Wild gains 5 meters per minute while the deer is resting. Note that the answer is rounded up.

2)

Returns: -1

3)

Returns: 7515

4)

Returns: -1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

IBEvaluator

Simple Math

Used in:

SRM 182

Used as:

Division II Level One

Writer:

dgarthur

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2306

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4730&pm=2306

Problem Statement

For the International Baccalaureate (IB) diploma, students are assigned integer grades between 1 and 7 inclusive, based on exams taken at the end of high school. Unfortunately, these results are never available in time to assist universities with admissions decisions. To counteract this problem, IB teachers are required to predict in advance how well each student will perform on the exams. As these predictions can have an enormous impact on a student's future, schools are naturally very interested in evaluating their accuracy.

Create a class IBEvaluator that contains a method getSummary, which is given a int[] predictedGrades and a int[] actualGrades. Corresponding elements in these arrays will represent the predicted and final grades, respectively, achieved by each student. The method should return a int[] with 7 elements, giving the percentage (rounded down) of predicted grades that differ from the actual grades by each value between 0 and 6 inclusive. Thus, element 0 of the return value should be the percentage of predictions that were correct, element 1 should be the percentage of predictions that differed by 1, etc.

Definition

Class:	IBEvaluator
Method:	getSummary
Parameters:	int[], int[]
Returns:	int[]
Method signature:	int[] getSummary(int[] predictedGrades, int[] actualGrades)
(be sure your method is public)

Constraints

-

predictedGrades and actualGrades will each contain between 1 and 50 elements inclusive.

-

predictedGrades and actualGrades will contain the same number of elements.

-

Each element of predictedGrades will be between 1 and 7 inclusive.

-

Each element of actualGrades will be between 1 and 7 inclusive.

Examples

0)

{1,5,7,3}

{3,5,4,5}

Returns: { 25,  0,  50,  25,  0,  0,  0 }

The grade distribution is shown below.

Student | Predicted grade | Actual grade | Difference
--------+-----------------+--------------+-----------
   1    |        1        |       3      |     2
   2    |        5        |       5      |     0
   3    |        7        |       4      |     3
   4    |        3        |       5      |     2

Out of four predictions, one (25%) is off by 0 points, two (50%) are off by 2 points, and one (25%) is off by 3 points.

1)

{1,1,1}

{5,6,7}

Returns: { 0,  0,  0,  0,  33,  33,  33 }

Note that percentages are rounded down.

2)

{3}

{3}

Returns: { 100,  0,  0,  0,  0,  0,  0 }

3)

{1,5,3,5,6,4,2,5,7,6,5,2,3,4,1,4,6,5,4,7,6,6,1}

{5,1,3,2,6,4,1,7,5,2,7,4,2,6,5,7,3,1,4,6,3,1,7}

Returns: { 17,  13,  21,  17,  21,  4,  4 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SquareCode

Encryption/Compression, String Manipulation

Used in:

SRM 180

Used as:

Division I Level Two

Writer:

Eeyore

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2303

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4720&pm=2303

Problem Statement

When Bob learned that he was to be sent abroad to work on an oil rig, he resolved that he would write regularly to his girlfriend.

"We'll have to encrypt our correspondence," he told Alice, "so that my tender feelings remain unknown to the rest of the crew."

Alice showed Bob a simple kind of text encryption that makes use of a square cardboard grille divided into equal-sized cells, exactly one quarter of which are punched out to make holes. For example, a six-by-six grille might be configured as follows, where '.' stands for a hole and 'X' for a cell that has been left intact.


               XXXXXX
               .XXXX.
               X.XX..
               XXX.XX
               X.XXXX
               XX.XX.

To encrypt a message, Bob begins writing plaintext into the grille, one character per hole, proceeding from left to right within each row and running through the rows from top to bottom. Once all holes are filled, he rotates the grille ninety degrees clockwise, and continues the message where he left off. After two more quarter turns, he has written a full square of coded text, and must begin a new one. Upon receipt of the message, Alice uses an identical grille to decrypt each square. If, for example, Bob's plaintext were "supercalifragilisticexpialadociously", Alice would receive the following code.


               idocfc
               sriaeu
               gpxoer
               piicau
               laslla
               iylsti

Not just any grille will do for this purpose, as Bob discovered when he tried to make one by cutting out holes at random. He found that this haphazard grille wouldn't let him write out a full square of text in the prescribed manner. After fewer than four quarter-turns, some holes revealed previously written characters. Alice assured him that this was a grave flaw. An encoding grille must permit one to fill the entire square by making three quarter-turns, and it must show each cell of the square exactly once. Bob, alas, had a lyrical soul and not a mathematical one. He could not perceive the properties that make a grille suitable for use with this encryption technique. Can you?

You are given a String[] describing a grille row by row, in the style shown above, with no more than a quarter of its holes punched out. If it is not possible to make a complete and valid encoding grille from this configuration by punching out zero or more additional holes, then return an empty String[]. Otherwise, punch out the necessary holes in the upper-left quadrant to make a complete and valid grille, and return it in the same format as the input.

Definition

Class:	SquareCode
Method:	completeIt
Parameters:	String[]
Returns:	String[]
Method signature:	String[] completeIt(String[] grille)
(be sure your method is public)

Constraints

-

grille contains between 2 and 50 elements, inclusive

-

grille contains an even number of elements

-

if grille contains exactly n elements, then every element of grille consists of n characters

-

every character in grille is either '.' or 'X'

-

no more than one quarter of the characters in grille are '.'

Examples

0)

{"XX..",
 "XX.X",
 ".XXX",
 "XXXX"}

Returns: { "XX..",  "XX.X",  ".XXX",  "XXXX" }

No additional holes are punched:

{"XX..",
 "XX.X",
 ".XXX",
 "XXXX" }

This was already a good grille.

1)

{"XXX.",
 "XX.X",
 ".XXX",
 "XXXX"}

Returns: { "XXX.",  ".X.X",  ".XXX",  "XXXX" }

One additional hole is punched:


{"XXX.",
 ".X.X",
 ".XXX",
 "XXXX"}

The grille could have been completed by punching a hole in one of four locations. We chose the leftmost, topmost one.

2)

{"XXX.",
 "XX.X",
 ".X.X",
 "XXXX"}

Returns: { }

An empty String[] is returned:

{}

The given grille reveals the same character location more than once.

3)

{"XXXXXX",
 "XXXXX.",
 "XXXX..",
 "XXX.XX",
 "X.XXXX",
 "XX.XX."}

Returns: { "XXXXXX",  ".XXXX.",  "X.XX..",  "XXX.XX",  "X.XXXX",  "XX.XX." }

Two additional holes are punched:


{"XXXXXX",
 ".XXXX.",
 "X.XX..",
 "XXX.XX",
 "X.XXXX",
 "XX.XX." }

4)

{"XXX.XX",
 ".XXXX.",
 "X.XXX.",
 "XXX.XX",
 "X.XXXX",
 "XX.XX."}

Returns: { }

5)

{"XXXXX.XX",
 "XXXX.XXX",
 "XXX..X.X",
 ".XXXXXXX",
 "XXXXXXXX",
 "XXXXXXXX",
 "X.XXXXXX",
 "XXXXXXXX"}

Returns: 
{ "....X.XX",
 ".XX..XXX",
 "X....X.X",
 ".XX.XXXX",
 "XXXXXXXX",
 "XXXXXXXX",
 "X.XXXXXX",
 "XXXXXXXX" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BettingMoney

Simple Math, Simulation

Used in:

SRM 191

Used as:

Division II Level One

Writer:

Ishan

Testers:

lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2297

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4775&pm=2297

Problem Statement

You run a gambling business in which people place bets on the margin of victory in a football game. At the end of the day, the company would like to know what the day's net gain has been.

Just as in any other betting system, people place certain amounts as their bets and if they guess correctly, they get their money back plus a pre-specified percentage of their bet; otherwise they lose the money they bet.

You are given a int[], amounts, the i^th element of which is the number of dollars people have placed on a victory margin of i (i = 0 refers to the first element). You are also given a int[], centsPerDollar, the i^th element of which is the number of cents the company has to pay for every dollar the people bet on a victory margin of i, if the final outcome is a victory margin of i. Finally, you are given an int, finalResult, which is the final margin of victory. You have to determine what the net gain for the day was and return the amount in cents.

For example, if amounts were {10,20,30}, it would mean that people placed $10 on a draw outcome, $20 on a victory margin of 1 and $30 on a victory margin of 2, and if centsPerDollar were {20,30,40}, it would mean the people would win 20 cents per dollar bet if the match were a draw, 30 cents per dollar if the victory margin were 1 and 40 cents per dollar if the victory margin were 2.

Suppose the final result is a victory margin of 1 (i.e., finalResult = 1). Then the people who guessed the outcome as a margin of 0 or 2 were wrong and the company receives the amounts they bet, $10+$30. However, the people who guessed that the outcome would be a margin of 1 were correct, and they receive money from the company according to the amount they bet (20 dollars) and the pre-set payoff percentage (30 cents per dollar) . This amounts to 20*30 = 600 cents. Hence, the day's net gain is 40 dollars - 600 cents = 3400 cents. You should return 3400.

Definition

Class:	BettingMoney
Method:	moneyMade
Parameters:	int[], int[], int
Returns:	int
Method signature:	int moneyMade(int[] amounts, int[] centsPerDollar, int finalResult)
(be sure your method is public)

Notes

-

Keep in mind that it is not relevant which team wins. Only the margin of victory matters.

-

A victory margin of 0 and a draw are the same thing.

-

There are 100 cents in a dollar.

-

If the company has to pay more than it receives, the day's net gain will be negative.

Constraints

-

amounts will contain between 1 and 50 elements, inclusive.

-

centsPerDollar will contain the same number of elements as amounts.

-

finalResult will be between 0 and n-1, inclusive, where n is the number of elements in amounts.

-

Each element of amounts will be between 0 and 5000, inclusive.

-

Each element of centsPerDollar will be between 0 and 5000, inclusive.

Examples

0)

{10,20,30}

{20,30,40}

Returns: 3400

The case explained in the problem statement above.

1)

{200,300,100}

{10,10,10}

Returns: 49000

The company gains 200+300 = 500 dollars from the people who bet on margins of 0 and 1. The company loses 100*10 = 1000 cents to the people who bet on a victory margin of 2. Hence, the net gain is 49000 cents.

2)

{100,100,100,100}

{5,5,5,5}

Returns: 29500

3)

{5000,5000}

{100,2}

Returns: 0

4)

{100}

{10}

Returns: -1000

The company doesn't gain anything! It has to pay the people who bet on the only outcome possible. It pays 100*10 cents. Hence, the net gain is -1000. (Negative indicates loss.)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Display

Math

Used in:

SRM 189

Used as:

Division I Level One , Division II Level Two

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2295

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4765&pm=2295

Problem Statement

We want to display a scatterplot in a 1000x1000 window. However, our points may have x and y values anywhere between -1,000,000,000 and 1,000,000,000. So, in order to display our data in a reasonable fashion, we want to make it fit in the window. Your task is, given the x and y values of the data, scale and translate the data so that the lowest x value is 0, and the highest is 1000. Do the same thing for the y values, being careful to preserve the relative distances in both the x and y directions. For example, if x = {-100, 0, 50, 100}, then it should be changed to {0,500,750,1000}. Note that changing the points may result in non-integral values, which should be rounded to the nearest integer (.5 rounds up). The return value should be a String[], each of whose elements is formatted as "<x> <y>", where <x> and <y> are the scaled and translated values of the corresponding elements of the input. <x> and <y> should be separated by exactly one space and have no extra leading zeros.

Definition

Class:	Display
Method:	transform
Parameters:	int[], int[]
Returns:	String[]
Method signature:	String[] transform(int[] x, int[] y)
(be sure your method is public)

Constraints

-

Each element of x and y will be between -1,000,000,000 and 1,000,000,000, inclusive.

-

x will contain at least two distinct values.

-

y will contain at least two distinct values.

-

x and y will contain the same number of elements.

-

x and y will each contain between 2 and 50 elements, inclusive.

Examples

0)

{-100, 0, 50, 100}

{-100, 0, 50, 100}

Returns: { "0 0",  "500 500",  "750 750",  "1000 1000" }

If we translate all the points +100 in both the x and y directions, and then scale all the coordinates up by a factor of 5, we find that they meet our requirements.

1)

{0,2000,1}

{0,2001,1}

Returns: { "0 0",  "1000 1000",  "1 0" }

2)

{-1000000000,1000000000,500000,499999}

{-1000000000,1000000000,500000,499999}

Returns: { "0 0",  "1000 1000",  "500 500",  "500 500" }

3)

{-53,652,-6132,673,74,-473,373,736363,234,234,234}

{-6464,36464,-43,373,363,-37633,2022,-644,2520,2520,2520}

Returns: 
{ "8 421",
 "9 1000",
 "0 507",
 "9 513",
 "8 513",
 "8 0",
 "9 535",
 "1000 499",
 "9 542",
 "9 542",
 "9 542" }

4)

{0,1001,2000}

{0,999,2000}

Returns: { "0 0",  "501 500",  "1000 1000" }

Be sure to round up when the fractional part is .5.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Scale

Math, String Manipulation

Used in:

TCCC '04 Qual. 3

Used as:

Division I Level Two

Writer:

lars2520

Testers:

schveiguy , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2294

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5002&pm=2294

Problem Statement

*** You may only submit a given problem once - no resubmissions will be accepted. ***

A common image editing task is to scale an image. For example, given an image 1024 pixels wide, and 768 pixels high, you might want to reduce it to 400x300 so it takes up less disk space. In this problem, you will be given an image as a String[], where each element represents a row of pixels, and each character represents a single pixel (the colors are simply ASCII values between 32 and 126, inclusive). Your task is to scale the image so that it is x pixels wide, and y pixels high. To determine the colors of the new pixels, you should draw a grid over the image such that there are x columns and y rows. Each region of the grid will then represent a single pixel, whose color is the weighted average of all the colors within it (0.5 rounds up). The weight of each color is equal to the area it covers in the region. For example, consider the input {"AB","BC"}, with x = y = 3. Here is a zoomed in view of the scaled image (with grid):

   AA | AB | BB
   AA | AB | BB
  ----+----+----
   AA | AB | BB
   BB | BC | CC
  ----+----+----
   BB | BC | CC
   BB | BC | CC

Now, taking the average value of each pixel in the scaled image, we end up with:

   ABB
   BBC
   BCC

Definition

Class:	Scale
Method:	scale
Parameters:	int, int, String[]
Returns:	String[]
Method signature:	String[] scale(int x, int y, String[] image)
(be sure your method is public)

Notes

-

Each character represents a color, as given by its ASCII value. The average of colors is just the average of the ASCII values.

-

Note that grid lines may go through the pixels in the original image.

Constraints

-

x and y will be between 1 and 100, inclusive.

-

x * y will be less than or equal to 8000.

-

image will contain between 1 and 50 elements, inclusive.

-

Each element of image will contain between 1 and 50 characters, inclusive.

-

Each element of image will contain the same number of characters.

-

Each character in image will have ASCII value between 32 and 126, inclusive.

Examples

0)

{"AB","BC"}

Returns: { "ABB",  "BBC",  "BCC" }

The example from the problem statement.

1)

{"AB","BC"}

Returns: { "AB",  "AB",  "BC",  "BC" }

2)

{"......",
 ".X....",
 ".X....",
 ".X....",
 ".X....",
 ".XXXX.",
 "......"}

Returns: 
{ "...................................................",
 "...................................................",
 "...................................................",
 "...................................................",
 "...................................................",
 "...................................................",
 "........@RRRRRRRR..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX..................................",
 "........CXXXXXXXX:::::::::::::::::::::::::4........",
 "........CXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXC........",
 "........CXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXC........",
 "........CXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXC........",
 "........CXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXC........",
 "........CXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXC........",
 "........@RRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR@........",
 "...................................................",
 "...................................................",
 "...................................................",
 "...................................................",
 "...................................................",
 "..................................................." }

3)

{"...AAA...",
 "...AAA..."}

Returns: { ".;;.",  ".;;.",  ".;;.",  ".;;." }

4)

{"......",
 ".X....",
 ".X....",
 ".X....",
 ".X....",
 ".XXXX.",
 "......"}

Returns: { "44..",  "<<..",  "<@40",  "4@@4" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Commission

Math

Used in:

TCCC '04 Qual. 3

Used as:

Division I Level One

Writer:

lars2520

Testers:

schveiguy , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2293

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5002&pm=2293

Problem Statement

*** You may only submit a given problem once - no resubmissions will be accepted. ***

Salesmen and saleswomen often work for a commission. In other words, they get to keep a certain percentage of the sales they make. You have a saleswoman working for you who gets a whopping 20% commission, which cuts deep into your profit margins. You are considering replacing her with a cheaper salesman who will keep commission% of his sales. Out of each sale, cost% of the sale goes towards the cost of your products and other overhead. Your current saleswoman sells $sales of products a year. Your task is to determine how much the potential salesman would have to sell in a year to make you the same profit.

Definition

Class:	Commission
Method:	equivalentSales
Parameters:	double, double, double
Returns:	double
Method signature:	double equivalentSales(double sales, double cost, double commission)
(be sure your method is public)

Notes

-

Your result must have relative or absolute error of less than 1e-9.

-

The commission is based on the gross sale, not the part of the sale that is above and beyond the cost. Therefore, if sales were $1000, your current saleswoman's commission would be $200.

-

Note that neither sales nor the return value need to be in whole cents.

Constraints

-

sales will be between 1 and 1e10, inclusive.

-

cost will be between 0.5 and 79.5, inclusive.

-

commission will be between 0.5 and 19.5, inclusive.

Examples

0)

100.555

70.0

10.0

Returns: 50.2775

If you hire the new salesman, your profit margin will double from 10% to 20%. Thus, in order to make the same profits, he needs only sell half as much.

1)

74.3

11.5

Returns: 303801.971830986

Your profit from your current saleswoman is $43139.88. If the potential salesman sells a little over $303801.97, your profit will also be the same.

2)

10000000000

79.5

19.5

Returns: 5.0E9

Note that the exact answer is $5E9, but a return of $4.999999999999823E9, for example, has an error of $0.000177 which is a relative error of much less than 1e-9.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RandomFA

Dynamic Programming, Graph Theory, Math

Used in:

SRM 178

Used as:

Division I Level Two

Writer:

brett1479

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2287

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4710&pm=2287

Problem Statement

A Randomized Finite Automaton (RFA) works as follows. The RFA maintains a variable, called its state, which is initially set to 0. When an input character ('a', 'b', or 'c') is fed into the RFA, it must determine which new value is to be assigned to its state. This determining process is governed by a list of rules stored in the RFA. For example, if the RFA is in state 2 and has received an 'a' as input, the RFA would consult element 2 of rulesa. Each element of rulesa is of the form "st:prob st:prob ...", where st denotes a value to be assigned to the state variable, and prob denotes the percentage (out of 100) of such an assignment occurring. If the given probabilities do not add up to 100, the remaining probability is the chance of changing state to 999. If a state (not 999) is missing from a rule, then its prob is assumed to be 0. Once state is 999, regardless of future input, it remains on 999. The machine has analogously defined rulesb, and rulesc defining what to do on 'b' or 'c' accordingly.

When processing an input string, each character is processed in order, left to right, one at a time. Assuming all input strings of length maxLength or fewer (including the string of length 0) are equally likely, return the probability the RFA will be on state finalState once the string is completely processed. The probability returned will be a double, between 0 and 1 inclusive. Results must be accurate to 1e-9.

Definition

Class:	RandomFA
Method:	getProbability
Parameters:	String[], String[], String[], int, int
Returns:	double
Method signature:	double getProbability(String[] rulesa, String[] rulesb, String[] rulesc, int finalState, int maxLength)
(be sure your method is public)

Constraints

-

rulesa will contain between 1 and 50 elements inclusive.

-

rulesa, rulesb, and rulesc all contain the same number of elements.

-

Each element of rulesa, rulesb, and rulesc contain between 0 and 50 characters inclusive.

-

Each element of rulesa, rulesb, and rulesc is a single space delimited list of pairs. Each pair is of the form (quotes for clarity) "st:prob" where,

st is an integer, with no extra leading zeros, between 0 and (size of rulesa-1) inclusive, and

prob is a positive integer, with no leading zeros.

-

The prob values in a single element of rulesa, rulesb, or rulesc will sum up to a value between 0 and 100 inclusive.

-

No 2 pairs in a single element of rulesa, rulesb, or rulesc will have the same st value.

-

finalState will be between 0 and (size of rulesa-1) inclusive, or 999.

-

maxLength will be between 0 and 10 inclusive.

Examples

0)

{"0:100"}

{""}

{""}

Returns: 0.5

The 4 strings that need to be considered are (quotes for clarity) "", "a", "b", and "c". Of those 4, the first 2 will end up on state 0, while the latter 2 will end up on state 999. 2 out of 4 produces a probability of .5 .

1)

{"1:100","0:100"}

{"1:100","0:100"}

{"1:100","0:100"}

Returns: 0.75

Here all even length strings will result in state 0, and odd length strings will result in state 1. Of the 40 strings considered, 1 has length 0, 3 have length 1, 9 have length 2, and 27 have length 3. Thus 30/40=.75 of them have odd length.

2)

{"1:25 2:25 3:25 4:25","0:100","0:100","0:100","0:100"}

{"","","","",""}

{"","","","",""}

Returns: 0.0020604395604395605

All strings that contain a 'b', or 'c' are sent to 999. The strings containing only 'a's begin on state 0, and are evenly distributed between states 1,2,3 and 4 after the first 'a'. After the second 'a' they are all returned to state 0. Examining this pattern, we see that strings that end on state 3 must contain only 'a's and have odd length. Of those, only a quarter of them actually make it to state 3. There are 3 strings consisting of only 'a's that have odd lengths less than or equal 5. This makes 3 out of the total 364 strings. The returned probability is thus 3/364*.25 = .0021 approx.

3)

{"1:25 2:25 3:25 4:25","0:100","0:100","0:100","0:100"}

{"","","","",""}

{"","","","",""}

Returns: 0.9835164835164837

The same problem as before, but now we want the strings that will end on 999. This will be any string of positive length that has a 'b' or 'c'. There are 358 of these, resulting in a probability of 358/364 = .984 approx.

4)

{"2:9 0:7 3:4 1:2 5:35","2:9 0:7 3:4 1:2 5:35",
 "2:9 0:7 3:4 1:2 5:35","2:9 0:7 3:4 1:2 5:35",
 "2:9 0:7 3:4 1:2 5:35","2:9 0:7 3:4 1:2 5:35"}

{"0:10 4:7 5:1","0:10 4:7 5:1","0:10 4:7 5:1",
 "0:10 4:7 5:1","0:10 4:7 5:1","3:79 2:10"}

{"1:100","2:100","3:100","4:100","5:100","0:100"}

Returns: 0.002676338903044717

A more complex example.

5)

{"2:9 0:7 3:4 1:2 5:35","2:9 0:7 3:4 1:2 5:35",
 "2:9 0:7 3:4 1:2 5:35","2:9 0:7 3:4 1:2 5:35",
 "2:9 0:7 3:4 1:2 5:35","2:9 0:7 3:4 1:2 5:35"}

{"0:10 4:7 5:1","0:10 4:7 5:1","0:10 4:7 5:1",
 "0:10 4:7 5:1","0:10 4:7 5:1","3:79 2:10"}

{"1:100","2:100","3:100","4:100","5:100","0:100"}

Returns: 0.0

Same as before, but only the empty string is considered.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WaterLevel

Math

Used in:

SRM 196

Used as:

Division II Level Three

Writer:

dgoodman

Testers:

zoidal , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2263

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5071&pm=2263

Problem Statement

The lake where we vacation sometimes floods. As soon as the level reaches the maximum level that can be contained by the banks of the lake, the additional water covers a fixed floodplain area, which enlarges the area of the lake. Below are views of the lake from the side, with water indicated by X's.


   |              |          |              |
   |___        ___|          |XXXXXXXXXXXXXX|
       |      |                  |XXXXXX|
       |      |                  |XXXXXX|
       |XXXXXX|                  |XXXXXX|
       |XXXXXX|                  |XXXXXX|

       (not flooded)             (flooded)

The amount of evaporation depends on the surface area. When the lake is not flooded, the evaporation is evapNormal units of water per day. When the lake is flooded, the evaporation is evapFlood units per day. The lake never goes dry and never extends beyond the floodplain.

Assume that the lake is initially full but not flooded. Create a class WaterLevel that contains a method netAmt that is given evapNormal, evapFlood, and int[] rain, the amounts of rain that fell on each day during our vacation. The method returns the net increase (a positive value) or decrease (a negative value) in the units of water in the lake during our vacation. The i-th element of rain tells how many units of water fell during the entire i-th day. You should assume that it rains at a constant rate throughout the day.

Definition

Class:	WaterLevel
Method:	netAmt
Parameters:	int, int, int[]
Returns:	double
Method signature:	double netAmt(int evapNormal, int evapFlood, int[] rain)
(be sure your method is public)

Notes

-

A return value with either an absolute or relative error of less than 1.0E-9 is considered correct.

Constraints

-

evapNormal will be between 0 and 1000 inclusive

-

evapFlood will be between evapNormal and 1000 inclusive

-

rain will contain between 1 and 50 elements inclusive

-

each element of rain will be between 0 and 1000 inclusive

Examples

0)

{0,60,0,0}

Returns: -35.0

After the first day, 20 units have evaporated so we are 20 units below flood stage. After the first half of the second day, 30 units of rain have fallen while 10 units have evaporated, so we have reached flood stage. By the end of the day another 30 have fallen and 20 (40 / 2) have evaporated leaving us 10 units above flood stage. On the third day, we leave flood stage after 1/4 of a day. By the end of the day we are 15 units below flood stage. On the fourth day 20 units evaporate leaving us 35 units below flood stage.

1)

{0,60}

Returns: 10.5

After the first day, we are 20 units below flood stage. We reach flood stage after half of the next day. During the last half of the day 30 units of rain fall while 19.5 units evaporate.

2)

{0}

Returns: -20.0

3)

{0,600}

Returns: 0.0

After the first day, the level is 200 below flood stage due to evaporation. Halfway through the second day, 300 units have rain have fallen and 100 units have evaporated so we have just reached flood stage. After that we are at a stable equilibrium in which the level does not change.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RussianDolls

Advanced Math

Used in:

TCCC '04 Wildcard

Used as:

Division I Level Two

Writer:

schveiguy

Testers:

lbackstrom , brett1479 , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2258

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5079&pm=2258

Problem Statement

Note to plugin users: there are html elements in this statement that will not appear correct in plugins. Please use the statement to view them.

Russian Nesting Dolls are a set of dolls which nest inside each other. The dolls are constructed in such a way that each doll will fit comfortably inside any larger doll, and no two dolls are the same size. There are a finite number of ways to nest dolls inside one another so that a specific subset of the dolls is visible. For example, with 3 dolls, there is only one way that they could be nested such that only the largest doll is visible, but there are 2 ways to nest the dolls if the largest and medium doll are visible (depending on which of the two larger dolls the smallest doll is inside). In addition, if you are just given how many dolls are visible, there may be even more ways that the dolls could be nested. For example, if you know there are 2 dolls visible in a 3-doll set, there are 3 ways they could be nested (see example 0).

Your clever friend has used an entire set of N nesting dolls in an arrangement on a table. He assures you that all the nesting dolls are on the table, but you can only see a subset of the dolls. In addition, he has placed a piece of cardboard in front of some of the dolls so that you cannot see which ones they are, and he tells you how many are behind the board. He asks you how many possible ways he could have arranged the dolls such that the current configuration is on the table.

Each doll has a number painted on it from 1 to N, which identifies the size of the doll. You can fit a doll labeled i inside a doll labeled j as long as i < j. Your program will be given an int N, identifying how many dolls there are in the set, a int[] visible, identifying which dolls you can see on the table, and an int hidden, identifying how many more dolls would be visible if the board was removed. Two arrangements are different if any doll is nested immediately inside a different doll, or is nested in one arrangement but not in the other.

Definition

Class:	RussianDolls
Method:	arrangements
Parameters:	int, int[], int
Returns:	long
Method signature:	long arrangements(int N, int[] visible, int hidden)
(be sure your method is public)

Notes

-

The constraints are constructed so the return value will be <= 2⁶³ - 1.

Constraints

-

N will be between 2 and 25, inclusive.

-

hidden will be between 0 and N, inclusive.

-

visible will have between 0 and N-hidden elements, inclusive.

-

Each element of visible will be between 1 and N, inclusive.

-

There will be no repeated elements in visible.

-

There will be at least one configuration which is possible given the arguments.

Examples

0)

{}

Returns: 3

There are three dolls, two of which are behind the board. Since no dolls are showing, the third doll must be nested inside one of the other two. There are three possibilities:

1 and 3 are behind the board, 2 is nested inside 3

2 and 3 are behind the board, 1 is nested inside 2

2 and 3 are behind the board, 1 is nested inside 3

1)

{2}

Returns: 2

In this case, doll 2 is showing. Since there is only one doll behind the board, it must be doll 3. The only unknown is doll 1. It could either be nested in doll 3 or doll 2.

2)

{9}

Returns: 255

Dolls 1-8 could either be behind the board or inside doll 9. However, the case where 1-8 are all inside of 9 is not possible, because then there wouldn't be a doll behind the board. So the answer is 2⁸ - 1.

3)

{13,5,2,18}

Returns: 7163268480

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RGBColor

Simple Math

Used in:

SRM 176

Used as:

Division II Level One

Writer:

Running Wild

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2251

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4685&pm=2251

Problem Statement

When doing any work with visual media it is often very useful to have the complement of a color on hand to create contrast and bring the focus of a picture to a particular place. To create the complement of a color on a computer, each of the red, green, and blue values of a color are inverted. Each of the red, green, and blue values of a color can range from 0 to 255, inclusive. If a particular component of one color is 50, then that component of its complement is 255-50=205.

Although this generally works well, it doesn't generate good complements for grey colors that have all three components right around 128. To fix this you will return an alternate complement for grey colors. If each component of a color and its corresponding component of the color's complement differ by 32 or less, then make the complement of each component by either adding 128 to a component's value, or by subtracting 128 from a component's value, whichever one results in a legal value. For example, the color {120,130,140} would have the complement {125,105,115}, but each component in the color and the complement differ by 32 or less, so we make the complement {248,2,12}.

Create a class RGBColor with a method getComplement that takes a int[] rgb representing the red, green, and blue values of a color, in that order, and returns a int[] representing the red, green, and blue values of the complement of that color, in that same order.

Definition

Class:	RGBColor
Method:	getComplement
Parameters:	int[]
Returns:	int[]
Method signature:	int[] getComplement(int[] rgb)
(be sure your method is public)

Constraints

-

rgb will contain exactly three elements.

-

Each element of rgb will be a value between 0 and 255, inclusive.

Examples

0)

{255,0,0}

Returns: { 0,  255,  255 }

The complement of red is cyan.

1)

{115,115,143}

Returns: { 243,  243,  15 }

The complement of this bluish-grey would normally have been {140,140,112}. But since each component of the complement would have been within 32 of the corresponding component of rgb we return the alternate complement instead.

2)

{115,115,144}

Returns: { 140,  140,  111 }

Also a bluish-grey, but in this case the blue component of the complement differs by 33 from the blue component of rgb, just enough so that we don't need to return the alternate complement.

3)

{153,12,55}

Returns: { 102,  243,  200 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RaceCalculator

Brute Force, Simple Math, Simulation

Used in:

SRM 184

Used as:

Division I Level One

Writer:

Running Wild

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2250

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4740&pm=2250

Problem Statement

If a runner races a distance D in time T, and later races a distance 2D, that runner will likely take more than 2T time to finish it. An examination of how times change with distances for a given runner can lead to the following approximation for the time it will take that runner to finish a given distance. Given two races with distances D₁ and D₂ (D₁<D₂) which a runner ran in times T₁ and T₂ (T₁<T₂) , respectively, the approximate time it will take a runner to run a distance D is given by: T₁*e^(ln(T₂/T₁)*ln(D₁/D)/ln(D₁/D₂)).

While it is clear which of a runner's races for a given distance is the best (the one that he or she ran the fastest), it isn't so clear what race is the best over all distances. This equation can help give an objective measure of that, however. If a runner has raced distances of D₁...D_n, with corresponding times of T₁...T_n, then any pair of two distances with their times will be able to approximate the rest of the times with the equation from above. Any other time will have a percent error from this approximation given by (actualTime-expectedTime)/expectedTime. Take the highest percent error for a time over all possible approximations, and this is that race's 'badness'. The race with the lowest badness is considered the best race.

Create a class RaceCalculator with a method bestRace that takes a int[] distances and a int[] times and returns an int that is the index of the best race specified by the input. Each value in distances will correspond to the value in times of the same index. All distances are in meters and all times are in seconds.

Definition

Class:	RaceCalculator
Method:	bestRace
Parameters:	int[], int[]
Returns:	int
Method signature:	int bestRace(int[] distances, int[] times)
(be sure your method is public)

Notes

-

In C++ e^x can be done with exp(x), and the natural log, ln(x), can be done with log(x), both functions are in math.h.

-

In C# e^x can be done with Math.Exp(x), and the natural log, ln(x), can be done with Math.Log(x). The Math class is in the System namespace.

-

In Java e^x can be done with Math.exp(x), and the natural log, ln(x), can be done with Math.log(x).

-

In Visual Basic e^x can be done with Exp(x), and the natural log, ln(x), can be done with Log(x), both functions are in the System.Math namespace.

Constraints

-

distances and times will both contain between 3 and 50 elements, inclusive.

-

distances and times will contain the same number of elements.

-

Every element in distances and times will be between 1 and 100000, inclusive.

-

No value in distances will occur more than once.

-

If the i-th value in distances is less than the j-th value in distances, then the i-th value of times will be less than the j-th value of times.

-

To avoid rounding issues, no two races' badnesses will be within 1e-9 of each other.

-

To make the approximation reliable, all speeds (distance/time), including those generated by the approximation, will be between 0.1 meter/second and 100 meters/second, inclusive.

Examples

0)

{1600,3200,16000}

{299,655,4020}

Returns: 2

This person runs 1.6 km in 4:59, 3.2 km in 10:55, and 16 km in 1:07:00. The expected times for each distance (always using the approximation based on the results of the other two races) are about 4:59.8 for the 1.6 km, 10:53.7 for the 3.2 km, and 1:07:26.0 for the 16 km. This results in badnesses of roughly -0.002767 for the 1.6 km, 0.001939 for the 3.2 km, and -0.006414 for the 16 km.

1)

{1600,2000,3200,3000,5000,9600}

{234,306,499,462,802,1629}

Returns: 3

Steve Prefontaine was probably the best American runner of all time. Here are his times for the 1.6 km, 2 km, 3 km, 3.2 km, 5 km, and 9.6 km. The badnesses of the respective races are about:

{0.0727,0.0747,0.0115,0.003,0.033,0.081}

2)

{1000,2000,3000,4000}

{160,330,510,750}

Returns: 2

3)

{1000,50000,10000,5000}

{200,70010,2250,1080}

Returns: 2

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ClockWalk

Simple Math

Used in:

SRM 175

Used as:

Division II Level One

Writer:

Eeyore

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2241

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4680&pm=2241

Problem Statement

Let's walk around the clock. We start at twelve o'clock and flip a coin. If it comes up heads, we step forward by one hour. If it's tails, we step one hour backward. We flip the coin a second time, but now we step two hours forward in the case of heads, or two hours backward for tails. On the third flip, we step three hours forward or backward on the same principle. In general, then, the nth flip decides the direction in which we step n hours: we move forward on heads, and backward on tails.

You are given a String describing a sequence of coin flips such that the nth character is either 'h', meaning that the nth flip is heads, or 't' to signify that the nth flip is tails. Return the hour at which we end up by following the above procedure.

Definition

Class:	ClockWalk
Method:	finalPosition
Parameters:	String
Returns:	int
Method signature:	int finalPosition(String flips)
(be sure your method is public)

Notes

-

The clock has an ordinary twelve-hour dial, numbered from 1 to 12.

-

Stepping forward means that we advance clockwise around the dial; to step backward is to advance counterclockwise.

Constraints

-

flips contains between 5 and 50 characters, inclusive

-

each character in flips is either 'h' or 't'

Examples

0)

"hhthh"

Returns: 9

We step forward to one o'clock on the first flip of the coin, and to three o'clock on the second flip. The third flip sends us back to twelve o'clock. On the fourth flip, we step forward to four o'clock. With the fifth and final flip, we arrive at nine o'clock.

1)

"hhtht"

Returns: 11

As before, the initial sequence "hhth" takes us to four o'clock. The fifth flip sends us backward to eleven o'clock.

2)

"hthth"

Returns: 3

Having stepped one hour forward, two backward, and three forward, we arrive at two o'clock. Stepping backward four hours and forward five, we end up at three o'clock.

3)

"hthhhhh"

Returns: 12

4)

"hthhthtththhtttthttthhhthtttthh"

Returns: 6

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ProbabilityTree

Math

Used in:

SRM 174

Used as:

Division II Level Three

Writer:

LunaticFringe

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2234

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4675&pm=2234

Problem Statement

Probability trees are a useful tool in mathematics to help determine conditional probabilities of complex events. Each node in a probability tree represents an event. We write P(X) to mean "the probability that event X occurs", and P(~X) to mean "the probability that event X does not occur". If a node is at the root of the tree, it has a single number associated with it (between 0.0 and 1.0, inclusive) which represents the likelihood of this event taking place. All other nodes on the tree have two numbers attached to them: the probability of this event happening if the parent node's event occurs, and the probability of this event happening if the parent node's event does not occur. If the current node is A and the parent node is B, these probabilities are referred to as P(A|B) (probability of A given B) and P(A|~B) (probability of A given not-B), respectively.

For example, here is a tree with only two nodes:

To calculate the probability of event 1 occurring (whether or not event 0 occurs), one can use this rule:

P(A) = P(A|B) * P(B) + P(A|~B) * P(~B)

The following diagram shows a more complete list of probabilities which can be derived:

Note that the sum of two opposite events is always equal to 1. P(1) was calculated as follows:

P(1) = P(1|0) * P(0) + P(1|~0) * P(~0) = (0.4 * 0.7) + (0.6 * 0.1) = 0.34

You will be given a String[] tree, representing a probability tree. The first element of tree represents the root node, and will be a single integer between 1 and 99, inclusive, representing the percent likelihood of the event taking place. Each successive element of tree will be of the form "<parent> <prob1> <prob2>", where <parent> is the zero-based index of the parent node in tree, and <prob1> and <prob2> are P(A|B) and P(A|~B) for this node, respectively. You will also be given two percentages, lowerBound and upperBound. Your method should return a int[] containing every node X, in ascending order, such that lowerBound < P(X) < upperBound.

Definition

Class:	ProbabilityTree
Method:	getOdds
Parameters:	String[], int, int
Returns:	int[]
Method signature:	int[] getOdds(String[] tree, int lowerBound, int upperBound)
(be sure your method is public)

Constraints

- tree will contain between 1 and 50 elements, inclusive.

- Each element of tree will contain between 1 and 8 characters, inclusive.

- The first element of tree will contain a single integer between 1 and 99, inclusive, with no leading zeroes.

- All other elements of tree will contain three space-separated integers of the form "<parent> <prob1> <prob2>", with no unnecessary leading zeroes.

- <parent> will be an integer between 0 and N-1, inclusive, where N is the number of elements in tree.

- <prob1> and <prob2> will be between 1 and 99, inclusive.

- All nodes in tree will be connected, directly or indirectly, to the root node.

- lowerBound will be between 0 and 99, inclusive.

- upperBound will be between 1 and 100, inclusive.

- lowerBound will be strictly less than upperBound.

- No event's likelihood will be within 1e-9 of lowerBound or upperBound.

Examples

0)

{"40","0 70 10"}

Returns: { 0,  1 }

This is the example from the problem statement. The probability of event 0 is 0.4, and the probability of event 1 is 0.34, both of which are within the specified range.

1)

{"20","2 50 50","0 50 50"}

Returns: { 1,  2 }

Both event 1 and event 2 have 50% probabilities of happening, regardless of what happens at their parents.

2)

{"10","0 99 41","1 40 3","2 91 43"}

Returns: { }

event | probability (rounded)
------+------------
 0    | 0.10
 1    | 0.47
 2    | 0.20
 3    | 0.53

3)

{"79","0 64 52","1 70 87","0 38 99","1 24 8"}

Returns: { 0,  1,  2,  3 }

4)

{"51",
 "29 58 3",
 "6 56 86",
 "18 97 1",
 "44 99 25",
 "33 69 90",
 "27 67 49",
 "32 15 19",
 "33 1 21",
 "45 12 33",
 "29 24 40",
 "45 86 74",
 "40 30 65",
 "0 18 27",
 "1 90 65",
 "0 47 62",
 "40 81 72",
 "42 25 56",
 "45 16 81",
 "8 94 92",
 "29 41 92",
 "24 4 29",
 "32 56 91",
 "20 16 77",
 "1 35 79",
 "45 77 61",
 "6 50 19",
 "20 69 43",
 "4 6 16",
 "15 55 26",
 "42 73 90",
 "40 8 49",
 "33 16 33",
 "15 95 47",
 "9 66 40",
 "25 80 39",
 "35 72 70",
 "27 10 36",
 "40 36 10",
 "32 2 48",
 "33 44 23",
 "22 51 45",
 "25 8 43",
 "18 32 96",
 "45 41 74",
 "0 51 6",
 "18 48 15"}

Returns: 
{ 0,  1,  2,  3,  4,  5,  6,  7,  9,  10,  11,  12,  13,  14,  15,  16,  17,  18,  20,  21,  23,  24,  25,  26,  27,  28,  29,  31,  32,  33,  34,  35,  36,  37,  38,  39,  40,  41,  42,  43,  44,  45,  46 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RangeGame

Math, String Parsing

Used in:

SRM 174

Used as:

Division I Level Two

Writer:

LunaticFringe

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2233

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4675&pm=2233

Problem Statement

Imagine a game consisting of two billion doors (numbered starting at 1), behind some of which lie fabulous cash prizes. There are a limited number of patterns to the placement of the prizes, which the contestant knows in advance. All doors initially begin closed. Before the game begins, the host secretly selects one of the patterns from the list at random (all with equal probability), and puts prizes behind the doors specified by the pattern. For example, if the host chose the pattern "3-4 9 12-15", he would put prizes behind doors 3, 4, 9, 12, 13, 14, and 15 (and nowhere else).

Two things happen every turn. First, the contestant decides which door is currently most likely to contain a prize, and secretly records this choice. (If two or more doors both have the greatest likelihood of containing a prize, he chooses the door with the lowest number.) The second part of a turn consists of the host opening one or more doors, all of which are revealed to be empty. For example, if the host gave the hint "2 7-10", this would indicate that he opened doors 2, 7, 8, 9, and 10 and there were no prizes behind any of them.

In specific, the following grammar is used for this problem:

<doors> ::= <range> | <range><sp><doors> <range> ::= <num> | <num><to><num> (the first num must be strictly less than the second num)<num> ::= integer between 1 and 2000000000, inclusive, with no leading zeroes <sp> ::= ' ' <to> ::= '-'

Given a String[] possible, containing the possible placements of prizes, and a String[] hints, the N hints given during the course of the game, your method should return a int[] containing N+1 elements. Each element should describe the most likely position of a prize at that point in the game. The first element represents your guess before any hints are given; the last element represents your guess taking every hint into account. Remember to break ties by choosing the lowest numbered door, if multiple doors are all the most likely.

Definition

Class:	RangeGame
Method:	bestDoors
Parameters:	String[], String[]
Returns:	int[]
Method signature:	int[] bestDoors(String[] possible, String[] hints)
(be sure your method is public)

Notes

- Each element of possible has an equal chance of being the pattern that is chosen by the host. This means that if one pattern appears on the list twice, it is twice as likely of being chosen as a pattern which appears on the same list only once.

Constraints

- possible will contain between 2 and 50 elements, inclusive.

- Each element of possible will contain between 1 and 50 characters, inclusive.

- Each element of possible will conform to the rules of <doors>, as specified in the grammar above.

- For each element of possible, the ranges contained therein will be non-overlapping and in ascending order.

- hints will contain between 0 and 50 elements, inclusive.

- Each element of hints will contain between 2 and 50 characters, inclusive.

- Each element of hints will conform to the rules of <doors>, as specified in the grammar above.

- For each element of hints, the ranges contained therein will be non-overlapping and in ascending order.

- The information given in hints will always be consistent with at least one pattern in possible.

Examples

0)

{"1-100","100-200","200-300"}

{"50-75","250-1000"}

Returns: { 100,  200,  100 }

There are three possible patterns of prizes: doors 1-100, doors 100-200, or doors 200-300. Before any hints are given, you know that doors 100 and 200 are more likely than the rest; the odds of a prize being in either of them are 2/3, whereas the odds of a prize being in any other door 1-300 is only 1/3. Doors 100 and 200 are the most likely, so your first guess should be 100 (since it is smaller).

Then the host reveals that there are no prizes behind doors 50-75. Pattern "1-100" is now no longer an option. You now know for sure that there is a prize in door 200, whereas the odds for any other door 100-300 is only 1/2. Therefore, 200 is the second element of the return list.

Finally, the host opens doors 250-1000 and shows them all to be empty. You now know the pattern must be "100-200", so you choose the smallest door of this group, 100, to be your final answer.

1)

{"100-900 1111","200-800 2222","300-700 3333","4444"}

{"2000-4000","500"}

Returns: { 300,  100,  4444 }

Before any hints are given, doors 300-700 are the most likely to contain prizes. The first hint tells you that doors 2222 and 3333 are empty, leaving only the first and last patterns as options. The second hint eliminates the first pattern, so the only prize must be in room 4444.

2)

{"346591240","858005279","1321831520","1453846384","1972718383","530431653-1848872872"}

{"1400000000-2000000000","400000000-600000000"}

Returns: { 858005279,  346591240,  346591240 }

Beware of large numbers and ranges!

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EngineersPrimes

Advanced Math

Used in:

SRM 181

Used as:

Division II Level Three

Writer:

antimatter

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2017

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4725&pm=2017

Problem Statement

A prime number is a number whose only divisors are 1 and itself. A sublinear polynomial-time algorithm has been shown to exist that determines primality or non-primality with certainty, unlike the previous probablistic tests, but it is extremely complicated. There must be an easier way.

In engineering, exact solutions are often not required, only good approximations. Thus, an "Engineer's Prime" of order N is any number that is divisible by none of the first N primes, since the smallest primes are easy to remember: 2, 3, 5, and so on. Note that 1 is not considered a prime in this case.

Given an int N, your method should return the smallest Engineer's Prime of order N that is not prime.

Definition

Class:	EngineersPrimes
Method:	smallestNonPrime
Parameters:	int
Returns:	long
Method signature:	long smallestNonPrime(int N)
(be sure your method is public)

Notes

-

1 is not to be considered prime.

Constraints

-

N will be between 1 and 100000, inclusive.

Examples

0)

Returns: 49

The first three primes are 2, 3, and 5. Next, look through the numbers after 5 that are not divisible by any of those first three primes. These are, in order, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, and 49, all of which are prime except the last.

1)

Returns: 9

The first odd number that is not prime.

2)

Returns: 2886601

3)

Returns: 247716121

4)

Returns: 10971096049

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Rounder

Math

Used in:

SRM 195

Used as:

Division II Level One

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2016

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5070&pm=2016

Problem Statement

Most of the time when rounding a given number, it is customary to round to some multiple of a power of 10. However, there is no reason why we cannot use another multiple to do our rounding to. For example, you could round to the nearest multiple of 7, or the nearest multiple of 3.

Given an int n and an int b, round n to the nearest value which is a multiple of b. If n is exactly halfway between two multiples of b, return the larger value.

Definition

Class:	Rounder
Method:	round
Parameters:	int, int
Returns:	int
Method signature:	int round(int n, int b)
(be sure your method is public)

Constraints

-

n will be between 1 and 1000000, inclusive.

-

b will be between 2 and 500, inclusive.

Examples

0)

Returns: 10

This is a standard rounding base. We round up because 5 is an equal distance between 0 and 10.

1)

Returns: 0

2)

Returns: 99

100 is closer to 99 than 102.

3)

Returns: 123459

4)

Returns: 49

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Harmony

Brute Force, Math

Used in:

SRM 176

Used as:

Division II Level Three

Writer:

Running Wild

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2015

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4685&pm=2015

Problem Statement

A chord in music is formed by playing three or more notes at the same time. The sound of the chord depends of the ratio of each note in the chord to the others. The ratios between frequencies in harmonious chords can be expressed as rational numbers with small denominators (2/1, 3/2, 5/4, etc...), whereas the ratios between frequencies in discordant chords can only be expressed as rational numbers with large denominators (8/7, 16/9, etc...). Ratios between frequencies are always represented by reduced fractions with the smaller number in the denominator. Create a class Harmony with a function mostHarmonious that takes a int[] frequencies representing the frequencies of various notes and returns a int[] that contains the three elements from frequencies that form the most harmonious chord, sorted from lowest to highest frequency.

A chord C1 is more harmonious than a chord C2 if the largest denominator of the ratios in C1 is smaller than the largest denominator of the ratios in C2. If these values are the same, then compare the second largest denominator of each chord in the same way, and then the third largest if necessary. If two chords have the same denominators, compare the lowest frequency of each chord, and return the chord with the lower frequency. If they are the same, then compare the second lowest frequency of each chord in the same way, and then the third lowest, if necessary.

An example: a chord C1 has notes with frequencies 200, 250, and 400. The ratios of these notes are 5/4, 2/1, and 8/5. A chord C2 has notes with frequencies 200, 320, and 350. The ratios of these notes are 8/5, 7/4, and 5/4. The denominators of the ratios in C1 are 1, 4, and 5, and for C2 they are 4, 4, and 5. C1 is the more harmonious of the two, because although both chords have the same largest and second largest denominator, C1's third largest denominator is less than C2's third largset denominator.

Definition

Class:	Harmony
Method:	mostHarmonious
Parameters:	int[]
Returns:	int[]
Method signature:	int[] mostHarmonious(int[] frequencies)
(be sure your method is public)

Constraints

-

frequencies will contain between 3 and 50 elements, inclusive.

-

Every element of frequencies will be a value between 1 and 10000, inclusive.

Examples

0)

{200,250,400,320,350}

Returns: { 200,  250,  400 }

These are the frequencies used in the example above. The most harmonious chord has ratios 8/5 (400/250), 5/4 (250/200), and 2/1 (400/200).

1)

{440, 320, 750,660, 500,550}

Returns: { 440,  550,  660 }

The best chord here is an A major triad.

2)

{1960,1000,3050,2341,7253,7864,2000,2352,2940,1534,7234}

Returns: { 1960,  2352,  2940 }

The best chord here is a G minor triad. Notice that even though the frequencies 1000 and 2000 are available, which had a ratio of 2/1, there is nothing else they could be used with that would also have a low ratio.

3)

{100,200,300,400,500,600,700,800,900,1000}

Returns: { 100,  200,  400 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Deranged

Advanced Math

Used in:

SRM 176

Used as:

Division I Level Two

Writer:

Running Wild

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=2013

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4685&pm=2013

Problem Statement

A derangement of n numbers is a permutation of those numbers in which none of the numbers appears in its original place. For example, the numbers {1,2,3} can be deranged into {2,3,1} and {3,1,2}. We can modify this slightly for n numbers that are not necessarily distinct by saying that no number in the derangement can be in the place that a number of the same value was in in the original ordering. So the numbers {1,1,2,2,3} could be deranged into {2,2,1,3,1}, {2,2,3,1,1}, {2,3,1,1,2}, and {3,2,1,1,2}. Create a class Deranged with a function numDerangements that takes a int[] nums and return the number of derangements of nums.

Definition

Class:	Deranged
Method:	numDerangements
Parameters:	int[]
Returns:	long
Method signature:	long numDerangements(int[] nums)
(be sure your method is public)

Notes

-

The return value will fit in a 64-bit unsigned integer.

Constraints

-

nums will contain between 1 and 15 elements, inclusive.

-

nums will only contain values between 0 and the number of elements in nums - 1, inclusive.

Examples

0)

{1,1,2,2,3}

Returns: 4

The example from above.

1)

{0,0,0,1,1,1}

Returns: 1

The only derangement is {1,1,1,0,0,0}.

2)

{0,0,0,1,1,1,1}

Returns: 0

There is no way to arrange the numbers such that no 1 is where a 1 was originally.

3)

{0,0,0,0,0,0,0,1,1,1,1,1,1,1,2}

Returns: 14

4)

{0,5,4,2,3,6,6}

Returns: 640

5)

{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14}

Returns: 481066515734

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BadParser

Simple Math, String Parsing

Used in:

TCO04 Round 1

Used as:

Division I Level Two

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1995

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5878&pm=1995

Problem Statement

You and a partner have teamed up for a coding project. He is writing the front-end of an arithmetic expression parser, and you are writing the back-end. The expressions are pretty simple, with normal arithmetic operations and no parentheses. As usual, he stayed up too late and made a terrible oversight. His parser spits out an expression tree where the precedence and associativity of the operators may be ignored. For example, let's say his program is given the expression "5+2-3-4*2". Each operator is supposed to be left associative, but his program could spit out the wrong tree:

       His tree                    Correct Tree
          +                             -
        /   \                        /     \
       5     -                     -         *
           /   \                 /   \     /   \
          2     -               +     3   4     2
              /   \           /   \
             3     *         5     2
                 /   \
                4     2

The expressions should be interpreted as follows:

1) As usual, the order of operations gives * and / highest precedence whereas + and - have lowest. * and / have equal precedence. In addition, + and - have equal precedence.
2) Amongst operations of equal precedence, process the leftmost operation first.

Adhering to these rules, the input above would be processed to produce the Correct Tree. In such a tree, lower nodes are processed before higher nodes. The value of a number node is the number itself. The value of an operation node is that operation applied to the values of its left and right subnodes (the value of the left subnode belongs on the left side of the operation). The value of the tree is the value of the top node (called the root node). Unfortunately, your partner's front-end may have violated rules 1 and 2 numerous times. Luckily the ordering of his tree is not messed up. This means that an inorder traversal of the tree beginning with the root will produce the original expression. Inorder traversal pseudocode follows:

InorderTraverse(node) {
	if (left subtree of node exists) 
		InorderTraverse(root of left subtree)
	Print the contents of node
	if (right subtree of node exists) 
		InorderTraverse(root of right subtree)
}

Your program will take a String[] badTree describing his tree, and will return an int which is the correct value of the expression he parsed. All operations are integer operations so division truncates results. For example 5/3=1, and -5/3 = -1.

Each element of badTree will be in one of two forms (quotes for clarity):

1) "op X Y" : op is one of *,/,+,-. X,Y are integers referencing other elements of badTree (0-indexed). X refers to the node's left child and Y refers to the node's right child.
2) "N" : N is a non-negative integer with no extra leading zeros.

Definition

Class:	BadParser
Method:	evaluate
Parameters:	String[]
Returns:	int
Method signature:	int evaluate(String[] badTree)
(be sure your method is public)

Constraints

-

badTree will contain between 1 and 50 elements inclusive.

-

Each element of badTree will be in one of the following forms (quotes for clarity):

1) "op X Y" where X and Y are integers, with no extra leading zeros, between 0 and M-1 inclusive. op must be *,+,-, or /. Here M denotes the number of elements in badTree.

2) "N" where N is a nonnegative integer with no extra leading zeros between 0 and 1000 inclusive.

-

The elements of badTree will describe a single tree, with element 0 acting as root.

-

The return value, and the value of any subtree of the correct tree will all be between -100000 and 100000 inclusive.

-

The computation of the return value, and the value of any subtree of the correct tree will not require division by 0.

Examples

0)

{"+ 1 2","5","- 3 4","2","- 5 6","3","* 7 8","4","2"}

Returns: -4

The example in the problem statement.

1)

{"- 1 2","5","- 3 4","2","- 5 6","3","* 7 8","4","2"}

Returns: -8

The example in the problem statement with the + replaced by a -.

2)

{"* 1 2","5","- 3 4","2","- 5 6","3","* 7 8","4","2"}

Returns: -1

The example in the problem statement with the + replaced by a *.

3)

{"99"}

Returns: 99

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ScheduleStrength

Math, Sorting, String Parsing

Used in:

SRM 265

Used as:

Division I Level One , Division II Level Two

Writer:

HardCoder

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1993

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8007&pm=1993

Problem Statement

A common way to rank athletic teams is based on each team's winning percentage. However, when two teams have similar percentages, the team that played against better opponents will be ranked above the team that had easier opponents. The measure of how difficult a team's opponents are, is known as the team's strength of schedule. A team that has faced tough opponents is said to have a strong schedule, and a team with poor opponents is said to have a weak schedule.

We will use the cumulative winning percentage of Team X's opponents (the teams that Team X played against) as a measure of Team X's strength of schedule. This percentage is the number of wins recorded by Team X's opponents divided by the total games they played, excluding games that were played against Team X.

Given a String[] of teams that contains the name of each team and a String[] results that indicates the outcome of games played during the season, return a String[] containing the names of the teams, ordered from strongest schedule to weakest. Teams with equivalent schedule strengths should appear in increasing alphabetical order.

Element i of results corresponds to team i whose name is found in teams at index i. Character j of element i of results will be one of 'W', 'L' or '-' respectively indicating whether team i won, lost, or did not play a game against team j.

Definition

Class:	ScheduleStrength
Method:	calculate
Parameters:	String[], String[]
Returns:	String[]
Method signature:	String[] calculate(String[] teams, String[] results)
(be sure your method is public)

Constraints

- teams will contain between 3 and 50 elements, inclusive.

- teams and results will contain the same number of elements.

- Each element of teams will contain between 1 and 50 characters, inclusive.

- Each element of teams will only contain uppercase letters ('A'-'Z').

- Each element of teams will be distinct.

- Each element of results will contain N characters, where N is the number of elements in teams.

- Each element of results will only contain 'W', 'L' and '-'.

- The ith character of the ith element of results will be '-'.

- If the jth character of the ith element of results is 'W' then the ith character of the jth element of results will be 'L', and vice versa.

- Every team will play at least two games.

Examples

0)

{"BEARS",
 "GIANTS",
 "COWBOYS",
 "BRONCOS",
 "DOLPHINS",
 "LIONS"}

{"-WLWW-",
 "L-WL-W",
 "WL---W",
 "LW--L-",
 "L--W--",
 "-LL---"}

Returns: {"BEARS", "DOLPHINS", "BRONCOS", "COWBOYS", "GIANTS", "LIONS" }

This season's results gives us the following win/loss records:

        wins - losses
BEARS      3 - 1
GIANTS     2 - 2  (1 loss to the BEARS)
COWBOYS    2 - 1  (1 win against the BEARS)
BRONCOS    1 - 2  (1 loss to the BEARS)
DOLPHINS   1 - 1  (1 loss to the BEARS)
LIONS      0 - 2  (did not play the BEARS)

The BEARS's opponents are the GIANTS, COWBOYS, BRONCOS and DOLPHINS. Their combined win/loss record is 6-6 (6 wins, 6 losses), but when we exclude games played against the BEARS, this record becomes 5-3. So, the BEARS have a schedule strength of 5/8 = .625

Here are the cumulative records and winning percentages calculated for each team:

           Record    Winning %
BEARS      5 - 3    5/8 = .625
GIANTS     4 - 4    4/8 = .5
COWBOYS    4 - 3    4/7 = .5714
BRONCOS    4 - 3    4/7 = .5714
DOLPHINS   3 - 2    3/5 = .6
LIONS      2 - 3    2/5 = .4

1)

{"BEARS",
 "COWBOYS",
 "GIANTS",
 "PACKERS"}

{"-LLW",
 "W-WW",
 "WL--",
 "LL--"}

Returns: {"GIANTS", "BEARS", "COWBOYS", "PACKERS" }

2)

{"AZTECS",
 "COUGARS",
 "COWBOYS",
 "FALCONS",
 "HORNEDFROGS",
 "LOBOS",
 "RAMS",
 "REBELS",
 "UTES"}

{"---L-L--W",
 "--LL-LWL-",
 "-W--WWLLW",
 "WW---L--W",
 "--L--W-L-",
 "WWLWL-LW-",
 "-LW--W-L-",
 "-WW-WLW--",
 "L-LL-----"}

Returns: 
{"HORNEDFROGS",
"COUGARS",
"RAMS",
"LOBOS",
"REBELS",
"UTES",
"COWBOYS",
"AZTECS",
"FALCONS" }

3)

{"E", "D", "C", "B", "Z"}

{
"--LLL",
"---LL",
"W---L",
"WW---",
"WWW--"
}

Returns: {"D", "E", "C", "Z", "B" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PokerDeck

Brute Force, Math

Used in:

SRM 265

Used as:

Division I Level Three

Writer:

HardCoder

Testers:

PabloGilberto , brett1479 , Olexiy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1981

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8007&pm=1981

Problem Statement

Poker is usually played with a standard deck of 52 cards. Each card is marked with one of 13 face values and one of 4 suits. In a common version of poker, a player receives a hand of five cards. Hands that match certain combinations, or patterns, have specific names like "FULL HOUSE" or "ROYAL FLUSH". The less likely it is that a particular hand will be dealt, the better that hand is.

You want to play poker with some friends, but your little sister has been using all the cards in the house to perform magic tricks. It seems the only trick she has perfected is a disappearing act which makes it impossible to find a complete deck of cards. You and your friends gather as many cards as you are able to find and put them into a single deck. This, however, might change the probability of getting certain poker hands. Given a String[] decks that lists the contents of the partial decks that were gathered, calculate the odds of getting each poker hand from the new combined deck. Return a String[] containing the names of each poker hand in order of increasing probability so that the best hand is listed first. Hands that have an equal chance of being dealt should be listed in alphabetical order. Hands that have no chance of being dealt should be excluded from the results.

Each element in decks is a list of cards separated by spaces. Each card will be in the format <face><suit> where <face> is one of the 13 face values, listed in increasing consecutive order ( 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A ) and <suit> is one of ( C, D, H, S ).

The possible hands from a combined deck are:

"ONE PAIR" - two of the five cards have the same face value (2C 4S 5H 8C 8D)
"TWO PAIR" - two of one face value and two of a different face value (4H 4S 5H 8C 8D)
"THREE OF A KIND" - three cards of the same face value (2C 4S 8H 8C 8D)
"FOUR OF A KIND" - four cards of the same face value (2C 8S 8H 8C 8D)
"FULL HOUSE" - three of one face value and two of a different face value (8H 8C 8D 4C 4S)
"FLUSH" - five cards of the same suit (2C 5C 7C QC AC)
"STRAIGHT" - five cards with consecutive face values (8C 9S 10C JH QD)
             The ace may be used as the low card in a straight (AD 2C 3S 4C 5H)
             However, wrapping is not allowed (QC KC AC 2D 3C)
"STRAIGHT FLUSH" - matches both a FLUSH and a STRAIGHT (7H 8H 9H 10H JH)
"ROYAL FLUSH" - ten, jack, queen, king, ace of the same suit (10S JS QS KS AS)
"FIVE OF A KIND" - all five cards with the same face value (6C 6D 6C 6S 6H)
"NOTHING" - a hand that does not match any of these combinations (2C 7D 8H 10C AS)

Since the order in which cards are dealt does not matter, a hand containing ( QD 9S JH 8C 10C ) is identical to ( 8C 9S 10C JH QD ) and both would be classified as a "STRAIGHT". A hand that matches more than one of the descriptions listed above is classified with the name that appears lowest. For instance, the hand ( 3C 3D 3H KC KD ) would be classified as a "FULL HOUSE" even though it also matches the descriptions for "THREE OF A KIND" and "ONE PAIR".

Definition

Class:	PokerDeck
Method:	getRanking
Parameters:	String[]
Returns:	String[]
Method signature:	String[] getRanking(String[] decks)
(be sure your method is public)

Notes

- The same card may appear multiple times in an element of decks

Constraints

- decks will have between 1 and 50 elements, inclusive.

- Each element of decks will have between 2 and 50 characters, inclusive.

- Each element of decks will contain valid cards with a single space between cards.

- The first character and the last character of each element of decks will not be a space.

- A valid card will be formatted as <face><suit>

- <face> will be one of ( 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A ).

- <suit> will be one of ( C, D, H, S ).

- decks will represent at least 5 cards.

Examples

0)

{"AC 2C 3C 4C 5C 6C 7C 8C 9C 10C JC QC KC",
 "AD 2D 3D 4D 5D 6D 7D 8D 9D 10D JD QD KD",
 "AH 2H 3H 4H 5H 6H 7H 8H 9H 10H JH QH KH",
 "AS 2S 3S 4S 5S 6S 7S 8S 9S 10S JS QS KS"}

Returns: 
{"ROYAL FLUSH",
"STRAIGHT FLUSH",
"FOUR OF A KIND",
"FULL HOUSE",
"FLUSH",
"STRAIGHT",
"THREE OF A KIND",
"TWO PAIR",
"ONE PAIR",
"NOTHING" }

This is a standard deck of cards, which will result in the following odds:

    ROYAL FLUSH:       4/2598960
 STRAIGHT FLUSH:      36/2598960
 FOUR OF A KIND:     624/2598960
     FULL HOUSE:    3744/2598960
          FLUSH:    5108/2598960
       STRAIGHT:   10200/2598960
THREE OF A KIND:   54912/2598960
       TWO PAIR:  123552/2598960
       ONE PAIR: 1098240/2598960
        NOTHING: 1302540/2598960

1)

{"AS 2C 3C 4C 5C 7D 7H 8C 8D 8H 10S JS QS KS"}

Returns: 
{"FLUSH",
"FULL HOUSE",
"ROYAL FLUSH",
"STRAIGHT",
"TWO PAIR",
"THREE OF A KIND",
"ONE PAIR",
"NOTHING" }

This deck results in the following odds:

          FLUSH:    1/2002
     FULL HOUSE:    1/2002
    ROYAL FLUSH:    1/2002
       STRAIGHT:    1/2002
       TWO PAIR:   27/2002
THREE OF A KIND:   54/2002
       ONE PAIR:  660/2002
        NOTHING: 1257/2002

2)

{"AS AS AS AS AS AS AS AS AS AS AS",
 "AS AS AS AS AS AS AS AS AS AS AS",
 "AS AS AS AS AS AS AS AS AS AS AS",
 "2C 4C 6C 8C"}

Returns: {"NOTHING", "ONE PAIR", "THREE OF A KIND", "FOUR OF A KIND", "FIVE OF A KIND" }

3)

{"QC QH QD 6S 6H"}

Returns: {"FULL HOUSE" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ProgressBar

Simple Math, String Manipulation

Used in:

SRM 173

Used as:

Division II Level One

Writer:

Yarin

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1975

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4670&pm=1975

Problem Statement

Installation programs often run several tasks, one after another. Each task is assigned an integer, the expected execution time of this task. During the installation, a progress bar shows the user what percentage of the installation time has elapsed. In this problem, the bar will be represented by a string containing exactly 20 characters. If X% of the installation has been completed, then the leftmost X% of these characters should be a '#', while the remaining characters should be '.'. If necessary, round down the number of '#' characters to the nearest integer less than or equal to the actual value (see example 0). The bar starts at 0% and is only updated each time a task finishes execution.

Create a class ProgressBar containing the method showProgress which takes a int[] taskTimes, the expected execution time for each task in the order they are run, and an int tasksCompleted, the number of these tasks that have been completed. The method should return a String containing exactly 20 characters showing the progress bar according to the descriptions above.

Definition

Class:	ProgressBar
Method:	showProgress
Parameters:	int[], int
Returns:	String
Method signature:	String showProgress(int[] taskTimes, int tasksCompleted)
(be sure your method is public)

Constraints

-

taskTimes will contain between 1 and 50 elements, inclusive.

-

Each element in taskTimes will be between 1 and 1000, inclusive.

-

tasksCompleted will be between 0 and the number of elements in taskTimes, inclusive.

Examples

0)

{19,6,23,17}

Returns: "##############......"

This installation consist of 4 tasks, and the expected execution times for these are 19, 6, 23 and 17, respectively. Since the first 3 tasks have been completed, the total execution time for the installation so far has been 19+6+23 = 48 and the total expected time is 19+6+23+17 = 65. Thus 48/65 = 73.84615% of the installation has been completed, so the first 20*0.7384615 = 14.76923 = 14 (round down) characters in the string should be '#', and the remaining 6 should be '.'. Thus the method returns "##############......"

1)

{2,3,7,1,4,3}

Returns: "#############......."

The installation has run for 2+3+7+1 = 13 units and the total execution is 2+3+7+1+4+3 = 20.

2)

{553,846,816,203,101,120,161,818,315,772}

Returns: "##########.........."

3)

{7,60,468,489,707,499,350,998,1000,716,457,104,597,583,396,862}

Returns: "...................."

4)

{419,337,853,513,632,861,336,594,94,367,336,297,966,627,399,433,846,859,80,2}

Returns: "###################."

Even though about 99.98% of the installation has been completed, the last character should still be a '.' since we always round down.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BaseballLineup

Advanced Math, Dynamic Programming

Used in:

TCO '03 Finals

Used as:

Division I Level Two

Writer:

lars2520

Testers:

zoidal , NGBronson , brett1479 , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1972

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4711&pm=1972

Problem Statement

Baseball is a sport played on a diamond with three bases, first second and third, and a home plate. Players start at home plate, and attempt to hit a ball and run around all three of the bases in order, and end up back at home plate. If a player gets back to home plate, then a run is scored. There are 6 things that can happen to a player when he attempts to hit the ball:

The player may get an out, in which case the next batter steps up, and the runners on base do not move (unless it is the third out of the inning, see below).
The player may be walked, and end up at first base. If there was a player on first base, that player would advance to second. If there were players on first and second, they would advance to second and third base respectively. If there were players on all three bases, the player on third base would score a run and the players on first and second would advance to second and third base respectively. In other words, when a walk occurs, a player only advances when another player advances to the base he is on. Thus, if there were players on first and third bases, and a player was walked, only the player on first would advance.
The player may hit a single. In this case, the player who hit the ball ends up on first base. If there was a player on first base, that player would advance to second. Each player who was on second or third base would make it to home plate and score a run. (So, if there were players on both second and third, two runs would score.)
The player may hit a double, and end up on second base. Each player who was on base scores a run.
The player may hit a triple, and end up on third base. Each player who was on base scores a run.
The player may hit a home run, in which case he and all of the players on base score runs.

A game of baseball goes 9 innings. Each inning consists of 3 outs (outs have no effect until there are 3 of them in an inning). Players take turns batting in order, starting with player 1 (indexed from 1) in the first inning, and continue to bat until there are 3 outs. Once 3 outs have been made, the inning ends and any runners who were on base are no longer on base. In the next inning, the batting order picks up where it left off. So, if player 4 made the last out in the 3rd inning, then player 5 would bat first in the 4th inning. Furthermore, after player 9 bats, it is then player 1's turn.

Your task is, given the stats of all 9 players on a team, return the expected number of runs that team will score in 9 innings. For each player you will be given a String, formatted as "<outs> <walks> <singles> <doubles> <triples> <homeRuns>". Each term in the String will be an integer representing the number of each event per 1000 appearances. Thus, the sum of all the terms in each String will be 1000. For example, "646 107 141 37 0 69" would indicate that 646/1000 times the players gets out, 107/1000 times the player is walked, 141/1000 times the player gets a single, and so on.

Here is an example of how an inning might go, assuming that player 3 is the first batter of the inning and that we start with 0 runs:

player | action   | outs | runs | runners on
-------+----------+------+------+-----------
 3     | walk     | 0    | 0    | first
 4     | out      | 1    | 0    | first
 5     | double   | 1    | 1    | second
 6     | walk     | 1    | 1    | first and second
 7     | single   | 1    | 2    | first and second
 8     | out      | 2    | 2    | first and second
 9     | home run | 2    | 5    | none
 1     | walk     | 2    | 5    | first
 2     | walk     | 2    | 5    | first and second
 3     | out      | 3    | 5    |

In the next inning, player 4 would bat first. Note that there would be no one on base at the beginning of the next inning, despite the fact that there were two players on base at the end of this inning.

In order to make things a little simpler, we will only allow 20 batters to hit in a single inning. So, after the 20th batter of an inning hits, the inning ends, regardless of how many outs there are. Thus, if every player hits a home run in every at bat, the team will score 20 runs per inning.

Definition

Class:	BaseballLineup
Method:	expectedRuns
Parameters:	String[]
Returns:	double
Method signature:	double expectedRuns(String[] stats)
(be sure your method is public)

Notes

-

Your result must have absolute or relative error less than 1e-9.

Constraints

-

stats will contain exactly 9 elements.

-

Each element of stats will be formatted as "<outs> <walks> <singles> <doubles> <triples> <homeRuns>".

-

Each of the terms in each element of stats will represent a non-negative integer, with no extra leading 0's.

-

The sum of the integers in each element of stats will be 1000.

Examples

0)

{"652 77 185 53 13 20",
 "649 58 213 74 1 5",
 "646 107 141 37 0 69",
 "650 100 159 55 1 35",
 "683 64 160 49 3 41",
 "663 76 184 43 2 32",
 "712 80 111 63 0 34",
 "693 99 135 48 2 23",
 "824 16 112 16 0 32"}

Returns: 4.799858944836131

The stats of the Cubs' starting lineup in game 7.

1)

{"1 0 0 0 0 999",
 "1 0 0 0 0 999",
 "1 0 0 0 0 999",
 "1 0 0 0 0 999",
 "1 0 0 0 0 999",
 "1 0 0 0 0 999",
 "1 0 0 0 0 999",
 "1 0 0 0 0 999",
 "1 0 0 0 0 999"}

Returns: 179.81995685471114

Here, players hit home runs almost every single time. Thus, since there are at most 20 at bats per inning, they are expected to score almost 20 runs per inning, for almost 180 during the whole game.

2)

{"0 0 1000 0 0 0",
 "0 0 1000 0 0 0",
 "0 0 1000 0 0 0",
 "0 0 1000 0 0 0",
 "0 0 1000 0 0 0",
 "0 0 1000 0 0 0",
 "0 0 1000 0 0 0",
 "0 0 1000 0 0 0",
 "0 0 1000 0 0 0"}

Returns: 162.0

3)

{"0 0 1000 0 0 0",
 "0 0 0 1000 0 0",
 "0 0 1000 0 0 0",
 "0 0 0 1000 0 0",
 "0 0 1000 0 0 0",
 "0 0 0 1000 0 0",
 "0 0 1000 0 0 0",
 "0 0 0 1000 0 0",
 "1000 0 0 0 0 0"}

Returns: 151.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BadClock

Math

Used in:

SRM 172

Used as:

Division I Level One , Division II Level Two

Writer:

Eeyore

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1969

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4665&pm=1969

Problem Statement

According to Lewis Carroll, a clock that has stopped is more accurate than one that is five minutes behind. He argues that the former is right twice a day, whereas the latter never shows the correct time. Then again, a clock that is always five minutes behind is in a sense perfectly accurate, and therefore an extraordinary specimen. More usually, a clock is ahead or behind because it runs at the wrong rate, so that its absolute discrepancy from the true time is steadily changing. If left unregulated, such a clock will show the true time at regular but perhaps lengthy intervals.

You are given two Strings of the form "hh:mm:ss". The first represents exactly the true time, while the second is exactly the time shown by an ill-tuned clock. This is an analog clock whose hour, minute, and second hands sweep continuously around the dial at a speed that is too fast or too slow by a constant factor. Both times are given in the North American style, where the hour ranges between 1 and 12, inclusive. Given an int specifying the non-zero number of seconds that the clock gains every hour, calculate the number of hours that elapse before it agrees with the true time. Your answer, a double, must be correct with either absolute or relative precision of 1.0e-9 (one billionth).

Definition

Class:	BadClock
Method:	nextAgreement
Parameters:	String, String, int
Returns:	double
Method signature:	double nextAgreement(String trueTime, String skewTime, int hourlyGain)
(be sure your method is public)

Notes

-

If hourlyGain is negative, the clock falls behind by a fixed number of seconds every hour.

-

It is not the case that the clock makes discrete jumps every so often. Rather, the hands of the clock are moving smoothly and continuously at a constant rate that is too slow or too fast relative to the true time.

Constraints

-

trueTime and skewTime each contain exactly eight characters in the format "hh:mm:ss", where the substring "hh" is a zero-padded integer between 1 and 12, inclusive, and "mm" and "ss" are zero-padded integers between 0 and 59, inclusive

-

hourlyGain is either between -1800 and -1, inclusive, or between 1 and 3600, inclusive

Examples

0)

"07:07:07"

"07:07:07"

Returns: 0.0

The clock is already showing the true time.

1)

"11:59:58"

"12:03:28"

-3

Returns: 70.0

This clock loses three seconds every hour, and will catch up with the true time in exactly 70 hours.

2)

"12:03:28"

"11:59:58"

Returns: 70.0

This clock gains three seconds per hour.

3)

"03:03:02"

"03:01:47"

Returns: 15.0

4)

"03:03:02"

"03:01:47"

-5

Returns: 8625.0

5)

"07:08:09"

"09:08:07"

-321

Returns: 22.42367601246106

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PassingGrade

Simple Math

Used in:

SRM 185

Used as:

Division II Level One

Writer:

vorthys

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1962

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4745&pm=1962

Problem Statement

You are studying for the final exam in a tough course, and want to know how many points you need to score on the final to pass the course. You know how many points you earned on each assignment (pointsEarned), how many points were possible on each assignment (pointsPossible), and how many points are possible on the final exam (finalExam). You need to earn a minimum of 65% of the total possible points to pass the course. Assume your score on the final exam will be an integral number of points between 0 and finalExam, inclusive. Return the number of points you need to score on the final to pass the course, or -1 if it is impossible for you to pass the course.

Definition

Class:	PassingGrade
Method:	pointsNeeded
Parameters:	int[], int[], int
Returns:	int
Method signature:	int pointsNeeded(int[] pointsEarned, int[] pointsPossible, int finalExam)
(be sure your method is public)

Constraints

-

pointsEarned contains between 1 and 20 elements, inclusive.

-

pointsPossible contains the same number of elements as pointsEarned.

-

Each element of pointsPossible is between 1 and 1000, inclusive.

-

Element i of pointsEarned is between 0 and element i of pointsPossible, inclusive.

-

finalExam is between 1 and 3000, inclusive.

Examples

0)

{55,77,82,60}

{100,100,100,100}

Returns: 181

If you score 181 points on the final, then you will finish the course with exactly 65% of the possible points.

1)

{ 1, 2, 3, 4 }

{ 2, 3, 4, 5 }

Returns: 4

If you score 4 points on the final, then you pass with 66.7% of the total possible points, but if you score 3 points on the final, then you fail with 61.9% of the possible points.

2)

{ 1, 2, 2, 1 }

{ 9, 9, 9, 9 }

Returns: -1

Even if you score 9 points on the final, you still fail with 33.3% of the possible points.

3)

{ 7, 8, 7, 6 }

{ 8, 8, 8, 8 }

Returns: 0

You will pass even if you score 0 points on the final.

4)

{ 17, 23, 50, 200, 19, 56, 83, 91, 77, 9, 0 }

{ 20, 30, 50, 250, 20, 70, 100, 100, 100, 10, 10 }

Returns: 129

5)

{600,600,600,600,600,600,600,600,600,600,
 600,600,600,600,600,600,600,600,600,600}

{1000,1000,1000,1000,1000,1000,1000,1000,
 1000,1000,1000,1000,1000,1000,1000,1000,
 1000,1000,1000,901}

Returns: 2886

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GoldMine

Greedy, Math

Used in:

SRM 169

Used as:

Division I Level Three

Writer:

huntergt

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1957

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4650&pm=1957

Problem Statement

Aurum Nugget, Inc. has just purchased some new gold mines. They have a number of miners available to work in the mines, and would like to allocate the miners in such a way as to maximize their profit. Each mine can support a maximum of 6 miners, and contains a maximum of 6 major ore deposits. After the miners have been allocated to mines, the company earns (or loses) money as follows:

If a mine has fewer miners than ore deposits, the company will earn $60 per miner allocated to that mine.
If a mine has the same number of miners as ore deposits, the company will earn $50 per miner allocated to that mine.
If a mine has more miners than ore deposits, the company will earn $50 for each miner up to the number of ore deposits, and will lose $20 for each extra miner allocated to that mine.

Even if it will lose money, the company must employ every available worker at one of its mines.

Write a class GoldMine with a method getAllocation that takes in a String[] mines and a int miners. Each element of mines will be in the form "<p0>, <p1>, <p2>, <p3>, <p4>, <p5>, <p6>" (quotes for clarity) where each <pn> is a three digit number (with leading 0s if necessary.) Each <pn> represents the probability (as a percentage) that n deposits are present in the mine, and all <pn>'s within a mine will always add up to 100. miners is the number of employees the company must allocate. The method should return a int[] indicating the number of miners to place in each mine in order to maximize the expected profit (where element i in the returned int[] corresponds to element i of mines). If there are multiple allocations which maximize expected profit, return the allocation which places more miners in earlier mines. More specifically, when comparing two different allocations X₀, X₁, X₂, ..., X_n and Y₀, Y₁, Y₂, ..., Y_n that yield the same expected profit, let i be the smallest index such that X_i is not equal to Y_i. Then if X_i > Y_i, allocation X₀, X₁, X₂, ..., X_n is preferred to allocation Y₀, Y₁, Y₂, ..., Y_n.

For example, suppose the company has 4 miners available, and purchased the following two mines:

	"000, 030, 030, 040, 000, 000, 000"
        "020, 020, 020, 010, 010, 010, 010"

The first mine has a 30 percent chance of containing 1 ore deposit, a 30 percent chance of containing 2 ore deposits, and a 40 percent chance of containing 3 ore deposits. The second mine has a 20 percent chance of containing 0 ore deposits, a 20 percent chance of containing 1 ore deposit, a 20 percent chance of containing 2 ore deposits, a 10 percent chance of containing 3 ore deposits, a 10 percent chance of containing 4 ore deposits, a 10 percent chance of containing 5 ore deposits, and a 10 percent chance of containing 6 ore deposits.

In this scenario, the company can make the most money by allocating two miners at each mine, yielding an expected profit of 153:

	First Mine
	   0.3*30 + 0.3*100 + 0.4*120 =
           9 + 30 + 48 = 87

	Second Mine
           0.2*(-40) + 0.2*30 + 0.2*100 + 0.1*120 + 0.1*120 + 0.1*120 + 0.1*120 = 
           -8 + 6 + 20 + 12 + 12 + 12 + 12 = 66

	Total Profit
	   87 + 66 = 153

The method would have returned { 2, 2 }. Other allocations would have yielded:

	{ 0, 4 } :  75
	{ 1, 3 } : 132
	{ 3, 1 } : 129
	{ 4, 0 } :  67

Definition

Class:	GoldMine
Method:	getAllocation
Parameters:	String[], int
Returns:	int[]
Method signature:	int[] getAllocation(String[] mines, int miners)
(be sure your method is public)

Notes

-

Each mine can support a maximum of 6 miners.

Constraints

-

mines will contain between 1 and 50 elements, inclusive

-

each element of mines will contain exactly 33 characters

-

each element of mines will contain only digits ('0'-'9'), commas (',') and spaces (' ')

-

each element of mines will be in the form "<p0>, <p1>, <p2>, <p3>, <p4>, <p5>, <p6>" (quotes for clarity) where each <pn> is a three digit number (with leading 0s if necessary.) Each <pn> represents the probability (as a percentage) that n deposits are present in the mine, and all <pn>'s within a mine will always add up to 100

-

miners will be between 1 and (6 * the number of elements in mines), inclusive

Examples

0)

{ "000, 030, 030, 040, 000, 000, 000",
  "020, 020, 020, 010, 010, 010, 010" }

Returns: { 2,  2 }

This is the example from the problem statement.

1)

{ "100, 000, 000, 000, 000, 000, 000",
  "100, 000, 000, 000, 000, 000, 000",
  "100, 000, 000, 000, 000, 000, 000",
  "100, 000, 000, 000, 000, 000, 000",
  "100, 000, 000, 000, 000, 000, 000" }

Returns: { 6,  2,  0,  0,  0 }

There are no deposits in any mines. However, since the company must employ every available worker, it loses $160 ($20 per worker). The proper allocation places 6 workers in the first mine and 2 workers in the second mine, since that is the allocation that places more workers in earlier mines and the maximum number of workers a mine can support is 6.

2)

{ "050, 000, 000, 000, 000, 050, 000",
  "050, 000, 000, 000, 000, 050, 000",
  "050, 000, 000, 000, 000, 050, 000",
  "050, 000, 000, 000, 000, 050, 000",
  "050, 000, 000, 000, 000, 050, 000",
  "050, 000, 000, 000, 000, 050, 000",
  "050, 000, 000, 000, 000, 050, 000",
  "050, 000, 000, 000, 000, 050, 000",
  "050, 000, 000, 000, 000, 050, 000",
  "050, 000, 000, 000, 000, 050, 000" }

Returns: { 4,  4,  4,  4,  4,  4,  4,  2,  0,  0 }

Each mine has a 50 percent chance of containing no deposits and a 50 percent chance of containing 5 deposits. The expected value from a mine like this is maximized with 4 workers. Since we allocate workers to earlier mines first, the early mines are filled with 4 workers each, and the remaining 2 miners are placed in the next available mine.

3)

{ "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004",
  "026, 012, 005, 013, 038, 002, 004" }

Returns: 
{ 2,  2,  2,  2,  2,  2,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1 }

4)

{ "100, 000, 000, 000, 000, 000, 000",
  "090, 010, 000, 000, 000, 000, 000",
  "080, 020, 000, 000, 000, 000, 000",
  "075, 025, 000, 000, 000, 000, 000",
  "050, 050, 000, 000, 000, 000, 000",
  "025, 075, 000, 000, 000, 000, 000",
  "020, 080, 000, 000, 000, 000, 000",
  "010, 090, 000, 000, 000, 000, 000",
  "000, 100, 000, 000, 000, 000, 000",
  "000, 090, 010, 000, 000, 000, 000",
  "000, 080, 020, 000, 000, 000, 000",
  "000, 075, 025, 000, 000, 000, 000",
  "000, 050, 050, 000, 000, 000, 000",
  "000, 025, 075, 000, 000, 000, 000",
  "000, 020, 080, 000, 000, 000, 000",
  "000, 010, 090, 000, 000, 000, 000",
  "000, 000, 100, 000, 000, 000, 000",
  "000, 000, 090, 010, 000, 000, 000",
  "000, 000, 080, 020, 000, 000, 000",
  "000, 000, 075, 025, 000, 000, 000",
  "000, 000, 050, 050, 000, 000, 000",
  "000, 000, 025, 075, 000, 000, 000",
  "000, 000, 020, 080, 000, 000, 000",
  "000, 000, 010, 090, 000, 000, 000",
  "000, 000, 000, 100, 000, 000, 000",
  "000, 000, 000, 100, 000, 000, 000",
  "000, 000, 000, 090, 010, 000, 000",
  "000, 000, 000, 080, 020, 000, 000",
  "000, 000, 000, 075, 025, 000, 000",
  "000, 000, 000, 050, 050, 000, 000",
  "000, 000, 000, 025, 075, 000, 000",
  "000, 000, 000, 020, 080, 000, 000",
  "000, 000, 000, 010, 090, 000, 000",
  "000, 000, 000, 000, 100, 000, 000",
  "000, 000, 000, 000, 090, 010, 000",
  "000, 000, 000, 000, 080, 020, 000",
  "000, 000, 000, 000, 075, 025, 000",
  "000, 000, 000, 000, 050, 050, 000",
  "000, 000, 000, 000, 025, 075, 000",
  "000, 000, 000, 000, 020, 080, 000",
  "000, 000, 000, 000, 010, 090, 000",
  "000, 000, 000, 000, 000, 100, 000",
  "000, 000, 000, 000, 000, 090, 010",
  "000, 000, 000, 000, 000, 080, 020",
  "000, 000, 000, 000, 000, 075, 025",
  "000, 000, 000, 000, 000, 050, 050",
  "000, 000, 000, 000, 000, 025, 075",
  "000, 000, 000, 000, 000, 020, 080",
  "000, 000, 000, 000, 000, 010, 090",
  "000, 000, 000, 000, 000, 000, 100" }

Returns: 
{ 0,  0,  0,  1,  1,  1,  1,  1,  1,  1,  1,  1,  2,  2,  2,  2,  2,  2,  2,  2,  3,  3,  3,  3,  3,  3,  3,  3,  3,  4,  4,  4,  4,  4,  4,  4,  4,  4,  5,  5,  5,  5,  5,  5,  5,  5,  5,  5,  6,  6 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CrossCountry

Simple Math, String Manipulation

Used in:

SRM 171

Used as:

Division I Level One , Division II Level Two

Writer:

Running Wild

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1950

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4660&pm=1950

Problem Statement

You are the coach of a high school cross country team. You are hosting a cross country meet at your school this weekend, and you need to be ready to score the meet. Since it is a bit of a pain to do by hand, especially for large meets, you are going to write a program to do it for you. Given the number of teams and the order in which the runners finish, determine the order in which each team places.

Capital letters will represent the teams in finishOrder and in the return value. The first team is 'A', the second team is 'B', and so on. The place in which the five fastest runners on a team finish is added together (first place=1, second place=2, etc...), and that is the team's score (a team must have at least five runners finish to place). Lower scores beat higher scores, and in the event of a tie the sixth fastest runners of each team are compared, and the team whose sixth fastest runner finished earlier wins the tie. If two teams tie and only one has a sixth runner, that team wins the tie. If two teams tie and neither has a sixth runner, the team who's letter comes first alphabetically wins the tie.

You will be given an int, numTeams, which is the number of teams competing, and a String, finishOrder, which is the order in which the runners finish. You are to return a String that lists the teams in the order they placed in the meet. If a team has fewer than 5 runners finish, do not include it in the return value.

For example, if finishOrder="AABBABBABBA", then team A's runners finish 1st, 2nd, 5th, 8th, and 11th, for a team score of 27 points. Team B's runners finish 3rd, 4th, 6th, 7th, 9th, and 10th, for a team score of 29 points (notice that only team B's first 5 runners are scored). In this case the return value would be "AB".

Definition

Class:	CrossCountry
Method:	scoreMeet
Parameters:	int, String
Returns:	String
Method signature:	String scoreMeet(int numTeams, String finishOrder)
(be sure your method is public)

Notes

-

If a team has fewer than 5 runners finish, don't remove that team's runners from finishOrder before calculating the score of the other teams.

Constraints

-

numTeams will be between 2 and 10, inclusive.

-

finishOrder will be between 10 and 50 characters, inclusive.

-

finishOrder will contain only the first numTeams capital letters ('A','B',...).

-

finishOrder will not contain more than seven occurrences of the same character.

Examples

0)

"AABBABBABBA"

Returns: "AB"

The example from above.

1)

"CCCBBBBBAAACC"

Returns: "BC"

In this case team A does not qualify because only 3 of its runners finish. Team B beats team C with a score of 30-31. Remember not to remove team A's runners, doing this would have team C win over team B with a score of 25-30.

2)

"ABDCBADBDCCDBCDBCAAAC"

Returns: "BDCA"

3)

"BDHCEAJBIDBCCHGCBDJEBAAHEGAGGADHGIECJEHAEBDADJCDHG"

Returns: "BCDAHEG"

4)

"BABCAABABAB"

Returns: "AB"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CombinationLock

Math, Simulation

Used in:

SRM 181

Used as:

Division I Level One , Division II Level Two

Writer:

antimatter

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1945

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4725&pm=1945

Problem Statement

Combination locks are convenient, because of their design. A combination lock consists of a small wheel to input the combination, and a latch to actually lock things together. The wheel contains consecutive numbers equally spaced around its edge, starting from zero and increasing clockwise. The outer casing of the lock has a small notch. To open the lock, you must rotate the wheel and align the numbers on the wheel with the notch in a specific order.

TopLock, a small company manufacturing combination locks, has recently decided to change its lock setup to give more security than the competitors. Many typical combination locks have a set of three numbers which you must input in order. TopLock locks will have a variable combination length which will be no less than three. In addition, they will be changing the number of numbers on the wheel, which will be between 10 and 100, inclusive.

To open a lock, you must follow the algorithm outlined below:

1. Set the current rotation direction to counterclockwise, and set N to the number of numbers in the combination.
2. Rotate the wheel N full turns in the current rotation direction, where a full turn is a 360 degree spin that leaves the notch pointing at the same number.
3. Continue to rotate the wheel in the current rotation direction until the notch is pointing at the next number in the combination, which successfully inputs that number. Note that by rotating the wheel counter-clockwise, the number that the notch points to will increase.
4. If there are no more numbers to input, open the lock, you're finished! Otherwise, reverse the current rotation direction, decrease N by one, and go back to step 2.

It is guaranteed that no two adjacent numbers in combo will be the same, so as to avoid ambiguity in step 3. Also, the starting position of the lock, start, will not be the same as the first number in combo.

Given a int[] combo, indicating the combination of the lock, an int size, the number of numbers on the wheel, and an int start, indicating the number that the notch starts off pointing at, your method should return a double indicating the total number of degrees turned to open the lock.

For example, if combo = {10,20,30}, size = 40, and start = 6, you would first rotate the wheel three times counterclockwise and then 4 units to the 10, for a total of 3 * 360 + 4 * (360 / 40) = 1116 degrees, and then you would rotate twice clockwise and 30 units to the 20, and then once counterclockwise and 10 units to the 30. Your method would in this case return 1116 + 990 + 450 = 2556.

Definition

Class:	CombinationLock
Method:	degreesTurned
Parameters:	int[], int, int
Returns:	double
Method signature:	double degreesTurned(int[] combo, int size, int start)
(be sure your method is public)

Notes

-

The numbers on the combination wheel start at 0 and go to (size - 1), increasing clockwise.

-

Double return values must be correct to within an absolute or relative difference of 1e-9.

Constraints

-

combo will have between 3 and 50 elements, inclusive.

-

Each element of combo will be between 0 and (size - 1), inclusive, and no two consecutive elements will be the same.

-

size will be between 10 and 100, inclusive.

-

start will be between 0 and (size - 1), inclusive, and will not be the same as the first element in combo (i.e., the one with index 0)

Examples

0)

{10,20,30}

Returns: 2556.0

Explained above.

1)

{0,50,99}

Returns: 2642.4

2)

{0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9}

Returns: 79344.0

3)

{64,93,87,3,22,53,64,53,11,90,11,59,30,6,11,17,72,0,38,55}

Returns: 79166.59793814432

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RPG

Simple Math, String Manipulation

Used in:

SRM 171

Used as:

Division II Level One

Writer:

Running Wild

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1944

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4660&pm=1944

Problem Statement

When playing many classic role playing games you often write die rolls in the form "ndx", where n indicates the number of dice of size x to be rolled. A die of size x is an x-sided die that has a distinct number between 1 and x, inclusive, on each of its sides. For example, "2d8" would mean "roll two eight sided dice". Given a String[] representing the dice to roll, return a int[] representing the minimum, maximum, and average die rolls (in that order). Round the value of the average die roll down to the highest integer less than or equal to the actual value. For example, the input {"1d8","3d4","2d6"} would have a minimum of 6 (if all the dice turned up ones), a maximum of 32 (if all the dice turned up their highest values), and an average of 19. The return value would be {6, 32, 19}.

Definition

Class:	RPG
Method:	dieRolls
Parameters:	String[]
Returns:	int[]
Method signature:	int[] dieRolls(String[] dice)
(be sure your method is public)

Constraints

-

dice will contain between 1 and 5 elements, inclusive.

-

Each element of dice will be formatted "ndx" (quotes for clarity only), where 'n' is an integer between 1 and 10, inclusive, 'd' is the character 'd', and 'x' is an integer between 2 and 20, inclusive. Neither 'n' nor 'd' will have leading zeros.

Examples

0)

{"3d6"}

Returns: { 3,  18,  10 }

Standard roll for creating characters stats in a popular RPG. The minimum value is when three 1's are rolled, the maximum value is when all 6's are rolled, and the average value is given by 3*(6+1)/2, which rounds down to 10.

1)

{"3d4","1d6"}

Returns: { 4,  18,  11 }

Be careful not to round the value of intermediate results. The average roll of "3d4" is 3*(1+4)/2=7.5, and the average roll of "1d6" is 1*(1+6)/2=3.5. The average of them both is 11, but rounding before adding them together will yield 10, which is incorrect.

2)

{"6d5","10d10","10d20"}

Returns: { 26,  330,  178 }

3)

{"1d2","2d2","4d2","6d2","8d2"}

Returns: { 21,  42,  31 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StairClimb

Simple Math

Used in:

SRM 168

Used as:

Division II Level One

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1937

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4645&pm=1937

Problem Statement

You are climbing a staircase. The staircase consists of some number of flights of stairs separated by landings. A flight is a a continuous series of stairs from one landing to another. You are a reasonably tall athletic person, so you can climb a certain number of stairs in one stride. However, after each flight, there is a landing which you cannot skip because you need to turn around for the next flight (which continues in the opposite direction).

You will be given the number of stairs in each flight in a int[] flights. Element 0 of flights represents the number of stairs in the first flight, element 1 is the number of stairs in the second flight, etc. You will also be given an int stairsPerStride, which is how many continuous stairs you climb in each stride. If it takes two strides to turn around at a landing, return the number of strides to get to the top of the staircase. You do not need to turn at the top of the staircase.

Definition

Class:	StairClimb
Method:	stridesTaken
Parameters:	int[], int
Returns:	int
Method signature:	int stridesTaken(int[] flights, int stairsPerStride)
(be sure your method is public)

Constraints

-

flights has between 1 and 50 elements, inclusive.

-

Each element of flights is between 5 and 30, inclusive.

-

stairsPerStride is between 2 and 5, inclusive.

Examples

0)

{15}

Returns: 8

A simple staircase with 15 steps. In 7 strides, you've climbed 14 steps. However, you still have one step left, so you must use an additional stride to get to the top.

1)

{15,15}

Returns: 18

This time, there are two flights with a landing in between. 8 strides to get to the first landing, 2 strides to turn around, and 8 more strides to get to the top makes 8+2+8=18 strides.

2)

{5,11,9,13,8,30,14}

Returns: 44

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

WhichData

Brute Force, Math

Used in:

TCO '03 Round 4

Used as:

Division I Level One

Writer:

brett1479

Testers:

lbackstrom , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1933

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4705&pm=1933

Problem Statement

You have just received a int[] sampleData from the laboratory. You know that the variance of this data should be varNum/varDen, where varNum and varDen are ints. Note that varNum/varDen need not be an integer. Your method will return which nonempty subset of the elements from sampleData produces a variance closest to the variance you expected. This subset may be the entire sampleData. The variance of a subset of the sampleData can be calculated via the following formula. Let s(i) denote the ith element of the subset (assuming some method of indexing into the subset), and let n denote the size of the subset. Then

     mean = ( s(0) + s(1) + s(2) + ... + s(n-1) )/n
     varsum = (mean-s(0))^2 + (mean-s(1))^2 + ... + (mean-s(n-1))^2
     variance = varsum/n

The subset will be returned as a int[], whose elements are the values of the subset, sorted in nondescending order. If two subsets are equally far from the expected variance, choose the one whose return value comes first lexicographically. A int[] X comes lexicographically before a int[] Y if there is a position j such that, X[i]=Y[i] for all i<j, and X[j]<Y[j]. If X is a proper prefix of Y, it occurs lexicographically before it.

Definition

Class:	WhichData
Method:	bestVariance
Parameters:	int[], int, int
Returns:	int[]
Method signature:	int[] bestVariance(int[] sampleData, int varNum, int varDen)
(be sure your method is public)

Notes

- doubles will provide enough precision to properly solve this problem. Given two subsets, s1 and s2, the difference between |variance(s1)-varNum/varDen| and |variance(s2)-varNum/varDen| will be either 0, or greater than 1e-9, where variance(x) is the variance of subset x.

Constraints

- varNum will be between 0 and 10000 inclusive.

- varDen will be between 1 and 10000 inclusive.

- sampleData will contain between 2 and 16 elements inclusive.

- Each element of sampleData will be between -10000 and 10000 inclusive.

Examples

0)

{1,2,3,4,5,6,7,8}

Returns: { 1,  2,  3,  4,  5 }

The variance should be 40/20 = 2. The set of numbers {1,2,3,4,5} has

	mean = (1+2+3+4+5)/5 = 3
	varsum = 2^2 + 1^2 + 0^2 + 1^2 + 2^2 = 10
	variance = 10/5 = 2

1)

{1,2,3,4,5,6,7,8}

Returns: { 1,  2,  4,  5,  8 }

2)

{-10000,10000,-9999,9999,-9998,9000}

Returns: { -10000,  -9998 }

3)

{-10000,10000,-9999,9999,-9998,9998,1,1,2,2}

Returns: { -10000,  -9998 }

4)

{500,500,500,500,500,500,500,580,
 100,100,100,100,100,100,100,180}

Returns: { 100,  100,  100,  100,  100,  100,  100,  180 }

5)

{10,10,10,10,10,10}

Returns: { 10 }

6)

{2,5,8,15,-14,0,-2,3,0,-10,-3,-9,6,-13,4,-1}

Returns: { -14,  -10,  -3,  -1,  0,  0,  2,  3,  4,  5 }

7)

{-14,-3,-1,10,-5,0,13,6,11,9,5,6,3,-2,0,2}

Returns: { -5,  -3,  -2,  -1,  0,  2,  5,  6,  6,  11 }

8)

{0,-13,15,5,5,-7,-6,-7,-8,4,-12,-13,14,9,-3,-1}

Returns: { -13,  -13,  -12,  -7,  -7,  -6,  -3,  4,  5,  5 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TerribleEncryption

Math

Used in:

SRM 221

Used as:

Division I Level One

Writer:

AdminBrett

Testers:

PabloGilberto , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1924

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5867&pm=1924

Problem Statement

You and your friends have decided to create your own encryption scheme (bad idea). An encrypted message consists of 3 parts:

1) A String called the pool
2) A int[] called the data
3) A int[] called the keys

To decrypt character i of the message, first find the smallest positive integer k such that

          (data[i] * k) % keys[i] = 1

Above % denotes the modulus operator. Character i of the message will be character j in pool, where j is given by

          j = k % (length of pool)

Return the decrypted String. Constraints will ensure that the ith element of data is relatively prime to the ith element of keys. In other words, the largest positive integer that divides data[i] and keys[i] will be 1, for all i.

Definition

Class:	TerribleEncryption
Method:	decrypt
Parameters:	String, int[], int[]
Returns:	String
Method signature:	String decrypt(String pool, int[] data, int[] keys)
(be sure your method is public)

Constraints

-

pool will contain between 2 and 50 characters inclusive.

-

Each character in pool will be a letter ('A'-'Z', 'a'-'z').

-

data will contain between 1 and 50 elements inclusive.

-

keys will contain the same number of elements as data.

-

Each element of data will be between 1 and 100000 inclusive.

-

Each element of keys will be between 2 and 5000 inclusive.

-

Element i of keys will be relatively prime to element i of data.

Examples

0)

"ABCDEFGHIJKLMNOPQRSTUVWXYZ"

{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}

{17,17,17,17,17,17,17,17,17,17,17,17,17,17,17}

Returns: "BJGNHDFPCMOKELI"

1)

"AEIOUAEIOUaeiouaeiou"

{1,2,3,4,5,6,7,8,9,10,1,2,3,4,5}

{2,3,4,5,6,7,8,9,10,11,13,15,16,17,18}

Returns: "EIOUAEIOUaEOeoe"

2)

"abcdeffedcbaABCDEFFEDCBA"

{10,10,10,10,10,10,10,10,10,10,10}

{3,7,11,13,17,19,23,29,31,37,41}

Returns: "bfbeAcedecB"

3)

"abcdefghijklmnopqrstuvwxyz"

{11,11,11,11,11,11,11,11,11,11,11,11,11,11,11}

{2,3,4,5,6,7,8,9,10,12,13,14,15,16,17}

Returns: "bcdbfcdfblgjldo"

4)

"HmmBlahHmmBlah"

{1,1,1,1,1,1,1}

{10,9,8,7,6,5,4}

Returns: "mmmmmmm"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Carbon14

Math

Used in:

TCO '03 Round 2

Used as:

Division I Level One

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1916

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4703&pm=1916

Problem Statement

A common way to determine the age of ancient organic artifacts is called Carbon-14 Dating. Carbon-14 is a radioactive isotope of carbon which is found in a relatively constant concentration in all living organisms. Once an organism dies, however, the carbon-14 in the remains of that organism begins to decay, and the concentration of carbon-14 in the remains starts to decrease. Thus, by comparing the concentration of carbon-14 in a neolithic wooden tool, for example, to the concentration typically found in living organisms, we can determine what percentage of the carbon-14 has decayed, and based on this, the age of the tool.

Radioactive isotopes generally decay according to the following function, where e is the base of the natural logarithm (about 2.718281828459045), t is the amount of time that has elapsed since the organism died, and k is a constant that is different for each isotope:

final concentration = initial concentration * (e ^ (- t / k))

In the case of carbon-14, k = 8267, when time is measured in years.

In this problem, you will be given a measurement, concentration, from an ancient artifact representing (final concentration / initial concentration) * 10,000 (so 543 would mean that the ratio of the two concentrations was 0.0543). You will also be given an int, err, indicating how far off this measurement could be. Your task is to determine a lower bound and an upper bound on the age of the artifact (in years). You should return a int[] with two elements. The first element should be the lower bound on the age of the artifact, and the second element should be the upper bound on its age. The lower bound should be rounded down (floor) and the upper bound should be rounded up (ceiling).

For example, if concentration were 5000 and err were 100, then the lower bound on the age of the artifact would come from assuming the true ratio of concentrations was 0.51, and the upper bound on the age of the artifact would come from assuming that the ratio of concentrations was 0.49. For these two concentrations, we get ages of 5566.54 and 5897.26, respectively. Thus we would return {5566, 5898}

Definition

Class:	Carbon14
Method:	dateRange
Parameters:	int, int
Returns:	int[]
Method signature:	int[] dateRange(int concentration, int err)
(be sure your method is public)

Notes

- Recall that ln(e^x) = x, where ln is the natural logarithm function.

Constraints

- concentration will be between 1 and 9999, inclusive.

- err will be between 0, inclusive, and min(concentration, 10000-concentration), exclusive.

- Neither the lower nor the upper bounds on the age will be within 1e-6 of an integer, prior to rounding.

Examples

0)

Returns: { 5566,  5898 }

The example from the problem statement.

1)

Returns: { 5730,  5731 }

With 0 error, we calculate the age of the artifact as 5730.25 years, giving us a lower bound of 5730 and an upper bound of 5731. For this reason, 5730 years is called the half-life of carbon-14 - after 5730 years, there is half as much of it as there was originally.

2)

Returns: { 76141,  76142 }

3)

Returns: { 8740,  8827 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RecurrenceRelation

Simple Math, Simulation

Used in:

SRM 170

Used as:

Division I Level One , Division II Level Two

Writer:

antimatter

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1915

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4655&pm=1915

Problem Statement

Consider a sequence {x₀, x₁, x₂, ...}. A relation that defines some term x_n in terms of previous terms is called a recurrence relation. A linear recurrence relation is one where the recurrence is of the form x_n = c_k-1x_n-1 + c_k-2x_n-2 + ... + c₀x_n-k, where all the c_i are real-valued constants, k is the length of the recurrence relation, and n is an arbitrary positive integer which is greater than or equal to k.

You will be given a int[] coefficients, indicating, in order, c₀, c₁, ..., c_k-1. You will also be given a int[] initial, giving the values of x₀, x₁, ..., x_k-1, and an int N. Your method should return x_N modulo 10.

Note that the value of X modulo 10 equals the last digit of X if X is non-negative. However, if X is negative, this is not true; instead, X modulo 10 equals ((10 - ((-X) modulo 10)) modulo 10). For example, (-16) modulo 10 = ((10 - (16 modulo 10)) modulo 10) = (10 - 6) modulo 10 = 4.

More specifically, if coefficients is of size k, then the recurrence relation will be

x_n = coefficients[k - 1] * x_n-1 + coefficients[k - 2] * x_n-2 + ... + coefficients[0] * x_n-k.

For example, if coefficients = {2,1}, initial = {9,7}, and N = 6, then our recurrence relation is x_n = x_n-1 + 2 * x_n-2 and we have x₀ = 9 and x₁ = 7. Then x₂ = x₁ + 2 * x₀ = 7 + 2 * 9 = 25, and similarly, x₃ = 39, x₄ = 89, x₅ = 167, and x₆ = 345, so your method would return (345 modulo 10) = 5.

Definition

Class:	RecurrenceRelation
Method:	moduloTen
Parameters:	int[], int[], int
Returns:	int
Method signature:	int moduloTen(int[] coefficients, int[] initial, int N)
(be sure your method is public)

Notes

-

(a + b) modulo x = ( (a modulo x) + (b modulo x) ) modulo x for any values of a, b, and x.

Constraints

-

coefficients will have between 1 and 10 elements, inclusive.

-

initial will have the same number of elements as coefficients.

-

Each element of coefficients will be between -1000 and 1000, inclusive.

-

Each element of initial will be between -1000 and 1000, inclusive.

-

N will be between 0 and 100000, inclusive.

Examples

0)

{2,1}

{9,7}

Returns: 5

As described in the problem statement.

1)

{1,1}

{0,1}

Returns: 4

This is the famous Fibonacci sequence, which goes 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

2)

{2}

{1}

Returns: 6

This sequence is 1, 2, 4, 8, 16, ...

3)

{2}

{1}

Returns: 6

Watch out for overflow.

4)

{25,143}

{0,0}

Returns: 0

This sequence will always be zero.

5)

{9,8,7,6,5,4,3,2,1,0}

{1,2,3,4,5,6,7,8,9,10}

Returns: 5

6)

{901,492,100}

{-6,-15,-39}

Returns: 4

Watch out for negative numbers.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Swimmers

Simple Math

Used in:

SRM 169

Used as:

Division II Level One

Writer:

huntergt

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1888

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4650&pm=1888

Problem Statement

A group of swimmers are stretching along the shores of a river. In just a few moments, they are all going to plunge in, swim downstream (with the current) for a specific distance (unique to each swimmer), and return back (against the current) to their starting points. Relative to a person on the shore, the speed at which each swimmer travels when swimming downstream is the swimmer's speed plus the speed of the current, and the speed at which each swimmer travels when swimming upstream is the swimmer's speed minus the speed of the current. Assume that no time elapses when a swimmer turns around to make the return trip.

Write a class Swimmers with a method getSwimTimes which takes a int[] distances (meters relative to the shore) each swimmer will be swimming, a int[] speeds (meters per second) at which they swim, and an int current representing the speed (meters per second) of the current in the river. Element i in distances corresponds to element i in speeds. The method should return a int[] of the times (rounded down to the nearest integer less than or equal to the actual value) that the roundtrip swim took for each swimmer, or "-1" if the trip is impossible to make. Element i in the returned int[] should correspond to element i in distances and speeds.

Definition

Class:	Swimmers
Method:	getSwimTimes
Parameters:	int[], int[], int
Returns:	int[]
Method signature:	int[] getSwimTimes(int[] distances, int[] speeds, int current)
(be sure your method is public)

Constraints

-

distances contains between 0 and 50 elements, inclusive

-

each element of distances will be between 0 and 10000, inclusive

-

speeds will have the same number of elements as distances

-

each element of speeds will be between 0 and 100, inclusive

-

current will be between 0 and 100, inclusive

Examples

0)

{ 300, 300, 300 }

{ 1, 2, 3 }

Returns: { -1,  -1,  360 }

The current is 2 meters per second, and each swimmer is going to swim 300 meters with the current followed by 300 meters back to their starting point. The first swimmer only swims at 1 meter per second, so it will be impossible to return to the starting point. The second swimmer matches the speed of the current, but will never be able to travel the return trip. The third swimmer swims at 3 meters per second, so will travel the 300 meters at 5 meters per second with the current and 1 meter per second against the current. This results in 60 seconds for the downstream trip and 300 seconds for the upstream trip, for a total of 360 seconds.

1)

{ 500, 500 }

{ 4, 5 }

Returns: { 333,  238 }

The first swimmer travels 500 meters downstream at 6 meters/second, resulting in 83 and 1/3 seconds. The upstream trip is done at 2 meters/second and takes 250 seconds. This results in a total time of 333 and 1/3 seconds. The integer portion of this is 333 seconds. The second swimmer travels 500 meters downstream at 7 meters/sec and takes 71 and 3/7 seconds. The upstream trip is done at 3 meters/second and takes 166 and 2/3 seconds. This results in 238 and 2/21 seconds. The integer portion of this is 238 seconds.

2)

{ 0, 0 }

{ 1, 2 }

Returns: { 0,  0 }

All the swimmers are swimming a distance of 0 meters, so it takes 0 seconds to finish.

3)

{ 0, 1 }

{ 0, 0 }

Returns: { 0,  -1 }

Watch out for division by zero!

4)

{ 7507, 7517, 7523, 7529, 7537, 7541, 7547, 7549, 7559, 7561, 7573, 7577, 7583,
  7589, 7591, 7603, 7607, 7621, 7639, 7643, 7649, 7669, 7673, 7681, 7687, 7691,
  7699, 7703, 7717, 7723, 7727, 7741, 7753, 7757, 7759, 7789, 7793, 7817, 7823,
  7829, 7841, 7853, 7867, 7873, 7877, 7879, 7883, 7901, 7907, 7919 }

{ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
  73, 79, 83, 89, 97, 99, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30,
  32, 34, 36, 38, 40, 42, 44, 46, 48, 51 }

Returns: 
{ -1,  -1,  -1,  8108,  1950,  1474,  1014,  882,  705,  544,  507,  420,  377,  359,  328,  290,  260,  252,  229,  216,  210,  195,  185,  173,  159,  155,  -1,  -1,  4409,  2413,  1717,  1354,  1127,  969,  852,  764,  692,  635,  585,  543,  507,  476,  449,  424,  402,  383,  365,  349,  334,  314 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Workshop

Brute Force, Simple Math

Used in:

SRM 166

Used as:

Division II Level One

Writer:

dimkadimon

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1880

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4635&pm=1880

Problem Statement

You work in a workshop which makes garden instruments from metal. At the end of each working day there remains a pile of scrap metal that cannot be used to make anything useful. Because you dislike the idea of throwing things away (even scrap metal), you decide to utilize this metal to make some triangular picture frames that can be sold at the local market.

Given a int[] pieces where each element represents the length of a straight metallic piece, return the number of possible different picture frames that can be made from those pieces. Two picture frames are considered to be identical if each of their corresponding sides is equal in length. If no picture frames can be created from pieces then return 0.

Definition

Class:	Workshop
Method:	pictureFrames
Parameters:	int[]
Returns:	int
Method signature:	int pictureFrames(int[] pieces)
(be sure your method is public)

Notes

-

A triangle can be formed if, and only if, for every pair of its sides the sum of that pair is longer than the third side.

Constraints

-

pieces will have between 0 and 50 elements inclusive.

-

Each element in pieces will be between 1 and 10000 inclusive.

-

pieces will not have any repeated elements.

Examples

0)

{1,2,3,4,5}

Returns: 3

We can form picture frames with the following sides: {2, 3, 4}, {2, 4, 5} and {3, 4, 5}. So we can form 3 different picture frames.

1)

{8,5,3}

Returns: 0

8 + 5 is longer than 3 and 8 + 3 is longer than 5, but 5 + 3 is not longer than 8. Thus we cannot form a single picture frame from these pieces.

2)

{4,23,76,22,87,3,1,99}

Returns: 7

3)

{10000,9999,9998,9997,9996,1,2,3,4,5}

Returns: 43

4)

{100}

Returns: 0

We cannot form any picture frames with just one piece of metal.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NumberGuesser

Math, Simulation

Used in:

SRM 168

Used as:

Division I Level One , Division II Level Two

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1869

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4645&pm=1869

Problem Statement

Select two numbers between 1 and 9998, inclusive, which have the same exact group of non-zero digits, but are not the same number. For example, you could use 1234 and 4321, or 91 and 901. Now, subtract the smaller of the two numbers from the larger. Finally, pick one of the non-zero digits in the result, and remove the digit from the number. If the resulting number is less than 100, prepend enough zeros so that it has 3 digits. It turns out, that given the remaining 3 digits, one can always determine the digit removed. (See examples for clarification)

You will be given a String leftOver, which contains the three digits left over after the above algorithm is run. You must return the digit which was removed.

Definition

Class:	NumberGuesser
Method:	guess
Parameters:	String
Returns:	int
Method signature:	int guess(String leftOver)
(be sure your method is public)

Notes

-

Although it may not be obvious, there is only one answer for each input.

-

You can only remove a non-zero digit when running the algorithm.

-

HINT: work backwards from the input.

Constraints

-

leftOver will consist of exactly 3 characters.

-

Each character of leftOver will be a digit '0'-'9'.

-

The input will be possible to acheive by performing the algorithm stated above.

Examples

0)

"087"

Returns: 3

Take the number 4321 and subtract 1234, you get 3087. Remove the 3, and the resulting digits are 087.

1)

"099"

Returns: 9

One possible way to achieve this is by using the numbers 1000 and 1.

2)

"191"

Returns: 7

4525 - 2554 = 1971

also, you could get this with:

1900 - 109 = 1791

or

7900 - 709 = 7191

3)

"689"

Returns: 4

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LongNumber

Advanced Math

Used in:

SRM 166

Used as:

Division I Level Three

Writer:

dimkadimon

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1863

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4635&pm=1863

Problem Statement

We generate two infinitely long numbers. The first number is generated by writing down all positive consecutive integers, while the second is generated by writing down all of their squares. We then find the sum of these two numbers. Here are the first 33 digits of the calculation:

  123456789101112131415161718192021...
+ 149162536496481100121144169196225...
= 272619325597593231536305887388246...

The first digit of the result is 2, the second digit is 7, the third is 2 and so on.

Given an int k, return the digit at position k of the resulting number, where the first digit is at position 1.

Definition

Class:	LongNumber
Method:	findDigit
Parameters:	int
Returns:	int
Method signature:	int findDigit(int k)
(be sure your method is public)

Constraints

-

k will be between 1 and 2147483647 inclusive.

Examples

0)

Returns: 2

1)

Returns: 1

2)

Returns: 5

3)

Returns: 6

4)

1780243932

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BritishCoins

Simple Math

Used in:

SRM 165

Used as:

Division II Level One

Writer:

Unknown

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1862

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4630&pm=1862

Problem Statement

Prior to 1971, Britain used a system of coins that can be traced back to the time of Charlemagne. The three main units of coinage were the penny, the shilling, and the pound. There were 12 pennies in a shilling and 20 shillings in a pound. Given a number pence of pennies, convert this amount into pounds, shillings, and pennies by first converting as many pennies as possible into pounds, and then converting as many of the remaining pennies as possible into shillings. Return a int[] of size three containing the number of pounds, the number of shillings, and the number of pennies, in that order.

Definition

Class:	BritishCoins
Method:	coins
Parameters:	int
Returns:	int[]
Method signature:	int[] coins(int pence)
(be sure your method is public)

Constraints

-

pence is between 0 and 10000, inclusive.

Examples

0)

Returns: { 2,  4,  5 }

First, we make 2 pounds, leaving 53 pence. Then, we make 4 shillings, leaving 5 pence.

1)

Returns: { 0,  0,  0 }

2)

Returns: { 0,  0,  6 }

3)

Returns: { 17,  0,  11 }

4)

Returns: { 41,  13,  4 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Orchard

Simple Math, Simple Search, Iteration

Used in:

SRM 167

Used as:

Division II Level Three

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1859

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4640&pm=1859

Problem Statement

My orchard is arranged in a square, with the rows and columns numbered 1, 2, ..., n. I need software to choose the location where the next tree should be planted.

I want the next tree not to be interfered with by existing trees or by the activities of the neighboring landowners. Therefore, I want to choose the location for which the shortest orthogonal path that goes either to a tree or out of the orchard is as long as possible. By an orthogonal path I mean a sequence of steps that go along rows and/or columns (not diagonally). If there are several locations that have the same shortest orthogonal path, break the tie by choosing the smallest row number, and, if necessary, break any remaining tie by choosing the smallest column number.

The existing layout of the orchard is shown by a String[] orchard in which the elements correspond to rows 1, 2, ..., n. Within each element of orchard, the characters correspond to columns 1, 2, ..., n. The character 'T' indicates an existing tree at that row and column, while '-' indicates an available location.

Create a class Orchard that contains a method nextTree that is given a String[] orchard and returns a int[] with two elements giving the row and column of the chosen location. The first element of the return should give the row, and the second element should give the column.

Definition

Class:	Orchard
Method:	nextTree
Parameters:	String[]
Returns:	int[]
Method signature:	int[] nextTree(String[] orchard)
(be sure your method is public)

Constraints

-

orchard contains n elements, where n is between 1 and 50 inclusive

-

each element of orchard contains exactly n characters

-

each element of orchard contains only the characters 'T' and '-'

-

at least one element of orchard contains a character '-'

Examples

0)

{ "----" , "T---" , "----" , "----" }

Returns: { 2,  3 }

    ----  row 1
    T---  row 2
    ----  row 3
    ----  row 4

The edge locations all have a path of length 1 out of the orchard. The four central locations have a shortest path of 2 out of the orchard. Among these four, the one in row 2 column 2 has a path of 1 to the tree. Among the other 3 locations, the one in row 2 is preferred to the ones in row 3.

1)

{"---T--","------","------","----T-","------","------"}

Returns: { 3,  3 }

    ---T--
    ------
    ------
    ----T-
    ------
    ------

The location at row 3, column 3 has a shortest orthogonal path of 3. In fact it has paths of length 3 to each of the 2 existing trees and also to the outside of the orchard.

2)

{"------------","------------","------------","------------",
"------------","------------","------------","------------",
"------------","------------","------------","------------"}

Returns: { 6,  6 }

3)

{"-T----T",
 "T---T--",
 "-----TT",
 "---TT--",
 "T-----T",
 "-------",
 "T-T--T-"}

Returns: { 2,  3 }

The location at row 2, column 3 has a shortest path of length two both to the outside of the orchard and to several trees.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PointSystem

Advanced Math

Used in:

SRM 174

Used as:

Division I Level Three

Writer:

LunaticFringe

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1849

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4675&pm=1849

Problem Statement

The game of tennis has a rather unusual scoring system. It can be simplified to the following rule: "If a player has at least four points, and is at least two points ahead of his opponent, that player wins the game." For example, 4-1 and 6-4 are winning scores, whereas 3-0 and 5-4 are not.

We can generalize this class of point systems by introducing two variables, pointsToWin and pointsToWinBy. The new rule is "If a player has at least pointsToWin points, and is at least pointsToWinBy points ahead of his opponent, that player wins the game." For example, the common practice of taking "best two out of three" falls into this class, where pointsToWin = 2 and pointsToWinBy = 1.

You would like to know, given a particular point system and the skills of two players, the probability of an upset. An "upset" is defined as a game where a player of lesser skill beats a player of greater skill. Given an int skill, representing the percent likelihood that the worse player beats the better player on any particular turn, along with pointsToWin and pointsToWinBy, you should return a double between 0 and 1 indicating the odds of an upset.

Definition

Class:	PointSystem
Method:	oddsOfWinning
Parameters:	int, int, int
Returns:	double
Method signature:	double oddsOfWinning(int pointsToWin, int pointsToWinBy, int skill)
(be sure your method is public)

Constraints

- pointsToWin will be between 1 and 10, inclusive.

- pointsToWinBy will be between 1 and 5, inclusive.

- skill will be between 1 and 50, inclusive.

Examples

0)

Returns: 0.352

This is the 'best two out of three' game. There are exactly three possible ways for an upset to occur:

1) The worse player scores two consecutive points, with probability 0.4*0.4 = 0.16

2) The better player scores one point, and then the worse player scores two consecutive points, with probability 0.6*0.4*0.4 = 0.096

3) The worse player scores one point, the better player scores one point, and then finally the worse player a second point, with probability 0.4*0.6*0.4 = 0.096

Thus, the total probability is 0.16+0.096+0.096 = 0.352

1)

Returns: 0.4999999999999998

When the probability is 50, clearly each player is the same, so each player has a 50% chance of winning.

2)

Returns: 0.035714285714285705

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BirthdayOdds

Math

Used in:

SRM 174

Used as:

Division I Level One , Division II Level Two

Writer:

LunaticFringe

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1848

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4675&pm=1848

Problem Statement

Here is an interesting factoid: "On the planet Earth, if there are at least 23 people in a room, the chance that two of them have the same birthday is greater than 50%." You would like to come up with more factoids of this form. Given two integers (minOdds and daysInYear), your method should return the fewest number of people (from a planet where there are daysInYear days in each year) needed such that you can be at least minOdds% sure that two of the people have the same birthday. See example 0 for further information.

Definition

Class:	BirthdayOdds
Method:	minPeople
Parameters:	int, int
Returns:	int
Method signature:	int minPeople(int minOdds, int daysInYear)
(be sure your method is public)

Notes

-

Two people can have the same birthday without being born in the same year.

-

You may assume that the odds of being born on a particular day are (1 / daysInYear).

-

You may assume that there are no leap years.

Constraints

-

minOdds will be between 1 and 99, inclusive.

-

daysInYear will be between 1 and 10000, inclusive.

-

For any number of people N, the odds that two people will have the same birthday (in a room with N people, on a planet with daysInYear days in each year) will not be within 1e-9 of minOdds. (In other words, you don't need to worry about floating-point precision for this problem.)

Examples

0)

Returns: 4

We must be 75% sure that at least two of the people in the room have the same birthday. This is equivalent to saying that the odds of everyone having different birthdays is 25% or less.

If there is only one person in the room, the odds are 5/5 or 100% that nobody shares a birthday.
If there are two people in the room, the odds are 5/5 * 4/5 = 80% that nobody shares a birthday. This is because the second person has 4 "safe" days on which his birthday could fall, out of 5 possible days in the year.
If there are three people in the room, the odds of no overlap are 5/5 * 4/5 * 3/5 = 48%.
If there are four people in the room, the odds are 5/5 * 4/5 * 3/5 * 2/5 = 19.2%. This means that you can be (100% - 19.2%) = 80.8% sure that two or more of them do, in fact, have the same birthday.

We only need to be 75% sure of this, which was untrue for three people but true for four. Therefore, your method should return 4.

1)

Returns: 23

The factoid from the problem statement. If there are 22 people in a room, the odds of a shared birthday are roughly 47.57%. With 23 people, these odds jump to 50.73%, which is greater than or equal to the 50% needed.

2)

Returns: 4

Another example from planet Earth. The odds of a repeat birthday among only four people are roughly 1.64%.

3)

Returns: 184

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CalendarRecycle

Math, Simple Search, Iteration

Used in:

SRM 163

Used as:

Division II Level Two

Writer:

Eeyore

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1847

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4620&pm=1847

Problem Statement

Jane is visiting your cubicle when she spies the Elvis calendar hanging on your wall.

"That's not right, is it?" she asks rhetorically.

Your Elvis calendar says that September 8 is a Sunday, but it's actually a Monday. Elvis Presley, the King of Rock 'n' Roll, is no liar. It's just that you bought the calendar last year. This is a 2002 calendar, whereas the current year is 2003. The dates no longer match the days of the week! But there will come a year when every date falls on the same day of the week as in 2002, and the King will reign again.

Given an int representing a year between 2002 and 9999, return the closest future year with which it shares a calendar. Jane reminds you that there are 30 days in April, June, September, and November. The remaining months, with the exception of February, have 31 days. February has 29 days in leap years, and 28 days otherwise. Leap years are divisible by four, and not divisible by 100 unless they are also divisible by 400. For example, 2004 and 2400 are leap years, but 2003 and 2100 are not. Jane also points out that there are only 14 possible calendars.

Definition

Class:	CalendarRecycle
Method:	useAgain
Parameters:	int
Returns:	int
Method signature:	int useAgain(int year)
(be sure your method is public)

Constraints

-

year is between 2002 and 9999, inclusive

Examples

0)

Returns: 2013

Your 2002 Elvis calendar will be valid again in 2013.

The following table shows the day of the week that September 8th falls on each year from 2002 to 2013.

Year | Day
-----+-----
2002 | Sunday
2003 | Monday
2004 | Wednesday
2005 | Thursday
2006 | Friday
2007 | Saturday
2008 | Monday
2009 | Tuesday
2010 | Wednesday
2011 | Thursday
2012 | Saturday
2013 | Sunday

1)

Returns: 2019

After 2013, your 2002 Elvis calendar will next be valid in 2019.

2)

Returns: 2036

3)

Returns: 10010

4)

Returns: 2531

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PaperFold

Brute Force, Simple Math

Used in:

SRM 162

Used as:

Division I Level One , Division II Level Two

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1846

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4615&pm=1846

Problem Statement

You have a piece of paper that you need to fold to fit into a box with a given width and length. Each time you fold the paper, you can fold it in half across either its width or length, but you can only fold the paper 8 times (after 8 times, the paper is too dense to fold again).

You will be given a int[] paper, which contains the width and length of the paper in inches, and a int[] box, which contains the width and length of the box in inches. In both cases, the first element is the width and the second element is the length. Your method should return the fewest number of folds which would allow you to fit the paper into the box. You can rotate the paper 90 degrees if it will fit with fewer folds, but the paper must lie completely flat inside the box. If the paper cannot be fit into the box with 8 folds or fewer, return -1.

Definition

Class:	PaperFold
Method:	numFolds
Parameters:	int[], int[]
Returns:	int
Method signature:	int numFolds(int[] paper, int[] box)
(be sure your method is public)

Notes

-

After the paper is folded, it is possible that it has fractional dimensions.

-

The paper will fit into the box even if one or both of the dimensions are exactly the same as the corresponding box dimensions.

Constraints

-

paper will contain exactly two elements.

-

box will contain exactly two elements.

-

Each element of paper and box will be between 1 and 10000, inclusive.

Examples

0)

{8, 11}

{6, 10}

Returns: 1

By folding the paper so that the length is reduced from 11 to 5.5 inches, it will fit inside the box if you rotate it 90 degrees.

1)

{11, 17}

{6, 4}

Returns: 4

There are two ways to fold the paper so that it fits within the box.

First, you could fold the width in half to get 5.5 inches, and then fold the length in half three times to get 2.125 inches.

Second, you could fold the width in half twice to get 2.25 inches, and then fold the length in half twice to get 4.25 inches. In this case, you must also rotate 90 degrees to fit the paper in.

2)

{11, 17}

{5, 4}

Returns: 4

Now, you must use the second method to get it to fit: Fold the width and length each twice, and rotate 90 degrees. If you try fitting without rotating, it would take 5 folds.

3)

{1000,1000}

{62,63}

Returns: -1

Folding in each direction 4 times, you can get the paper down to 62.5 x 62.5. However, this will not fit into the box because neither dimension fits in 62.

4)

{100,30}

{60,110}

Returns: 0

5)

{1895, 6416}

{401, 1000}

Returns: 5

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SMBus

Simple Math, Simulation

Used in:

SRM 162

Used as:

Division II Level Three

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1841

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4615&pm=1841

Problem Statement

On most modern PC systems, there is a 2-wire bus called the System Management Bus, or SMBus, which is based on the I²C protocol. This bus is used to talk to multiple devices on the system such as temperature sensors, or batteries. The most significant achievement of the I²C protocol is that it requires no more than 2 wires, and is not susceptible to collisions (unlike other hardware protocols, like ethernet). Collisions occur when two masters (devices which transmit messages) try to transmit at the same time and the resulting data is invalid. For I²C, the first bit transmitted by one master which is different than the bit transmitted by another master causes an "arbitration" to occur. The data being transmitted on the bus is the logic and-ed value of all the data being transmitted by the masters. Therefore, if one master is transmitting a '1' and another is transmitting a '0', the '0' will be transmitted and the '1' will not. The master transmitting the '1' detects that it is not able to transmit, and stops transmitting. The arbitration is not detected by the master transmitting the '0', or by the slave receiving the '0', so the message can continue without any collisions.

Since '0' bits that occur earlier in messages always win, the master transmitting the lowest byte always wins arbitration. For example, if one master was transmitting "01234", and another master was transmitting "01245", both masters would transmit the first three bytes, but the first master would win arbitration on the fourth data byte, since '3' is less than '4'.

Multiple masters can start transmissions at the same time, but if a transmission has already started, another master cannot start one in the middle of the transmission. Therefore, if one master is transmitting "01234", and has already transmitted the '0', another master wanting to transmit "1234" cannot start its transmission until the first master is finished.

The speed of transmission of each master is also allowed to vary. The speed at which each byte is transferred is determined by the slowest transmitting master. If a master loses arbitration of the bus, it continues to drive the clock signal (which determines the speed) for the remainder of the current byte, but then stops driving the clock for the rest of the transmission. In other words, the speed that each byte is transmitted at is determined by the slowest master attempting to transmit during that byte, even if the master loses arbitration during that byte.

Given the description of the I²C protocol above, you are to simulate multiple masters transmitting messages on the bus, and return how long it takes to transmit them. You will be given a String[] messages, where each element is a message to be transmitted by a master device, and the messages consist of numeric digits '0'-'9'. You will also be given a int[] times, where each element is the number of milliseconds it takes for the corresponding master to transmit a byte. The master transmitting element i of messages is described by element i of times. Each master that loses arbitration will retry transmitting its message after the current message is finished. Note that all masters try transmitting their messages at the very beginning of the simulation.

Definition

Class:	SMBus
Method:	transmitTime
Parameters:	String[], int[]
Returns:	int
Method signature:	int transmitTime(String[] messages, int[] times)
(be sure your method is public)

Constraints

-

messages will contain between 1 and 50 elements, inclusive.

-

Each element of messages will contain between 1 and 50 characters, inclusive.

-

Each element of messages will consist only of numeric digits '0'-'9', inclusive.

-

No element of messages will be a prefix of, or be exactly the same as, any other element of messages.

-

times will contain the same number of elements as messages.

-

Each element of times will be between 1 and 100, inclusive.

Examples

0)

{"123","124","134"}

{1,2,3}

Returns: 25

Here is a graph of the bytes that are transmitted, which masters are transmitting for each byte, and how long each byte takes to transmit. '-' means the master is transmitting, and '+' means the master was driving clock, but lost arbitration:

Data:       123124134
Master1:    ---
Master2:    --+---
Master3:    -+ -+ ---
Time taken: 332332333

For the first message, all masters successfully transmit the first byte. Since the slowest is 3 milliseconds, the first byte takes 3 milliseconds to transfer. On the second byte, the third master is arbitrated out since the other two transmit a lower byte. However, the third master still drives the clock for the byte, so it is transmitted at 3 milliseconds. The third byte is transmitted by the first two masters, and even though the second master loses arbitration, it drives the clock at 2 milliseconds. The total time for the first message is therefore 3+3+2 = 8 milliseconds long.

At this point, the second and third master still haven't transmitted their messages. The second message again takes 8 milliseconds because the third master is arbitrated out on the second byte.

The final message is transmitted only by the third master, and therefore takes 9 milliseconds to transmit. The total time for the entire sequence is 8+8+9=25 milliseconds.

1)

{"012", "1234", "1233", "1223", "1123"}

{4,1,5,2,9}

Returns: 94

Again, here is a graph which displays the bytes transmitted, which masters are transmitting, and the resulting times for each byte. '-' means the master is transmitting and '+' means the master is driving clock, but lost arbitration:

Data:       0121123122312331234
Master1:    ---
Master2:    +  -+  --+ ---+----
Master3:    +  -+  --+ ----
Master4:    +  -+  ----
Master5:    +  ----
Time taken: 9449999555255551111

2)

{"0002019289019101039663222896280025447",
 "00201873554718989597528841094293294387326",
 "010699029378761", "0110118", "011143279122561420",
 "001046384966198", "00200570375817801109530240012",
 "0003163277589822", "01100240744590150136673219652442108",
 "012033596872642679096489479354", "0121059494098",
 "00001002303019117948961792176", "00216399923558", "02014",
 "00224999120803846121427603894967637446889670369",
 "01101009414735635151893037596051740080475886",
 "0000101211809647472761605153430927981533514",
 "176845042961739039392207791589",
 "02000047506929386333221966659552927385017901842706",
 "021001117450487502127241076595509511",
 "021010776262723557108100899515",
 "0210114830738951774606917781619656",
 "0211798433083855430", "00000005842153604632996228135814",
 "0001000766929248550736138555144997170272757787",
 "0001010247593342056062432721557",
 "01100004828618452515832113396660046634951",
 "0132559984733529872911444204991646138116334788",
 "0224149857349431864906523152249992",
 "00001142929552573133212195441932219",
 "0011090498947092002457447355036811372647896489218",
 "000001275414757476198997466", "00010014",
 "00111025861963467834393486017602553072649743",
 "000102085", "00120882661783539",
 "01100018938145727291185020",
 "01100191373790478446634214244459341793", "0001129060",
 "001111287431066271555393813846448",
 "011010160778408696098486370196313", "0002125146381515395"}

{42, 86, 47, 86, 32, 95, 2, 98, 17, 58, 31, 32, 85, 77,
 87, 61, 1, 20, 15, 80, 20, 95, 55, 87, 52, 14, 55, 68,
 2, 66, 67, 3, 28, 97, 100, 67, 65, 20, 28, 77, 93, 64}

Returns: 71048

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Equity

Advanced Math

Used in:

TCO '03 Semifinals 3

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

lbackstrom , schveiguy , vorthys

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1833

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4708&pm=1833

Problem Statement

We are given k candy bars to divide up among n people. Each bar may be left whole, split into 2 equal pieces, or split into 3 equal pieces. We must distribute all the candy to the people, but we want to be as fair as possible. Define the "inequity" of a distribution of the candy to be the difference between the minimum amount received by a person and the maximum amount received by a person. We want to minimize the inequity.

Among solutions that have minimum inequity, we want to choose the one that has the fewest pieces. Each whole bar counts as one piece, while each split bar counts as either two or three pieces depending on how it was split. Create a class Equity that contains a method minPieces that takes n, the number of people, and k, the number of candy bars, and returns the smallest number of pieces that we will need in order to divide the candy bars with minimum inequity.

Definition

Class:	Equity
Method:	minPieces
Parameters:	int, int
Returns:	int
Method signature:	int minPieces(int n, int k)
(be sure your method is public)

Constraints

-

n will be between 1 and 1000 inclusive

-

k will be between 1 and 1000 inclusive

Examples

0)

Returns: 18

Split 2 of the bars into thirds, and 3 of the bars into halves. Give 6 of the people a third of a bar and a half of a bar each. Give the other 6 people a whole bar each. This results in an inequity of 1 - (1/2+1/3) = 1/6 which is the minimum possible inequity. There are 18 pieces: 6 thirds, 6 halves, and 6 wholes.

1)

Returns: 12

Give each person a third of a bar.

2)

Returns: 3

The best we can do is to give 3 people a third, and the other 9 nothing.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PowSum

Simple Math

Used in:

TCO '03 Round 1

Used as:

Division I Level One

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1821

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4702&pm=1821

Problem Statement

Given an int low, an int high, and an int pow, return the sum of i^j, for all i between low and high, inclusive, and all j between 1 and pow, inclusive.

Definition

Class:	PowSum
Method:	getSum
Parameters:	int, int, int
Returns:	int
Method signature:	int getSum(int low, int high, int pow)
(be sure your method is public)

Constraints

- low will be between -100 and 100, inclusive.

- high will be between low and 100, inclusive.

- pow will be between 1 and 10, inclusive.

- The return value will fit in a signed 32 bit datatype.

Examples

0)

Returns: 20

 1^1 + 2^1 + 3^1 + 1^2 + 2^2 + 3^2 = 
 1 + 2 + 3 + 1 + 4 + 9 =
 20

1)

-12

Returns: 1637738440

Note that intermediate values may exceed the 32 bit restriction.

2)

-100

Returns: 676700

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

CalendarISO

Search

Used in:

SRM 163

Used as:

Division I Level Three

Writer:

Eeyore

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1811

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4620&pm=1811

Problem Statement

According to the International Organization for Standardization (ISO), the first calendar week of a year is the one that includes the first Thursday of that year, and the last calendar week of a year is the week immediately preceding the first calendar week of the next year. It follows from this definition that some years have 52 calendar weeks, while others have 53. The calendar weeks are numbered in succession from 1 to 52 or 53, as the case may be. Each week begins on a Monday and ends on a Sunday. Observe that a week may spill over from one year into another. For example, if January 1 of some year is a Wednesday, then ISO week 1 of that year includes the last Monday and Tuesday of the previous year. Similarly, if December 31 of some year is a Saturday, then the last ISO week of that year includes the first Sunday of the following year.

The months of April, June, September, and November are 30 days long. The others have 31 days, with the exception of February, which has 29 days in leap years and 28 days otherwise. A leap year is one that is divisible by 4, except if it is divisible by 100 and not divisible by 400. For example, 1996 and 2000 are leap years, but 2099 and 2100 are not. These rules were introduced by Pope Gregory XIII (hence the name "Gregorian calendar") on October 15, 1582, and are part of the calendar standard promulgated today by the ISO.

Mathematicians and programmers have been familiar with this standard for some time, and have developed efficient methods to calculate ISO week numbers. It is rumored, however, that all the library routines are about to become obsolete. Your newspaper's gossip column states that the ISO council, at its next annual congress in Geneva, will announce a three-day shift in the mapping of dates to weekdays, effective retroactively and into the future. Under this ruling, September 8, 2003 ceases to be a Monday and will henceforth be a Thursday, with all other dates remapped to agree with the order of the weekdays. The ISO standard will remain unchanged in every other respect.

Given three int values specifying the year, month, and day of a date between the introduction of the Gregorian calendar and the last day of the year 9999, inclusive, calculate the ISO number of the week within which it falls under the new mapping.

Definition

Class:	CalendarISO
Method:	weekNumber
Parameters:	int, int, int
Returns:	int
Method signature:	int weekNumber(int year, int month, int day)
(be sure your method is public)

Notes

-

Months, days, and ISO weeks are all numbered starting from 1.

Constraints

-

year is between 1582 and 9999, inclusive

-

month is between 1 and 12, inclusive

-

day is valid for the given month and year

-

the given date is between October 15, 1582 and December 31, 9999, inclusive

Examples

0)

Returns: 51

When Isaac Newton was born on December 25, 1642, people called it Thursday. With the mapping of weekdays specified above, the same date becomes a Sunday. Therefore, the last ISO week of 1642 begins on Monday, December 26, 1642, and ends on Sunday, January 1, 1643. Because 1642 doesn't have 53 weeks under this mapping, its last week has ISO number 52. In consequence, the immediately preceding Sunday must fall in ISO week 51.

1)

Returns: 9

Napoleon escaped from the isle of Elba on February 26, 1815.

2)

Returns: 1

The Y2K bug failed to cripple the world economy on January 1, 2000.

3)

Returns: 32

The 29th Olympic Games will open in Beijing on August 8, 2008.

4)

Returns: 27

July 4, 2276 will be the quincentenary of the Declaration of Independence.

5)

Returns: 1

6)

Returns: 1

7)

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PermutationValues

Advanced Math, Recursion, Search

Used in:

SRM 161

Used as:

Division I Level Three

Writer:

brett1479

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1808

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4610&pm=1808

Problem Statement

You will be given two int[]s lows and highs describing a group of integer ranges. lows[i] and highs[i] represent the lower and upper inclusive bounds for the ith range of numbers. None of the ranges will overlap. The total group of numbers used in this problem will be the combination of the ranges given in lows and highs.

You will also be given a numeric String lexPos and a String[] retInts containing numeric Strings. Assume you listed all possible permutations of the given group of numbers in ascending lexicographical order (no repeated permutations). Find the permutation A that is in position lexPos lexicographically. Return a int[] with the same number of elements as retInts whose kth element is A[retInts[k]]. lexPos is a 0-based index into the list of possible permutations. Each element of retInts is a 0-based index into the relevant permutation.

In a lexicographical ordering, permutations are ordered by their first elements, with ties broken by their second elements, further ties broken by their third elements, and so forth. If lexPos is greater than the total possible number of lexicographical orderings (without repeats) T, then use lexPos%T instead of lexPos (% denotes mod).

Definition

Class:	PermutationValues
Method:	getValues
Parameters:	int[], int[], String, String[]
Returns:	int[]
Method signature:	int[] getValues(int[] lows, int[] highs, String lexPos, String[] retInts)
(be sure your method is public)

Notes

-

Each element of retInts and lexPos will fit in a long.

Constraints

-

lows will contain between 1 and 50 elements inclusive

-

highs will contain the same number of elements as lows

-

lexPos will be between 0 and (2^63)-1 inclusive

-

lexPos will contain only digits (0-9), will not have extra leading zeros, and will not contain whitespace

-

lexPos will contain between 1 and 50 characters inclusive

-

retInts will contain between 1 and 50 elements inclusive

-

Each element of lows will be between -2^31 and (2^31)-1 inclusive

-

Each element of highs will be between -2^31 and (2^31)-1 inclusive

-

Element k of lows will not be greater than element k of highs

-

No two ranges will overlap

-

Each element of retInts will contain only digits (0-9), will not have extra leading zeros, and will not contain whitespace

-

Each element of retInts will contain between 1 and 50 characters inclusive

-

Each element of retInts will be between 0 and tot-1 inclusive, where tot is the total amount of numbers in all ranges combined

Examples

0)

{1}

{4}

"0"

{"0","1","2","3"}

Returns: { 1,  2,  3,  4 }

The 0th permutation lexicographically is the sequence 1,2,3,4.

1)

{1}

{3}

"5"

{"0","1","2"}

Returns: { 3,  2,  1 }

The 6 possible permutations, in order, are :

0) 1, 2, 3

1) 1, 3, 2

2) 2, 1, 3

3) 2, 3, 1

4) 3, 1, 2

5) 3, 2, 1

lexPos is 5 so you return the 0th, 1st, and 2nd elements of permutation 5

2)

{1,16}

{5,20}

"1000000"

{"0","1","2","3","4","5","6","7","8","9","1","2","3"}

Returns: { 3,  18,  19,  4,  20,  2,  16,  17,  1,  5,  18,  19,  4 }

Notice the repeated elements in retInts

3)

{1}

{5}

"100000000000001"

{"0","1","2","3","4"}

Returns: { 2,  4,  5,  3,  1 }

lexPos is very big.

4)

{-1000000000,500000}

{0,2000000000}

"99999999999999999"

{"2999500000","1234123","123344","9293939","2999500001","2999499950"}

Returns: { 1999999987,  -998765877,  -999876656,  -990706061,  1999999982,  1999999949 }

5)

{9}

{9}

"999999"

{"0"}

Returns: { 9 }

6)

{0,-100,101}

{99,-11,100000000}

"100000000000009"

{"4","100000087","7"}

Returns: { -96,  99999993,  -93 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Inchworm

Simple Math, Simulation

Used in:

SRM 163

Used as:

Division II Level One

Writer:

Eeyore

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1799

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4620&pm=1799

Problem Statement

The inchworm is a creature of regular habits. She inches forward some distance along the branch of a tree, then stops to rest. If she has stopped at a leaf, she makes a meal of it. Then she inches forward the same distance as before, and repeats this routine until she has reached or passed the end of the branch.

Consider an inchworm traveling the length of a branch whose leaves are spaced at uniform intervals. Depending on the distance between her resting points, the inchworm may or may not be able to eat all of the leaves. There is always a leaf at the beginning of the branch, which is where the inchworm rests before setting out on her journey.

You are given three int values that specify, in inches: the length of the branch; the distance traveled by the inchworm between rests; and the distance between each consecutive pair of leaves. Given that the inchworm only eats at rest, calculate the number of leaves she will consume.

Definition

Class:	Inchworm
Method:	lunchtime
Parameters:	int, int, int
Returns:	int
Method signature:	int lunchtime(int branch, int rest, int leaf)
(be sure your method is public)

Notes

-

The inchworm starts by gobbling up the leaf at the beginning of the branch.

-

If there is a leaf at the end of the branch, the inchworm eats it only if it falls at a resting point.

Constraints

-

branch is between 1 and 1000000 (one million), inclusive

-

rest is between 1 and 1000, inclusive

-

leaf is between 1 and 1000, inclusive

Examples

0)

Returns: 3

Leaves grow 0, 4, and 8 inches from the beginning of the branch. The inchworm eats them all.

1)

Returns: 2

The inchworm misses the leaves growing at distances 4 and 8, but eats those at 0 and 12.

2)

Returns: 1

The inchworm eats only the leaf at the outset.

3)

Returns: 2

The inchworm eats the leaves at the beginning and end of the branch.

4)

Returns: 1

The inchworm eats only the leaf at the outset.

5)

Returns: 48

6)

Returns: 48

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LCMRange

Brute Force, Math

Used in:

SRM 162

Used as:

Division II Level One

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1792

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4615&pm=1792

Problem Statement

The least common multiple of a group of integers is the smallest number that can be evenly divided by all the integers in the group. Given two ints, first and last, find the least common multiple of all the numbers between first and last, inclusive.

Definition

Class:	LCMRange
Method:	lcm
Parameters:	int, int
Returns:	int
Method signature:	int lcm(int first, int last)
(be sure your method is public)

Constraints

-

first will be between 1 and 12, inclusive.

-

last will be between first and 12, inclusive.

Examples

0)

Returns: 60

The following statements show how 60 can be divided by all numbers from 1 to 5:

1*60 = 60

2*30 = 60

3*20 = 60

4*15 = 60

5*12 = 60

1)

Returns: 20

Although 60 would be a common multiple for 4 and 5, 20 is the least common multiple.

2)

Returns: 27720

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Salary

Math, String Parsing

Used in:

SRM 157

Used as:

Division I Level One , Division II Level Two

Writer:

Yarin

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1786

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4590&pm=1786

Problem Statement

Often employees at a company time stamp their arrivals and departures, so when the month is over the boss can check how much each employee has worked. Given the time stamps for a single employee during a single day as well as his (or her) hourly wage, calculate how much the employee has earned that day.

The time stamps are given in the format "hh:mm:ss" (quotes for clarity only) where hh is the hour (between 00 and 23 inclusive), mm is the minute (between 00 and 59 inclusive) and ss is the second (between 00 and 59 inclusive). All these numbers have exactly two digits. The arrival time stamps are inclusive, and the departure time stamps are exclusive, so an employee arriving at 09:00:00 one day and departing 17:30:00 the same day has worked exactly 8 hours 30 minutes 0 seconds during that interval.

An employee working during evenings (between 18:00:00 and 23:59:59, inclusive) or nights (between 00:00:00 and 05:59:59, inclusive) gets paid one and a half times as much during that period.

Create a class Salary containing the method howMuch which takes a String[], arrival, and a String[], departure, the arrival and departures times of an employee, respectively, as well an int wage, the hourly wage (in cents). Your method should return an int representing the total amount (in cents) the employee earned during the time he or she worked. The amount should be rounded down to the largest integer less than or equal to the actual amount. Element i in arrival corresponds to element i in departure.

Definition

Class:	Salary
Method:	howMuch
Parameters:	String[], String[], int
Returns:	int
Method signature:	int howMuch(String[] arrival, String[] departure, int wage)
(be sure your method is public)

Constraints

-

arrival will contain between 1 and 10 elements, inclusive.

-

departure will contain between 1 and 10 elements, inclusive.

-

arrival will contain the same number of elements as departure.

-

All elements in arrival and departure will be in the form "hh:mm:ss" (quotes for clarity only) satisfying the constraints given above.

-

All time stamps will be strictly increasing; that is, arrival[0]<departure[0]<arrival[1]<departure[1] and so on.

-

wage will be between 100 and 10000, inclusive.

Examples

0)

{"08:00:00","13:00:00","19:27:32"}

{"12:00:00","17:00:00","20:48:10"}

Returns: 10015

This employee worked 4 hours, took a break and then worked 4 more hours. Later he got back to work and worked 1 hour, 20 minutes and 38 seconds overtime. The salary becomes (4+4)*1000 + (1+20/60+38/3600)*1000*1.5 = 10015.83333 which is rounded down to 10015.

1)

{"01:05:47","16:48:12"}

{"09:27:30","21:17:59"}

Returns: 33920

2)

{"00:00:00"}

{"23:59:59"}

Returns: 299995

3)

{"10:00:00"}

{"18:00:00"}

Returns: 80000

Notice that 18:00:00 is exclusive, so the last second was not overtime.

4)

{"22:19:46"}

{"23:12:46"}

Returns: 7049

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BombSweeper

Simple Math, Simple Search, Iteration

Used in:

SRM 156

Used as:

Division I Level One , Division II Level Two

Writer:

LunaticFringe

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1778

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4585&pm=1778

Problem Statement

The game of BombSweeper is a single-player game played on a rectangular grid. Each square in the grid is either a bomb (represented by 'B') or empty space (represented by '.'). The true identity of each square is hidden when the game begins. The object of the game is to correctly determine both the number of bombs on the board and their positions.

You are trying to write a program which predicts the percent likelihood that you will win a given game of BombSweeper. You've recently become so good at the game that your success or failure depends only on your first few moves. To start, you pick a random square on the gameboard and uncover it. If the square you uncover is a bomb, you lose the game. If the square is not a bomb, but one or more of its horizontal, vertical, and diagonal neighbors is, you are no better off than when you started and you must take another turn. If the square is not a bomb, and none of its (up to) eight neighbors are bombs either, then you win the game.

Given a String[] board, representing the game board, return a number between 0.0 and 100.0, inclusive, representing the percent likelihood of you winning the game.

Definition

Class:	BombSweeper
Method:	winPercentage
Parameters:	String[]
Returns:	double
Method signature:	double winPercentage(String[] board)
(be sure your method is public)

Notes

- In calculating the probability, let wins be the number of non-bomb squares which have no bomb neighbors, and let losses be the number of bombs on the board. The odds of winning are then (wins / (wins + losses)), which returns a number between 0.0 and 1.0, inclusive.

- As long as you calculate wins and losses correctly, you need not worry about minor double imprecisions.

- Your solution need only be accurate to 1e-9 (relative or absolute). Thus, if your result is within 1e-9 (relative or absolute) of the result shown, your result will be judged correct.

Constraints

- board will contain between 1 and 50 elements, inclusive.

- Each element of board will contain between 1 and 50 characters, inclusive.

- Each element of board will contain the same number of characters.

- Each character in board will be either '.' or 'B'.

Examples

0)

{".....",
 ".....",
 "..B..",
 ".....",
 "....."}

Returns: 94.11764705882354

If you uncover the bomb in the center of the gameboard, you lose. If you uncover one of the eight squares surrounding the bomb, you would need to take another turn. If you uncover one of the 16 squares on the perimeter of the gameboard, you would win, since none of these squares has a neighboring square which is a bomb. Since there are 16 ways to win and only 1 way to die, your odds of winning are 16/17, or about 94.1%.

1)

{"BBBBB",
 "B...B",
 "B...B",
 "B...B",
 "BBBBB"}

Returns: 5.882352941176471

As far as your odds of winning are concerned, this board is the opposite of the previous one. The only way to win is to uncover the square in the exact center of the gameboard, while any of the 16 bombs on the perimeter will cause you to lose. 1/17 is about 0.0588, or about 5.88%.

2)

{".........",
 ".B..B..B.",
 ".........",
 ".........",
 ".B..B..B.",
 ".........",
 ".........",
 ".B..B..B.",
 "........."}

Returns: 0.0

Every square on this board is either a bomb, or has a bomb as a neighbor. Therefore, there is no way to win.

3)

{".........................",
 ".........................",
 ".........................",
 "........................."}

Returns: 100.0

Now there are no bombs, so any square you uncover will cause you to win.

4)

{"......B.......B..B...........................B....",
 "..............B..................BB..B............",
 "B.B.B.............B.....B..............B..........",
 "...................B...B....................BB....",
 "...B.....B.........................B.......B.....B",
 "B.B.........B.....B.......B..B......B.B...B.BB....",
 "..B...................BB...............B..........",
 ".........B...B................B..B................",
 ".......BB.......B....B................B.....BBB...",
 ".......BB..........B..............B......BB.......",
 "...................BB.....................B.......",
 "...B.B.B......B..............B...B......B.........",
 "B................B................................",
 "....B..........B.....B..BB....B...............BB..",
 "..B....B.....B.............B.....B............B...",
 "...................B.B........B..B.........B.B....",
 ".....B.....B......................................",
 "...........BB......BB...B.B........B...B..........",
 ".....BBB..........................................",
 ".B...........B....B...BB......B......B...B.B......",
 "..................B........BB................B....",
 "...............................B..B....BBB.B....B.",
 "..........B.......................................",
 ".....B..........B....BB......B.B......B......B....",
 ".....B..................B........B................",
 "............B.....B..B....BB...B....BB........B...",
 "..B.................B.........B...................",
 ".BB..............B................................",
 "...B....B..................B.................B....",
 "......B...B......B......................B.B.......",
 "..............B..................B.......B........",
 ".....B........BB...B.....B........................",
 ".......B......B.B..B..........B...........B....B..",
 "B...B...........B...B...B......B.B...B..B......B..",
 "....B..B.....B.B.......BB..B............B.B....B..",
 "B.......B..........B.........B...B.BB......B......",
 "....B...............................B.............",
 ".....B.B..........................................",
 "..........B............B......B.B..B....B.........",
 "....B...B.......................B.................",
 "B.................B...........B..B....B...........",
 "...B.....B........................................",
 "...B..B......................................BBB..",
 ".B...B....................................B....B..",
 "...B...B..........B...B.B.........................",
 ".....B.............B...BB..........B..BBB.BB......",
 "....................B.....B.......................",
 "........B..BB..........B.B....B...........B......B",
 ".........B.....BB..B.............B....BB..........",
 "....B..B..............B...B..B..........B........."}

Returns: 77.67558528428094

This board has 267 bombs, 1304 empty spaces with bomb neighbors, and 929 empty spaces without bomb neighbors. (929 / (929 + 267)) is about 0.7768.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DiskSpace

Simple Math, Sorting

Used in:

SRM 156

Used as:

Division II Level One

Writer:

LunaticFringe

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1777

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4585&pm=1777

Problem Statement

As of late, your usually high-performance computer has been acting rather sluggish. You come to realize that while you have plenty of free disk space on your machine, it is split up over many hard drives. You decide that the secret to improving performance is to consolidate all the data on your computer onto as few hard drives as possible.

Given a int[] used, representing the amount of disk space used on each drive, and a corresponding int[] total, representing the total capacity of each drive mentioned in used, you should attempt to pack the data onto as few hard drives as possible. You may assume that the data consists of very small files, such that splitting it up and moving parts of it onto different hard drives never presents a problem. Return the minimum number of hard drives that still contain data after the consolidation is complete.

Definition

Class:	DiskSpace
Method:	minDrives
Parameters:	int[], int[]
Returns:	int
Method signature:	int minDrives(int[] used, int[] total)
(be sure your method is public)

Constraints

- used will contain between 1 and 50 elements, inclusive.

- used and total will contain the same number of elements.

- Each element of used will be between 1 and 1000, inclusive.

- Each element of total will be between 1 and 1000, inclusive.

- used[i] will always be less than or equal to total[i], for every valid index i.

Examples

0)

{300,525,110}

{350,600,115}

Returns: 2

In this example, the computer contains three hard drives:

Hard drive 1: 350 MB total, 300 MB used, 50 MB free
Hard drive 2: 600 MB total, 525 MB used, 75 MB free
Hard drive 3: 115 MB total, 110 MB used, 5 MB free

One way to pack the data onto as few drives as possible is as follows. First, move 50 MB from hard drive 3 to hard drive 1, completely filling it up. Next, move the remaining 60 MB from hard drive 3 to hard drive 2. There are still two hard drives which contain data after this process, so your method should return 2.

1)

{1,200,200,199,200,200}

{1000,200,200,200,200,200}

Returns: 1

One way to consolidate the data would be to move the 1 MB from hard drive 1 to hard drive 4. However, this is a poor choice, as it results in only one free hard drive and five hard drives which still contain data. A better decision is to move all the data from the other five hard drives onto hard drive 1. Now there is only one hard drive which contains data. Since this is the optimal strategy, the method returns 1.

2)

{750,800,850,900,950}

{800,850,900,950,1000}

Returns: 5

No matter how the files get moved around, all five drives will still contain data at the end.

3)

{49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,
 49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49,49}

{50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,
 50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50,50}

Returns: 49

To consolidate this data, you would select one hard drive, and transfer 1 MB of data from it to each other drive. This results in 49 completely full hard drives and one empty drive.

4)

{331,242,384,366,428,114,145,89,381,170,329,190,482,246,2,38,220,290,402,385}

{992,509,997,946,976,873,771,565,693,714,755,878,897,789,969,727,765,521,961,906}

Returns: 6

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MostProfitable

Simple Math

Used in:

SRM 153

Used as:

Division II Level One

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1774

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4570&pm=1774

Problem Statement

When selling goods, it is important to know exactly how much it costs to acquire each item. A number of distributed costs, such as marketing often make this difficult, but not impossible. If a business can figure out how much an item costs, with some accuracy, then it can easily calculate the profit margins for the item. This information, combined with sales figures, can be used to determine which items are the most important to a business. In this problem you will be given the costs, prices, and number of sales for a number of items. Each element of costs represents the total costs accrued from selling a single item. The corresponding elements (ones with the same index) of prices and sales represent the prices at which single items are sold, and the number of sales of each item that have occurred in some time period, respectively. You are to return the name of the item (the corresponding element of items) that provides the business with the most profits. If there is a tie for the most profitable item, return the one that comes earliest in items (lowest index). If no item provides the business with positive profits you should return the empty String.

Definition

Class:	MostProfitable
Method:	bestItem
Parameters:	int[], int[], int[], String[]
Returns:	String
Method signature:	String bestItem(int[] costs, int[] prices, int[] sales, String[] items)
(be sure your method is public)

Constraints

-

costs, prices, sales, and items will all contain the same number of elements.

-

costs, prices, sales, and items will contain between 1 and 50 elements, inclusive.

-

Each element of costs and prices will be between 1 and 1,000,000, inclusive.

-

Each element of sales will be between 0 and 1,000, inclusive.

-

Each element of items will have between 1 and 50 characters, inclusive.

-

Each character of each element of items will have ASCII value between 32 and 126, inclusive. (All of the characters that can be easily made with a regular keyboard.)

Examples

0)

{100,120,150,1000}

{110,110,200,2000}

{20,100,50,3}

{"Video Card","256M Mem","CPU/Mobo combo","Complete machine"}

Returns: "Complete machine"

This business makes 200 on video cards, loses 1000 on memory, makes 2500 on CPU/Mobo combos, and makes 3000 on complete machines. Since 3000 is the highest, you should return "Complete machine".

1)

{100}

{100}

{134}

{"Service, at cost"}

Returns: ""

The only product given is sold at cost, so there are no items which give positive profit.

2)

{38,24}

{37,23}

{1000,643}

{"Letter","Postcard"}

Returns: ""

3)

{10,10}

{11,12}

{2,1}

{"A","B"}

Returns: "A"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Inventory

Math

Used in:

SRM 153

Used as:

Division I Level One , Division II Level Two

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1772

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4570&pm=1772

Problem Statement

Inventory control is an important part of any business that maintains an inventory. On the one hand, businesses want to have enough of a product in stock that they can ship orders immediately. However, they do not want to have so much of a product in stock that all of their capital is tied up in that product. To deal with this, businesses often maintain a small stock, and replenish that stock as it is sold on a monthly basis. In other words, every month the business orders or produces more of a product so that it has some of the product in stock for the next month.

In this problem, a business wants to place a standing monthly order so that a certain number of items are delivered to it each month. Your task is to help the business determine how large a standing order to place. You will be given a int[], sales, representing the number of items that the business sold for each of a number of months, and are to determine how many they can expect to sell in an average month. Unfortunately, the business may have run out of items some months, so this is not as simple as just taking the average of the number of items sold each month.

You will be given a int[], daysAvailable, whose elements represent the number of days that the item was available in each of the months (elements of daysAvailable correspond to elements of sales with the same index). You should assume that, if the item was not available for a whole month, the business would have continued to sell the item at the same rate during the days of the month that it was not available as it did during the days the item was available, had sufficient stock been present. So, for example, if the business sold 5 items in the first half of a month, and then ran out, you can assume that they would have sold 10 items that month, if they had been available.

On months when the item was available for zero days, you can tell nothing about the number of items that might have sold, so you should not include these months in your calculation. Also, for simplicity, you may assume that all months have 30 days. Thus, if the item were in stock for exactly half of the month this would be represented by a 15 in daysAvailable. Furthermore, if the expected number of sales per month is not a whole number, you should round up since it is probably better to have one too many items than it is to have one too few.

Definition

Class:	Inventory
Method:	monthlyOrder
Parameters:	int[], int[]
Returns:	int
Method signature:	int monthlyOrder(int[] sales, int[] daysAvailable)
(be sure your method is public)

Notes

-

While it is possible to solve this problem without using any double arithmetic, the last constraint ensures that the simpler solution using doubles will work if an epsilon is used properly (pay special attention to the last example). In other words, once you have computed the expected number of sales, you should subtract a small number (like 1e-9) from this number before rounding up.

Constraints

-

daysAvailable and sales will have the same number of elements.

-

daysAvailable and sales will both have between 1 and 50 elements, inclusive.

-

Each element of daysAvailable will be between 0 and 30, inclusive.

-

Each element of sales will be between 0 and 10,000, inclusive.

-

If an element of daysAvailable is 0, the corresponding element of sales will also be 0.

-

At least one element of daysAvailable will be greater than 0.

-

The expected number of sales, prior to rounding, will not be within 1e-9 of an integer, unless the expected number is exactly an integer.

Examples

0)

{5}

{15}

Returns: 10

If 5 items are sold in 15 days (half a month), then 10 items could have been sold in a full month.

1)

{75,120,0,93}

{24,30,0,30}

Returns: 103

The expected number of sales per month is 102.25. Rounding up, we get 103.

2)

{8773}

{16}

Returns: 16450

3)

{1115,7264,3206,6868,7301}

{1,3,9,4,18}

Returns: 36091

Watch out for double imprecision. The expected number of sales per month, without rounding, is exactly 36091.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Collision

Advanced Math

Used in:

SRM 153

Used as:

Division I Level Two

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1771

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4570&pm=1771

Problem Statement

You are working on the backend of a particular system in which you want to assign a unique ID to each client. However, the system is distributed, and there are a number of components, each of which must be able to assign IDs to clients. In other words, you want to have each of the components assign the IDs with as little communication between the components as possible. You have decided that it is more important to keep the system distributed than it is to ensure that all of the clients have unique IDs. Thus, you are considering having each of the components independently assign IDs randomly from a large pool of possible IDs, and synchronizing the assigned IDs at the end of each day. In other words, each component will update its list of available IDs at the end of each day, based on the IDs assigned by all of the components.

Now, there are two ways that you can do this. The first is to have each of the components assign a random ID each time from the list of available IDs obtained at the beginning of each day. In other words, have components without any memory of which IDs they have assigned during the day, which may assign the same ID more than once during the day. The second way to assign the IDs is to have the components each remember which IDs they have assigned, so that no component assigns the same ID more than once. This way, two different components may assign the same ID, but no one component will assign an ID more than once. Now, it turns out that the first system is slightly cheaper to implement, but it will clearly result in more collisions (a collision occurs when the same ID is assigned to multiple clients). So, to help decide which system to implement, you want to run a simulation.

Your task is to simulate both systems and figure out the probability that some ID is assigned to more than one client in both of the systems, and then return the difference in the two probabilities. You will be given an int, ids, which represents the number of IDs in the pool of possible IDs that each component may assign at the beginning of some day (all components draw IDs from the same pool). You will also be given a int[], assignments, each of whose elements represents the number of IDs that some component assigns during the day. You are to return a double representing the difference in the probabilities between the two systems.

Definition

Class:	Collision
Method:	probability
Parameters:	int[], int
Returns:	double
Method signature:	double probability(int[] assignments, int ids)
(be sure your method is public)

Notes

-

Your result need not be precisely the same as the result shown in the examples. As long as your result is within 1e-9 of the result in the example, your submission will be evaluated as correct.

-

If more IDs are assigned than there are total IDs, return 0, since there must be a collision in this case.

Constraints

-

ids will be between 1000 and 2147483647, inclusive.

-

assignments will contain between 2 and 50 elements, inclusive.

-

Each element of assignments will be between 0 and 10,000, inclusive.

Examples

0)

{20,20}

Returns: 0.2113618990410422

The probability that there will be no collision if the components have memory is about 0.45362802928706036.

The probability that there will be no collision if the components do not have memory is about 0.6649899283281026.

1)

{123,456}

Returns: 0.3769052883184334

2)

{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000}

2147483647

Returns: 0.0069090268185510555

3)

{1005,1005}

Returns: 0.0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MarginCalculator

Simple Math

Used in:

SRM 154

Used as:

Division II Level One

Writer:

Unknown

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1768

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4575&pm=1768

Problem Statement

Margin is defined as the percentage of the selling price of an item or group of items which is profit. For example, if an item costs $80 and is sold for $100, then there is $20 profit, or 20% margin.

You will be given a String[], items, which is all of the items sold in a single transaction. Each String in items will be formatted as follows: "nnn.nn nnn.nn" (quotes for clarity), where each n is a digit between '0' and '9' inclusive. Each String will be exactly 13 characters in length. The first number listed is the price the customer paid for the item. The second number is what the cost to the store of the item was.

You will create a class MarginCalculator with a method percent which will calculate the percentage of margin on the transaction and return it as an int, rounded down to the greatest integer less than the actual value.

For example, let's say you were given the following String[]:

   { "012.99 008.73",
     "099.99 050.00",
     "123.45 101.07" }

The total cost is $159.80. The total price is $236.43. That means $76.63 was made on this sale. This would be a 32.41128% margin. Since we are rounding down, you would return 32.

Definition

Class:	MarginCalculator
Method:	percent
Parameters:	String[]
Returns:	int
Method signature:	int percent(String[] items)
(be sure your method is public)

Notes

-

The cost for some items may be greater than the price they was sold for. However, the sum of the prices of all the items in the transaction will be greater than the sum of the costs of all items.

Constraints

-

items will contain between 1 and 50 elements, inclusive.

-

Every String in items will be exactly 13 characters in length.

-

Every String in items will be formatted as "nnn.nn nnn.nn" where each n is a digit between '0' and '9' inclusive, thus the range for each price will be between "000.00" and "999.99" inclusive (all quotes for clarity).

-

The total price of all items will be greater than the total cost of all items.

-

The total price of all items will be greater than 0.

-

The percent of margin, prior to rounding, will not be within 1e-5 of an integer.

Examples

0)

{"012.99 008.73","099.99 050.00","123.45 101.07"}

Returns: 32

This is the example from above.

1)

{"000.00 049.99","999.99 936.22","033.99 025.64","249.99 211.87"}

Returns: 4

The total price is $1283.97. The total cost is $1223.72. The margin prior to rounding is 4.6924772%.

2)

{"822.77 704.86","829.42 355.45","887.18 949.38"}

Returns: 20

The margin prior to rounding is 20.8587169%.

3)

{"612.72 941.34","576.46 182.66","787.41 524.70","637.96 333.23","345.01 219.69",
 "567.22 104.77","673.02 885.77"}

Returns: 23

The margin prior to rounding is 23.9925711%.

4)

{"811.22 275.32","433.89 006.48","141.28 967.41","344.47 786.23","897.47 860.61",
 "007.42 559.29","255.72 460.00","419.35 931.19","419.25 490.52","199.78 114.44",
 "505.63 276.58","720.96 735.00","719.90 824.46","816.58 195.94","498.68 453.05",
 "399.48 921.39","930.88 017.63","422.20 075.39","380.22 917.27","630.83 995.87",
 "821.07 126.87","715.73 985.62","246.23 134.64","168.28 550.33","707.28 046.72",
 "117.76 281.87","595.43 410.45","345.28 532.42","554.24 264.34","195.73 814.87",
 "131.98 041.28","595.13 939.47","576.04 107.70","716.00 404.75","524.24 029.96",
 "673.49 070.97","288.09 849.43","616.34 236.34","401.96 316.33","371.18 014.27",
 "809.63 508.33","375.68 290.84","334.66 477.89","689.54 526.35","084.77 316.51",
 "304.76 015.91","460.63 636.56","357.84 436.20","752.24 047.64","922.10 573.12"}

Returns: 10

The margin prior to rounding is 10.4737522%.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FixedPointTheorem

Simple Math, Simulation

Used in:

SRM 152

Used as:

Division II Level One

Writer:

leadhyena_inran

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1765

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4565&pm=1765

Problem Statement

The fixed-point theorem is one of those cornerstones of mathematics that reaches towards all disciplines, and oddly enough it is also closely related to the ability of any program to Quine itself (or to print out its own source code). Put simply, the fixed-point theorem states that with certain restrictions on a real-valued function F, there is always a point such that X=F(X). Taking the fixed-point theorem further, you can show that any function that meets certain restrictions will start to cycle through values if you keep on feeding it its own output (doing this with programs and their output is one way of producing programs that Quine themselves).

One simple function that does this is the logistic function F(X)=R*X*(1-X) in the interval [0,1] for certain values of R. For example, if you start with the value X=.25 and feed it into F to get a new X, then feed that value into F to get yet another X, and so on, the values of X that are produced will converge to a small set of values that will eventually repeat forever, called a cycle.

Your program will be given a double R between 0.1 and 3.569 inclusive. Starting with X=.25, generate the first 200,000 iterations of F using the given value of R, which will stabilize values of X. Then generate 1000 more values, and return the range of these values (highest value - lowest value). In other words, you will be finding the range of the values produced between iterations 200,001 and 201,000 inclusive.

Definition

Class:	FixedPointTheorem
Method:	cycleRange
Parameters:	double
Returns:	double
Method signature:	double cycleRange(double R)
(be sure your method is public)

Notes

- Don't worry about overflow. With the given values it'll never happen.

Constraints

- R will be a value between 0.1 and 3.569 inclusive.

- R will always be a value such that the process stated above will produce a result accurate to 1e-9 (absolute or relative).

Examples

0)

0.1

Returns: 0.0

At low numbers, there exists only one point in the cycle, so the answer is 0.0.

1)

3.05

Returns: 0.14754098360655865

2)

3.4499

Returns: 0.4175631735867292

3)

3.55

Returns: 0.5325704489850351

4)

3.565

Returns: 0.5454276003030636

5)

3.5689

Returns: 0.5489996297493569

6)

3.00005

Returns: 0.004713996108955176

Make sure you're iterating 200,000 times.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DotNotation

String Parsing

Used in:

SRM 152

Used as:

Division I Level Three

Writer:

leadhyena_inran

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1762

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4565&pm=1762

Problem Statement

In Chapter 7 of W.V. Quine's book "Mathematical Logic", Quine speaks about the necessity of parentheses but also of their obsfucating nature. To combat this he introduces "a graphical notation of dots". Where parentheses determine the outside boundaries of operands by marking them directly, dot notation does this by placing dots on each side of the operator. The left operand of the operator is determined by the number of dots prefixed to the operator; the operand is the substring with its end at the beginning of the prefixed dots and with its beginning at the end of the next larger grouping of dots suffixed to another operator, or at the beginning of the expression whichever comes first. The right side of the operator is determined likewise; it is the substring starting at the end of the suffixed dots and has its end at the beginning of the next larger grouping of dots prefixed to another operator or at the end of the expression, whichever comes first.

To be specific, all dot notation will be a <DotNotation> of this form (quotes added for clarity):

<DotNotation> := <Number> | <DotNotation><Dots><Operator><Dots><Number>

<Dots> := "" | <Dots>"."

<Operator> := "+" | "-" | "*" | "/"

<Number> := exactly one of "0123456789"

If an operator's operands reach across the entire expression, the operator is said to be dominant. Evaluation in dot notation involves finding the dominant operator, evaluating the left and right operands of that operator, and then evaluating that operator last. For example: in the dot notation expression "2*.1+3", "2" is the left operand of the '*' (consider no dots as a grouping of 0 dots) and "1+3" is the right operand of the '*', so this can be read with parentheses as "2*(1+3)", the '*' is dominant, and the expression evaluates to 8. Likewise, "2*.1..+3" refers to the expression "(2*1)+3", the '+' is dominant, and the expression evaluates to 5.

Dot notation can be ambiguous if there is more than one dominating operator. For example, in the expression "3+.5.*7" either operator may be dominant (both operators reach across the entire expression unopposed) so this could be parenthesized as either "3+(5*7)" or "(3+5)*7" and the expression could evaluate to either 38 or 56 respectively. There are even expressions that have no dominating operator, such as "1+...2....*.8..+7". Since there is no way to parenthesize this expression consistent with its dot notation, it cannot be legally evaluated.

You will be given a String in dot form, and you'll need to return the number of unique integers that the expression can evaluate to. For this problem, a specific evaluation is illegal if any part of the evaluation involves division by 0, any operand evaluates to a value that is less than -2000000000 or greater than 2000000000, or if the expression has no dominating operator thus preventing evaluation. If all possible evaluations of the dot notation are illegal return 0.

Definition

Class:	DotNotation
Method:	countAmbiguity
Parameters:	String
Returns:	int
Method signature:	int countAmbiguity(String dotForm)
(be sure your method is public)

Notes

- There is no normal order of operations in this problem; thus a+b*c is ambiguous.

Constraints

- dotForm will be between 1 and 25 characters long, inclusive.

- dotForm will be a <DotNotation> as described above.

Examples

0)

"2"

Returns: 1

A single digit by itself has only one interpretation.

1)

"9+5*3"

Returns: 2

This could be read (9+5)*3 or as 9+(5*3). Keep in mind that no order of operations is to be assumed.

2)

"9+5.*3"

Returns: 1

Here, the dot prefixed to the * gives it dominance, and this can only be read as (9+5)*3.

3)

"1+2.*.3+4"

Returns: 1

The * is dominant here, so this is read as (1+2)*(3+4), and 21 is the only number it can be evaluated to.

4)

"9*8+7*6-5+4*3/2./9"

Returns: 99

5)

"1+...2....*.8..+7"

Returns: 0

Notice here how none of the operators in the expression can be dominating. Since none of these operators are dominating, none of these operators may be evaluated last, meaning that there is no valid interpretation of this expression.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PermutationCounter

Advanced Math, Recursion, Search

Used in:

SRM 162

Used as:

Division I Level Three

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1752

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4615&pm=1752

Problem Statement

You have a group of non-zero digits, which are not necessarily unique. If you can insert '0' digits wherever you wish, there are an infinite number of integers which have exactly those non-zero digits. For example, given the group of digits {1, 2}, you can create the numbers 12, 21, 102, 120, 201, 210, 1002, 1020, etc. Given a potentially large number n in String format, return how many numbers that use the same exact non-zero digits are less than it. Leading zeros are not allowed.

Definition

Class:	PermutationCounter
Method:	count
Parameters:	String
Returns:	long
Method signature:	long count(String n)
(be sure your method is public)

Constraints

-

n will have between 1 and 50 characters, inclusive.

-

n will consist only of digit characters ('0' - '9').

-

n will not start with a '0'.

-

There will be at most 2^63 - 1 integers with the same non-zero digits as n that are less than n

Examples

0)

"1020"

Returns: 7

From the problem statement above, we see that there are 7 values less than the given value.

1)

"50000000000000"

Returns: 13

Since there is only one non-zero digit in this number, the only way to increment the number is by inserting a zero after the 5. Therefore, the sequence is: 5, 50, 500, 5000, ..., 50000000000000.

2)

"1030000040000"

Returns: 1414

3)

"1901712530271201432987123"

Returns: 141588146596382454

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EyeDrops

Math

Used in:

SRM 167

Used as:

Division II Level One

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1750

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4640&pm=1750

Problem Statement

Note to plugin users: There is an image in the problem examples. Please use the applet to view it.

After laser surgery, I was instructed to put drops in my eyes 6 times a day, spacing them as far apart as possible. Considering that I sleep for some period each day, it required some calculation to come up with an optimal schedule. Recognizing that I get similar instructions every time I get medication from the doctor, it became clear that a computer program was needed.

Create a class EyeDrops that contains a method closest that is given sleepTime, the number of hours that the patient sleeps each day, and k, the number of doses required each day. The method returns the number of minutes between the closest doses, when the schedule is chosen to make this period as large as possible. You should assume that the patient sleeps for the same continuous period each day.

The schedule that you choose will be applied for multiple days, so the period between closest doses may be between doses on different days.

Definition

Class:	EyeDrops
Method:	closest
Parameters:	int, int
Returns:	double
Method signature:	double closest(int sleepTime, int k)
(be sure your method is public)

Notes

-

The returned value must have a relative error of less than 1.0E-9

Constraints

-

sleepTime must be between 0 and 23 inclusive

-

k must be between 1 and 50 inclusive

Examples

0)

Returns: 720.0

You can take one dose when you wake up, and the next one 12 hours later.

1)

Returns: 450.0

Take your medicine when you wake up, when you go to sleep, and halfway in between.

2)

Returns: 1440.0

3)

Returns: 128.57142857142856

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Gauss

Advanced Math, Search

Used in:

SRM 151

Used as:

Division I Level Three

Writer:

Wernie

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1745

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4560&pm=1745

Problem Statement

Carl Friedrich Gauss (1777-1855) is considered to be one of the greatest mathematicians ever. There is a nice story about him being at elementary school: The teacher wanted to keep the class busy and assigned to them the task of adding all whole numbers from 1 to 100. While the other kids were just about to start their additions, Gauss already presented the result, 5050. He noticed that the numbers can be grouped into 50 pairs of value 101 (1+100, 2+99, ...), and from this he deduced that the sum of all natural numbers from 1 to n equals n(n+1)/2.

Now let's consider adding consecutive numbers not only starting at 1 but at any natural number. E.g. if you start at 13 and add three consecutive numbers, you get 13+14+15 = 42. Now can 42 also be achieved by adding two or more consecutive numbers starting at a different number? Yes, it can: 3+4+5+6+7+8+9 = 9+10+11+12 = 42.

Given a number target, return all intervals representing a sequence of two or more consecutive natural numbers (positive integers) that add up to target. The intervals have to be sorted by ascending lower interval limits. The interval representing the sequence a + (a+1) + ... + (b-1) + b is the String "[a, b]" (quotes for clarity; there is a single space between the comma and b).

Definition

Class:	Gauss
Method:	whichSums
Parameters:	String
Returns:	String[]
Method signature:	String[] whichSums(String target)
(be sure your method is public)

Notes

- The value of target fits into a long.

Constraints

- target represents a natural number between 1 and 10^11, inclusive, without leading zeros.

Examples

0)

"42"

Returns: { "[3, 9]",  "[9, 12]",  "[13, 15]" }

This is the example from the problem statement.

1)

"4"

Returns: { }

There are no 2 or more consecutive natural numbers that add up to 4.

2)

"17"

Returns: { "[8, 9]" }

3)

"55"

Returns: { "[1, 10]",  "[9, 13]",  "[27, 28]" }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DivDigits

Simple Math, String Manipulation

Used in:

SRM 148

Used as:

Division II Level One

Writer:

Unknown

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1741

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4545&pm=1741

Problem Statement

Create a class DivDigits containing a method howMany which takes as an argument an int number and returns how many digits in number that number itself is divisible by. Count all occurences of such digits in the number, not just the first. See examples for more information.

Definition

Class:	DivDigits
Method:	howMany
Parameters:	int
Returns:	int
Method signature:	int howMany(int number)
(be sure your method is public)

Notes

-

No number is divisible by 0.

Constraints

-

number will be an int between 10000 and 999999999, inclusive (between 5 and 9 digits, inclusive).

Examples

0)

Returns: 3

12345 is divisible by 1, 3, and 5.

1)

Returns: 3

661232 is divisible by 1 and 2.

2)

Returns: 0

52527 is not divisible by 5, 2, or 7.

3)

730000000

Returns: 0

Nothing is divisible by 0. In this case, the number is also not divisible by 7 or 3.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Birthday

Simple Math, String Parsing

Used in:

SRM 151

Used as:

Division II Level Two

Writer:

Wernie

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1739

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4560&pm=1739

Problem Statement

Forgetting a close friend's birthday is quite embarrassing, but forgetting it two years in a row is a catastrophe. So what can a coder do to prevent this from happening again? Well, the thing he possibly can do best: code...

Given a String date (the current date) and a String[] birthdays, a list of people's birthdays and names, return a String, the date of the next occurring birthday, starting from the current date.

date is in the format "MM/DD" (quotes for clarity), where MM represents the two-digit month and DD represents the two-digit day (leading zero if necessary). Each element of birthdays is in the format "MM/DD <Name>" (quotes for clarity), where MM/DD is the date of <Name>'s birthday. <Name> is a sequence of characters from 'A'-'Z' and 'a'-'z'. There is exactly one space character between the date and <Name>. The date returned also has to be in the format "MM/DD" (quotes for clarity).

Definition

Class:	Birthday
Method:	getNext
Parameters:	String, String[]
Returns:	String
Method signature:	String getNext(String date, String[] birthdays)
(be sure your method is public)

Constraints

-

birthdays contains between 1 and 50 elements, inclusive.

-

Each element of birthdays contains between 7 and 50 characters, inclusive.

-

date and each element of birthdays follow the format described in the problem statement.

-

All dates are legal dates and neither date nor any date in birthdays is the 29th of February.

Examples

0)

"06/17"

{"02/17 Wernie", "10/12 Stefan"}

Returns: "10/12"

1)

"06/17"

{"10/12 Stefan"}

Returns: "10/12"

2)

"02/17"

{"02/17 Wernie", "10/12 Stefan"}

Returns: "02/17"

3)

"12/24"

{"10/12 Stefan"}

Returns: "10/12"

4)

"01/02"

{"02/17 Wernie",
 "10/12 Stefan",
 "02/17 MichaelJordan",
 "10/12 LucianoPavarotti",
 "05/18 WilhelmSteinitz"}

Returns: "02/17"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TopCan

Geometry, Math

Used in:

SRM 209

Used as:

Division I Level Two

Writer:

Wernie

Testers:

PabloGilberto , lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1729

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5855&pm=1729

Problem Statement

This problem contains an image.

TopCan, Inc. is a major producer of food. It produces all kinds of food than can be filled into a can: pineapples, mushrooms, peas, etc. However, business is not going well, so they are looking for ways to make production cheaper. An important expense factor is the amount of material needed for producing the can, which directly depends on the surface area of the can. Currently, cans are produced in all imaginable shapes and sizes, but to reduce cost, the company thinks about producing only cans in the shape of a cylinder (as shown below). So to be able to decide whether production should be changed TopCan wants to know, for a given volume, the minimal surface area possible of such a can. As the company's brightest employee, this task has been assigned to you.

Given an int volume, return a double, the minimal surface area possible of a cylinder that has the given volume.

Definition

Class:	TopCan
Method:	minSurface
Parameters:	int
Returns:	double
Method signature:	double minSurface(int volume)
(be sure your method is public)

Notes

-

Consider the material the can is made of to be infinitely thin.

-

Some formulas for your convenience:

r: radius of the circle being the base of the cylinder

h: height of the cylinder

Volume V = h * PI * r²

Surface S = 2 * PI * r * (r + h)

-

If not provided by a library, use the value of 2*acos(0) for PI.

-

Reminder:

If your result is within 10^-9 of the expected result, your solution will be evaluated as correct.

If your result is between (1+10^-9)*expected and (1-10^-9)*expected, it will be evaluated as correct.

Constraints

-

volume will be between 1 and 100000, inclusive.

Examples

0)

Returns: 25.694955950835347

For a volume of 10, the cylinder has a height of about 2.3351 and the base circle has a radius of about 1.1675.

1)

Returns: 40.78820010663257

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Time

Simple Math, String Manipulation

Used in:

SRM 144

Used as:

Division II Level One

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1708

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4515&pm=1708

Problem Statement

Computers tend to store dates and times as single numbers which represent the number of seconds or milliseconds since a particular date. Your task in this problem is to write a method whatTime, which takes an int, seconds, representing the number of seconds since midnight on some day, and returns a String formatted as "<H>:<M>:<S>". Here, <H> represents the number of complete hours since midnight, <M> represents the number of complete minutes since the last complete hour ended, and <S> represents the number of seconds since the last complete minute ended. Each of <H>, <M>, and <S> should be an integer, with no extra leading 0's. Thus, if seconds is 0, you should return "0:0:0", while if seconds is 3661, you should return "1:1:1".

Definition

Class:	Time
Method:	whatTime
Parameters:	int
Returns:	String
Method signature:	String whatTime(int seconds)
(be sure your method is public)

Constraints

-

seconds will be between 0 and 24*60*60 - 1 = 86399, inclusive.

Examples

0)

Returns: "0:0:0"

1)

Returns: "1:1:1"

2)

Returns: "1:30:36"

3)

Returns: "23:59:59"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Archimedes

Math, Simulation

Used in:

SRM 151

Used as:

Division I Level One

Writer:

Wernie

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1693

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4560&pm=1693

Problem Statement

The Greek mathematician Archimedes of Syracuse (287-212 B.C.) was most likely the first in finding a way to systematically (iteratively) approximate the value of Pi, the ratio between the perimeter and the diameter of a circle.

He inscribed and circumscribed regular polygons in/around a circle and calculated their perimeter. These are lower (inscribed polygon) and upper (circumscribed polygon) bounds for the perimeter of the circle, and therefore can be used to calculate lower and upper bounds for Pi. He then found a formula for directly calculating the perimeter of inscribed and circumscribed polygons with 2*n sides only using the values previously calculated for polygons with n sides.

You now have a slightly simpler task, considering only inscribed polygons. You are given an int numSides, the number of sides of a regular polygon that is inscribed in a circle. Return a double, the approximated value for Pi when the perimeter of that polygon is used as an approximation for the perimeter of the circle.

[Image showing a circle with an 8-sided regular polygon inscribed]

Definition

Class:	Archimedes
Method:	approximatePi
Parameters:	int
Returns:	double
Method signature:	double approximatePi(int numSides)
(be sure your method is public)

Notes

-

Perimeter of a circle: 2 * PI * radius

-

Perimeter of a n-sided regular polygon: n * sidelength

-

Reminder how doubles are evaluated:

If your result is within 1e-9 of the expected result, your solution will be evaluated as correct.

If your result is between (1+1e-9) * expected and (1-1e-9) * expected, it will be evaluated as correct.

Constraints

-

numSides will be between 3 and 100000, inclusive.

Examples

0)

Returns: 2.598076211353316

1)

Returns: 3.0614674589207183

2)

Returns: 3.1415926362832276

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Yahtzee

Simple Math, Simple Search, Iteration

Used in:

SRM 146

Used as:

Division II Level One

Writer:

lbackstrom

Testers:

PabloGilberto , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1692

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4535&pm=1692

Problem Statement

This task is about the scoring in the first phase of the die-game Yahtzee, where five dice are used. The score is determined by the values on the upward die faces after a roll. The player gets to choose a value, and all dice that show the chosen value are considered active. The score is simply the sum of values on active dice.

Say, for instance, that a player ends up with the die faces showing 2, 2, 3, 5 and 4. Choosing the value two makes the dice showing 2 active and yields a score of 2 + 2 = 4, while choosing 5 makes the one die showing 5 active, yielding a score of 5.

Your method will take as input an int[] toss, where each element represents the upward face of a die, and return the maximum possible score with these values.

Definition

Class:	Yahtzee
Method:	maxPoints
Parameters:	int[]
Returns:	int
Method signature:	int maxPoints(int[] toss)
(be sure your method is public)

Constraints

-

toss will contain exactly 5 elements.

-

Each element of toss will be between 1 and 6, inclusive.

Examples

0)

{ 2, 2, 3, 5, 4 }

Returns: 5

The example from the text.

1)

{ 6, 4, 1, 1, 3 }

Returns: 6

Selecting 1 as active yields 1 + 1 = 2, selecting 3 yields 3, selecting 4 yields 4 and selecting 6 yields 6, which is the maximum number of points.

2)

{ 5, 3, 5, 3, 3 }

Returns: 10

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Sets

Math

Used in:

SRM 159

Used as:

Division II Level Two

Writer:

dimkadimon

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1685

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4600&pm=1685

Problem Statement

A set of numbers is a collection of numbers with no repeated elements. We can define the following set operations:

The UNION of two sets A and B is a set containing all the elements that are either in A or in B.

The INTERSECTION of two sets A and B is a set containing all the elements that are in both A and B.

The SYMMETRIC DIFFERENCE of two sets A and B is a set containing all the elements that are either in A or in B, but not containing elements that are in both A and B.

Given two int[]s representing sets A and B, and an operation applied on them, return a int[] representing the resulting set sorted in ascending order. If the result is an empty set then return an empty int[]. operation will be one of the following: "UNION", "INTERSECTION", "SYMMETRIC DIFFERENCE".

Definition

Class:	Sets
Method:	operate
Parameters:	int[], int[], String
Returns:	int[]
Method signature:	int[] operate(int[] A, int[] B, String operation)
(be sure your method is public)

Constraints

-

A will have between 0 and 50 elements inclusive.

-

B will have between 0 and 50 elements inclusive.

-

each element in A will be between -1000000 and 1000000 inclusive.

-

each element in B will be between -1000000 and 1000000 inclusive.

-

A will not have any repeated elements.

-

B will not have any repeated elements.

-

operation will be one of the following: "UNION", "INTERSECTION", "SYMMETRIC DIFFERENCE".

Examples

0)

{1,2,3,4}

{3,4,5,6}

"INTERSECTION"

Returns: { 3,  4 }

The only elements that are both in A and in B are 3 and 4.

1)

{1,2,3,4}

{3,4,5,6}

"UNION"

Returns: { 1,  2,  3,  4,  5,  6 }

Here we return all the elements that are either in A or in B.

2)

{432,756,123}

{534,76,1209}

"INTERSECTION"

Returns: { }

There are no common elements, so we must return an empty set.

3)

{6,5,7,4}

{7,6,4,10}

"SYMMETRIC DIFFERENCE"

Returns: { 5,  10 }

Elements 4, 6, 7 are in both sets, thus they cannot be in our answer. However we can include elements 5 and 10.

4)

{342,654,897,312,76,23,78}

{21,43,87,98,23,756,897,234,645,876,123}

"SYMMETRIC DIFFERENCE"

Returns: { 21,  43,  76,  78,  87,  98,  123,  234,  312,  342,  645,  654,  756,  876 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Bonuses

Simple Math, Simulation

Used in:

SRM 145

Used as:

Division I Level One

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1677

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4530&pm=1677

Problem Statement

You have a certain amount of money to give out as a bonus to employees. The trouble is, who do you pick to receive what bonus? You decide to assign a number of points to each employee, which corresponds to how much they helped the company in the last year. You are given an int[] points, where each element contains the points earned by the corresponding employee (i.e. points[0] is the number of points awarded to employee 0). Using this, you are to calculate the bonuses as follows:

- First, add up all the points, this is the pool of total points awarded.

- Each employee gets a percentage of the bonus money, equal to the percentage of the point pool that the employee got.

- Employees can only receive whole percentage amounts, so if an employee's cut of the bonus has a fractional percentage, truncate it.

- There may be some percentage of bonus left over (because of the fractional truncation). If n% of the bonus is left over, give the top n employees 1% of the bonus. There will be no more bonus left after this. If two or more employees with the same number of points qualify for this "extra" bonus, but not enough bonus is left to give them all an extra 1%, give it to the employees that come first in points.

The return value should be a int[], one element per employee in the order they were passed in. Each element should be the percent of the bonus that the employee gets.

Definition

Class:	Bonuses
Method:	getDivision
Parameters:	int[]
Returns:	int[]
Method signature:	int[] getDivision(int[] points)
(be sure your method is public)

Constraints

-

points will have between 1 and 50 elements, inclusive.

-

Each element of points will be between 1 and 500, inclusive.

Examples

0)

{1,2,3,4,5}

Returns: { 6,  13,  20,  27,  34 }

The total points in the point pool is 1+2+3+4+5 = 15.

Employee 1 gets 1/15 of the total pool, or 6.66667%, Employee 2 gets 13.33333%, Employee 3 gets 20% (exactly), Employee 4 gets 26.66667%, and Employee 5 gets 33.33333%. After truncating, the percentages look like:

{6,13,20,26,33}

Adding up all the fractional percentages, we see there is 2% in extra bonuses, which go to the top two scorers. These are the employees who received 4 and 5 points.

1)

{5,5,5,5,5,5}

Returns: { 17,  17,  17,  17,  16,  16 }

The pool of points is 30. Each employee got 1/6 of the total pool, which translates to 16.66667%. Truncating for all employees, we are left with 4% in extra bonuses. Because everyone got the same number of points, the extra 1% bonuses are assigned to the four that come first in the array.

2)

{485, 324, 263, 143, 470, 292, 304, 188, 100, 254, 296,
 255, 360, 231, 311, 275,  93, 463, 115, 366, 197, 470}

Returns: 
{ 8,  6,  4,  2,  8,  5,  5,  3,  1,  4,  5,  4,  6,  3,  5,  4,  1,  8,  1,  6,  3,  8 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ExerciseMachine

Math, String Parsing

Used in:

SRM 145

Used as:

Division II Level Two

Writer:

schveiguy

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1675

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4530&pm=1675

Problem Statement

You are writing firmware for an exercise machine. Each second, a routine in your firmware is called which decides whether it should display the percentage of the workout completed. The display does not have any ability to show decimal points, so the routine should only display a percentage if the second it is called results in a whole percentage of the total workout.

Given a String time representing how long the workout lasts, in the format "hours:minutes:seconds", return the number of times a percentage will be displayed by the routine. The machine should never display 0% or 100%.

Definition

Class:	ExerciseMachine
Method:	getPercentages
Parameters:	String
Returns:	int
Method signature:	int getPercentages(String time)
(be sure your method is public)

Constraints

- time will be a String formatted as "HH:MM:SS", HH = hours, MM = minutes, SS = seconds.

- The hours portion of time will be an integer with exactly two digits, with a value between 00 and 23, inclusive.

- The minutes portion of time will be an integer with exactly two digits, with a value between 00 and 59, inclusive.

- The seconds portion of time will be an integer with exactly two digits, with a value between 00 and 59, inclusive

- time will not be "00:00:00".

Examples

0)

"00:30:00"

Returns: 99

The standard 30 minute workout. Each one percent increment can be displayed every 18 seconds.

1)

"00:28:00"

Returns: 19

The 28 minute workout. The user completes 5 percent of the workout every 1 minute, 14 seconds.

2)

"23:59:59"

Returns: 0

This is the longest workout possible, given the constraints. No percentages are ever displayed on the screen.

3)

"00:14:10"

Returns: 49

4)

"00:19:16"

Returns: 3

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Lottery

Advanced Math

Used in:

SRM 144

Used as:

Division I Level Two

Writer:

LunaticFringe

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1659

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4515&pm=1659

Problem Statement

In most states, gamblers can choose from a wide variety of different lottery games. The rules of a lottery are defined by two integers (choices and blanks) and two boolean variables (sorted and unique). choices represents the highest valid number that you may use on your lottery ticket. (All integers between 1 and choices, inclusive, are valid and can appear on your ticket.) blanks represents the number of spots on your ticket where numbers can be written.

The sorted and unique variables indicate restrictions on the tickets you can create. If sorted is set to true, then the numbers on your ticket must be written in non-descending order. If sorted is set to false, then the numbers may be written in any order. Likewise, if unique is set to true, then each number you write on your ticket must be distinct. If unique is set to false, then repeats are allowed.

Here are some example lottery tickets, where choices = 15 and blanks = 4:

{3, 7, 12, 14} -- this ticket is unconditionally valid.
{13, 4, 1, 9} -- because the numbers are not in nondescending order, this ticket is valid only if sorted = false.
{8, 8, 8, 15} -- because there are repeated numbers, this ticket is valid only if unique = false.
{11, 6, 2, 6} -- this ticket is valid only if sorted = false and unique = false.

Given a list of lotteries and their corresponding rules, return a list of lottery names sorted by how easy they are to win. The probability that you will win a lottery is equal to (1 / (number of valid lottery tickets for that game)). The easiest lottery to win should appear at the front of the list. Ties should be broken alphabetically (see example 1).

Definition

Class:	Lottery
Method:	sortByOdds
Parameters:	String[]
Returns:	String[]
Method signature:	String[] sortByOdds(String[] rules)
(be sure your method is public)

Constraints

- rules will contain between 0 and 50 elements, inclusive.

- Each element of rules will contain between 11 and 50 characters, inclusive.

- Each element of rules will be in the format "<NAME>:_<CHOICES>_<BLANKS>_<SORTED>_<UNIQUE>" (quotes for clarity). The underscore character represents exactly one space. The string will have no leading or trailing spaces.

- <NAME> will contain between 1 and 40 characters, inclusive, and will consist of only uppercase letters ('A'-'Z') and spaces (' '), with no leading or trailing spaces.

- <CHOICES> will be an integer between 10 and 100, inclusive, with no leading zeroes.

- <BLANKS> will be an integer between 1 and 8, inclusive, with no leading zeroes.

- <SORTED> will be either 'T' (true) or 'F' (false).

- <UNIQUE> will be either 'T' (true) or 'F' (false).

- No two elements in rules will have the same name.

Examples

0)

{"PICK ANY TWO: 10 2 F F"
,"PICK TWO IN ORDER: 10 2 T F"
,"PICK TWO DIFFERENT: 10 2 F T"
,"PICK TWO LIMITED: 10 2 T T"}

Returns: 
{ "PICK TWO LIMITED",
 "PICK TWO IN ORDER",
 "PICK TWO DIFFERENT",
 "PICK ANY TWO" }

The "PICK ANY TWO" game lets either blank be a number from 1 to 10. Therefore, there are 10 * 10 = 100 possible tickets, and your odds of winning are 1/100.

The "PICK TWO IN ORDER" game means that the first number cannot be greater than the second number. This eliminates 45 possible tickets, leaving us with 55 valid ones. The odds of winning are 1/55.

The "PICK TWO DIFFERENT" game only disallows tickets where the first and second numbers are the same. There are 10 such tickets, leaving the odds of winning at 1/90.

Finally, the "PICK TWO LIMITED" game disallows an additional 10 tickets from the 45 disallowed in "PICK TWO IN ORDER". The odds of winning this game are 1/45.

1)

{"INDIGO: 93 8 T F",
 "ORANGE: 29 8 F T",
 "VIOLET: 76 6 F F",
 "BLUE: 100 8 T T",
 "RED: 99 8 T T",
 "GREEN: 78 6 F T",
 "YELLOW: 75 6 F F"}

Returns: { "RED",  "ORANGE",  "YELLOW",  "GREEN",  "BLUE",  "INDIGO",  "VIOLET" }

Note that INDIGO and BLUE both have the exact same odds (1/186087894300). BLUE is listed first because it comes before INDIGO alphabetically.

2)

{}

Returns: { }

Empty case

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

HardwareOptimize

Dynamic Programming, Math, String Manipulation, String Parsing

Used in:

TCCC '03 Semifinals 1

Used as:

Division I Level Three

Writer:

brett1479

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1640

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4491&pm=1640

Problem Statement

When you are compiling code to a target architecture there are hardware specific optimizations that can be made. In this problem we will be taking a string of source text and compiling it to some variable architecture. The source text will be given as a String expression. expression should be a well-parenthesized mathematical formula that conforms to the following grammar:

<EXPR> ::= '('<EXPR><OP><EXPR>')' | <INT>
<OP> ::= '+' | '-' | '/' | '*'
<INT> ::= a positive integer with no leading 0s between 1 and 100, inclusive

For example, 9, (1+(2+((3+2)-2))), and ((1*2)/2) conform to the grammar while (1+2+3), (0+2), and ((1+2)) do not.

If expression does not conform to the above grammar your method should return -2. If it does conform, you will then have to determine which instructions should be used to implement the expression. The machine capabilities will be given in a String[] instructions. Each element will conform to the following grammar:

<INST> ::= <COST>':'<VAREXPR>
<VAREXPR> ::= '('<VAREXPR><OP><VAREXPR>')' | 'X'
<OP> ::= '+' | '-' | '/' | '*'
<COST> ::= a positive integer with no leading 0s between 1 and 100, inclusive

An example element could be 10:(X+X) meaning that there is an instruction that will add 2 operands together at a cost of 10. Another example could be 12:(X*(X-X)) meaning that it will cost 12 to multiply 1 operand by the difference of two others. Each element of instruction will thus represent the possible operations the underlying hardware can perform along with their cost. Since instructions of the form "COST:X" are meaningless they will not be allowed as input. If the given expression cannot be computed on the given hardware your method should return -1. Otherwise it should return the minimum cost required to compute all of the operations in the expression. For example:

expression = "((1+2)*(3+(4-2)))"
instructions = {"5:(X+X)",
                "5:(X-X)",
                "6:(X*X)",
                "7:((X+X)*X)"}

Using instruction 0 on the (1+2) portion of the expression and instruction 1 on the (4-2) portion of the expression will produce the intermediate expression (3*(3+2)). Then applying expression 0 to the (3+2) portion we get the intermediate expression (3*5). Finally applying instruction 2 we get an expression that no longer contains any operations and is thus complete. The total cost of this method is 5+5+5+6 = 21. Alternatively we could have used instruction 1, then 0, and finally 3 for a smaller cost of 17. Your method should thus return 17, the minimum possible cost. The cost of applying no operations is 0. For example:

expression = "84"
instructions = {"10:(X+X)"}

Since the expression only consists of a number, there are no operations to be processed, so the cost is simply 0.

Note that you are not allowed to apply any simplifications to the expression (i.e. no associativity, commutativity, distributivity, or identity laws). This means (3+(4*5)) cannot be processed by an instruction like 4:((X*X)+X).

Definition

Class:	HardwareOptimize
Method:	bestCost
Parameters:	String, String[]
Returns:	int
Method signature:	int bestCost(String expression, String[] instructions)
(be sure your method is public)

Constraints

-

expression will contain between 1 and 50 characters inclusive

-

expression will only contain characters from the string (quotes for clarity) "0123456789+*/-()"

-

instructions will contain between 0 and 50 elements inclusive

-

Each element of instructions will contain between 7 and 50 characters inclusive

-

Each element of instructions will only contain characters from the string (quotes for clarity) "0123456789:()X+*/-"

-

Each element of instructions will adhere to the format stated above

-

There will be no elements of instructions of the form "COST:X"

Examples

0)

"((1+2)*(3+(4-2)))"

{"5:(X+X)",
 "5:(X-X)",
 "6:(X*X)",
 "7:((X+X)*X)"}

Returns: 17

1)

"(1+2+3)"

{}

Returns: -2

2)

"((0+0)*(0+0))"

{"10:(X+X)"}

Returns: -2

3)

"(((1+1)+((1+1)+(1+1)))+(((1+1)+(1+1))+((1+1)+1)))"

{"10:(X+X)","19:(X+(X+X))"}

Returns: 117

4)

"23"

{}

Returns: 0

5)

"(1+2)"

{}

Returns: -1

6)

"(1/(1-1))"

{"1:(X-X)","1:(X/X)"}

Returns: 2

7)

"((1*1)+1)"

{"10:(X*X)", "10:(X+X)", "5:(X+(X*X))"}

Returns: 20

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

ContinuedFractions

Advanced Math

Used in:

SRM 165

Used as:

Division I Level Two

Writer:

vorthys

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1630

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4630&pm=1630

Problem Statement

Any irrational number greater than 1 can be written as

    Q[0] +             1
           ------------------------
           Q[1] +         1
                  -----------------
                  Q[2] +      1
                         ----------
                         Q[3] +  1
                                ---
                                ...

for some infinite sequence Q[0],Q[1],Q[2],Q[3],... where each Q[i] is a positive integer. This method of writing a number is called a continued fraction, and each Q[i] is called a partial quotient. A remarkable fact from number theory is that, whenever the square root of a non-square positive integer is written in this form, the sequence of partial quotients is periodic. In other words, there exists some number K such that Q[J+K] = Q[J] for all J > 0. Notice that the repeating pattern begins at Q[1]; the initial partial quotient, Q[0], is not involved in the repetition.

We will represent such a periodic continued fraction as the finite sequence {Q[0],Q[1],...,Q[K]}, where K is the size of the shortest repeating pattern. For example, the square root of 2 has partial quotients 1,2,2,2,... and would be written as {1,2}. Similarly, the square root of 8 has partial quotients 2,1,4,1,4,... and would be written as {2,1,4}. Your task is to take a non-square positive integer n, and calculate its representation as a periodic continued fraction. Several sample calculations will be presented from which you should be able to generalize an algorithm. Although you are not required to follow the same algorithm as the sample calculations, it is highly suggested that you do so. Note that, for the purposes of this problem, the periodic continued fraction will always contain fewer than 100 elements.

Here is a sample calculation showing that the square root of 2 is {1,2}:

  Step 0: Calculate Q[0] from sqrt(2).

      sqrt(2) = 1 + sqrt(2)-1
                    ---------
                        1

      Q[0] is 1.  The remainder is (sqrt(2)-1)/1.

  Step 1: Calculate Q[1] from (sqrt(2)-1)/1.

      sqrt(2)-1         1                    1                  1               1
      --------- = ------------- = --------------------- = ------------- = -------------
          1             1             1       sqrt(2)+1     sqrt(2)+1     2 + sqrt(2)-1
                    ---------     --------- * ---------     ---------         ---------
                    sqrt(2)-1     sqrt(2)-1   sqrt(2)+1          1                1

      Q[1] is 2.  The remainder is (sqrt(2)-1)/1.

  Step 2: Calculate Q[2] from (sqrt(2)-1)/1.  (Same as Step 1!)

Substituting the result of Step 1 into the result of Step 0, we get

  sqrt(2) = 1 +    1
                -------
                2 + ...

and at this point the pattern repeats, so the square root of 2 is {1,2}.

Notice that, at every step, the partial quotient is chosen to force the remainder between 0 and 1 (exclusive), and that there is only one way to do this. Also notice that, in Step 1, we made essential use of the identity (A-B)*(A+B) = A*A - B*B.

Here is a more elaborate example, showing that the square root of 41 is {6,2,2,12}:

Step 0: Calculate Q[0] from sqrt(41).

    sqrt(41) = 6 + sqrt(41)-6
                   ----------
                        1

    Q[0] is 6.  The remainder is (sqrt(41)-6)/1.

Step 1: Calculate Q[1] from (sqrt(41)-6)/1.

    sqrt(41)-6          1                    1                     1                1
    ---------- = -------------- = ----------------------- = -------------- = --------------
         1              1              1       sqrt(41)+6     sqrt(41)+6     2 + sqrt(41)-4
                   ----------     ---------- * ----------     ----------         ----------
                   sqrt(41)-6     sqrt(41)-6   sqrt(41)+6          5                  5

    Q[1] is 2.  The remainder is (sqrt(41)-4)/5.

Step 2: Calculate Q[2] from (sqrt(41)-4)/5.

    sqrt(41)-4          1                    1                     1                1
    ---------- = -------------- = ----------------------- = -------------- = --------------
         5              5              5       sqrt(41)+4     sqrt(41)+4     2 + sqrt(41)-6
                   ----------     ---------- * ----------     ----------         ----------
                   sqrt(41)-4     sqrt(41)-4   sqrt(41)+4          5                  5

    Q[2] is 2.  The remainder is (sqrt(41)-6)/5.

Step 3: Calculate Q[3] from (sqrt(41)-6)/5.

    sqrt(41)-6          1                    1                     1                1
    ---------- = -------------- = ----------------------- = -------------- = ---------------
         5              5              5       sqrt(41)+6     sqrt(41)+6     12 + sqrt(41)-6
                   ----------     ---------- * ----------     ----------          ----------
                   sqrt(41)-6     sqrt(41)-6   sqrt(41)+6          1                   1

    Q[3] is 12.  The remainder is (sqrt(41)-6)/1.

Step 4: Calculate Q[4] from (sqrt(41)-6)/1.  (Same as Step 1!)

Substituting the result of each step into the result of the previous step, we get

  sqrt(41) = 6 +       1
                ----------------
                2 +      1
                    ------------
                    2 +    1
                        --------
                        12 + ...

and at this point the pattern repeats, so the square root of 41 is {6,2,2,12}.

Notice that the remainders are always of the form (sqrt(n)-d)/m, for some integers d and m. It might sometimes appear that the remainder has the form c*(sqrt(n)-d)/m, but it will always be possible to eliminate the c.

Definition

Class:	ContinuedFractions
Method:	squareRoot
Parameters:	int
Returns:	int[]
Method signature:	int[] squareRoot(int n)
(be sure your method is public)

Notes

- Because we have restricted each partial quotient to be a positive integer, each square root has a unique representation as a periodic continued fraction.

Constraints

- n is between 2 and 1000, inclusive.

- n is not a square number. For example, n is not 4, 9, or 16.

Examples

0)

Returns: { 1,  2 }

The first example above.

1)

Returns: { 6,  2,  2,  12 }

The second example above.

2)

Returns: { 7,  1,  14 }

3)

Returns: { 12,  1,  1,  3,  12,  3,  1,  1,  24 }

4)

Returns: { 22,  1,  1,  1,  2,  6,  11,  6,  2,  1,  1,  1,  44 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TeamPhoto

Advanced Math, Sorting

Used in:

SRM 167

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1614

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4640&pm=1614

Problem Statement

It's time to line up for the team photo. We want all the team members, plus the head coach and the two assistant coaches to be in the photo. We want the head coach in the middle and the two assistant coaches on the two ends. But we don't want to have much disparity in heights between adjacent people.

Let's line up to minimize the sum of the absolute height differences of adjacent people. If there is an even number of people, the coach can go in either center position. Create a class TeamPhoto that contains method minDiff that takes int[] height, the heights of all the people, and returns the minimum possible sum of adjacent absolute height differences.

height lists the coach first, then the two assistant coaches, then the team members.

Definition

Class:	TeamPhoto
Method:	minDiff
Parameters:	int[]
Returns:	int
Method signature:	int minDiff(int[] height)
(be sure your method is public)

Constraints

-

height has between 5 and 50 elements inclusive

-

each element of height is between 10 and 100 inclusive

Examples

0)

{80,82,81,50,90,65}

Returns: 79

The coach has a height of 80 and must be in one of the two middle positions, with the assistant coaches (82 and 81) on the two ends. The best lineup is 81,65,50,80,90,82 with the minDiff calculated as |81-65| + |65-50| + |50-80| + |80-90| + |90-82| = 79. There are other ways to achieve this minDiff.

1)

{70,82,91,50,50,50,50,50,50}

Returns: 113

Line up in the order 82,50,50,50,70,50,50,50,91

2)

{13, 17, 11, 12, 10}

Returns: 10

One optimal way to line up is 17, 12, 13, 10, 11 making the sum of the absolute differences 5 + 1 + 3 + 1 = 10

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TickTick

Math, Search

Used in:

SRM 177

Used as:

Division I Level One

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1609

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4690&pm=1609

Problem Statement

Our computer clock is not continuous. It "ticks" every millisecond and keeps track of how many ticks have occurred since the beginning of the "epoch" (Jan 1, 1970). The clocktime does not change between ticks.

Time is continuous, and events (such as interrupts from hardware devices and the starting of a program) can happen anytime. We have a program that experiences a sequence of events. At each event in our program, our logic gets the current clocktime and compares it with the clocktime stored from the previous event. It outputs either 'D' or 'S' indicating whether the current clocktime is Different or the Same as the previous event's clocktime. (The first event after the program starts generates the first 'S' or 'D' based on comparison with the clocktime at the start of the program.)

Because the first tick during our program can occur anytime within one millisecond after the start of the program, the string of 'D's and 'S's output from our program cannot be predicted, even given the exact timing of the program. Create a class TickTick that contains a method count that is given event, a String[] of the times of events relative to the start of the program, and returns the number of different output sequences that might be generated. The event times are given in milliseconds elapsed since the start of the program, formatted to contain digits and exactly one decimal point.

Time is continuous, so exact coincidences do not occur (or occur with probability 0). You should not consider the possibility that a tick occurs at exactly the same time as an event or at the exact start of the program. The constraints on event guarantee that two different events can never be exactly an integral number of milliseconds apart.

Definition

Class:	TickTick
Method:	count
Parameters:	String[]
Returns:	int
Method signature:	int count(String[] events)
(be sure your method is public)

Constraints

-

events has between 1 and 50 elements inclusive

-

each element of events has length between 2 and 8, and contains exactly one decimal point '.'. All the other characters are digits '0'-'9'

-

no element of events has a value equal to an integer

-

no two elements of events have values that differ by an integer

-

the elements of events have values that are strictly increasing

Examples

0)

{".222","00.223","1.221","4.220"}

Returns: 4

If the clock's first tick occurs approximately .100 milliseconds after the start of the program, then the clocktime at time .222 will be Different from the clocktime at the start. The clocktime at .223 will be the same as at .222, the clocktime at 1.221 will be different from the clocktime at .223 since a tick occurs at 1.100. The clocktime at 4.220 will always be different from the clocktime at 1.221. So in this case, the program generates DSDD. Similarly,

   if the clock's first tick is at .2215, DSSD
   if the clock's first tick is at .2225, SDSD
   if the clock's first tick is at .2235, SSDD

These are the only possible sequences that can be generated.

1)

{"4.220112","4.221","4.222","4.223"}

Returns: 4

DSSS, DSSD, DSDS, DDSS

2)

{"123456.1","123456.7"}

Returns: 2

If the first tick occurs at .05 after the program starts, the output would be DS while if it occurs .5 after the program starts, then the output would be DD. These are the only possible results.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Pricing

Brute Force, Simple Math

Used in:

SRM 149

Used as:

Division II Level Three

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1600

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4550&pm=1600

Problem Statement

Market differentiation in its simplest form is a system of charging different prices to different customers for the same product. To maximize the total sales revenue, we would like to charge each customer individually, charging the highest price that that customer would be willing to pay. Usually we have to divide the customers into a few groups, and charge the same price to everyone in a group (e.g. business class, economy class, etc.).

We have a list of all the potential customers for our product and the most that each customer is willing to pay. We have decided to differentiate them into four or fewer (non-overlapping) groups. Everyone within each group will be offered the same price. Our goal is to choose the groups and prices optimally to maximize our total sales revenue.

Create a class Pricing that contains a method maxSales that takes a int[] price containing the highest price that each potential customer is willing to pay, and returns the maximum sales revenue we can generate by differentiating our customers into four or fewer groups.

Definition

Class:	Pricing
Method:	maxSales
Parameters:	int[]
Returns:	int
Method signature:	int maxSales(int[] price)
(be sure your method is public)

Constraints

-

price must contain between 1 and 50 elements inclusive

-

each element of price must be between 0 and 1000 inclusive

Examples

0)

{9,1,5,5,5,5,4,8,80}

Returns: 120

Charge 80 to the one customer willing to pay 80.
Charge 8 to the 2 customers willing to pay 8 or 9.
Charge 5 to the 4 customers willing to pay 5.
Charge 4 to the one customer willing to pay 4.

Total sales revenue = 1*80 + 2*8 + 4*5 + 1*4. (We can put the customer who is willing to pay 1 into any of these groups since he will not buy anything at these prices.)

1)

{17,50,2}

Returns: 69

We use just three groups, each containing one customer. We charge each customer the most she is willing to pay. Total sales revenue = 1*17 + 1*50 + 1*2

2)

{130,110,90,13,6,5,4,3,0}

Returns: 346

Charge each of the 4 customers willing to pay between 4 and 13 a price of 4, thereby getting a total of 16 from them. Then charge the most we can to each of the three customers who are willing to pay a lot. 4*4 + 90 + 110 + 130 = 346

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RectangularGrid

Math

Used in:

SRM 146

Used as:

Division I Level One , Division II Level Two

Writer:

dimkadimon

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1589

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4535&pm=1589

Problem Statement

Given the width and height of a rectangular grid, return the total number of rectangles (NOT counting squares) that can be found on this grid.

For example, width = 3, height = 3 (see diagram below):

 __ __ __
|__|__|__|
|__|__|__|
|__|__|__|

In this grid, there are 4 2x3 rectangles, 6 1x3 rectangles and 12 1x2 rectangles. Thus there is a total of 4 + 6 + 12 = 22 rectangles. Note we don't count 1x1, 2x2 and 3x3 rectangles because they are squares.

Definition

Class:	RectangularGrid
Method:	countRectangles
Parameters:	int, int
Returns:	long
Method signature:	long countRectangles(int width, int height)
(be sure your method is public)

Notes

-

rectangles with equals sides (squares) should not be counted.

Constraints

-

width and height will be between 1 and 1000 inclusive.

Examples

0)

Returns: 22

See above

1)

Returns: 31

 __ __ __ __ __
|__|__|__|__|__|
|__|__|__|__|__|

In this grid, there is one 2x5 rectangle, 2 2x4 rectangles, 2 1x5 rectangles, 3 2x3 rectangles, 4 1x4 rectangles, 6 1x3 rectangles and 13 1x2 rectangles. Thus there is a total of 1 + 2 + 2 + 3 + 4 + 6 + 13 = 31 rectangles.

2)

Returns: 2640

3)

Returns: 0

4)

Returns: 81508708664

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GreedyChange

Advanced Math, Dynamic Programming

Used in:

TCCC '03 Round 3

Used as:

Division I Level Two

Writer:

lars2520

Testers:

brett1479 , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1579

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4474&pm=1579

Problem Statement

Many monetary systems have the nice property that, when giving change, a greedy algorithm will always produce the fewest number of coins possible. In other words, if you are trying to produce a certain amount of change, then something like the following algorithm will produce the fewest coins possible:

number of coins = 0;
while(amount>0){
	find the largest coin, c, that is less than or equal to amount;
	subtract the value of c from amount and increment the number of coins;
}

For example, the American monetary system with coins valued at 1, 5, 10, and 25 cents has this property. However, it is not difficult to construct values of coins that do not have this property. If the values of your coins are 1, 3 and 4, then you can make 6 with two 3's. The algorithm above, on the other hand, will use 3 coins - a 4 and two 1's.

Your task is to write a class GreedyChange, with a method smallest that takes a int[], denominations, representing the values of the various coins in some monetary system. You should return the smallest amount of money for which the greedy algorithm does not produce the fewest coins possible. If the greedy algorithm always produces the fewest coins possible, return -1. To guarantee that the greedy algorithm always works (terminates), there will always be a coin worth 1.

Definition

Class:	GreedyChange
Method:	smallest
Parameters:	int[]
Returns:	int
Method signature:	int smallest(int[] denominations)
(be sure your method is public)

Constraints

-

denominations will contain between 1 and 50 elements, inclusive.

-

Each element of denominations will be between 1 and 500,000, inclusive.

-

At least one of the elements of denominations will be 1.

Examples

0)

{1,25,10,5}

Returns: -1

In this system, the greedy algorithm always produces an optimal result.

1)

{1,3,4}

Returns: 6

If we need to make 6, the greedy algorithm does so as 4 + 1 + 1. However, the optimal solution is 3 + 3.

2)

{1,10,10,20,25}

Returns: 30

Note that elements may be repeated.

3)

{1,15,25}

Returns: 30

4)

{1,2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50,
52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,84,86,88,90,92,94,96,500000}

Returns: -1

5)

{500000,499999,1}

Returns: 999998

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Optimizer

Math, String Manipulation, String Parsing

Used in:

TCCC '03 Round 4

Used as:

Division I Level Three

Writer:

lars2520

Testers:

brett1479 , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1574

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4482&pm=1574

Problem Statement

Compilers often optimize source code to make programs run faster. One common optimization is to evaluate constant expressions while compiling. For example, when compiling the expression "a * 4 * 3", you can first reduce it to "a * 12" before compiling it to machine code. You are to write a class Optimizer with a method reduce that takes a String, expression, and determines the minimum cost of evaluating the expression after it has been fully reduced. For this problem, we will only be considering add and multiply operations on a machine that takes 1 cycle to perform an add operation, and 10 cycles to perform a multiply operation. You should reduce the expression according to the following specifications:

- Multiplication and addition are both commutative, e.g. "a * b" = "b * a" and "a + b" = "b + a".
- Multiplication and addition are both associative, e.g. "(a * b) * c" = "a * (b * c)" and "(a + b) + c" = "a + (b + c)".
- We have no guarantees that the values of the variables will stay the same throughout the computations, so an expression such as "3 * a + 4 * a" can not be reduced to "7 * a". In other words, you should treat each occurrence of a variable as if it was a unique variable.
- "<expression> + 0" is always "<expression>", and "<expression> * 1" is always "<expression>". Similarly, "<expression> * 0" is always 0.
- Any reductions that you make must follow directly from commutativity, associativity, the above rule, or from evaluating part of an expression that does not contain any variables. Thus, you may not reduce "a * 2" into "a + a" or vice versa, but you may reduce "(3 + 4) * a" to "7 * a" because you are evaluating a part of the expression that does not contain any variables.

Your method should reduce the expression as much as possible, following the above rules, and return the number of cycles required to evaluate the reduced expression, given that each addition takes 1 cycle, and each multiplication takes 10 cycles. When performing reductions, you must follow standard operator precedence rules: terms in parentheses are evaluated first, then multiplication, then addition.

The input string will be a well-formed <expression> conforming to the following grammar:

<expression> ::= <expression><op><expression> |
                       <sp><expression><sp> | 
                       (<expression>) | <var> | <num>
<var> ::= a sequence of one or more lowercase letters ('a'-'z')
<num> ::= a sequence of one or more digits ('0'-'9')
<op> ::= '*' | '+'
<sp> ::= zero or more spaces (' ')

Definition

Class:	Optimizer
Method:	reduce
Parameters:	String
Returns:	int
Method signature:	int reduce(String expression)
(be sure your method is public)

Notes

-

Be sure to only apply the reductions mentioned in the problem statement. In particular, note that we are not applying the distrubutive property of addition and multiplication. See example 7.

-

A common way to represent the structure of the expression is to build a tree, where each internal node represents an operation ('+' or '*') and each leaf represents a variable or number.

Constraints

-

expression will contain between 1 and 50 characters, inclusive.

-

expression will conform to the grammar defined above.

-

Each <num> will represent an integer between 0 and 2^32-1, inclusive.

-

The numbers in fully reduced expressions will not exceed 2^32-1.

Examples

0)

"  alpha*beta+5*006  "

Returns: 11

This can be reduced to "alpha * beta + 30", which has one multiplication and one addition.

1)

"a * b * 00 + 1 * 5"

Returns: 0

This can simply be reduced to "5" which requires no evaluation.

2)

"dx + a * b * 0 + 1 * c"

Returns: 1

3)

"5 * (3 + 4 + c) + (a + c) * (c + d)"

Returns: 24

This can be reduced to "5 * (7 + c) + (a + c) * (c + d)" which has 4 additions and 2 multiplications. Note that we can not reduce "5 * (7 + c)" to "35 + 5 * c" because that reduction is a property of distributivity, and is not one of the allowed reductions.

4)

"9 * ((4 + 4)) * (7) * (3 + 1) + 504"

Returns: 0

There are no variables here, so the compiler can evaluate the whole expression and reduce it to "2520"

5)

"((((aa))))"

Returns: 0

6)

"(1 + 0 * a) * c + (0 + 0 * b) * d"

Returns: 0

7)

"5 * d + 5 * b"

Returns: 21

Remember that we are not applying the distributive property, so we cannot reduce this to "5 * (d + b)".

8)

"(a*5)*4+((a+4)+5)"

Returns: 12

Note that we can first change this to "a*(5*4)+(a+(4+5))" and then to "a*20+a+9".

9)

"(a*5)*(b*6)"

Returns: 20

10)

"(1)+0+1*(w+6)*1"

Returns: 1

We can reduce this to "w + 7"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

InterestingDigits

Math

Used in:

SRM 150

Used as:

Division I Level One , Division II Level Two

Writer:

vorthys

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1523

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4555&pm=1523

Problem Statement

The digits 3 and 9 share an interesting property. If you take any multiple of 3 and sum its digits, you get another multiple of 3. For example, 118*3 = 354 and 3+5+4 = 12, which is a multiple of 3. Similarly, if you take any multiple of 9 and sum its digits, you get another multiple of 9. For example, 75*9 = 675 and 6+7+5 = 18, which is a multiple of 9. Call any digit for which this property holds interesting, except for 0 and 1, for which the property holds trivially.

A digit that is interesting in one base is not necessarily interesting in another base. For example, 3 is interesting in base 10 but uninteresting in base 5. Given an int base, your task is to return all the interesting digits for that base in increasing order. To determine whether a particular digit is interesting or not, you need not consider all multiples of the digit. You can be certain that, if the property holds for all multiples of the digit with fewer than four digits, then it also holds for multiples with more digits. For example, in base 10, you would not need to consider any multiples greater than 999.

Definition

Class:	InterestingDigits
Method:	digits
Parameters:	int
Returns:	int[]
Method signature:	int[] digits(int base)
(be sure your method is public)

Notes

-

When base is greater than 10, digits may have a numeric value greater than 9. Because integers are displayed in base 10 by default, do not be alarmed when such digits appear on your screen as more than one decimal digit. For example, one of the interesting digits in base 16 is 15.

Constraints

-

base is between 3 and 30, inclusive.

Examples

0)

Returns: { 3,  9 }

All other candidate digits fail for base=10. For example, 2 and 5 both fail on 100, for which 1+0+0=1. Similarly, 4 and 8 both fail on 216, for which 2+1+6=9, and 6 and 7 both fail for 126, for which 1+2+6=9.

1)

Returns: { 2 }

2)

Returns: { 2,  4,  8 }

3)

Returns: { 5,  25 }

4)

Returns: { 29 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Dragons

Math, Simulation

Used in:

SRM 147

Used as:

Division I Level Two

Writer:

axchma

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1520

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4540&pm=1520

Problem Statement

There is a small cube planet somewhere. On each side of the cube there lives a four-armed dragon. It is time for dinner now. Each dragon sits in front of his bowl with food.

During each round, the following happens: Each dragon is trying to steal food from his neighbors (living on four neighboring sides of the cube). He spreads his four arms there (each arm goes to each separate neighbor). As other dragons do the same, four hands meet in each bowl of food. Four hands fight for a while and each takes one quarter of the food in this bowl to its own bowl. Hence, each round the food distribution changes.

Given the initial amount of food in each bowl and the number of rounds, return the amount of food the dragons' boss Snaug will have after these rounds.

In more detail:

The initial amount of food will be given in the following order: front, back, up, down, left, right. The dragons' boss Snaug lives on the "up" side of the cube. If the answer is an integer, return this integer. If the answer is a fraction, return the answer in the format X/Y, where X and Y are integers without common factors. Extra leading zeroes shouldn't be present in your answer.

Example.

Suppose that the initial distribution of food is the following: 0, 0, 4, 0, 0, 0. That is Snaug has 4 and everybody else has 0 amount of food in their bowls. After the first round the distribution of food will be the following: 1, 1, 0, 0, 1, 1, that is every neighbor of Snaug steals from him one quarter of his food. After the second round the distribution of food will be the following: 1/2, 1/2, 1, 1, 1/2, 1/2.

Definition

Class:	Dragons
Method:	snaug
Parameters:	int[], int
Returns:	String
Method signature:	String snaug(int[] initialFood, int rounds)
(be sure your method is public)

Constraints

-

initialFood has exactly 6 elements

-

each element of initialFood is between 0 and 1,000 inclusive

-

rounds is between 0 and 45 inclusive

Examples

0)

{0, 0, 4, 0, 0, 0}

Returns: "1"

See the explanation above

1)

{0, 0, 4, 0, 0, 0}

Returns: "1/2"

2)

{1000, 1000, 1000, 1000, 1000, 1000}

Returns: "1000"

When everybody has the same amount of food, they continue to have the same amount of food after each round

3)

{1, 2, 3, 4, 5, 6}

Returns: "7/2"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BinaryCardinality

Simple Math, Sorting

Used in:

SRM 166

Used as:

Division I Level One , Division II Level Two

Writer:

dimkadimon

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1519

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4635&pm=1519

Problem Statement

The cardinality of a binary number is given as the total number of "ones" it contains. For example, the cardinality of binary 10100 (decimal 20) is 2, because there are 2 "ones". The cardinality of binary 11110 (decimal 30) is 4, because there are 4 "ones".

Given a int[] of decimal numbers arrange them in ascending order of binary cardinality and return this arranged int[]. If two numbers have the same binary cardinality, then the smaller number must come first in the arranged int[].

Definition

Class:	BinaryCardinality
Method:	arrange
Parameters:	int[]
Returns:	int[]
Method signature:	int[] arrange(int[] numbers)
(be sure your method is public)

Constraints

-

numbers will have between 1 and 50 elements inclusive.

-

each element of numbers will be between 0 and 1000000 inclusive.

Examples

0)

{4}

Returns: { 4 }

There is only one element in the array, so it must be returned.

1)

{31,15,7,3,2}

Returns: { 2,  3,  7,  15,  31 }

We start by converting the above set of decimals into binary numbers. We get the following array: {11111, 1111, 111, 11, 10}. Now we can calculate the cardinality of each number: {5, 4, 3, 2, 1}. So 2 has the lowest binary cardinality, followed by 3, 7, 15 and finally 31.

2)

{10,9,8,7,6,5,4,3,2,1}

Returns: { 1,  2,  4,  8,  3,  5,  6,  9,  10,  7 }

The cardinality array is {2, 2, 1, 3, 2, 2, 1, 2, 1, 1}. Note that although 10 and 3 have the same cardinality of 2, 3 must come earlier because it is smaller in value.

3)

{811385,340578,980086,545001,774872,855585,13848,863414,419523,190151,784903,127461}

Returns: 
{ 13848,  340578,  545001,  855585,  419523,  811385,  127461,  190151,  774872,  863414,  784903,  980086 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FryingHamburgers

Math

Used in:

SRM 159

Used as:

Division I Level One

Writer:

dimkadimon

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1517

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4600&pm=1517

Problem Statement

In order to cook hamburgers, a chef must fry them 5 minutes on each side. However, the two 5 minute intervals do not have to happen consecutively.

panSize indicates how many hamburgers can fit into the given pan, while hamburgers represents the number of hamburgers that need to be fried. Given panSize and hamburgers return the minimum amount of time (in minutes) required to fry all the hamburgers.

Definition

Class:	FryingHamburgers
Method:	howLong
Parameters:	int, int
Returns:	int
Method signature:	int howLong(int panSize, int hamburgers)
(be sure your method is public)

Constraints

-

panSize is between 1 and 1000 inclusive.

-

hamburgers is between 0 and 1000 inclusive.

Examples

0)

Returns: 15

We will assume that the three hamburgers given are A, B and C. The chef could fry A and B on one side, taking up 5 minutes. Then remove B and fry A on its second side together with C on its first side. After 5 minutes, remove A and fry B and C on their second sides for another 5 minutes. The total time used is 15 minutes.

1)

Returns: 15

We will assume that the four hamburgers given are A, B, C and D. The chef could fry A, B and C on one side, taking up 5 minutes. Then remove C and fry A and B on their second side together with D on its first side. So after a total of 10 minutes A and B are completely fried, while C and D are fried on one side only. Finally, the chef fries C and D on their second side, taking another 5 minutes. The total time used is 15 minutes.

2)

Returns: 10

3)

Returns: 0

There are no hamburgers, so we do not have to fry anything.

4)

Returns: 35

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

GoldenChain

Advanced Math

Used in:

SRM 147

Used as:

Division II Level Three

Writer:

axchma

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1355

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4540&pm=1355

Problem Statement

Background

I remember a chain problem from my childhood. Suppose you have four sections of a golden chain. Each consists of three links joined together in a line. You would like to connect all four sections into a necklace. The obvious solution is to cut the last link of each section and use it to connect the first section to the second one, then the second to the third, then the third to the fourth, then the fourth to the first one. If you want to minimize the number of cuts, you can do better. You can cut one of the three link sections into its individual links. Using the three loose links you can join the three remaining sections together.

Your task is, given the lengths of the sections, to return the minimum number of cuts to make one big circular necklace out of all of them.

Definition

Class:	GoldenChain
Method:	minCuts
Parameters:	int[]
Returns:	int
Method signature:	int minCuts(int[] sections)
(be sure your method is public)

Constraints

-

sections has between 1 and 50 elements inclusive

-

each element of sections is between 1 and 2,147,483,647 inclusive

-

the sum of all elements of sections is between 3 and 2,147,483,647 inclusive

Examples

0)

{3,3,3,3}

Returns: 3

1)

{2000000000}

Returns: 1

2)

{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,
21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,
38,39,40,41,42,43,44,45,46,47,48,49,50}

Returns: 42

3)

{20000000,20000000,2000000000}

Returns: 3

4)

{10,10,10,10,10,1,1,1,1,1}

Returns: 5

5)

{1,10}

Returns: 1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BenfordsLaw

Math, Simulation

Used in:

SRM 155

Used as:

Division II Level Two

Writer:

vorthys

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1348

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4580&pm=1348

Problem Statement

Pick a random financial transaction from the ledger of a typical business and there is about a 30% chance that the first non-zero digit of the amount of money involved is a 1. This counter-intuitive fact is a result of Benford's Law, discovered by astronomer Simon Newcomb in the late 1800's and rediscovered by physicist Frank Benford in the early 1900's. They found that real world data are not evenly distributed. Instead, given a random number related to some natural or social phenomenon satisfying certain conditions, the probability that the first non-zero digit of the number is D is log₁₀(1 + 1/D).

Increasingly, financial auditors are using Benford's Law to detect possible fraud. Given a record of the financial transactions of a company, if some leading digit appears with a frequency that significantly differs from that predicted by Benford's Law, it is a signal that those transactions deserve a closer look.

Create a class BenfordsLaw with a method questionableDigit that takes a int[] transactions and an int threshold and returns the smallest digit that appears as the first non-zero digit of numbers in transactions with a frequency that is at least threshold times more or less than its expected frequency (e.g., more than three times the expected frequency or less than one-third the expected frequency when threshold=3). If no such digit exists, return -1.

For example, consider the data

    5236    7290     200    1907    3336
    9182      17    4209    8746    7932
    6375     909    2189    3977    2389
    2500    1239    3448    6380    4812

The following chart gives the actual frequency of each leading digit, and its expected frequency according to Benford's law.

    digit    | 1    2    3    4    5    6    7    8    9
    ---------|---------------------------------------------
    actual   | 3    4    3    2    1    2    2    1    2
    expected | 6.02 3.52 2.50 1.94 1.58 1.34 1.16 1.02 0.92

Assuming a threshold of 2, there are two digits that are questionable: the leading digit 1 appears less than half as often as expected and the leading digit 9 appears more than twice as often as expected. Since 1 is smaller than 9, the answer is 1.

Note that, although the expected frequencies have been rounded to two decimal places in the above table for the purposes of presentation, you should perform all such calculations without rounding. Errors of up to 0.000001 in the expected frequencies will not affect the final answer.

Definition

Class:	BenfordsLaw
Method:	questionableDigit
Parameters:	int[], int
Returns:	int
Method signature:	int questionableDigit(int[] transactions, int threshold)
(be sure your method is public)

Notes

-

In the formula for Benford's Law, log₁₀ means the base-10 logarithm.

Constraints

-

transactions contains between 1 and 50 elements, inclusive.

-

Each element of transactions is between 1 and 999999999, inclusive.

-

threshold is between 2 and 10, inclusive.

-

Errors of up to 0.000001 in calculating the expected frequencies will not affect the final answer.

Examples

0)

{ 5236,7290,200,1907,3336,9182,17,4209,8746,7932,
  6375,909,2189,3977,2389,2500,1239,3448,6380,4812 }

Returns: 1

The example above.

1)

{ 1,10,100,2,20,200,2000,3,30,300 }

Returns: 2

2 and 3 appear more than twice as often as expected, and 4 through 9 appear less than half as often as expected. 2 is the smallest of these digits.

2)

{ 9,87,765,6543,54321,43219,321987,21987,1987,345,234,123 }

Returns: -1

3)

{ 1,2,3,4,5,6,7,8,7,6,5,4,3,2,1 }

Returns: 9

4)

{ 987,234,1234,234873487,876,234562,17,
  7575734,5555,4210,678234,3999,8123 }

Returns: 8

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RoadWork

Math, Sorting

Used in:

TCCC '03 NE/SE Regional

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1307

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4462&pm=1307

Problem Statement

Federal repaving contracts have been awarded to various contractors to fix a number of sections of the nation's highway system. Each contract specifies a single section, giving its starting and ending location. The number of feet of highway in that section is the ending location minus the starting location. For example, a section whose start is 2000 and whose end is 2001 is just one foot long. We need software to protect the public from the possibility that contracts might be granted for overlapping sections, leaving the government to pay multiple times for fixing that part.

We want a program that will examine the contracts and will tell us how many feet of highway have been included in more than one contract. Create a class RoadWork that contains a method fraudFeet that takes int[] start and int[] end as input and returns the number of feet of highway that are included in more than one contract. Corresponding elements of start and end give the starting and ending location of a contract.

Definition

Class:	RoadWork
Method:	fraudFeet
Parameters:	int[], int[]
Returns:	int
Method signature:	int fraudFeet(int[] start, int[] end)
(be sure your method is public)

Notes

-

Keep in mind that the highways can potentially be very long (2,000,000,000 feet) and that your program must run in 8 seconds, and use less than 64 MB of memory.

Constraints

-

start contains between 1 and 50 elements inclusive

-

end contains the same number of elements as start

-

each element of end is greater than the corresponding element of start

-

each element of start and end is between 0 and 2,000,000,000 inclusive

Examples

0)

{50,50,50}

{58,58,60}

Returns: 8

All three contracts cover the section from 50 to 58

1)

{171234,12,20,30}

{171236,20,30,40}

Returns: 0

2)

{12,32,92}

{991,161,1093}

Returns: 959

32 to 92 is covered by the first 2 contracts, 92 to 161 is covered by all the contracts, and 161 to 991 is covered by the first and last contract. The answer is (92-32) + (161-92) + (991-161)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Ordered

Math

Used in:

TCCC '03 Round 3

Used as:

Division I Level One

Writer:

brett1479

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1287

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4474&pm=1287

Problem Statement

Given a int[] values containing positive integers return (quotes for clarity):

"ASCENDING mean" if the numbers are in increasing order and there are no repeated values,
"DESCENDING mean" if the numbers are in decreasing order and there are no repeated values,
"NONASCENDING freq" if the numbers are in decreasing order and contain repeated values,
"NONDESCENDING freq" if the numbers are in increasing order and contain repeated values,
or "NOTHING" if the numbers are none of the above.

where mean is a reduced fraction representing the average of the numbers formatted as (quotes for clarity) "numerator/denominator"

and freq is the number of times the most frequently occurring value occurred in the sequence.

Neither numerator nor denominator should have any leading zeros. For example (quotes for clarity):

values = {1,2,4,11}       return "ASCENDING 9/2" since the average is 18/4 = 9/2
values = {1,2,2,2,3,4}   return "NONDESCENDING 3"  since 2 occurred 3 times
values = {6,5,1}         return "DESCENDING 4/1" since the average is 12/3 = 4/1
values = {5,5,4,4,1}     return "NONASCENDING 2" since 5 occurred twice
values = {1,2,3,4,1}     return "NOTHING" since no other choice is possible

Definition

Class:	Ordered
Method:	getType
Parameters:	int[]
Returns:	String
Method signature:	String getType(int[] values)
(be sure your method is public)

Notes

-

Be sure that you spell everything correctly.

Constraints

-

values must contain between 2 and 50 elements inclusive

-

At least 2 elements of values must be distinct

-

Each element of values must be between 1 and 1000 inclusive

Examples

0)

{1,2,4,11}

Returns: "ASCENDING 9/2"

Increasing order with no repeats

1)

{1,2,2,2,3,4}

Returns: "NONDESCENDING 3"

Increasing order but the 2 is repeated 3 times

2)

{6,5,1}

Returns: "DESCENDING 4/1"

Decreasing order with no repeats

3)

{5,5,4,4,1}

Returns: "NONASCENDING 2"

Decreasing order but there are repeats

4)

{1,2,3,4,1}

Returns: "NOTHING"

The sequence increases at first but decreases at the end

5)

{1000,999,998}

Returns: "DESCENDING 999/1"

Decreasing with no repeats

6)

{999,1000,1000,1000,1000,1000}

Returns: "NONDESCENDING 5"

7)

{1,1000,1,1000,1,1000}

Returns: "NOTHING"

8)

{1,2,3,4,5,6,7,8,9,10,
11,12,13,14,15,16,17,18,19,20,
21,22,23,24,25,26,27,28,29,30,
31,32,33,34,35,36,37,38,39,40,
41,42,43,44,45,46,47,48,49,51}

Returns: "ASCENDING 638/25"

9)

{2,2,1}

Returns: "NONASCENDING 2"

10)

{1,2,2}

Returns: "NONDESCENDING 2"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TimeSlicing

Advanced Math, Dynamic Programming

Used in:

TCCC '03 Semifinals 3

Used as:

Division I Level Three

Writer:

vorthys

Testers:

Logan , lbackstrom , brett1479 , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1256

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4493&pm=1256

Problem Statement

Concurrency can be simulated on a single processor using the technique of time-slicing, giving each process a chance to run for some small, fixed interval before switching to the next process. For example, two processes might take turns executing for 10 milliseconds each until both have finished. However, switching between processes is expensive, so it is sometimes desirable to allow a process to execute more than one time slice in a row. On the other hand, to preserve the illusion of parallel execution, it is desirable that no process have to wait too long before getting a chance to run. One way to balance these conflicting desires is to set a limit K on the number of time slices a process might wait between turns. More precisely, no process that still needs more time slices will ever wait more than K time slices before getting a chance to run.

Consider two processes, A and B, that both need to run for N time slices. Given N and K, your task is to determine how many ways there are to schedule A and B such that A gets the first time slice and B gets the last time slice. For example, if N=3 and K=3, there are six possible schedules:

     AAABBB
     AABABB
     AABBAB
     ABAABB
     ABABAB
     ABBAAB

If K is reduced to 2, then the AAABBB schedule is eliminated, leaving five possible schedules.

Your task is to write a method that takes two integers, N (the number of time slices needed by each process) and K (the maximum number of time slices an unfinished process is willing to wait), and returns the number of possible schedules as a long (see examples).

Definition

Class:	TimeSlicing
Method:	howMany
Parameters:	int, int
Returns:	long
Method signature:	long howMany(int N, int K)
(be sure your method is public)

Constraints

-

N is between 1 and 30, inclusive.

-

K is between 1 and 30, inclusive.

Examples

0)

Returns: 5

The example above.

1)

Returns: 12

The twelve possible schedules are

   AABAABBB    ABAABABB    ABBAABAB
   AABABABB    ABAABBAB    ABBABAAB
   AABABBAB    ABABAABB
   AABBAABB    ABABABAB
   AABBABAB    ABABBAAB

Notice in the first schedule (AABAABBB) that process B runs for three time slices in a row even though K=2. This is legal because process A has already finished.

2)

Returns: 1

3)

Returns: 33246459524

4)

Returns: 30067266499540954

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Mandelbrot

Math, Simulation

Used in:

TCO '03 Qual. Round 2

Used as:

Division I Level Two

Writer:

lars2520

Testers:

brett1479 , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1172

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4701&pm=1172

Problem Statement

A complex number is one of the form a+bi, where a and b are real numbers, and i represents the square root of -1. We call a the real part of the complex number, and b the imaginary part. When multiplying two complex numbers a+bi and c+di, the result is (a*c-b*d)+(a*d+b*c)i. When adding two complex numbers, a+bi and c+di, the result is (a+c)+(b+d)i. Finally, the magnitude of a complex number, a+bi, is sqrt(a*a+b*b).

The Mandelbrot set is a set of complex numbers. To determine whether or not a complex number, C = a+bi, is in the Mandelbrot set, we use the following recurrence:

Z₀ = C

Z_n+1 = Z_n*Z_n+C

If, for all n greater than or equal to 0, the magnitude of Z_n is less than or equal to 2, then the complex number represented by C = a+bi is in the Mandelbrot set.

You will be given an int, max, representing the maximum value of n to check. For example, if max were 10, you would be required to check Z_n for all 0 <= n <= 10. You will also be given two doubles, a and b, representing the real and imaginary parts of Z₀, respectively. If the magnitude of Z_n is always less than or equal to 2, for all 0 <= n <= max, you should return -1. Otherwise, you should return the smallest n such that the magnitude of Z_n is greater than 2.

Definition

Class:	Mandelbrot
Method:	iterations
Parameters:	int, double, double
Returns:	int
Method signature:	int iterations(int max, double a, double b)
(be sure your method is public)

Constraints

- max will be between 1 and 30, inclusive.

- a will be between -2 and 2, inclusive.

- b will be between -2 and 2, inclusive.

- To prevent rounding errors, the magnitude of Z_n will not be within 1e-3 of 2, for any n between 0 and n', inclusive, where n' is the smallest number (or max) such that the magnitude of Z_n' is greater than 2.

Examples

0)

Returns: 1

Here, Z₀ = 1 + 1i

Thus, Z₁ = 1 - 1 + 1i + 1i + 1 + 1i = 1 + 3i. The magnitude of 1+3i is sqrt(1*1 + 3*3) = sqrt(10) > 2. Therefore, the return is 1.

1)

-1

-1

Returns: 2

Z₀ = -1 - 1i

Z₁ = -1 + 1i

Z₂ = -1 - 3i

2)

.25

.25

Returns: -1

In this example, the magnitude of Z_n is never more than 2.

3)

-1.9

Returns: -1

4)

.375

.3

Returns: 21

5)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

FleasFleas

Recursion, Simple Math

Used in:

TCCC '03 W/MW Regional

Used as:

Division I Level One

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1144

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4464&pm=1144

Problem Statement

My dog has fleas. I suspect that his fleas have fleas. I suspect that his fleas' fleas have fleas!

Assume that every infested creature (either a dog or a flea) is infested with n fleas and that k of these are themselves infested (with smaller fleas). At each smaller size, n stays the same but k decreases by 5 (but never becomes negative).

For example, suppose that n is 30 and k is originally 7. Then my dog is infested by 30 fleas of which 7 are infested with tiny fleas. Each of those 7 is infested with 30 tiny fleas of which 2 are infested with 30 miniscule fleas. No miniscule flea is infested (since 2-5 is not positive). Calculating the entire population we get 23 uninfested fleas + 7 infested fleas + 196 uninfested tiny fleas + 14 infested tiny fleas + 420 minuscule uninfested fleas = 660 fleas of all sizes.

Create a class FleasFleas that contains method population that takes an int n, the number of full-sized fleas on my dog, and an int k, the number of those that are themselves infested, and returns the total flea population on my dog. If the population is more than 10,000,000 return -1.

Definition

Class:	FleasFleas
Method:	population
Parameters:	int, int
Returns:	int
Method signature:	int population(int n, int k)
(be sure your method is public)

Constraints

-

n is between 1 and 100 inclusive

-

k is between 0 and n inclusive

Examples

0)

Returns: 660

As described in the Problem Statement

1)

Returns: 400

There are 100 full-sized fleas, 3 of which have 100 tiny fleas each

2)

Returns: -1

3)

Returns: 45800

4)

Returns: 100

5)

Returns: 9970464

6)

Returns: 6

7)

Returns: 30

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Permutation

Graph Theory, Math, String Manipulation

Used in:

SRM 160

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1135

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4605&pm=1135

Problem Statement

A permutation of the letters in an alphabet can be described by a string that contains each letter exactly once. For example, CABD describes the permutation of ABCD that maps A to C, B to A, C to B, and D to D. If we repeatedly apply that permutation, we will get the sequence ABCD,CABD,BCAD,ABCD,CABD,BCAD,ABCD,... This permutation is cyclic with length 3.

We want to find the permutation of the first n letters of

    ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz

that has the longest cycle. Create a class Permutation that contains the method best that takes the number of characters n as input and returns the lexicographically first permutation that has the maximum possible cycle length.

"Lexicographically first" means the String that would sort first among all the permutations of maximum cycle length, using the ASCII sequence (which sorts uppercase letters before lowercase letters).

Definition

Class:	Permutation
Method:	best
Parameters:	int
Returns:	String
Method signature:	String best(int n)
(be sure your method is public)

Constraints

-

n is between 1 and 52 inclusive

Examples

0)

Returns: "ACBEFD"

This permutation has cycle length 6. So does BDEFCA, but ACBEFD is lexicographically first. The cycle is: ABCDEF -> ACBEFD -> ABCFDE -> ACBDEF -> ABCEFD -> ACBFDE -> ABCDEF

1)

Returns: "BCAEFGD"

This is the lexicographically first permutation with cycle length 12

2)

Returns: "BCDEAGHIJKLFNOPQRSTMVWXYZabcU"

3)

Returns: "A"

4)

Returns: "BCAEFGHD"

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

NoZero

Advanced Math

Used in:

TCCC '04 Qual. 2

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

lbackstrom , schveiguy

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1107

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5001&pm=1107

Problem Statement

*** You may only submit a given problem once - no resubmissions will be accepted. ***

A no-zero number system uses only the digits 1 through 9. So counting begins with 1, the first "counting number", and continues:

1,2,3,4,5,6,7,8,9,11,12,...,19,21,...,98,99,111,112,...

So, in this system 9 is the ninth counting number and 11 is the tenth counting number.

As usual, addition can be defined by reference to the counting sequence. Addition of the i-th counting number and the j-th counting number is defined to mean the (i+j)-th counting number. Thus, in this system 5 + 8 = 14, since 5 is the fifth counting number, 8 is the eighth, and 14 is the thirteenth counting number. Subtraction is the reverse of addition. Create a class NoZero that contains the method subtract that takes two no-zero numbers, big and small, and returns the no-zero value that results from calculating big - small.

Definition

Class:	NoZero
Method:	subtract
Parameters:	int, int
Returns:	int
Method signature:	int subtract(int big, int small)
(be sure your method is public)

Constraints

-

big and small do not contain the digit 0

-

big is between 1 and 999,999,999 inclusive

-

small is between 1 and 999,999,999 inclusive

-

big is greater than small

Examples

0)

Returns: 1

This big and small are adjacent in the counting sequence. So 99 + 1 = 111 and 111 - 99 = 1.

1)

Returns: 8

2)

Returns: 79

3)

Returns: 12

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Coherence

Advanced Math

Used in:

TCCC '03 Int'l Regional

Used as:

Division I Level Two

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1106

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4466&pm=1106

Problem Statement

We want to display a two-color pattern on a rectangular array of pixels, with k of the pixels in the foreground color. We want to choose the pattern so that it minimizes the boundary between the foreground and the background.

The length of the boundary is the number of vertical and horizontal pixel edges that separate a foreground pixel from a background pixel. For example, this picture shows a rectangular array with three rows and six columns that has 5 foreground pixels (indicated by 'X'). The boundary in this case has length equal to 6: the upper left X is adjacent to 1 background pixel, the upper middle X is adjacent to 1, the rightmost X is adjacent to 3, the lower left X is adjacent to 0, and the lower right X is adjacent to 1.

   - - - - - -
   X X X - - -
   X X - - - -

Create a class Coherence that contains the method minBndry that takes three int inputs, numRows (the height of the array), numCols (the width of the array), and k (the number of foreground pixels), and returns the length of the minimum possible boundary.

Definition

Class:	Coherence
Method:	minBndry
Parameters:	int, int, int
Returns:	int
Method signature:	int minBndry(int numRows, int numCols, int k)
(be sure your method is public)

Constraints

-

numRows is between 1 and 30 inclusive

-

numCols is between 1 and 30 inclusive

-

k is between 0 and numRows*numCols inclusive

Examples

0)

Returns: 5

  X X X - - -
  X X - - - -
  - - - - - -
  - - - - - -
  - - - - - -
  - - - - - -

The upper right foreground pixel has 2 boundary edges, the bottom right one has 2 boundary edges, and the bottom left one has 1 boundary edge.

1)

Returns: 4

 X X X X - -
 X X X X - -
 X X X X - -
 X X X X - -

2)

Returns: 0

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Regions

Advanced Math

Used in:

SRM 179

Used as:

Division I Level Two , Division II Level Three

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1099

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4715&pm=1099

Problem Statement

Our world consists of rows and columns of identical square regions. We have a list of regions that we want to visit, starting from the center of the first region in the list and going in straight lines to the center of each successive region. Every time we cross from one region into the interior of another region (even if we have previously visited it) we will be charged a tax.

Create a class Regions that contains the method numTaxes that takes int[]s rows and columns of the regions on our list and returns the number of taxes we will have to pay. The i-th elements of rows and columns give the location of the i-th region that we must visit. If we must pay more than 2,000,000,000 taxes (!) then return -1.

Definition

Class:	Regions
Method:	numTaxes
Parameters:	int[], int[]
Returns:	int
Method signature:	int numTaxes(int[] row, int[] col)
(be sure your method is public)

Notes

-

We are not charged a tax if we just touch the boundary of a region.

Constraints

-

rows has between 1 and 50 elements inclusive.

-

columns has the same number of elements as rows.

-

Each element of rows and or columns is between 0 and 1,000,000,000 inclusive.

Examples

0)

{4,2,3}

{4,2,6}

Returns: 7

Going from the center of 4,4 to the center of 2,2 we pay tax when we enter region 3,3 and when we enter region 2,2. Going from the center of 2,2 to the center of 3,6 we pay tax as we enter 2,3 then 2,4 then 3,4 then 3,5 then 3,6.

1)

{0,1000000000,0}

{0,1000000000,0}

Returns: 2000000000

We enter each region along the diagonal on the first leg, a total of 1,000,000,000 regions. On the way back we go back down the diagonal but we still have to pay taxes.

2)

{0,10,10}

{0,2,2}

Returns: 10

The first leg enters (1,0),(2,0),(3,1),(4,1),(5,1),(6,1),(7,1),(8,2),(9,2),(10,2). The second leg just stays within region (10,2), paying no additional taxes.

3)

{0,1000000000,6}

{0,999999999,18}

Returns: -1

Each of the two legs enters almost 2 billion regions, so the sum of the taxes along this path is greater than 2 billion.

4)

{999999999,1,999999999,999999999}

{1,1,1,6}

Returns: -1

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SumSort

Advanced Math, Search, Sorting

Used in:

TCI '02 Semifinals 2

Used as:

Division I Level Three

Writer:

brett1479

Testers:

alexcchan , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1075

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4371&pm=1075

Problem Statement

Given an inclusive range of numbers you will first sort them in ascending order by their digit sum (sum of their decimal digits). Ties are settled by the numbers' values, lower numbers first. You will then return the value at location pos (0-based) in the newly sorted list. For example:

rangeLow = 0

rangeHigh = 10

pos = 3

The sorted range is : 0,1,10,2,3,4,5,6,7,8,9. The value at position 3 is 2. Note that 10 comes before 2 since the digit sum of 10 is 1 whereas the digit sum of 2 is 2. Also note that 10 comes after 1 even though they have the same digit sum since 10 is greater than 1.

Definition

Class:	SumSort
Method:	valueAt
Parameters:	int, int, int
Returns:	int
Method signature:	int valueAt(int rangeLow, int rangeHigh, int pos)
(be sure your method is public)

Constraints

-

rangeLow will be between 0 and 1000000000 (10^9) inclusive

-

rangeHigh will be between 0 and 1000000000 (10^9) inclusive

-

rangeLow will be less than or equal to rangeHigh

-

pos will be between 0 and (rangeHigh - rangeLow) inclusive

Examples

0)

Returns: 2

This is the example above

1)

Returns: 79

The numbers are sorted as:

80, 81, 90, 82, 91, 83, 92, 84, 93, 85, 86, 78, 87, 79, 88, 89

2)

Returns: 2520

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Calculate

String Parsing

Used in:

TCO '03 Round 2

Used as:

Division I Level Three

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1019

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4703&pm=1019

Problem Statement

You must write a class Calculate, with a method calc, which takes a String expression, where expression is a mathematical expression. You should calculate the value of the expression, using the standard order of operations:

Always evaluate expressions in parentheses first.
Exponentiation next.
Multiplication and division next.
Addition and subtraction last.

Operators with the same precedence should be evaluated from left to right. So 2^3^2 = (2^3)^2 = 64, and 3-2+1 = (3-2)+1 = 2

Thus, if expression = "1+2*3^(1+1)-2", we first calculate (1+1), and get "1+2*3^2-2". Next we apply exponentiation and get "1+2*9-2". Then multiplication and division gives us "1+18-2". Last, addition and subtraction, left to right, gives 17.

Furthermore, you will be given a String[] variables each of whose elements represents a variable which may be used in expression. Each element of variables will be formatted as "<variable> <value>", where <variable> is a sequence of 1 or more letters ('a'-'z' and 'A'-'Z'), and <value> is an integer. For example, if variables = {"x 1", "y 11"}, and expression = "x*y+3*x", we substitute the values for the variables to get 1*11+3*1 = 14.

The expression will conform to the following grammar:

<expression> ::= (<expression>) | <expression><op><expression> | <val>
<op>::= '+'|'-'|'/'|'*'|'^'
<val>::= a sequence of 1 or more digits or a <variable> from variables

Definition

Class:	Calculate
Method:	calc
Parameters:	String, String[]
Returns:	int
Method signature:	int calc(String expression, String[] variables)
(be sure your method is public)

Notes

-

All of the intermediate and final results of both division and exponentiation will be integers between -2^31 and 2^31 - 1, inclusive. (see constraints)

-

Variable names are case sensitive.

Constraints

-

expression will include only the characters '0' to '9', '+', '-', '*', '/', '^', '(', and ')' and letters ('a'-'z' and 'A'-'Z').

-

expression will be well-formed, conforming to the grammar in the problem statement.

-

The final result, and all intermediate results will be integers in the range -2^31 to 2^31-1, inclusive. This includes all numbers and variables, so "0*10000000000" is not allowed, nor is "0*a", {"a 10000000000"}.

-

expression will not result in division by 0 or 0^x, for x less than or equal to 0.

-

variables will have between 0 and 50 elements, inclusive.

-

Each element of variables will be formatted as "<variable> <value>", where <variable> is a sequence of 1 or more letters ('a'-'z' and 'A'-'Z'), and <value> is an integer between -2^32 and 2^32-1, inclusive (possibly with leading zeros).

-

No two elements of variables will have the same <variable>.

-

Each variable in expression will be found in variables.

-

expression will contain between 1 and 50 characters, inclusive.

-

Each element of variables will contain between 3 and 50 characters, inclusive.

Examples

0)

"x*y+3*x"

{"x 1", "y 11"}

Returns: 14

The example from the problem statement.

1)

"x^p*2^(2^p)/t^p^t+xx*n^v"

{"x 53", "xx 32", "p 3","t 2","n -1","v -21"}

Returns: 595476

2)

"t^003^t"

{"t 00000000000002","a 999999999"}

Returns: 64

Substituting, we get 2^3^2 = 8^2 = 64.

3)

"(8*(Aa^(aA-1230))-aA^2+((00)))*(0-1)"

{"aA 01234","Aa 98"}

Returns: -736371772

4)

"0-2+t^30+t^30+1"

{"t 2"}

Returns: 2147483647

The largest possible result.

5)

"1+(0-t)^31-1"

{"t 2"}

Returns: -2147483648

The smallest possible result.

6)

"((5-x+1^x))"

{"x -100"}

Returns: 106

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Decimal

Advanced Math

Used in:

TCI '02 Round 1 B

Used as:

Division I Level Three

Writer:

lars2520

Testers:

alexcchan , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=1016

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4325&pm=1016

Problem Statement

A rational number is a number which can be expressed as a ratio of two integers. In addition, all rational numbers can be expressed as a decimal number with some repeating periodic part (in some cases the repeating part is 0). For example 1/7 = 0.1428571428571428... with 142857 repeating itself infinitely. Other fractions have some finite number of non-repeating digits before the periodic part begins. For example, 1/6 = 0.166666... starts with a 1 and then settles into repeating 6's.

Your task is to write a class Decimal with a method find that takes four int's: lower, upper, lowerLength, and upperLength. Your method must find all integers n between lower and upper, inclusive, where the repeating portion of the decimal representation of 1/n has between lowerLength and upperLength digits, inclusive. You should return all of the numbers you find in a int[] sorted in increasing order.

Definition

Class:	Decimal
Method:	find
Parameters:	int, int, int, int
Returns:	int[]
Method signature:	int[] find(int lower, int upper, int lowerLength, int upperLength)
(be sure your method is public)

Constraints

-

lower and upper will be between 1 and 1000000, inclusive.

-

upper will be greater than or equal to lower.

-

The difference between upper and lower will be at most 100.

-

lowerLength and upperLength will be between 1 to 1000000, inclusive.

-

upperLength will be greater than or equal to lowerLength.

Examples

0)

Returns: { 1,  2,  3,  4,  5,  6,  8,  9,  10 }

1/1 = 1.00000...
1/2 = 0.50000...
1/3 = 0.33333...
1/4 = 0.25000...
1/5 = 0.20000...
1/6 = 0.16666...
1/8 = 0.12500...
1/9 = 0.11111...
1/10 = 0.10000...

Thus, all of the numbers other than 7 eventually settle into a repeating sequence of exactly 1 digit.

1)

Returns: { 55,  56 }

1/55 = 0.01818... (18 is repeating)
1/56 = 0.017857142857142... (857142 is repeating)

Both of these numbers have between 1 and 10 digits in its repeating part.

2)

Returns: { 204,  209,  212,  228,  237,  247,  248,  255,  265,  266,  272,  279,  285 }

3)

Returns: { 999983 }

The repeating part of 1/999983 is 999982 digits long!

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Travel

Brute Force, Geometry, Graph Theory

Used in:

TCI '02 Semifinals 3

Used as:

Division I Level One

Writer:

lars2520

Testers:

alexcchan , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=996

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4372&pm=996

Problem Statement

A traveling salesman has recently decided to go international and sell his wares around the globe. He has done in depth research and has come up with a list of cities which he thinks will provide the best market for his goods. In planning his trip, the salesman wants to minimize the total distance he has to travel because he does not particularly like traveling (which is unfortunate for him, as he is a traveling salesman) and furthermore, he figures the less distance he has to travel, the cheaper his trip will be. However, this salesman is not particularily good at math, and so you must write a computer program to help him find his way in the least distance.

You will be given a set of cities defined by their longitudes and latitudes. In addition, you will be given the radius of the planet that this traveling salesman resides on. Assume that there are direct flights, both ways, between every pair of cities that the salesman wants to visit, and that the flights follow the shortest path possible (over the surface of the planet). In addition, the first element of the input String[] will be the city in which the salesman lives, and thus his trip must start and end at this city.

Each city is defined by two numbers, a latitude and a longitude. The latitude is the number of degrees above the equator, with 90 being the north pole, and -90 being the south pole. The longitude is the number of degrees east or west of some arbitrary, predefined point. Thus, 90 degrees east is one quarter of the way around the globe in the eastern direction.

If the result is not an integer, round it to the nearest integer (.5 rounds up)

Definition

Class:	Travel
Method:	shortest
Parameters:	String[], int
Returns:	int
Method signature:	int shortest(String[] cities, int radius)
(be sure your method is public)

Notes

-

Assume the planet is a perfect sphere.

-

To find the cartesion coordinates of a city, assuming the center of the planet is at (0,0,0), use the following formulas:

x = r*cos(latitude)*cos(longitude)

y = r*cos(latitude)*sin(longitude)

z = r*sin(latitude)

Constraints

-

cities contains between 2 and 9 elements, inclusive.

-

Each element of cities represents a unique point on the globe.

-

Each element of cities is formatted as "<latitude> <longitude>" where <latitude> is an integer in the range -90 to 90, inclusive, and <longitude> is an integer in the range -180 to 180, inclusive.

-

radius is an integer between 1 and 1,000, inclusive.

-

to avoid rounding errors, the shortest path, prior to rounding, will not be within 0.001 of <x>+0.5 for any integer <x>.

Examples

0)

{"0 0","0 1"}

Returns: 35

The two cities are located one degree apart at the same latitude

1)

{"0 0","0 1","0 -1","-1 0","1 0","-1 -1","1 1","1 -1","-1 1"}

Returns: 0

2)

{"40 -82","-27 -59","-40 48"
,"26 -12","-31 -37","-30 42"
,"-36 -23","-26 71","-19 83","8 63"}

Returns: 4505

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BlueMoons

Math, Simulation

Used in:

SRM 189

Used as:

Division I Level Three

Writer:

lars2520

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=945

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4765&pm=945

Problem Statement

For the purposes of this problem, there are exactly 29.53 days between two full moons. A blue moon occurs whenever there is a full moon twice in one calendar month (January, February, etc). For example, if a full moon occurs at some point on January 1^st, then another one will occur at some point on January 30^th or 31^st (depending on what time it occurred on the 1^st). The second one is the blue moon.

Given an interval from one month to another, you are to determine how many blue moons there are between those two months, inclusive. To solve this you must know the following:

Every year has 12 months.
In a normal year, the number of days in each month are, in order starting with January, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31
In leap years, the second month (February) has 29 days instead of 28.
Leap years occur every year that is divisible by 4 except for years that are divisible by 100 but not divisible by 400. Thus 1996 was a leap year, as was 2000 (2000 is divisible by 400), but not 1700, 1800, or 1900 (1700, 1800 and 1900 are divisible by 100 but not divisible by 400).

Your task is to write a method, count, which takes a String, interval, and another String, fullMoon, as input and determines how many blue moons there are in that interval. interval will be formatted as "MM/YYYY to MM/YYYY" where "MM" represents the month (January is "01" and December is "12") and "YYYY" represents the year. fullMoon will represent a specific time at which there was a full moon and will be formatted as "DD.DD/MM/YYYY" where "MM" and "YYYY" are formatted the same as they are in interval. "DD.DD" represents the day of the month, as a fraction. Thus "01.00" would mean 12 AM on the first day of the month. "01.50" would be exactly half way through the first day of the month (12 NOON). Thus, if fullMoon were "05.75/05/2002", this would mean that there was a full moon precisely 3 quarters of the way through the 5^th day of the 5^th month of 2002 (6 PM May 5^th 2002).

Definition

Class:	BlueMoons
Method:	count
Parameters:	String, String
Returns:	int
Method signature:	int count(String interval, String fullMoon)
(be sure your method is public)

Notes

-

If a full moon occurs at 12AM (Midnight) it is part of the day which has just started, not the one that has just finished.

Constraints

-

interval will be formatted exactly as "MM/YYYY to MM/YYYY", with no leading, trailing, or extra spaces.

-

fullMoon will be formatted exactly as "DD.DD/MM/YYYY", with no leading or trailing spaces.

-

Each MM will contain leading 0's, if necessary, to have exactly 2 digits.

-

DD.DD will contain leading and trailing 0's if necessary so that it is always formatted as "DD.DD"

-

All dates and times will be valid times since 1900, inclusive. Thus "MM" will be between "01" and "12", inclusive, "YYYY" will be between "1900" and "9999" inclusive, and "DD.DD" will be between "01.00" and "31.99" (depending on the month, the upper bound for the day could be lower), inclusive.

Examples

0)

"01/2002 to 05/2002"

"28.95/01/2002"

Returns: 0

Given that there was a full moon at the specified time, there are no blue moons during this period.

1)

"01/2002 to 05/2002"

"01.00/01/2002"

Returns: 2

2)

"01/2002 to 01/2002"

"02.46/01/2002"

Returns: 1

3)

"01/2002 to 01/2002"

"01.00/02/2002"

Returns: 0

Note that fullMoon need not be within interval.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

UGroupOrder

Advanced Math

Used in:

TCI '02 Round 1 A

Used as:

Division I Level Two

Writer:

brett1479

Testers:

alexcchan , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=903

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4324&pm=903

Problem Statement

Two integers are relatively prime if they have no common factors other than 1. For example, 8 and 6 are not relatively prime since they are both divisible by 2. 27 and 10 are relatively prime since they have no common factors other than 1. Note that 1 is relatively prime to all numbers.

The Nth U-group is a special group of integers denoted U(N). An integer B is in U(N) if:

1) 0 < B < N

2) B is relatively prime to N

All arithmetic done in U(N) is performed modulo N. This means:

If C and D are in U(N) then: C*D means (C*D) mod N

The order of an element K in a U-group U(N) is the smallest positive integer E such that:

(K^E) mod N = 1

where ^ denotes exponentiation

In other words, how ever many times you have to multiply K times itself mod N to get 1. In a U-group, every element will have a finite order.

Given N you are going to return the order of each element in U-group U(N).

For example:

N = 8

U(N) = {1,3,5,7}

Orders = {1,2,2,2} since

(1^1) mod 8 = 1 mod 8 = 1

(3^2) mod 8 = (3*3) mod 8 = 9 mod 8 = 1

(5^2) mod 8 = (5*5) mod 8 = 25 mod 8 = 1

(7^2) mod 8 = (7*7) mod 8 = 49 mod 8 = 1

See examples for further clarification.

Create a class UGroupOrder that contains the method findOrders, which takes an int N and returns a int[] containing the order of each corresponding element in U(N).

Definition

Class:	UGroupOrder
Method:	findOrders
Parameters:	int
Returns:	int[]
Method signature:	int[] findOrders(int N)
(be sure your method is public)

Notes

-

The index of each returned element corresponds to the elements of U(N). The first element of U(N) corresponds to the first element in the return value. The second element of U(N) corresponds to the second element in the returned value ...

-

Note that (a*b) mod N = ((a mod N)*(b mod N)) mod N

Constraints

-

N will be between 2 and 51 inclusive

Examples

0)

Returns: { 1,
  6,
  3,
  6,
  3,
  2 }

1^1 mod 9 = 1

2^6 mod 9 = 1

4^3 mod 9 = 1

5^6 mod 9 = 1

7^3 mod 9 = 1

8^2 mod 9 = 1

1)

Returns: { 1,
  2,
  2,
  2 }

This is the example given in the problem statement.

2)

Returns: { 1,
  4,
  2,
  4,
  4,
  2,
  4,
  2 }

3)

Returns: 
{ 1,
  8,
  4,
  16,
  16,
  8,
  16,
  16,
  4,
  16,
  2,
  8,
  16,
  16,
  16,
  8,
  8,
  16,
  16,
  16,
  8,
  2,
  16,
  4,
  16,
  16,
  8,
  16,
  16,
  4,
  8,
  2 }

4)

Returns: { 1,
  4,
  4,
  2 }

5)

Returns: { 1 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

QuadraticRoots

Brute Force, Simple Math

Used in:

TCO '03 Round 3

Used as:

Division I Level One

Writer:

brett1479

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=893

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4704&pm=893

Problem Statement

A quadratic equation has the format ax^2 + bx + c = 0 where a != 0. To solve this equation the quadratic formula is used:

x = (-b (+|-) sqrt(b^2 - 4ac)) / 2a ,

where (+|-) means plus or minus, sqrt means square root, and x is the solution.

Given a list of values for a, b and c your method will return a sorted int[] of all integer solutions to the corresponding quadratic equations. The sorted values should be in ascending order with no repeats. For example, if

    a = {1} ,
    b = {2,3} ,
and c = {2,1} ,

your method would have to solve the quadratic equations corresponding to all combinations of values from a, b and c. This would amount to solving:

 x^2 + 2x + 2 = 0  (Solutions : not integers)
 x^2 + 2x + 1 = 0  (Solutions : -1)
 x^2 + 3x + 2 = 0  (Solutions : -2,-1)  
 x^2 + 3x + 1 = 0  (Solutions : not integers)  .

Notice that all combinations have been tried. The return value would be {-2,-1}.

Definition

Class:	QuadraticRoots
Method:	findRoots
Parameters:	int[], int[], int[]
Returns:	int[]
Method signature:	int[] findRoots(int[] a, int[] b, int[] c)
(be sure your method is public)

Constraints

-

a, b, and c will each contain between 1 and 50 elements inclusive.

-

Each element of a will be nonzero, between -10000 and 10000 inclusive.

-

Each element of b and c will be between -10000 and 10000 inclusive.

-

The returned int[] will contain at most 100 elements.

Examples

0)

{1}

{2,3}

{2,1}

Returns: { -2,  -1 }

Example from above.

1)

{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}

{1}

{1}

Returns: { }

No roots here.

2)

{1}

{0}

{-1,-2,-3,-4,-5,-6,-7,-8,-9,-10,-11,-12,-13,-14,-15,-16}

Returns: { -4,  -3,  -2,  -1,  1,  2,  3,  4 }

3)

{1,1,2,2,3,3,4,4}

{1,1,2,2,3,3,4,4}

{1,1,2,2,3,3,4,4}

Returns: { -3,  -2,  -1 }

Tons of repeats.

4)

{1,10000,-10000}

{0,1,10000,-10000}

{0,1,10000,-10000}

Returns: { -10000,  -100,  -1,  0,  1,  100,  10000 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TupleLine

Math, Search

Used in:

TCCC '03 NE/SE Regional

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=890

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4462&pm=890

Problem Statement

An "n-dimensional grid of size k" contains k^n cells. Each cell can be represented as an n-tuple of values from the set {0,1,...,k-1}. For example a 2-dimensional grid of size 3 is just a 3 x 3 square, with cells (0,0) (0,1) (0,2) (1,0) (1,1) (1,2) (2,0) (2,1) and (2,2). A 3-dimensional grid of size 5 is a cube containing 125 cells. Cell (0,2,2) is the cell in row 0, column 2, layer 2.

Higher dimensions get a little harder to describe geometrically, but not algebraically! Every cell in an n-dimensional grid can be uniquely represented by an n-tuple specifying the "row" "column" "layer" "plane" "hyper-row" etc. (English fails us at about the same point as geometry fails us). We can define a straight line in an n-dimensional grid algebraically. It is a set of distinct cells that can be placed in a sequence such that the difference between each pair of adjacent cells is the same throughout the sequence. Of course, the difference between two n-tuples is an n-tuple. A maximal line in an n-dimensional grid of size k is a line containing k cells.

In a 3-dimensional grid of size 4, one example of a maximal straight line is (3,0,1),(2,1,1),(1,2,1),(0,3,1) which is a straight line of length 4. The difference between each pair of adjacent cells in the sequence is (-1,1,0).

You want to create a maximal line in your n-dimensional grid by adding to a collection of cells that have already been chosen. Create a class TupleLine that contains the method quickLine that takes an int size and a String[] chosen as inputs and returns the smallest number of additional cells that you could choose to form a maximal line in the grid.

Each String in chosen is a sequence of digits indicating a particular cell. For example, "410" would indicate the cell at row 4, column 1, layer 0 in a 3-dimensional grid whose size is at least 5 (since it has a row 4). The dimension of the grid is always the same as the length of each String in chosen.

Definition

Class:	TupleLine
Method:	quickLine
Parameters:	int, String[]
Returns:	int
Method signature:	int quickLine(int size, String[] chosen)
(be sure your method is public)

Constraints

-

size is between 3 and 9 inclusive

-

chosen contains between 1 and 50 elements inclusive

-

each character in each element of chosen is a digit whose value is less than size

-

each element in chosen contains the same number of characters, n. n is the dimension of the grid and is between 2 and 9 inclusive

Examples

0)

{"00","02","21"}

Returns: 2

    X - X -         X X X X
    - - - -         - - - -
    - X - -         - X - -
    - - - -         - - - -

The left-hand picture shows the original situation. The right-hand picture shows the only way of completing a maximal line by adding two X's.

1)

{"00","32","21","32"}

Returns: 3

    X - - -
    - - - -
    - X - -
    - - X -

There are lots of ways to form a maximal line with 3 more cells. Note that the cell "32" appears twice in chosen but, of course, this does not help us to form a maximal line.

2)

{"0022","0202","0112","0000","0112"}

Returns: 0

These first three cells already form a maximal line in this 4-dimensional grid.

3)

{"2355846","6355842","3355848"}

Returns: 7

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Average

Simple Math, Simple Search, Iteration

Used in:

SRM 89

Used as:

Division II Level One

Writer:

dgoodman

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=818

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4165&pm=818

Problem Statement

You have acquired a list of the math and verbal test scores from all the children in the county. Write a class Average that contains a method belowAvg that takes two int[], math and verbal, representing the math and verbal scores of all of the children in the county, and returns the number of children who have a composite score which is below average in the county.

The composite score is defined to be the sum of a child's math and verbal scores.

Definition

Class:	Average
Method:	belowAvg
Parameters:	int[], int[]
Returns:	int
Method signature:	int belowAvg(int[] math, int[] verbal)
(be sure your method is public)

Notes

-

each element of math corresponds to the element with the same index in verbal.

-

the number of children is the length of math and verbal.

Constraints

-

math and verbal will contain the same number of elements.

-

math will contain between 1 and 50 elements, inclusive.

-

each value in math and in verbal is between 200 and 800, inclusive.

Examples

0)

{200,250,700,700}

{400,400,400,400}

Returns: 2

The composite scores of the 4 children are 600, 650, 1100, and 1100 and the average composite score is 862.5, so 2 of the children are below average.

1)

{500,400}

{300,400}

Returns: 0

Both children have the same composite score 800 which is also the average. Neither are below average

2)

{293}

{799}

Returns: 0

3)

{400,400,400,400,400,400,401}

{400,400,400,400,400,400,400}

Returns: 6

The average composite score is just above 800, so 6 of the 7 children are below average.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

StockSales

Advanced Math

Used in:

SRM 202

Used as:

Division I Level Three

Writer:

dgoodman

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=762

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5848&pm=762

Problem Statement

For tax purposes I need to trade some stock, generating as small a positive amount of revenue as possible. I can buy or sell any integer quantity of each stock (I can "sell short", which means that I can sell more of a stock than I have).

Create a class StockSales that contains a method getAmounts that is given a int[] values, the prices of the stocks I am willing to trade, and that returns the amounts of each stock that I should buy or sell. In the return, positive amounts represent amounts to sell, while negatives represent amounts to buy.

To make the answer unique, choose the amounts in order. Choose each amount to have the smallest possible absolute value (considering all the earlier choices). If both the negative and positive amount is available, choose the positive amount.

Definition

Class:	StockSales
Method:	getAmounts
Parameters:	int[]
Returns:	int[]
Method signature:	int[] getAmounts(int[] values)
(be sure your method is public)

Constraints

-

values contains between 1 and 50 elements inclusive.

-

Each element in values is between 1 and 1,000,000 inclusive.

Examples

0)

{6,12,17}

Returns: { 0,  -7,  5 }

The smallest positive revenue is 1. We can trade 0 of the first stock and still achieve this. Choose -7 for the second stock since -7 is the smallest (absolute value) coefficient of 12 that allows us to get revenue of 1: 0*6 + -7*12 + 5*17 = 1.

1)

{10,4}

Returns: { 1,  -2 }

The smallest positive revenue is 2. Both {1,-2} and {-1,3} achieve this. {1,-2} is chosen by the tie breaking rule that says to choose the positive amount in preference to the same negative amount. 1*10 + -2*4 = 2, the minimum revenue possible.

2)

{79}

Returns: { 1 }

3)

{60,60,60,60,60,60,60}

Returns: { 0,  0,  0,  0,  0,  0,  1 }

4)

{17,19,37,11,22,110}

Returns: { 0,  0,  3,  0,  0,  -1 }

5)

{1000000,499999}

Returns: { -249999,  499999 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

PairwiseSums

Brute Force, Math

Used in:

SRM 182

Used as:

Division I Level Three

Writer:

dgarthur

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=595

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4730&pm=595

Problem Statement

Given a list of numbers, A = {a₀, a₁, ..., a_n-1}, its pairwise sums P are defined to be all numbers of the form a_i + a_j for 0 <= i < j < n. For example, if

A = {1,2,3,4},

then

P = {1+2, 1+3, 1+4, 2+3, 2+4, 3+4} = {3, 4, 5, 5, 6, 7}.

The order of the terms in P is ignored, and both A and P may contain duplicates.

In general, it is very easy to compute the pairwise sums of a list, but it is much more difficult to perform this operation in reverse, extracting the original list given its pairwise sums. That is where you come in. Create a class PairwiseSums that contains a method reverse, which takes a String[] sums. Each element in sums will consist of space-separated integers. The method should consider the list P containing all the integers in all the elements of sums. If there is exactly one non-decreasing int[] of non-negative integers, A, such that P contains precisely the pairwise sums for A, the method should return A. Otherwise, it should return an empty int[].

Definition

Class:	PairwiseSums
Method:	reverse
Parameters:	String[]
Returns:	int[]
Method signature:	int[] reverse(String[] sums)
(be sure your method is public)

Constraints

-

sums will contain between 1 and 50 elements inclusive.

-

Each element of sums will contain between 1 and 50 characters inclusive.

-

There will be a total of at least three integers in sums.

-

Each element of sums will contain at least one integer.

-

Each character in sums will either be a space (' '), or a digit ('0'-'9').

-

Each integer in sums will be between 0 and 1000 inclusive, and will have no leading 0's.

-

Each element of sums will have precisely one space between consecutive integers, and will have no leading or trailing spaces.

Examples

0)

{"3 5 4 7 6 5"}

Returns: { 1,  2,  3,  4 }

This is the example from the problem statement.

1)

{"0", "1000", "1000"}

Returns: { 0,  0,  1000 }

Note that A can contain 0 and duplicates, but it cannot contain negative integers or fractions.

2)

{"15 30 45 60"}

Returns: { }

There exists no A whose collection of pairwise sums contains precisely four elements.

3)

{"5 6 7 9 10 11"}

Returns: { }

A could be either {1,4,5,6} or {2,3,4,7}, so {} is returned.

4)

{"910 689 882 565 922 815 457 674 495 653 755 948",
 "631 988 881 523 740 561 719 727 410 767 660 302",
 "519 340 498 603 960 853 495 712 533 691 643 536",
 "178 395 216 374 893 535 752 573 731 428 645 466",
 "624 287 108 266 325 483 304"}

Returns: { 35,  73,  143,  231,  252,  267,  393,  422,  460,  488,  500 }

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

MatArith

Math

Used in:

TCI '02 Round 2

Used as:

Division I Level Two

Writer:

chogyonim

Testers:

alexcchan , lbackstrom

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=511

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=4335&pm=511

Problem Statement

Let an R by C (also notated as RxC) matrix mean a matrix with R rows and C columns. Also, for x between 1 and R, inclusive, and y between 1 and C inclusive, let element (x,y) represent the element at the xth row and yth column (both 1-indexed) of a given R by C matrix.

Matrix multiplication works as follows:

For an L by M matrix A and an M by N matrix B, define an L by N matrix P such that A * B = P, and each element (x,y) of matrix P is equal to the sum of the product of each element of the xth row of A with the equivalently indexed element of the yth column of B.

For example, say we have a 4x2 matrix A and a 2x3 matrix B:

A={{ a1, a2 },
   { a3, a4 },
   { a5, a6 },
   { a7, a8 }}

B={{ b1, b2, b3 },
   { b4, b5, b6 }}

Then 4x3 matrix P = A * B =
{{ b1*a1+b4*a2, b2*a1+b5*a2, b3*a1+b6*a2 },
 { b1*a3+b4*a4, b2*a3+b5*a4, b3*a3+b6*a4 },
 { b1*a5+b4*a6, b2*a5+b5*a6, b3*a5+b6*a6 },
 { b1*a7+b4*a8, b2*a7+b5*a8, b3*a7+b6*a8 }}

Matrix addition works as follows:

For an L by M matrix A and an L by M matrix B, define an L by M matrix S such that A + B = S, and each element (x,y) of matrix C is equal to the sum of the two elements (x,y) in A and B.

For example, say we have a 2x3 matrix A and a 2x3 matrix B:

A={{ a1, a2, a3 },
   { a4, a5, a6 }}

B={{ b1, b2, b3 },
   { b4, b5, b6 }}

Then 2x3 matrix S = A + B =
{{ a1+b1, a2+b2, a3+b3 }
 { a4+b4, a5+b5, a6+b6 }}

Write a method multiply which takes three String[] inputs representing matrix A, matrix B, and matrix C. Each element will be a String representing a row of that matrix as follows:

"I1 I2 I3 I4 I5 ... IN" (quotes added for clarity)

where each I is an integer.

The fourth argument is a String representing an equation between A, B, and C.

Return the String[] represention of the solution matrix to the equation, in the same form as the inputs.

The equation follows the standard order of operations. That is, first do any multiplications, going left to right. Then do any additions, going left to right. After each multiplication or addition, put an intermediate matrix in place of the two argument matrices. For example (quotes added for clarity):

"A*B+C*A"

You would first multiply A*B, and replace those two matrices with an intermediate matrix M:

"M+C*A"

You would then multiply C*A, and replace those two matrices with an intermediate matrix N:

"M+N"

You would finally add M+N, returning the final result.

If the equation is not valid for the given matrices, return an empty String[]. The equation is not valid if:

*at any point, two matrices (A, B, C, or any intermediates) must be multiplied, in which the number of rows in the second matrix is not equal to the number of columns in the first matrix.

*at any point, two matrices (A, B, C, or any intermediates) must be added, but do not have the same dimensions.

*at any point, one of the intermediate matrices contains a value that is greater than 2147483647 or less than -2147483648.

In summary, given the 3 matrices and an equation involving those three matrices, return the resulting matrix in the described String[] format, or an empty String[] if the equation is not valid for the given matrices.

Definition

Class:	MatArith
Method:	calculate
Parameters:	String[], String[], String[], String
Returns:	String[]
Method signature:	String[] calculate(String[] A, String[] B, String[] C, String equation)
(be sure your method is public)

Notes

-

The return must be formatted exactly as the inputs. That means no leading/trailing or extra spaces.

Constraints

-

Each String[] will contain 1 to 10 element, inclusive.

-

Each element of A, B and C will contain between 1 and 50 characters, inclusive.

-

All elements of A, B and C will be a space-delimited list of integers, with one space between integers, and no leading or trailing spaces.

-

All elements of A, B and C will contain only the numbers [0-9] inclusive, the negative sign ('-') and spaces.

-

The number of integers represented by each element of A, B and C will be between 1 and 10, inclusive.

-

The number of integers represented by each element of A will be the same as the number of integers represented by every other element of A.

-

The number of integers represented by each element of B will be the same as the number of integers represented by every other element of B.

-

The number of integers represented by each element of C will be the same as the number of integers represented by every other element of C.

-

Each integer represented in A, B or C will be between -10 and 10, inclusive.

-

Each integer represented in A, B or C will be a correctly formatted integer, without leading zeros.

-

equation will contain between 1 and 49 characters, inclusive.

-

equation can only contain the capital letters 'A', 'B', and 'C', and the two operands '+' and '*'.

-

The first and last characters of equation will be letters, and each pair of consecutive letters in equations will have exactly one operand between them.

Examples

0)

{"1 2 3","2 3 4"}

{"1 2","3 4","5 6"}

{"1"}

"A*B"

Returns: { "22 28",  "31 40" }

A*B={{ 1*1+2*3+3*5, 1*2,2*4,3*6 },
     { 2*1+3*3+4*5, 2*2+3*4+4*6 }}

1)

{"1 2 3","2 3 4"}

{"1 2","3 4","5 6"}

{"1"}

"A+B+C"

Returns: { }

A+B is calculated first, but the two matrices do not have the same dimensions.

2)

{"3 5 7","5 4 3","-2 3 2"}

{"3"}

{"1 1 1","2 5 2","3 5 -3"}

"A+C"

Returns: { "4 6 8",  "7 9 5",  "1 8 -1" }

A+C={{ 3+1,  5+1, 7+1  },
     { 2+5,  5+4, 2+3  },
     { -2+3, 3+5, 2+-3 }}

3)

{"10 0","0 0"}

{"0"}

{"0"}

"A*A*A*A*A*A*A*A*A"

Returns: { "1000000000 0",  "0 0" }

4)

{"10 0","0 0"}

{"0"}

{"0"}

"A*A*A*A*A*A*A*A*A*A"

Returns: { }

An intermediate value (10,000,000,000) is greater than 2,147,483,647.

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

AlephNull

Advanced Math

Used in:

TCCC '02 W/MW Reg. Quart.

Used as:

Division I Level Three

Writer:

wyzmo

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=445

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=61&pm=445

Problem Statement

PROBLEM STATEMENT

The logician Charles Sanders Pierce proposed a procedure for generating and
ordering all of the positive rational numbers. A rational number is an integer
divided by an integer (n/m where both n and m are integers and m does not equal
zero). 

The procedure proceeds as follows. Start with the two rationals 0/1 and 1/0
(disregarding the fact that 1/0 is not a valid number). Call this generation 1.
To produce the next generation, insert a new rational in between each pair of
rationals in the current generation by summing the numerators (the number being
divided) of the adjacent rationals to produce the new numerator, and by summing
the denominators (the number doing the dividing) of the adjacent rationals to
produce the new denominator. By repeating this procedure indefinitely, all of
the positive rational numbers will be produced in order in their simplest
rational form. 

The first few generations proceed as follows:

G1: 0/1 1/0
G2: 0/1 1/1 1/0
G3: 0/1 1/2 1/1 2/1 1/0
G4: 0/1 1/3 1/2 2/3 1/1 3/2 2/1 3/1 1/0
G5: 0/1 1/4 1/3 2/5 1/2 3/5 2/3 3/4 1/1 4/3 3/2 5/3 2/1 5/2 3/1 4/1 1/0 

Code a method that given a generation number and a zero based index, returns
the numerator and denominator of the rational number at the position indicated
by the index within the generation. If the index is not within the range of
values for the given generation, return the special error value having zero for
both the numerator and denominator.

DEFINITION
Class: AlephNull
Parameters: int, int
Returns: int[]
Method signature: int[] rational(int generation, int item)

(be sure your method is public)

TopCoder will ensure the validity of the inputs.  Inputs are valid if all of
the following criteria are met:

* generation is from 1 to 30 inclusive.
* item is from 0 to 999999999 inclusive. 

HINT
The number of elements in a given generation can be computed as follows:
elements = (2 ^ (generation - 1)) + 1. (The '^' symbol indicates
exponentiation. For example:
Generation 1: 2^0 + 1 = 2 
Generation 2: 2^1 + 1 = 3 
Generation 3: 2^2 + 1 = 5 
Generation 4: 2^3 + 1 = 9
Generation 9: 2^8 + 1 = 257

EXAMPLES
E1:  1,0        ==> [0,1]
E2:  1,1        ==> [1,0]
E3:  1,2        ==> [0,0]      //error value
E4:  4,1        ==> [1,3]
E5:  4,6        ==> [2,1]
E6:  5,11       ==> [5,3]
E7:  8,70       ==> [9,7]
E8:  10,467     ==> [43,12]
E9:  23,4190316 ==> [438,43]
E10: 30,100     ==> [7,157]

Definition

Class:	AlephNull
Method:	rational
Parameters:	int, int
Returns:	int[]
Method signature:	int[] rational(int param0, int param1)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Intervals

Math, String Parsing

Used in:

TCCC '02 W/MW Reg. Quart.

Used as:

Division I Level Two

Writer:

wyzmo

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=444

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=61&pm=444

Problem Statement

PROBLEM STATEMENT

An interval is a set of consecutive integers. The lowest and highest integers,
separated by a single colon, (the character ':'), are used to represent the
interval. The low number appears first, before the ':'. The high number appears
second, after the ':'. For example, the interval "1:3" represents the set of
integers 1, 2, and 3. (double quotes are for clarity). The interval "100:199"
represents the set of integers greater than or equal to 100 and less than or
equal to 199. The interval "5:5" respresents the set containing the single
integer 5. Note that the high value of the interval must always be greater than
or equal to the low value of the interval. 

Write a method that takes a list of intervals and partitions the intervals so
that every interval in the result:

* is pairwise disjoint (no two intervals contain the same integer), 
* every integer appearing in the original input is represented exactly once in
exactly one of the resulting intervals, 
* no integer appears in a result interval that does not also appear in at least
one input interval, 
* the minimum number of resulting intervals is used, 
* each interval in the orignal input can be recreated by combining one or more
intervals from the result. 

Return the intervals ordered by the low value of each range. Note that the
input may contain duplicate intervals, but the result will not. 

DEFINITION
Class: Intervals
Parameters: String[]
Returns: String[]
Method signature: String[] partition(String[] intervals);

(be sure your method is public)

TopCoder will ensure the validity of the inputs.  Inputs are valid if all of
the following criteria are met:

* The input will contain from 0 to 20 elements, inclusive.
* Each element of intervals will contain two integers (no leading zeros)
separated by a single colon (character ':').
* Each element of intervals will have neither leading nor trailing spaces.
* Each integer in an interval will be from 0 to 9999, inclusive.
* The high value of each interval will be greater than or equal to the low
value of that interval.

EXAMPLES

E1: {1:5,3:8} ==> {1:2,3:5,6:8} 

The input has two intervals. The first interval contains the integers 1, 2, 3,
4 and 5. The second interval contains the integers 3, 4, 5, 6, 7, and 8. Since
two input intervals contain the integers 3, 4, and 5, the intervals are not
pairwise disjoint. By creating the new interval, "3:5", and removing the
elements 3, 4, and 5 from the two original intervals, the original intervals
are now correctly partitioned into the three intervals "1:2", "3:5", and "6:8".
Note that other partitionings are possible, such as {1:2,3:4,5:5,6:8} which
uses four intervals, but the minimum number of partitions must be used. A
partitioning such as {1:2,3:6,7:8} is incorrect because the interval "1:5" from
the original input cannot be formed by combining one or more of the result
intervals. Thus, the only correct solution is the list of intervals
{1:2,3:5,6:8}. 
  
E2: {} ==> {} 
E3: {0:9999} ==> {0:9999} 
E4: {10:21,10:21} ==> {10:21}
E5: {6:10,3:10} ==> {3:5,6:10} 
E6: {1:10,3:5} ==> {1:2,3:5,6:10}
E7: {6:7,1:8,2:4,5:7,2:3} ==> {1:1,2:3,4:4,5:5,6:7,8:8}
E8: {1:99,6:10,3:10} ==> {1:2,3:5,6:10,11:99}

Definition

Class:	Intervals
Method:	partition
Parameters:	String[]
Returns:	String[]
Method signature:	String[] partition(String[] param0)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

DiceChecker

Math, Simple Search, Iteration

Used in:

TCCC '02 Reg. Semifinal

Used as:

Division I Level One

Writer:

jay_peg

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=355

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=62&pm=355

Problem Statement

PROBLEM STATEMENT

The results of rolling a die a number of times is given.  If one particular
value comes up more than 1/4 of the time, or comes up less than 1/10 of the
time, the die is considered to be loaded (Loaded means weighted in such a way
as to make the die show a particular number more or less often than is
statistically acceptable).  

Given a sample of die rolls, decide whether or not the die is loaded, and if
so, return the numbers that came up too many or too few times.

DEFINITION

Class Name: DiceChecker
Method Name: badValues
Parameters: int[]
Returns: int[]

Method signature: int[] badValues(int[] values)
Be sure your method is public.

TopCoder will ensure the validity of the inputs.  Inputs are valid if all of
the following criteria are met:
 *values has between 1 and 50 elements, inclusive.
 *each element of values is between 1 and 6, inclusive.

Return an int[] that contains the numbers between 1 and 6 (inclusive) that were
in the int[] too few or too many times.

NOTES
 - If the die is not loaded, return an empty int[].
 - Sort the output ascending ( { 1, 2 }, not { 2, 1 } ).

Examples:

values: { 1, 2, 3, 4, 5, 6, 1, 2, 3, 4 }
1 comes up 1/5 of the time.
2 comes up 1/5 of the time.
3 comes up 1/5 of the time.
4 comes up 1/5 of the time.
5 comes up 1/10 of the time.
6 comes up 1/10 of the time.
No value comes up more than 1/4 of the time or less than 1/10 of the time.
The die is not loaded so return {} (empty int[]).

values: { 3, 1, 5 }
1 comes up 1/3 of the time.
2 does not comes up.
3 comes up 1/3 of the time.
4 does not comes up.
5 comes up 1/3 of the time.
6 does not comes up.
2, 4, and 6 come up less than 1/10 of the time, and 1, 2, and 3 come up more
than 1/4 of the time so return { 1, 2, 3, 4, 5, 6 }.

values : { 1, 1, 1, 1, 1, 1, 1, 2, 2, 2 }
1 comes up 7/10 of the time.
2 comes up 3/10 of the time.
3 does not comes up.
4 does not comes up.
5 does not comes up.
6 does not comes up.
All values are out of the range specified for an unloaded die (> 1/4 or < 1/10).
return { 1, 2, 3, 4, 5, 6 }.

values : { 1, 1, 3, 3, 4, 4, 2, 2, 5, 5, 6, 6 }
1 comes up 1/6 of the time.
2 comes up 1/6 of the time.
3 comes up 1/6 of the time.
4 comes up 1/6 of the time.
5 comes up 1/6 of the time.
6 comes up 1/6 of the time.

All values are in the range specified for an unloaded die (> 1/4 or < 1/10)
return {}.

Definition

Class:	DiceChecker
Method:	badValues
Parameters:	int[]
Returns:	int[]
Method signature:	int[] badValues(int[] param0)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

RuleEngine

Advanced Math, Brute Force, String Parsing

Used in:

TCCC '02 Reg. Semifinal

Used as:

Division I Level Three

Writer:

jay_peg

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=352

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=62&pm=352

Problem Statement

PROBLEM STATEMENT:

A rule engine is simply a warehouse of tests.  Based on the result of these
tests, actions are taken.  When a set of rules causes an action to be taken,
the rule set is said to "fire".

EXAMPLE Rule Sets:

Example 1:
If the monkey is hungry and the monkey has a banana in it's hand, then the
monkey eats the banana.  The rule set has two rules:
IF:
	(RULE) monkey is hungry
	(RULE) monkey has banana
THEN:
	(ACTION) monkey eats banana.

Example 2:
If X = 2, and Y is between 10 and 15, and Z = 5, then Z = 4.  The rule set has
three rules:
IF:
	(RULE) X = 2
	(RULE) Y between 10 and 15
	(RULE) Z = 5
THEN:
	(ACTION) set Z = 4

DEFINITION:

It is often very important to know when a given state will cause two different
rule sets to fire.  You will be given two rule sets.  Determine whether there
are any data sets that will cause both rule sets to fire. If so, return the
number of such sets within a set of given bounds.  If not, return "0".
The elements of the rule sets are of the form "<X><comparison>data1,data2" or
"<X><comparison>data1" where <comparison> can be "==", "<", "<=", ">", ">=",
"!=", or "B". <X> is a variable name, a single capital letter 'A'-'Z'. The
element would be TRUE if the comparison of the value in <X> to data1 (or data1
and data2) was true. If all elements of the rule set are TRUE, then the rule
set fires (Double-quotes and angle-brackets are for clarity only).

<comparison> legend:
==	X == data1
<	X < data1
<=	X <= data1
>	X > data1
>=	X >= data1
!=	X != data1
B	X is between data1 and data2, inclusive

X represents an integer variable whose range of possible values are specified
by the below rules.

Method signature: String countSets(String[] ruleSet1, String[] ruleSet2)
Be sure your method is public.

TopCoder will enforce the validity of the inputs.  Inputs are considered valid
if all of the following criteria are met:
  *ruleSet1 and ruleSet2 each have between 1 and 7 elements, inclusive.
*each element of ruleSet1 and ruleSet2 is either of the form
"<X><comparison><data1>" where <comparison> is not the letter "B", or of the
form "<X>B<data1>,<data2>" (quotes and angle-brackets are shown for clarity,
they do not appear in the input).
  *<X> is a letter between 'A' and 'Z', inclusive (upper-case only).
*<data1> and <data2> are integers between -9 and 9, inclusive.  Leading zeros
are possible.
  *<comparison> is one of the following: "==", "<", "<=", ">", ">=", "!=", "B".
*If the <comparison> code is 'B', then <data1> will be less than or equal to
<data2>.

Return the number of distinct data sets made up of values between -10 and 10,
inclusive that will cause both rules to fire.
Format the return value as a String.

WORKED EXAMPLES:

ruleSet1 = { "A<1", "B>2" }, ruleSet2 = { "A>1", "BB1,2" }.
Here ruleSet1 will fire if the value in A is less than 1, and the value in B is
greater than 2.  ruleSet2 will fire if the value in A is greater than 1, and
the value in B is between 1 and 2.  The rule sets are mutually exclusive, for A
cannot be both greater than and less than 1 so return "0".

ruleSet1 = { "A<0" }, ruleSet2 = { "A<0" }.
Both rulesets will fire for any value of A between -10 and -1, inclusive.
There are 10 such values, so return "10".

ruleSet1 = { "A==1", "X>=4", "F<1" }, ruleSet2 = { "X>=5", "ZB2,9" }.
ruleSet1 will fire when A is 1, X is greater or equal to 4, and F is less than
1.  ruleSet2 will fire when X is greater than or equal to 5, and Z is between 2
and 9, inclusive.  Both rule sets will fire when:
A is 1.
X is greater than or equal to 5.
F is less than or equal to 0.
Z is between 2 and 9, inclusive.

Hence, the rule sets are not mutually exclusive, so calculate the number of
distinct data sets that can cause the rule set to fire, in which the values are
between -10 and 10, inclusive:

A can only be 1 (1 possible element).
X can be between 5, and 10 inclusive (6 possible elements).
F can be between -10 and 0 inclusive (11 possible elements). 
Z can be between 2 and 9 inclusive (8 possible elements).

The number of distinct data sets that can cause both rule sets to fire within
the given bounds is: 1 * 6 * 11 * 8 = 528.  Return "528".

TEST CASES:

{ "A<1", "B==2", "C>4", "D>=6", "E<=9", "FB1,2", "J!=6" }, { "E>9" } returns "0".
{ "A<01", "B==2", "C>4", "D>=2", "E<=9", "FB1,2", "J!=6" }, { "A<9", "B>=2" }
returns "475200".
{ "A<=9", "B<=9", "C<=9", "D<=9", "E<=9", "F<=9", "G<=9" }, { "H<=9", "I<=9",
"J<=9", "K<=9", "L<=9", "M<=9", "N<=9" } returns "1638400000000000000".
{ "KB-09,5", "K<3" }, { "Y>4" } returns "72".

Definition

Class:	RuleEngine
Method:	countSets
Parameters:	String[], String[]
Returns:	String
Method signature:	String countSets(String[] param0, String[] param1)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Multiples

Brute Force, Simple Math

Used in:

SRM 201

Used as:

Division II Level One

Writer:

zoidal

Testers:

lbackstrom , brett1479

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=343

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=5872&pm=343

Problem Statement

You are to create a class Multiples with a method number, which takes three ints: min, max, and factor.

Given a range of integers from min to max (inclusive), determine how many numbers within that range are evenly divisible by factor.

Definition

Class:	Multiples
Method:	number
Parameters:	int, int, int
Returns:	int
Method signature:	int number(int min, int max, int factor)
(be sure your method is public)

Notes

-

If x is evenly divisble by y, there exists some integer k such that k * y = x.

Constraints

-

min will be between -1000000 and 1000000, inclusive.

-

max will be between -1000000 and 1000000, inclusive.

-

max will be greater than or equal to min.

-

factor will be between 1 and 1000, inclusive.

Examples

0)

Returns: 3

The numbers 0, 5, and 10 are evenly divisible by 5, so this returns 3.

1)

Returns: 6

The numbers 9, 12, 15, 18, 21, 24 are evenly divisible by 3, so this returns 6.

2)

-123456

Returns: 780

3)

-75312

Returns: 34515

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Birds

Simple Math, Simple Search, Iteration, Sorting

Used in:

TCCC '02 Reg. Semifinal

Used as:

Division I Level Two

Writer:

jay_peg

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=330

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=62&pm=330

Problem Statement

PROBLEM STATEMENT:

A Bird is considered migratory if it can be found in two regions in different
parts of the year.  Of course, it must stay in those regions for a minimum
amount of time (one day in Barbados does not make a migration).  The bird can
travel inside those regions and that travel is unimportant (The bird can leave
Alaska for Florida and spend some time in both southern and northern Florida
but those COULD just be considered part of spending time in Florida).  The bird
can also travel when not in those regions and that travel can be ignored (The
bird can spend the summer in Alaska and the winter in Brazil, and if the bird
is in England in the spring, who cares?).  In this problem we will specify that
the time a bird must spend in a region is at least 90 days.  The distance
between these regions must be at least 1000 miles for the bird to be considered
migratory.

To put it precisely, the bird is migratory if there exist 2 blocks of time in
the same calendar year that are each at least 90 contiguous days in length in
which all areas the bird is at in time period 1 are at least 1000 miles away
from all areas the bird is at in time period 2.

Write a class Birds which contains a method isMigratory.  isMigratory should
determine whether the given set of bird moves describe a migratory bird.  If
so, return 1, otherwise return 0.

Example:

If the bird is in New York in January, and in Connecticut from February through
April, and then spends the rest of the year in Brazil, (which is at least 1000
miles from both New York and Connecticut) that Bird would be considered
migratory because it is spending 31 + 28 + 31 + 30 = 120 consecutive days in
the region containing New York and Connecticut and 365 - 120 = 245 consecutive
days in Brazil.

DEFINITION:

Class Name: Birds
Method Name: isMigratory
Parameters: String[]
Returns: int

Method Signature: int isMigratory(String[] birdMoves)
(be sure your method is public)

TopCoder will enforce the following rules:
 *birdMoves has between 1 and 15 elements, inclusive.
 *each element of birdMoves will contain between 1 and 50 characters, inclusive.
*each String in birdMoves is of the form
"<gridCoordinateX>,<gridCoordinateY>,<month>,<day>" where <gridCoordinateX>,
<gridCoordinateY>, <month>, and <day> all represent integer values.  (The
quotes and angle-brackets are for clarity only).
*<gridCoordinateX> and <gridCoordinateY> will each be between 0 and 30000,
inclusive.  The pair <gridCoordinateX>, <gridCoordinateY> represents a location
where the bird begins to reside at the point in time represented by the pair
<month>, <day>.
 *<month> will be between 1 and 12, inclusive.
*<day> will be appropriate to the month on a non leap year.  That is, if
<month> is 2, then <day> will be restricted to being between 1 and 28, inclusive.
 *grid coordinates represent one mile for each unit.
*the distance between a grid cordinate (x1, y1) and (x2, y2) is given by the
square root of the value ((x2 - x1)^2 + (y2 - y1)^2).
 *two different elements of birdMoves cannot contain the same date.

NOTES:
 *Sort birdMoves by date.
*Assume that the bird begins to exist on the earliest day given in the
birdMoves.
 *The bird begins that day at the associated grid coordinate.
*Then, the bird moves instantly, at midnight on the date represented by the
next element of birdMoves to the position represented by the next element of
birdMoves.
*The bird will exist at the location given by the last element of birdMoves
until and including the entire day of December 31.
*January(1), March(3), May(5), July(7), August(8), October(10), December(12)
each have 31 days.
 *April(4), June(6), September(9), November(11) each have 30 days.
 *February(2) has 28 days.

WORKED EXAMPLES:

birdMoves = { "0,0,1,1", "1000,1000,6,1" }
The bird is at grid coordinate (0,0) from January 1 through May 31.  Then, the
bird is at grid coordinate (1000,1000) through December 31.  The distance
between (0,0) and (1000,1000) is sqrt( (1000 - 0) ^ 2  +  (1000 - 0) ^ 2 ) =
sqrt(2000000) >= 1000.  The number of days spent at (0,0) is 31 + 28 + 31 + 30
+ 31 = 151 >= 90, and the number of days spent at (1000,1000) is 365 - 151 =
214 >= 90.  Return 1.

birdMoves = { "0,0,1,1", "100,100,6,1" }
The bird is at grid coordinate (0,0) from January 1 through May 31.  Then, the
bird is at grid coordinate (100,100) through December 31.  The distance between
(0,0) and (100,100) is sqrt( (100 - 0) ^ 2  +  (100 - 0) ^ 2 ) = sqrt(20000) <
1000.  Return 0.

birdMoves = { "1000,0,2,1", "1000,1000,1,1", "10000,30000,7,1" }
The bird is at (1000,1000) for 31 days, then at (1000,0) for 150 days, then at
(10000,30000) for 184 days.
The distance from (1000,0) to (10000,30000) is 31320.919...
Thus, the bird spends 150 consecutive days (at 1000,0) at least 1000 miles away
from where the bird spends 184 consecutive days (at 10000,30000).  Return 1.

{ "30000,30000,9,1", "0,0,1,1", "1000,1000,5,1" } returns 1.
In this case, the bird is migratory based on any of three distance checks.  The
bird spends 4 months at (0,0), 4 months at (1000,1000), and 4 months at
(30000,30000).  Each of these three spots is at least 1000 miles from the
others.  The amount of time spent by the bird in each spot is at least 90 days.
 Return 1.

TEST CASES:

{ "0,0,1,1", "00708,708,6,1" } returns 1.
{ "200,400,7,1", "100,0,1,1", "200,200,3,1", "0,400,11,1", "407,308,5,1",
"100,600,9,1" } returns 0.

Definition

Class:	Birds
Method:	isMigratory
Parameters:	String[]
Returns:	int
Method signature:	int isMigratory(String[] param0)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

LongCalc

Math, String Parsing

Used in:

TCI '01 Semifinals 3

Used as:

Division I Level Three

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=212

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=55&pm=212

Problem Statement

THIS PROBLEM WAS TAKEN FROM THE SEMIFINALS OF THE TOPCODER INVITATIONAL
TOURNAMENT

PROBLEM STATEMENT 
Create a class LongCalc that will perform arithmetic operations on two whole
numbers, represented by Strings. The operation to be performed is indicated by
op, which will be 1 for addition, 2 for subtraction, 3 for multiplication, and
4 for integer division. The value returned from this operation will be a
numeric value held in a String (which may begin with a negative sign if
necessary).

DEFINITION
Class Name: LongCalc
Method Name: process
Parameters: String, String, int
Returns: String
Method signature (be sure your method is public): String process(String a,
String b, int op);  

The operation that will be performed is <a op b>.

TopCoder will ensure the validity of the inputs.  Inputs are valid if all of
the following criteria are met:
- Both a and b will consist of only digits, and that the first digit of each
number is greater than 0.
- Both a and b will have length between 1 and 50, inclusive.
- op will be either 1, 2, 3, or 4

JAVA NOTE
java.math.* will not be allowed

EXAMPLES
process("100", "50", 1) -> "150"
process("100000000000000000000000000000000",
"400000000000000000000000000000000", 1) -> "500000000000000000000000000000000"
process("3", "4", 2) -> "-1"
process("29", "465", 3) -> "13485"
process("15", "2", 4) -> "7"

Definition

Class:	LongCalc
Method:	process
Parameters:	String, String, int
Returns:	String
Method signature:	String process(String param0, String param1, int param2)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Networking

Dynamic Programming, Graph Theory, Math

Used in:

TCI '01 Finals

Used as:

Division I Level Three

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=209

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=57&pm=209

Problem Statement

THIS PROBLEM WAS TAKEN FROM THE FINALS OF THE TOPCODER INVITATIONAL TOURNAMENT

PROBLEM STATEMENT
A network consists of a system of numNodes nodes, numbered from 0 to
numNodes-1, and connections between those nodes.  A connection has a chance of
being up and a chance of being down. Implement a class Networking that contains
a method getProbability which calculates the chance that there will be a path
from node 0 to node numNodes-1 such that each connection in the path is up.
(See the examples to see how probabilities can be calculated)

DEFINITION
Class Name: Networking
Method Name: getProbability
Parameters: int, String[]
Returns: double
Method signature (be sure your method is public):  double getProbability(int
numNodes, String[] connections);

numNodes is an int representing the number of nodes.
connections is a String[] representing the connections.  The elements will be
of the form "N1 N2 P" where N1 and N2 represent the numbers of the two nodes
the connection connects, and P is the probability the connection will be up.
There will be precisely one space between N1 and N2 and one space between N2
and P.  The nodes are numbered from 0 to numNodes-1. Every connection connects
two nodes (or possibly a node to itself).

OUTPUT
A double representing the probability there exists a path from node 0 to node
numNode-1 such that every connection in the path is up. Your result must be
within 10^-6 of our solution's result (tolerance for double inaccuracies).

NOTES
* A "path" is a series of one or more connections such that each successive
connection starts at the node where the previous connection ended.
* The connections are bi-directional.
* There can be multiple (parallel) connections connecting two nodes.

TopCoder will ensure the validity of the inputs.  Inputs are valid if all of
the following criteria are met:
* numNodes is an integer between 2 and 10, inclusive.
* Elements of connections are of the form described in the input above.
* connections has between 0 and 20 elements, inclusive.
* P is a decimal value between 0 and 1 inclusive with exactly one digit before
the decimal point and two digits after the decimal point.
* N1 and N2 are single integer digits between 0 and numNodes-1, inclusive.

EXAMPLES
* Nodes are in series. For example, if numNodes = 3 and connections = {"0 1
0.20", "1 2 0.10"}, the network looks as follows (letters are added for
clarity):
 ___             ___              ___
|   |   0.20    |   |    0.10    |   |   
| 0 |-----------| 1 |------------| 2 |
|___|     a     |___|      b     |___|

In this case, the probability of a connection from 0 to 2 is the probability
that a AND b are up. The AND relationship corresponds to multiplication.
Therefore, to calculate this all you need to do is mutliply the probability of
0->1 by the probability of 1->2. 
                (0.20 * 0.10) = 0.02
So the method should return 0.02.


* Nodes are in parallel. If numNodes = 4 and connections = {"0 1 0.10", "1 3
0.20", "0 2 0.30", "2 3 0.40"}, the network looks as follows:
                 ___
                |   |
     0.10 /-----| 1 |-----\  0.20
         /      |___|      \
 ___    / a               b \  ___
|   |  /                     \|   |
| 0 | /                       | 3 |
|___| \                      /|___|
       \         ___        /
        \ c     |   |    d /
         \------| 2 |-----/
       0.30     |___|       0.40

In order for this to happen, either a and b have to be up, or c and d have to
be up. The probability a connection exists from 0 to 3 now becomes the
probability that (a AND b are up) OR (c AND d are up). 

This equals P(a AND b up) OR P(c AND d up) = P(a up)*P(b up) + P(c up)*P(d up)
- P(a and b and c and d up) = 0.1 * 0.2 + 0.3 * 0.4 - 0.1 * 0.2 * 0.3 * 0.4 =
0.1376.

(The probability that they are all up is subtracted out at the end because it
is added as both P(a AND b up) and P(c AND d up)).

* If numNodes=2 and connections = {"0 1 0.80"}, there is a path from node 0 to
node 1 when the connection is up, so the method should return 0.8.


* If numNodes=3 and connections = {"0 2 0.50", "0 2 0.50", "0 1 0.10", "1 2
0.20","1 1 0.60"}, there is a path from node 0 from node 2 if either of the
first two connections are up or if both the 3rd and 4th connection are up, so
the method should return 0.755.  Note the connection from node 1 to node 1 does
not affect the result.


* If numNodes=4 and connections = {"0 2 0.06", "3 1 1.00", "1 3 0.50", "1 2
0.00"}, the method should return 0.0.


* If numNodes=4 and connections = {"0 1 0.10", "1 3 0.20", "0 2 0.30", "2 3
0.40", "1 2 0.60"}, the method should return 0.17048.
This can be calculated by reducing the network as follows:

The original network looks like:
                ___
          _____|   |_____     
    0.10 /     | 1 |     \  0.20
        /      |___|      \
 ___   / a       |       b \  ___
|   | /          |e         \|   |
| 0 |/           |0.60       | 3 |
|___|\           |          /|___|
      \         _|_        /
       \ c     |   |    d /
        \______| 2 |_____/
      0.30     |___|       0.40

This solution can be found by reducing the network.  
The chance the network is up is P(e up)*P(Network up, given e up) + P(e
down)*P(Network up, given e down).

P(Network up, given e up):

Given e up, the network becomes:

         0.10           0.20
       ______         ________
 ___  /  a   \  ___  /    b   \  ___
|   |/        \|   |/          \|   |
| 0 |\   c    /|1,2|\     d    /| 3 |
|___| \______/ |___| \________/ |___|
         0.30           0.40

The probability this is up is :

P((a OR c up) AND (b OR d up)) =
P(a OR c up) * P(b OR d up) =
(0.1+ 0.3- 0.1 * 0.3) * (0.2 + 0.4-0.2 * 0.4) = 0.1924

Given e down, the network becomes:
                 ___
                |   |
     0.10 /-----| 1 |-----\  0.20
         /      |___|      \
 ___    / a               b \  ___
|   |  /                     \|   |
| 0 | /                       | 3 |
|___| \                      /|___|
       \         ___        /
        \ c     |   |    d /
         \------| 2 |-----/
       0.30     |___|       0.40

And low and behold, this is the network from the last example, and the
probability of it being up is: 0.1376

Therefore, the probability of the entire network being up is:
P(e up)*P(Network up, given e up) + P(e down)*P(Network up, given e down) =
0.6 * 0.1924 + 0.4 * 0.1376 = 0.17048
The method should return 0.17048.

Definition

Class:	Networking
Method:	getProbability
Parameters:	int, String[]
Returns:	double
Method signature:	double getProbability(int param0, String[] param1)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Clock

Math

Used in:

TCI '01 Round 3

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=189

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=52&pm=189

Problem Statement

PROBLEM STATEMENT
Implement a class Clock, which contains a method getAngles.  getAngles takes a
String in the form "HH:MM:SS" representing a time of day.  getAngles returns an
int[] holding the angles that the hour hand, minute hand, and the seconds hand
make, clockwise, from 12:00:00 to the hand.  At 12:00:00 all hands are at 0
degrees. If the angle is not a whole number of degrees, simply truncate the
decimal part. 

DEFINITION
Class Name: Clock
Method Name: getAngles
Parameters: String
Returns: int[]
Method signature (be sure your method is public):  int[] getAngles(String time);

TopCoder will ensure the validity of the inputs.  Inputs are valid if all of
the following criteria are met:
- The input String is in the form "HH:MM:SS"
- HH is an integer between 01 and 12, inclusive, representing hours.
- MM is an integer between 00 and 59, inclusive, representing minutes.
- SS is an integer between 00 and 59, inclusive, representing seconds.

NOTES
-  The element located at index zero of the return int[] should represent the
angle that the hour hand made from 12:00:00 to the hour hand.
-  The element located at index one of the return int[] should represent the
angle that the minute hand made from 12:00:00 to the minute hand.
-  The element located at index two of the return int[] should represent the
angle that the seconds hand made from 12:00:00 to the seconds hand.
-  The seconds hand makes one full rotation every minute, the minute hand makes
one full rotation every hour, and the hour hand makes one full rotation every
twelve hours. 
-  Keep in mind that the hour and minute hands are continuously moving.  For
example, the number of degrees returned for the minute and hour hands at
01:07:00 will not be the same as the number of degrees returned for the minute
and hour hands at 01:08:00. 


EXAMPLES
"06:00:00" getAngles returns [180, 0, 0]
"08:30:00" getAngles returns [255, 180, 0]
"10:17:55" getAngles returns [308, 107, 330]

Definition

Class:	Clock
Method:	getAngles
Parameters:	String
Returns:	int[]
Method signature:	int[] getAngles(String param0)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

BitChecker

Simple Math, Simulation

Used in:

TCI '01 Round 3

Used as:

Division I Level Two

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=182

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=52&pm=182

Problem Statement

PROBLEM STATEMENT

When a binary message is transmitted across a network, there is always a chance
that the message might be corrupted by the time it is received.  In order for
the receiver to determine if an error occurred during transmission, the
transmitter sends an additional shorter message, called the key.  The key is
functionally derived from the first message and is used by the receiver to
perform a check based on both of these messages.

Suppose there is an original binary message M, and the derived binary message
key K. The verification check is accomplished by performing a bitwise
operation. Let R be the "residue", which is the result of performing this
bitwise operation on M and K. The bitwise operation is performed as follows:

1. Align K beneath M, starting with the left-most nonzero bit of M. 
2. Execute an XOR operation on M and K where XOR(x,y)=0 (zero) if x is the same
as y, and XOR(x,y)=1 (one) if x is different than y.  Let R equal the result of
this step.
3. Repeat steps 1 and 2 on each newly derived R until |R| is equal to |K|-1. If
|R| is less than |K|-1, left-pad R with 0's (zeros) until the final |R| is
equal to |K|-1.

If the final residue is all zeros, the message was transmitted correctly.
Otherwise, an error occurred.

Create a class BitChecker that contains the method getResidue, which takes two
binary Strings, M and K as input and returns a binary String representing the
final residue. 

DEFINITION
Class: BitChecker
Parameters: String, String
Returns: String
Method signature (be sure your method is public):  String getResidue(String M,
String K);


NOTES
- Assume the key message is always received correctly.
- Let |K| be the length of K.
- Let |M| be the length of M counting from the leftmost nonzero bit to the
right most bit (inclusive).
- Let |R| be the length of R counting from the leftmost nonzero bit to the
right most bit (inclusive).



TopCoder will ensure the validity of the inputs.  Inputs are valid if all of
the following criteria are met:
- The |M| > |K|.
- The leftmost bit in K must be 1.
- Each bit of both M and K can only be a 1 (one) or 0 (zero).
- M can be of length 3 - 50 (inclusive) counting from the leftmost nonzero bit
to the rightmost bit (inclusive).
- K can be of length 2 - 49 (inclusive) counting from the leftmost nonzero bit
to the rightmost bit (inclusive).
	
EXAMPLES
Here's an example, with M = 10011010010011 and K = 10011:

10011010010011
10011
-----
00000010010011
      10011
      -----
00000000001011 
          Method returns 1011 

Here's another example, with M = 11010110111110 and K = 10011:
11010110111110
10011
-----
01001110111110
 10011
 -----
00000010111110
      10011
      -----
00000000100110
        10011
        -----
00000000000000 

Method returns 0000

Definition

Class:	BitChecker
Method:	getResidue
Parameters:	String, String
Returns:	String
Method signature:	String getResidue(String param0, String param1)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

EndOfContest

Math, String Parsing

Used in:

TCI '01 Round 2

Used as:

Division I Level Two

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=178

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=51&pm=178

Problem Statement

Class Name: EndOfContest
Method Name: calcEarnings
Parameters: String[], int[]
Returns: String[]

Implement a class EndOfContest, which contains a method calcEarnings:

The method signature is (be sure your method is public):
String[] calcEarnings(String[] scores, int[] money)

TopCoder will check the following to be sure input is valid:
* scores - a String[] of between 1 and 20 (inclusive) elements of the form
"NAME: SCORE".  NAME has length between 1 and 20 (inclusive) and may only
contain letters (a-z and A-Z, inclusive).  No duplicate NAMEs can appear in the
String[] scores. SCORE is a floating point value with 2 places after the
decimal point.  NOTE: SCORE must always have 2 places after the decimal point.
SCORE is between -1000.00 and 10000.00 (inclusive).
* money - an int[] of between 1 and 20 (inclusive) elements.  The 0th element
is the earnings of the first place (highest score) winner, the 1st element is
the earnings of the second place winner.  The elements of money[] are between 1
and 100000 (inclusive).

The return value is a String[] of the form "NAME: PLACE, EARNINGS" where PLACE
is an int representing the place (final standing) the person came in and
EARNINGS is a floating point value truncated to an int.

The PLACE rules are:
*The person with the highest score comes in 1st place, second highest score
comes in 2nd, et cetera.
*If p people have the same score and there are x scores higher than that score,
all p people come in (x+1)th place.  The person(s) with the next score less
than the p peoples score, comes in (x+1+p)th place.

The money winning rules are:
*If there are no ties, the person with the highest score gets the first place
prize (element 0 of the money int[]), the person with the second highest score
gets the second place prize (element 1 of the money int[]), et cetera.
*If p people are tied for xth place, they equally split the sum of the prize
money of places x through p+x-1, inclusive.
*All winnings are truncated to ints. NOTE: The cents are removed, they are not
added to any other winnings.
*No one with a score less than or equal to zero can earn any money at all.
This rule has first precedence, so even if someone with 0 points comes in first
place, they can earn no money.

The order of names in the returned String[] should be the same as the order of
the names in the scores String[].
If there are more elements in scores than in money, it should be assumed the
earnings are 0 for places that do not have elements in money.

Examples:
If scores=
   {"ads: 550.34",
    "talub: 2102.98",
    "romana: 1123.21",
    "mike: -1000.00",
    "td: 1123.21",
    "dok: 1123.21",
    "dwarfsleepy: 812.12"}
and
  money=
  {300,
   150,
   75}
Then talub came in first place alone and won 300 dollars
romana, td, and dok tied for second so they equally split the sum of 2nd, 3rd,
and 4th places (150 + 75 + 0 = 225) so they win 225/3 = 75 dollars.
no one else won any money.

The returned String[] should be:
{"ads: 6, 0",
 "talub: 1, 300",
 "romana: 2, 75",
 "mike: 7, 0",
 "td: 2, 75",
 "dok: 2, 75",
 "dwarfsleepy: 5, 0"
}
If scores=
   {"buddy: 100.00",
    "carl: 0.00",
   }
and
   money=
   {10,20,30}

Then buddy came in first place and won 10 dollars and no one else got a
positive score so no one else won money and the returned String[] should be:
  {"buddy: 1, 10",
   "carl: 2, 0"}
---------------------------------------------------------
If scores=
   {"a: 100.00",
    "b: 100.00",
    "c: 100.00",
    "d: 100.00",
    "e: 100.00",
    "f: 100.00",
    "g: 100.00"}
and
   money=
   {1000,500}
Then everyone tied for first place, so they all win (1000+500)/7= 214 dollars
(remember to truncate to an int) and the returned String[] should be:
  {"a: 1, 214",
   "b: 1, 214",
   "c: 1, 214",
   "d: 1, 214",
   "e: 1, 214",
   "f: 1, 214",
   "g: 1, 214"}

Definition

Class:	EndOfContest
Method:	calcEarnings
Parameters:	String[], int[]
Returns:	String[]
Method signature:	String[] calcEarnings(String[] param0, int[] param1)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Prerequisites

Graph Theory, String Parsing

Used in:

TCI '01 Round 1

Used as:

Division I Level Three , Division II Level Three

Writer:

lars2520

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=164

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=50&pm=164

Problem Statement

***Note:  Please keep programs under 7000 characters in length.  Thank you


Class Name: Prerequisites
Mathod Name: orderClasses
Parameters: String[]
Returns: String[]

You are a student at a college with the most unbelievably complex prerequisite
structure ever. To help you schedule your classes, you decided to put together
a program that returns the order in which the classes should be taken.  

Implement a class Prerequisites which contains a method orderClasses.  The
method takes a String[] that contains the classes you must take and returns a
String[] of classes in the order the classes should be taken so that all
prerequisites are met.

String[] elements will be of the form (and TopCoder will ensure this):
"CLASS: PRE1 PRE2 ..." where PRE1 and PRE2 are prerequisites of CLASS.  CLASS,
PRE1, PRE2, ... consist of a department name (3 or 4 capital letters, A-Z
inclusive) followed by a class number (an integer between 100 and 999,
inclusive).  The department name should be immediately followed by the class
number with no additional characters, numbers or spaces (i.e. MATH217).  It is
not necessary for a class to have prerequisites.  In such a case, the colon is
the last character in the String.  

You can only take one class at a time, therefore, use the following rules to
determine which class to take :
1) Any prerequisite class(es) listed for a class must be taken before the class
can be taken.
2) If multiple classes can be taken at the same time, you take the one with the
lowest number first, regardless of department.
3) If multiple classes with the same number can be taken at the same time, you
take the department name which comes first in alphabetical order.  
4) If the inputted course schedule has errors, return a String[] of length 0.
There is an error if it is impossible to return the classes in an order such
that all prerequisites are met, or if a prerequisite is a course that does not
have its own entry in the inputted String[].

Examples of valid input Strings are:
"CSE111: CSE110 MATH101"
"CSE110:"

Examples of invalid input Strings are:
"CS117:" (department name must consist of 3 - 4 capital letters, inclusive)
"cs117:" (department name must consist of 3 - 4 capital letters, inclusive)
"CS9E11:" (department name must be letters only)
"CSE110: " (no trailing spaces allowed)
"CSE110: CSE101 " (no trailing spaces allowed)
"MATH211: MAM2222" (class number to large)
"MATH211: MAM22" (class number to small)
"ENGIN517: MATH211" (department name to large)

Here is the method signature (be sure your method is public):
String[] orderClasses(String[] classSchedule);

TopCoder will make sure classSchedule contains between 1 and 20 Strings,
inclusive, all of the form above.  The Strings will have between 1 and 50
characters, inclusive.  TopCoder will check that the syntax of the Strings are
correct: The Strings will contain a valid class name, followed by a colon,
possibly followed by a series of unique prerequisite classes separated by
single spaces.  Also, TopCoder will ensure that each class has at most one
entry in the String[]. 

Examples:
If classSchedule={
"CSE121: CSE110",
"CSE110:",
"MATH122:",
}
The method should return: {"CSE110","CSE121","MATH122"}

If classSchedule={
"ENGL111: ENGL110",
"ENGL110: ENGL111"
}
The method should return: {}

If classSchedule=[
"ENGL111: ENGL110"
}
The method should return: {}

If classSchedule={
"CSE258: CSE244 CSE243 INTR100"
"CSE221: CSE254 INTR100"
"CSE254: CSE111 MATH210 INTR100"
"CSE244: CSE243 MATH210 INTR100"
"MATH210: INTR100"
"CSE101: INTR100"
"CSE111: INTR100"
"ECE201: CSE111 INTR100"
"ECE111: INTR100"
"CSE243: CSE254"
"INTR100:"
}
The method should return:
{"INTR100","CSE101","CSE111","ECE111","ECE201","MATH210","CSE254","CSE221","CSE2
43","CSE244","CSE258"}

Definition

Class:	Prerequisites
Method:	orderClasses
Parameters:	String[]
Returns:	String[]
Method signature:	String[] orderClasses(String[] param0)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

SquareDigits

Brute Force, Math

Used in:

TCI '01 Round 1

Used as:

Division I Level Two , Division II Level Two

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=163

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=50&pm=163

Problem Statement

***Note:  Please keep programs under 7000 characters in length.  Thank you


Class Name: SquareDigits
Method Name: smallestResult
Parameters: int
Returns: int

Define the function S(x) as the sum of the squares of the digits of x.   
For example: S(3)=3*3=9 and S(230)=2*2+3*3+0*0=13.

Define the set T(x) to be the set of unique numbers that are produced by
repeatedly applying S to x.  That is: S(x), S(S(x)), S(S(S(x))), etc... 
For example, repeatedly applying S to 37:
S(37)=3*3+7*7=58.  
S(58)=5*5+8*8=89.
S(89)=145.
S(145)=42. 
S(42)=20.
S(20)=4.
S(4)=16.
S(16)=37. 
Note this sequence will repeat so we can stop calculating now and: 
T(37)={58,89,145,42,20,4,16,37}.
However, note T(x) may not necessarily contain x.  

Implement a class SquareDigits, which contains a method smallestResult.  The
method takes an int, n, as a parameter and returns the smallest int, x, such
that T(x) contains n.

The method signature is (be sure your method is public): 
int smallestResult(int n); 

TopCoder will ensure n is non-negative and is between 0 and 199 inclusive.

Examples:
If n=0: S(0) = 0, so T(0)={0}, so the method should return 0.

If n=2: T(0) through T(10) do not contain the value 2.  If x=11, however:
S(11)=1*1+1*1=2, so T(11) contains 2, and the method should return 11.

If n=10: T(0) through T(6) do not contain 10.  If x=7:
S(7)=49.
S(49)=97.
S(97)=130.
S(130)=10.
S(10)=1.
and it starts to repeat... 
so T(7) is {49,97,130,10,1}, which contains 10, and the method should return 7.

n=1 -> x=1 
n=19 -> x=133
n=85 -> x=5
n=112 -> x=2666

Definition

Class:	SquareDigits
Method:	smallestResult
Parameters:	int
Returns:	int
Method signature:	int smallestResult(int param0)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Expressions

Used in:

SRM 10

Used as:

Division I Level Two , Division II Level Two

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=92

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=3009&pm=92

Problem Statement

Class Name: Expressions
Method Name: evaluate
Parameters: String
Returns: int

Implement a class Expressions, which contains a method evaluate.  The method
takes a String as a parameter representing a mathematic expression and returns
the int that is is equivalent to the expression.

The expression contains non-negative integers and the operands *, +, - , /, and
parenthesis ( ). There is no white space in the expression.  The division (/)
is integer division (that is any remainder is truncated). Remember: Parentheses
are highest priority, then * and / are medium priority, then + and - are the
lowest priority.  When there are parentheses inside parentheses, the inner
parentheses are evaluated first.  When dealing with operands of equal priority,
evaluation occurs from left to right.

Here is the method signature.
public int evaluate(String expression);

expression is of length between 1 and 50.  It contains digits and the symbols
*, +, -, /, (, ) and represents a valid expression with no division by 0
(TopCoder will check this).

Example:
"6+2*(3*(1+1))-6/(2+3)" -> 17.

Definition

Class:	Expressions
Method:	evaluate
Parameters:	String
Returns:	int
Method signature:	int evaluate(String param0)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Schedule

Used in:

SRM 6

Used as:

Division I Level Three , Division II Level Three

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=80

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=3005&pm=80

Problem Statement

Class Name: Schedule
Method Name: maxClubs
Paramaters: String[]
Returns: int

Ed is an over achieveing, over active college student.  He wants to be in as
many clubs as possible.   Each club has a meeting time, and in order to be in a
club, Ed has to attend the club's meeting, in its entirety.  Each club meets
weekly, one day a week.  Also, being the overachiever he is, Ed has invented a
teleportation system so the time it takes him to get from meeting to meeting is
negligable.  That is, if one club's meeting ends at 10:00 and another club's
meeting starts at 10:00, Ed can be in both clubs.

Implement a class Schedule which contains a method maxClubs.  maxClubs takes a
String[] as a parameter.  The String[] contains the times of clubs' meetings.
The method returns an int that is the maximum number of clubs Ed can be in.

Each element in the String[] represents one club's information and is a String
of the form:
"CLUBNAME d hh:mm LENGTH". (The quotes are for clarity and are not part of the
String).
CLUBNAME is the name of the club and consists of only letters (at least 1 and
at most 20).
d is the day of the meeting.  It is a number from 1 to 7.  1 is Sunday, 2 is
Monday ... 7 is Saturday.
hh:mm is the starting time of the club's meeting, in military time.  It
consists of two numerical digits representing the hour, a colon, and two more
numerical digits representing the minute.  The hour is between 00 and 23,
inclusive.  The minute is between 00 and 59, inclusive.
LENGTH is the length of the meeting in hours.  The length of the meeting is an
integer between 1 and 24, inclusive.

Note:
-There is exactly one space beween CLUBNAME and d, between d and hh:mm, and
between hh:mm and LENGTH.
-Club names are not necessarily unique.
-The solution must run in under 6 seconds on TopCoder's tester.
-If the String[] is empty, Ed can be in 0 clubs.

The method signature is:
public int maxClubs(String[] meetingtimes);

meetingtimes has at most 14 elements.  Each element is a String of the form
given above (TopCoder will check this).

Examples:
If meetingtimes={"MATHTEAM 2 11:00 3","CHESSCLUB 2 12:00 1","FIGURESKATING 2
13:00 2"}, Ed can maximize the number of clubs he is in by being in CHESSCLUB
and FIGURESKATING and the method returns the maximum number of clubs he can be
in: 2.

Definition

Class:	Schedule
Method:	maxClubs
Parameters:	String[]
Returns:	int
Method signature:	int maxClubs(String[] param0)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Race

Simple Math

Used in:

TCCC '01 Semifinals 3

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=73

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=2007&pm=73

Problem Statement

 Class Name: Race
Method Name: closestCheckPoint
Parameters: int[], int[], int[]
Returns: int

Three runners are running a race.  There are n checkpoints numbered 0
through n-1 along the course of the race.  The time each runner crosses each
checkpoint is recorded, in seconds since the beginning of the race.  As the
race progresses, the time counts up. 
Implement a class Race, which contains a method closestCheckPoint.  The
method takes three int[]'s as parameters.  The int[]'s contain the times the
runners crossed the checkpoints, in seconds, one int[] for each runner.  The
0th element of the first int[] is the time the first runner crossed the 0th
checkpoint.  The 0th element of the second int[] is the time the second runner
crossed the 0th checkpoint, etc... The method returns an int that is the number
of the checkpoint at which the three runners are closest (the time between the
first and last runners' arrivals at the checkpoint is the minimum).  If there
are multiple checkpoints with the same closeness, the last (highest numbered)
of these checkpoints is returned.

The method signature is:
public int closestCheckPoint(int[] runner1, int[] runner2, int[] runner3);
*runner1, runner2, and runner3 will have the same number of elements.  There
will be at least 1 element and at most 100 elements in each int[].  The
elements will be between 0 and 30000.

Note:
-Keep in mind runners may cheat and therefore the int[] may not be an
increasing sequence.

Examples:
runner1 = {10,40,90}
runner2 = {12,37,87}
runner3 = {15,32,88}
returns: 2

runner1 = {3,4,5,8}
runner2 = {3,4,6,8}
runner3 = {3,5,7,8}
returns: 3

Definition

Class:	Race
Method:	closestCheckPoint
Parameters:	int[], int[], int[]
Returns:	int
Method signature:	int closestCheckPoint(int[] param0, int[] param1, int[] param2)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

Weekday

Math

Used in:

TCCC '01 Round 3

Used as:

Division I Level One

Writer:

Unknown

Testers:

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=46

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=2002&pm=46

Problem Statement

Given that January 1, 1990 falls on a Monday, determine which weekday a given
date (restricted to the years 1990-1999) falls on.

The program will take as input three integers representing a valid month, day,
and year, from the years 1990-1999. The output will be a string containing a
case sensitive day of the week :

         (Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday)

Here are the number of days for each month in 1990-1999 :

(Jan, Mar, May, Jul, Aug, Oct, Dec) = 31; (Apr, Jun, Sep, Nov) = 30;
(Feb)=28 except on 1992, 1996 (Feb)=29  (leap year)

NOTE : You are not allowed to use any external libraries for this problem
       (ie no import statements)

Here is the method signature :

public String getDay(int month, int day, int year);

We will check to make sure the input to this problem is valid.
(ie date validity, year restriction, etc)

Example :

Input : 4 26 1999
Output : Monday

Definition

Class:	Weekday
Method:	getDay
Parameters:	int, int, int
Returns:	String
Method signature:	String getDay(int param0, int param1, int param2)
(be sure your method is public)

This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2010, TopCoder, Inc. All rights reserved.

TopCoder.com Algorithm Problems Searcher

Found 934 results

ProductAndSum

Brute Force, Dynamic Programming, Math

Used in:

Used as:

Writer:

Testers:

Problem url:

Problem stats url:

Problem Statement

Definition

Constraints

Examples

FractalPicture

Brute Force, Geometry, Recursion, Simple Math, Simulation

Used in:

Used as:

Writer:

Testers:

Problem url:

Problem stats url:

Problem Statement

Definition

Notes

Constraints

Examples

GeometricProgressions

Math, Simulation

Used in:

Used as:

Writer:

Testers:

Problem url:

Problem stats url:

Problem Statement

Definition

Constraints

Examples

ColorfulRabbits

Simple Math

Used in:

Used as:

Writer:

Testers:

Problem url:

Problem stats url:

Problem Statement

Definition

Constraints

Examples

OneDimensionalBalls

Graph Theory, Simple Math, Simple Search, Iteration

Used in:

Used as:

Writer:

Testers:

Problem url:

Problem stats url:

Problem Statement

Definition

Constraints

Examples

AdditionGame

Greedy, Simple Math, Simple Search, Iteration

Used in:

Used as:

Writer:

Testers:

Problem url:

Problem stats url:

Problem Statement

Definition

Constraints

Examples

FoxStones

Math

Used in:

Used as:

Writer: